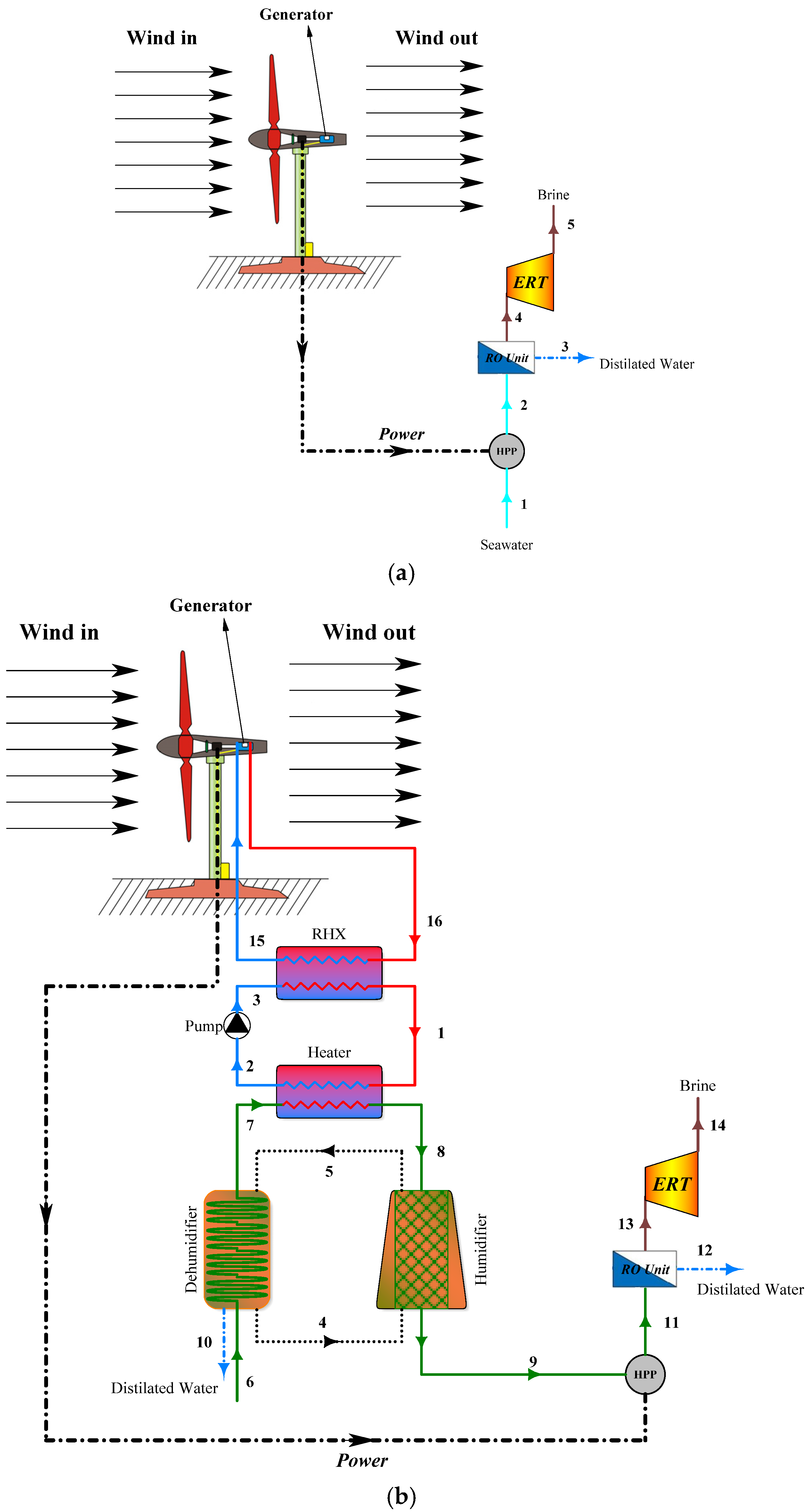
5.2. Parametric Study
In the previous sub-section, the inferiorities and superiorities of the hybrid HDH-RO unit driven by various wind turbines were discussed, as well as in what way utilizing waste heat from the generator of a wind turbine for seawater desalination under the designed condition is economical. In this part, a parametric study is conducted to identify how the performance and cost metrics of the WT/HDH-RO unit can deteriorate or improve by re-adjusting the assumed input data. For this purpose, a GW-136/4.5 wind turbine model is selected, and analysis is conducted for this model. The main input data affecting the design condition around the basic points are the wind speed, desalination flow ratio, humidifier and dehumidifier effectiveness, desalination top temperature, and the TTD of the heater.
Figure 4 displays the altering trend of total freshwater rate, RO-to-HDH distilled water ratio, the unit cost of freshwater produced by the HDH sub-unit and RO sub-unit, APR, net power, SWP of the system, SWC of the hybrid unit, total exergy efficiency, the unit cost of total freshwater, TUCP, and total exergoeconomic factor with wind speed. According to
Figure 4, although more freshwater is produced as the wind speed rises (since more power is supplied to the RO unit and more heat, dissipating from the generator of the wind turbine, is captured by the HDH unit), the ratio of the freshwater produced by the HDH system to that produced by the RO unit remains unchanged. This is simply because of the linear proportionality assumption made between the power and the waste heat in the applied model. In addition, the wind turbine operates at a constant maximal speed (and hence the same capacity) at wind speeds higher than the rated speed, and hence, freshwater capacity does not rise thereafter. Thus, the maximum freshwater capacity that can be obtained during the operation of the GW-136/4.5 is 4.025 m
3/h. It is accepted that the unit cost associated with freshwater produced by the HDH and RO units decreases with the rise of the wind speed, since the capacity of the operating wind turbine increases, and hence it is more economical to use mechanical or thermal energies produced by the wind turbine for freshwater production at large capacities. However, the most critical point is the quantitative distribution of the unit cost between the distilled water produced by the direct supply of mechanical energy from the wind turbine and the waste heat dissipating from the generator of the wind turbine. According to
Figure 4b, the cost of the freshwater produced by the HDH unit is inordinately higher than that produced by the RO unit. As a result, although the total freshwater rate produced through the operation of the HDH-RO unit is higher than that produced by installing a solo RO unit (as discussed in
Table 7), the freshwater produced by capturing the waste heat of the generator of the wind turbine is substantially more expensive than when the power of the wind turbine is directly supplied to a mechanical desalination unit (here, an RO unit). Hence, although the idea of seawater desalination via capturing waste thermal energy of the generator of the wind turbine sounds interesting, and is explored in previous studies [
5,
8], no comparison is made between the unit cost of freshwater produced by each method, and the previous conclusions achieved through the analysis were incomplete. It should be noted that this conclusion is achieved with the use of a liquid-liquid cooling unit employed on the generator, and any other consideration in terms of the cooling technique might result in a less inordinate cost difference. The high unit cost of freshwater produced by the HDH unit is mainly due to the high unit cost of the steam produced after cooling down the generator, although here it is assumed that the wind turbine setup has previously been established, and the bottoming components are added on (i.e., no capital cost is considered in the cost balance equation of the wind turbine and generator, and as a result, the obtained unit cost for the steam is vastly lower when the full investment cost is accounted for).
The results expressed in
Figure 4 also reveal that the total exergy efficiency has reached a peak at a specific wind speed value. Quantitatively speaking, the total exergy efficiency has reached its maximum value of 32.49% at
uw = 9.85 m/s. The results of varying the exergy efficiency with the wind speed also show that the setup reveals high second-law performance at low wind speeds despite the fact that the freshwater capacity and its cost have deteriorated at this condition. That is, there is a conflicting trend between the first- and second-law metrics, or between the second-law and cost metrics, versus any change in the wind speed.
As seen earlier, the unit cost of the freshwater obtained by delivering the thermal energy of the generator of the wind turbine to the HDH unit was substantially higher than that produced by the direct supply of power to the RO unit. By accounting for the cost associated with the generated power along with the freshwater cost, one can define a single cost metric for the whole set-up, which is TUCP, as defined by Equation (66). According to the altering trend of TUCP with the wind speed, it can be stated that the TUCP can reach its minimum value of 9.47
$/GJ at a wind speed of 10.43 m/s. The wind speed at which the TUCP reaches minimum is the beginning of the point where the total freshwater cost is less affected by the wind speed (as two plots in
Figure 4f show), and hence the rise in the net power cost shows its dominant effect hereafter on the TUCP.
A complete cost analysis of an energy system should reveal the products’ operating cost, along with the investment cost and the cost penalty associated with the destruction, and losses occurring within the system. The varying trend of operating costs of the proposed system with wind speed was studied by introducing TUCP, or total freshwater cost. However, to have a thorough cost evaluation we have presented a variation trend of the investment cost rate and the exergoeconomic factor with the wind speed. We should reiterate that the initial capital cost of the wind turbine is not included in the total investment cost (as we have assumed that the wind turbine is previously installed). A high investment cost at high wind speed values is evident, since the scale of the required components (such as heat or mass exchangers) increases, but it remains constant for the wind speeds higher than the rated value since the capacity is unchanged. Furthermore, the significant impact of the investment cost relative to the cost rate associated with exergy destruction and loss decreases as the wind speed rises. However, it should be stated that even at low wind speeds, the value of the exergoeconomic factor is still below 50%, and hence lowering the total cost of the plant via managing the cost penalty associated with exergy destruction and loss of the system is still the top priority.
Figure 5 displays the altering trend of the total freshwater rate, RO-to-HDH distilled water ratio, unit cost of freshwater produced by the HDH sub-unit and RO sub-unit, APR, net power, SWP, SWC of the hybrid desalination unit, exergy efficiency, the unit cost of total freshwater, TUCP, and total exergoeconomic factor, with a desalination flow ratio at three different dehumidifier efficiencies of 0.7, 0.85, and 1. According to
Figure 5, for each dehumidifier effectiveness level, the total freshwater rate has reached its peak value at different desalination flow ratios. In addition, as reported in previous similar studies that have investigated the effects of the dehumidifier effectiveness and desalination flow ratio on the freshwater capacity [
8,
31,
32], this maximal freshwater capacity occurs at a higher desalination flow ratio as the dehumidifier effectiveness increases. Once the freshwater capacity increases with the rise of the desalination flow ratio at
up to the peak, the freshwater rate also slightly decreases thereafter, indicating the fact that setting the desalination flow ratio beyond the optimal value is advisable, since it provides rather a conservative result and the desalination capacity is less affected by any unintentional maladjustment of the optimal point in the real operation scenario. Furthermore, the results portrayed in
Figure 5a indicate that increasing the dehumidifier effectiveness (with the same increment step) from 0.85 to 1 is more effective than when it is increased from 0.7 to 0.85, especially when
.
The contribution of each desalination sub-unit to the total freshwater capacity at different quantitative values of the desalination flow ratio, and three dehumidifier effectivenesses of 0.7, 0.85, and 1, is expressed in
Figure 5b. As
Figure 5b reveals, the contribution of the freshwater produced by the RO module relative to that produced by the HDH unit has its lowest amount around the optimal desalination flow ratio (where the total freshwater rate is maximal). It should be emphasized that the freshwater produced by each unit has a maximum point relative to the desalination flow ratio near the same optimal desalination flow ratio. However, the freshwater produced by the HDH unit hugely affects the RO-to-HDH flow ratio, due to its high varying rate.
To understand how the unit cost of the freshwater produced by each desalination unit is affected through varying the desalination flow ratio and the dehumidifier effectiveness, please see
Figure 5c,d. First and foremost, a comparison between the unit cost of the freshwater produced via each unit substantiates the previous concluding remark about the high cost of the freshwater of the HDH unit compared to the RO unit. The aggregated unit cost of the freshwater (
Figure 5k) shows a similar trend of change to each individual unit cost, due to the same varying behavior of both parameters, and its quantitative value is very similar to that of the HDH unit, due to its dominant cost.
With the rise of the desalination flow ratio, the humidity of the humidified air leaving the humidifier increases, while the dry air mass flow rate decreases substantially. By considering the rise in the freshwater rate at low desalination flow ratios and the drop in the freshwater rate at high desalination flow ratios, via increasing the desalination flow ratio along with the decrease in the dry air flow rate, through this change, it can be declared that the APR of the hybrid HDH-RO unit increases considerably and continuously at low dehumidifier effectiveness, and its increment rate decreases at higher dehumidifier effectiveness. That is, at the APR increases with the rise of the desalination flow ratio at lower desalination flow ratio values, while it slightly decreases and remains nearly constant thereafter.
Three additional significant metrics, including of the net power, SWC of the hybrid HDH-RO desalination unit, and SWP of the whole setup, are also included here, and their varying trend with the change of the desalination flow ratio and dehumidifier effectiveness is plotted in
Figure 5f–h, respectively. On this basis, since the power produced by the wind turbine is constant and independent of any change in the desalination flow ratio and dehumidifier effectiveness, only the power recovered by the ERT is changing. Accordingly, the power produced by the ERT has a maximum value with the change of the desalination flow ratio and increases as the dehumidifier effectiveness increases. As a result, it affects the net power inversely, and hence the net power will have a minimum point versus a broad change of the desalination flow ratio, where the severity of the drop in the net power at lower desalination flow ratios and higher dehumidifier effectiveness is relatively high, although the scale of the power recovered by the ERT is meaningfully smaller than the power generated by the wind turbine. Due to the direct relationship of the SWP to the net power and inverse relationship with the total freshwater rate, the SWP of the system will be affected in the same direction from both of these influential parameters, and hence its altering trend versus the desalination flow ratio and dehumidifier effectiveness will resemble that of the net power. The same altering trend is predictable for the SWC of the hybrid HDH-RO desalination system, since it is inversely affected by the total freshwater rate and the ERT power.
According to the altering trend of TUCP with the desalination flow ratio at different values of dehumidifier effectiveness, it can be stated that the TUCP can reach its maximum value at , while increasing at two different increment rates at . Therefore, by operating the HDH unit with a low desalination flow ratio, one can considerably lower the TUCP, although lowering the dehumidifier effectiveness to pursue lowering the TUCP is effective as well. However, there is a conflicting trend of interest in the TUCP, and the unit cost associated with total freshwater, in terms of selecting the ultimate values of dehumidifier effectiveness or the desalination flow ratio that must be taken into account prior to the final decision. Since the altering trend of the unit cost of the total freshwater rate is hugely affected by the desalination flow ratio as well as the dehumidifier effectiveness, its varying trend can be prioritized over the TUCP in the ultimate design stage. The exergoeconomic factor, defined as the ratio of the investment cost rate to the cost rate associated with exergy destruction and loss, as well as the investment cost rate, has reached a peak value as its varying tendency with the desalination flow ratio is investigated. It should be stated that through the range of the investigated parameters, the value of the exergoeconomic factor is still below 50%, and hence, lowering the total cost of the plant via lowering the cost penalty associated with the destruction and losses of the exergy of the system is still the top priority. Since the operating and maintenance cost of the wind turbine (as the topping system) remains unchanged with the change of the desalination flow ratio or the dehumidifier effectiveness, the exergoeconomic factor changes slightly through this alteration and cannot be lowered significantly with each of these two design parameters.
Figure 6 displays the altering trend of the total freshwater rate, RO-to-HDH distilled water ratio, unit cost of freshwater produced by the HDH sub-unit and RO sub-unit, APR, net power, SWP, SWC of the hybrid unit, the unit cost of total freshwater, TUCP, and total exergoeconomic factor, with a desalination flow ratio at three different humidifier effectiveness levels of 0.7, 0.85, and 1. The variation trend of the exergy efficiency is excluded here, due to its very slight change.
According to
Figure 6, for each humidifier effectiveness, the total freshwater rate has reached its peak value at different desalination flow ratios. As also reported in previous similar studies investigating the influence of humidifier effectiveness and desalination flow ratio on the freshwater capacity [
8,
31,
32], this maximal freshwater capacity occurs at higher desalination flow ratios as the humidifier effectiveness increases. In addition, as has been demonstrated in these studies [
8,
31,
32], once we compare the results of
Figure 5a and
Figure 6a, it can be stated that the influence of the dehumidifier effectiveness on the freshwater capacity is more meaningful than that of the humidifier effectiveness. The altering trend of all metrics versus the humidifier effectiveness is the same as the dehumidifier effectiveness, for nearly the same reasons which were explained previously, except for the following differences. In contrast to the observation that the freshwater capacity slightly decreased with the rise of the desalination flow ratio at
from the maximal point thereafter, here it has dropped significantly, like the varying trend observed at lower humidifier effectiveness levels. Furthermore, despite the different increment/decrement rate seen in
Figure 5a for different values of dehumidifier effectiveness,
Figure 6a shows that increasing the humidifier effectiveness (with the same increment step) from 0.85 to 1 has the same effect when it is increased from 0.7 to 0.85. Hence, the altering shape of the total freshwater rate with desalination flow ratio is independent of the humidifier effectiveness. In addition, in contrast to the results captured in
Figure 5e,
Figure 6e indicates that the variation of the APR with the desalination flow ratio at all humidifier effectiveness levels is similar, with nearly the same varying slope but with an up- or downward shift relative to each other. Hence, the altering shape of the APR with the desalination flow ratio is independent of the humidifier effectiveness. In addition, as
Figure 5k indicated, the TUCP reached its maximum value at
, while it increased by two different increment rates at
. However, here the alteration pattern of the TUCP with the desalination flow ratio is the same for all three investigated humidifier effectiveness levels.
Figure 7 displays the altering trend of the total freshwater rate, RO-to-HDH distilled water ratio, unit cost of freshwater produced by the HDH sub-unit and RO sub-unit, APR, net power, SWP, SWC of the hybrid unit, unit cost of total freshwater, TUCP, and total exergoeconomic factor with desalination top temperature at four different TTDs of the heater at 5, 10, 15, and 20 K. The altering trend of the total exergy efficiency is excluded here, due to its constant trend with the TTD of the heater and the desalination top temperature. According to
Figure 7, the total freshwater rate increases with the drop of the desalination top temperature or TTD of the heater. It should be noted that at low values of the TTD of the heater, the amount of fresh water can be enhanced more significantly than is the case when the system works at higher TTDs of the heater. That is, when decreasing the TTD of the heater with a constant decrement step of 5 K, decreasing from 10 K to 5 K is more effective than when it is decreased from 20 K to 15 K, especially at lower desalination top temperatures.
The contribution of each desalination sub-unit to total freshwater capacity at different quantitative values of the desalination top temperature and four TTDs of the heater of 5 K, 10 K, 15 K, and 20 K is expressed in
Figure 7b. As
Figure 7b reveals, varying the TTD of the heater makes no contribution to the proportion of the freshwater produced by the RO module, relative to that produced by the HDH unit. The RO-to-HDH freshwater ratio only decreases with the rise of the desalination top temperature, since the contribution of the HDH unit at a high scale of the operating temperature will obviously increase its role in the total freshwater rate.
To understand how the unit cost of the freshwater produced by each desalination unit is affected through varying the desalination top temperature and the TTD of the heater, please see
Figure 7c,d. First and foremost, a comparison between the unit cost of the freshwater produced via each unit substantiates the previously made concluding remark about the high cost of the freshwater of the HDH unit compared to the RO unit. In addition, by setting the operating desalination top temperature at higher values, one can expect to lower the high unit cost of freshwater of the HDH unit relative to that of the RO unit, although it is still high and is not economical. The aggregated unit cost of the freshwater (
Figure 7i) shows a similar trend of change to the unit cost of the freshwater of the HDH unit, due to the dominant role of this element.
With the rise of the desalination top temperature, the humidity of the air leaving the humidifier increases, while the dry air mass flow rate decreases substantially. By considering the drop in the freshwater rate and the dry air mass flow with the rise of the desalination top temperature, it can be stated that the APR of the hybrid HDH-RO unit will decrease continuously. Regarding the altering trend of the net power, since the power produced by the wind turbine is constant with the change of the desalination top temperature and the TTD of the heater, only the power produced by the ERT meaningfully decreases (although the power consumed by the pump is decreasing as well) with the rise of the desalination top temperature or TTD of the heater. Therefore, the net power will increase with the rise of the desalination top temperature or TTD of the heater. It should be noted that at low values of TTD of the heater the amount of the net power can be enhanced more significantly than the case when the system works at a higher TTD of the heater. That is, increasing the TTD of the heater with a constant increment step of 5 K from 5 K to 10 K is more effective than when it is increased from 15 K to 20 K.
Due to the direct relationship of the SWP with the net power, and its inverse relationship with the total freshwater rate, the SWP of the system will be affected in the same direction from both of these influential parameters, and hence, its altering trend versus those of the desalination top temperature and TTD of the heater will resemble that of the net power. The same altering trend is predictable for the SWC of the hybrid HDH-RO desalination system, since it is inversely affected by the total freshwater rate and the ERT power, and hence, both SWP and SWC will increase with the rise of the desalination top temperature and TTD of the heater.
According to the altering trend of TUCP with the desalination top temperature at different values of the TTD of the heater, it can be stated that the TUCP decreases with the rise of the desalination top temperature. Meanwhile, the TUCP first increases as the TTD of the heater increases from 5 K to 10 K, and hence decreases as the TTD of the heater increases from 10 K to 20 K. Therefore, there is a conflicting trend of interest in the TUCP and the unit cost associated with total freshwater in terms of selecting the ultimate values of the TTD of the heater, which must be taken into account prior to the final decision. Since the altering trend of the unit cost of the total freshwater rate is hugely affected by the TTD of the heater, its varying trend can be prioritized over the TUCP in the ultimate design stage. The exergoeconomic factor increases with the rise of the desalination top temperature, while it is increased as the TTD of the heater increases from 5 K to 10 K, and hence is decreased as the TTD of the heater increases from 10 K to 20 K. It should be stated that through the range of these two investigated parameters (i.e., and ), the value of the exergoeconomic factor is still below 50%, and hence, lowering the cost penalty associated with the destruction and losses of the exergy of the system is still the top priority.