State-Aware Stochastic Optimal Power Flow
Abstract
:1. Introduction
- 1.
- Proposing and formulating the novel state-aware stochastic optimal power flow (SA-SOPF) problem with a given affine feedback policy. The formulation is aimed to minimize joint objective of expectation of state deviation and generation cost;
- 2.
- Learning distributionally robust (DR) affine policy using the Gaussian process. This DR policy can be employed for different uncertainty distributions without retraining. The analytical form of policy is then expressed as a function of DA base-solution to be incorporated in SA-SOPF;
- 3.
- Developing convex relaxation of SA-SOPF with modified objective function for incorporating real-time objective. This relaxation handles the non-convexity of proposed SA-SOPF, formulated based on complete AC power flow to incorporate the voltage variable.
2. State-Aware Stochastic Optimal Power Flow
Constraints
3. Affine Policy for RT Operation
Distributionally Robust Affine Policy Learning
4. Convex Relaxation SA-SOPF
4.1. RT Stage Reformulation
4.2. Convexification of SA-SOPF
5. Results and Discussion
5.1. 14-Bus System
- Case I: Uniform distribution of uncertain net-load vector , within variation of base-load of each node;
- Case II: Normal distribution of uncertain net-load vector with base-load as mean and of the base-load taken as standard deviation for each node;
- Case III: Weibull distribution of uncertain net-load vector with base-load selected as scale and times the base-load taken as shape parameter for each node.
- Case IV: Normal distribution of uncertain net-load vector with times base-load as mean and of the base-load taken as standard deviation for each node.
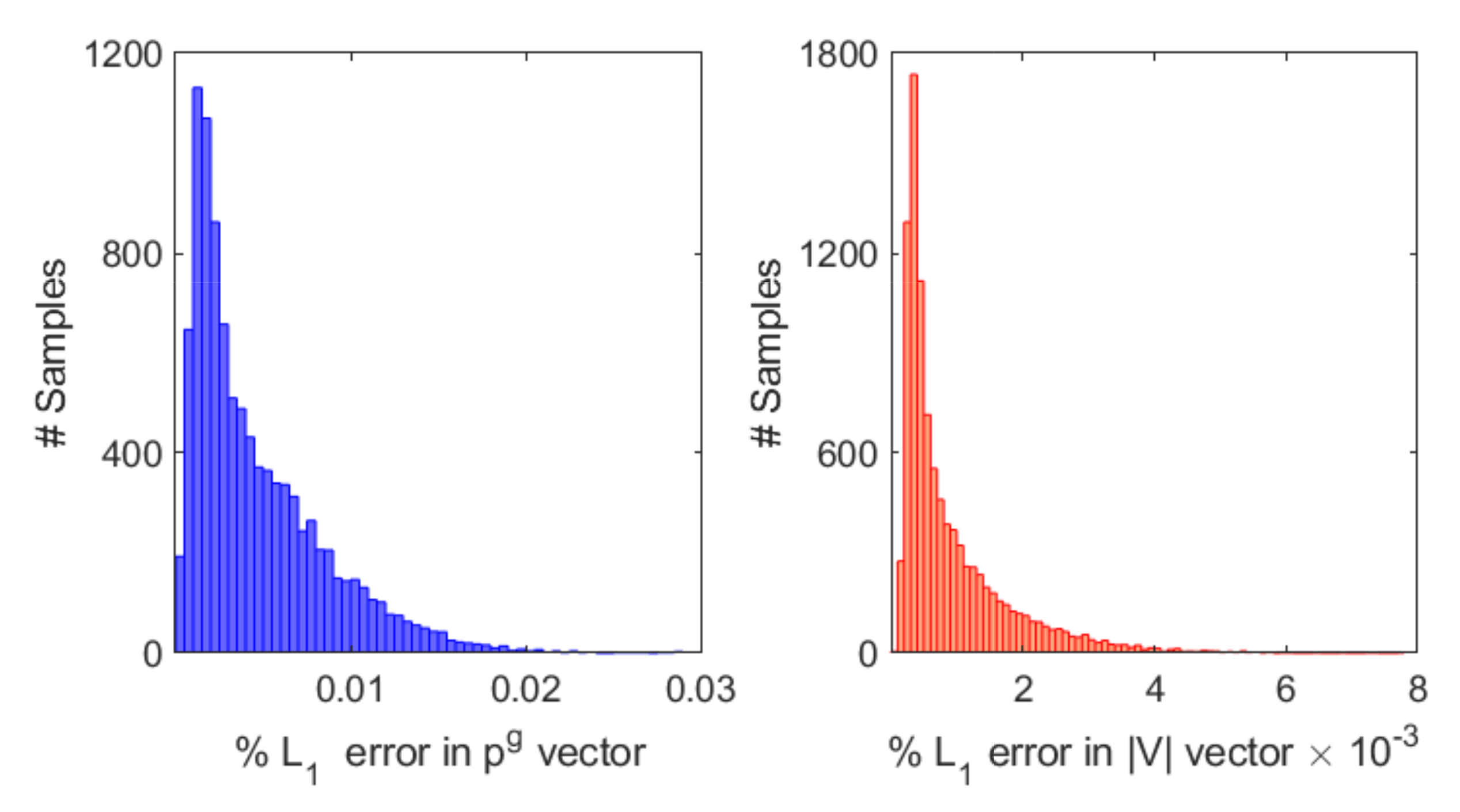
5.2. 30-Bus System
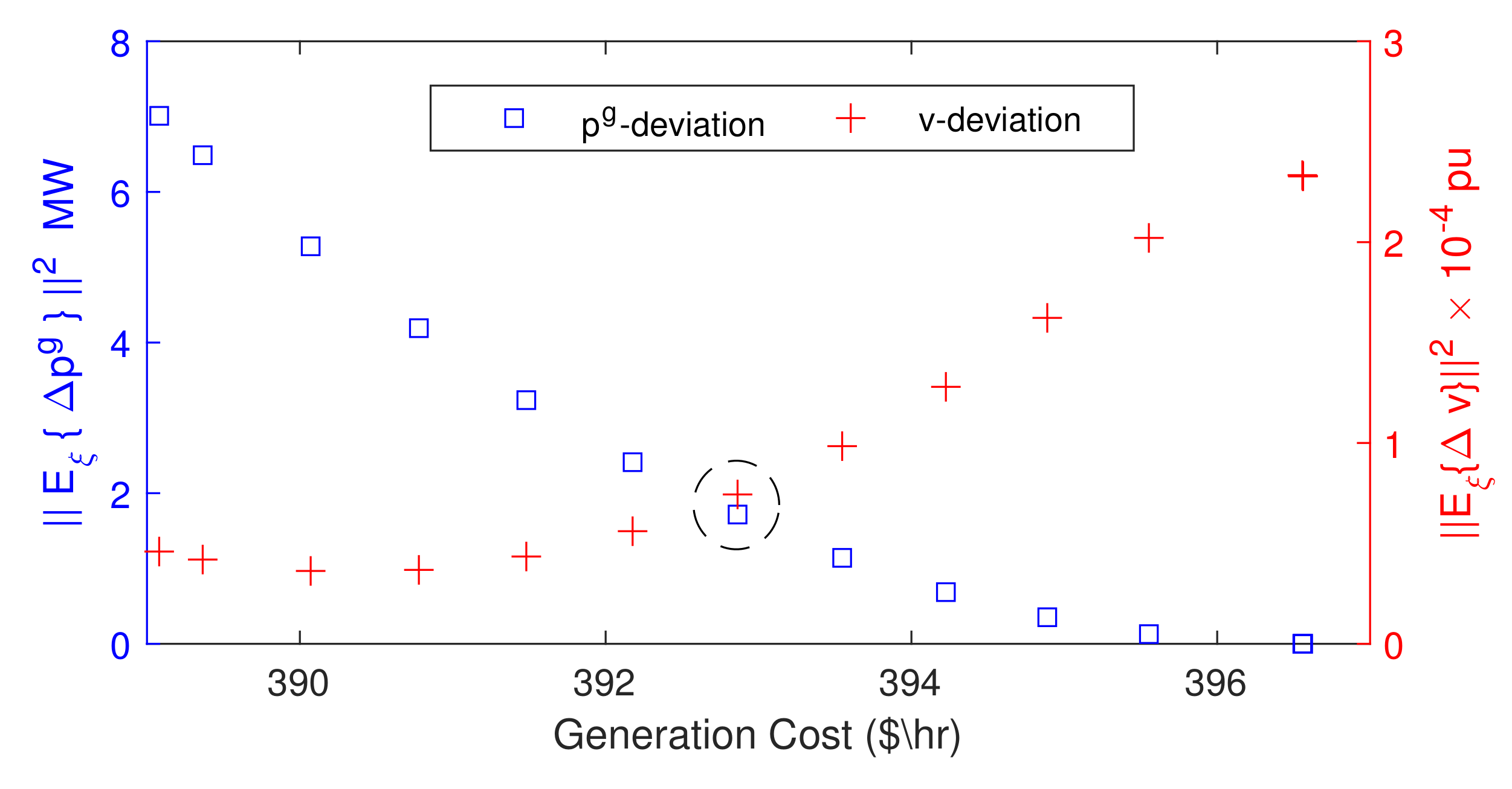
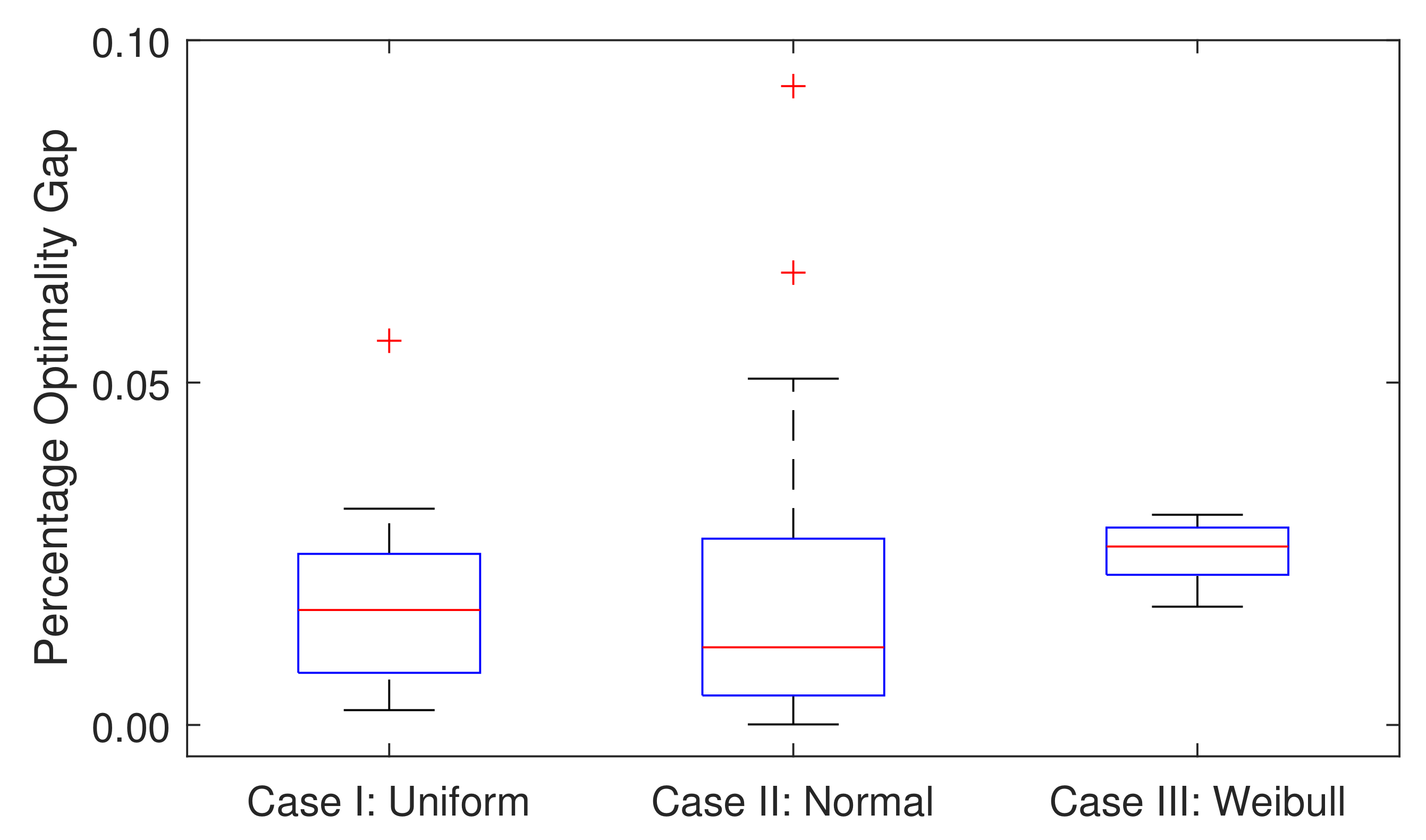
5.3. Optimality Gap and Computation Time
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Mezghani, I.; Misra, S.; Deka, D. Stochastic AC optimal power flow: A data-driven approach. Electr. Power Syst. Res. 2020, 189, 106567. [Google Scholar] [CrossRef]
- Dandurand, B.; Kim, K.; Schanen, M. Toward a scalable robust security-constrained optimal power flow using a proximal projection bundle method. Electr. Power Syst. Res. 2020, 189, 106681. [Google Scholar] [CrossRef]
- Baker, K.; Toomey, B. Efficient relaxations for joint chance constrained AC optimal power flow. Electr. Power Syst. Res. 2017, 148, 230–236. [Google Scholar] [CrossRef] [Green Version]
- Arrigo, A.; Ordoudis, C.; Kazempour, J.; De Grève, Z.; Toubeau, J.F.; Vallée, F. Optimal Power Flow Under Uncertainty: An Extensive Out-of-Sample Analysis. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Bucharest, Romania, 29 September–2 October 2019; pp. 1–5. [Google Scholar]
- Yong, T.; Lasseter, R. Stochastic optimal power flow: Formulation and solution. In Proceedings of the Power Engineering Society Summer Meeting, Seattle, WA, USA, 16–20 July 2000; Volume 1, pp. 237–242. [Google Scholar]
- Roald, L.; Andersson, G. Chance-constrained AC optimal power flow: Reformulations and efficient algorithms. IEEE Trans. Power Syst. 2017, 33, 2906–2918. [Google Scholar] [CrossRef] [Green Version]
- Vrakopoulou, M.; Margellos, K.; Lygeros, J.; Andersson, G. A Probabilistic Framework for Reserve Scheduling and N-1 Security Assessment of Systems with High Wind Power Penetration. IEEE Trans. Power Syst. 2013, 28, 3885–3896. [Google Scholar] [CrossRef]
- Mühlpfordt, T.; Faulwasser, T.; Hagenmeyer, V. Solving stochastic ac power flow via polynomial chaos expansion. In Proceedings of the IEEE Conference on Control Applications (CCA), Buenos Aires, Argentina, 19–22 September 2016; pp. 70–76. [Google Scholar]
- Louca, R.; Bitar, E. Stochastic AC optimal power flow with affine recourse. In Proceedings of the IEEE 55th CDC, Las Vegas, NV, USA, 12–14 December 2016; pp. 2431–2436. [Google Scholar]
- Baghsorkhi, S.S.; Hiskens, I.A. Impact of wind power variability on sub-transmission networks. In Proceedings of the IEEE PESGM, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Bienstock, D.; Shukla, A. Variance-aware optimal power flow: Addressing the tradeoff between cost, security, and variability. IEEE Trans. Control. Netw. Syst. 2019, 6, 1185–1196. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Roald, L.A. Towards an AC optimal power flow algorithm with robust feasibility guarantees. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar]
- Mieth, R.; Dvorkin, Y. Data-driven distributionally robust optimal power flow for distribution systems. IEEE Control Syst. Lett. 2018, 2, 363–368. [Google Scholar] [CrossRef] [Green Version]
- Louca, R.; Bitar, E. Robust AC optimal power flow. IEEE Trans. Power Syst. 2018, 34, 1669–1681. [Google Scholar] [CrossRef] [Green Version]
- Lorca, A.; Sun, X.A. The Adaptive Robust Multi-Period Alternating Current Optimal Power Flow Problem. IEEE Trans. Power Syst. 2018, 33, 1993–2003. [Google Scholar] [CrossRef]
- Guo, Y.; Baker, K.; Dall’Anese, E.; Hu, Z.; Summers, T.H. Data-based distributionally robust stochastic optimal power flow—Part I: Methodologies. IEEE Trans. Power Syst. 2018, 34, 1483–1492. [Google Scholar] [CrossRef] [Green Version]
- Venzke, A.; Halilbasic, L.; Markovic, U.; Hug, G.; Chatzivasileiadis, S. Convex relaxations of chance constrained AC optimal power flow. IEEE Trans. Power Syst. 2017, 33, 2829–2841. [Google Scholar] [CrossRef] [Green Version]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Lavaei, J.; Low, S.H. Zero duality gap in optimal power flow problem. IEEE Trans. Power Syst. 2012, 27, 92–107. [Google Scholar] [CrossRef] [Green Version]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- Pareek, P.; Nguyen, H.D. Probabilistic robust small-signal stability framework using Gaussian process learning. Electr. Power Syst. Res. 2020, 188, 106545. [Google Scholar] [CrossRef]
- Pareek, P.; Yu, W.; Nguyen, H. Optimal Steady-state Voltage Control using Gaussian Process Learning. IEEE Trans. Ind. Inform. 2020. [Google Scholar] [CrossRef]
- Wiesemann, W.; Kuhn, D.; Sim, M. Distributionally robust convex optimization. Oper. Res. 2014, 62, 1358–1376. [Google Scholar] [CrossRef]
- Pareek, P.; Nguyen, H.D. Gaussian Process Learning-based Probabilistic Optimal Power Flow. IEEE Trans. Power Syst. 2021, 36, 541–544. [Google Scholar] [CrossRef]
- Coffrin, C.; Hijazi, H.L.; Van Hentenryck, P. Strengthening the SDP relaxation of AC power flows with convex envelopes, bound tightening, and valid inequalities. IEEE Trans. Power Syst. 2016, 32, 3549–3558. [Google Scholar] [CrossRef]
- Pareek, P.; Nguyen, H.D. A Convexification Approach for Small-Signal Stability Constrained Optimal Power Flow. IEEE Trans. Control of Network Syst. 2021. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2010, 26, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Madani, R.; Sojoudi, S.; Lavaei, J. Convex relaxation for optimal power flow problem: Mesh networks. IEEE Trans. Power Syst. 2014, 30, 199–211. [Google Scholar] [CrossRef]
- Löfberg, J. YALMIP : A Toolbox for Modeling and Optimization in MATLAB. In Proceedings of the CACSD Conference, Taipei, Taiwan, 2–4 September 2004. [Google Scholar]
- Rasmussen, C.E.; Nickisch, H. Gaussian processes for machine learning (GPML) toolbox. J. Mach. Learn. Res. 2010, 11, 3011–3015. [Google Scholar]
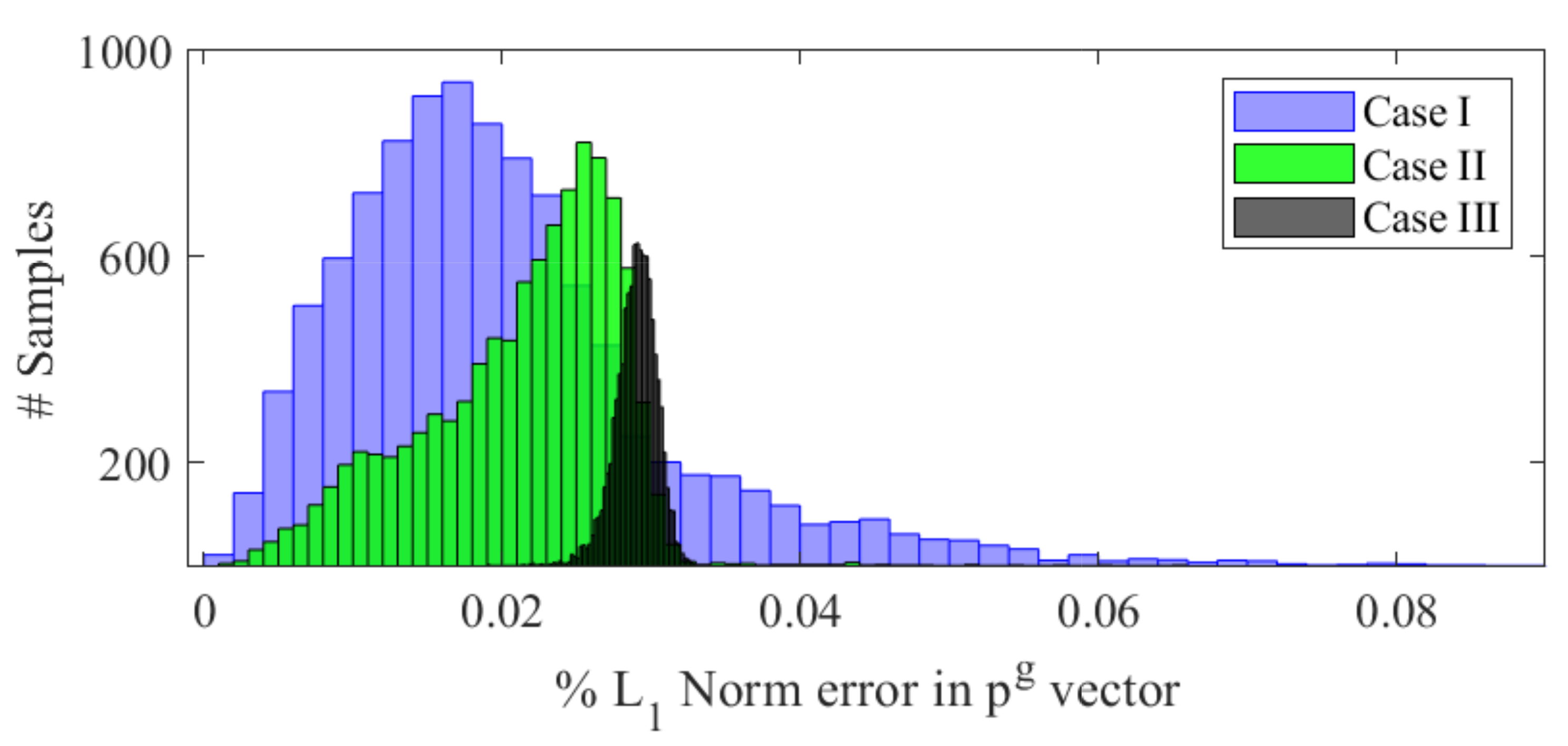


| Case I | 5.7438 $/hr | 0.0349 MW | −0.6680 pu |
| Case II | 5.7440 $/hr | 0.0189 MW | −0.6672 pu |
| Case III | 5.7721 $/hr | −0.1975 MW | −0.6586 pu |
| ACOPF | 6429.31 $/hr | 204.13 MW | 0.6709 pu |
| SA-SOPF-Pareto | 6730.55 $/hr | 61.92 MW | 0.0185 pu |
| Change | 4.685% | −69.66% | −97.24% |
| ACOPF | 388.22 $/h | 17.305 MW | 0.087818 pu |
| SA-SOPF-Pareto | 392.86 $/h | 1.716 MW | pu |
| Change | 1.195% | −90.08% | −99.915% |
| System | Learning (s) | SA-SOPF (s) |
|---|---|---|
| 14-bus | 2.41 + 16.88 = 19.29 | 0.157 |
| 30-bus | 4.01 + 38.01 = 42.02 | 2.325 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pareek, P.; Nguyen, H.D. State-Aware Stochastic Optimal Power Flow. Sustainability 2021, 13, 7577. https://doi.org/10.3390/su13147577
Pareek P, Nguyen HD. State-Aware Stochastic Optimal Power Flow. Sustainability. 2021; 13(14):7577. https://doi.org/10.3390/su13147577
Chicago/Turabian StylePareek, Parikshit, and Hung D. Nguyen. 2021. "State-Aware Stochastic Optimal Power Flow" Sustainability 13, no. 14: 7577. https://doi.org/10.3390/su13147577
APA StylePareek, P., & Nguyen, H. D. (2021). State-Aware Stochastic Optimal Power Flow. Sustainability, 13(14), 7577. https://doi.org/10.3390/su13147577







