Proton Exchange Membrane Fuel Cells Modeling Using Chaos Game Optimization Technique
Abstract
:1. Introduction
2. Modeling of The PEMFCS Methods
3. Problem Formulation
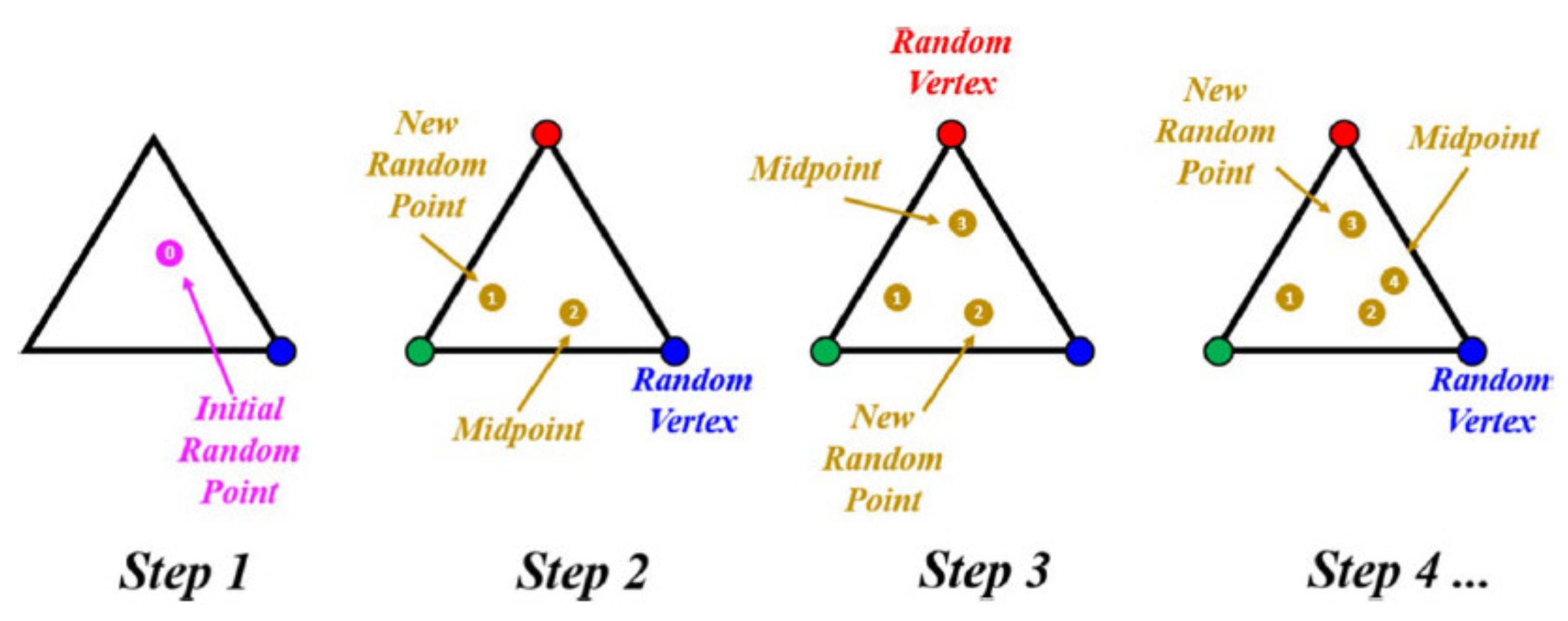
4. The Chaos Game Optimization Algorithm
4.1. Inspiration
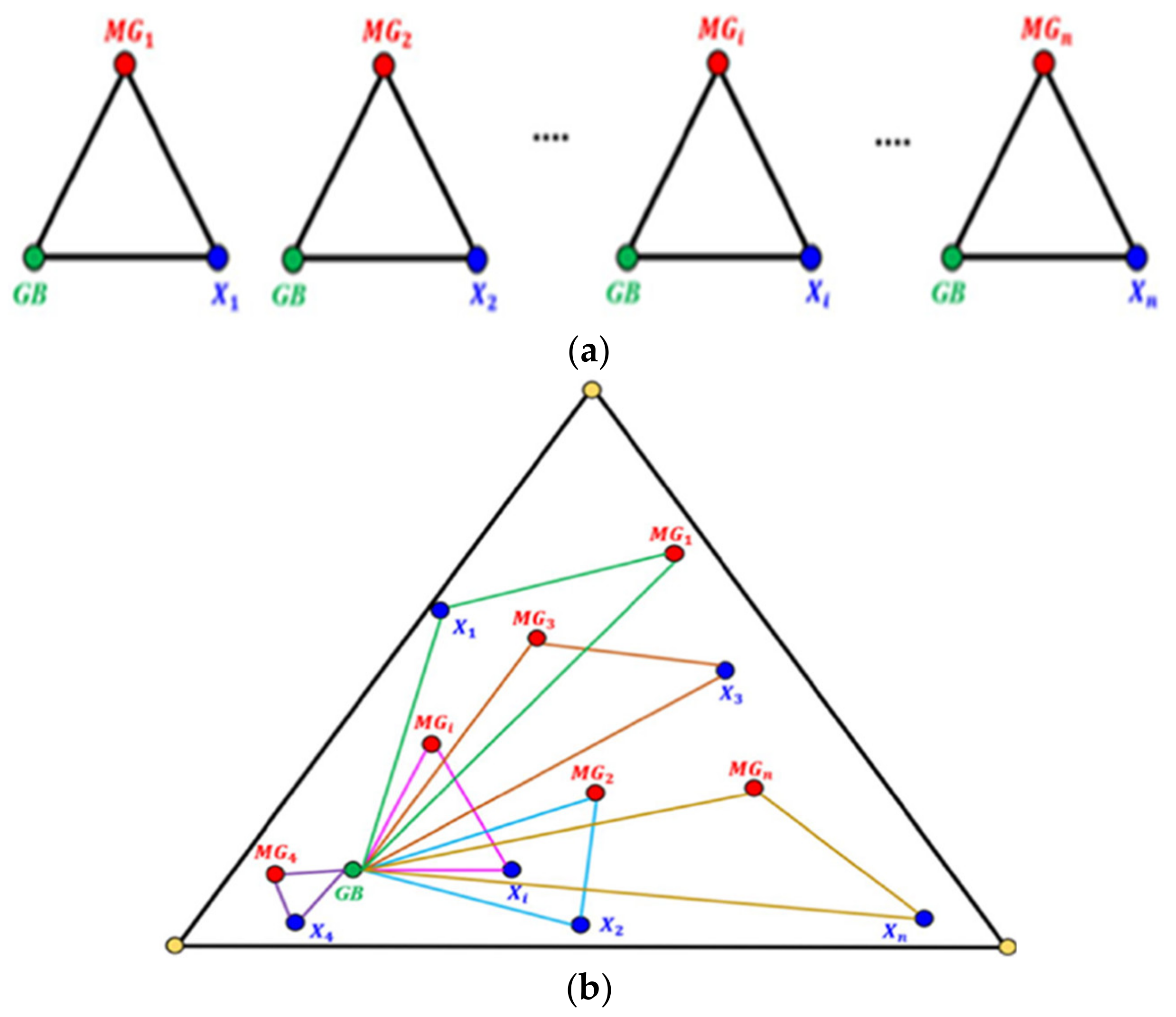
4.2. Mathematical Model
- The Global Best (GB) found so far;
- The Mean Group (MGi) which is the mean values of random seeds;
- The solution candidate ().
| Generate random initial population () of seeds () | |||
| Calculate fitness for each seed | |||
| Calculate GB | |||
| While (t < max. number of iterations) | |||
| for i = 1: number of initial seeds | |||
| Find | |||
| Create temporary triangles with, GB, and | |||
| Determine , , and | |||
| Determine new candidates using Equations (9)–(10). | |||
| if new candidates exceed the limits | |||
| Modify the candidates and amend them | |||
| end if | |||
| Calculate the fitness for the new seeds | |||
| if new candidates have better fitness than the initial ones | |||
| Substitute the worst initial eligible seeds by the new seeds | |||
| end if | |||
| Update GB if a better fitness is obtained | |||
| end for | |||
| t = t + 1 | |||
| end while | |||
| return GB | |||
5. Simulation Results
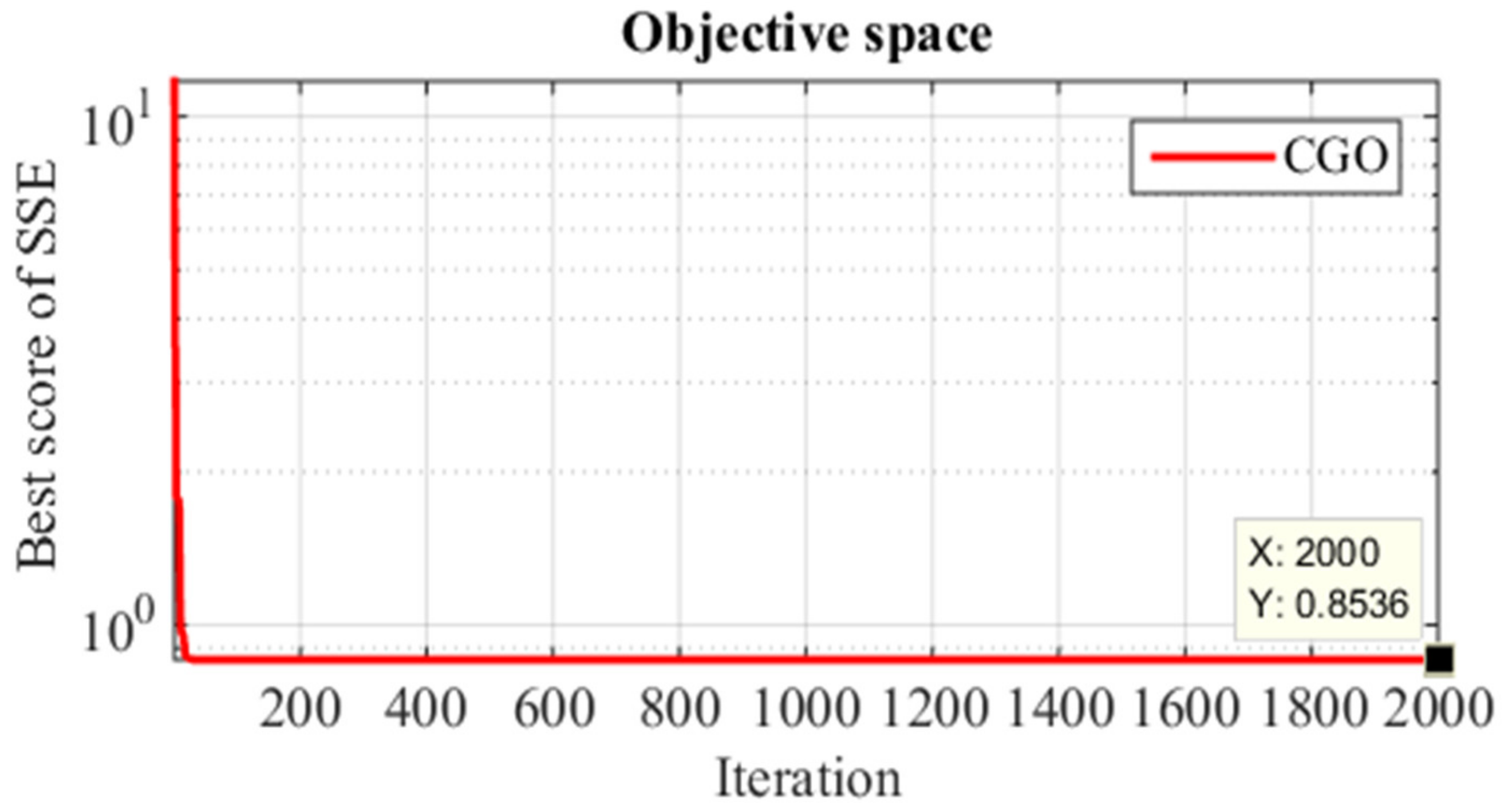
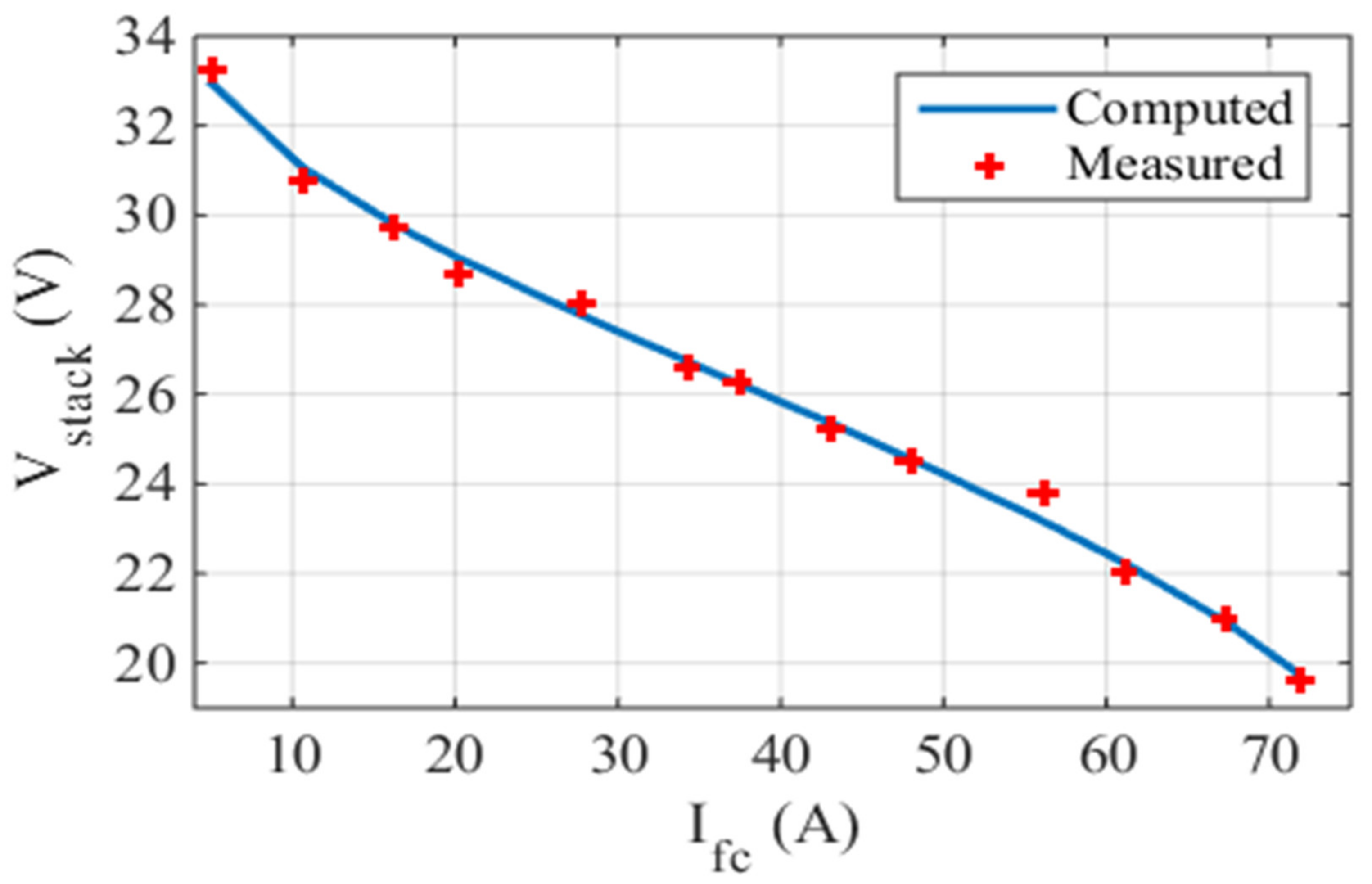
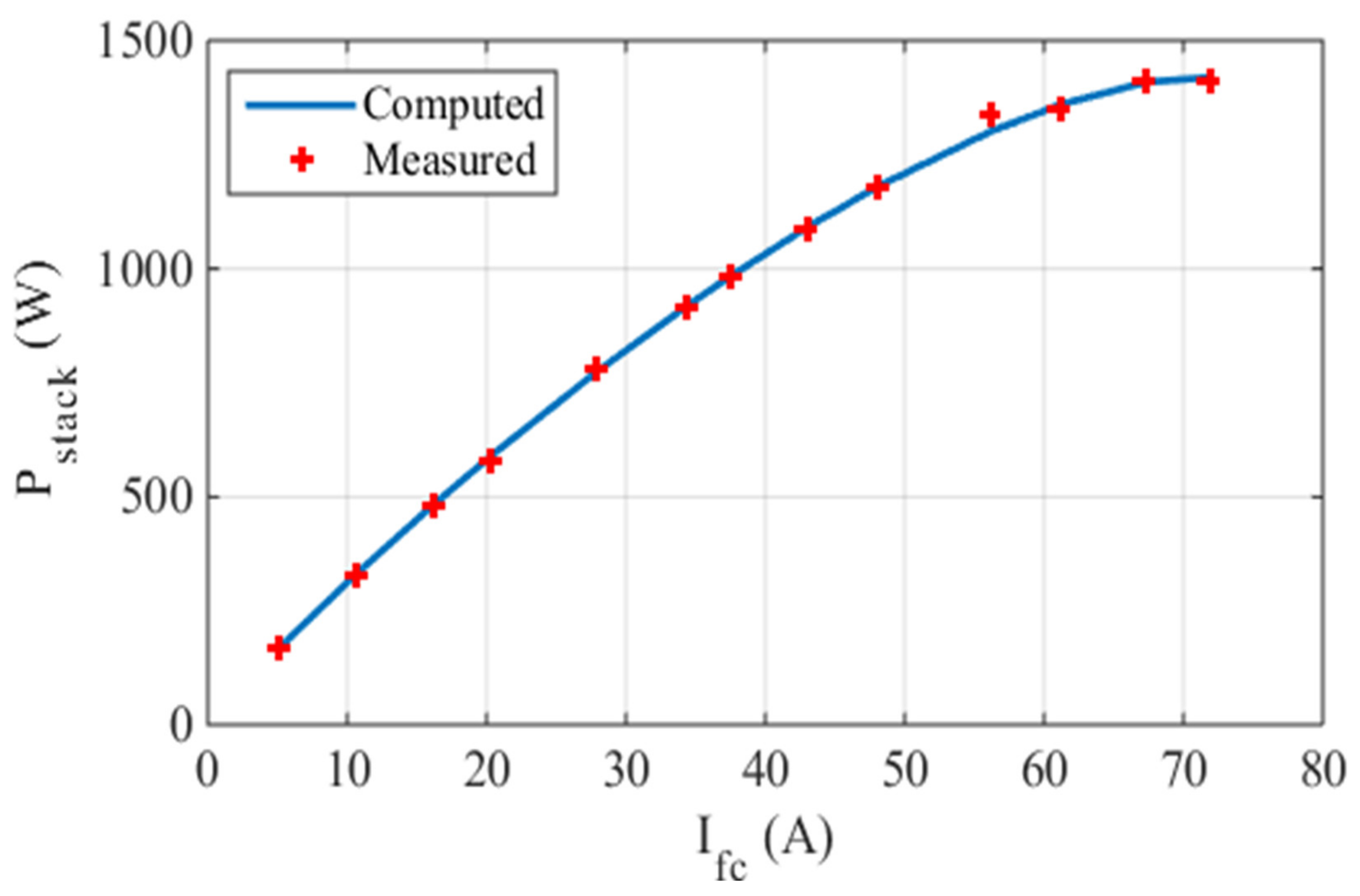
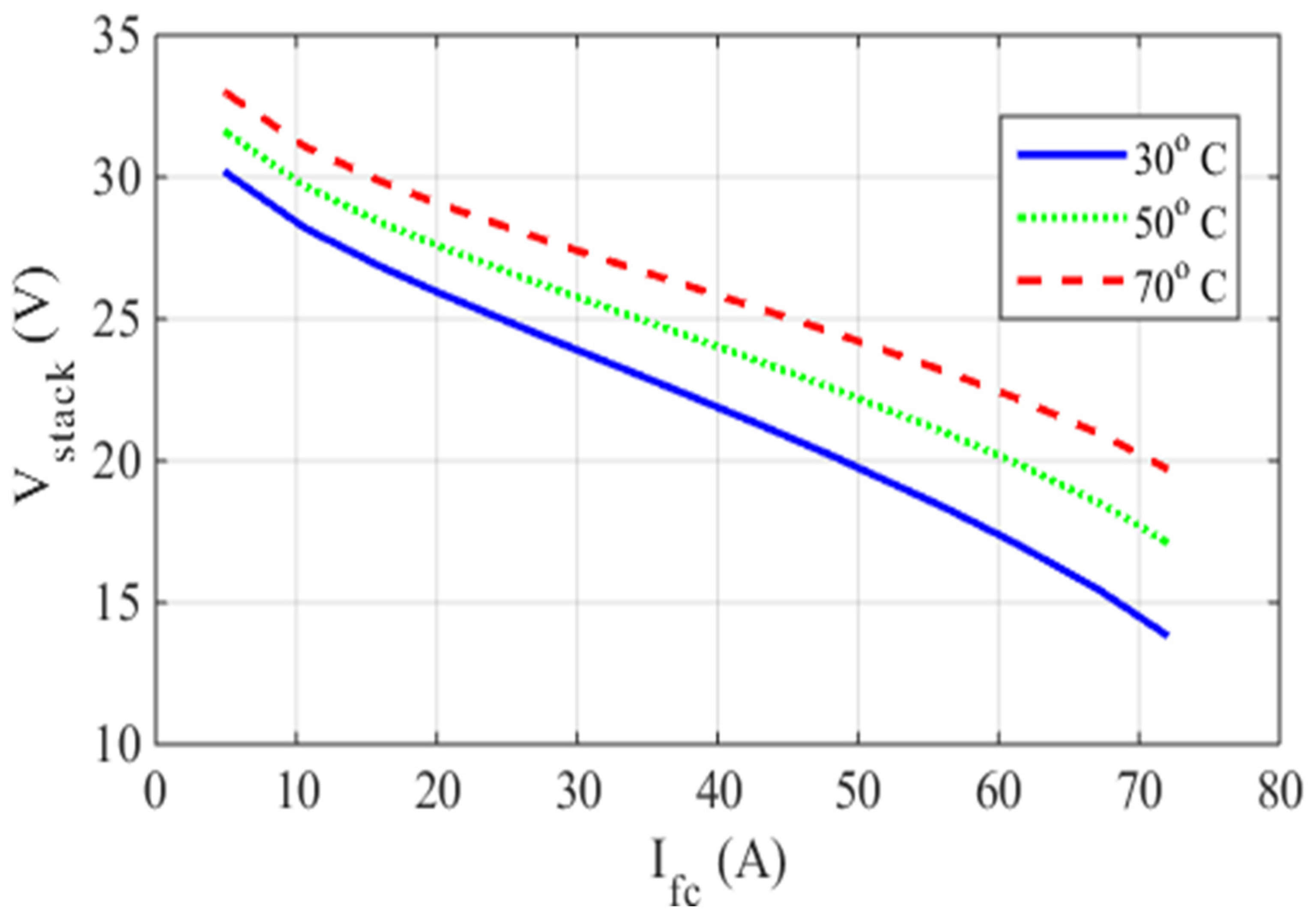
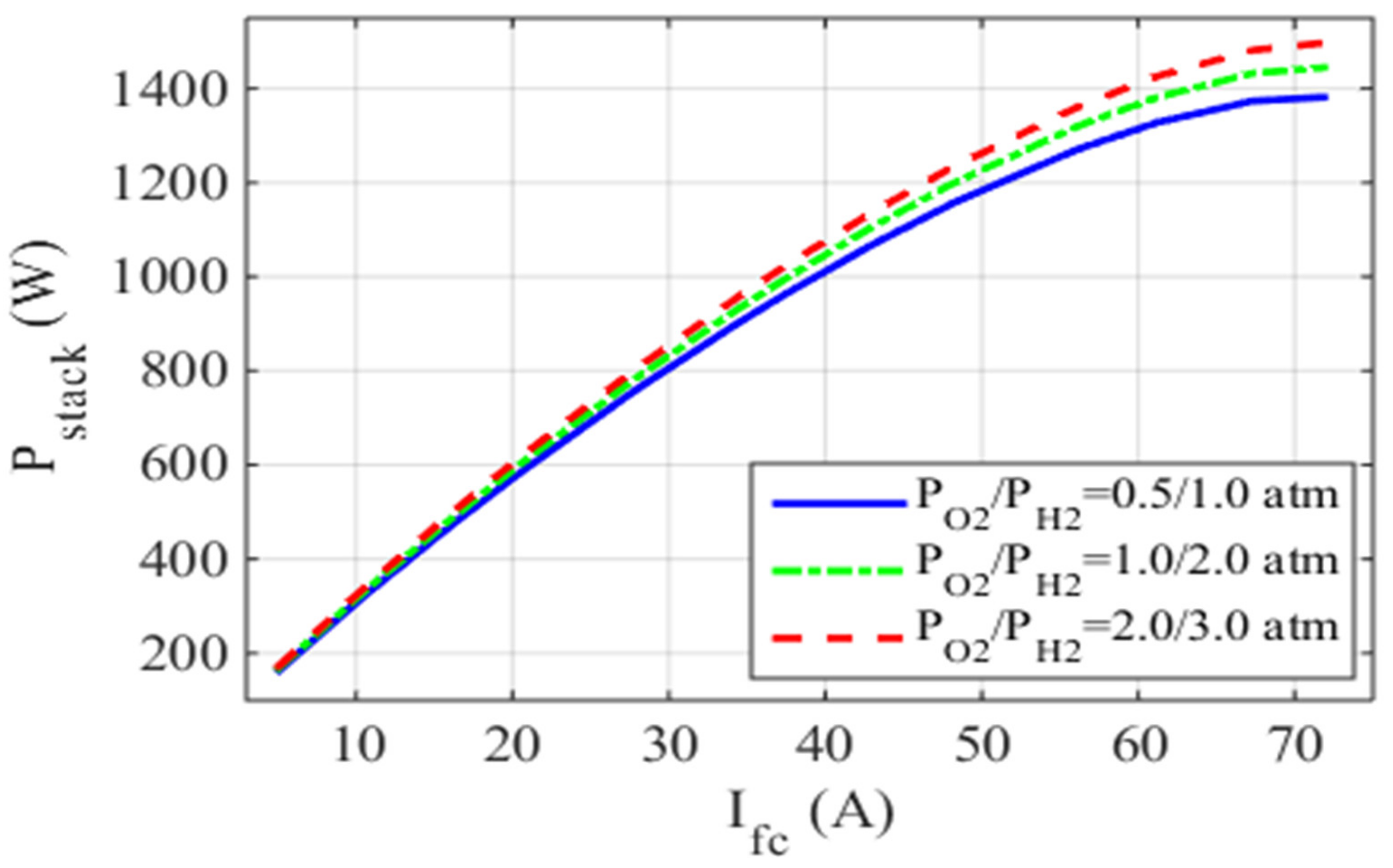
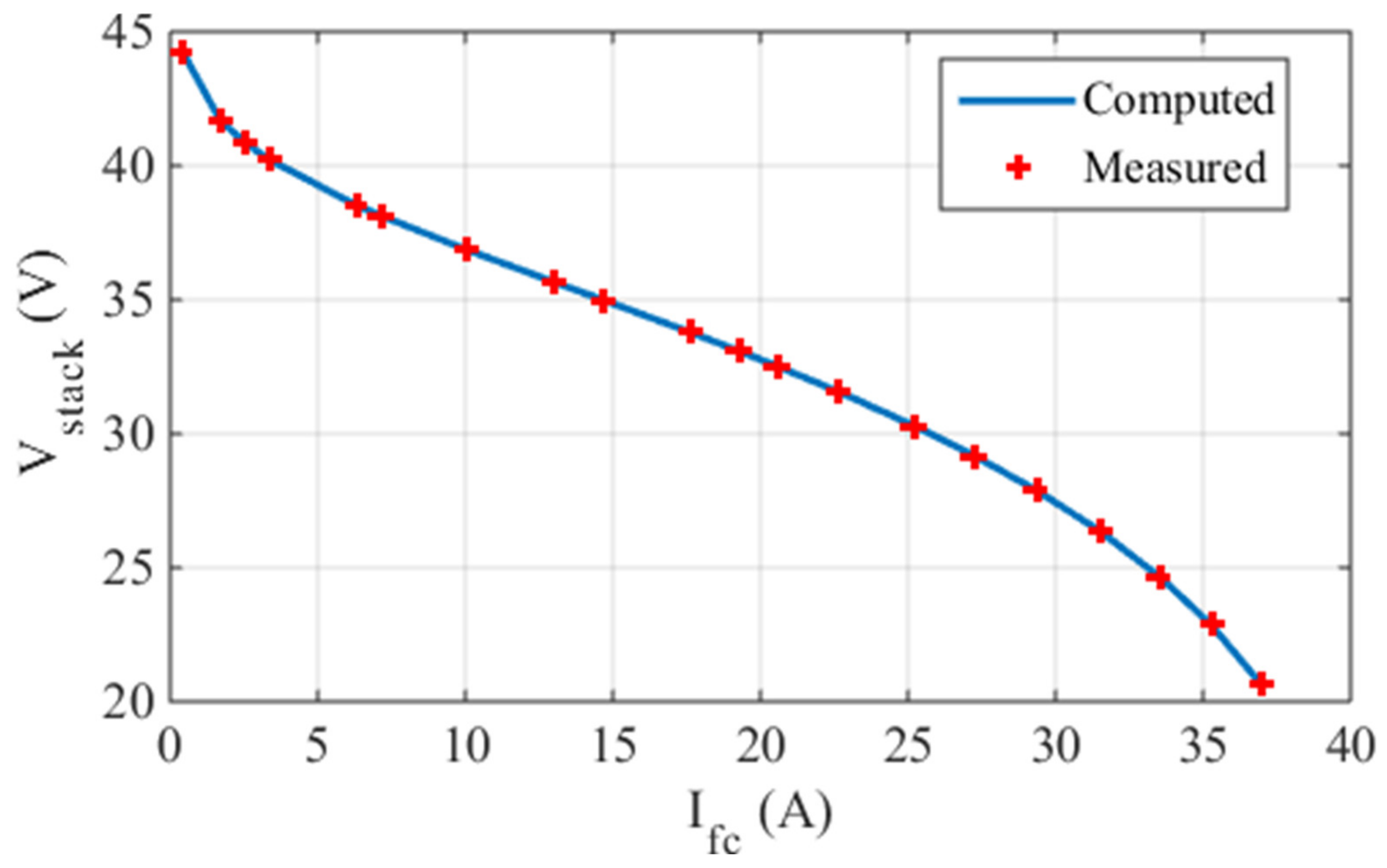
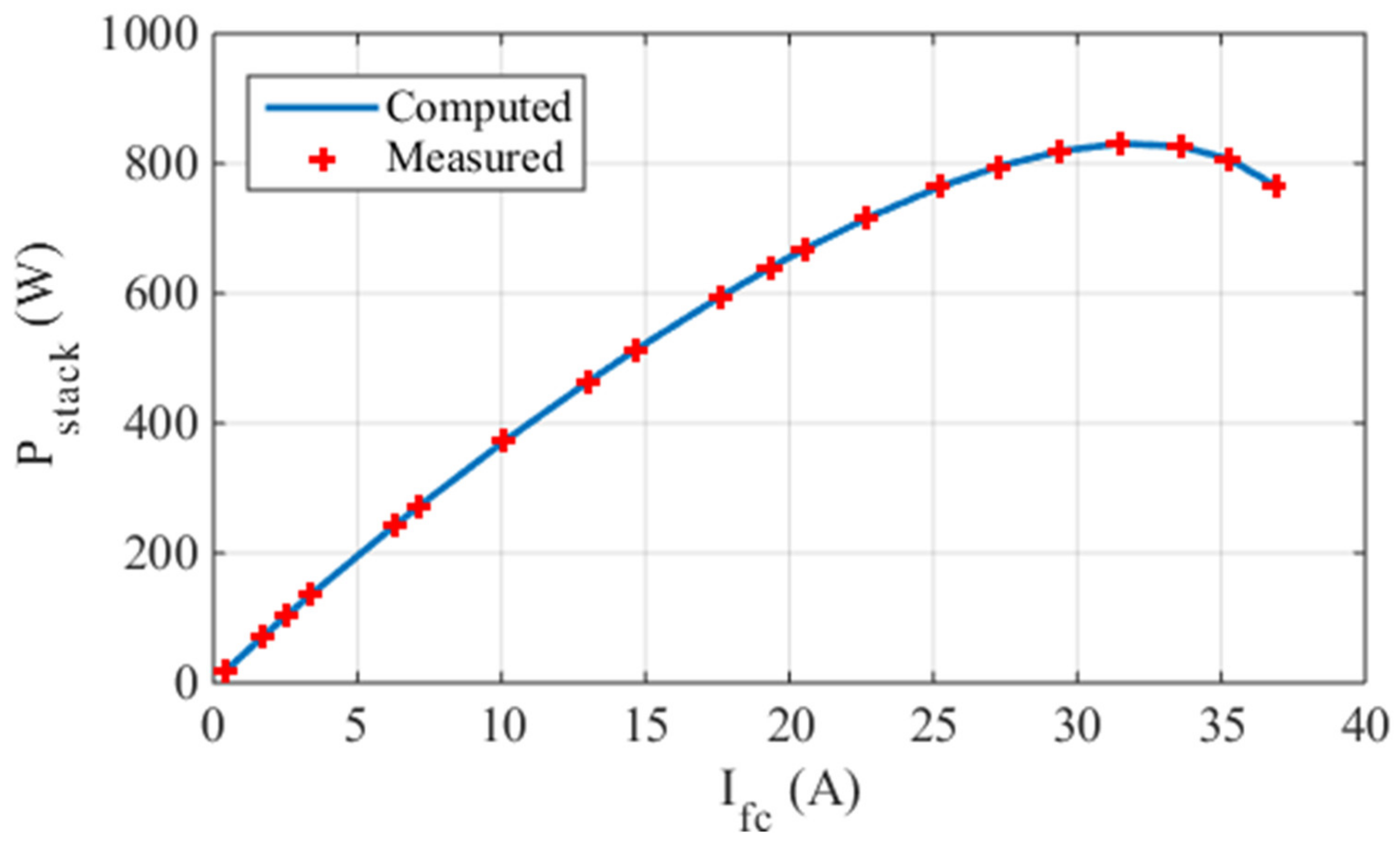
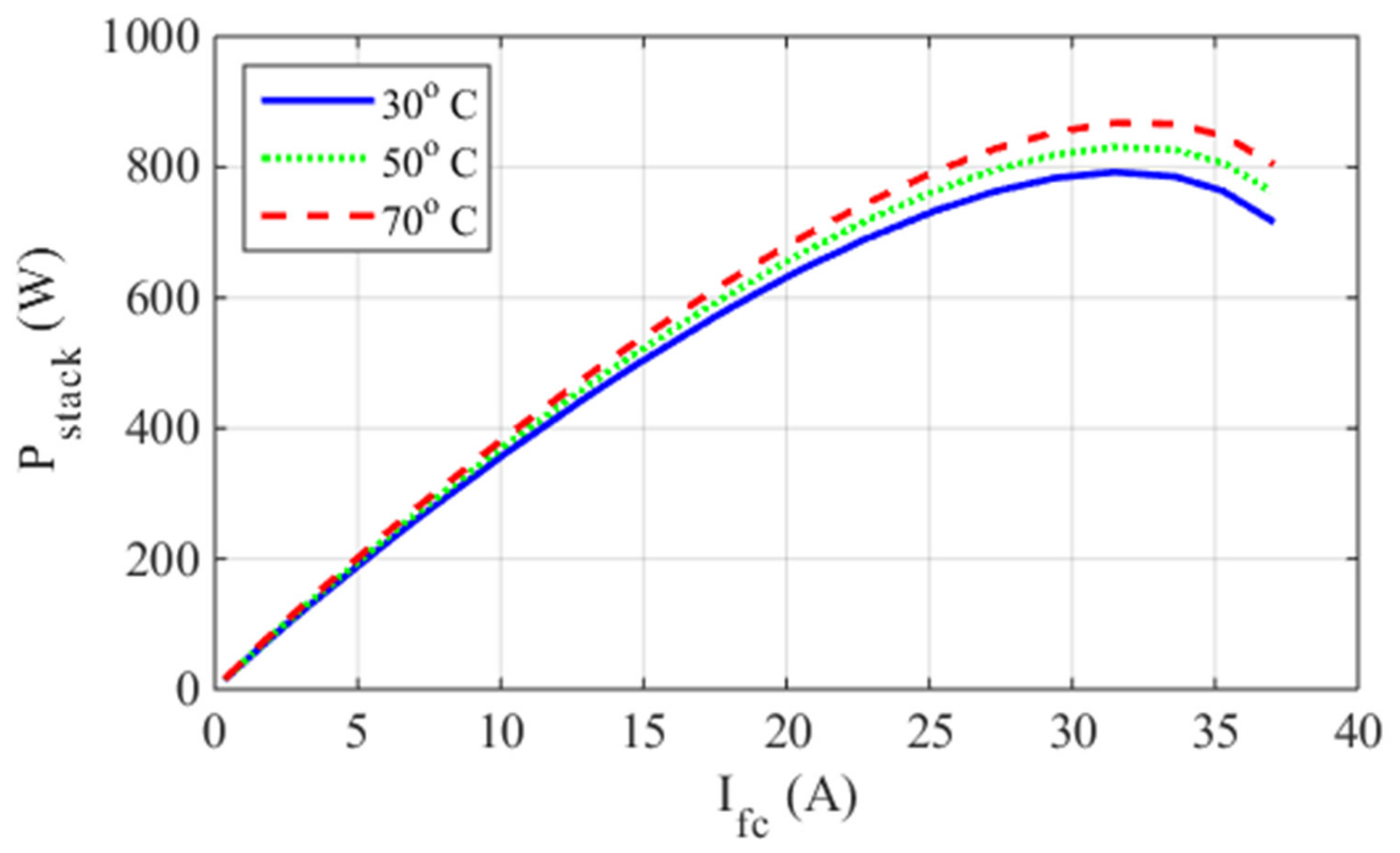
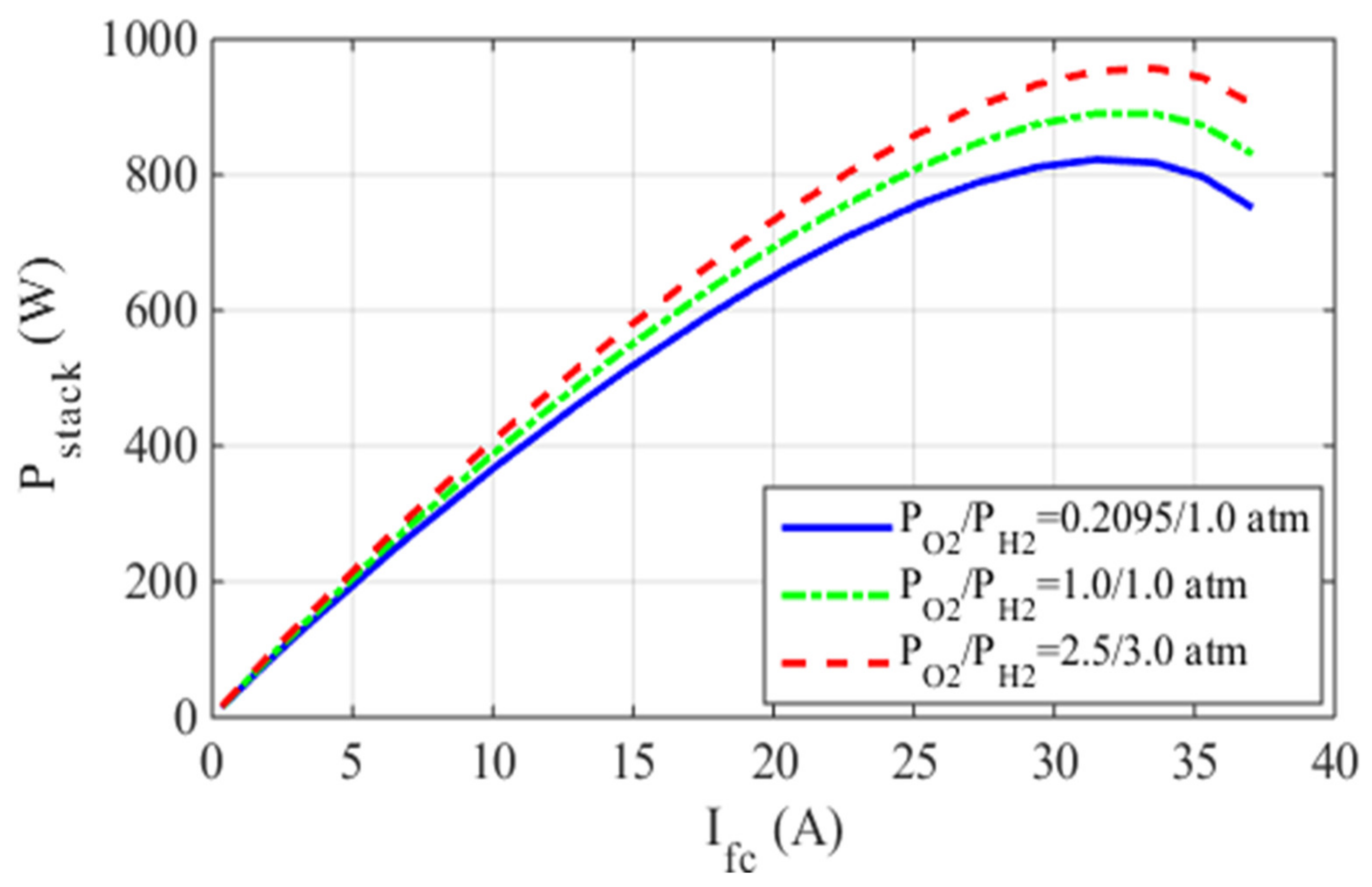
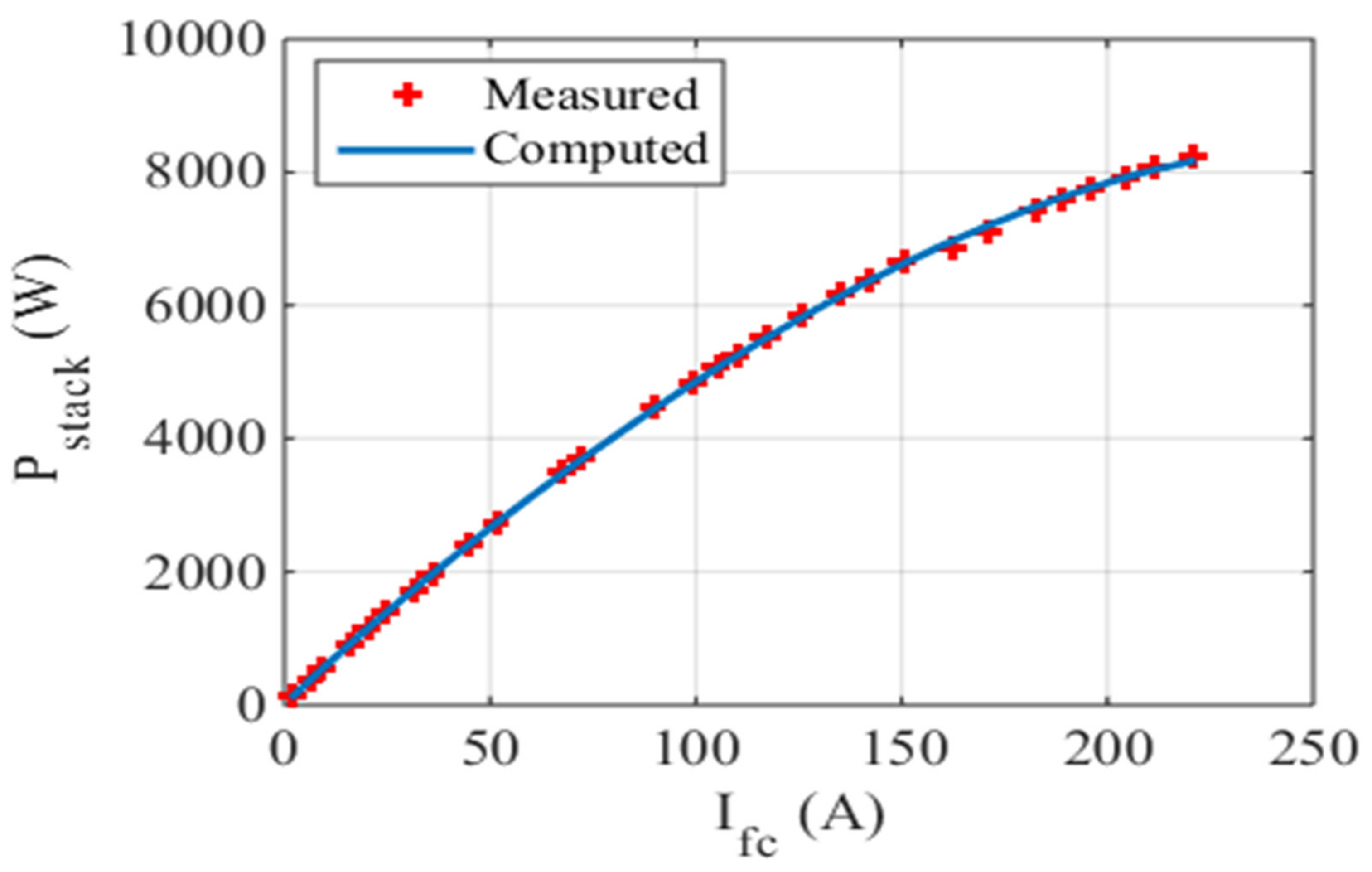
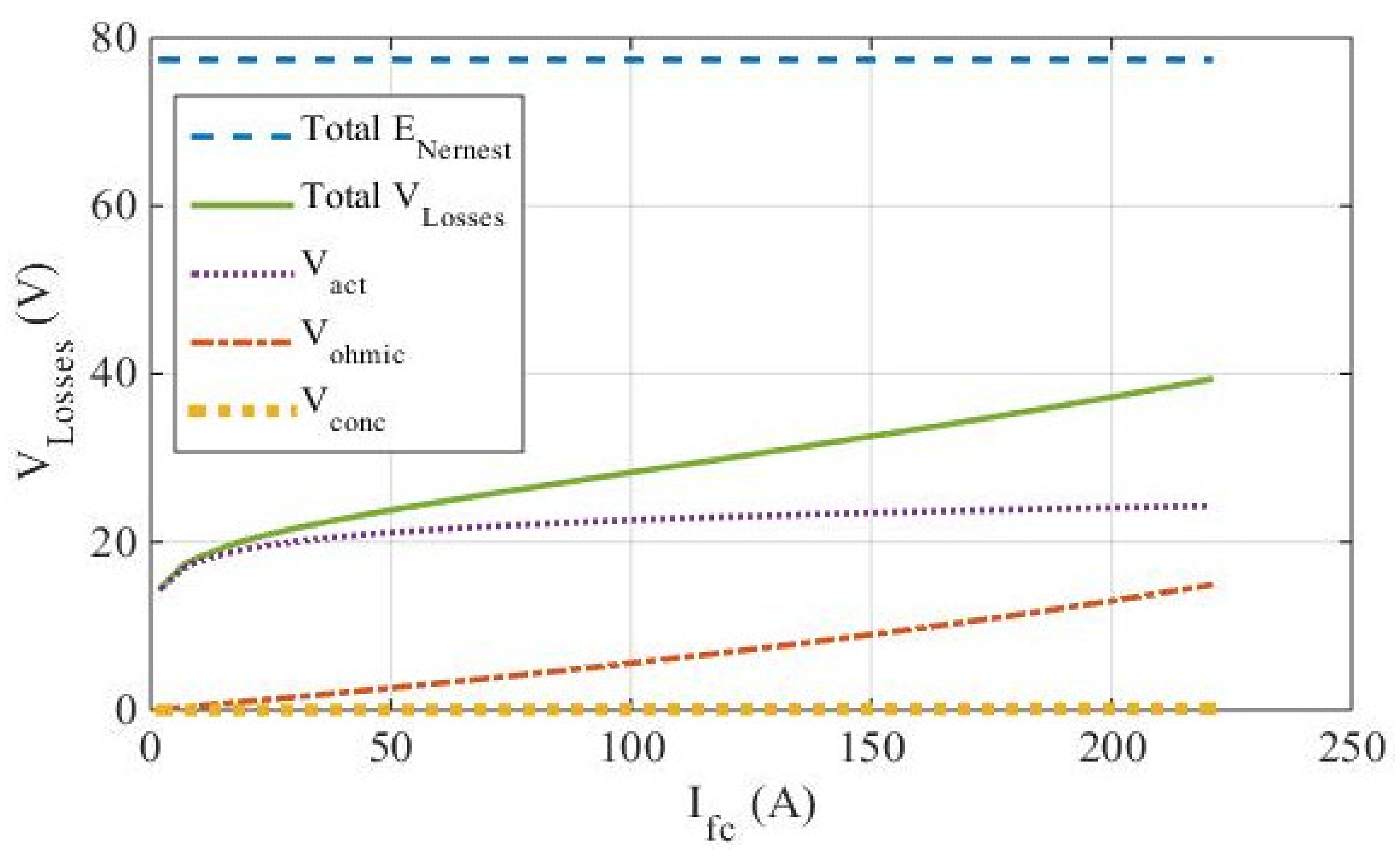
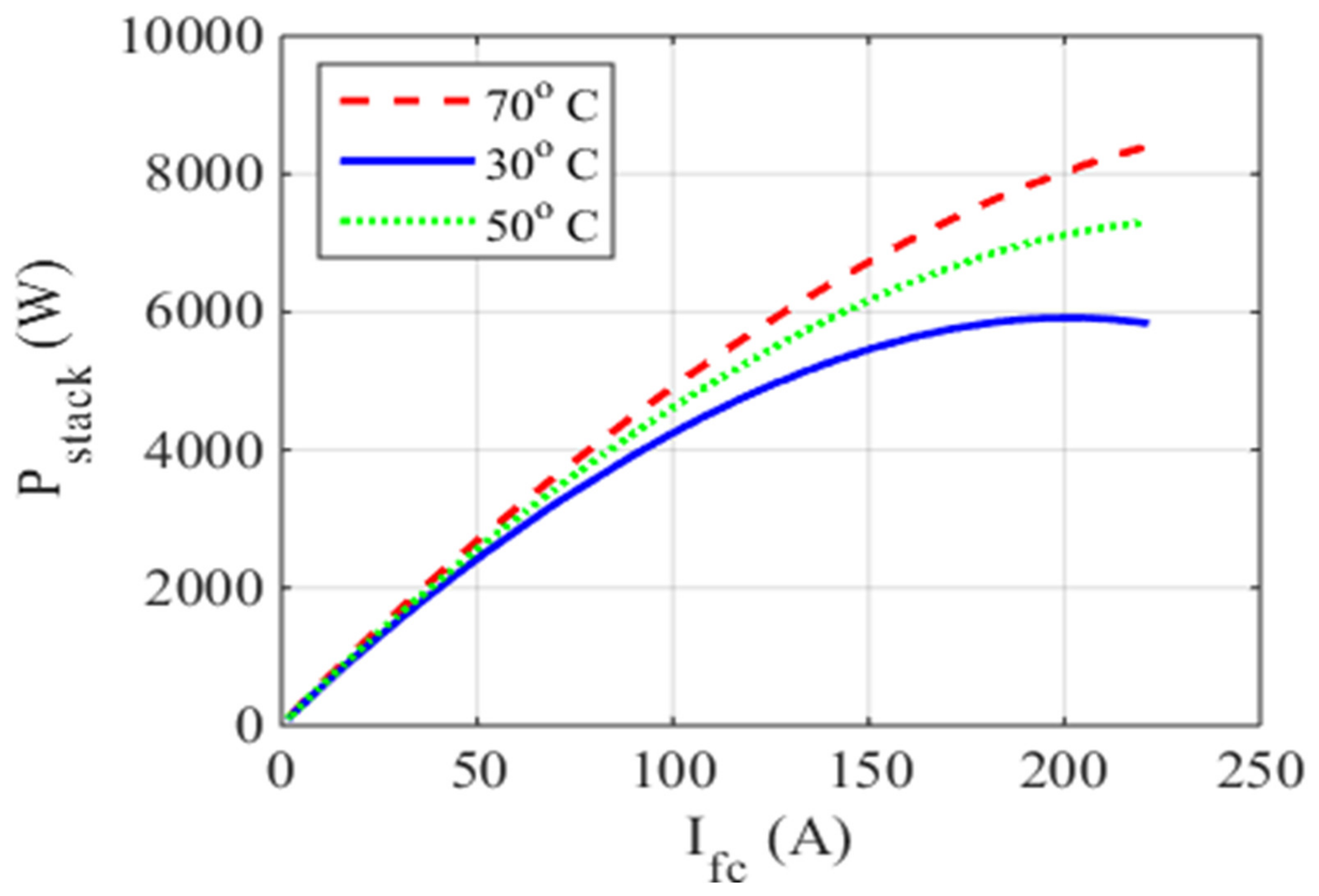
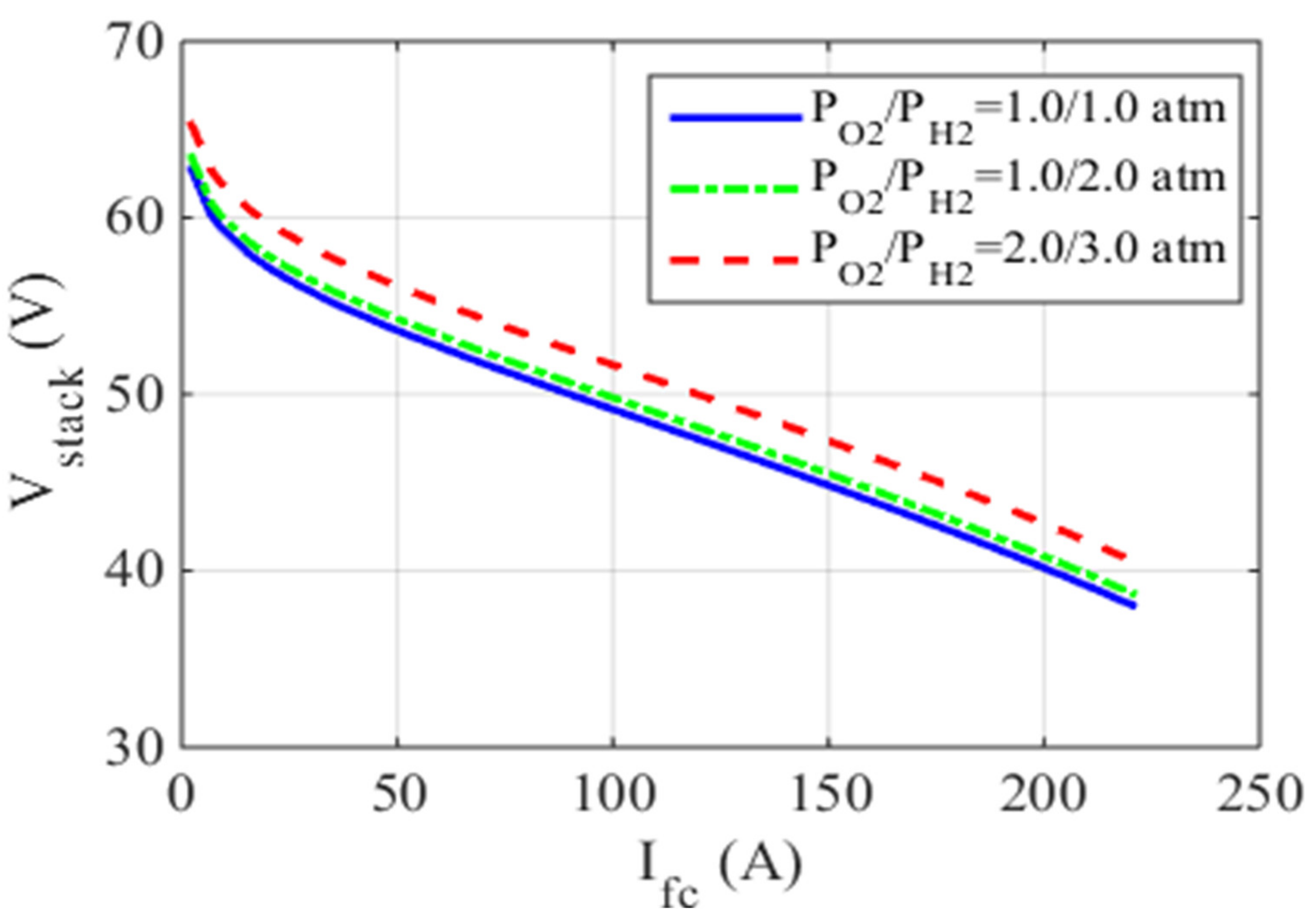
5.1. Case One: The Ballard Mark V
5.2. Case Two: The AVISTA SR-12 500 W
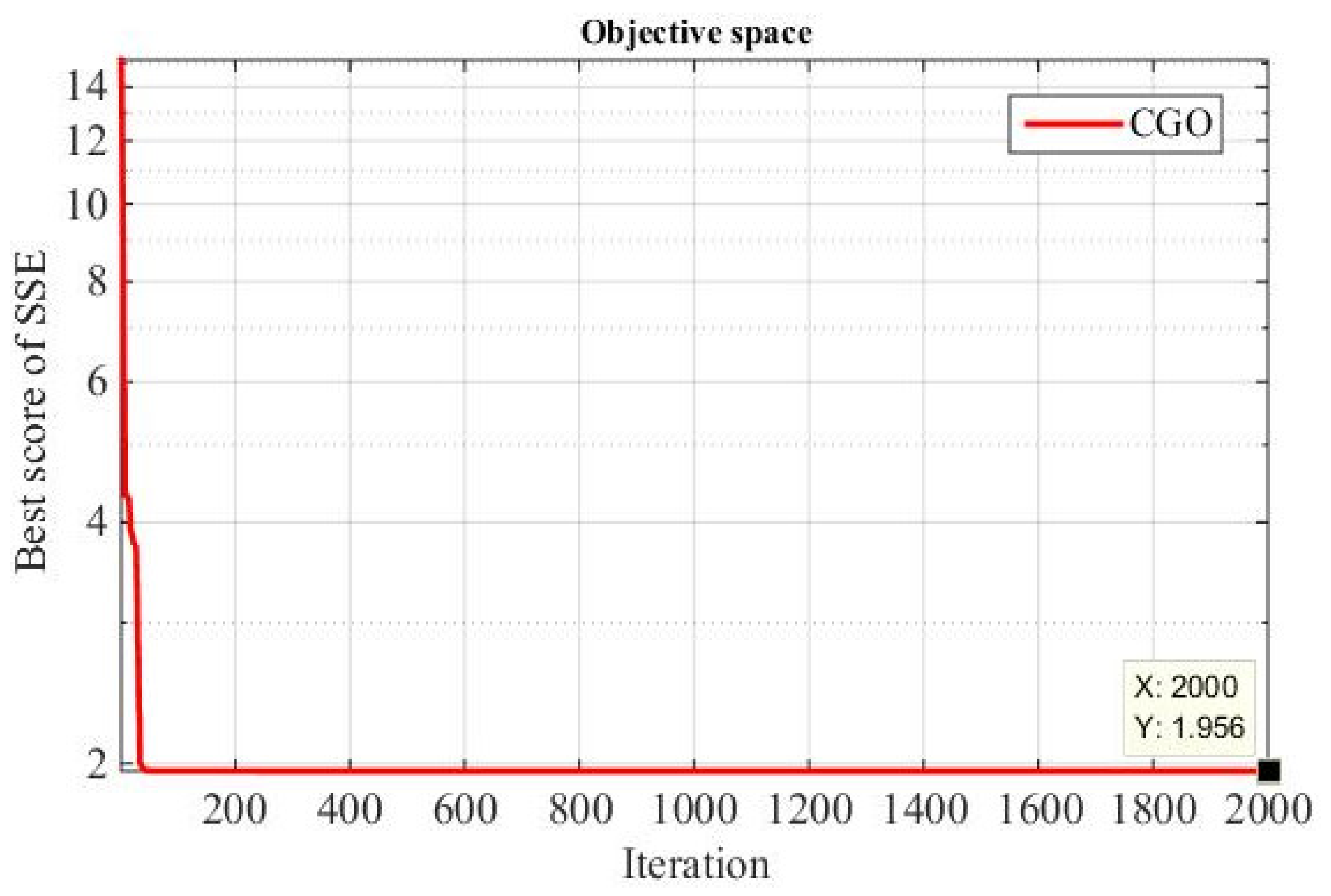
5.3. Case Three: The 6 kW Nedstack PS6
5.4. Robustness Statistical Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CGO | Chaos Game Optimization Algorithm |
| FC | Fuel Cells |
| FF | Fitness Function |
| NLOP | Nonlinear Optimization Problem |
| PEMFC | Proton Exchange Membrane Fuel Cell |
| SSE | Sum of Squared Errors |
References
- Shen, J.; Zhengkai, T.; Siew, H.C. Evaluation criterion of different flow field patterns in a proton exchange membrane fuel cell. Energy Convers. Manag. 2020, 213, 112841. [Google Scholar] [CrossRef]
- Hussien, A.M.; Mekhamer, S.F.; Hasanien, H.M. Cuttlefish Optimization Algorithm based Optimal PI Controller for Performance Enhancement of an Autonomous Operation of a DG System. In Proceedings of the 2020 2nd International Conference on Smart Power & Internet Energy Systems (SPIES), Bangkok, Thailand, 15–18 September 2020. [Google Scholar]
- Seleem, S.I.; Hasanien, H.M.; El-Fergany, A.A. El-Fergany. Equilibrium optimizer for parameter extraction of a fuel cell dynamic model. Renew. Energy 2021, 169, 117–128. [Google Scholar] [CrossRef]
- Sohani, A.; Naderi, S.; Torabi, F.; Sayyaadi, H.; Akhlaghi, Y.G.; Zhao, X.; Talukdar, K.; Said, Z. Application based multi-objective performance optimization of a proton exchange membrane fuel cell. J. Clean. Prod. 2020, 252, 119567. [Google Scholar] [CrossRef]
- Chen, H.; Liu, B.; Liu, R.; Weng, Q.; Zhang, T.; Pei, P. Optimal interval of air stoichiometry under different operating parameters and electrical load conditions of proton exchange membrane fuel cell. Energy Convers. Manag. 2020, 205, 112398. [Google Scholar] [CrossRef]
- Agwa, A.M.; El-Fergany, A.A.; Sarhan, G.M. Steady-state modeling of fuel cells based on atom search optimizer. Energies 2019, 12, 1884. [Google Scholar] [CrossRef] [Green Version]
- Kandidayeni, M.; Macias, A.; Khalatbarisoltani, A.; Boulon, L.; Kelouwani, S. Benchmark of proton exchange membrane fuel cell parameters extraction with metaheuristic optimization algorithms. Energy 2019, 183, 912–925. [Google Scholar] [CrossRef]
- El-Hay, E.A.; El-Hameed, M.A.; El-Fergany, A.A. El-Fergany. Improved performance of PEM fuel cells stack feeding switched reluctance motor using multi-objective dragonfly optimizer. Neural Comput. Appl. 2019, 31, 6909–6924. [Google Scholar] [CrossRef]
- Derbeli, M.; Barambones, O.; Farhat, M.; Ramos-Hernanz, J.A.; Sbita, L.; Derbeli, M.; Barambones, O.; Farhat, M.; Ramos-Hernanz, J.A.; Sbita, L. Robust high order sliding mode control for performance improvement of PEM fuel cell power systems. Int. J. Hydrog. Energy 2020, 45, 29222–29234. [Google Scholar] [CrossRef]
- Karanfil, G. Importance and applications of DOE/optimization methods in PEM fuel cells: A review. Int. J. Energy Res. 2020, 44, 4–25. [Google Scholar] [CrossRef]
- Gong, X.; Dong, F.; Mohamed, M.A.; Abdalla, O.M.; Ali, Z.M. A secured energy management architecture for smart hybrid microgrids considering PEM-fuel cell and electric vehicles. IEEE Access 2020, 8, 47807–47823. [Google Scholar] [CrossRef]
- Fathy, A.; Elaziz, M.A.; Alharbi, A.G. A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell. Renew. Energy 2020, 146, 1833–1845. [Google Scholar] [CrossRef]
- Pan, M.; Li, C.; Liao, J.; Lei, H.; Pan, C.; Meng, X.; Huang, H. Design and modeling of PEM fuel cell based on different flow fields. Energy 2020, 207, 118331. [Google Scholar] [CrossRef]
- Chugh, S.; Chaudhari, C.; Sonkar, K.; Sharma, A.; Kapur, G.; Ramakumar, S. Experimental and modelling studies of low temperature PEMFC performance. Int. J. Hydrog. Energy 2020, 45, 8866–8874. [Google Scholar] [CrossRef]
- Taleb, M.A.; Béthouxb, O.B.; Godoy, E. Identification of a PEMFC fractional order model. Int. J. Hydrog. Energy 2017, 42, 1499–1509. [Google Scholar] [CrossRef]
- Lyu, Z.; Meng, H.; Zhu, J.; Han, M.; Sun, Z.; Xue, H.; Zhao, Y.; Zhang, F. Comparison of off-gas utilization modes for solid oxide fuel cell stacks based on a semi-empirical parametric model. Appl. Energy 2020, 270, 115220. [Google Scholar] [CrossRef]
- Geem, Z.W.; Noh, J.S. Parameter estimation for a proton exchange membrane fuel cell model using GRG technique. Fuel Cell 2016, 16, 640–645. [Google Scholar] [CrossRef]
- Chavan, S.; Talange, D.B. Talange. Modeling and performance evaluation of PEM fuel cell by controlling its input parameters. Energy 2017, 138, 437–445. [Google Scholar] [CrossRef]
- Rao, Y.; Shao, Z.; Ahangarnejad, A.H.; Gholamalizadeh, E.; Sobhani, B. Shark Smell Optimizer applied to identify the optimal parameters of the proton exchange membrane fuel cell model. Energy Convers. Manag. 2019, 182, 1–8. [Google Scholar] [CrossRef]
- Priya, K.; Sathishkumar, K.; Rajasekar, N. A comprehensive review on parameter estimation techniques for Proton Exchange Membrane fuel cell modelling. Renew. Sustain. Energy Rev. 2018, 93, 121–144. [Google Scholar] [CrossRef]
- Talatahari, S.; Azizi, M. Optimization of constrained mathematical and engineering design problems using chaos game optimization. Comput. Ind. Eng. 2020, 145, 106560. [Google Scholar] [CrossRef]
- Mann, R.F.; Amphlett, J.C.; Hooper, M.A.I.; Jensen, H.M.; Peppley, B.A.; Roberge, P.R. Development and application of a generalised steady-state electrochemical model for a PEM fuel cell. J. Power Sources 2000, 86, 173–180. [Google Scholar] [CrossRef]
- El-Fergany, A. Electrical characterisation of proton exchange membrane fuel cells stack using grasshopper optimiser. IET Renew. Power Gener. 2017, 12, 9–17. [Google Scholar] [CrossRef]
- Saleh, I.M.M.; Ali, R.; Zhang, H. Simplified mathematical model of proton exchange membrane fuel cell based on horizon fuel cell stack. J. Mod. Power Syst. Clean Energy 2016, 4, 668–679. [Google Scholar] [CrossRef] [Green Version]
- El-Fergany, A.A. Extracting optimal parameters of PEM fuel cells using salp swarm optimizer. Renew. Energy 2018, 119, 641–648. [Google Scholar] [CrossRef]
- Talatahari, S.; Azar, B.F.; Sheikholeslami, R.; Gandomi, A. Imperialist competitive algorithm combined with chaos for global optimization. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1312–1319. [Google Scholar] [CrossRef]
- Shaheen, M.A.; Hasanien, H.M.; Alkuhayli, A. A novel hybrid GWO-PSO optimization technique for optimal reactive power dispatch problem solution. Ain Shams Eng. J. 2021, 12, 621–630. [Google Scholar] [CrossRef]
- Shaheen, M.; Mekhamer, S.F.; Hasanien, H.M.; Talaat, H.E.A. Optimal Power Flow of Power Systems Using Hybrid Firefly and Particle Swarm Optimization Technique. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; pp. 232–237. [Google Scholar]
- El-Fergany, A.A.; Hasanien, H.M.; Agwa, A.M. Semi-empirical PEM fuel cells model using whale optimization algorithm. Energy Convers. Manag. 2019, 201, 112197. [Google Scholar] [CrossRef]
- Zhang, G.; Jiao, K. Three-dimensional multi-phase simulation of PEMFC at high current density utilizing Eulerian-Eulerian model and two-fluid model. Energy Convers. Manag. 2018, 176, 409–421. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Transient search optimization: A new meta-heuristic optimization algorithm. Appl. Intell. 2020, 50, 3926–3941. [Google Scholar] [CrossRef]
- Fawzi, M.; El-Fergany, A.A.; Hasanien, H.M. Hasanien. Effective methodology based on neural network optimizer for extracting model parameters of PEM fuel cells. Int. J. Energy Res. 2019, 43, 8136–8147. [Google Scholar] [CrossRef]









| Item | Value |
|---|---|
| No. of series cells | 35 |
| Membrane thickness | 178 μm |
| 50.6 cm2 | |
| Thermal limit of the current | 70 A |
| Maximum current density | 1.5 A/cm2 |
| Parameter | CGO | HOA | WOA [29] | GHO [23] |
|---|---|---|---|---|
| (V) | −1.192042466678 | −0.8532 | −1.1978 | −0.8532 |
| (V/K) | 3.6124342507723 | 3.3244899099 | 4.4183 | 3.4173 |
| (V/K) | 4.0797209285374 | 9.1704275491 | 9.7214 | 9.8 |
| (V/K) | −16.283043067932 | −15.445073095 | −16.273 | −15.9555 |
| λ | 23 | 22.999998286 | 23 | 22.8458 |
| (mΩ) | 0.1 | 0.249053165 | 0.1002 | 0.1 |
| β | 0.0136000000000001 | 0.0136 | 0.0136 | 0.0136 |
| Population size | 50 | 20 | 50 | 60 |
| Number of iterations | 2000 | 2000 | 2000 | 2000 |
| Computation time (s) | 119.38140 | 11.4236416 | 111 | 95.5 |
| SSE | 0.8536075155595 | 0.9424006399 | 0.8537 | 0.871 |
| Parameter | CGO | WOA [29] | NNO [32] | GHO [23] |
|---|---|---|---|---|
| (V) | −1.1053135621 | −0.8902 | −1.0596 | −1.1997 |
| (V/K) | 3.506655471 | 3.3088 | 3.7435 | 4.2695 |
| (V/K) | 6.726482341 | 9.75455 | 9.6902 | 9.8 |
| (V/K) | −10.634713544 | −10.33 | −19.302 | −10.1371 |
| λ | 21.517713112 | 22.8311 | 20.8772 | 23 |
| (mΩ) | 0.272639115 | 0.5677 | 0.1 | 0.4638 |
| β | 0.150008476 | 0.1464 | 0.0161 | 0.1486 |
| Population size | 50 | NR | NR | NR |
| Number of iterations | 2000 | 200 | NR | NR |
| Computation time (s) | 116.798459 | 38.3 | 33 | 12.5 |
| SSE | 0.000142098 | 0.0111 | 0.0117 | 0.0478 |
| Item | Value |
|---|---|
| No. of series cells | 65 |
| Membrane thickness | 1.78 mm |
| 240 cm2 | |
| Max. current density | 5 A/cm2 |
| Parameter | CGO | NNA [32] | SSO [21,25] | GA [23] |
|---|---|---|---|---|
| (V) | −1.14692894516 | −0.8535 | −0.9719 | −1.1997 |
| (V/K) | 3.27982148359 | 2.4316 | 3.3487 | 3.4172 |
| (V/K) | 3.6043948463 | 3.7545 | 7.9111 | 3.6 |
| (V/K) | −9.54 | −9.54 | −9.5435 | −9.54 |
| λ | 13.013946837 | 13.0802 | 13 | 13 |
| (mΩ) | 0.1 | 0.1 | 0.1 | 0.1376 |
| β | 0.0136 | 0.0136 | 0.0534 | 0.0359 |
| Population size | 50 | NR | NR | NR |
| Number of iterations | 2000 | NR | NR | NR |
| Computation time (s) | 91.7770779 | NR | NR | NR |
| SSE | 1.955524791 | 2.14487 | 2.18067 | 2.4089 |
| Run No. | Case One |
|---|---|
| 1 | 0.853607516 |
| 2 | 0.853607516 |
| 3 | 0.853607516 |
| 4 | 0.853607516 |
| 5 | 0.853607516 |
| 6 | 0.853607516 |
| 7 | 0.853607516 |
| 8 | 0.853607516 |
| 9 | 0.853607516 |
| 10 | 0.853607516 |
| 11 | 0.853607516 |
| 12 | 0.853607516 |
| 13 | 0.853607516 |
| 14 | 0.853607516 |
| 15 | 0.853607516 |
| 16 | 0.853607516 |
| 17 | 0.853607516 |
| 18 | 0.853607516 |
| 19 | 0.853607516 |
| 20 | 0.853607516 |
| 21 | 1.087297383 |
| 22 | 0.853607516 |
| 23 | 0.853607516 |
| 24 | 0.853607516 |
| 25 | 0.853607516 |
| 26 | 0.853607516 |
| 27 | 0.853607516 |
| 28 | 0.853607516 |
| 29 | 0.853607516 |
| 30 | 0.853607516 |
| Max | 1.087297383 |
| Median | 0.861397178 |
| Min | 0.853607516 |
| Standard Dev. | 0.042665737 |
| Variance | 0.001820365 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsaidan, I.; Shaheen, M.A.M.; Hasanien, H.M.; Alaraj, M.; Alnafisah, A.S. Proton Exchange Membrane Fuel Cells Modeling Using Chaos Game Optimization Technique. Sustainability 2021, 13, 7911. https://doi.org/10.3390/su13147911
Alsaidan I, Shaheen MAM, Hasanien HM, Alaraj M, Alnafisah AS. Proton Exchange Membrane Fuel Cells Modeling Using Chaos Game Optimization Technique. Sustainability. 2021; 13(14):7911. https://doi.org/10.3390/su13147911
Chicago/Turabian StyleAlsaidan, Ibrahim, Mohamed A. M. Shaheen, Hany M. Hasanien, Muhannad Alaraj, and Abrar S. Alnafisah. 2021. "Proton Exchange Membrane Fuel Cells Modeling Using Chaos Game Optimization Technique" Sustainability 13, no. 14: 7911. https://doi.org/10.3390/su13147911







