A P-Hub Location Problem for Determining Park-and-Ride Facility Locations with the Weibit-Based Choice Model

Abstract

Park and ride (P&R) facilities provide intermodal transfer between private vehicles and public transportation systems to alleviate urban congestion. This study developed a mathematical programming formulation for determining P&R facility locations. A recently developed Weibit-based model was adopted to represent the traveler choice behavior with heterogeneity. The model’s independence of irrelevant alternatives (IIA) property was explored and used to linearize its nonlinear probability. Some numerical examples are provided to demonstrate a feature of the proposed mixed integer linear programing (MILP). The results indicate a significant impact of route-specific perception variance on the optimal P&R facility locations in a real-size transportation network.

1. Introduction

Park and ride (P&R) facilities are a significant component of the public transportation system in many cities around the world. The facility has been recognized as part of sustainable development for many decades. With globalization, economic growth brings more business activities [1], and the desire to use public transportation more frequently depends on the ease of car access [2,3]. Hence, the selection of P&R facility locations becomes essential in encouraging drivers to transfer from their private vehicles to public transportation to alleviate traffic congestion in the urban areas [4].

The mathematical programming (MP) approach plays an important role in the P&R facility location problem. The optimal facility location is determined through the interaction of the travel choice behavior and the level of service (LOS) of the P&R locations in a transportation network. The pioneer location model was provided by [5], which assumes an all-or-nothing (AON) assignment (i.e., all travel demands are entirely assigned to the closest facility). Several studies relaxed the AON assumption using the attractiveness of the facility to determine the assignment [6,7]. Most of these studies adopted the gravity-based model [8,9] and the random utility maximization (RUM) model. The gravity-based model usually considers the attractiveness through the negative exponential impedance or the negative power impedance of the distance. The RUM model considers the attractiveness through the travelers’ perception. The travelers’ observed utility is measured and incorporated with the unobserved utility [10]. A market share for the open facility is determined based on the travelers’ choice behavior that maximizes their individual utilities. The well-known multinomial Logit (MNL) model is usually adopted to represent such choice behavior for the parking selection [11,12]. Benati and Hansen [13] provided a MNL model-based MP and a linear reformulation of the nonlinear MNL probability in the facility location problem. Haase [14] adopted the MNL model with a constant substitution pattern to provide a linear reformulation. Aros-Vera et al. [15] utilized this method for P&R facility location in a hypernetwork [16], where the level of service (LOS) or travel cost of each intermodal transport journey is considered through the performance of links, and hence routes, in a one-dimensional transportation network. The study in [17] employed a similar linear reformulation of Benati and Hansen [13] to give an alternative formulation. In all these approaches, Haase and Muller [18] argued that the constant substitution pattern assumption seems to be superior to other formulations. Further, Liu and Meng [19] and Liu et al. [20] provided the bus-based P&R facility location. Pineda et al. [21] integrated the traffic and public transportation systems for the P&R facility location.

The drawbacks of the MNL model include: (1) inability to consider the similarity between the choice alternatives and (2) inability to consider the heterogeneity [22]. These two drawbacks stem from the independently and identically distributed (IID) assumption embedded in the random error term of the MNL model [23]. In the hypernetwork, the MNL model cannot account for route similarity (route correlation or route overlapping) [20,24,25,26] and the heterogeneous perception variance from different trip lengths [22,27]. It has been shown that heterogeneity is an important factor of the P&R facility location selection [28].

In this study, we developed a mathematical programming (MP) formulation to consider the travelers’ heterogeneity in selecting a P&R facility location. The multinomial Weibit (MNW) model [29] was adopted to account for the heterogeneity among the intermodal journey alternatives. The independence of irrelevant alternatives (IIA) property of MNW was explored and used to provide a linear reformulation of its non-linear choice probability. Application of the proposed mixed integer linear programing (MILP) is demonstrated in a real-size transportation network. The numerical examples indicate a significant impact of heterogeneous perception variance on the optimal P&R facility locations. The MNW route-specific perception variance as a function of trip length is more sensitive to a change in distance-based public transport fare structure, and hence, the P&R facility location selection.

The paper is organized as follows. Section 2 provides a list of notations used in this study. Section 3 gives some background of the MNL and MNW models. In Section 4, the proposed MILP is developed with a rigorous proof. Section 5 shows two numerical examples to demonstrate features of the proposed model and its applicability in a realistic transportation network. Section 6 concludes this paper.

2. Notation

Table 1. Notation list.

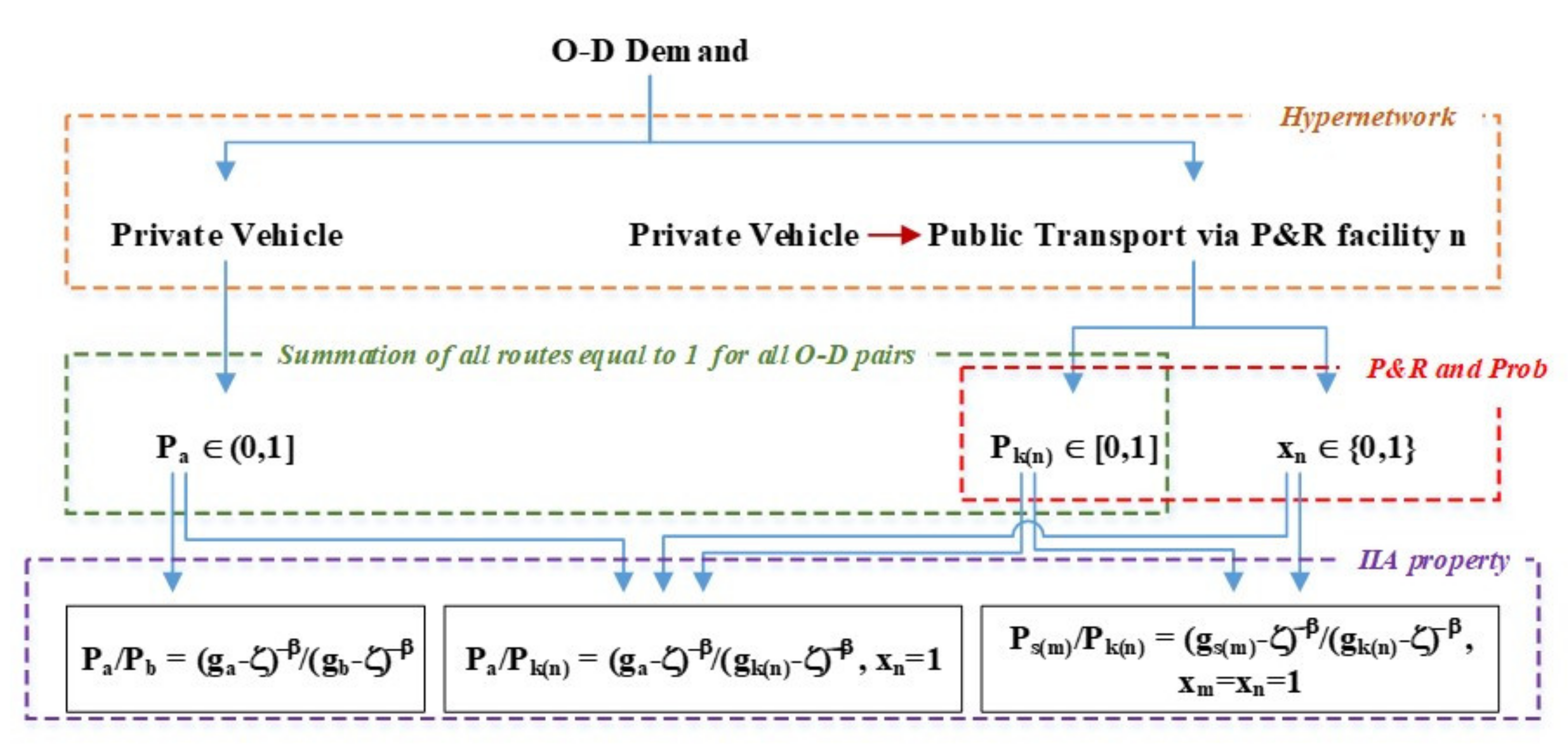
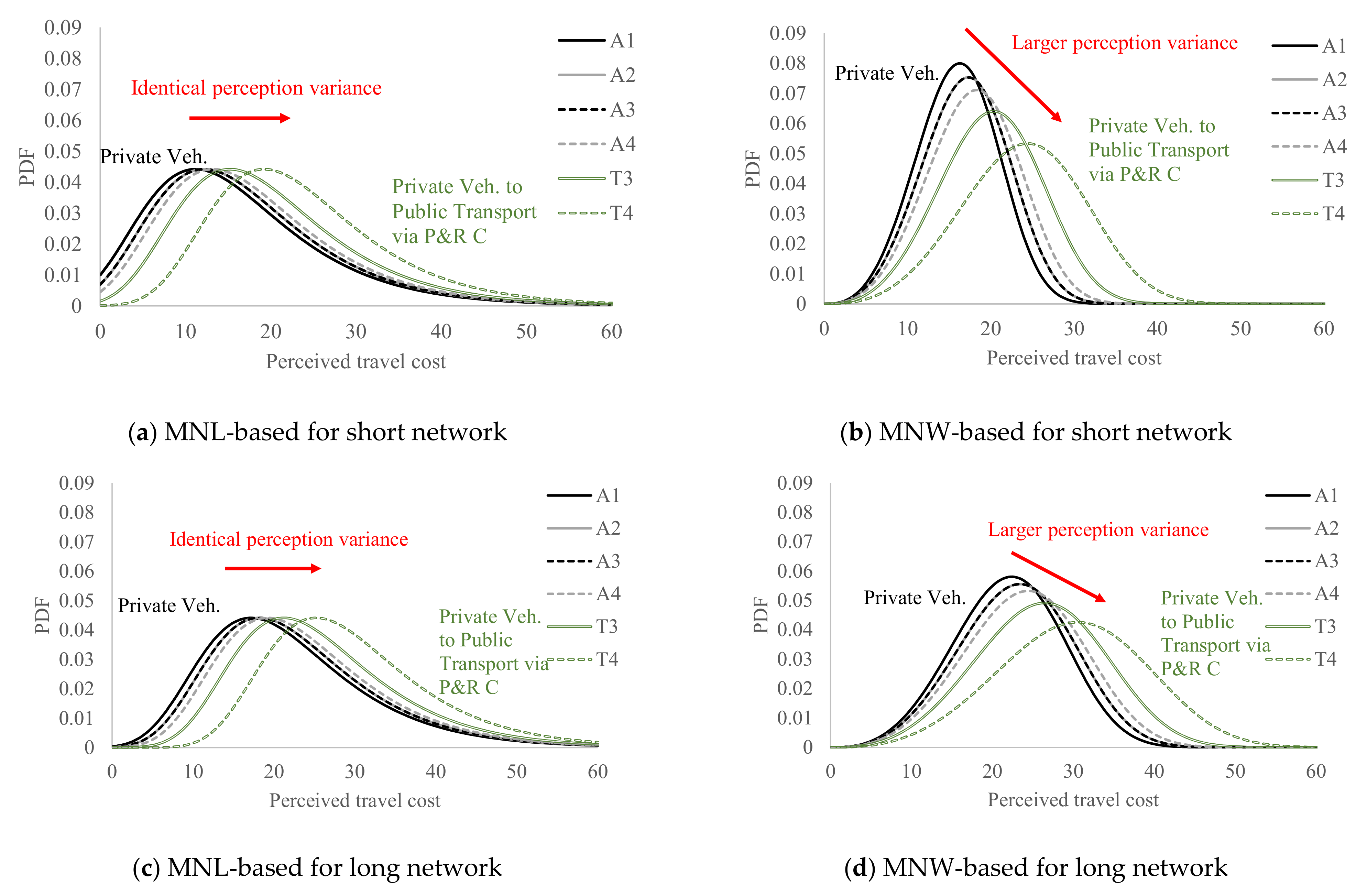
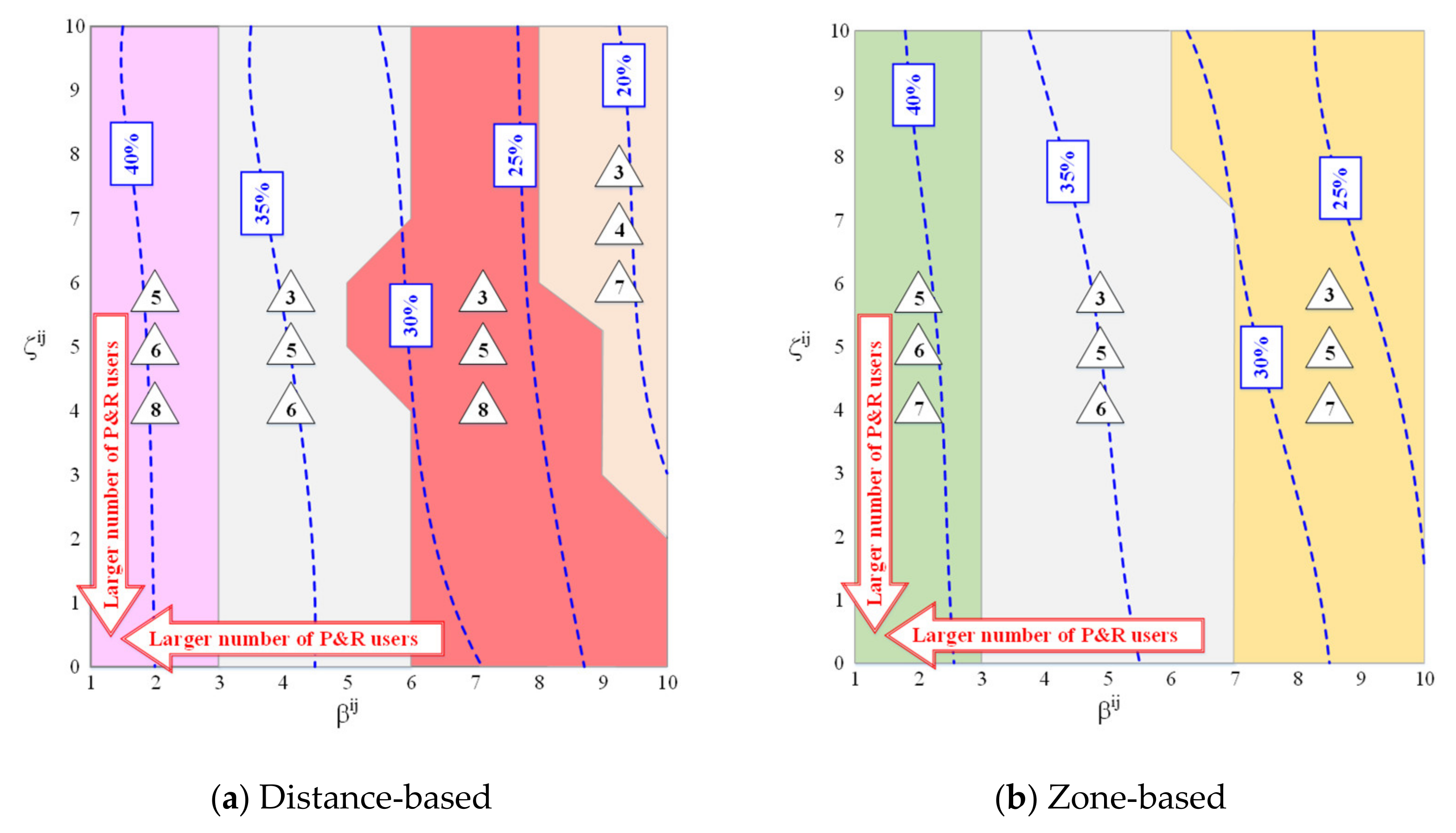
Type	Symbol	Definition
Set	IJ	Set of origin-destination (O-D) pairs
	$R_{ij}$	Set of routes between O-D pair ij∈IJ
	N	Set of potential park and ride (P&R) facility locations
	$R_{ij}^{T\left(n\right)}$	Set of public transport routes via P&R n∈N between O-D pair ij∈IJ ($R_{ij}^{T\left(n\right)}\subset R_{ij}$)
	$R_{ij}^A$	Set of auto routes between O-D pair ij∈IJ ($R_{ij}^A\subset R_{ij}$)
Variable	$P_{k\left(n\right)}^{ij}$	Probability of choosing route k∈$R_{ij}^{T\left(n\right)}$ passing through P&R n∈N between O-D pair ij∈IJ
	$P_a^{ij}$	Probability of choosing route a∈$R_{ij}^A$ between O-D pair ij∈IJ
	$x_n$	Binary variable for P&R facility at location n∈N
Parameter	θ	Multinomial Logit (MNL) model dispersion parameter
	${\beta }^{ij}$	Multinomial Weibit (MNW) model shape parameter between O-D pair ij∈IJ
	${\zeta }^{ij}$	Multinomial Weibit (MNW) model location parameter between O-D pair ij∈IJ
	$g_r^{ij}$	Travel cost on route r∈Rij between O-D pair ij∈IJ
	p	Number of P&R facilities

provides a notation list. Sets, variables, and parameters are presented. Some notations are used intensively in Section 4, especially the variables.

3. Multinomial Logit Model and Multinomial Weibit Model

This section provides some background of the multinomial Logit (MNL) model and the multinomial Weibit (MNW) model in the context of a hypernetwork.

3.1. Multinomial Logit Model

The MNL model is derived from the Gumbel distributed route perceived travel cost. Let $F_r^{ij}$ be the cumulative distribution function (CDF) for route r ∈ R_ij between O-D pair ij ∈ IJ; $g_r^{ij}$ be the mean travel cost on route r ∈ R_ij between O-D pair ij ∈ IJ; and ${({\sigma }_r^{ij})}^2$ be the variance on route r ∈ R_ij between O-D pair ij ∈ IJ.

Table 2. Gumbel distribution and its characteristics.

CDF ($F_r^{ij}$)	$1-\exp \left(-\exp \left({\theta }_r^{ij}\left(t-{\zeta }_r^{ij}\right)\right)\right)$
Mean ($g_r^{ij}$)	${\zeta }_r^{ij}-\frac{\gamma }{{\theta }_r^{ij}}$
Variance ${({\sigma }_r^{ij})}^2$	$\frac{{\pi }^2}{6{\theta }_r^{i{j}^2}}$

provides the Gumbel CDF, its mean, and its variance. The Gumbel CDF and its mean are a function of the location parameter ${\zeta }_r^{ij}$ and scale parameter ${\theta }_r^{ij}$. Meanwhile, the variance is a function of only ${\theta }_r^{ij}$. Note that γ is the Euler constant.

With the independently distributed assumption, a joint Gumbel distribution can be expressed as

$$H^{ij}={\displaystyle \prod _{r\in R_{ij}}{F}_r^{ij}}$$

(1)

The route choice probability can be determined by

$$P_r^{ij}={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{H}_r^{ij}dx}$$

(2)

where $H_r^{ij}=\partial H^{ij}/\partial x_r^{ij}$ and $x_r^{ij}$ is the random route travel cost. Following [30], we have

$$P_r^{ij}={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\theta }_r^{ij}{e}^{{\theta }_r^{ij}\left(x-{\zeta }_r^{ij}\right)}\exp \left[-{\displaystyle \sum _{k\in R_{ij}}\left(e^{{\theta }_k^{ij}\left(x-{\zeta }_k^{ij}\right)}\right)}\right]dx}$$

(3)

Setting ${\theta }_r^{ij}=\theta$ for all routes between all O-D pairs, we have

$$P_r^{ij}=\frac{\exp \left(-\theta {\zeta }_r^{ij}\right)}{{\displaystyle \sum _{k\in R_{ij}}\exp \left(-\theta {\zeta }_k^{ij}\right)}}$$

(4)

Relating ${\zeta }_r^{ij}$ to the mean route travel cost, we have the MNL model, i.e.,

$$P_r^{ij}=\frac{\exp \left(-\theta g_r^{ij}\right)}{{\displaystyle \sum _{k\in R_{ij}}\exp \left(-\theta g_k^{ij}\right)}}$$

(5)

Furthermore, the MNL model exhibits the independence of irrelevant alternatives (IIA) property [22], in which the probability ratio of each route pair is unaffected by the change in other route travel costs, i.e.,

$$\frac{P_r^{ij}}{P_l^{ij}}=\frac{\exp \left(-\theta g_r^{ij}\right)}{{\displaystyle \sum _{k\in R_{ij}}\exp \left(-\theta g_k^{ij}\right)}}/\frac{\exp \left(-\theta g_l^{ij}\right)}{{\displaystyle \sum _{k\in R_{ij}}\exp \left(-\theta g_k^{ij}\right)}}=\frac{\exp \left(-\theta g_r^{ij}\right)}{\exp \left(-\theta g_l^{ij}\right)}$$

(6)

Note that the Gumbel variance is a function of ${\theta }_r^{ij}$ alone. By setting ${\theta }_r^{ij}=\theta$ (i.e., the identically distributed assumption) in Equation (4), a closed-form probability expression for the MNL model can be derived with the following identical perception variance for all routes between all O-D pairs:

$${\left({\sigma }_r^{ij}\right)}^2=\frac{{\pi }^2}{6{\theta }^2}$$

(7)

This identical perception variance does not allow heterogeneity among the alternatives in the hypernetwork. All routes are assumed to have the same and fixed perception variance, and travelers are assumed to be insensitive to different trip lengths.

3.2. Multinomial Weibit Model

The MNW model was developed from the Weibull distribution.

Table 3. Weibull distribution and its characteristics.

CDF ($F_r^{ij}$)	$1-\exp \left[-{\left(\frac{t-{\zeta }_r^{ij}}{{\theta }_r^{ij}}\right)}^{{\beta }_r^{ij}}\right]$
Mean ($g_r^{ij}$)	${\zeta }_r^{ij}+{\theta }_r^{ij}\Gamma \left(1+\frac{1}{{\beta }_r^{ij}}\right)$
Variance ${({\sigma }_r^{ij})}^2$	${\theta }_r^{i{j}^2}\left[\Gamma \left(1+\frac{2}{{\beta }_r^{ij}}\right)-{\Gamma }^2\left(1+\frac{1}{{\beta }_r^{ij}}\right)\right]$

provides the Weibull CDF, its mean, and its variance. For the Weibull distribution, its CDF, mean, and variance are function of the location parameter ${\zeta }_r^{ij}$, scale parameter ${\theta }_r^{ij}$, and shape parameter ${\beta }_r^{ij}$, where Γ() is the Gamma function.

Following the same derivation of the MNL model, we have

$$P_r^{ij}={\displaystyle \underset{{\zeta }_r^{ij}}{\overset{+\infty }{\int }}{\beta }_r^{ij}\frac{{\left(x-{\zeta }_r^{ij}\right)}^{{\beta }_r^{ij}-1}}{{\left({\phi }_r^{ij}\right)}^{{\beta }_r^{ij}}}\exp \left(-{\displaystyle \sum _{k\in R_{ij}}{\left(\frac{x-{\zeta }_k^{ij}}{{\phi }_k^{ij}}\right)}^{{\beta }_k^{ij}}}\right)dx}$$

(8)

By setting ${\beta }_r^{ij}={\beta }^{ij}$ and ${\zeta }_r^{ij}={\zeta }^{ij}$, a closed-form probability expression for the MNW model can be expressed as follows:

$$P_r^{ij}=\frac{{\left({\theta }_r^{ij}\right)}^{{\beta }^{ij}}}{{\displaystyle \sum _{k\in R_{ij}}{\left({\theta }_k^{ij}\right)}^{{\beta }^{ij}}}}$$

(9)

Relating the scaling parameter to its mean, the MNW model can be rewritten as

$$P_r^{ij}=\frac{{\left(g_r^{ij}-{\zeta }^{ij}\right)}^{{\beta }^{ij}}}{{\displaystyle \sum _{k\in R_{ij}}{\left(g_k^{ij}-{\zeta }^{ij}\right)}^{{\beta }^{ij}}}}$$

(10)

Unlike the MNL model, setting ${\beta }_r^{ij}={\beta }^{ij}$ and ${\zeta }_r^{ij}={\zeta }^{ij}$ does not require the identically distributed assumption. Hence, the MNW model can have individual (i.e., non-identical) perception variance as follows [27,31]:

$${\left({\sigma }_r^{ij}\right)}^2=\frac{{\left(g_r^{ij}-{\zeta }^{ij}\right)}^2}{{\Gamma }^2\left(1+\frac{1}{{\beta }^{ij}}\right)}\left[\Gamma \left(1+\frac{2}{{\beta }^{ij}}\right)-{\Gamma }^2\left(1+\frac{1}{{\beta }^{ij}}\right)\right]$$

(11)

Each route in the hypernetwork has a route-specific variance as a function of mean route cost, location, and shape parameters. The larger the route cost, the higher the perception variance.

4. MNW P-Hub Problem for P&R Facility Location

In this section, we propose a mathematical programming (MP) formulation for the P&R facility location problem based on the MNW choice behavior [29]. This study considers two choice alternatives for a journey, including (1) private vehicle (or auto) and (2) public transport via a P&R facility [14,15,18]. We assume that congestion is moderate, and travelers using public transport exclusively have no impact on the two choices.

The MNW route choice probability of travelers choosing to use a P&R facility n on route k between O-D pair ij can be expressed as

$$P_{k\left(n\right)}^{ij}=\frac{x_n{(g_{k\left(n\right)}^{ij}-{\zeta }^{ij})}^{-{\beta }^{ij}}}{{\displaystyle \sum _{m\in N}{\displaystyle \sum _{r\left(m\right)\in R_{ij}^{T\left(m\right)}}{x}_m{(g_{r\left(m\right)}^{ij}-{\zeta }^{ij})}^{-{\beta }^{ij}}+}}{\displaystyle \sum _{s\in R_{ij}^A}{(g_s^{ij}-{\zeta }^{ij})}^{-{\beta }^{ij}}}}$$

(12)

where $R_{ij}^{T\left(n\right)}$ is a set of routes between O-D pair ij interchanging between private vehicles and public transport at P&R facility n∈N; $R_{ij}^A$ is a set of routes for private vehicles between O-D pair ij; and x_n is a binary variable for the P&R facility n∈N, which has route $k\left(n\right)\in R_{ij}^{T\left(n\right)}$, n∈N passing through. If P&R facility n is selected (open), x_n = 1 and $P_{k\left(n\right)}^{ij}$ ∈ (0,1]. If P&R facility n is not selected (close), x_n = 0 and $P_{k\left(n\right)}^{ij}$ = 0. On the other hand, the probability of selecting a journey from i to j with a private vehicle with the route travel cost of $g_a^{ij}$ is

$$P_a^{ij}=\frac{{(g_a^{ij}-{\zeta }^{ij})}^{-{\beta }^{ij}}}{{\displaystyle \sum _{m\in N}{\displaystyle \sum _{r\left(m\right)\in R_{ij}^{T\left(m\right)}}{x}_m{(g_{r\left(m\right)}^{ij}-{\zeta }^{ij})}^{-{\beta }^{ij}}+}}{\displaystyle \sum _{s\in R_{ij}^A}{(g_s^{ij}-{\zeta }^{ij})}^{-{\beta }^{ij}}}}$$

(13)

Consider the following MP formulation:

$$\max Z={\displaystyle \sum _{ij\in IJ}{\displaystyle \sum _{n\in N}{\displaystyle \sum _{k\left(n\right)\in R_{ij}^{T\left(n\right)}}{q}_{ij}{P}_{k\left(n\right)}^{ij}}}}$$

(14)

s.t.

$${\displaystyle \sum _{n\in N}{x}_n}=p$$

(15)

$${\displaystyle \sum _{n\in N}{\displaystyle \sum _{k\left(n\right)\in R_{ij}^{T\left(n\right)}}{P}_{k\left(n\right)}^{ij}}}+{\displaystyle \sum _{a\in R_{ij}^A}{P}_a^{ij}}=1, \forall ij\in IJ$$

(16)

$$x_n\in \left\{0,1\right\} , \forall n\in N$$

(17)

and Equations (12) and (13), where q_ij is a given travel demand between O-D pair ij. The objective function in Equation (14) is to maximize the number of P&R users, and hence reduce the overall number of private vehicles in the study area [14,15]. Equation (15) constrains the number of P&R facilities to p. Equation (16) is the route choice probability conservation and Equation (17) declares the P&R facility location decision variables are binary.

To develop a mixed integer linear program (MILP) for the above MP, Equations (12) and (13) were linearized as follows. Like the MNL model, the MNW model also exhibits the IIA property, i.e.,

$$\frac{P_r^{ij}}{P_l^{ij}}=\frac{{\left(g_r^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\displaystyle \sum _{\forall l\in R_{ij}}{\left(g_l^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}}/\frac{{\left(g_l^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\displaystyle \sum _{\forall l\in R_{ij}}{\left(g_l^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}}=\frac{{\left(g_r^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_l^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}$$

(18)

The probability $P_a^{ij}$ is always greater than zero. Meanwhile. the probability $P_{k\left(n\right)}^{ij}$ has a value between 0 to 1. This probability will be greater than 0 only if x_n = 1 as presented in Figure 1. We can state the following condition:

$$P_{k\left(n\right)}^{ij}\le x_n, \forall k\left(n\right)\in R_{ij}^{T\left(n\right)},n\in N,ij\in IJ$$

(19)

Hence, we can rewrite the probability ratio as follows:

$$P_b^{ij}=\frac{{\left(g_b^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_a^{ij} \mathrm{for} \mathrm{all} \mathrm{private} \mathrm{vehicle} \mathrm{routes}.$$

(20)

$$P_{s\left(m\right)}^{ij}=\frac{{\left(g_{s\left(m\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_{k\left(n\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_{k\left(n\right)}^{ij} \mathrm{if} x_m=1 \mathrm{and} x_n=1.$$

(21)

$$P_a^{ij}=\frac{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_{k\left(n\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_{k\left(n\right)}^{ij} if x_n=1.$$

(22)

Since the private vehicle route choice probability is greater than zero, the IIA property in Equation (20) is always satisfied. In contrast, the IIA property for the routes using the P&R facility is related to x_n. Equation (21) is satisfied only when the P&R locations m and n are both selected. If only one of them is selected, all probabilities will be zero. Similarly, Equation (22) is satisfied only when the P&R location n is selected. If not, $P_{k\left(n\right)}^{ij}$ = 0 and $P_a^{ij}$ = 0 cannot simultaneously occur. Therefore, the term (1 − x_n) was added to Equations (21) and (22) [14,15,32], and we have

$$P_b^{ij}=\frac{{\left(g_b^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_a^{ij}, \forall a,b\in R_{ij}^A,ij\in IJ$$

(23)

$$\begin{gathered} P_{s\left(m\right)}^{ij}\le \frac{{\left(g_{s\left(m\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_{k\left(n\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_{k\left(n\right)}^{ij}+\left(1-x_n\right), \\ \forall k\left(n\right)\in R_{ij}^{T\left(n\right)},s\left(m\right)\in R_{ij}^{T\left(m\right)},m,n\in N,ij\in IJ \end{gathered}$$

(24)

$$\begin{gathered} P_a^{ij}\le \frac{{\left(g_r^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_{k\left(n\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_{k\left(n\right)}^{ij}+\left(1-x_n\right), \\ \forall k\left(n\right)\in R_{ij}^{T\left(n\right)},n\in N,a\in R_{ij}^A,ij\in IJ, \end{gathered}$$

(25)

$$\begin{gathered} P_{k\left(n\right)}^{ij}\le \frac{{\left(g_{k\left(n\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_a^{ij}, \\ \forall k\left(n\right)\in R_{ij}^{T\left(n\right)},n\in N,a\in R_{ij}^A,ij\in IJ \end{gathered}$$

(26)

The maximization of the P&R users in the objective function would work with Equations (24)–(26) to obtain the MNW IIA property in Equations (21) and (22). A number of equations for each O-D pair according to Equations (23)–(26) can be determined by

$${}_{\left|R_{ij}\right|}{P}_2{-}_{\left|R_{ij}^A\right|}{C}_2=\frac{\left|R_{ij}\right|!}{\left(\left|R_{ij}\right|-2\right)!}-\frac{\left|R_{ij}^A\right|!}{2!\left(\left|R_{ij}^A\right|-2\right)!}$$

(27)

The second term is according to Equation (23) with an equal sign. Thus, under the same number of routes, the O-D with more private vehicle routes has a fewer number of equations for these constraints.

Proposition 1.

The mixed integer linear program (MILP) in Equations (14)–(17) and (19), and Equations (23)–(26) generates the maximum number of P&R facility users under the MNW travel choice behavior.

Proof. 

Assume that there are at least two routes connecting each O-D pair, one for the private vehicles only and the other for the vehicles using the P&R facility locations. We separate them into two cases: (a) x_n = 0 and (b) x_n = 1. □

Case (a): When x_n = 0, $P_{k\left(n\right)}^{ij}=0$, $P_a^{ij}\le 1$ from Equation (25), $P_{s\left(m\right)}^{ij}\le 1$ from Equation (24), and $P_a^{ij}\ge 0$ from Equation (26). With the probability conservation for each O-D pair in Equation (16) and the IIA property, we have the MNW travel choice behavior, i.e.,

$$\begin{array}{l}\frac{{\left(g_{r\left(m\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_{s\left(m\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_{s\left(m\right)}^{ij}+\cdots +\frac{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_{s\left(m\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_{s\left(m\right)}^{ij}+\hspace{0.17em}\cdots \\ +\frac{{\left(g_{s\left(m\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_a^{ij}+\cdots +\frac{{\left(g_b^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_a^{ij}+\cdots =1\\ ,\hspace{0.17em}\forall r\left(m\right),s\left(m\right)\in R_{ij}^{T\left(m\right)},m\in N,a,b\in R_{ij}^A,ij\in IJ\end{array}$$

(28)

This equation provides the MNW travel choice model in Equations (12) and (13).

Case (b): When x_n = 1, $P_a^{ij}\le \frac{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_{k\left(n\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_{k\left(n\right)}^{ij}$, $P_{k\left(n\right)}^{ij}\le \frac{{\left(g_k^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_a^{ij}$, and $P_{s\left(m\right)}^{ij}\le \frac{{\left(g_{s\left(m\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_{k\left(n\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_{k\left(n\right)}^{ij}$.

This results in the IIA property of the MNW model in Equation (18). From Equation (16),

$$\begin{array}{l}\frac{{\left(g_{r\left(n\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_{k\left(n\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_{k\left(n\right)}^{ij}+\cdots +\frac{{\left(g_{l\left(m\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_{k\left(n\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_{k\left(n\right)}^{ij}+\cdots \\ +\frac{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_{k\left(n\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_{k\left(n\right)}^{ij}+\cdots +\frac{{\left(g_{k\left(n\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_a^{ij}+\cdots ,\\ +\frac{{\left(g_{r\left(m\right)}^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_a^{ij}+\cdots +\frac{{\left(g_b^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{{\left(g_a^{ij}-{\zeta }^{ij}\right)}^{-{\beta }^{ij}}}{P}_a^{ij}+\cdots =1\\ ,\forall r\left(n\right),k\left(n\right)\in R_{ij}^{T\left(n\right)},l\left(m\right)\in R_{ij}^{T\left(m\right)},m,n\in N,a,b\in R_{ij}^A,ij\in IJ.\end{array}$$

(29)

Similarly, we have the MNW travel choice model in Equations (12) and (13). Hence, the MILP in Equations (14)–(17) and (19), and Equations (23)–(26) gives the optimum number of the P&R facility users under the MNW choice behavior. This completes the proof.

5. Numerical Results

In this section, some features of the proposed MNW-based P-hub location model for determining optimal locations of P&R facilities were investigated through two networks. A small network was used to examine the features of the MNW-based model embedded in the P-hub location model. A real-size network in the city of Chiang Mai, Thailand, was employed to test the location of P&R facilities under different fare structures. Without loss of generality, the MNL parameter θ was set to 0.1 and the MNW parameters were set as ${\beta }^{ij}$ = 3.7 and ${\zeta }^{ij}$ = 0 unless specified otherwise. IBM-ILOG CPLEX 12.10.0 [33] was used to solve the problem.

5.1. Small Network

Two small networks in Figure 2 were used to compare the MNL and MNW choice models for locating the P&R facility and investigate the effect of MNW model’s parameters. These two networks have one O-D pair from node A to node D with a travel demand of 1000 travelers and two candidate P&R facility sites at node B and node C. There are 4 private vehicle routes (on the street) and 2 routes for each P&R facility. The link travel cost is 2 units larger in the long network.

5.1.1. Comparison between MNL-Based and MNW-Based Models

We begin with a comparison between the MNW-based model and the MNL-based model [15]. With p = 1, both models give the same optimal P&R facility location at node C for both short and long networks shown in

Table 4. Optimal solution of MNL and MNW for both short and long networks.

Choice Model	Short Network		Long Network
	P&R Facility Location	Number of P&R Users	P&R Facility Location	Number of P&R Users
MNL	C	244.02	C	244.02
MNW	C	210.21	C	180.44

. According to the identically distributed assumption, the MNL-based model cannot account for the overall trip length of the two networks (i.e., the MNL probabilities only depend on the absolute cost difference in Equation (5)) and allocate the same number of P&R users to both short and long networks. On the other hand, the MNW model assigns different numbers of P&R users to the two networks. It provides a higher number of P&R users at node C in the short network due to a smaller perception variance (see Equation (11)). As reflected in Figure 3, the difference in the perceived travel cost probability density function (PDF) seems to be more obvious in the short network (Figure 3b) than in the long network (Figure 3d) for the MNW model.

5.1.2. Effect of the MNW Model Parameters

In this section, we investigate the effect of the MNW model parameters ${\beta }^{ij}$ and ${\zeta }^{ij}$) on the optimal locations of P&R facilities. It appears that the change in both parameters has no significant impact on the optimal location results in the two small networks as shown in Figure 4. The optimal location of a P&R facility remains at node C for all values of ${\beta }^{ij}$ and ${\zeta }^{ij}$. However, the number of P&R users varies as ${\beta }^{ij}$ or ${\zeta }^{ij}$ increases. In general, increasing either ${\beta }^{ij}$ or ${\zeta }^{ij}$ decreases the route perception variance and subsequently decreases the number of P&R users. Since all private vehicle routes are shorter than the routes through the P&R facility, this reduction on the route-specific perception variance would also decrease the number of P&R users.

In addition, parameter ${\beta }^{ij}$ seems to have a larger influence on the number of P&R users. From Equation (11), ${\beta }^{ij}$ governs the overall perception variance. With ${\zeta }^{ij}$= 0, the coefficient of variation (CoV) κ of all routes is solely dependent on ${\beta }^{ij}$, i.e.,

$$\kappa =\frac{{\sigma }_r^{ij}}{g_r^{ij}}=\frac{\sqrt{\Gamma \left(1+\frac{2}{{\beta }^{ij}}\right)-{\Gamma }^2\left(1+\frac{1}{{\beta }^{ij}}\right)}}{\Gamma \left(1+\frac{1}{{\beta }^{ij}}\right)}$$

(30)

The increasing ${\beta }^{ij}$ decreases the CoV κ of all routes. Meanwhile, ${\zeta }^{ij}$ affects the CoV κ of each route as follows:

$$\kappa =\frac{{\sigma }_r^{ij}}{g_r^{ij}}=\frac{\left(g_r^{ij}-{\zeta }^{ij}\right)}{g_r^{ij}\Gamma \left(1+\frac{1}{{\beta }^{ij}}\right)}\sqrt{\Gamma \left(1+\frac{2}{{\beta }^{ij}}\right)-{\Gamma }^2\left(1+\frac{1}{{\beta }^{ij}}\right)}$$

(31)

As ${\zeta }^{ij}$ > 0, the shorter route has a smaller CoV κ.

5.2. Chiang Mai Transportation Network

The Chiang Mai public transportation master plan, Thailand [34,35] shown in Figure 5 was used to demonstrate the proposed model in a real-world setting. This transportation network has 3 light rail transit (LRT) lines: red line (line 1), green line (line 2), and blue line (line 3). The service distance of each LRT line is approximately 15 km. There are 304 O-D pairs with a potential daily travel demand of 38,314 travelers using the P&R facilities in the opening year 2024. Each O-D pair has an origin outside the city and a destination in the downtown area, i.e., the central business district (CBD). Eight candidate sites are proposed for constructing the P&R facilities along the LRT corridors. The total number of routes is 1841 routes, including 1233 private vehicle routes and 608 routes for public transport via P&R facilities.

Two fare structures are under consideration for implementation: (1) distance-based and (2) zone-based. The distance-based fare has an entrance fee of 15 Baht (33 Baht is approximately 1 USD) with an additional 1 Baht for each kilometer travelled. The maximum charge for the distance-based fare is capped at 40 Baht. The zone-based fare divides the city of Chiang Mai into 3 zones. Zone 1 covers the historical area and the tourist popular spots. Zone 2 is the CBD area, including the commercial area, several universities, and high-rise residential buildings. Zone 3 is in the outskirts of the CBD with low-rise residential buildings. The fare is 10 Baht for a journey within the same zone. An additional 15 Baht is charged for a journey between zones as presented in

Table 5. Zone-based fare structure in Thai Baht.

From/To	1	2	3
1	10	25	40
2	25	10	25
3	40	25	10

.

The results of the MNL-based and MNW-based models are presented in

Table 6. Number of P&R facilities, their corresponding locations, and P&R users for the Chiang Mai transportation network under two fare structures.

p	Fare Structure	Distance-Based		Zone-Based
	Choice Model	MNL	MNW	MNL	MNW
4	P&R users	30.05%	39.53%	31.56%	40.44%
	P&R facility site	3, 5, 6, 7	3, 5, 6, 8	3, 4, 5, 7	3, 5, 6, 7
3	P&R users	28.61%	35.23%	30.06%	36.28%
	P&R facility site	3, 5, 7	3, 5, 6	3, 5, 7	3, 5, 6
2	P&R users	24.17%	27.13%	26.39%	28.81%
	P&R facility site	3, 5	3, 6	3, 5	3, 5
1	P&R users	14.84%	17.66%	14.17%	17.58%
	P&R facility site	6	6	3	6

. A larger number of P&R facilities (p) can potentially provide a higher number of P&R users. The resulting number of P&R users from the MNL-based model is less than that of the MNW-based model. The identically distributed assumption embedded in the MNL model assigns more traffic flow to the shorter routes, and most of the shorter routes are the private vehicle routes. As such, the routes passing through the P&R facilities receive less traffic flow, and hence fewer P&R users. Further, each model can result in different P&R facility locations irrespective of the fare structure scheme. The identically distributed assumption and the multiple O-D pairs are combined to generate different optimal P&R facility locations for the MNL-based and MNW-based models. This confirms that the travelers’ heterogeneity is an important factor for the P&R facility location selection [28].

In addition, each model may obtain different locations of P&R facilities under different fare structure schemes. In the distance-based fare structure, travelers need to pay more for a longer journey while they are encouraged to make a journey within the same zone for the zone-based fare structure. As a result, each fare structure scheme has different P&R users at the optimum solution shown in Figure 6. When p = 1, the P&R facility is located at site 6 for both fare structures. For p > 1, site 6 and site 5 seem to dominate in the distance-based scheme and the zone-based scheme, respectively. This is because most potential travelers are commuting from the east to the CBD. Site 6 offers a smaller travel cost to the CBD area. Meanwhile, site 5 is in zone 2, where the majority of such travelers are commuting to.

Apart from the number and locations of P&R facilities, the travel response is different for each fare structure. We use p = 3 to explain this issue through the travel distance probability density function (PDF) in Figure 7. Despite the same three P&R locations (i.e., 3, 5 and 6) being selected for both fare structures, the P&R users travel longer on the average under the zone-based fare structure. Furthermore, the travel distance variance is also higher under this fare structure. This can be explained by the fact that zone 2 covers about 20 km of the LRT network, allowing the travelers to make a journey within the CBD area without incurring an additional charge. All these results reveal that the choice model and fare structure can have a significant impact on not only the P&R facility locations but also the number of P&R users.

Next, the impact of ${\beta }^{ij}$ and ${\zeta }^{ij}$ was investigated. Unlike the small network, these MNW parameters affect the optimal solution as shown in Figure 8. The contour line presents the ratio of P&R users to the potential daily travel demand under p = 3. Both the P&R facility locations and the number of P&R users are altered when the values of ${\beta }^{ij}$ and ${\zeta }^{ij}$ are varied. A smaller value of ${\beta }^{ij}$ and/or ${\zeta }^{ij}$ tends to give a larger number of P&R users for each fare structure. However, the distance-based fare structure seems to be more sensitive to changes in ${\beta }^{ij}$ and ${\zeta }^{ij}$ than the zonal-based fare structure. This is because the MNW model can consider travelers’ heterogeneous perception variance. The difference in distance travelled is explicitly accounted for. Meanwhile, the zonal-based fare structure does not rely on the trip length, hence less impact on the MNW parameter changes.

6. Conclusions and Suggestions

This study developed a Weibit-based mathematical programming (MP) formulation to consider the park and ride (P&R) facility locations under moderate traffic congestion. The multinomial Weibit (MNW) model [29] was adopted to account for travelers’ heterogeneity. Its independence of irrelevant alternatives (IIA) property was explored and used to linearize the MNW choice probability. The numerical experiments demonstrated that the Weibit-based choice model could alleviate the homogeneous perception variance due to the identically distributed assumption embedded in the well-known multinomial Logit (MNL) model. The resulting differences between the MNL-based and MNW-based models could be presented not only from the optimal P&R facility location, but also the number of P&R users. Furthermore, a real-world case study was conducted to show the applicability of the proposed mixed integer linear programing (MILP) in a public transportation master plan in the city of Chiang Mai, Thailand. The trip-length-based route-specific perception variance in the MNW model provided a higher impact on the P&R facility location decision under a distance-based public transport fare scheme.

The number of constraints to account for the MNW IIA property increases exponentially with respect to the number of routes for each O-D pair. The correlation between the travel routes is another important factor that affects the route choice behavior [36]. Some other (route) choice models could be considered for future study, such as the cross nested Logit (CNL) model and paired combinatorial Logit (PCL) model [27,31,37,38,39]. Note that the IIA property may not hold for such models. Alternative approaches may be required. In addition, a smart parking system could be considered in the future P&R facility [40,41,42,43,44,45] as it could affect the travelers’ perception and hence the P&R facility location. To consider such travel behavior, an advanced behavioral choice model capable of accounting for the features of smart parking systems should be considered in future research [46,47,48].