Newly Elaborated Hybrid Algorithm for Optimization of Robot Arm’s Trajectory in Order to Increase Efficiency and Provide Sustainability in Production
Abstract
:1. Introduction
- (1)
- The application of industrial robots is needed in production companies in order to compensate for the lack of human resources (economic and social aspects of sustainability).
- (2)
- Industrial robots—as environmentally friendly, energy-efficient and innovative technologies—have the capability to significantly increase productivity, which results in reductions in specific production costs, including labor costs, energy costs, etc. The application of energy-efficient robots causes higher utilization of resources, energy-saving and less environmental damage (environmental and economic aspects of sustainability).
- (3)
- There are several industrial tasks for which industrial robots are more suitable than human workers, because the conditions of some workplaces can be hazardous for workers (e.g., chemical, ergonomic or physical hazards) and the safety of all workers has become a priority (social and economic aspects of sustainability) [12,13].
2. Materials and Methods
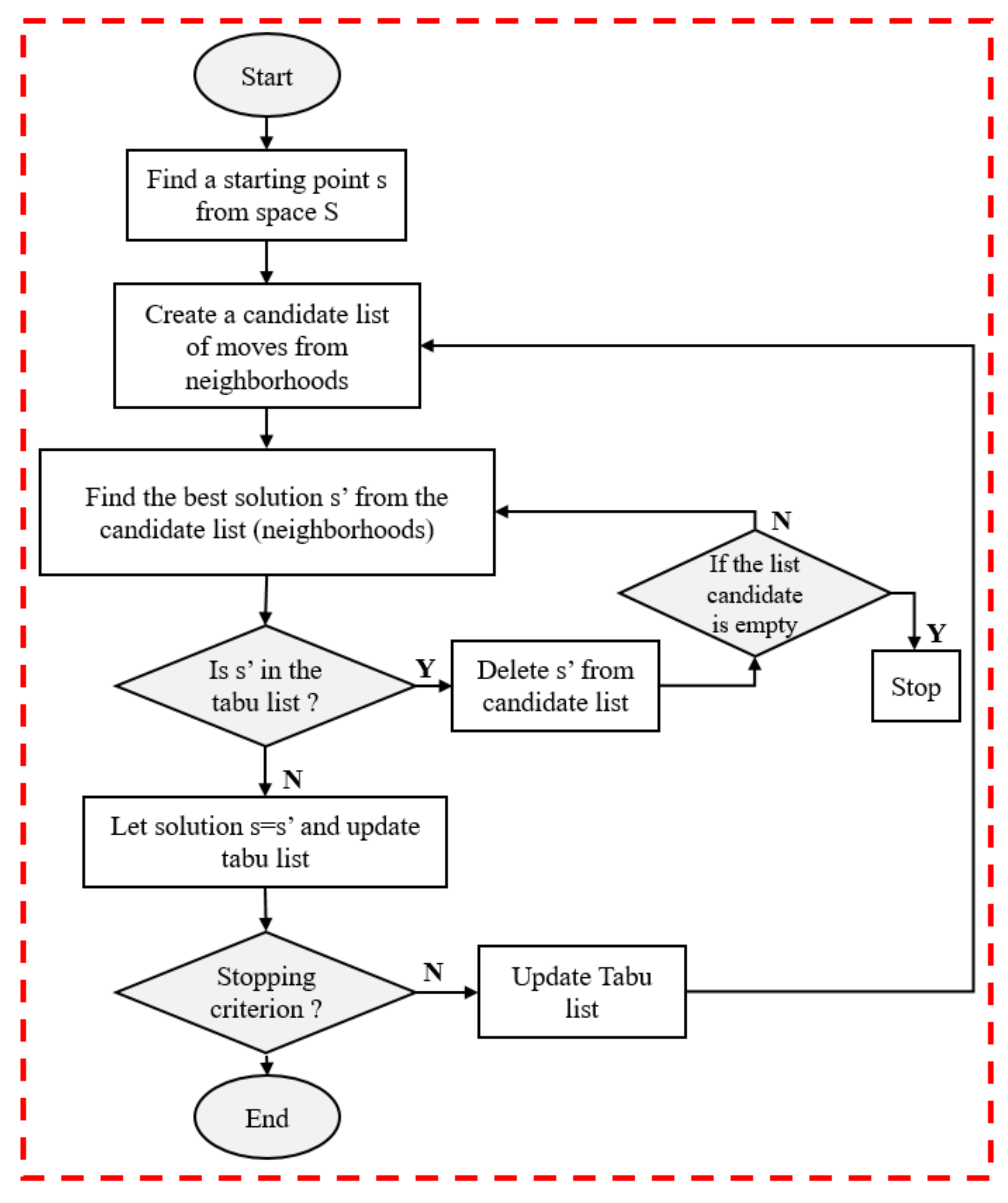
2.1. Tabu Search Algorithm Overview
3. Results—Hybrid Algorithm for Optimization of Robot Arm’s Trajectory
3.1. Tabu Search Based Hybrid Algorithm
3.1.1. Tabu Search Algorithm in Details
- 1.
- Let the initial state be n (storing a starting spline, whose ct is a large value, e.g., 1E20); let the best state found so far be n_GlobalBest, initialized by the value of n; let the TabuList be initialized with an empty list, so TabuList length tll is equal to 0; let the max value of tll be equal tllmax = 80 (this max value can be modified based on running experience); let the counter of false comparisons be cfc = 0, max value cfcmax = 80 (this max value can also be modified based on running experience); let the cycle variable k be initialized to 1; and let the maximum value of cycle variable kmax be 10,000.
- 2.
- If the stop criterion is met, return to the n_GlobalBest state, and stop.
- 3.
- Otherwise, let n_LocalBest be equal to the state having the minimal cycle time ctmin among the f() = ct values of neighbor states of n, excluding the states of the TabuList.
- 4.
- Update the TabuList with n state and let n new value be equal to n_LocalBest.
- 5.
- If (n_LocalBest.ct < n_GlobalBest.ct), then n_GlobalBest = n_LocalBest and cfc = 0; otherwise, let the counter of false comparisons be cfc = cfc + 1.
- 6.
- Increment the cycle variable k and repeat from step 2.
- A state is a record (structure) containing:
- −
- the spline from S to E through the actual internal control grid points P1,⋯, Pi,⋯, PN represented by N interpolated grid points (control points) in vector Vspline; and
- −
- the cycle time ct = f(spline) of traveling a trajectory—represented by the spline—is determined using the same f() iterative algorithm that was used to determine the minimal cycle time in whip-lashing theory [47].
- The TabuList is a vector of those tabu states that have been traversed in the search process in the last tll searching steps, where tll is the TabuList length. The state n_LocalBest among the non-tabu local neighbor states whose cycle time was the minimal ctmin is inserted in the beginning of the TabuList in the TabuList actualization step. The TabuList length is checked after insertion and if it is longer then tllmax, it is cut back to tllmax.
- The stop criterion includes three conditions:
- −
- k > kmax; OR
- −
- all neighbor states are included in the TabuList (no state to step in); OR
- −
- counter of the number of (n_GlobalBest.ct > n_LocalBest.ct) = false comparisons number cfc reaches cfcmax. (The local bests did not give a new global best in many checks.)
- The checking of the tabu condition can be simplified by handling the spline content of the used states only; the ct cycle time can be ignored.
- For the real robot, not every grid point will be used (e.g., at the border of the motion area or near obstacles), so not every neighbor state can be generated. (In the first version of the program, we supposed that the progress of the algorithm would not touch such non-existing splines.)
3.1.2. Point Insertion Method in Details
3.1.3. Grid Refinement Method in Details
3.2. Demonstration of Tabu Search Based Hybrid Optimization Algorithm in 2D
- 1.
- A lot of optimization methods and algorithms are available in the literature for trajectory optimization [27,28,29,30,31,32,33,34,35,36,37,38,39,40,42,49,50], but there cannot be found any algorithm which combines the Tabu Search Algorithm, the Point Insertion and the Grid Refinement methods simultaneously. The newly elaborated Hybrid Algorithm integrates, on the one hand, the search power of Tabu Search Algorithm [40,49,50] for the selection of the optimal trajectory from the space of possible trajectories that has the smallest cycle time. On the other hand, the Hybrid Algorithm utilizes the successive approximation of the Point Insertion and Grid Refinement algorithmic technologies to determine the optimal motion path of the robot arm more precisely [42].
- 2.
- Based on the synthesis of the existing literature, it can also be concluded that in the literature, the motion path planning and the trajectory optimization are discussed separately [27,48,52]. Different methods and algorithms are introduced in publications for the determination of the optimal motion path and the optimization of the robot arm trajectory. Although a lot of optimization algorithms are available [28,29,30,31,32,33,34,35,36,37,38,39,40], there cannot be found any algorithm which solves the two main tasks—both the trajectory optimization and the path planning tasks—in an integrated form simultaneously.
4. Discussion—Application of the Hybrid Algorithm for Optimization of Robot Arms’ Trajectory, Case Study
4.1. Parameters of the Optimization Task
- The RV-2AJ robot arm’s kinematic and dynamic properties.
- −
- The robot arm working space V, so the limiting surfaces of those points that can be reached by the gripper of the robot arm;
- −
- Vector of maximal allowed torques aT for every joint J of the robot arm.
- The object O to be conveyed.
- −
- The mass m of the O conveyed object;
- −
- The vector v that points from the gripper coordinate-system origin to the mass center of the conveyed object.
- Starting parameters.
- −
- The searched trajectory at the initial moment:
- The number N of the trajectory interpolated points including S and E (N > 2);
- coordinates of the trajectory interpolated points in a matrix ), where the coordinates of the starting point , ending point and trajectory inner points ).
- −
- Starting grid step gs.
- Stopping parameters.
- −
- Stopping criteria of Tabu Search;
- −
- Stopping criteria of the points number incrementation cycle.
4.2. Hybrid Algorithm Realization
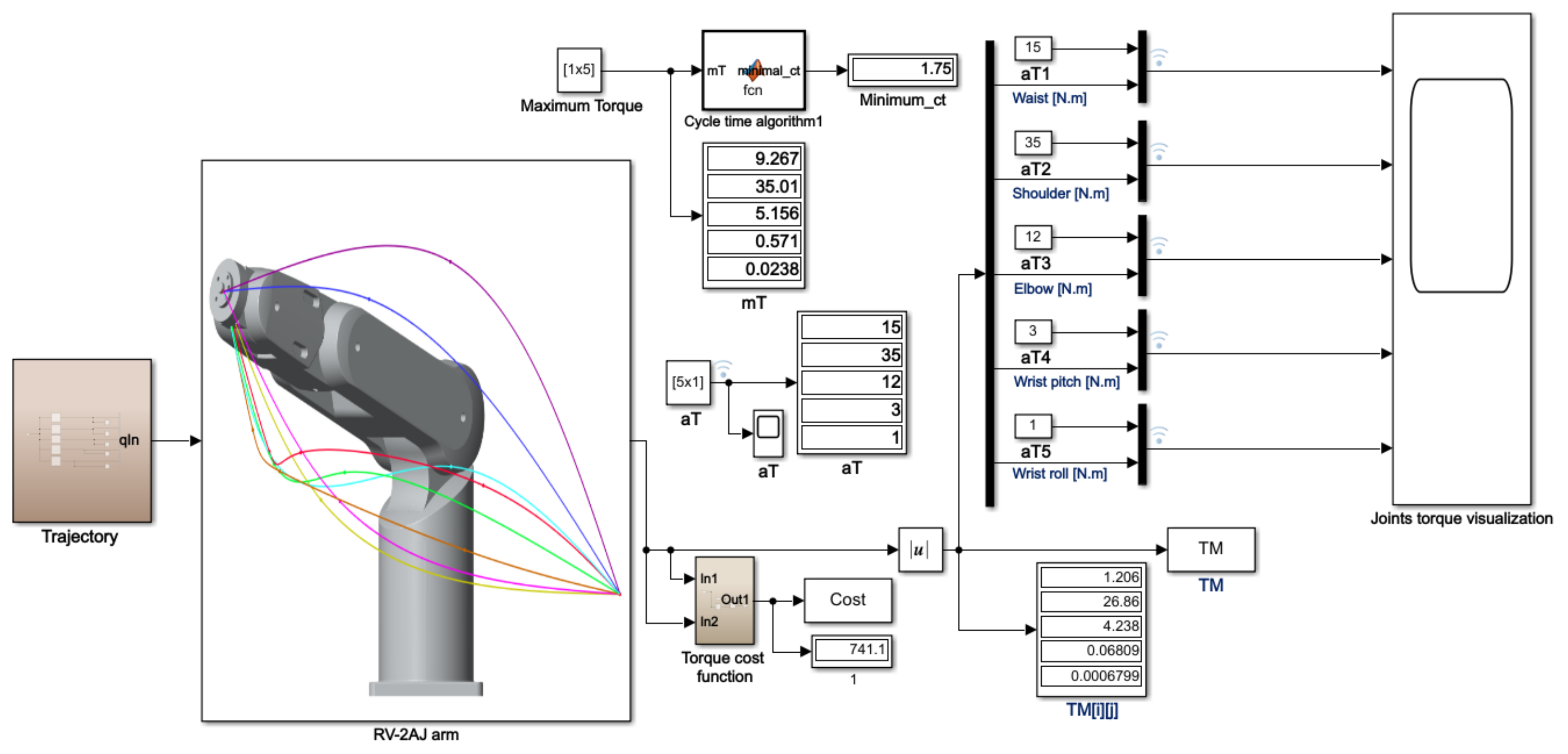
4.3. Case Study for Joints Torque Function Regarding Starting and Final Best Trajectories
- Trajectory block includes the inverse kinematic solution for the different position points connected using the spline function;
- RV-2AJ arm block includes the mechanical structure of the RV-2AJ robot arm with its given parameters and configuration;
- Torque cost function block produces the dot product of the torque matrix with its transpose, and this result can be used in the rare case that Tabu Search finds two or more trajectories with the same least cycle time, so it will choose the best one by comparing them by the minimum torque cost value;
- aT block describes the vector of allowable torques for each joint of the RV-2AJ robot arm;
- mT block describes the maximum torque in the iteration;
- Cycle time algorithm presents the core iterative algorithm of the whip-lashing theory responsible for determining the minimum cycle time (ct);
- TM (i)(j)block presents the vector of joints torque for each moment from the simulation;
- Joint torque visualization presents a scoop block that visualizes the joint torque diagrams.
5. Conclusions and Future Research
- (1)
- The findings and the results of the research and their applicability are the following:
- The authors elaborated a new Hybrid Algorithm for the optimization of a robot arm’s trajectory. This Hybrid Algorithm is based on the Tabu Search Algorithm and also uses two added methods—Point Insertion and Grid Refinement methods—simultaneously to determine that trajectory of the robot arm from the space of possible trajectories with the lowest cycle time between two given points, avoiding obstacles.
- The optimization of the robot arm’s trajectory by the application of the newly elaborated Hybrid Algorithm results in an even further reduction in cycle time and more efficient utilization of joints’ torque compared to the individual application of the Tabu Search Algorithm.
- Due to further reduction in the cycle time, the application of the new Hybrid Algorithm results in even higher efficiency improvement and provides a greater contribution to sustainable production compared to the individual application of the Tabu Search Algorithm.
- The efficiency of the Hybrid Algorithm was validated by a case study in which 32% shorter motion cycle time was obtained by the application of the new algorithm. The application of the Hybrid Algorithm was executed using MATLAB software by creating a dynamic model of a RV-2AJ Mitsubishi robot arm with 5 degrees of freedom.
- The minimization of motion cycle time causes significant increasing of the productivity in practice, which means that more final products can be produced in a given time interval. It results in the reduction of specific production costs, thereby reducing the final product’s cost. It can be concluded that the efficiency improvement results in cost saving for the production companies.
- The enterprises can use this cost saving for further development and can invest in environmentally friendly, energy-efficient technologies and equipment which can further improve sustainability in the production. In addition, smaller cycle times mean less demand against all infrastructure usage, heating and lighting of the manufacturing shop, standby time of error protection systems or readiness of special human resources such as troubleshooting teams. The gained time, energy and workforce can be used in other areas of production.
- (2)
- The main added values of the research are the following:
- The main contribution of the research is the elaboration of a new Hybrid Algorithm which can define the quasi-optimal path that has the lowest cycle time between the starting and ending points, avoiding given obstacles. This new algorithm results in an even further reduction in cycle time and more efficient utilization of joint torque compared to the individual application of the Tabu Search Algorithm.
- Further added value of the research is that the newly elaborated Hybrid Algorithm can solve the two main tasks—both the path planning task determining the best motion path and the dynamic task of the trajectory optimization using maximal allowed joint torques—in an integrated form simultaneously.
- The newly elaborated Hybrid Algorithm is an absolutely novel optimization algorithm in the recent literature and fills the previously mentioned gaps in this research field.
- (3)
- The application of the newly elaborated Hybrid Algorithm for the optimization of the robot arm’s trajectory has three main ways of contributing to sustainability in terms of environmental, social and economic aspects:
- The industrial robots—as environmentally friendly, energy-efficient and innovative technologies—have the capability to significantly increase productivity. In addition, the optimization of the robot arm trajectory by the application of the new Hybrid Algorithm results in an even further reduction in cycle time compared to the individual application of the Tabu Search Algorithm. Therefore, the shorter cycle time causes higher productivity. This efficiency improvement results in reduction of specific production costs (including labor costs, energy costs, etc.), thereby the reduction of the final product’s cost. The application of energy-efficient robots causes higher utilization of resources, energy-saving and less environmental damage.
- There are several industrial tasks for which industrial robots are more suitable than human workers, because the conditions of some workplaces can be hazardous for workers (e.g., chemical, ergonomic or physical hazards) and the safety of all workers has become a priority.
- Generally, the application of industrial robots is required at manufacturing companies in order to eliminate the lack of decreasing human resources.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Koberg, E.; Longoni, A. A systematic review of sustainable supply chain management in global supply chains. J. Clean. Prod. 2019, 207, 1084–1098. [Google Scholar] [CrossRef]
- Stock, T.; Seliger, G. Opportunities of Sustainable Manufacturing in Industry 4.0. Procedia CIRP 2016, 40, 536–541. [Google Scholar] [CrossRef] [Green Version]
- Grondys, K.; Androniceanu, A.; Dacko-Pikiewicz, Z. Energy management in the operation of enterprises in the light of the applicable provisions of the energy efficiency directive (2012/27/EU). Energies 2020, 13, 4338. [Google Scholar] [CrossRef]
- Benotsmane, R.; Kovács, G.; Dudás, L. Economic, Social Impacts and Operation of Smart Factories in Industry 4.0 Focusing on Simulation and Artificial Intelligence of Collaborating Robots. Soc. Sci. 2019, 8, 143. [Google Scholar] [CrossRef] [Green Version]
- Ghadimi, P.; Wang, C.; Lim, M.K. Sustainable supply chain modeling and analysis: Past debate, present problems and future challenges. Resour. Conserv. Recycl. 2019, 140, 72–84. [Google Scholar] [CrossRef]
- Walker, H.; Seuring, S.; Sarkis, J.; Klassen, R. Sustainable operations management: Recent trends and future directions. Int. J. Oper. Prod. Man. 2014, 34, 1–12. [Google Scholar] [CrossRef]
- Yawar, S.A.; Seuring, S. Management of Social Issues in Supply Chains: A Literature Review Exploring Social Issues, Actions and Performance Outcomes. J. Bus. Ethics 2017, 141, 621–643. [Google Scholar] [CrossRef]
- Kovács, G.; Illés, B. Development of an optimization method and software for optimizing global supply chains for in-creased efficiency, competitiveness, and sustainability. Sustainability 2019, 11, 1610. [Google Scholar] [CrossRef] [Green Version]
- Muangmee, C.; Dacko-Pikiewicz, Z.; Meekaewkunchorn, N.; Kassakorn, N.; Khalid, B. Green Entrepreneurial Orientation and Green Innovation in Small and Medium-Sized Enterprises (SMEs). Soc. Sci. 2021, 10, 136. [Google Scholar] [CrossRef]
- Szczepańska-Woszczyna, K.; Kurowska-Pysz, J. Sustainable Business Development Through Leadership in SMEs. Èkon. I Zarz. 2016, 8, 57–69. [Google Scholar] [CrossRef] [Green Version]
- Oncioiu, I.; Petrescu, A.G.; Bîlcan, F.R.; Petrescu, M.; Fülöp, M.T.; Topor, D.I. The influence of corporate governance systems on a company’s market value. Sustainability 2020, 12, 3114. [Google Scholar] [CrossRef] [Green Version]
- Benotsmane, R.; Dudás, L.; Kovács, G. Collaborating robots in industry 4.0 conception. IOP Conf. Ser. Mater. Sci. Eng. 2018, 448, 012023. [Google Scholar] [CrossRef]
- Kot, S. Sustainable Supply Chain Management in Small and Medium Enterprises. Sustainability 2018, 10, 1143. [Google Scholar] [CrossRef] [Green Version]
- Kun-Bodnár, K.; Kundrák, J.; Maros, Z. Machining of rotationally symmetric parts with abrasive waterjet cutting. IOP. Conf. Ser. Mater. Sci. 2018, 448, 012053. [Google Scholar] [CrossRef]
- Rosyidi, C.N.; Hapsari, S.N.; Jauhari, W.A. An integrated optimization model of production plan in a large steel manufacturing company. J. Ind. Prod. Eng. 2021, 38, 186–196. [Google Scholar] [CrossRef]
- Jaegler, Y.; Jaegler, A.; Mhada, F.Z.; Trentesaux, D.; Burlat, P. A new methodological support for control and optimization of manufacturing systems in the context of product customization. J. Ind. Prod. Eng. 2021, 38, 341–355. [Google Scholar] [CrossRef]
- Kundrák, J.; Karpuschewski, B.; Pálmai, Z.; Felhő, C.; Makkai, T.; Borysenko, D. The energetic characteristics of milling with changing cross-section in the definition of specific cutting force by FEM method. CIRP J. Manuf. Sci. Technol. 2021, 32, 61–69. [Google Scholar] [CrossRef]
- Lee, J.; Davari, H.; Singh, J.; Pandhare, V. Industrial Artificial Intelligence for industry 4.0-based manufacturing systems. Manuf. Lett. 2018, 18, 20–23. [Google Scholar] [CrossRef]
- Benyoucef, L.; Grabot, B. Artificial Intelligence Techniques for Networked Manufacturing Enterprises Management; Springer: London, UK, 2010. [Google Scholar]
- Karabegović, I. The role of industrial robots in the development of automotive industry in China. Int. J. Eng. Work. 2016, 3, 92–97. [Google Scholar]
- Kim, J.; Kim, S.R.; Kim, S.J.; Kim, D.H. A practical approach for minimum-time trajectory planning for industrial robots. Ind. Robot. Int. J. 2010, 37, 51–61. [Google Scholar] [CrossRef]
- Cservenák, Á. Simulation of a mobile robot’s motion. Acad. J. Manuf. Eng. 2021, 9, 80–88. [Google Scholar]
- Martínez, J.R.G.; Reséndiz, J.R.; Prado, M.Á.M.; Miguel, E.E.C. Assessment of jerk performance s-curve and trapezoidal ve-locity profiles. In Proceedings of the XIII International Engineering Congress, Santiago de Queretaro, Mexico, 15–19 May 2017; pp. 1–7. [Google Scholar]
- Liu, X.; Qiu, C.; Zeng, Q.; Li, A. Kinematics Analysis and Trajectory Planning of collaborative welding robot with multiple manipulators. Procedia CIRP 2019, 81, 1034–1039. [Google Scholar] [CrossRef]
- Fang, Y.; Hu, J.; Liu, W.; Shao, Q.; Qi, J.; Peng, Y. Smooth and time-optimal S-curve trajectory planning for automated robots and machines. Mech. Mach. Theory 2019, 137, 127–153. [Google Scholar] [CrossRef]
- Bobrow, J.E.; Martin, B.; Sohl, G.; Wang, E.C.; Park, F.C.; Kim, J. Optimal robot motions for physical criteria. J. Robot. Syst. 2001, 18, 785–795. [Google Scholar] [CrossRef]
- Gasparetto, A.; Boscariol, P.; Lanzutti, A.; Vidoni, R. Path planning and trajectory planning algorithms: A general overview. In Motion and Operation Planning of Robotic Systems; Carbone, G., Gomez-Bravo, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 29. [Google Scholar]
- Lozano-Perez, T.; Wesley, M.A. An algorithm for planning collision-free paths among polyhedral obstacles. Commun. ACM 1979, 22, 560–570. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M.; Jazar, R. Autonomous Robots Path Planning: An Adaptive Roadmap Approach. Appl. Mech. Mater. 2013, 373, 246–254. [Google Scholar] [CrossRef] [Green Version]
- Glavaški, D.; Volf, M.; Bonkovic, M. Mobile robot path planning using exact cell decomposition and potential field methods. WSEAS Trans. Circuits Syst. 2009, 8, 789–800. [Google Scholar]
- Torres, F.; Puente, S.; Díaz, C. Automatic cooperative disassembly robotic system: Task planner to distribute tasks among robots. Control Eng. Pract. 2009, 17, 112–121. [Google Scholar] [CrossRef]
- Zhu, Q.; Yan, Y.; Xing, Z. Robot Path Planning Based on Artificial Potential Field Approach with Simulated Annealing. In Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications, Jinan, China, 16–18 October 2006; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NY, USA, 2006; Volume 2, pp. 622–627. [Google Scholar]
- Beom, H.R.; Cho, H.S. A sensor-based navigation for a mobile robot using fuzzy logic and reinforcement learning. IEEE Trans. Syst. Man Cybern. 1995, 25, 464–477. [Google Scholar] [CrossRef]
- Janglová, D. Neural Networks in Mobile Robot Motion. Int. J. Adv. Robot. Syst. 2004, 1, 15–22. [Google Scholar] [CrossRef] [Green Version]
- Gerke, M. Genetic path planning for mobile robots. Proc. Amer. Control Conf. 1999, 4, 2424–2429. [Google Scholar]
- Garcia, M.P.; Montiel, O.; Castillo, O.; Sepúlveda, R.; Melin, P. Path planning for autonomous mobile robot navigation with ant colony optimization and fuzzy cost function evaluation. Appl. Soft Comput. 2009, 9, 1102–1110. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M. Sampling-Based Robot Motion Planning: A Review. IEEE Access 2014, 2, 56–77. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Glover, F. Tabu Search-Part I. ORSA J. Comp. 2019, 1, 190–206. [Google Scholar] [CrossRef] [Green Version]
- Brady, M.; Hollerbach, J.; Timothy, L.; Lozano-Pérez, T.; Mason, M.T. Robot Motion: Planning and Control; MIT Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Lewis, F.L.; Dawson, D.M.; Abdallah, C.T. Robot Manipulator Control: Theory and Practice, 2nd ed.; Marcel Dekker Inc.: New York, NY, USA, 2003. [Google Scholar]
- Sobrino, D.R.; Košťál, P.; Cagáňová, D.; Čambál, M. On the Possibilities of Intelligence Implementation in Manufacturing: The Role of Simulation. Appl. Mech. Mater. 2013, 309, 96–104. [Google Scholar] [CrossRef]
- Lin, C.; Chang, P.; Luh, J. Formulation and optimization of cubic polynomial joint trajectories for industrial robots. IEEE Trans. Autom. Control. 1983, 28, 1066–1074. [Google Scholar] [CrossRef]
- Benotsmane, R.; Kacemi, S.; Benachenhou, M.R. Calculation methodology for trajectory planning of a 6 axis manipulator arm. Ann. Fac. Eng. Hunedoara Int. J. Eng. 2018, 3, 27–32. [Google Scholar]
- Gupta, K.; Del Pobil, A.P. Practical Motion Planning in Robotics: Current Approaches and Future Directions; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Benotsmane, R.; Dudás, L.; Kovács, G. Trajectory Optimization of Industrial Robot Arms Using a Newly Elaborated “Whip-Lashing” Method. Appl. Sci. 2020, 10, 8666. [Google Scholar] [CrossRef]
- Balkan, T. A dynamic programming approach to optimal control of robotic manipulators. Mech. Res. Commun. 1998, 25, 225–230. [Google Scholar] [CrossRef]
- Glover, F.; Laguna, M. Tabu search principles. In Tabu Search; Springer: Boston, MA, USA, 1997; pp. 125–151. [Google Scholar]
- Alshibli, M.; El Sayed, A.; Kongar, E.; Sobh, T.M.; Gupta, S.M. Disassembly Sequencing Using Tabu Search. J. Intell. Robot. Syst. 2016, 82, 69–79. [Google Scholar] [CrossRef]
- Perutka, K. MATLAB for Engineers—Applications in Control, Electrical Engineering, IT and Robotics; Intech: Rijeka, Croatia, 2011. [Google Scholar]
- Cao, B.; Dodds, G.I. Time-optimal and smooth joint path generation for robot manipulators. In Proceedings of the International Conference on Control—Control ’94, Coventry, UK, 21–24 March 1994; pp. 1122–1127. [Google Scholar]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benotsmane, R.; Dudás, L.; Kovács, G. Newly Elaborated Hybrid Algorithm for Optimization of Robot Arm’s Trajectory in Order to Increase Efficiency and Provide Sustainability in Production. Sustainability 2021, 13, 8193. https://doi.org/10.3390/su13158193
Benotsmane R, Dudás L, Kovács G. Newly Elaborated Hybrid Algorithm for Optimization of Robot Arm’s Trajectory in Order to Increase Efficiency and Provide Sustainability in Production. Sustainability. 2021; 13(15):8193. https://doi.org/10.3390/su13158193
Chicago/Turabian StyleBenotsmane, Rabab, László Dudás, and György Kovács. 2021. "Newly Elaborated Hybrid Algorithm for Optimization of Robot Arm’s Trajectory in Order to Increase Efficiency and Provide Sustainability in Production" Sustainability 13, no. 15: 8193. https://doi.org/10.3390/su13158193
APA StyleBenotsmane, R., Dudás, L., & Kovács, G. (2021). Newly Elaborated Hybrid Algorithm for Optimization of Robot Arm’s Trajectory in Order to Increase Efficiency and Provide Sustainability in Production. Sustainability, 13(15), 8193. https://doi.org/10.3390/su13158193





