Next Article in Journal
Field and Numerical Study on Deformation and Failure Characteristics of Deep High-Stress Main Roadway in Dongpang Coal Mine
Previous Article in Journal
Decarbonizing the Cold Chain: Long-Haul Refrigerated Deliveries with On-Board Photovoltaic Energy Integration
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sustainability
Volume 13
Issue 15
10.3390/su13158488
sustainability-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effects of Water-Saving Irrigation on Hydrological Cycle in an Irrigation District of Northern China

by
Manfei Zhang
1,2,
Xiao Wang
1,2 and
Weibo Zhou
1,2,*
1
School of Water and Environment, Chang’an University, Xi’an 710054, China
2
Key Laboratory of Subsurface Hydrology and Ecological Effects in Arid Region, Chang’an University, Xi’an 710054, China
*
Author to whom correspondence should be addressed.
Sustainability 2021, 13(15), 8488; https://doi.org/10.3390/su13158488
Submission received: 28 April 2021 / Revised: 27 June 2021 / Accepted: 30 June 2021 / Published: 29 July 2021
Browse Figures
Versions Notes

Abstract

:
In an arid and semi-arid irrigation district, water-saving practices are essential for the sustainable use of water resources. The Soil and Water Assessment Tool (SWAT) was used to simulate hydrological processes under three water-saving scenarios for the Jinghui Canal irrigation district (JCID) in Northwest China. Due to the lack of available hydrometric stations in the study area, the model was calibrated by Moderate Resolution Imaging Spectroradiometer Global Evaporation (MOD16) from 2001 to 2010 on monthly scale. The simulation results showed that using MOD16 to calibrate the SWAT model was an alternative approach when hydro-meteorological data were lacking. It also revealed that the annual average surface runoff (SURQ) decreased by 4.13%, 8.37% and 12.08% and the percolation (PERC) increased by 3.67%, 7.59% and 11.19%, with the improvement of the water-saving degree (the effective utilization coefficient of irrigation water (EUCIW) increased by 0.1, 0.2 and 0.3). Compared with the above two components, the change in actual evapotranspiration (ET) was not obvious. From the perspective of the spatial scale, the changes in every component in the east regions were generally greater than those in the west regions. On a monthly scale, the change in every component was mainly during these two periods. The analysis results of water balance in the study area showed that the proportion of SURQ in water balance decreased (from 14.02% to 12.33%), while that of PERC increased (from 10.99% to 12.22%) after the application of the water-saving irrigation. The decrease in the variation in soil water content indicates that the improvement of the water-saving degree plays a positive role in maintaining the sustainable development of water resources in irrigated areas. This study demonstrates the potential to use remotely sensed evapotranspiration data for hydrological model calibration and validation in a sparsely gauged region with reasonable accuracy. The results of this study also provide a reference for the effect of water-saving irrigation in the irrigated area.

1. Introduction

Water is one of the essential natural resources for social and economic development. Global water resources are becoming increasingly vulnerable due to escalating water demand resulting from population growth, expanding industrialization and increased food production on account of varied human activities, climate and land use change impacts [1,2]. In semi-arid northwest China, the irrigation water use accounts for more than 80% of the total water consumption [3,4]. The overexploitation of water resources has led to serious eco-environmental problems (e.g., soil salinization and water quality degradation), especially in large-scale irrigation districts that play a significant role in satisfying food demands [5]. Unreasonable water management and decreasing water resources have led to conflicts of water uses among different economic sectors (e.g., agriculture vs. industry) and different parts of the region [6,7]. Therefore, it is urgent to implement effective measures to ensure the sustainable utilization of water resources.
One of the effective ways to relieve the contradiction between water supply and demand is to develop water-saving irrigation [8]. However, the application of water-saving irrigation can affect the regional hydrological cycle. A great deal of research has been committed to evaluating the impacts of water-saving measures on various hydrological cycle components. For instance, Mermoud et al. (2005) [9] established a 1-D vadose zone model to assess the impacts of different irrigation schedules and found that a decrease in the irrigation frequency resulted in an increase in transpiration, but a decrease in evaporation. Based on a groundwater balance model in the Yichang irrigation sub-district, the largest irrigation sub-district in the Hetao irrigation district, Yue et al. (2016) [10] assessed the impacts of water-saving on groundwater balance and the results showed that the application of water-saving measures conjunctively could result in a reduction in surface water diversions by up to 52% relative to the situation without any water-saving measures. By employing a MIKE-SHE model, Jiang et al. (2016) [11] analyzed the effects of water-saving irrigation on groundwater and revealed that increasing water-saving irrigation resulted in a decrease in groundwater level. Zhang et al. (2014) [12] implemented comprehensive observations of water balance components in an irrigated cropland of a typical oasis within the Tarim river basin and found that the groundwater dynamics were significantly altered by the application of water-saving irrigation. Most studies on effects of water-saving irrigation on the hydrological cycle were focused on groundwater. There are few quantitative studies on the multiple components of the hydrological cycle of irrigation district under the influence of water-saving irrigation, especially on surface hydrological cycle components.
In terms of research methods, the SWAT model has been proposed as a tool for estimating hydrological components including surface runoff [13,14,15], evapotranspiration (ET) [16,17], soil moisture [18,19,20], groundwater [21,22], and the amount of water divided from rainfall to runoff, evapotranspiration and groundwater [23,24]. Therefore, this study selected the SWAT model to construct a simulation model for the study area.
Generally, the SWAT model is calibrated using a few hydro-meteorological stations [22,23,24]. However, obtaining hydro-meteorological data is quite difficult in some ungauged areas. Therefore, to obtain credible model parameters and to better simulate watershed hydrological processes, it is necessary to perform the model auto-calibration procedure with other spatially heterogeneous observation data.
ET is one of the most important components of water balance, since changes in it would affect the whole water cycle. With the development of remote sensing, ET data are no longer difficult to obtain. With the help of remote sensing technology, energy data relating to the soil–vegetation–air interface can be extracted, and then combined with site-based meteorological data to calculate the regional ET based on the traditional algorithm [25]. Recently, many regional ET models have been developed, for example, the Reg model [26], Priestley–Taylor jet propulsion laboratory model (PT-JPL) [27], the Moderate Resolution Imaging Spectroradiometer Global Evaporation (MOD16) [28], and Global Land surface Evaporation Amsterdam Methodology (GLEAM) [29]. These datasets can be directly used to calibrate and validate hydrological models. For example, Immerzeel and Droogers (2008) [30] used a remote sensing-derived ET (based on MODIS data and the SEBAL model) to calibrate a SWAT in a catchment of the Krishna basin in Southern India and obtained an obvious credible performance. Rafiei Emam et al. (2017) [31] calibrated a SWAT model based on river discharge, actual evapotranspiration using MODIS products and crop yield in the A-Luoi district in Thua Thien Hue province of Vietnam. The results showed that the ET product of MODIS can be used for the calibration of the hydrological model in case of data scarcity. Ha et al. (2018) [32] used the ET and leaf area index to calibrate a SWAT model in the Day basin, which is a sub-basin of the transboundary Red River basin. Parajuli et al. (2017) [33] applied MOD16 ET data to evaluate the SWAT calibration. They demonstrated the use of satellite-based ET data to evaluate the SWAT performance, which can be applied in watersheds with a lack of meteorological data. In these studies, satellite-based ET data were used to optimize the hydrological model parameters, and the simulated results of the actual ET were good. Therefore, satellite-based ET datasets can be introduced to calibrate the SWAT model in some regions with scarce data.
Jinghui Canal irrigation district (JCID), located in Guanzhong basin of northwest China, is a representative canal-well combined irrigation area and also a major grain producing area in Shaanxi province. The water management here is crucial to sustainable development. The objectives of this paper are as follows: (1) introducing MOD16 to calibrate the SWAT model and simulating the hydrological cycle components including precipitation (PREC), surface runoff (SURQ), actual evapotranspiration (ET) and percolation (PERC) of JCID from 2001 to 2010; (2) evaluating the spatial and temporal dynamics of the hydrological cycle components; (3) assessing the impacts of water-saving irrigation on the hydrological cycle components. The results can provide a strong reference basis for the reasonable utilization of water resources in JCID and other similar regions.

2. Methods

2.1. Study Area

The JCID lies at a longitude of 108°34′34″ to 109°21′35″ N and latitude of 34°25′20″ to 34°41′40″ E in Shaanxi province, China (Figure 1). It has a total area of 1180 km2, including four counties (Jingyang, Gaolin, Sanyuan and Fuping) and two districts (Yanliang and Lingtong). The study area is surrounded by the Jing river, Wei river and Shi Chuan river. The Yeyu river and Qingyu river are distributed inside of the JCID. All of them flow into the Wei river at the eastern and southern parts of the study area. JCID is located in the continental semi-arid climate regions. The average annual precipitation is about 538.9 mm, approximately 50 to 60 percent of which occurs in summer (from June to August). The average annual temperature is 13.4 °C.
One of the irrigation water resources of JCID is the Jing river, which has an average annual runoff of 17.4 × 108 m3. Another irrigation water resource is the groundwater from unconfined aquifer. 29 irrigation ditches are distributed inside the study area, among which five ditches are the main ditches and 24 are the branch ditches (Figure 1). Figure 2 displays the runoff of Jing River, irrigation water and average groundwater depth over the JCID from 2001 to 2010. Under the condition that the runoff of the Jing river decreases and the groundwater depth increases, the irrigation water still increases. This indicates that it is necessary to further improve the degree of water-saving irrigation to ensure that the increase in groundwater depth can be restrained while meeting the irrigation requirements, which is conducive to the sustainable development of water resources in the irrigated areas.
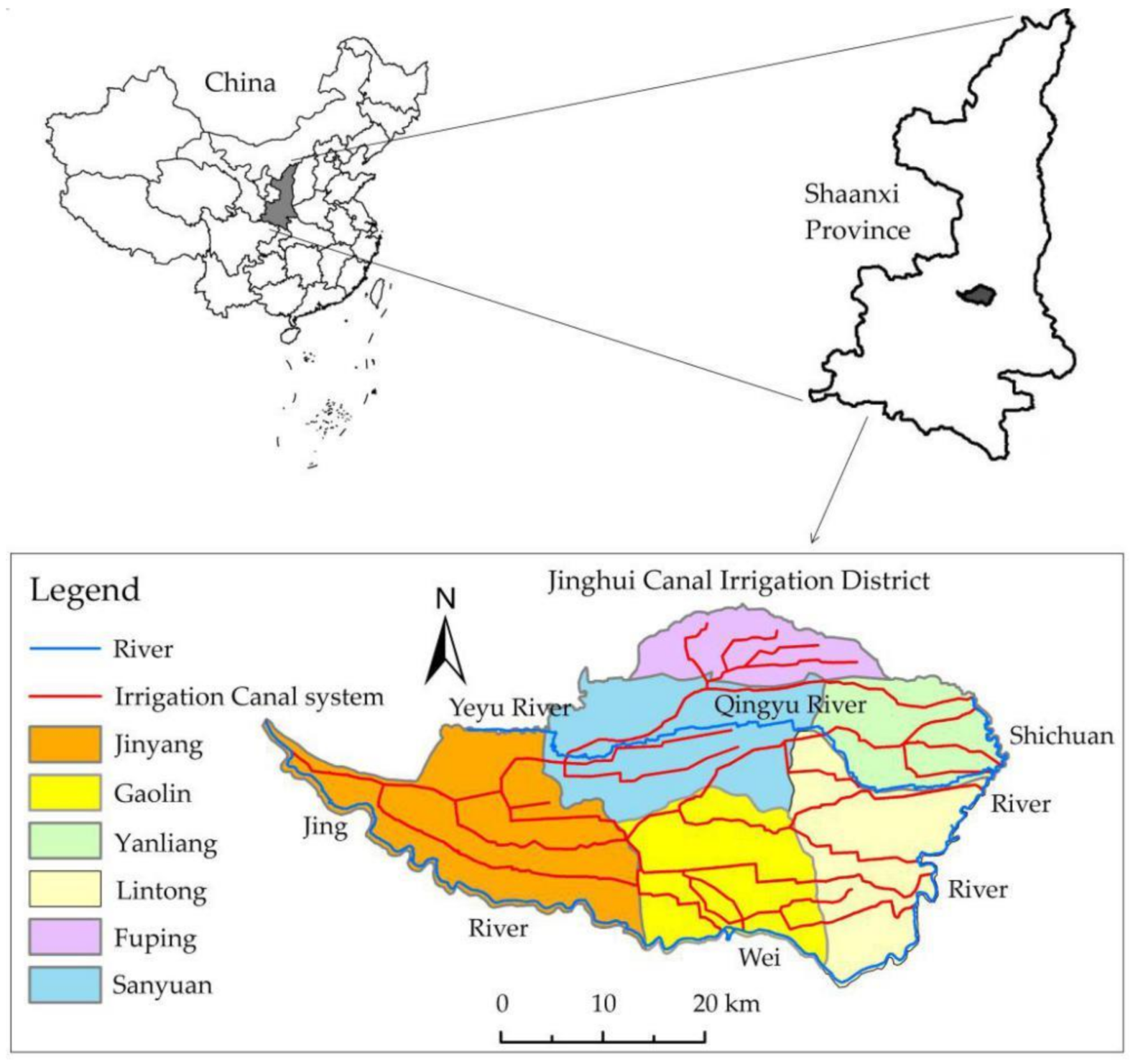
Wheat and corn are the main irrigated crop, whose planting areas account for 70% of the total planting area in the irrigation area.

2.2. Soil and Water Assessment Tool

The Soil and Water Assessment Tool (SWAT) [34] is a semi-distributed hydrological model, developed to forecast the impact of long-term land management measures on water, sediment and agricultural pollutants within a complex basin, containing multiple soil, land use and management conditions [35]. A watershed is divided into several sub-watersheds based on the topography, which are then subdivided into hydrologic response units (HRUs) based on the unique soil, land use and slope characteristics. The main module of this model includes climate, hydrology, soil temperature and attributes, plant growth nutrients, pesticides and land management [34,36].
A comprehensive description of the model can be found in a previous study [35]. According to the water-balance principle, the soil water balance in a SWAT can be described as:
S W t = S W 0 + ∑ i = 1 t R d a y − Q s u r f − E T a − W s e e p − Q g w
where t is the time (days), SWt is the final soil water content (mm), SW0 is the initial soil water content on day i (mm), Rday is the amount of precipitation on day i (mm), Qsurf is the amount of surface runoff on day i (mm), ETa is the amount of evapotranspiration on day i (mm), Wseep is the amount of water entering the vadose zone from the soil profile on day i (mm), and Qgw is the amount of return flow on day i (mm).

2.3. Input Datasets

2.3.1. Physiographical Maps

The Digital Elevation Model (DEM) is downloaded from the Geospatial Data Cloud (http://www.gscloud.cn/, accessed on 13 December 2020) with a resolution of 30 m (Figure 3a). The elevations of the study area range from 219 m to 680 m and nearly 90% of the total area range from 324 m to 444 m.
According to the DEM and the irrigation canal system, the JCID has been divided into 52 sub-watersheds (Figure 3a).
Land use data for 2003 were obtained from Landsat7 ETM data through human-computer interactive interpretation with a spatial resolution of 30 m (Figure 3b). Five types of land use are included in the study area, of which 62.32% is agricultural land (AGRL), 26.92% is residential-medium density land (URMD), 1.54% is water (WATR), 9.20% is pasture (PAST) and only 0.02% is covered by forest (FRST).
The soil map is obtained by clipping the Chinese Soil Database (V1.1) [37], which is based on the World Soil Database (HWSD) with a scale of 1:1,000,000 and a spatial resolution of 1 km (Figure 3c). Seven types of soil are distributed in the study area. The predominant soil is Fimic Anthrosols (46.80%), followed by Culumic Anthrosols (29.15%), Calcaric Fluvisols (17.85%), Calcaric Cambisols (2.95%), Gleyic Cambisols (2.76%) and Salic Fluvisols (0.50%).

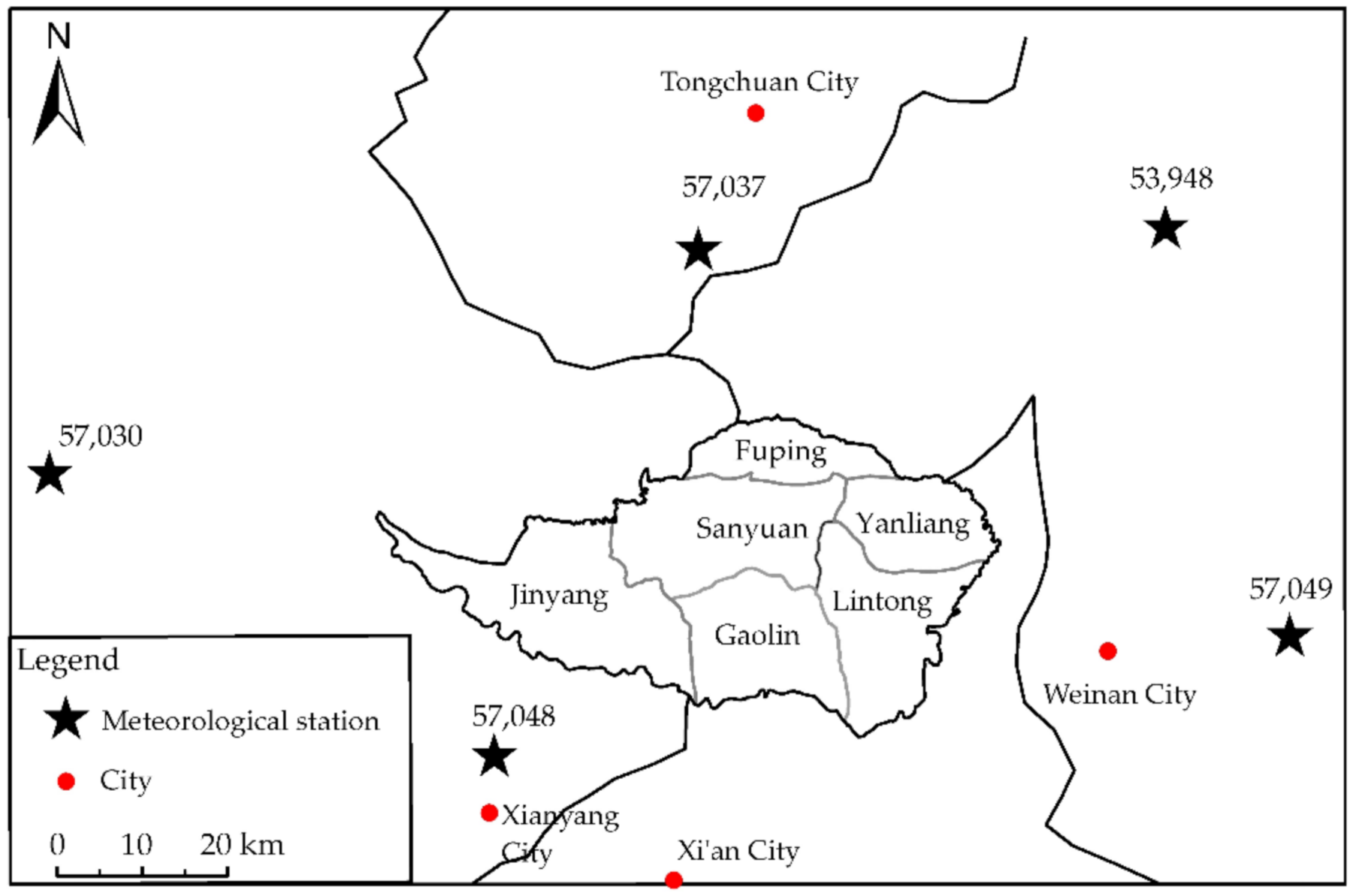
2.3.2. Meteorological Data

The meteorological data selected in this research are from the Daily Datasets of Surface Climate Data in China (V3.0), which are obtained from National Meteorological Information Center (https://data.cma.cn/, accessed on 16 December 2020). These datasets contain data from 699 basic meteorological stations in China, and include the daily data of air pressure, temperature, precipitation, evaporation, relative humidity, wind speed, and sunshine hours since January 1951. In this study, 5 traditional weather stations are selected to force the SWAT model (Figure 4).

2.3.3. Irrigation Data

The irrigation water in JCID is drawn from groundwater and water diversion from Jing River via an irrigation canal system including 5 main ditches and 24 branch ditches as shown in Figure 1. According to the collection and integrity of irrigation data obtained from Shaanxi Jinghui Canal Irrigation Administration, the irrigation measures from 2001 to 2010 are shown in Table 1. The irrigation data include the canal irrigation quantity and the well irrigation quantity of every year. In every selected year, the irrigation periods were divided into winter irrigation, spring irrigation and summer irrigation.
The final manifestation of water-saving reconstruction in irrigated areas is the influence on the irrigation efficiency. In China, effective utilization coefficient of irrigation water (EUCIW) was widely used to characterize the irrigation efficiency. It is a comprehensive technological efficiency indicator that reflects the quality of irrigation projects, the level of irrigation technology, and the level of water management, which generally refers to the ratio of the amount of water available for crop use by irrigation in the field and the total amount of water introduced by the canal head [38]. “Water available for crop use by irrigation in the field” refers to the change (increase) of soil moisture content in the soil root zone before and after irrigation [39]. That is to say, the higher the EUCIW value is, the more the increase in soil moisture content in the soil root zone after irrigation is, the higher the water-saving degree is. Therefore, the influence of water-saving reconstruction on the hydrological cycle can be simulated by changing the EUCIW.
In practice, the EUCIW can be increased by improving the anti-seep standards of the irrigation canals to decreasing the loss water through canal leakage in the process of water transportation. It also can be increased by changing the irrigation methods from the present surface irrigation to sprinkler irrigation, microspray irrigation and low pressure pipe irrigation to increasing the infiltration of irrigation water and preventing its confluence to the surface runoff. In fact, the above two methods had already began to be implemented. Under the present situation, the values of EUCIW (EUCIW0) which were obtained from Shaanxi Jinghui Canal Irrigation Administration changed from 0.522 in 2001 to 0.537 in 2010 as shown in Table 1. However, it is clearly that the water-saving degree of the irrigated area was not high enough at the time, as shown as Figure 2. Thus, it is necessary to continue to increase EUCIW to improve the water-saving degree of the irrigated area.
However, the effect of improving the water-saving degree via increasing EUCIW on the hydrological cycle at irrigation district level must be analyzed before making the relevant water-saving projects operational. Thus, three water-saving scenarios was set and described as follows:
Scenario 1: Based on the present situation, EUCIW was increased by 0.1 to improved the water-saving degree (EUCIW1 = EUCIW0 + 0.1).
Scenario 2: Based on Scenario 1, EUCIW was increased by 0.1 again to improved the water-saving degree (EUCIW2 = EUCIW0 + 0.2).
Scenario 3: Based on Scenario 2, EUCIW continued to increase by 0.1 to further improved the water-saving degree (EUCIW3 = EUCIW0 + 0.3).

2.3.4. Model Setup

Except the Qingyu river, all the other rivers are distributed at the edge of the irrigation area. Irrigation mainly depends on the irrigation canal system. Thus, the irrigation canal system was directly used to replace the natural water system, and then the irrigation area was divided into 52 sub-basins by the DEM-based method (Figure 3a). According to the distribution of land use classes, soil types and land slope, the 52 sub-basins were further subdivided into 364 HRUs. Next, a distributed hydrological model was established for JCID based on meteorological data and relevant irrigation data.

2.3.5. Model Calibration

Since there is no available hydrometric station in the study area, the calibration of the SWAT model was performed by comparing the SWAT modeled evapotranspiration (ETSWAT) with the actual evapotranspiration (ETa). In this paper, MOD16 was introduced as ETa, which is the most common global scale ET dataset. It is based on energy balance models and uses remote sensing data as the input. According to the regular arrangement of the satellite orbit number and the location of the study area, the relevant satellite orbit numbers (h26v05 and h27v05) were selected and downloaded online (http://files.ntsg.umt.edu/data/NTSG_Products/MOD16/, 21 December 2020) from 2001 to 2010 on a monthly scale. ETa was further extracted from MOD16 products and summarized in each sub-basin using ARCGIS (developed by Environmental Systems Research Institute Inc., Redlands, CA, USA).
The Sequential Uncertainty Fitting Algorithm (SUFI-2) is a frequently used and effective method for parameter calibration and uncertainty analysis [40,41]. SUFI-2 is based on a stochastic procedure for drawing independent parameter sets using Latin Hypercube sampling (LHS). A global sensitivity analysis based on the multiple regression method [42] was implemented, in which parameter sensitivities are determined by numerous rounds of LHS to obtain the most sensitive parameters by examining the resulting p-value and t-stat value. The t-stat provides a measure of sensitivity (larger values are more sensitive), and the p-value determines the significance of the parameters (the smaller the value, the more important the parameter). According to the theory of the SUFI-2 method, parameter uncertainties are expressed as the 95% prediction uncertainty (95 PPU), which is calculated at the 2.5% and 97.5% levels of the cumulative distribution of output variables through Latin hypercube sampling [43]. Two indicators were used to quantify the fit between the simulation result and observation value. One was the P-factor, which was the percentage of the observed data enveloped by the modeling result. Another one was the T-factor, which referred to the thickness of the 95PPU envelop. Theoretically, when the P-factor is 1, and the R-factor is 0, the modeling result exactly corresponds to the measured data.
Among the various evaluation indicators allowed in SUFI-2, the correlation coefficient (R2), percent bias index (PBIAS) and Nash–Sutcliffe coefficiency index (NSE) were selected.
The R2 is the percent of variance explained by the model. It represents the percentage of the variance in the measured data explained by the simulated data. R2 is computed as shown in Equation (2).
R 2 = ∑ i = 1 n O i − O ¯ M i − M ¯ ∑ i = 1 n O i − O ¯ 2 ∑ i = 1 n M i − M ¯ 2 2
where Mi and Oi represent the ith simulated and observed ET, M ¯ and O ¯ represent the mean value of the simulated and observed ET, and n is the total number of observations.
The PBIAS is the deviation of data being evaluated expressed as a percentage. It measures the average tendency of the simulated data to be larger or smaller than the observations [44]. Negative values indicate model overestimating and positive values indicate model underestimating. It ranges from −∞ to +∞, where low magnitude values indicate better simulations. It is computed in percentage terms, as shown in Equation (3).
P B I A S = ∑ i = 1 n M i − O i ∑ i = 1 n O i × 100
where Mi and Oi represent the ith simulated and observed ET, and n is the total number of observations.
The NSE quantifies the relative magnitudes of the residual variance compared to the measured data variance. It indicates how close the plots of the observed vs. the simulated data are to the 1:1 line. NSE ranges from −∞ to 1, and NSE of 1 represents the optimal value. NSE is computed as shown in Equation (4).
N S E = 1 − ∑ i = 1 n O i − M i 2 ∑ i = 1 n O i − O ¯ 2
where Mi and Oi represent the ith simulated and observed ET, O ¯ represent the mean value of the observed ET, and n is the total number of observations.
For R2, the best computed result can be obtained when it is 1. If R2 is less than 1, the closer it is to 1, the better the simulation is. The assessment standards of the other two indicators [43,45] are described in Table 2.
The calibration and validation of the SWAT in this study were performed by using the SWAT Calibration Uncertainty Procedures (SWAT-CUP) which combine the SUFI-2 with the SWAT [46]. For the calibration period, the model was run using meteorological data from 2001 to 2005 as the input, while the validation was conducted from 2006 to 2010.
During the model calibration, five iterations with 500 simulations each were performed. Based on the previous studies, 16 calibrated parameters were chosen [32,47,48], shown in Table 3. SOL_Z, SOL_AWC, SOL_BD, SOL_K and GWQMN were direct influencing factors of soil moisture change. CANMX, GW_REVAP, REVAPMN, ESCO, ESPO and SOL_ALB affected ET directly. Other parameters, including CN2, SURLAG, OV_N and ALPHA_BF, were selected because of their influences on the surface-subsurface hydrological processes and on the water availability for ET.

3. Results and Discussion

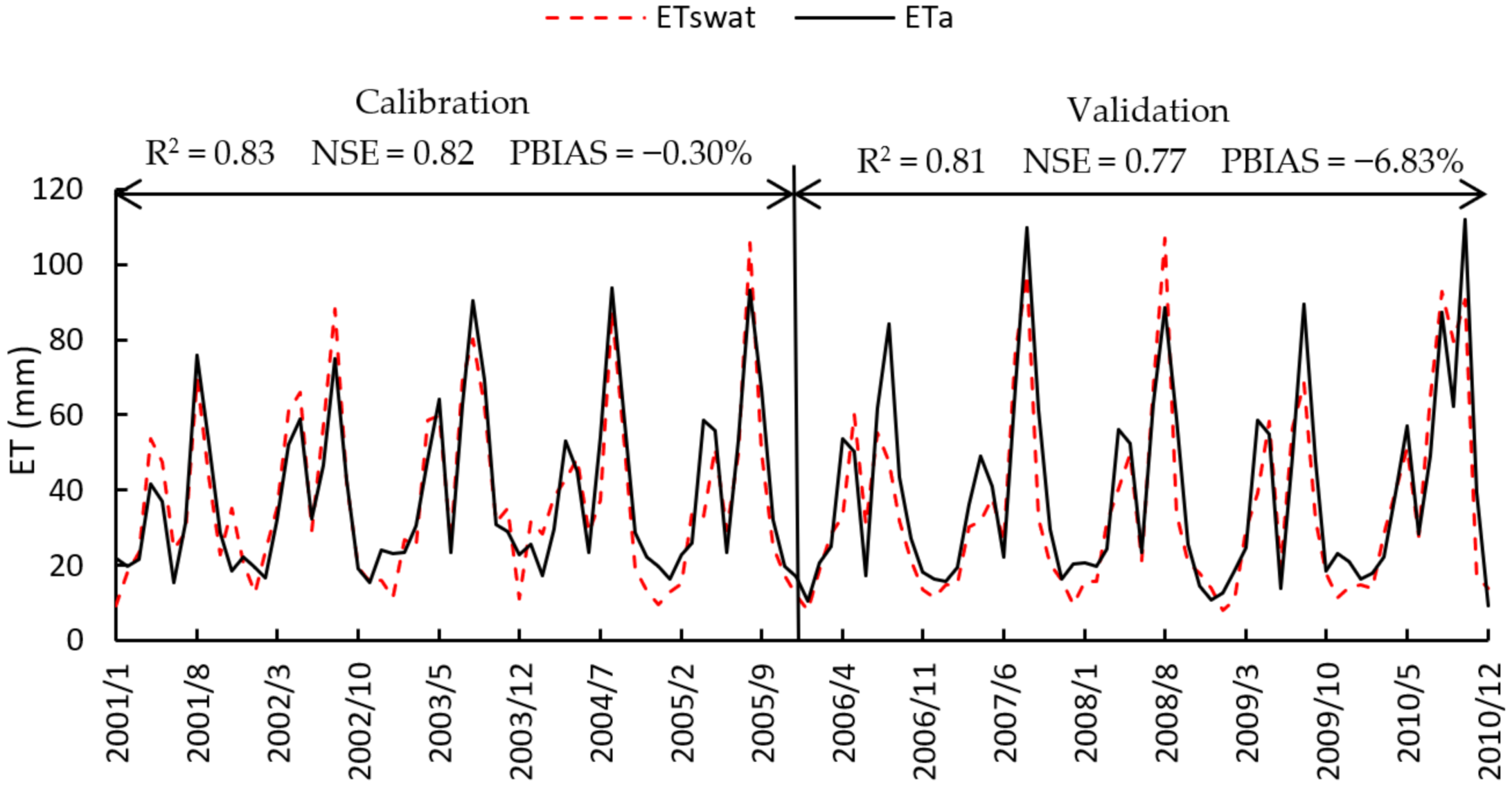
3.1. Calibration and Validation Results

Table 3 shows the selected SWAT parameters in the calibration process and their sensitivity statistics. According to the result of the sensitivity analysis, GWQMN was the most sensitive parameter for ET. This indicates that soil water content is the most important impact factor of the ET simulation for the SWAT model of JCID. It can be seen from Table 3 that CANMX, REVAPMN, GW_DELAY, SURLAG, GW_REVAP, ALPHA_BF and EPCO were more sensitive than the remaining parameters. CANMX and EPCO affected the simulation of ET by affecting evapotranspiration of plants. REVAPMN, GW_DELAY, GW_REVAP and ALPHA_BF were among the sensitive parameters indicating that the estimation of ET is affected by sub-surface hydrological process in JCID. SURLAG and ALPHA_BF were included in these parameters, revealing that surface hydrological process is also an important impact factor to ET in our study area.
Figure 5 shows the spatial distribution of subbasin scale R2, NSE, and PBIAS during the calibration and validation period, respectively.
During the calibration period, R2 ranged from 0.64 to 0.96 and the sub-basins with R2 value greater than 0.80 accounted for nearly 70% of the total 52 sub-basins. NSE ranged from 0.33 to 0.95, and the sub-basins with NSE value of more than 0.65 accounted for 90%. PBIAS yielded from −24% to 18%, and a |PBIAS| value of less than 25% accounted for 90%. In all, a model performance R2 > 0.8, NSE > 0.65 and PBIAS < ±25% was achieved in nearly 70% of the 52 sub-basins.
During the validation period, R2 ranged from 0.71 to 0.95 and the sub-basins with R2 value greater than 0.80 accounted for more than 67% of the total 52 sub-basins. NSE ranged from 0.30 to 0.95, and the sub-basins with NSE value of more than 0.65 accounted for nearly 85%. PBIAS yielded from −26% to 32%, and a |PBIAS| value of less than 25% accounted for 92%. In total, a model performance R2 > 0.8, NSE > 0.65 and PBIAS < ±25% was achieved in more than 67% of the 52 sub-basins.
The overall result of the model performance for the entire study area was satisfactory judging by the R2, NSE and PBIAS metrics in both the calibration and validation period.
Figure 6 shows the statistical indicators of the effect of the simulated average ET of the total 52 sub-basins during 2001 to 2010. The remote sensing-based calibration yielded acceptable NSE ranging from 0.82 for calibration and 0.77 for validation. R2 for calibration and validation was 0.83 and 0.81, while PBIAS ranged from −0.3% to −6.83%.
Using the guidelines in Moriasi et al. (2007) [43] and Van Liew et al. (2007) [45] for evaluating the SWAT model performance at a monthly time step, the PBIAS values showed a satisfactory model performance (PBIAS ≤ ±25) in the calibration/validation period. The negative PBIAS obtained in the calibration/validation of the SWAT model using the ET from MOD16 indicated a tendency for the SWAT model to overestimate monthly ET, or the MOD16 algorithm to underestimate the ET of the study area. The negative PBIAS result obtained using MOD16 for calibrating agrees with previous studies conducted in other regions of China. Zhang et al. (2020) applied the data of monitored runoff and remote sensing ET (MOD16) to calibrated the SWAT model in the Xixian basin located in the eastern China, and found that the annual ET estimate derived by the MOD16 algorithm was 14% less than the measured amount [49]. He et al. (2020) conduced accuracy verification and spatiotemporal comparison of three global high-resolution ET products (PML_V2, MOD16 and SSEBop_V4) in North China and found that the MOD16 product underestimated the ET of the study area [50]. From our results, it is agreed that the ET from MOD16 tends to underestimate ET.

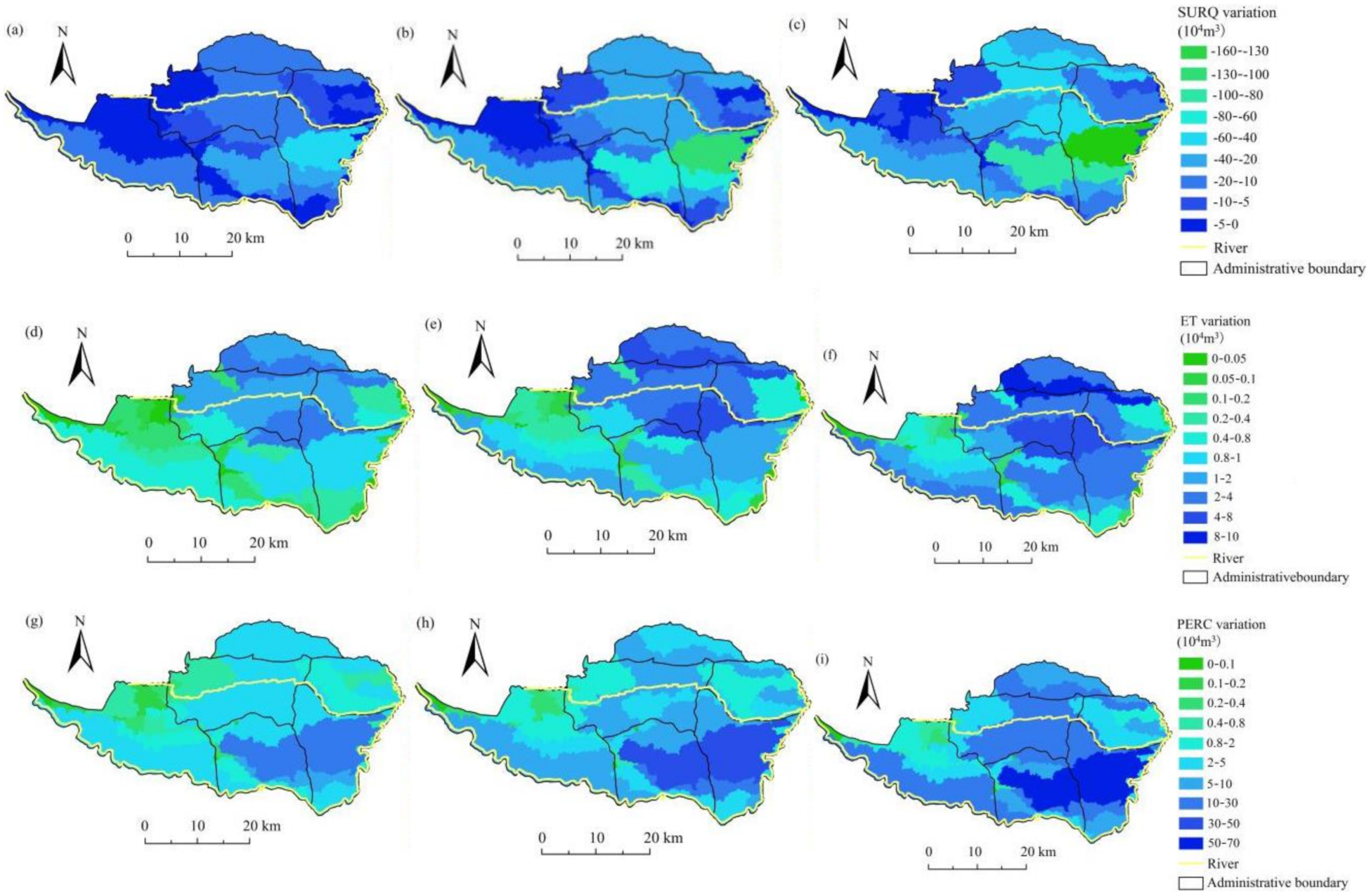
3.2. Impacts of Water-Saving Irrigation on Hydrological Cycle Components

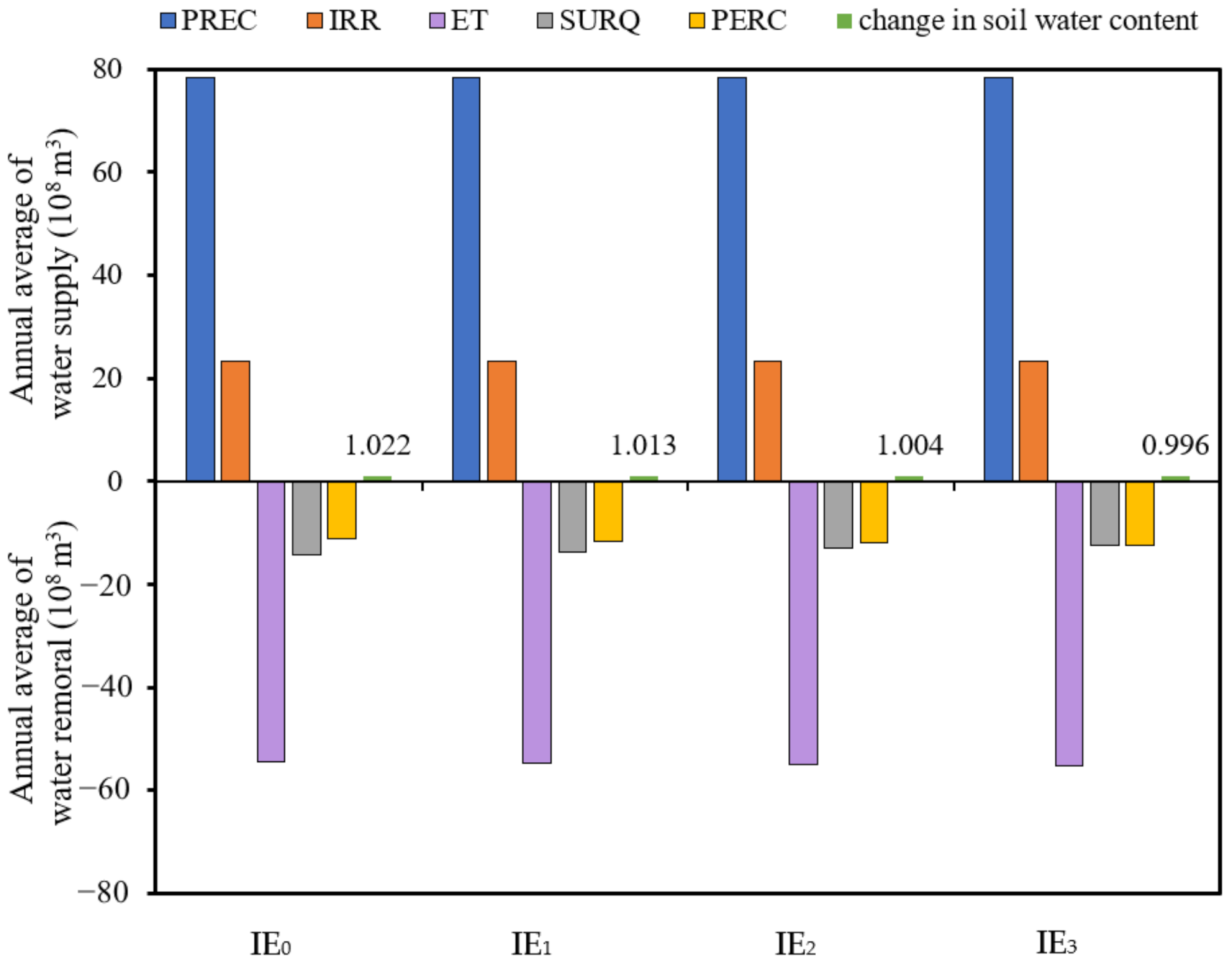
3.2.1. Annual Average Scale

According to the simulation results with the SWAT for JCID under various EUCIW values, the corresponding annual average values of SURQ, ET and PERC are shown in Figure 7a. In order to further analyze the degree of changes in every component, the annual average percentage changes in every component were calculated as shown in Figure 7b.
SURQ decreased gradually with the improvement of the water-saving degree. From Figure 7, the SURQ changed from 1.43 × 108 m3 to 1.25 × 108 m3 when the EUCIW increased by 0.1 to 0.3. The SURQ values decreased by 4.13%, 8.37% and 12.08% with the improvement of the water-saving degree. Similar results were also reported by Ahmadzadeh et al. (2016) [51]. They assessed the streamflow that joined Lake Urmia in the Zarrineh Rud catchment after water-saving measures and observed a slightly decreased annual streamflow.
In contrast to the simulation results of SURQ, PERC increased gradually with the improvement of the water-saving degree. The PERC changed from 1.12 × 108 m3 to 1.24 × 108 m3 and the values increased by 3.67%, 7.59% and 11.19% with the improvement of the water-saving degree. This was mainly caused by the increment of the water applied to the soil root zone through increasing EUCIW, which is beneficial to water infiltration but unfavorable to water confluence on the surface. The increase in the percolation results in an increase in the recharge to groundwater. In other words, the implementation of water-saving irrigation measures increased the groundwater recharge, which is consistent with the findings of Dai et al. (2013) [52]. According to their research, the increase in the irrigation water use coefficient is very effective in alleviating the falling of the groundwater level.
The ET changed from 5.45 × 108 m3 to 5.51 × 108 m3 and the annual average percentages of increase in ET under different scenarios were 0.43%, 0.84% and 1.18%, respectively. ET increased gradually with the improvement of the water-saving degree. Compared the simulation results of SURQ and PERC, the change in ET was not obvious, the reason for which was that the evaporation in the irrigation area is more affected by meteorological factors. The increase in EUCIW just affected the evaporation loss in the process of irrigation water transportation. Similar results were also reported by Ahmadzadeh et al. (2016) [51]. They simulated a slight increase in ET in the Zarrineh Rud catchment after water-saving measures. Clemmens and Allen (2005) also noted that some irrigation improvement techniques may not conserve water on a regional basis since ET of irrigated fields is normally not reduced and may actually be increased by improved uniformity and more careful control of water application [53].
The changes in each component of the hydrological cycle under various EUCIW on sub-basin scale are shown in Figure 8.
In Figure 8a,c, the decreased amounts of SURQ were between 0 and 53.81 × 104 m3 when EUCIW increased by 0.1. The values of that changed from between 0 and 107.38 × 104 m3 to between 0 and 155.06 × 104 m3 when EUCIW increased by 0.2 and 0.3. The decrease in SURQ became more obvious with the improvement of the water-saving degree. In Figure 8d,f, the increased amounts of ET were between 0 and 3.40 × 104 m3 when EUCIW increased by 0.1. The values of that changed from between 0 and 6.34 × 104 m3 to between 0 and 8.71 × 104 m3 when EUCIW increased by 0.2 and 0.3. The change in ET was not as obvious as that in SURQ. In Figure 8g,i, the increased amounts of PERC were between 0 and 20.49 × 104 m3 when EUCIW increased by 0.1. The values of that changed from between 0 and 41.94 × 104 m3 to between 0 and 63.02 × 104 m3 when EUCIW increased by 0.2 and 0.3. The increase in PERC became more evident with the improvement of the water-saving degree.
Combining the results and analysis on the whole irrigation area scale, it could be found that the change rules of every component on the sub-basin scale were same as those on the whole irrigation area scale. That is to say, the results are correct and universally applicable for the scenarios of increasing EUCIW.
In addition, it is clearly evident from Figure 8 that the variation values of every component in the east regions were generally greater the those in the west regions. All of these results can provide a reference for the managers of irrigation systems to avoid excessive improvement of the water-saving degree, which would lead to a large reduction in surface runoff, causing insufficient surface irrigation water consumption or a substantial increase in percolation, leading to a rise in the groundwater level, and thus increasing the risk of eco-environmental degradation. Therefore, appropriate EUCIW should be carefully considered in future studies.

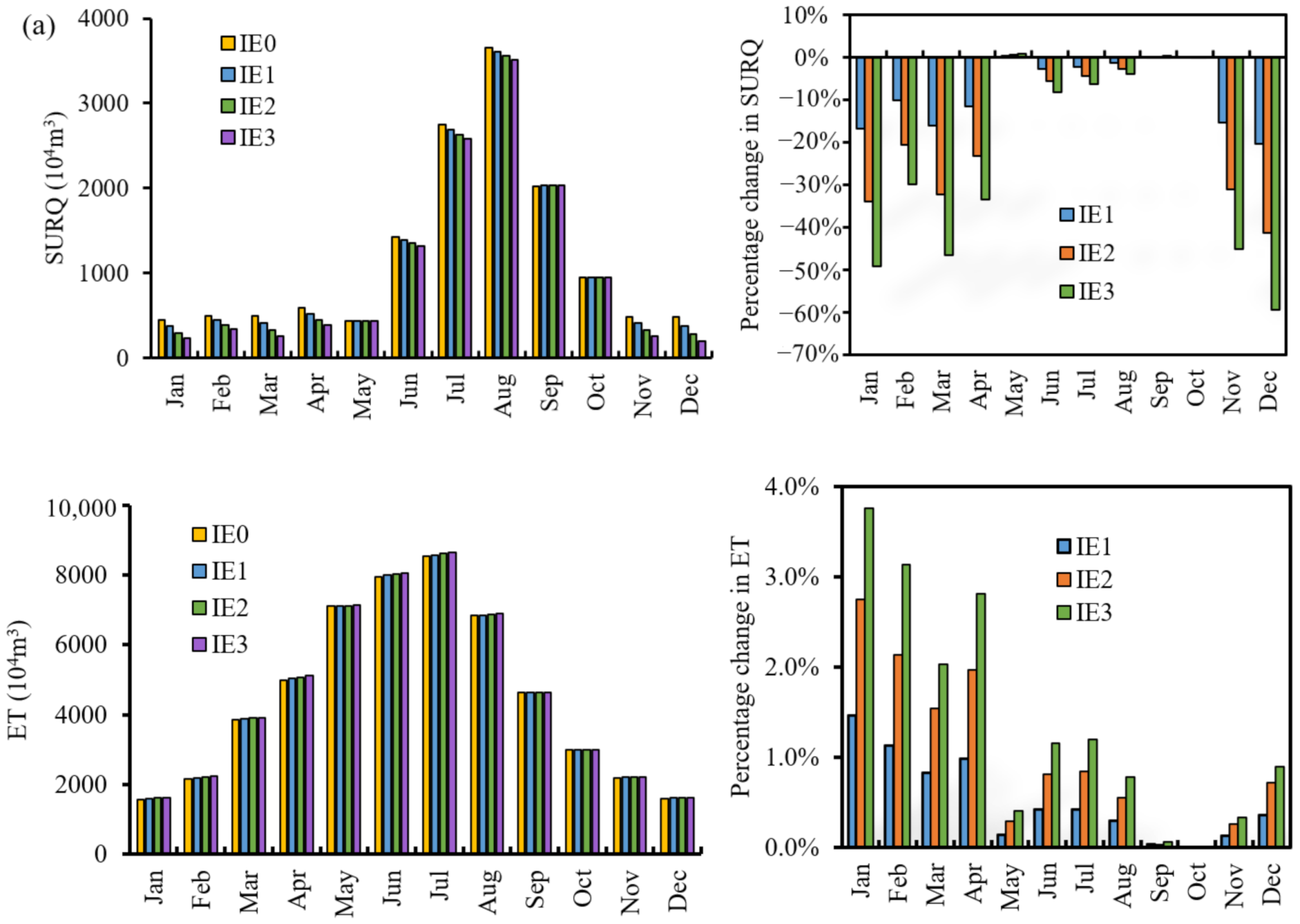
3.2.2. Monthly Average Scale

According to the simulation results with the SWAT for JCID under various EUCIW values, the corresponding average values of SURQ, ET and PERC in per month are shown in Figure 9. In order to further analyze the degree of changes in every component, the monthly average percentage changes in every component were calculated and are also shown in Figure 9a.
In general, the improvement of the water-saving degree caused a reduction in SURQ and increase in ET and PERC, which was in agreement with the results on the annual average scale. SURQ obviously changed between January to April and November to December (spring and winter irrigation period), while the situation was not obvious from June to August (summer irrigation period). In May, September and October, there was no change. Similar results were found for ET and PERC.
To analyze the reason for the above situation, the ratio of irrigation water quantity (IRR) and precipitation (PREC) in per month was calculated and shown in Figure 9b. It can be seen that IRR was greater than PREC between January to March and November to December. Although IRR was smaller than PREC in April, the ratio of IRR and PREC was also as high as 0.74. In these months, the effect of IRR on the hydrological cycle system was greater than the PREC, so the improvements to the water-saving degree had a great impact on the hydrological cycle system. PREC began to increase significantly in June and peaked in August. The amount of rainfall was much greater than that of irrigation during this period, so the influence of increasing the water-saving degree on the hydrological cycle system was not obvious. In May, September and October, there were no irrigation water applied to the study area, so the hydrological cycle components had not changed in these months.
That is to say, the effect of improving the water-saving degree on the hydrological cycle system was mainly during spring and winter irrigation period, and the degree of that on monthly scale depends on the amount of precipitation and irrigation.

3.2.3. Evaluation Impacts of Water Saving Irrigation on Hydrological Water Balance

To evaluate the impact of water-saving irrigation on the components of water balance over the whole irrigation area, the calibrated SWAT model was executed for the period of 2001–2010 for the current and water-saving irrigation scenarios. Figure 10 shows the total value changes in the components of water balance at the whole study area for the various EUCIW. As indicated in the figure, while the input to the irrigation area was PREC and IRR, the major output was ET, with the amount being about 50% of the total input. The next most significant output was surface runoff. In the current situation (EUCIW0), SURQ accounted for 14.02% of the total input volume, and the percentage of which were 13.44%, 12.85% and 12.33% in three scenarios. PERC was also an important output and its total amount accounted for 10.99% of the total input in current situation, the percentage values of which were 11.39%, 11.82% and 12.22% with the improvement of the water-saving degree. That is to say that with the improvement of the water-saving degree, the proportion of runoff in water balance decreased, while the proportion of percolation increased.
It also can be seen in Figure 10 that the change in soil water content decreased from 1.022 × 108 m3 (EUCIW0) to 0.996 × 108 m3 (EUCIW3) indicating that the input and output of soil water tended to be balanced. This reveals that the improvement of the water-saving degree plays a positive role in maintaining the sustainable development of water resources in irrigated areas.

4. Conclusions

Water-saving irrigation measures have significantly affected the hydrological cycle in irrigation areas. In this study, a SWAT model has been used to compute the water cycle components (surface runoff, actual evapotranspiration and percolation) of Jinghui Canal irrigated district from 2001 to 2010. Due to the lack of available hydrometric stations in the study area, satellite-based ET datasets (MOD16) were introduced as actual evapotranspiration to calibrate the SWAT model. Then, the water cycle components were simulated when the EUCIW was added by 0.1, 0.2 and 0.3 to analyze the effect of water-saving irrigation on the hydrological cycle. The major study findings include the following.
  • The overall result of the model performance for the entire study area was satisfactory judging by the R2, NSE and PBIAS metrics in both the calibration and validation period. It indicates that it is a good alternative method to introducing the satellite-based ET datasets to calibrating the SWAT model when hydro-meteorological are missing.
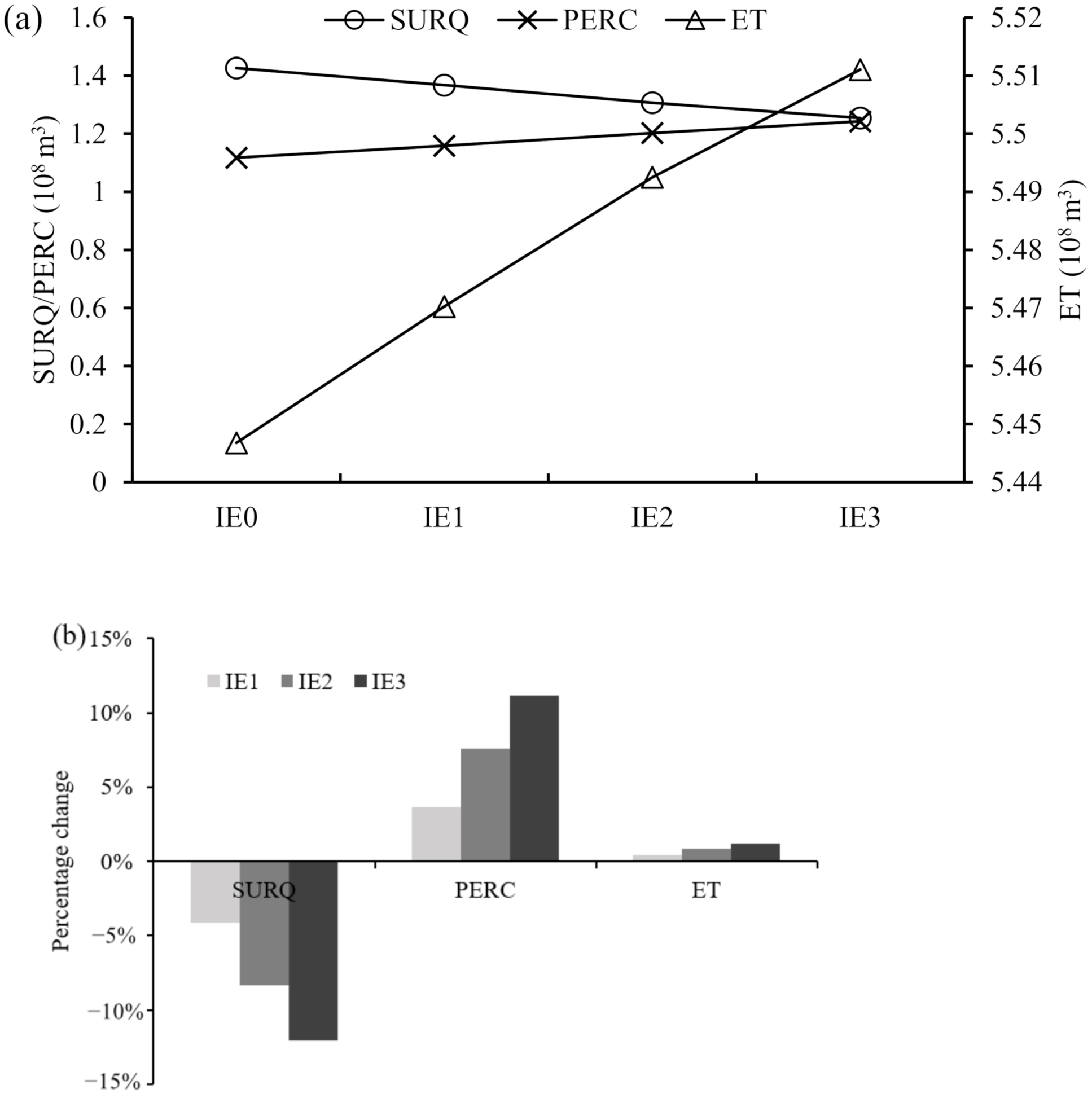
  • Improving the EUCIW was helpful in decreasing SURQ but increasing PERC, while it had no obvious effect on ET.
  • The main inputs of the irrigation area were PREC and IRR, while the main output was ET. The effect of the improvement of the water-saving degree on the hydrological cycle system was mainly during the periods when IRR was greater than PREC.
  • With the improvement of the water-saving degree, more input water resources (including PREC and IRR) were resupplied to groundwater through increasing PERC and less were converted to SURQ. The decrease in the value of the change in soil water content showed that the improvement of the water-saving degree plays a positive role on maintaining the sustainable development of water resources in irrigated areas.
The findings above contribute to a better understanding of the suitability of using freely available satellite-based actual evapotranspiration datasets in a sparsely gauged region for calibration/validation of the SWAT model. Moreover, the results of this paper are helpful in providing a reference for the managers of irrigation systems to avoid excessive improvement of EUCIW, which would lead to a large reduction in surface runoff causing insufficient surface irrigation water consumption or a substantial increase in percolation leading to a rise in groundwater level, and thus increasing the risk of eco-environmental degradation. Therefore, appropriate EUCIW should be carefully considered in future studies.

Author Contributions

Conceptualization, M.Z.; Data curation, M.Z. and X.W.; Formal analysis, M.Z.; Funding acquisition, W.Z.; Resources, W.Z.; Writing—original draft, M.Z.; Writing—review & editing, M.Z. and X.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by “The Twelfth Five-Year” National Science-technology Support Plan Projects (2011BAD29B01) and Shaanxi Province Natural Science Foundation of China (2014JM1030).

Institutional Review Board Statement

Not Applicable.

Informed Consent Statement

Not Applicable.

Data Availability Statement

Not Applicable.

Acknowledgments

This research was supported by “The Twelfth Five-Year” National Science-technology Support Plan Projects (2011BAD29B01) and Shaanxi Province Natural Science Foundation of China (2014JM1030). The authors sincerely thank the editors and reviewers for reviewing the manuscript and providing important comments to help improve this paper.

Conflicts of Interest

The authors have no conflict of interest to declare.

References

  1. Carroll, S.; Liu, A.; Dawes, L.; Hargreaves, M.; Goonetilleke, A. Role of Land Use and Seasonal Factors in Water Quality Degradations. Water Resour. Manag. 2013, 27, 3433–3440. [Google Scholar] [CrossRef] [Green Version]
  2. McDonald, R.; Weber, K.; Padowski, J.; Flörke, M.; Schneider, C.; Green, P.A.; Gleeson, T.; Eckman, S.; Lehner, B.; Balk, D.; et al. Water on an urban planet: Urbanization and the reach of urban water infrastructure. Glob. Environ. Chang. 2014, 27, 96–105. [Google Scholar] [CrossRef] [Green Version]
  3. Zhang, J.S.; Xu, J.X.; Zhang, Y.Q.; Wang, M.Q.; Cheng, Z.S. Water resources utilization and eco-environmental safety in Northwest China. J. Geogr. Sci. 2006, 16, 277–285. [Google Scholar] [CrossRef]
  4. Gonçalves, J.M.; Pereira, L.S.; Fang, S.X.; Dong, B. Modelling and multicriteria analysis of water-saving scenarios for an irrigation district in the upper Yellow River Basin. Agric. Water Manag. 2007, 94, 93–108. [Google Scholar] [CrossRef]
  5. Han, D.; Song, X.; Currell, M.J.; Cao, G.; Zhang, Y.; Kang, Y. A survey of groundwater levels and hydrogeochemistry in irrigated fields in the Karamay Agricultural Development Area, northwest China: Implications for soil and groundwater salinity resulting from surface water transfer for irrigation. J. Hydrol. 2011, 405, 217–234. [Google Scholar] [CrossRef]
  6. Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y.; et al. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef]
  7. Xu, X.; Huang, G.; Qu, Z.; Pereira, L.S. Assessing the groundwater dynamics and impacts of water-saving in the Hetao Irrigation District, Yellow River basin. Agric. Water Manag. 2010, 98, 301–313. [Google Scholar] [CrossRef]
  8. Belder, P.; Bouman, B.; Cabangon, R.; Guoan, L.; Quilang, E.; Yuanhua, L.; Spiertz, J.; Tuong, T. Effect of water-saving irrigation on rice yield and water use in typical lowland conditions in Asia. Agric. Water Manag. 2004, 65, 193–210. [Google Scholar] [CrossRef]
  9. Mermoud, A.; Tamini, T.D.; Yacouba, H. Impacts of different irrigation schedules on the water balance components of an onion crop in a semi-arid zone. Agric. Water Manag. 2005, 77, 282–295. [Google Scholar] [CrossRef]
  10. Yue, W.F.; Liu, X.Z.; Wang, T.J.; Chen, X.H. Impacts of water-saving on groundwater balance in a large scale arid irrigation district, Northwest China. Irrig. Sci. 2016, 34, 297–312. [Google Scholar] [CrossRef]
  11. Jiang, L.; Xue, L.; Liu, Y.; Li, W.; Chi, Y. Effects of water-saving irrigation on groundwater in arid basin based on MIKE SHE model. J. Irrig. Drain. 2016, 35, 59–65. [Google Scholar]
  12. Zhang, Z.; Hu, H.; Tian, F.; Yao, X.; Sivapalan, M. Groundwater dynamics under water-saving irrigation and implications for sustainable water management in an oasis: Tarim River basin of western China. Hydrol. Earth Syst. Sci. 2014, 18, 3951–3967. [Google Scholar] [CrossRef] [Green Version]
  13. Uniyal, B.; Jha, M.K.; Verma, A.K. Parameter identification and uncertainty analysis for simulating streamflow in a river basin of Eastern India. Hydrol. Process. 2015, 29, 3744–3766. [Google Scholar] [CrossRef]
  14. Easton, Z.M.; Fuka, D.R.; Walter, M.T.; Cowan, D.M.; Schneiderman, E.M.; Steenhuis, T.S. Re-conceptualizing the soil and water assessment tool (SWAT) model to predict runoff from variable source areas. J. Hydrol. 2008, 348, 279–291. [Google Scholar] [CrossRef]
  15. Manaswi, C.M.; Thawait, A.K. Application of soil and water assessment tool for runoff modeling of Karam River basin in Madhya Pradesh. Int. J. Sci. Eng. Technol. 2014, 3, 529–532. [Google Scholar]
  16. Sun, C.; Ren, L. Assessment of surface water resources and evapotranspiration in the Haihe River basin of China using SWAT model. Hydrol. Process. 2012, 27, 1200–1222. [Google Scholar] [CrossRef]
  17. Gao, Y.; Long, D. Intercomparison of remote sensing-based models for estimation of evapotranspiration and accuracy assessment based on SWAT. Hydrol. Process. 2008, 22, 4850–4869. [Google Scholar] [CrossRef]
  18. Chen, F.; Crow, W.T.; Starks, P.J.; Moriasi, D.N. Improving hydrologic predictions of a catchment model via assimilation of surface soil moisture. Adv. Water Resour. 2011, 34, 526–536. [Google Scholar] [CrossRef]
  19. Li, M.; Ma, Z.; Du, J. Regional soil moisture simulation for Shaanxi Province using SWAT model validation and trend analysis. Sci. China Earth Sci. 2010, 53, 575–590. [Google Scholar] [CrossRef]
  20. Narasimhan, B.; Srinivasan, R.; Arnold, J.G.; Di Luzio, M. Estimation of long-term soil moisture using a distributed parameter hydrologic model and verification using remotely sensed data. Trans. ASAE 2005, 48, 1101–1113. [Google Scholar] [CrossRef]
  21. Cheema, M.; Immerzeel, W.; Bastiaanssen, W. Spatial Quantification of Groundwater Abstraction in the Irrigated Indus Basin. Ground Water 2014, 52, 25–36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Zhang, X.; Ren, L.; Kong, X. Estimating spatiotemporal variability and sustainability of shallow groundwater in a well-irrigated plain of the Haihe River basin using SWAT model. J. Hydrol. 2016, 541, 1221–1240. [Google Scholar] [CrossRef]
  23. Xie, X.; Cui, Y. Development and test of SWAT for modeling hydrological processes in irrigation districts with paddy rice. J. Hydrol. 2011, 396, 61–71. [Google Scholar] [CrossRef]
  24. Goswami, S.; Kar, S. Simulation of water cycle components in the Narmada River basin by forcing SWAT model with CFSR data. Meteorol. Hydrol. Water Manag. 2017, 6, 13–25. [Google Scholar] [CrossRef]
  25. Jin, X.; Jin, Y. Calibration of a Distributed Hydrological Model in a Data-Scarce Basin Based on GLEAM Datasets. Water 2020, 12, 897. [Google Scholar] [CrossRef] [Green Version]
  26. Wang, Y.; Brubaker, K. Implementing a nonlinear groundwater module in the soil and water assessment tool (SWAT). Hydrol. Process. 2013, 28, 3388–3403. [Google Scholar] [CrossRef]
  27. Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
  28. Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
  29. Miralles, D.G.; Holmes, T.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
  30. Immerzeel, W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
  31. Emam, A.R.; Kappas, M.; Linh, N.H.K.; Renchin, T. Hydrological Modeling and Runoff Mitigation in an Ungauged Basin of Central Vietnam Using SWAT Model. Hydrology 2017, 4, 16. [Google Scholar] [CrossRef] [Green Version]
  32. Ha, L.T.; Bastiaanssen, W.G.M.; Van Griensven, A.; Van Dijk, A.I.J.M.; Senay, G.B. Calibration of Spatially Distributed Hydrological Processes and Model Parameters in SWAT Using Remote Sensing Data and an Auto-Calibration Procedure: A Case Study in a Vietnamese River Basin. Water 2018, 10, 212. [Google Scholar] [CrossRef] [Green Version]
  33. Parajuli, P.B.; Jayakody, P.; Ouyang, Y. Evaluation of Using Remote Sensing Evapotranspiration Data in SWAT. Water Resour. Manag. 2018, 32, 985–996. [Google Scholar] [CrossRef]
  34. Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
  35. Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute Technical Report No.406; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
  36. Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical Development, Applications, and Future Research Directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef] [Green Version]
  37. Fischer, G.; Nachtergaele, F.; Prieler, S.; van Velthuizen, H.T.; Verelst, L.; Wiberg, D. Global Agro-Ecological Zones Assessment for Agriculture (GAEZ 2008); IIASA: Laxenburg, Austria; FAO: Rome, Italy, 2008. [Google Scholar]
  38. Guo, A.; Jiang, D.; Zhong, F.; Ding, X.; Song, X.; Cheng, Q.; Zhang, Y.; Huang, C. Prediction of Technological Change under Shared Socioeconomic Pathways and Regional Differences: A Case Study of Irrigation Water Use Efficiency Changes in Chinese Provinces. Sustainability 2019, 11, 7103. [Google Scholar] [CrossRef] [Green Version]
  39. Feng, B.Q. Study on the Evaluation and Management of Irrigation Water Use Efficiency for Different Scales in Countrywide; China Institute of Water Resources & Hydropower Research (IWHR): Beijing, China, 2013. [Google Scholar]
  40. Abbaspour, K.C.; Johnson, C.A.; Van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
  41. Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
  42. Abbaspour, K.C. SWAT-CUP 2012. SWAT Calibration and Uncertainty Program—A User Manual; Eawag and Swiss Federal Institute of Aqutic Science and Technology: Dübendorf, Switzerland, 2014. [Google Scholar]
  43. Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
  44. Gupta, H.V.; Soroosh, S.; Patrice, O.Y. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
  45. Van Liew, M.W.; Veith, T.L.; Bosch, D.D.; Arnold, J.G. Suitability of SWAT for the Conservation Effects Assessment Project: Comparison on USDA Agricultural Research Service Watersheds. J. Hydrol. Eng. 2007, 12, 173–189. [Google Scholar] [CrossRef] [Green Version]
  46. Schuol, J.; Abbaspour, K.C.; Srinivasan, R.; Yang, H. Estimation of freshwater availability in the West African sub-continent using the SWAT hydrologic model. J. Hydrol. 2008, 352, 30–49. [Google Scholar] [CrossRef]
  47. Milewski, A.; Sultan, M.; Yan, E.; Becker, R.; Abdeldayem, A.; Soliman, F.; Gelil, K.A. A remote sensing solution for estimating runoff and recharge in arid environments. J. Hydrol. 2009, 373, 1–14. [Google Scholar] [CrossRef]
  48. Rajib, A.; Merwade, V.; Yu, Z. Multi-objective calibration of a hydrologic model using spatially distributed remotely sensed/in-situ soil moisture. J. Hydrol. 2016, 536, 192–207. [Google Scholar] [CrossRef] [Green Version]
  49. Zhang, Q.; Yue, Q.H.; Dong, X.H.; Yang, B.Y.; Wei, C.; Yu, D.; Zang, T. The application of remote sensing data to the SWAT model enhances its accuracy of evapotranspiration. J. Water Resour. Water Eng. 2020, 31, 37–44. [Google Scholar]
  50. He, S.; Tian, J.; Zhang, Y. Verification and comparison of three high-resolution surface evapotranspiration products in North China. Resour. Sci. 2020, 42, 2035–2046. [Google Scholar] [CrossRef]
  51. Ahmadzadeh, H.; Morid, S.; Delavar, M.; Srinivasan, R. Using the SWAT model to assess the impacts of changing irrigation from surface to pressurized systems on water productivity and water saving in the Zarrineh Rud catchment. Agric. Water Manag. 2016, 175, 15–28. [Google Scholar] [CrossRef]
  52. Dai, F.G.; Cai, H.J.; Liu, X.; Liang, H.W. Simulation of effect of water-saving renovation on spatial distribution of groundwater in Jinghui Canal irrigation area. J. Drain. Irrig. Mach. Eng. 2013, 31, 729–736. [Google Scholar]
  53. Clemmens, A.J.; Allen, R.G. Impact of Agricultural Water Conservation on Water Availability; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2005; pp. 1–14. [Google Scholar]
Sustainability 13 08488 g001 550
Figure 1. Location of the study area and the irrigation canal system distribution in the study area.
Figure 1. Location of the study area and the irrigation canal system distribution in the study area.
Sustainability 13 08488 g001
Sustainability 13 08488 g002 550
Figure 2. The runoff of the Jing river, irrigation water and average groundwater depth during the period of 2001–2010 in the Jinghui Canal irrigation district.
Figure 2. The runoff of the Jing river, irrigation water and average groundwater depth during the period of 2001–2010 in the Jinghui Canal irrigation district.
Sustainability 13 08488 g002
Sustainability 13 08488 g003 550
Figure 3. The DEM (a), land cover (b) and soil map (c) of the study area.
Figure 3. The DEM (a), land cover (b) and soil map (c) of the study area.
Sustainability 13 08488 g003
Sustainability 13 08488 g004 550
Figure 4. The distribution of 5 traditional weather stations.
Figure 4. The distribution of 5 traditional weather stations.
Sustainability 13 08488 g004
Sustainability 13 08488 g005 550
Figure 5. Performance metrics (R2, NSE, and PBIAS) result of SWAT during the calibration period (left) and the validation period (right).
Figure 5. Performance metrics (R2, NSE, and PBIAS) result of SWAT during the calibration period (left) and the validation period (right).
Sustainability 13 08488 g005
Sustainability 13 08488 g006 550
Figure 6. Comparison between simulated evapotranspiration (ETSWAT) and the actual evapotranspiration (ETa) based on MOD16 during both calibration and validation periods.
Figure 6. Comparison between simulated evapotranspiration (ETSWAT) and the actual evapotranspiration (ETa) based on MOD16 during both calibration and validation periods.
Sustainability 13 08488 g006
Sustainability 13 08488 g007 550
Figure 7. (a) The annual average values and (b) the annual average percentage of the hydrological cycle components in three scenarios from 2001 to 2010.
Figure 7. (a) The annual average values and (b) the annual average percentage of the hydrological cycle components in three scenarios from 2001 to 2010.
Sustainability 13 08488 g007
Sustainability 13 08488 g008 550
Figure 8. The spatial variations of (a–c) the annual average surface runoff (SURQ), (d–f) actual evapotranspiration (ET) and (g–i) percolation (PERC) in three scenarios respectively.
Figure 8. The spatial variations of (a–c) the annual average surface runoff (SURQ), (d–f) actual evapotranspiration (ET) and (g–i) percolation (PERC) in three scenarios respectively.
Sustainability 13 08488 g008
Sustainability 13 08488 g009a 550Sustainability 13 08488 g009b 550
Figure 9. (a) Monthly average values and percentage of increase or decrease in SURQ, ET and PERC under various values of EUCIW, and (b) the ratio of IRR and PREC on monthly average scale in the study area.
Figure 9. (a) Monthly average values and percentage of increase or decrease in SURQ, ET and PERC under various values of EUCIW, and (b) the ratio of IRR and PREC on monthly average scale in the study area.
Sustainability 13 08488 g009aSustainability 13 08488 g009b
Sustainability 13 08488 g010 550
Figure 10. The water balance of the irrigation area in the current and water-saving irrigation scenarios.
Figure 10. The water balance of the irrigation area in the current and water-saving irrigation scenarios.
Sustainability 13 08488 g010
Table
Table 1. Irrigation water quantity from 2001 to 2010.
Table 1. Irrigation water quantity from 2001 to 2010.
Irrigation YearCanal Irrigation Quantity
(104 m3)		Well Irrigation Quantity
(104 m3)		EUCIW0 *
WinterSpringSummerWinterSpringSummer
20014240420629504079404728380.522
20025268352327705703381429980.524
20033551298821054266359025290.523
20045186354325965203355426040.525
20053855486637123581452034480.528
20064858435034454704421233360.531
20075470304011235894327612100.532
20085486305945865209290443550.535
20095298482836194221384628830.535
20106030403838014630310129190.537
The winter irrigation time was between November of the previous year and February of the current year. The spring irrigation time was between March and April of the current year. The summer irrigation time was between June and August of the current year. The time frame of the well irrigation was the same for the canal irrigation. * EUCIW0 is the effective utilization coefficient of irrigation water obtained from Shaanxi Jinghui Canal Irrigation Administration from 2001 to 2010.
Table
Table 2. The assessment standards of PBIAS and NSE.
Table 2. The assessment standards of PBIAS and NSE.
Simulation ResultAbsolute Value of PBIASNSE
Very good|PBIAS| ≤ 10%NSE > 0.75
Good10% < |PBIAS| ≤ 15%0.65 < NSE ≤ 0.75
Satisfactory15% < |PBIAS| ≤ 25%0.50 < NSE ≤ 0.65
Unsatisfactory|PBIAS| > 25%NSE ≤ 0.50
Table
Table 3. Sensitivity rank and calibrated parameters with their optimal value of the SWAT model.
Table 3. Sensitivity rank and calibrated parameters with their optimal value of the SWAT model.
Parameter Name *Physical Meaningt-Statp-ValueFitted Value
V_GWQMN.gwThreshold depth of water in the shallow aquifer required for return flow to occur (mm)5.000.002675
V_CANMX.hruMaximum canopy storage (mm)3.390.0051.50
V_REVAPMN.gwThreshold depth of water in the shallow aquifer for “revap” to occur (mm)3.330.00122.50
V_GW_DELAY.gwGroundwater delay (days)3.320.00127.50
V_SURLAG.bsnSurface runoff lag time (days)3.040.0022.48
V_GW_REVAP.gwGroundwater “revap” coefficient2.610.010.06
V_ALPHA_BF.gwBaseflow alpha factor (days)2.110.040.66
V_EPCO.hruPlant uptake compensation factor1.330.190.65
R_SOL_Z.solDepth from soil surface to bottom of layer (mm)−0.560.58−0.24
R_SOL_K.solSaturated hydraulic conductivity (mm/h)0.490.620.02
R_SOL_ALB.solMoist soil albedo0.380.700.28
R_SOL_AWC.solAvailable water capacity of the soil layer (mm/mm)0.350.72−0.20
V_OV_N.hruManning’s “n” value for overland flow0.300.7728.35
R_CN2.mgtSCS runoff curve number for moisture condition 20.240.81−0.14
R_SOL_BD.solMoist bulk density (g/cm3)0.230.820.48
V_ESCO.hruSoil evaporation compensation factor0.150.880.51
(* The r parameter value is multiplied by 1 + a given value, and the v parameter value is replaced by a value from the given range).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Zhang, M.; Wang, X.; Zhou, W. Effects of Water-Saving Irrigation on Hydrological Cycle in an Irrigation District of Northern China. Sustainability 2021, 13, 8488. https://doi.org/10.3390/su13158488

AMA Style

Zhang M, Wang X, Zhou W. Effects of Water-Saving Irrigation on Hydrological Cycle in an Irrigation District of Northern China. Sustainability. 2021; 13(15):8488. https://doi.org/10.3390/su13158488

Chicago/Turabian Style

Zhang, Manfei, Xiao Wang, and Weibo Zhou. 2021. "Effects of Water-Saving Irrigation on Hydrological Cycle in an Irrigation District of Northern China" Sustainability 13, no. 15: 8488. https://doi.org/10.3390/su13158488

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop