Remaining Useful Life Prediction-Based Maintenance Decision Model for Stochastic Deterioration Equipment under Data-Driven
Abstract
:1. Introduction
2. Problem Description and Model Assumptions
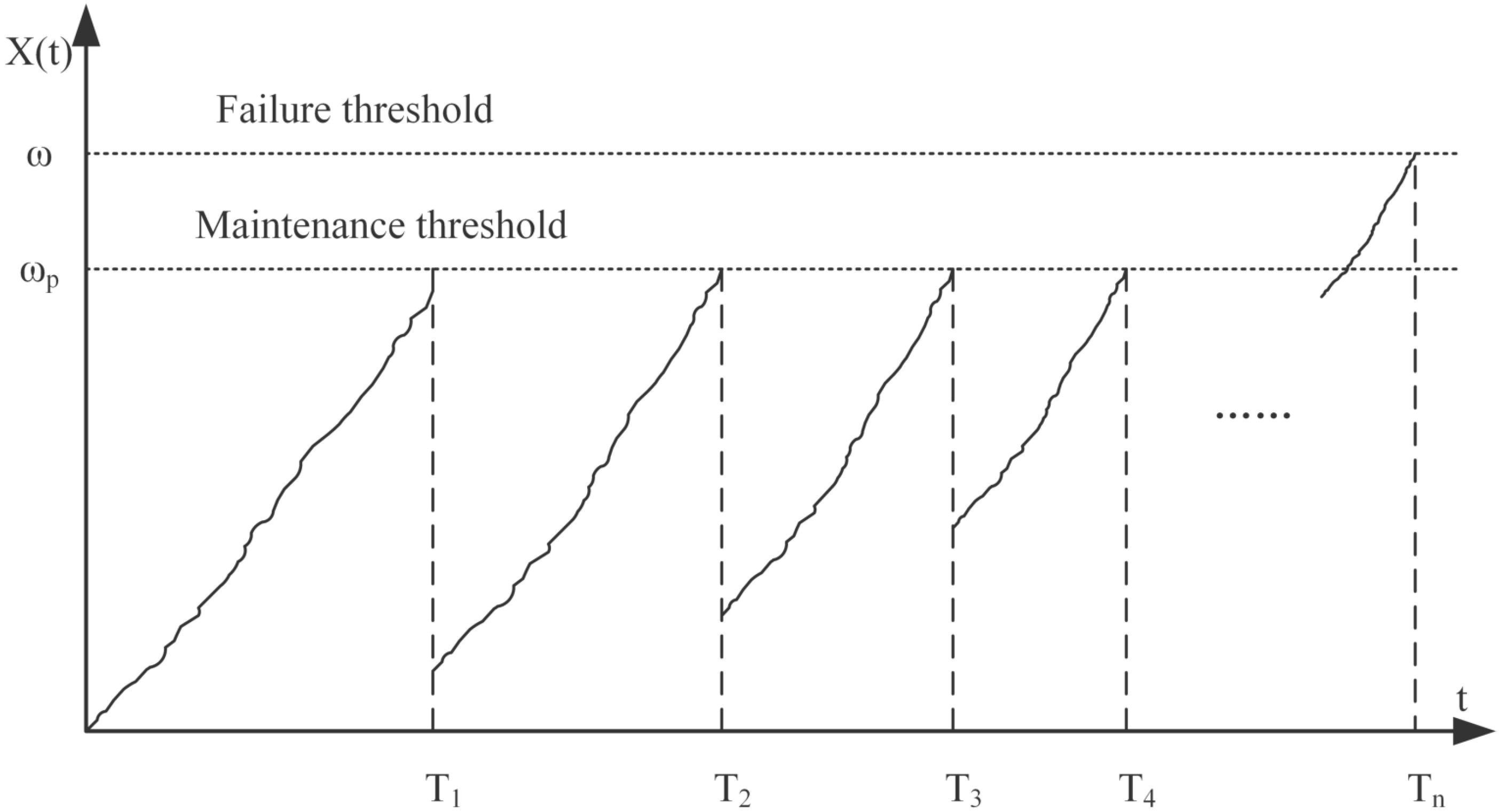
2.1. Problem Description
2.2. Model Assumptions
- (1)
- Preventive maintenance does not affect the degradation mechanism of the equipment itself and can slow down the process of equipment degradation. However, preventive maintenance activities are not unlimited. When the number of maintenance reaches the prescribed upper limit N, maintenance activities will no longer be carried out.
- (2)
- The status value of each period can be obtained through the detection method, and the replacement and repair time of the equipment under any maintenance means is ignored.
- (3)
- When equipment degradation is less than the preventive maintenance threshold , no maintenance, and the equipment usually operates.
- (4)
- When equipment degradation is greater than the preventive maintenance threshold , but the number of maintenance does not exceed N, we take preventive maintenance.
- (5)
- When the overall degradation exceeds the failure threshold , the system will fail, and time-sensitive replacement will be adopted.
3. Model Building
3.1. Non-Linear Drift Wiener Degradation Model
3.2. RUL Prediction Model
3.3. Maintenance Decision Model
3.3.1. Preventive Replacement
3.3.2. Failure Replacement
3.4. Parameter Estimation
3.4.1. Parameter Offline Estimation
3.4.2. Real-Time Parameter Estimation
4. Case Analysis and Discussion
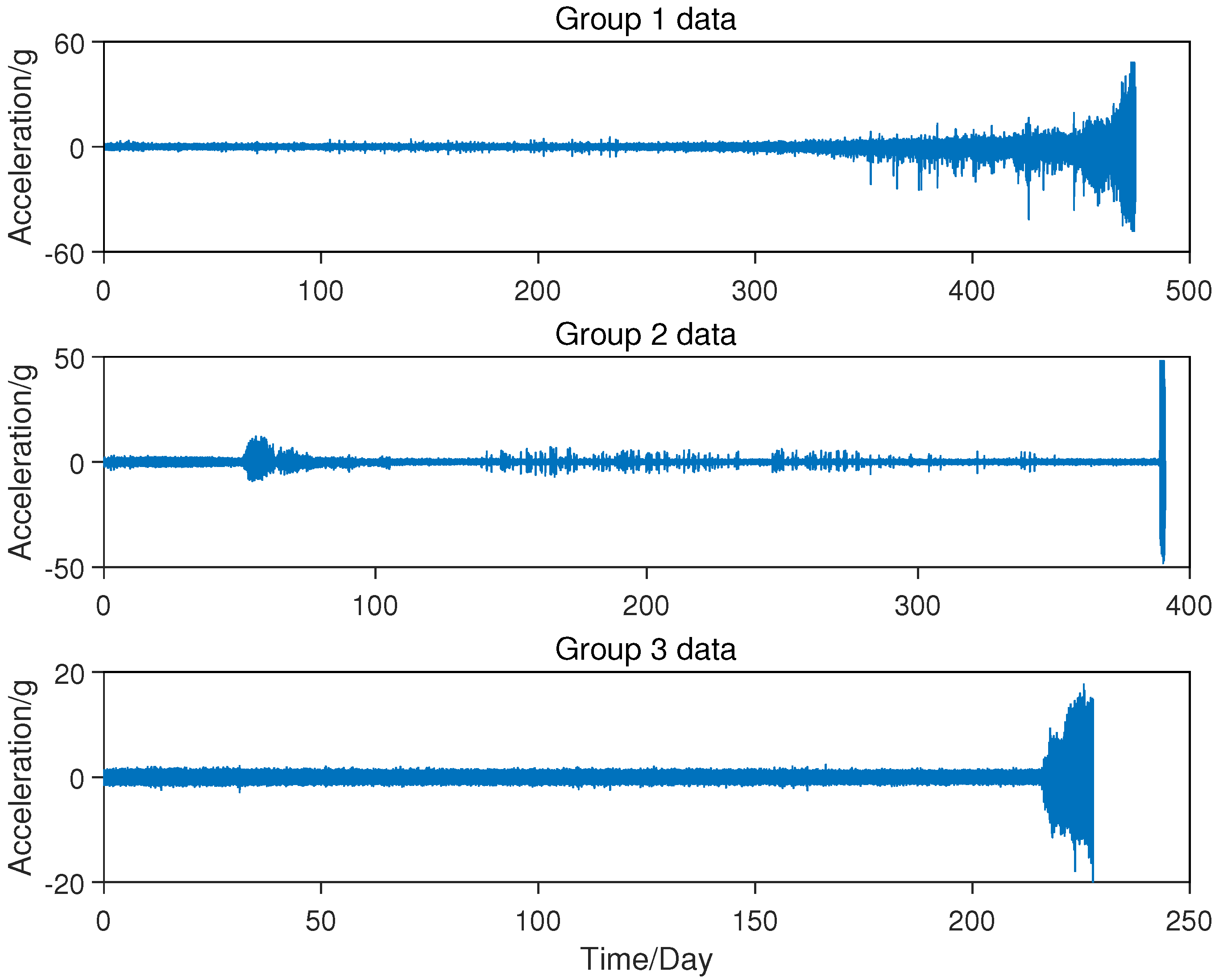
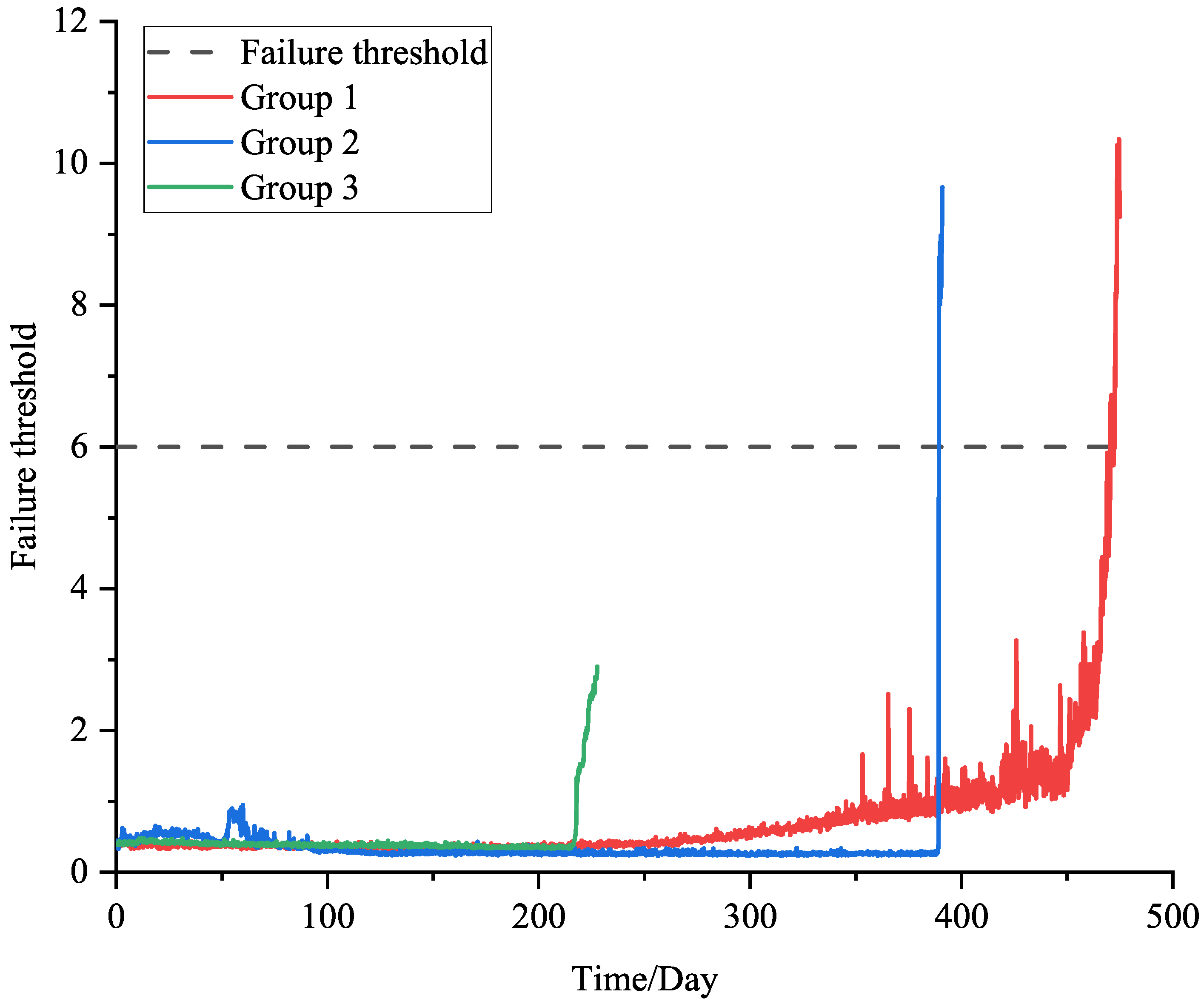
4.1. Case Analysis
4.2. RUL Prediction
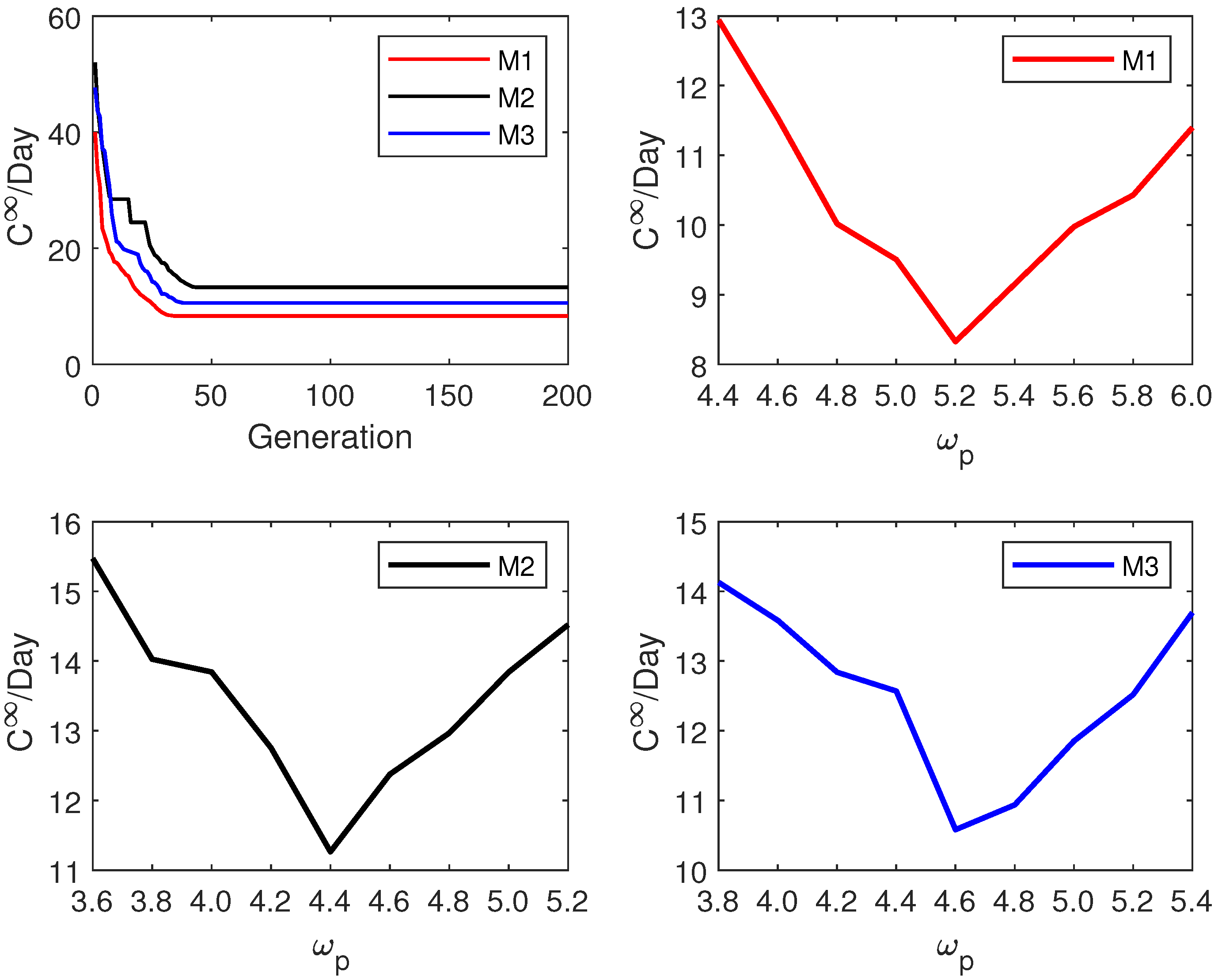
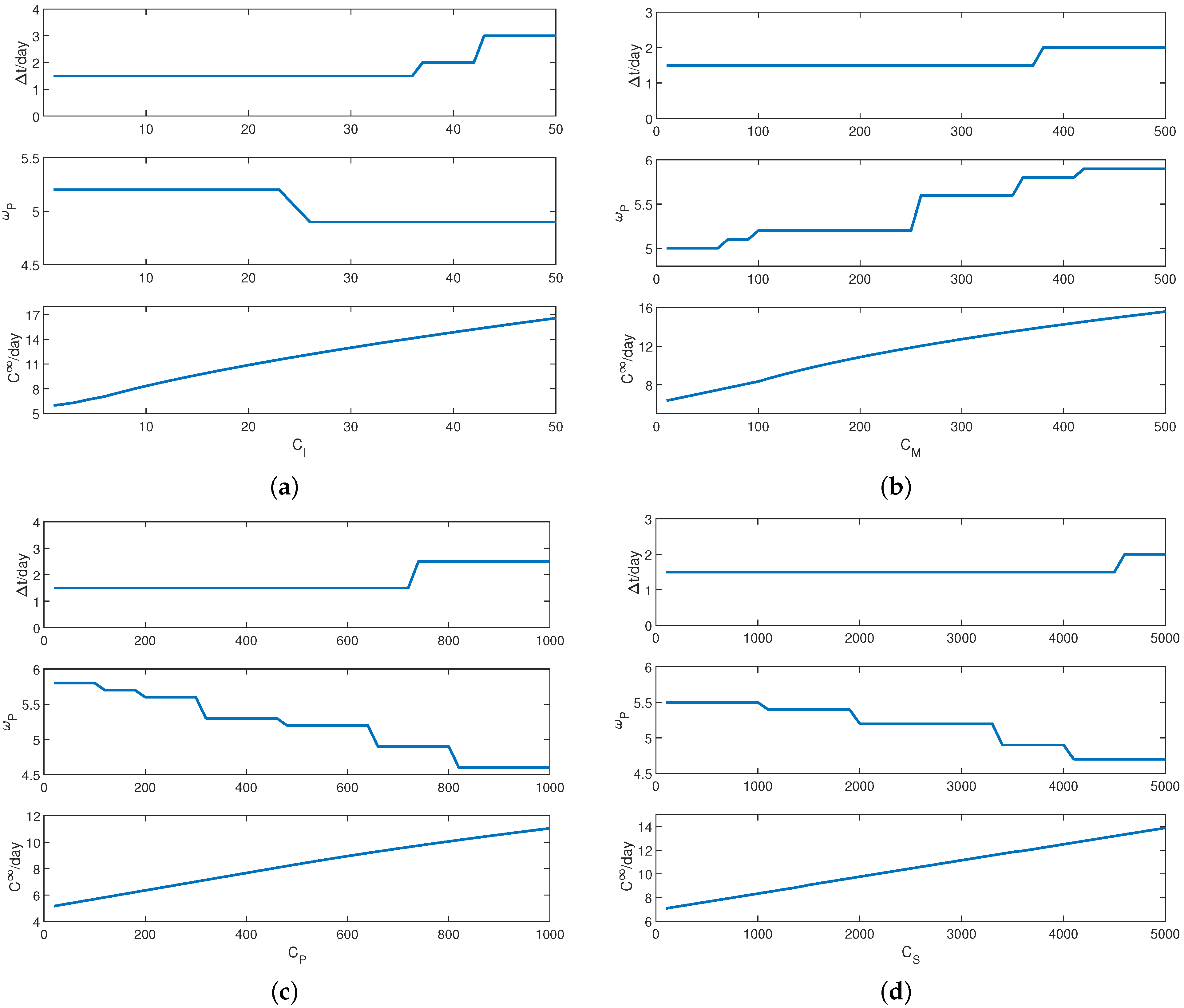
4.3. Decision Analysis
4.4. Discussion
5. Conclusions
- (1)
- For stochastic deterioration equipment, the nonlinear Wiener process can represent the true degradation process of the device more accurately than the linear Wiener process, which conforms to objective laws and effectively improves the accuracy of RUL prediction.
- (2)
- The introduction of online parameter updates can improve the accuracy and reliability of RUL prediction.
- (3)
- Based on the more accurate RUL prediction results, a more realistic optimal maintenance strategy can be formulated, reducing maintenance costs and prolonging the RUL of the equipment.
- (4)
- Inspection costs and preventive maintenance costs have a significant impact on maintenance strategies. Therefore, it is necessary to focus on controlling inspection costs and preventive maintenance costs to promote sustainable development in actual maintenance activities.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Iheukwumere-Esotu, L.O.; Yunusa-Kaltungo, A. Knowledge Criticality Assessment and Codification Framework for Major Maintenance Activities: A Case Study of Cement Rotary Kiln Plant. Sustainability 2021, 13, 4619. [Google Scholar] [CrossRef]
- Pei, H.; Hu, C.; Si, X.; Zhang, J.; Pang, Z.; Zhang, P. Summary of equipment remaining life prediction methods based on machine learning. Chin. J. Mech. Eng. 2019, 55, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Tichy, T.; Broz, J.; Belinova, Z.; Pirnik, R. Analysis of Predictive Maintenance for Tunnel Systems. Sustainability 2021, 13, 3977. [Google Scholar] [CrossRef]
- Liu, H.; Jia, W.; Zhang, D.; Tan, J. The Research Status and Challenges of Deep Learning in the Technology of Predicting the Remaining Service Life of Equipment. Comput. Integr. Manuf. Syst. 2021, 27, 34–52. [Google Scholar]
- Sarute, U.; Hathaikarn, M. A critical review on cellulose: From fundamental to an approach on sensor technology. Renew. Sustain. Energy Rev. 2015, 41, 401–412. [Google Scholar]
- Park, S.; Hamm, S.Y.; Kim, J. Performance Evaluation of the GIS-Based Data-Mining Techniques Decision Tree, Random Forest, and Rotation Forest for Landslide Susceptibility Modeling. Sustainability 2019, 11, 5659. [Google Scholar] [CrossRef] [Green Version]
- Kamble, S.S.; Gunasekaran, A.; Ghadge, A.; Raut, R. A performance measurement system for industry 4.0 enabled smart manufacturing system in SMMEs—A review and empirical investigation. Int. J. Prod. Econ. 2020, 229, 107853. [Google Scholar] [CrossRef]
- Ammar, Y.; Alqahtani, S.M.; Gupta, K.N. Warranty and maintenance analysis of sensor embedded products using internet of things in industry 4.0. Int. J. Prod. Econ. 2019, 208, 483–499. [Google Scholar]
- Jafari, L.; Makis, V. Joint optimal lot sizing and preventive maintenance policy for a production facility subject to condition monitoring. Int. J. Prod. Econ. 2015, 169, 156–168. [Google Scholar] [CrossRef]
- Lin, Y.; Li, X.; Hu, Y. Deep diagnostics and prognostics: An integrated hierarchical learning framework in PHM applications. Appl. Soft. Comput. 2018, 72, 555–564. [Google Scholar] [CrossRef]
- Rodrigues, L.R.; Yoneyama, T. A spare parts inventory control model based on Prognostics and Health monitoring data under a fill rate constraint. Comput. Ind. Eng. 2020, 148, 106724. [Google Scholar] [CrossRef]
- Ma, J.; Shang, P.; Zou, X.; Ma, N.; Ding, Y.; Sun, J.; Cheng, Y.; Tao, L.; Lu, C.; Su, Y.; et al. A hybrid transfer learning scheme for remaining useful life prediction and cycle life test optimization of different formulation Li-ion power batteries. Appl. Energy. 2021, 282, 116167. [Google Scholar] [CrossRef]
- Dawn, A.; Nam, H.; Kim, J. Practical options for selecting data-driven or physics-based prognostics algorithms with reviews. Eng. Syst. Saf. 2015, 133, 223–236. [Google Scholar]
- Omer, F.; Eker, F.; Ian, K. Physics-based prognostic modelling of filter clogging phenomena. Mech. Syst. Signal Proc. 2016, 75, 395–412. [Google Scholar]
- Guo, J.; Li, Z.; Li, M. A Review on Prognostics Methods for Engineering Systems. IEEE Trans. Reliab. 2020, 69, 1110–1129. [Google Scholar] [CrossRef]
- Sun, H.; Cao, D.; Zhao, Z. A Hybrid Approach to Cutting Tool Remaining Useful Life Prediction Based on the Wiener Process. IEEE Trans. Reliab. 2018, 67, 1294–1303. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N. A Hybrid Prognostics Approach for Estimating Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Reliab. 2020, 69, 401–412. [Google Scholar] [CrossRef]
- Feng, Y.; Mohamed, S.; Yan, S. Remaining useful life prediction of induction motors using nonlinear degradation of health index. Mech. Syst. Signal Proc. 2021, 148, 107183. [Google Scholar]
- Yang, X.; Fang, Z.; Li, X. Similarity-based information fusion grey model for remaining useful life prediction of aircraft engines. Grey Syst. Theory Appl. 2020. ahead-of-print. [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, X.; Si, C.; Lei, T.G. Degradation data analysis and remaining useful life estimation: A review on Wiener-process-based methods. Eur. J. Oper. Res. 2018, 271, 775–796. [Google Scholar] [CrossRef]
- Akhilesh, K.; Ratna, B.C.; Finn, T. An HMM and polynomial regression based approach for remaining useful life and health state estimation of cutting tools. Comput. Ind. Eng. 2019, 128, 1008–1014. [Google Scholar]
- Mosayeb, E.; Grall, E.; Shemehsavar, S. A dynamic auto-adaptive predictive maintenance policy for degradation with unknown parameters. Eur. J. Oper. Res. 2020, 282, 81–92. [Google Scholar] [CrossRef] [Green Version]
- Van, T.; Hong, T.; Bo-Suk, Y.; Tan, T. Machine performance degradation assessment and remaining useful life prediction using proportional hazard model and support vector machine. Mech. Syst. Signal Proc. 2012, 32, 320–330. [Google Scholar]
- Han, C.; Kong, X.G.; Chen, G.; Wang, Q.B.; Wang, R.B. Transferable convolutional neural network based remaining useful life prediction of bearing under multiple failure behaviors. Measurement 2021, 168, 108286. [Google Scholar]
- Chen, Z.; Wu, M.; Zhao, R. Machine Remaining Useful Life Prediction via an Attention Based Deep Learning Approach. IEEE Trans. Ind. Electron. 2021, 68, 2521–2531. [Google Scholar] [CrossRef]
- Meng, M.; Zhu, M. Deep Convolution-based LSTM Network for Remaining Useful Life Prediction. IEEE Trans. Ind. Inform. 2021, 17, 1658–1667. [Google Scholar]
- Singpurwalla, N.D. Survival in Dynamic Environments. Stat. Sci. 1995, 10, 86–103. [Google Scholar] [CrossRef]
- Lorton, A.; Fouladirad, M.; Grall, A. A methodology for probabilistic model-based prognosis. Eur. J. Oper. Res. 2013, 225, 443–454. [Google Scholar] [CrossRef]
- Zhang, M.; Ye, Z.; Xie, M. A condition-based maintenance strategy for heterogeneous populations. Comput. Ind. Eng. 2014, 77, 103–114. [Google Scholar] [CrossRef]
- Kleijnen, J.P. Regression and Kriging metamodels with their experimental designs in simulation: A review. Eur. J. Oper. Res. 2017, 256, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Feng, D.; Guan, J. Planning of step-stress accelerated degradation test based on non-stationary gamma process with random effects. Comput. Ind. Eng. 2020, 125, 467–479. [Google Scholar]
- Cao, Y.; Liu, S.; Fang, Z.; Dong, W. Modeling ageing effects in the context of continuous degradation and random shock. Comput. Ind. Eng. 2020, 145, 106539. [Google Scholar] [CrossRef]
- Li, F.; Li, H.; He, Y. Adaptive stochastic model predictive control of linear systems using Gaussian process regression. IET Contr. Theory Appl. 2020, 15, 683–693. [Google Scholar] [CrossRef]
- Davis, C.B.; Hans, C.M.; Santner, T.J. Prediction of non-stationary response functions using a Bayesian composite Gaussian process. Comput. Stat. Data Anal. 2021, 154, 107083. [Google Scholar] [CrossRef]
- He, D.; Liu, L.; Cao, M. A doubly accelerated degradation model based on the inverse Gaussian process and its objective Bayesian analysis. J. Stat. Comput. Simul. 2021, 91, 1485–1503. [Google Scholar] [CrossRef]
- Zhai, Q.; Ye, Z. RUL Prediction of Deteriorating Products Using an Adaptive Wiener Process Model. IEEE Trans. Ind. Inform. 2017, 13, 2911–2921. [Google Scholar] [CrossRef]
- Wen, Y.; Wu, J.; Das, D.; Tseng, T. Degradation modeling and RUL prediction using Wiener process subject to multiple change points and unit heterogeneity. Reliab. Eng. Syst. Saf. 2018, 176, 113–124. [Google Scholar] [CrossRef]
- Li, N.; Lei, Y.; Yan, T. A Wiener Process Model-based Method for Remaining Useful Life Prediction Considering Unit-to-Unit Variability. IEEE Trans. Ind. Electron. 2018, 66, 2092–2101. [Google Scholar] [CrossRef]
- Man, J.; Zhou, Q. Prediction of hard failures with stochastic degradation signals using Wiener process and proportional hazards model. Comput. Ind. Eng. 2018, 125, 480–489. [Google Scholar] [CrossRef]
- Wang, H.; Ma, X.; Zhao, Y. An improved Wiener process model with adaptive drift and diffusion for online remaining useful life prediction. Mech. Syst. Signal Proc. 2018, 125, 370–387. [Google Scholar] [CrossRef]
- Liu, D.; Wang, S. A degradation modeling and reliability estimation method based on Wiener process and evidential variable. Reliab. Eng. Syst. Saf. 2020, 202, 106957. [Google Scholar] [CrossRef]
- Zhang, M.; Gaudoin, O.; Xie, M. Degradation-based maintenance decision using stochastic filtering for systems under imperfect maintenance. Eur. J. Oper. Res. 2015, 245, 531–541. [Google Scholar] [CrossRef]
- Liu, B.; Xie, M.; Xu, Z.; Kuo, W. An imperfect maintenance policy for mission-oriented systems subject to degradation and external shocks. Comput. Ind. Eng. 2016, 102, 21–32. [Google Scholar] [CrossRef] [Green Version]
- Pei, H.; Hu, C.; Si, X.; Zhang, Z.; Du, D. Equipment maintenance decision-making model based on remaining life prediction information under imperfect maintenance. Acta Autom. Sin. 2018, 44, 719–729. [Google Scholar]
- Wang, Z.; Chen, Y.; Cai, Z.; Xiang, H.; Wang, L. Prediction of remaining life of imperfect maintenance equipment based on compound inhomogeneous Poisson process. Chin. J. Mech. Eng. 2020, 56, 14–23. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Wang, Z. Optimal Maintenance Decision Based on Remaining Useful Lifetime Prediction for the Equipment Subject to Imperfect Maintenance. IEEE Access 2020, 8, 6704–6716. [Google Scholar] [CrossRef]
- Tang, S.; Yu, C.; Xue, W.; Guo, X.; Si, X. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on the Wiener Process with Measurement Error. Energies 2014, 7, 520–547. [Google Scholar] [CrossRef] [Green Version]
- Gebraeel, N.Z.; Lawley, M.A.; Li, R.; Ryan, J.K. Residual-life distributions from component degradation signals: A Bayesian approach. IIE Trans. 2005, 37, 534–557. [Google Scholar] [CrossRef]
- Lee, M.-L.T.; Whitmore, G.A. Threshold Regression for Survival Analysis: Modeling Event Times by a Stochastic Process Reaching a Boundary. Stat. Sci. 2006, 21, 501–513. [Google Scholar] [CrossRef] [Green Version]
- Grall, A.; Dieulle, L.; Berenguer, C. Continuous-time predictive-maintenance scheduling for a deteriorating system. IEEE Trans. Reliab. 2001, 51, 141–150. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Pham, H. A Multi-Objective Optimization of Imperfect Preventive Maintenance Policy for Dependent Competing Risk Systems With Hidden Failure. IEEE Trans. Reliab. 2011, 60, 770–781. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, B.; Qin, Z. Recursive Extended Least Squares Parameter Estimation for Wiener Nonlinear Systems with Moving Average Noises. Circuits Syst. Signal Process. 2014, 32, 655–664. [Google Scholar] [CrossRef]
- Zio, E.; Peloni, G. Particle filtering prognostic estimation of the remaining useful life of nonlinear components. Reliab. Eng. Syst. Saf. 2011, 96, 403–409. [Google Scholar] [CrossRef]
- Patrick, N.; Rafael, G.; Kamal, M.; Emmanuel, R. An Experimental Platform for Bearings Accelerated Life Test. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 18 June 2012. [Google Scholar]
- Saxena, A.; Celaya, J.; Saha, B. Metrics for offlineevaluation of prognostic performance. Int. J. Progn. Health Manag. 2010, 1, 2153–2648. [Google Scholar]
- Thompson, P.A. An MSE statistic for comparing forecast accuracy across series. Int. J. Forecast. 1990, 6, 219–227. [Google Scholar] [CrossRef]


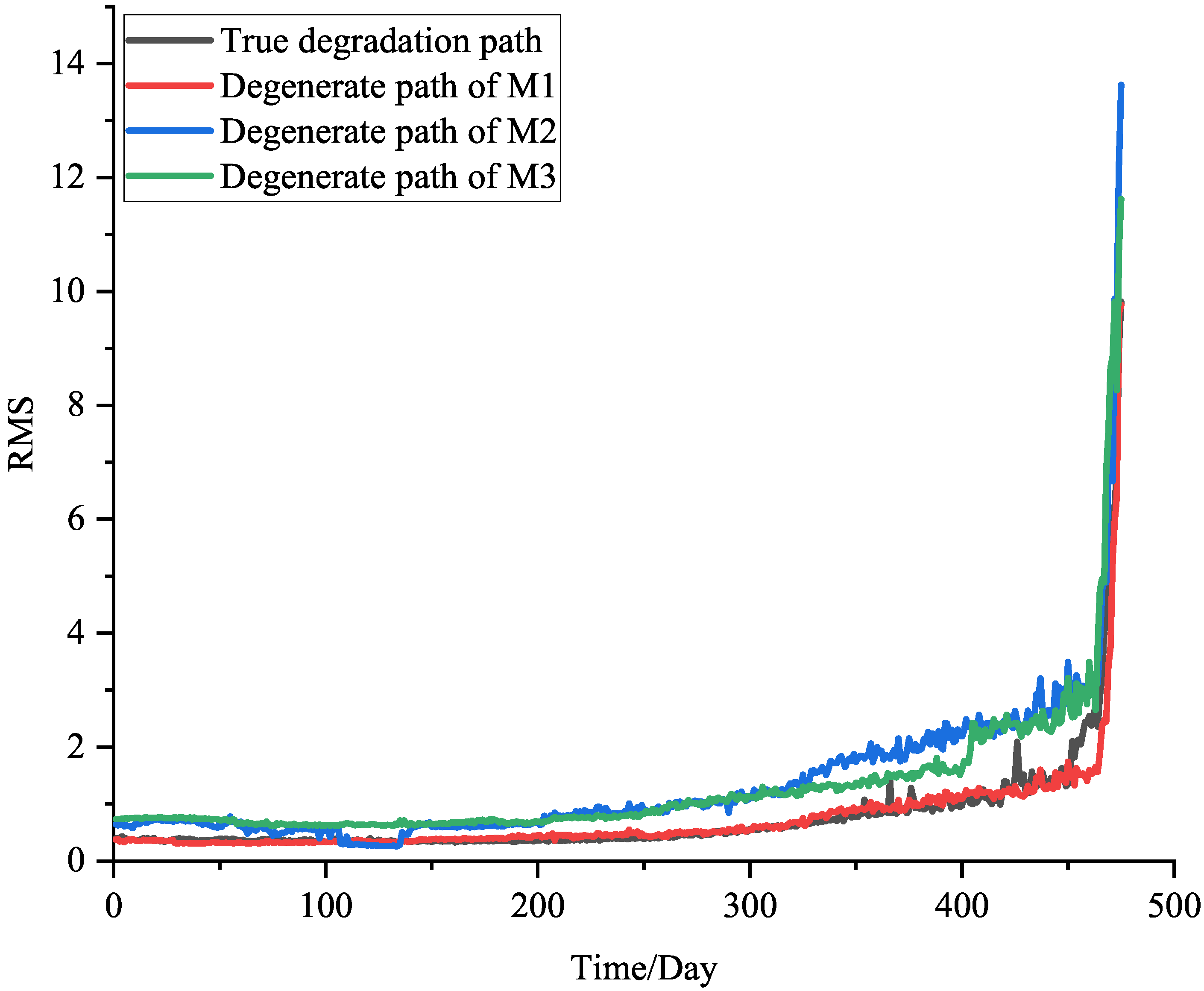
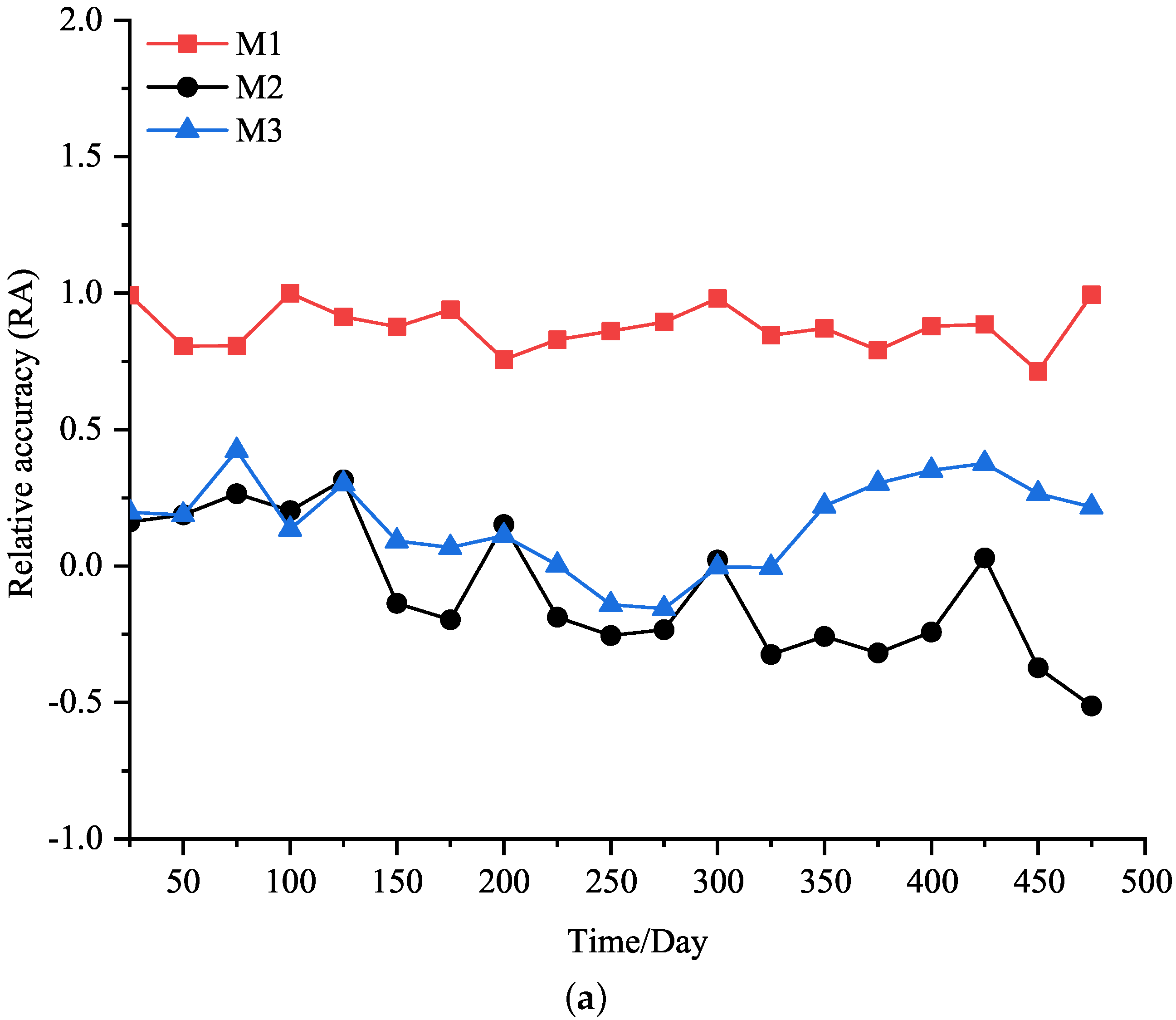
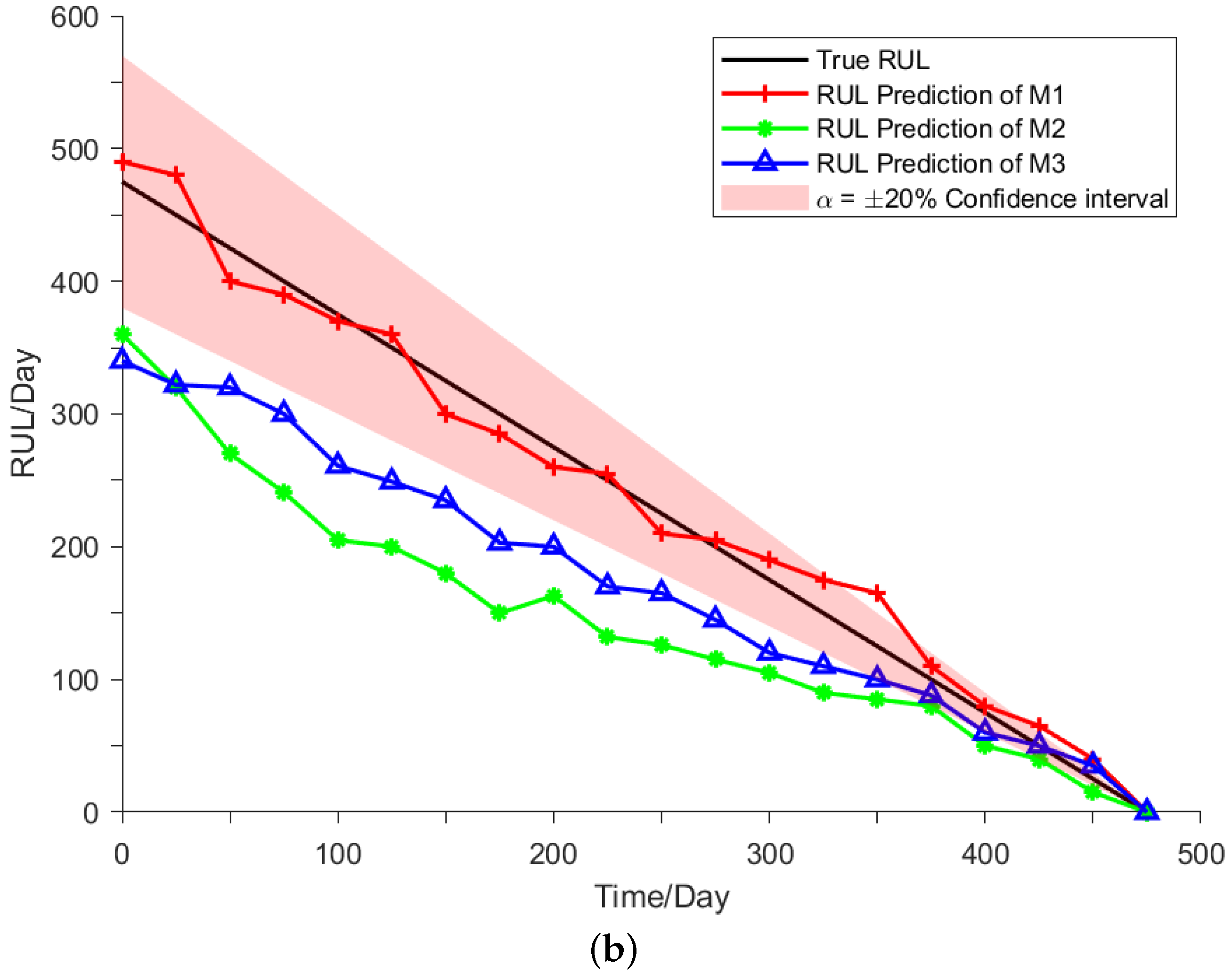
| Method | MAE | MAE Lift Rate | RMSE | RMSE Lift Rate |
|---|---|---|---|---|
| M1 | 0.240 | - | 0.378 | - |
| M2 | 0.548 | 56.20% | 0.703 | 46.23% |
| M3 | 0.485 | 50.52% | 0.621 | 24.30% |
| Parameter | ||||
|---|---|---|---|---|
| Cost/$ | 10 | 100 | 500 | 1000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Li, P.; Ming, S. Remaining Useful Life Prediction-Based Maintenance Decision Model for Stochastic Deterioration Equipment under Data-Driven. Sustainability 2021, 13, 8548. https://doi.org/10.3390/su13158548
Cao X, Li P, Ming S. Remaining Useful Life Prediction-Based Maintenance Decision Model for Stochastic Deterioration Equipment under Data-Driven. Sustainability. 2021; 13(15):8548. https://doi.org/10.3390/su13158548
Chicago/Turabian StyleCao, Xiangang, Pengfei Li, and Song Ming. 2021. "Remaining Useful Life Prediction-Based Maintenance Decision Model for Stochastic Deterioration Equipment under Data-Driven" Sustainability 13, no. 15: 8548. https://doi.org/10.3390/su13158548





