Optimization of Groundwater Exploitation in an Irrigation Area in the Arid Upper Peacock River, NW China: Implications for Sustainable Agriculture and Ecology
Abstract
:1. Introduction
2. Materials and Methods
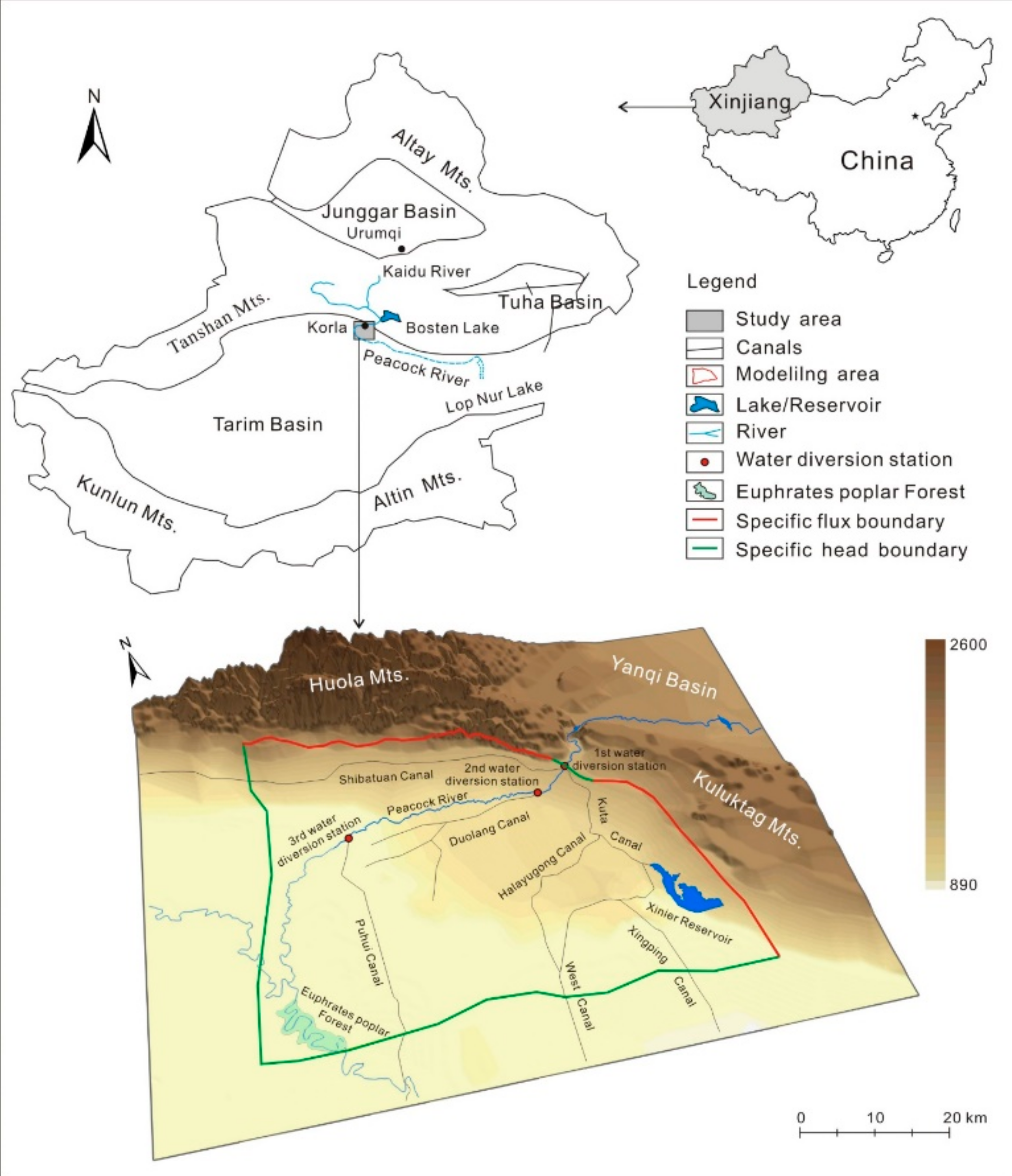
2.1. General Setting
2.2. Geology and Hydrogeology
2.3. Irrigation and Groundwater Overexploitation
2.4. River-Aquifer Interaction
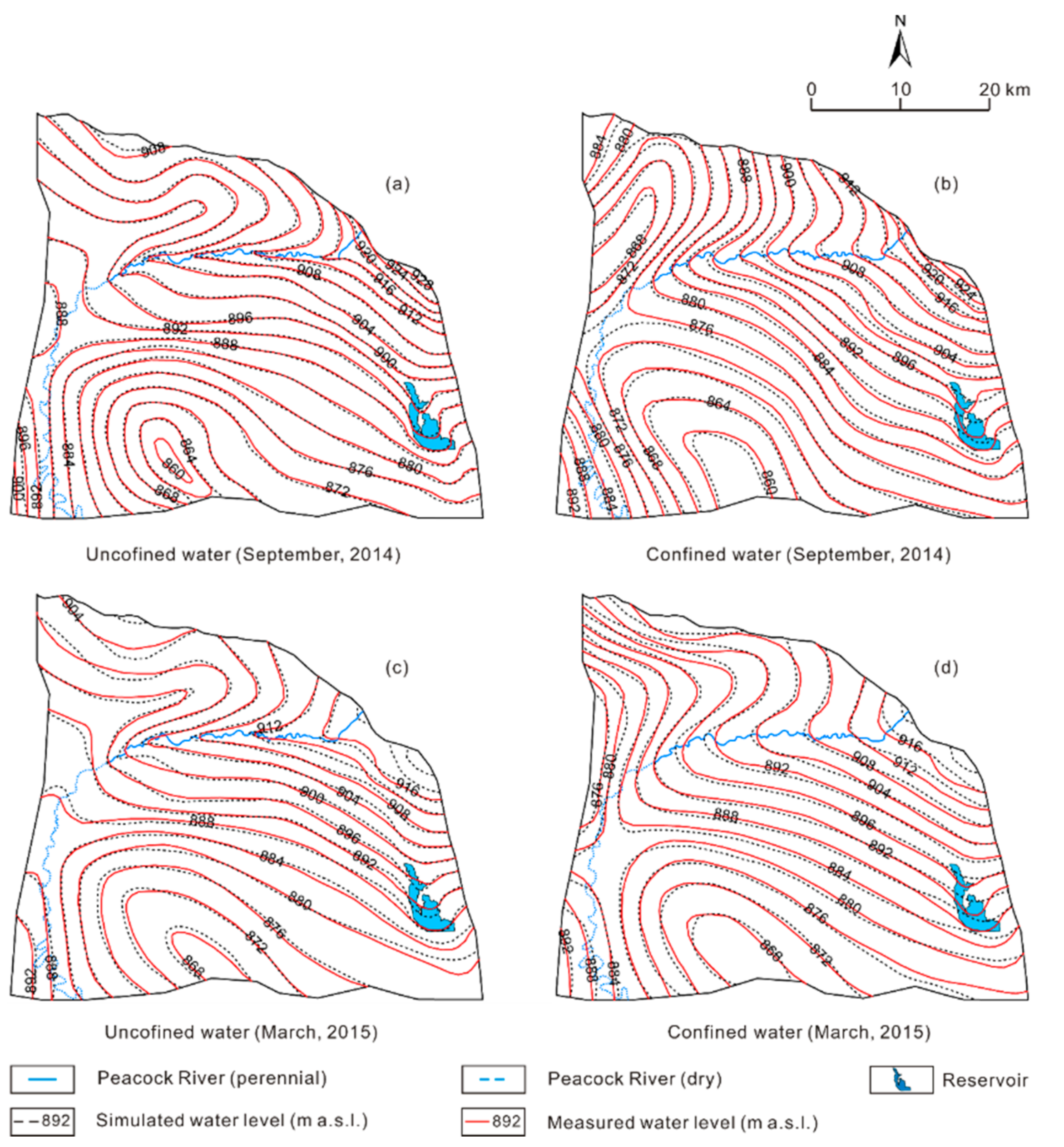
2.5. Numerical Modeling of the Groundwater Flow System
2.6. Sensitivity Analysis
2.7. Groundwater Management Schemes under Various Constraints
3. Results and Discussion
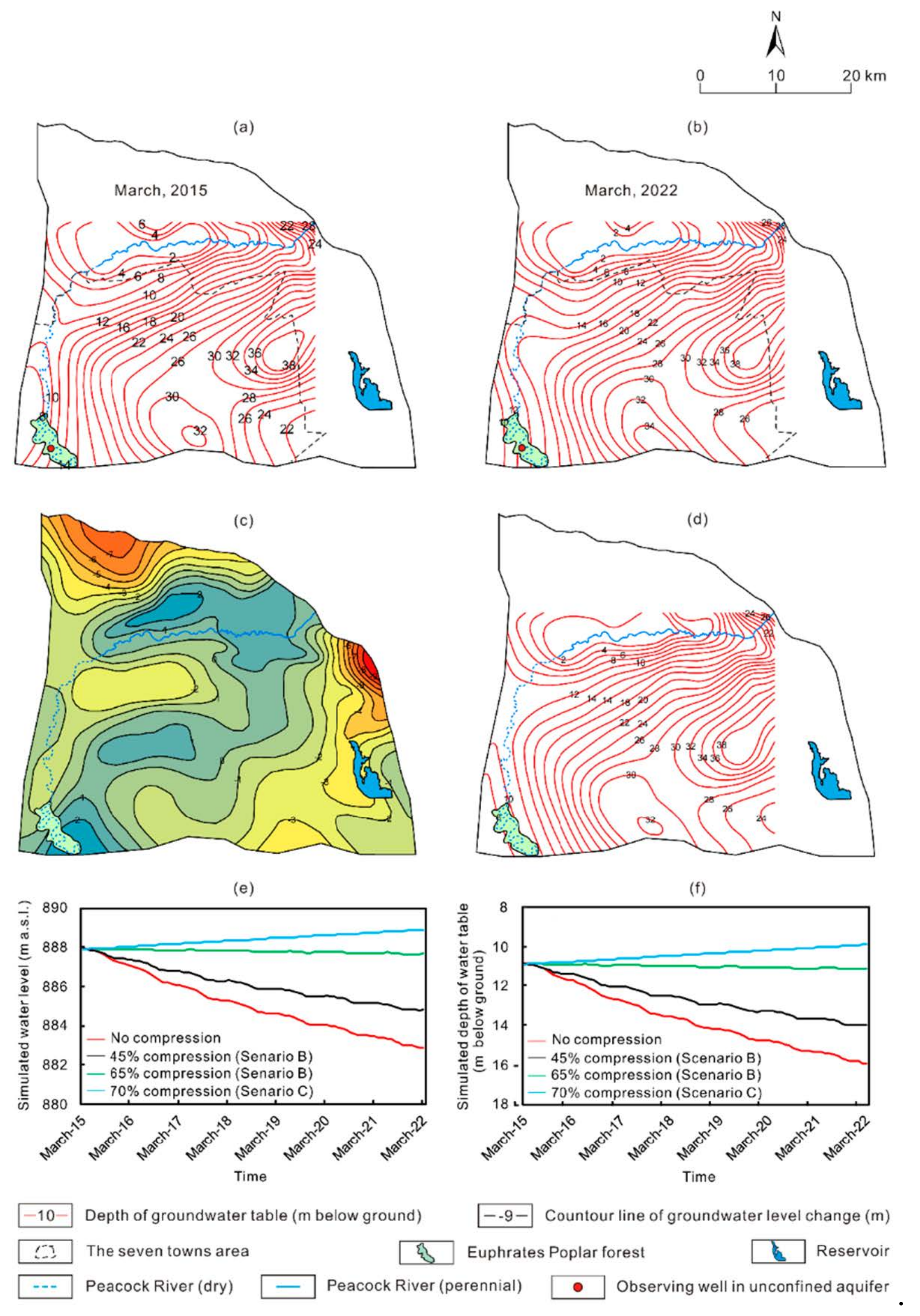
3.1. Scenario A: Current Conditions
3.2. Scenario B: Reducing Groundwater Exploitation
3.3. Scenario C: With Ecological Constraint
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, Y.L.; Shao, J.L. The Role of Ground Water in Arid/Semiarid Ecosystems, Northwest China. Groundwater 2005, 43, 471–477. [Google Scholar] [CrossRef]
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Doll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef] [Green Version]
- Abd-Elaty, I.; Ghanayem, H.M.; Zeleňáková, M.; Mésároš, P.; Saleh, O.K. Numerical Investigation for Riverbank Filtration Sustainability Considering Climatic Changes in Arid and Semi-Arid Regions; Case Study of RBF Site at Embaba, Nile Delta, Egypt. Sustainability 2021, 13, 1897. [Google Scholar] [CrossRef]
- Jasechko, S.; Perrone, D. Global groundwater wells at risk of running dry. Science 2021, 372, 418–421. [Google Scholar] [CrossRef] [PubMed]
- Lasagna, M.; Bonetto, S.M.R.; Debernardi, L.; De Luca, D.A.; Semita, C.; Caselle, C. Groundwater Resources Assessment for Sustainable Development in South Sudan. Sustainability 2020, 12, 5580. [Google Scholar] [CrossRef]
- Elshall, A.S.; Arik, A.D.; El-Kadi, A.I.; Pierce, S.; Ye, M.; Burnett, K.M.; Wada, C.A.; Bremer, L.L.; Chun, G. Groundwater sustainability: A review of the interactions between science and policy. Environ. Res. Lett. 2020, 15, 093004. [Google Scholar] [CrossRef]
- Wu, W.Y.; Lo, M.H.; Wada, Y.; Famiglietti, J.S.; Reager, J.T.; Yeh, P.J.F.; Ducharne, A.; Yang, Z.L. Nature Divergent effects of climate change on future groundwater availability in key mid–latitude aquifers. Nat. Commun. 2020, 11, 3710. [Google Scholar] [CrossRef]
- Morgenstern, U.; Daughney, C.J. Groundwater age for identification of baseline groundwater quality and impacts of land-use intensification—The National Groundwater Monitoring Programme of New Zealand. J. Hydrol. 2012, 456, 79–93. [Google Scholar] [CrossRef]
- Benini, L.; Antonellini, M.; Laghi, M.; Mollema, P.N. Assessment of water resources availability and groundwater salinization in future climate and land use change scenarios: A case study from a coastal drainage basin in Italy. Water Resour. Manag. 2016, 30, 731–745. [Google Scholar] [CrossRef]
- Ayenew, T.; Gebre, E.M.; Kebede, S.; Mamo, S. Integrated assessment of hydrogeology and water quality for groundwater-based irrigation development in the Raya Valley, northern Ethiopia. Water Int. 2013, 38, 480–492. [Google Scholar] [CrossRef]
- Custodio, E.; Andreu-Rodes, J.M.; Aragón, R.; Estrela, T.; Ferrer, J.; García-Aróstegui, J.L.; Manzano, M.; Rodríguez-Hernández, L.; Sahuquillo, A.; Del Villar, A. Groundwater intensive use and mining in south-eastern peninsular Spain: Hydrogeological, economic and social aspects. Sci. Total. Environ. 2016, 559, 302–316. [Google Scholar] [CrossRef] [Green Version]
- Alley, W.M.; Clark, B.R.; Ely, D.M.; Faunt, C.C. Groundwater Development Stress: Global-Scale Indices Compared to Regional Modeling by Indices Compared to Regional Modeling. Groundwater 2018, 56, 266–275. [Google Scholar] [CrossRef]
- Aksever, F.; Davraz, A.; Karaguzel, R. Groundwater balance estimation and sustainability in the Sandikli Basin (Afyonkarahisar/Turkey). J. Earth Syst. Sci. 2015, 124, 783–798. [Google Scholar] [CrossRef] [Green Version]
- Yosri, A.; Abd-Elmegeed, M.A.; Hassan, A.E. Assessing groundwater storage changes in the Nubian aquifer using GRACE data. Arab. J. Geosci. 2016, 9, 567. [Google Scholar] [CrossRef]
- Rateb, A.; Scanlon, B.R.; Pool, D.R.; Sun, A.; Zhang, Z.Z.; Chen, J.L.; Clark, B.; Faunt, C.C.; Haugh, C.J.; Hill, M.; et al. Comparison of Groundwater Storage Changes From GRACE Satellites With Monitoring and Modeling of Major US Aquifers. Water Resour. Res. 2020, 56, e2020WR02755. [Google Scholar] [CrossRef]
- Zhang, C.; Duan, Q.Y.; Yeh, P.J.F.; Pan, Y.; Gong, H.L.; Gong, W.; Di, Z.H.; Lei, X.H.; Liao, W.H.; Huang, Z.Y.; et al. The Effectiveness of the South–to–North Water Diversion Middle Route Project on Water Delivery and Groundwater Recovery in North China Plain. Water Resour. Res. 2020, 56, e2019WR026759. [Google Scholar] [CrossRef]
- Lezzaik, K.; Milewski, A. A quantitative assessment of groundwater resources in the Middle East and North Africa region. Hydrogeol. J. 2017, 26, 251–266. [Google Scholar] [CrossRef]
- Alam, S.; Gebremichael, M.; Li, R.; Dozier, J.; Lettenmaier, D.P. Can managed aquifer recharge mitigate the groundwater overdraft in California’s Central Valley? Water Resour. Res. 2020, 56, e2020WR027244. [Google Scholar] [CrossRef]
- Antonio, P.B.; Angela, V.; Fernando, S. Groundwater Sustainability Strategies in the Sierra de Gador–Campo de Dalias System, Southeast Spain. Water 2020, 11, 3262. [Google Scholar]
- Al-Amin, S.; Berglund, E.Z.; Mahinthakumar, G.; Larson, K.L. Assessing the effects of water restrictions on socio-hydrologic resilience for shared groundwater systems. J. Hydrol. 2018, 566, 872–885. [Google Scholar] [CrossRef]
- Quinn, N.W.T.; Oster, J.D. Innovations in Sustainable Groundwater and Salinity Management in California’s San Joaquin Valley. Sustainability 2021, 13, 6658. [Google Scholar] [CrossRef]
- Wurl, J.; Gámez, A.E.; Ivanova, A.; Lamadrid, M.A.I.; Hernández–Morales, P. Socio–hydrological resilience of an arid aquifer system, subject to changing climate and inadequate agricultural management: A case study from the Valley of Santo Domingo, Mexico. J. Hydrol. 2018, 559, 486–498. [Google Scholar] [CrossRef]
- Bouaamlat, I.; Larabi, A.; Faouzi, M. Hydrogeological investigation of an oasis–system aquifer in arid southeastern Morocco by development of a groundwater flow model. Hydrogeol. J. 2016, 24, 1479–1496. [Google Scholar] [CrossRef]
- Almuhaylan, M.R.; Ghumman, A.R.; Al–Salamah, I.S.; Ahmad, A.; Ghazaw, Y.M.; Haider, H.; Shafiquzzaman, M. Evaluating the Impacts of Pumping on Aquifer Depletion in Arid Regions Using MODFLOW, ANFIS and ANN. Water 2020, 12, 2297. [Google Scholar] [CrossRef]
- Song, J.; Yang, Y.; Sun, X.M.; Jin, L.; Wu, M.; Wu, J.F.; Wu, J.C. Basin–scale multi–objective simulation–optimization modeling for conjunctive use of surface water and groundwater in northwest China. Hydrol. Earth Syst. Sci. 2020, 24, 2323–2341. [Google Scholar] [CrossRef]
- Sefelnasr, A.; Gossel, W.; Wycisk, P. Groundwater management options in an arid environment: The Nubian Sandstone Aquifer System, Eastern Sahara. J. Arid. Environ. 2015, 122, 46–58. [Google Scholar] [CrossRef]
- Brush, C.F.; Dogrul, E.C.; Kadir, T.N. Development and Calibration of the California Central Valley Groundwater Surface Water Simulation Model (C2VSim), Version 3.02–CG; California Department of Water Resources: Sacramento, CA, USA, 2013; p. 196. [Google Scholar]
- Li, R.; Pun, M.; Bradley, J.; Ou, G.; Schneider, J.; Flyr, B.; Winter, J.; Chinta, S. Evaluating hydrologically connected surface water and groundwater using a groundwater model. J. Am. Water Resour. Assoc. 2016, 52, 799–805. [Google Scholar] [CrossRef]
- Lin, J.J.; Ma, R.; Hu, Y.L.; Su, Z.Y.; Wang, Y.X.; McCarter, C.P.R. Groundwater sustainability and groundwater/surface–water interaction in arid Dunhuang Basin, northwest China. Hydrogeol. J. 2018, 26, 1559–1572. [Google Scholar] [CrossRef]
- Wang, H.; Qin, D.Y.; Wang, Y.; Wang, F. Ecological status and its evolution trend in arid region of northwest China. J. Hydraul. Eng. 2004, 8, 8–14. [Google Scholar]
- He, K.; Wu, S.X.; Yang, Y.; Wang, D.; Zhang, S.Y.; Yin, N. Dynamic changes of land use and oasis in Xinjiang in the last 40 years. Arid Land Geogr. 2018, 41, 1333–1340. [Google Scholar]
- Ma, L.; Wei, X.M.; Bao, A.M.; Wang, S.F. Simulation of groundwater table dynamics based on Feflow in the Minqin Basin, China. J. Arid. Land 2012, 4, 123–131. [Google Scholar] [CrossRef]
- Wang, W.R.; Chen, Y.N.; Wang, W.H.; Jiang, J.X.; Cai, M.; Xu, Y.J. Evolution characteristics of groundwater and its response to climate and land–cover changes in the oasis of dried–up river in Tarim Basin. J. Hydrol. 2021, 594, 125644. [Google Scholar] [CrossRef]
- Chen, F.; Xu, X.Y.; Yang, Y.; Ding, Y.Y.; Li, J.Q.; Li, Y.Y. Investigation on the evolution trends and influencing factors of groundwater resources in China. Adv. Water Sci. 2020, 31, 811–819. [Google Scholar]
- The First Institute of Hydrogeology and Engineering Geology, Xinjiang Uygur Autonomous Region, The Second Institute of Hydrogeology and Engineering Geology, Xinjiang Uygur Autonomous Region. 1: 50,000 Hydrogeological Investigation of the Upper Peacock River; The First Institute of Hydrogeology and Engineering Geology, Xinjiang Uygur Autonomous Region, The Second Institute of Hydrogeology and Engineering Geology, Xinjiang Uygur Autonomous Region: Urumqi, China; Changji, China, 2015; pp. 135–139. [Google Scholar]
- Wei, X.; Zhou, J.L.; Zeng, Y.Y.; Feng, S.T.; Wang, Y. Dynamics and Influence Factors of Groundwater Depth in Korla with Intensive Exploitation. J. Yangtze River Sci. Res. Inst. 2019, 36, 46–59, 63. [Google Scholar]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. MODFLOW–2000, the U.S. Geological Survey Modular Ground–Water Model, User’s Guide to the Modularization Concepts and the Ground–Water Flow Process: U.S. Geological Survey Open–File Report 00–92. Available online: http://water.usgs.gov/nrp/gwsoftware/modflow2000/modflow2000.html (accessed on 4 September 2003).
- Yang, F.T.; Chen, Y.X.; Zhang, P.; Zhang, X. Report on Coefficients of Precipitation and Irrigation Infiltration in Korla City; Institute of Water Resources and Environment, Jilin University: Changchun, China, 2014; pp. 26–53. [Google Scholar]
- Zhao, Y.J. A Study on the Influence Factors and Calculation Method for Phreatic Water in Xinjiang Plain Area; Xinjiang Agricultural University: Urumqi, China, 2012; pp. 26–27. [Google Scholar]
- Prasad, Y.S.; Rao, B.V.; Surinaidu, L. Groundwater flow modeling and prognostics of Kandivalasa river sub-basin, Andhra Pradesh, India. Environ. Dev. Sustain. 2021, 23, 1823–1843. [Google Scholar] [CrossRef]
- Korla Municipal Bureau of Water Resources. Remediation Scheme of Groundwater Overexploitation Area in Korla City (2016–2030). Available online: http://www.xjkel.gov.cn/gk/gfxwj/fzbfw/190312.htm (accessed on 25 February 2018).
- Lei, M.; Zhou, J.L.; Wei, X.; Zhang, J.; Fan, W. Assessment of comprehensive control of groundwater over-exploitation areas of oasis city in arid region. Yellow River 2021, 43, 100–105. [Google Scholar]
- Liu, B. Groundwater Investigation of the Tarim Basin; Geology Press: Beijing, China, 2008; p. 234. ISBN 9787116059078-1-00580. [Google Scholar]
- Administration of City and Country Planning of Korla. Korla City Master Plan (2012–2030). Available online: http://www.xjkel.gov.cn/gk/kelfcflbgg/29189.htm (accessed on 27 February 2013).
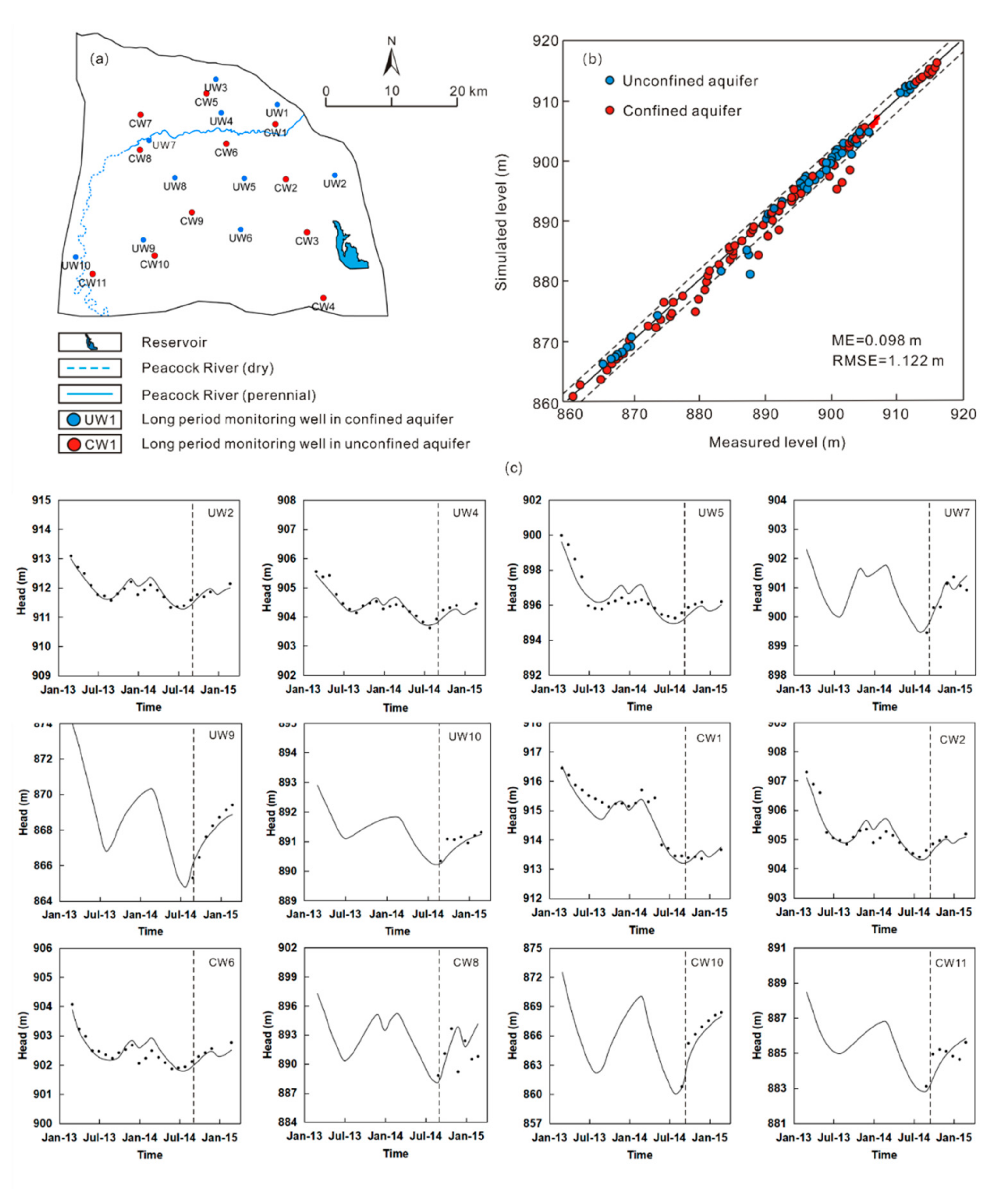
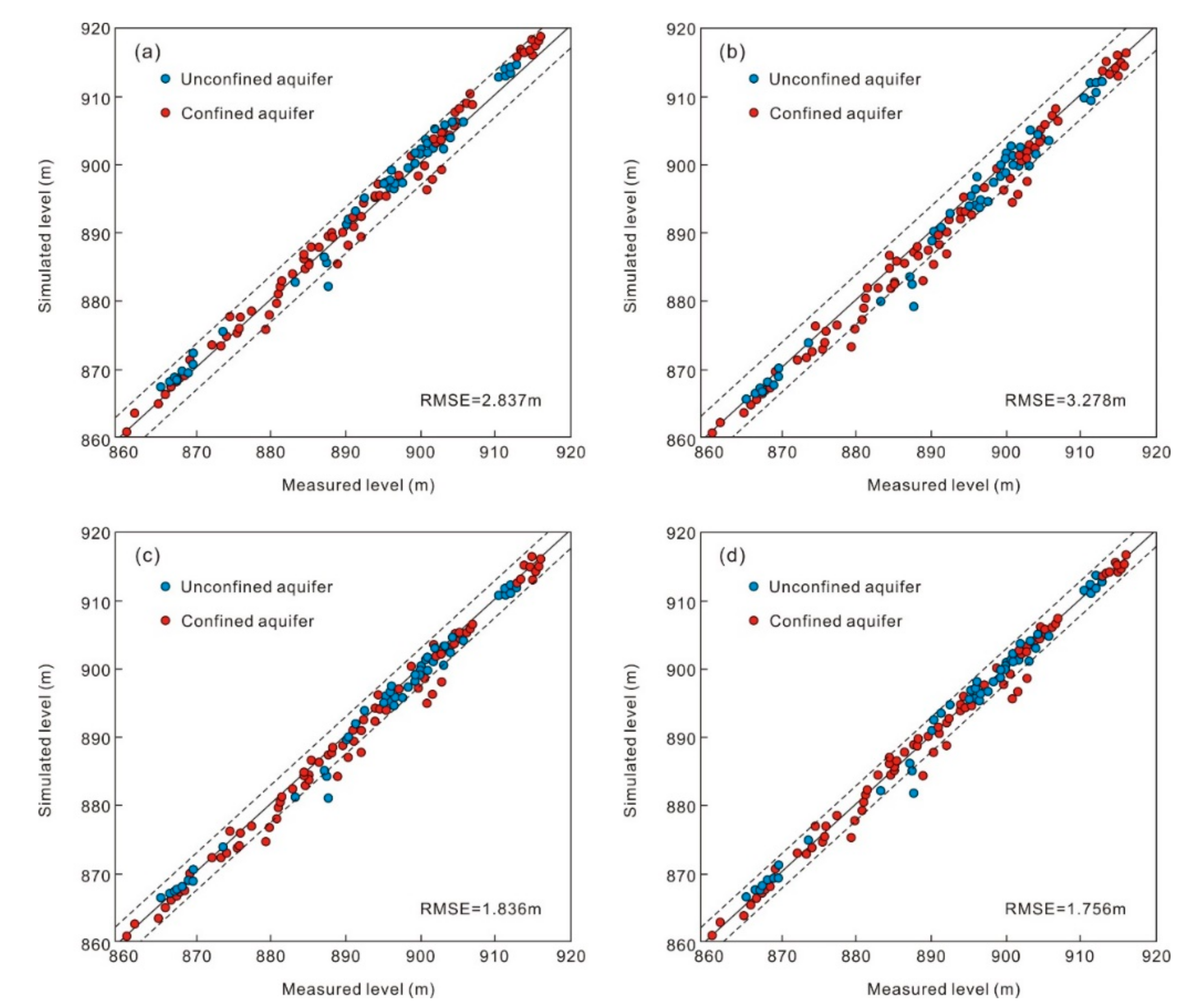

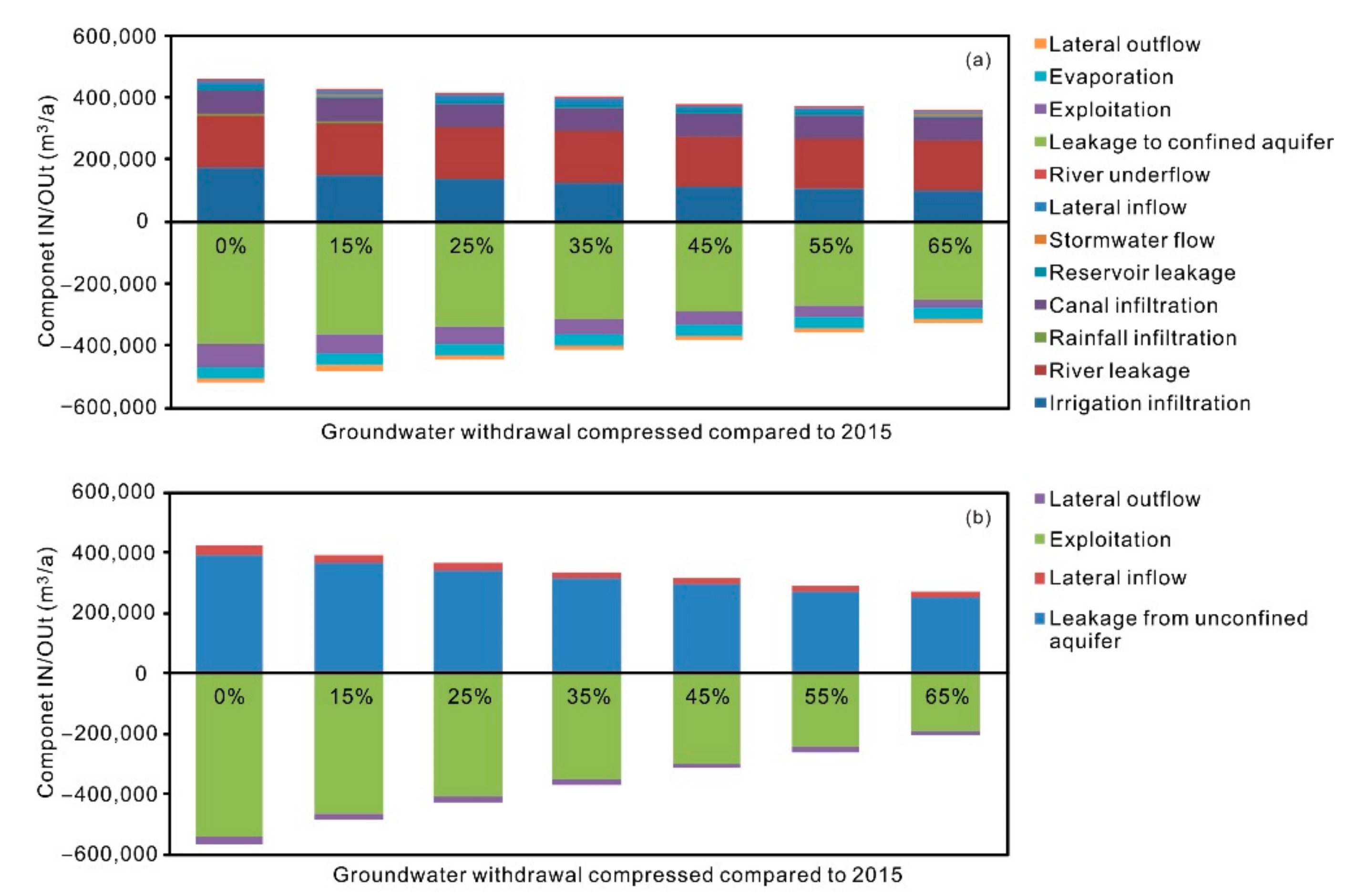
| River Reaches | Kv (m/d) | M (m) |
|---|---|---|
| 1st–2nd water diversion station | 40–100 | 0.01–0.05 |
| 2nd water diversion station–SG07 | 20–40 | 0.05–0.15 |
| SG07–3rd water diversion station | 5–20 | 0.15–0.25 |
| Component IN (103 m3/a) | Unconfined Aquifer | Confined Aquifer |
|---|---|---|
| Irrigation infiltration a | 172,239.8 | |
| River leakage | 172,721.2 | |
| Canal infiltration | 75,965.0 | |
| Lateral inflow b | 19,510.3 | 28,340.2 |
| Reservoir leakage b | 10,389.5 | |
| River underflow at mountain front a | 3531.6 | |
| Stormwater flow a | 944.1 | |
| Rainfall infiltration | 901.6 | |
| Leakage to unconfined/confined aquifer b | 392,717.6 | |
| Total IN | 456,203.0 | 421,057.8 |
| Component OUT (103 m3/a) | Unconfined aquifer | Confined aquifer |
| Exploitation a | 75,149.8 | 545,433.1 |
| Evaporation b | 35,395.3 | |
| Lateral outflow b | 17,894.4 | 23,275.4 |
| Leakage to unconfined/confined aquifer b | 392,716.3 | |
| Total OUT | 521,155.8 | 568,708.5 |
| Balance IN-OUT | −64,952.8 | −147,650.7 |
| Water budget of the study area | −212,603.5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Yang, F.; Chen, Y.; Zhang, P.; Zhang, X. Optimization of Groundwater Exploitation in an Irrigation Area in the Arid Upper Peacock River, NW China: Implications for Sustainable Agriculture and Ecology. Sustainability 2021, 13, 8903. https://doi.org/10.3390/su13168903
Su Y, Yang F, Chen Y, Zhang P, Zhang X. Optimization of Groundwater Exploitation in an Irrigation Area in the Arid Upper Peacock River, NW China: Implications for Sustainable Agriculture and Ecology. Sustainability. 2021; 13(16):8903. https://doi.org/10.3390/su13168903
Chicago/Turabian StyleSu, Yujuan, Fengtian Yang, Yaoxuan Chen, Pan Zhang, and Xue Zhang. 2021. "Optimization of Groundwater Exploitation in an Irrigation Area in the Arid Upper Peacock River, NW China: Implications for Sustainable Agriculture and Ecology" Sustainability 13, no. 16: 8903. https://doi.org/10.3390/su13168903
APA StyleSu, Y., Yang, F., Chen, Y., Zhang, P., & Zhang, X. (2021). Optimization of Groundwater Exploitation in an Irrigation Area in the Arid Upper Peacock River, NW China: Implications for Sustainable Agriculture and Ecology. Sustainability, 13(16), 8903. https://doi.org/10.3390/su13168903







