Advancements in Geo-Inclusions for Ballasted Track: Constitutive Modelling and Numerical Analysis
Abstract
:1. Introduction
2. Use of Waste Mixture for Subballast (Capping) Layer in Rail Tracks
2.1. Constitutive Modelling
2.1.1. Governing Equations
2.1.2. The Critical State
2.1.3. Bounding Surface and Loading Surface
2.1.4. Plastic Potential
2.1.5. Hardening Law
2.1.6. Parameters Calibration
2.2. Model Validation
3. Discrete Element Modelling (DEM) of Ballasted Tracks Stabilised with Rubber Mats
3.1. Modelling of Ballast Grains in DEM
3.2. Coupled Discrete-Continuum Modelling (DEM-FEM) for Ballasted Tracks with Rubber Mats
3.3. Particle Breakage
4. Conclusions
- A bounding surface model for SFS+CW+RC mixtures as a form of potential capping layer was introduced and validated based on laboratory data. The energy-absorbing characteristics of the mixture with different rubber contents were captured through an empirical relationship between the critical stress ratio () and the total work input (). The proposed model was also validated by considering other rubber-soil mixtures tested during previous studies [26,40]. The predicted stress-strain behaviour of the mixture was comparable with the laboratory observations. The observed properties of this compacted waste product could be considered favourable as an alternative capping medium to be adopted in railways, in lieu of traditional (geologic) materials.
- The changes of broken bonds (representing ballast breakage) and the re-distribution and re-orientation of contact forces to support the external loads were captured via the coupled DEM-FEM modelling. The predicted results were in satisfactory agreement with the large-scale laboratory data. The inclusion of rubber mats reduced the broken bonds and the magnitude of maximum contact forces, hence reducing ballast deformation and degradation.
- The constitutive and numerical modelling facilitated the analysis and investigation of track performance incorporating resilient recycled rubber materials (i.e., rubber crumbs and rubber shock mats). The proposed critical state surface capturing the energy-absorbing characteristics of the waste blends including RC is suitable for and can be extended to relevant studies on rubber-soil mixtures. The established DEM-FEM modelling provides a novel approach for further studies to look into the combined micro and macro-mechanical response of ballasted tracks considering ballast degradation. From an environmental sustainability perspective, the use of recycled waste products in track construction and rehabilitation will contribute not only to reduce waste disposal volumes to landfills, but also to more effective use of non-renewable natural resources, thereby reducing the carbon footprint of future rail infrastructure projects.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Indraratna, B.; Lackenby, J.; Christie, D. Effect of confining pressure on the degradation of ballast under cyclic loading. Geotechnique 2005, 55, 325–328. [Google Scholar] [CrossRef]
- Zhai, W.; Wei, K.; Song, X.; Shao, M. Experimental investigation into ground vibrations induced by very high speed trains on a non-ballasted track. Soil Dyn. Earthq. Eng. 2015, 72, 24–36. [Google Scholar] [CrossRef] [Green Version]
- Indraratna, B.; Nimbalkar, S.S.; Ngo, T.; Neville, T. Performance improvement of rail track substructure using artificial inclusions—Experimental and numerical studies. Transp. Geotech. 2016, 8, 69–85. [Google Scholar] [CrossRef] [Green Version]
- Tennakoon, N.; Indraratna, B.; Rujikiatkamjorn, C.; Nimbalkar, S.; Neville, T. The Role of Ballast-Fouling Characteristics on the Drainage Capacity of Rail Substructure. Geotech. Test. J. 2012, 35, 629–640. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Tutumluer, E. Discrete Element Modeling for fouled railroad ballast. Constr. Build. Mater. 2011, 25, 3306–3312. [Google Scholar] [CrossRef]
- Leng, J.; Gabr, M. Characteristics of Geogrid-Reinforced Aggregate Under Cyclic Load. Transp. Res. Rec. J. Transp. Res. Board 2002, 1786, 29–35. [Google Scholar] [CrossRef]
- Biabani, M.M.; Ngo, N.T.; Indraratna, B. Performance evaluation of railway subballast stabilised with geocell based on pull-out testing. Geotext. Geomembr. 2016, 44, 579–591. [Google Scholar] [CrossRef] [Green Version]
- Indraratna, B.; Qi, Y.; Tawk, M.; Heitor, A.; Rujikiatkamjorn, C.; Navaratnarajah, S.K. Advances in ground improvement using waste materials for transportation infrastructure. Proc. Inst. Civ. Eng. Ground Improv. 2020, 1–20. [Google Scholar] [CrossRef]
- Liu, C.; Indraratna, B.; Rujikiatkamjorn, C. An analytical model for particle-geogrid aperture interaction. Geotext. Geomembr. 2020, 49, 41–44. [Google Scholar] [CrossRef]
- Jayasuriya, C.; Indraratna, B.; Ngo, T. Experimental study to examine the role of under sleeper pads for improved performance of ballast under cyclic loading. Transp. Geotech. 2019, 19, 61–73. [Google Scholar] [CrossRef]
- Tawk, M.; Qi, Y.; Indraratna, B.; Rujikiatkamjorn, C.; Heitor, A. Behavior of a Mixture of Coal Wash and Rubber Crumbs under Cyclic Loading. J. Mater. Civ. Eng. 2021, 33, 04021054. [Google Scholar] [CrossRef]
- Koohmishi, M.; Azarhoosh, A. Hydraulic conductivity of fresh railway ballast mixed with crumb rubber considering size and percentage of crumb rubber as well as aggregate gradation. Constr. Build. Mater. 2020, 241, 118133. [Google Scholar] [CrossRef]
- Indraratna, B.; Ngo, N.T.; Nimbalkar, S.; Rujikiatkamjorn, C. Two Decades of Advancement in Process Simulation Testing of Ballast Strength, Deformation, and Degradation. In Railroad Ballast Testing and Properties; ASTM International: West Conshohocken, PA, USA, 2018; pp. 11–38. [Google Scholar] [CrossRef]
- Navaratnarajah, S.K.; Indraratna, B.; Ngo, N.T. Influence of Under Sleeper Pads on Ballast Behavior under Cyclic Loading: Experimental and Numerical Studies. J. Geotech. Geoenviron. Eng. 2018, 144, 04018068. [Google Scholar] [CrossRef]
- Leventhal, A.; de Ambrosis, L. Waste disposal in coal mining—A geotechnical analysis. Eng. Geol. 1985, 22, 83–96. [Google Scholar] [CrossRef]
- Qi, Y.; Indraratna, B.; Heitor, A.; Vinod, J.S. Closure to “Effect of Rubber Crumbs on the Cyclic Behavior of Steel Furnace Slag and Coal Wash Mixtures” by Yujie Qi, Buddhima Indraratna, Ana Heitor, and Jayan S. Vinod. J. Geotech. Geoenviron. Eng. 2019, 145, 07018035. [Google Scholar] [CrossRef] [Green Version]
- Xue, Y.; Wu, S.; Hou, H.; Zha, J. Experimental investigation of basic oxygen furnace slag used as aggregate in asphalt mixture. J. Hazard. Mater. 2006, 138, 261–268. [Google Scholar] [CrossRef] [PubMed]
- Malasavage, N.E.; Jagupilla, S.; Grubb, D.G.; Wazne, M.; Coon, W.P. Geotechnical Performance of Dredged Material—Steel Slag Fines Blends: Laboratory and Field Evaluation. J. Geotech. Geoenviron. Eng. 2012, 138, 981–991. [Google Scholar] [CrossRef]
- Khan, M.; Castel, A.; Akbarnezhad, A.; Foster, S.; Smith, M. Utilisation of steel furnace slag coarse aggregate in a low calcium fly ash geopolymer concrete. Cem. Concr. Res. 2016, 89, 220–229. [Google Scholar] [CrossRef]
- Yildirim, I.Z.; Prezzi, M. Geotechnical Properties of Fresh and Aged Basic Oxygen Furnace Steel Slag. J. Mater. Civ. Eng. 2015, 27, 04015046. [Google Scholar] [CrossRef]
- Chiaro, G.; Indraratna, B.; Tasalloti, S.A.; Rujikiatkamjorn, C. Optimisation of coal wash–slag blend as a structural fill. Proc. Inst. Civ. Eng. Ground Improv. 2015, 168, 33–44. [Google Scholar] [CrossRef] [Green Version]
- Qi, Y.; Indraratna, B.; Heitor, A.; Vinod, J.S. The Influence of Rubber Crumbs on the Energy Absorbing Property of Waste Mixtures. In Geotechnics for Transportation Infrastructure; Springer: Singapore, 2019; pp. 271–281. [Google Scholar] [CrossRef] [Green Version]
- Qi, Y.; Indraratna, B. Energy-Based Approach to Assess the Performance of a Granular Matrix Consisting of Recycled Rubber, Steel-Furnace Slag, and Coal Wash. J. Mater. Civ. Eng. 2020, 32, 04020169. [Google Scholar] [CrossRef]
- Kim, H.-K.; Santamarina, J.C. Sand–rubber mixtures (large rubber chips). Can. Geotech. J. 2008, 45, 1457–1466. [Google Scholar] [CrossRef] [Green Version]
- Mohajerani, A.; Burnett, L.; Smith, J.V.; Markovski, S.; Rodwell, G.; Rahman, T.; Kurmus, H.; Mirzababaei, M.; Arulrajah, A.; Horpibulsuk, S.; et al. Recycling waste rubber tyres in construction materials and associated environmental considerations: A review. Resour. Conserv. Recycl. 2020, 155, 104679. [Google Scholar] [CrossRef]
- Youwai, S.; Bergado, D.T. Strength and deformation characteristics of shredded rubber tire—Sand mixtures. Can. Geotech. J. 2003, 40, 254–264. [Google Scholar] [CrossRef]
- Indraratna, B.; Qi, Y.; Heitor, A. Evaluating the Properties of Mixtures of Steel Furnace Slag, Coal Wash, and Rubber Crumbs Used as Subballast. J. Mater. Civ. Eng. 2018, 30, 04017251. [Google Scholar] [CrossRef] [Green Version]
- Qi, Y.; Indraratna, B. The Influence of Rubber Inclusion on the Dynamic Response of Rail Track. J. Mater. Civ. Eng. 2021, in press. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, C.; Markine, V.; Jing, G.; Zhai, W. Calibration for discrete element modelling of railway ballast: A review. Transp. Geotech. 2020, 23, 100341. [Google Scholar] [CrossRef]
- Shi, C.; Zhao, C.; Zhang, X.; Guo, Y. Coupled discrete-continuum approach for railway ballast track and subgrade macro-meso analysis. Int. J. Pavement Eng. 2020, 1–16. [Google Scholar] [CrossRef]
- Huang, Z.-Y.; Yang, Z.-X.; Wang, Z.-Y. Discrete element modeling of sand behavior in a biaxial shear test. J. Zhejiang Univ. A 2008, 9, 1176–1183. [Google Scholar] [CrossRef]
- O’Sullivan, C.; Cui, L. Micromechanics of granular material response during load reversals: Combined DEM and experimental study. Powder Technol. 2009, 193, 289–302. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Spiryagin, M.; Cole, C.; McSweeney, T. Parallel computing in railway research. Int. J. Rail Transp. 2020, 8, 111–134. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhao, C.; Zhai, W. Importance of load frequency in applying cyclic loads to investigate ballast deformation under high-speed train loads. Soil Dyn. Earthq. Eng. 2019, 120, 28–38. [Google Scholar] [CrossRef]
- Ngo, T.; Indraratna, B. Analysis of Deformation and Degradation of Fouled Ballast: Experimental Testing and DEM Modeling. Int. J. Géoméch. 2020, 20, 06020020. [Google Scholar] [CrossRef]
- Nishiura, D.; Sakai, H.; Aikawa, A.; Tsuzuki, S.; Sakaguchi, H. Novel discrete element modeling coupled with finite element method for investigating ballasted railway track dynamics. Comput. Geotech. 2018, 96, 40–54. [Google Scholar] [CrossRef]
- Lim, N.-H.; Kim, K.-J.; Bae, H.-U.; Kim, S. DEM Analysis of Track Ballast for Track Ballast–Wheel Interaction Simulation. Appl. Sci. 2020, 10, 2717. [Google Scholar] [CrossRef] [Green Version]
- Qi, Y.; Indraratna, B.; Coop, M.R. Predicted Behavior of Saturated Granular Waste Blended with Rubber Crumbs. Int. J. Géoméch. 2019, 19, 04019079. [Google Scholar] [CrossRef] [Green Version]
- Qi, Y.; Indraratna, B.; Vinod, J.S. Behavior of steel furnace slag, coal wash, and rubber crumb mixtures with special relevance to stress–dilatancy relation. J. Mater. Civ. Eng. 2018, 30, 04018276. [Google Scholar] [CrossRef] [Green Version]
- Tasalloti, A.; Indraratna, B.; Rujikiatkamjorn, C.; Heitor, A.; Chiaro, G. A Laboratory Study on the Shear Behavior of Mixtures of Coal Wash and Steel Furnace Slag as Potential Structural Fill. Geotech. Test. J. 2015, 38, 361–372. [Google Scholar] [CrossRef] [Green Version]
- Dafalias, Y.F. Bounding Surface Plasticity. I: Mathematical Foundation and Hypoplasticity. J. Eng. Mech. 1986, 112, 966–987. [Google Scholar] [CrossRef]
- Carrera, A.; Coop, M.; Lancellotta, R. Influence of grading on the mechanical behaviour of Stava tailings. Géotechnique 2011, 61, 935–946. [Google Scholar] [CrossRef]
- Chávez, C.; Alonso, E. A Constitutive Model for Crushed Granular Aggregates Which Includes Suction Effects. Soils Found. 2003, 43, 215–227. [Google Scholar] [CrossRef] [Green Version]
- Zornberg, J.G.; Cabral, A.R.; Viratjandr, C. Behaviour of tire shred—Sand mixtures. Can. Geotech. J. 2004, 41, 227–241. [Google Scholar] [CrossRef]
- Russell, A.R.; Khalili, N. A bounding surface plasticity model for sands exhibiting particle crushing. Can. Geotech. J. 2004, 41, 1179–1192. [Google Scholar] [CrossRef]
- Fang, H.; Wang, W. A Three-Dimensional Multishear Bounding Surface Model of Granular Soil–Structure Interfaces under Monotonic and Cyclic Loading. J. Eng. Mech. 2020, 146, 04020068. [Google Scholar] [CrossRef]
- Wang, Z.-L. Bounding Surface Hypoplasticity Model for Granular Soils and Its Applications; University of California: Davis, CA, USA, 1990. [Google Scholar]
- Xiao, Y.; Sun, Z.; Stuedlein, A.; Wang, C.; Wu, Z.; Zhang, Z. Bounding surface plasticity model for stress-strain and grain-crushing behaviors of rockfill materials. Geosci. Front. 2020, 11, 495–510. [Google Scholar] [CrossRef]
- Kadivar, M.; Manahiloh, K.N.; Kaliakin, V.N. A Bounding Surface Based Constitutive Model for Unsaturated Granular Soils. Geo-Congress 2019: Geotechnical Materials, Modeling, and Testing; American Society of Civil Engineers: Reston, VA, USA, 2019. [Google Scholar]
- Kaliakin, V.N.; Dafalias, Y.F. Theoretical Aspects of the Elastoplastic-Viscoplastic Bounding Surface Model for Cohesive Soils. Soils Found. 1990, 30, 11–24. [Google Scholar] [CrossRef] [Green Version]
- Kan, M.E.; Taiebat, H.A.; Khalili, N. Simplified Mapping Rule for Bounding Surface Simulation of Complex Loading Paths in Granular Materials. Int. J. Géoméch. 2014, 14, 239–253. [Google Scholar] [CrossRef] [Green Version]
- Kan, M.E.; Taiebat, H.A. A bounding surface plasticity model for highly crushable granular materials. Soils Found. 2014, 54, 1188–1201. [Google Scholar] [CrossRef] [Green Version]
- Been, K.; Jefferies, M.G. A state parameter for sands. Géotechnique 1985, 35, 99–112. [Google Scholar] [CrossRef]
- Wroth, C.P.; Bassett, R.H. A Stress–Strain Relationship for the Shearing Behaviour of a Sand. Géotechnique 1965, 15, 32–56. [Google Scholar] [CrossRef]
- Li, X.S.; Dafalias, Y.F. Dilatancy for cohesionless soils. Géotechnique 2000, 50, 449–460. [Google Scholar] [CrossRef]
- Khalili, N.; Habte, M.; Zargarbashi, S. A fully coupled flow deformation model for cyclic analysis of unsaturated soils including hydraulic and mechanical hystereses. Comput. Geotech. 2008, 35, 872–889. [Google Scholar] [CrossRef]
- Sun, Y.; Xiao, Y.; Ju, W. Bounding surface model for ballast with additional attention on the evolution of particle size distribution. Sci. China Ser. E Technol. Sci. 2014, 57, 1352–1360. [Google Scholar] [CrossRef]
- Khalili, N.; Habte, M.A.; Valliappan, S. A bounding surface plasticity model for cyclic loading of granular soils. Int. J. Numer. Methods Eng. 2005, 63, 1939–1960. [Google Scholar] [CrossRef]
- Chen, J.Y.; Ummin, O.; Yu, T.; Qi, Y.J. Applications of Rayleigh Wave Detection Technique and Polymer Grouting Technology in Waterproof Construction. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2013. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Tutumluer, E.; Qian, Y.; Hashash, Y.M.; Ghaboussi, J.; Davis, D.D. Discrete element modelling of ballasted track deformation behaviour. Int. J. Rail Transp. 2013, 1, 57–73. [Google Scholar] [CrossRef]
- Tran, K.M.; Bui, H.H.; Sánchez, M.; Kodikara, J. A DEM approach to study desiccation processes in slurry soils. Comput. Geotech. 2020, 120, 103448. [Google Scholar] [CrossRef]
- Tran, V.D.H.; Meguid, M.; Chouinard, L.E. Discrete Element and Experimental Investigations of the Earth Pressure Distribution on Cylindrical Shafts. Int. J. Géoméch. 2014, 14, 80–91. [Google Scholar] [CrossRef]
- McDowell, G.R.; Bolton, M.D. On the micromechanics of crushable aggregates. Geotechnique 1998, 48, 667–679. [Google Scholar] [CrossRef] [Green Version]
- Lu, M.; McDowell, G.R. Discrete element modelling of ballast abrasion. Geotechnique 2006, 56, 651–655. [Google Scholar] [CrossRef]
- Ngo, T.; Indraratna, B.; Rujikiatkamjorn, C. DEM simulation of the behaviour of geogrid stabilised ballast fouled with coal. Comput. Geotech. 2014, 55, 224–231. [Google Scholar] [CrossRef] [Green Version]
- Yimsiri, S.; Soga, K. Micromechanics-based stress–strain behaviour of soils at small strains. Geotechnique 2000, 50, 559–571. [Google Scholar] [CrossRef]
- Ngo, N.T.; Indraratna, B.; Rujikiatkamjorn, C. Micromechanics-based investigation of fouled ballast using large-scale triaxial tests and discrete element modeling. J. Geotech. Geoenviron. Eng. 2017, 143, 04016089. [Google Scholar] [CrossRef] [Green Version]
- Suhr, B.; Marschnig, S.; Six, K. Comparison of two different types of railway ballast in compression and direct shear tests: Experimental results and DEM model validation. Granul. Matter 2018, 20, 70. [Google Scholar] [CrossRef] [Green Version]
- Cui, L.; O’sullivan, C. Exploring the macro-and micro-scale response of an idealised granular material in the direct shear apparatus. Géotechnique 2006, 56, 455–468. [Google Scholar] [CrossRef]
- Li, H.; McDowell, G. Discrete element modelling of two-layered ballast in a box test. Granul. Matter 2020, 22, 76. [Google Scholar] [CrossRef]
- Cheng, Y.; Bolton, M.; Nakata, Y. Grain crushing and critical states observed in DEM simulations. P&G05 2005, 2, 1393–1397. [Google Scholar]
- Bhandari, A.; Han, J. Investigation of geotextile–soil interaction under a cyclic vertical load using the discrete element method. Geotext. Geomembr. 2010, 28, 33–43. [Google Scholar] [CrossRef]
- Indraratna, B.; Ngo, T.; Rujikiatkamjorn, C. Performance of Ballast Influenced by Deformation and Degradation: Laboratory Testing and Numerical Modeling. Int. J. Géoméch. 2020, 20, 04019138. [Google Scholar] [CrossRef] [Green Version]
- Indraratna, B.; Salim, W.; Rujikiatkamjorn, C. Advanced Rail Geotechnology-Ballasted Track; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- AS:2758.7. Standard Australia, Aggregates and Rock for Engineering Purposes in Part 7. Railway Ballast. Australia. 2015. Available online: https://www.techstreet.com/standards/as-2758-7-2015?product_id=2058243 (accessed on 30 June 2015).
- Guo, N.; Zhao, J. A coupled FEM/DEM approach for hierarchical multiscale modelling of granular media. Int. J. Numer. Methods Eng. 2014, 99, 789–818. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Indraratna, B.; Ngo, N.T. Effect of increase in load and frequency on the resilience of railway ballast. Géotechnique 2019, 69, 833–840. [Google Scholar] [CrossRef] [Green Version]

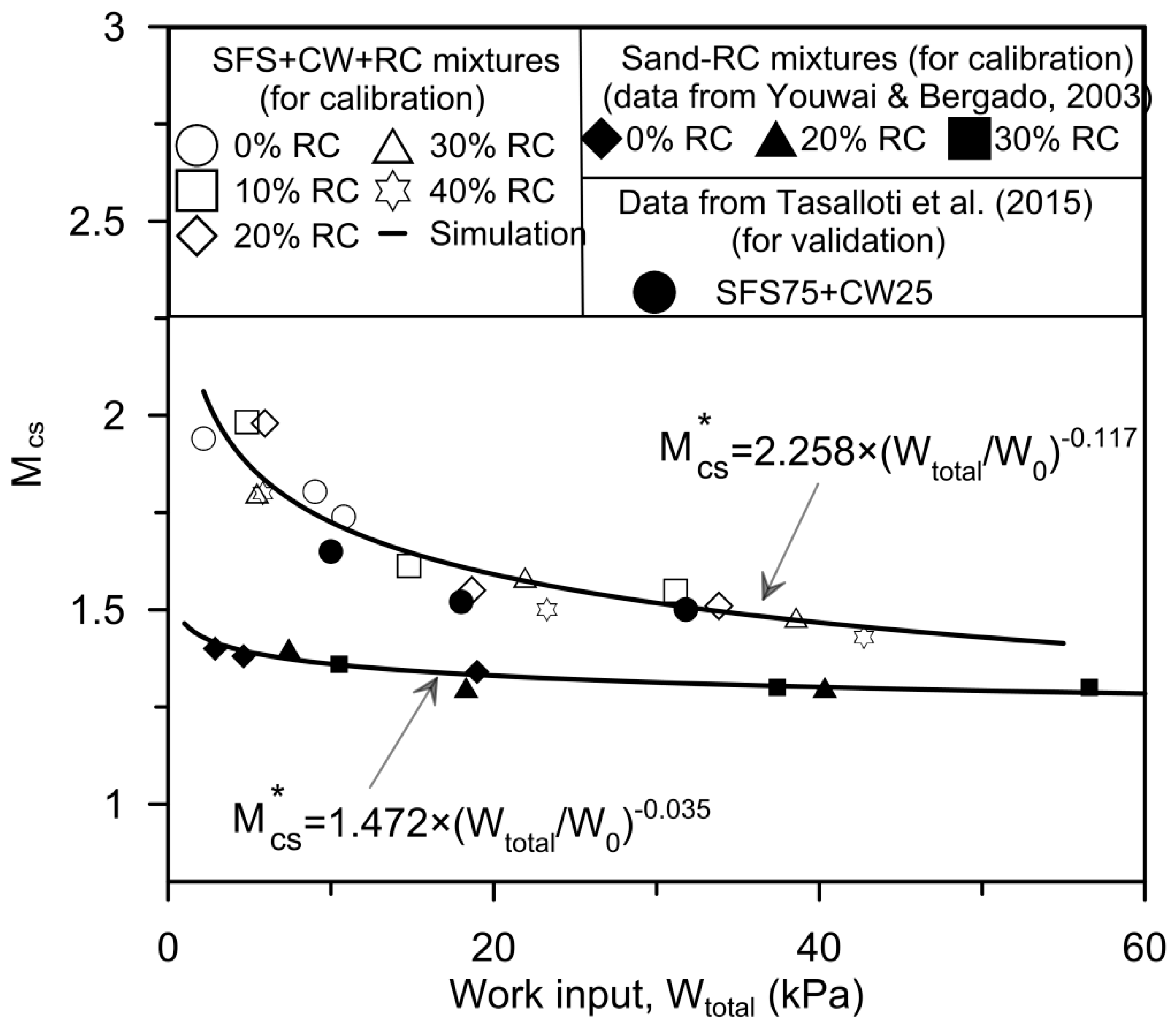
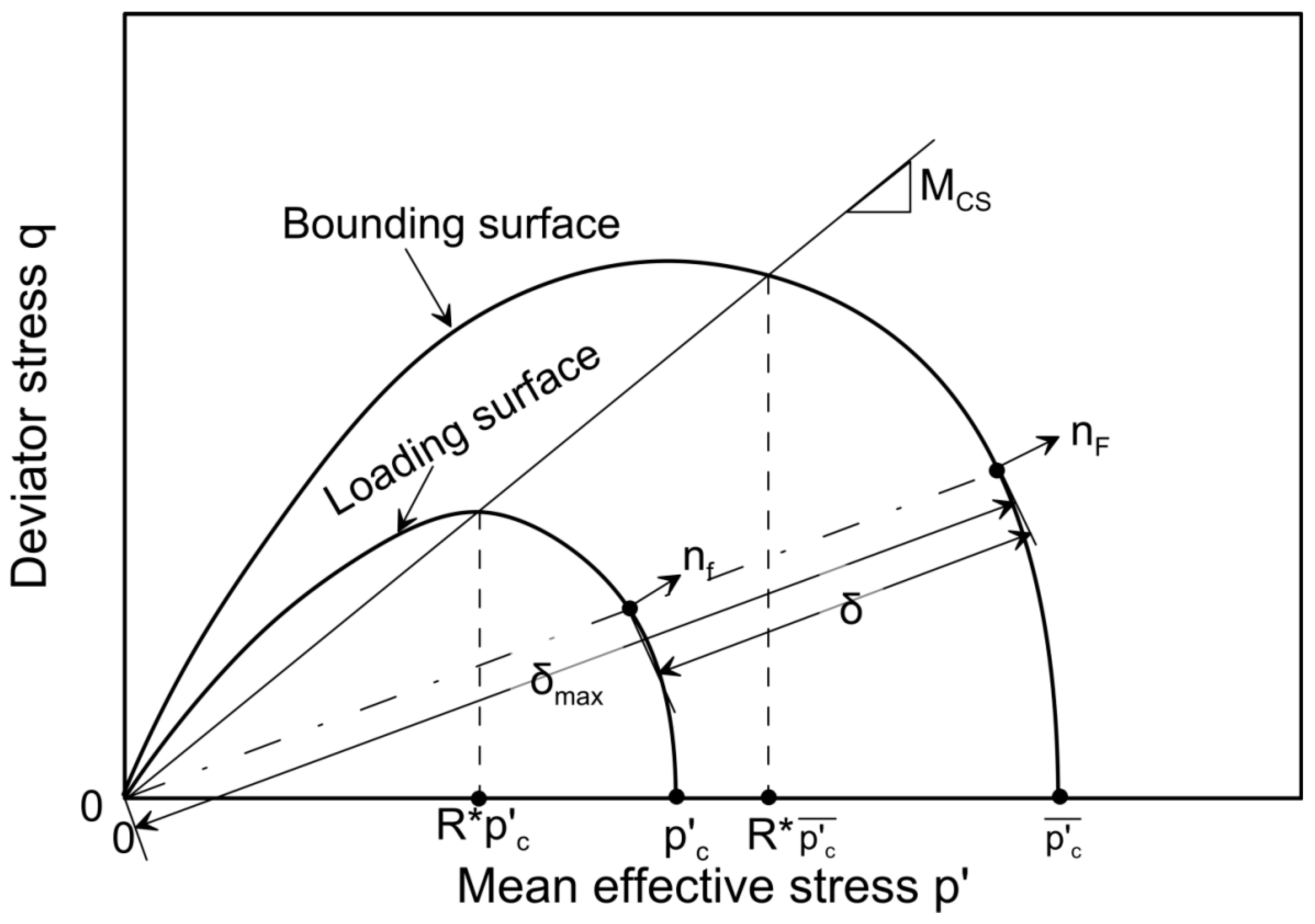
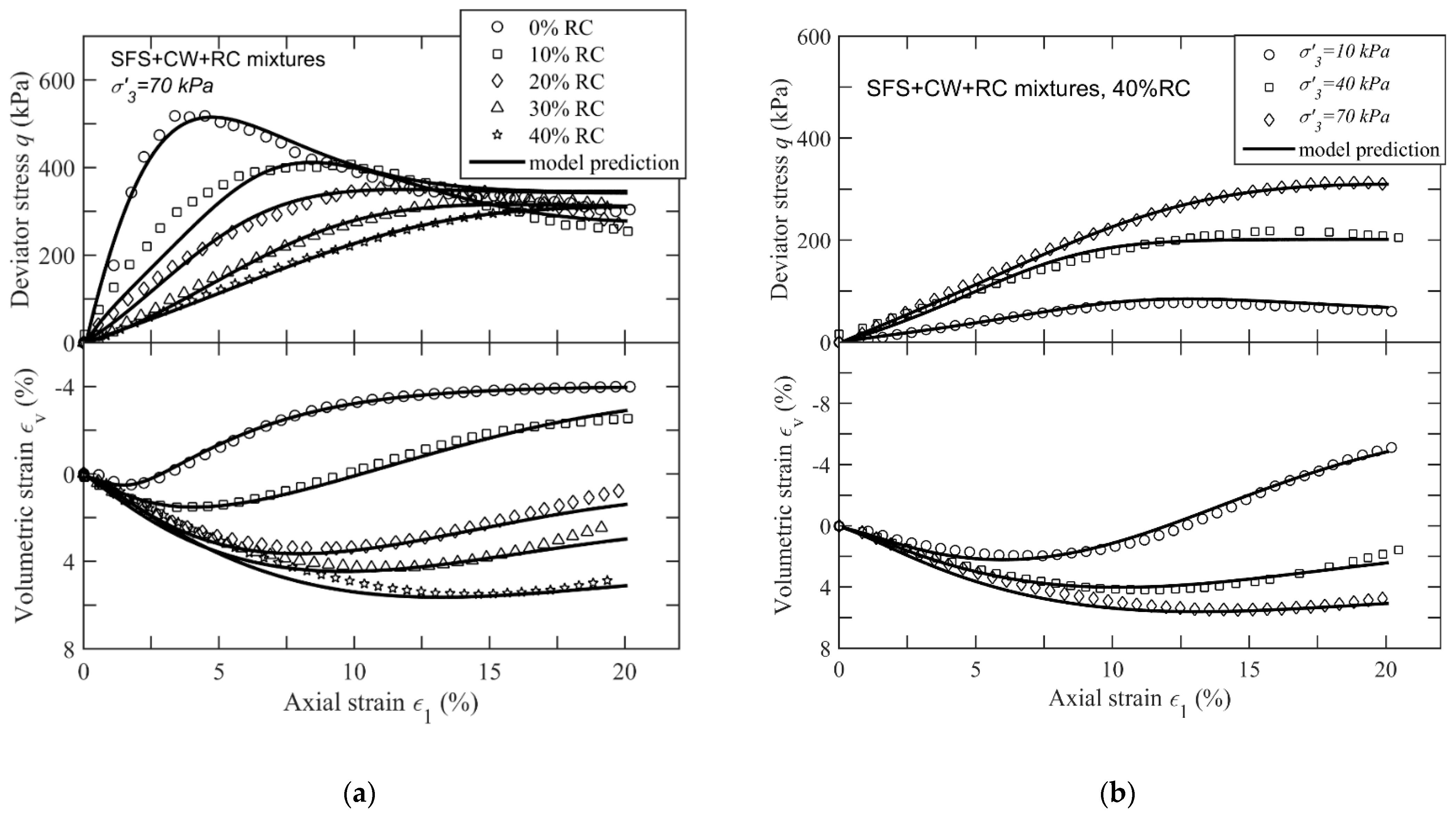
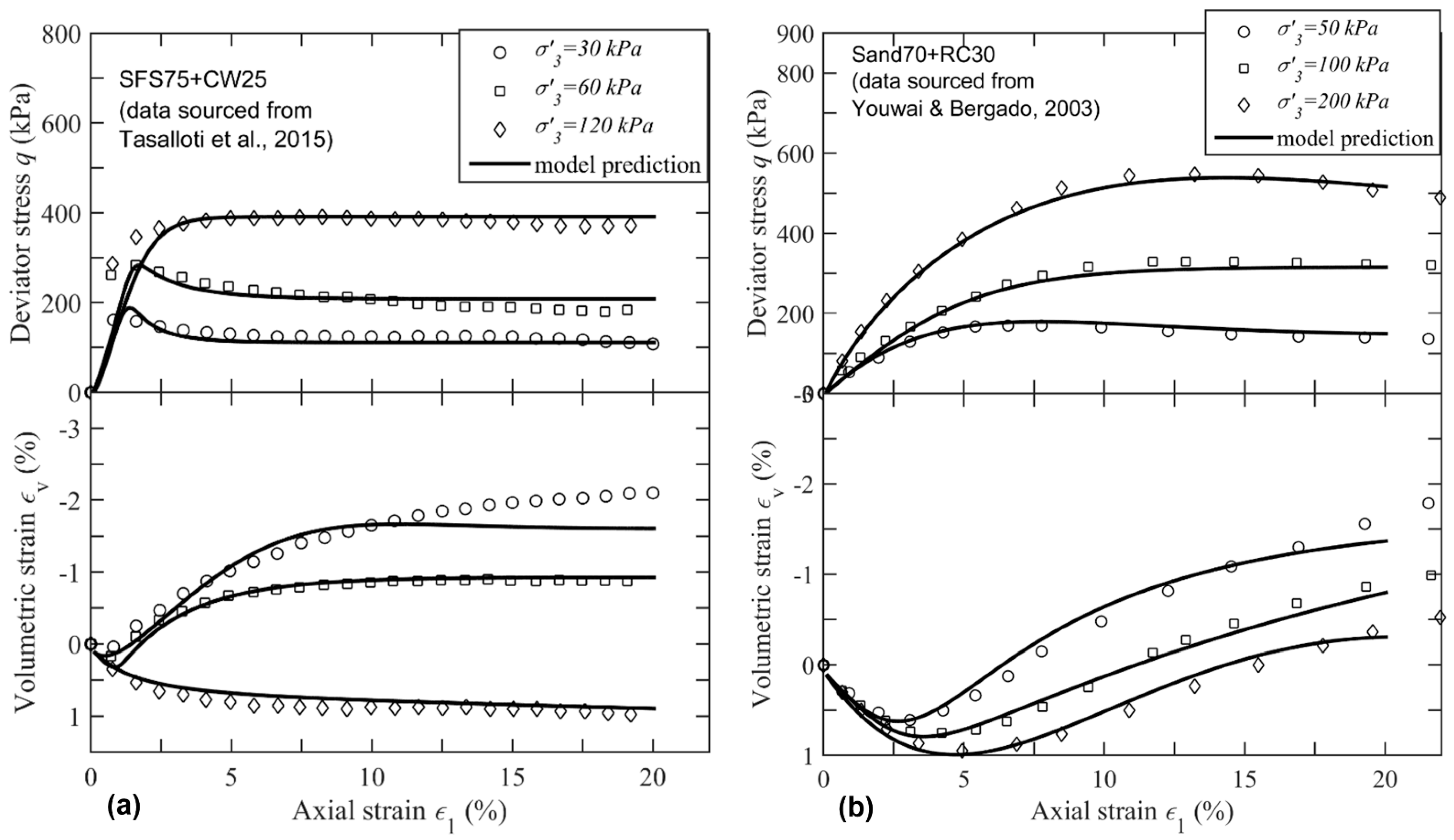
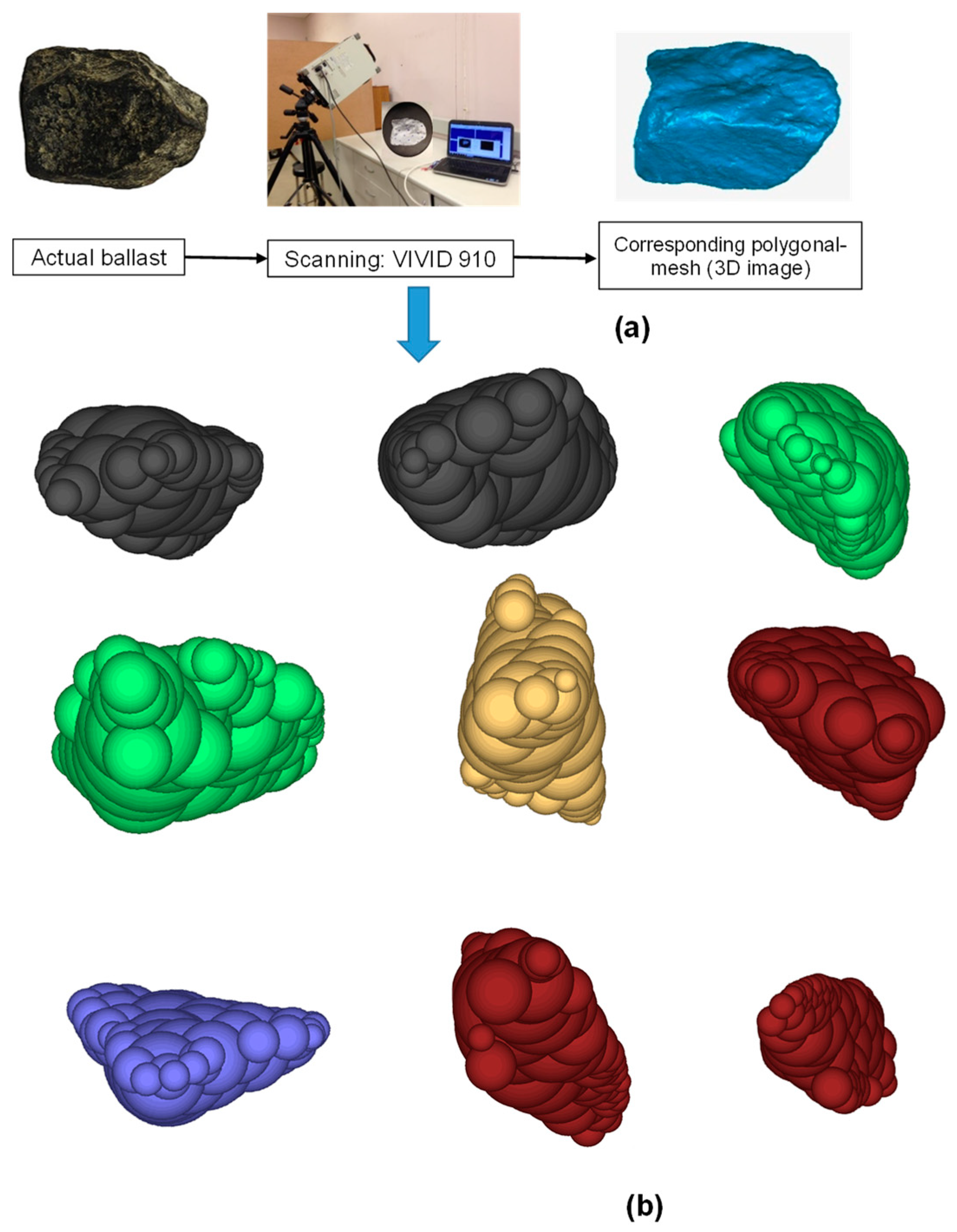
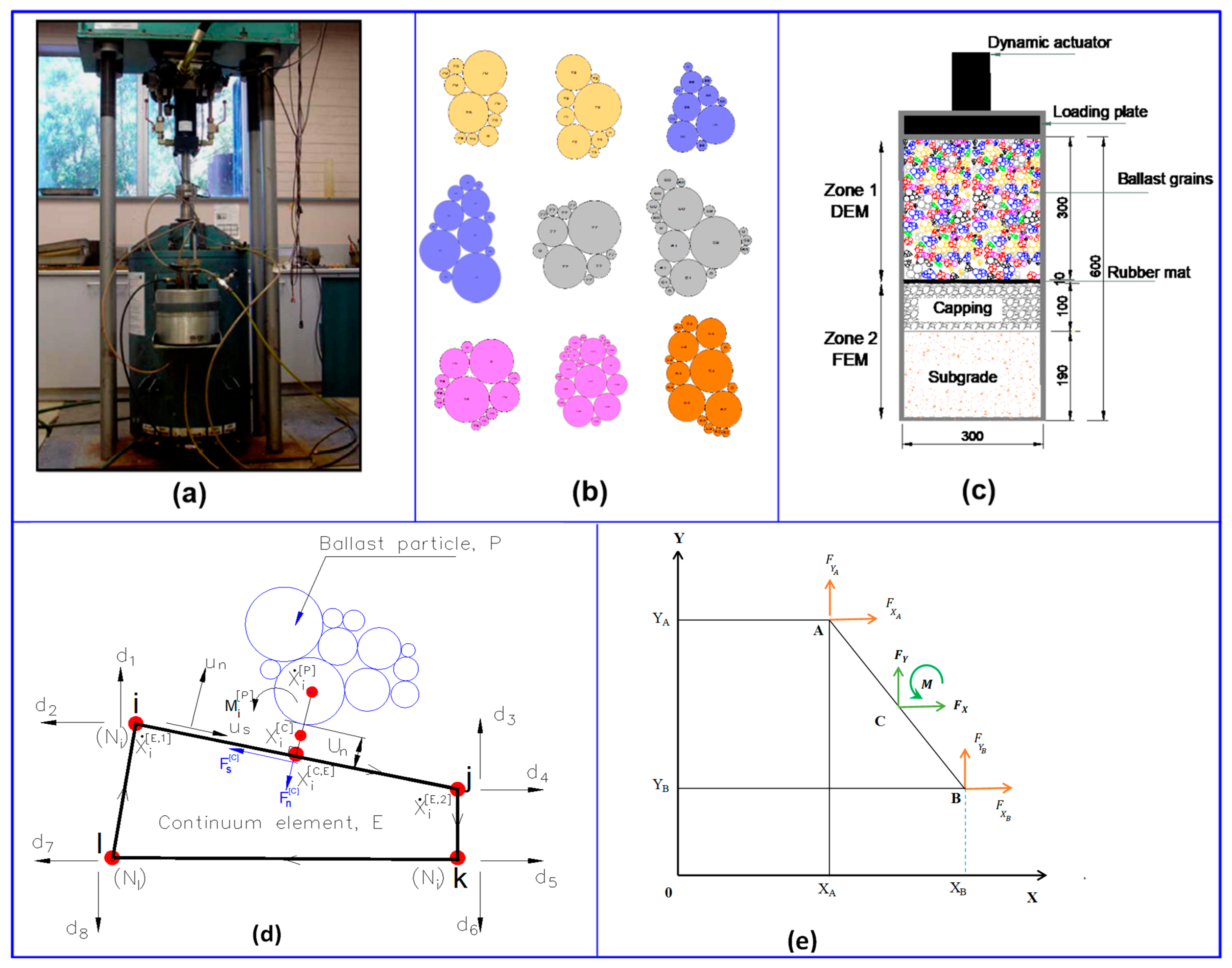
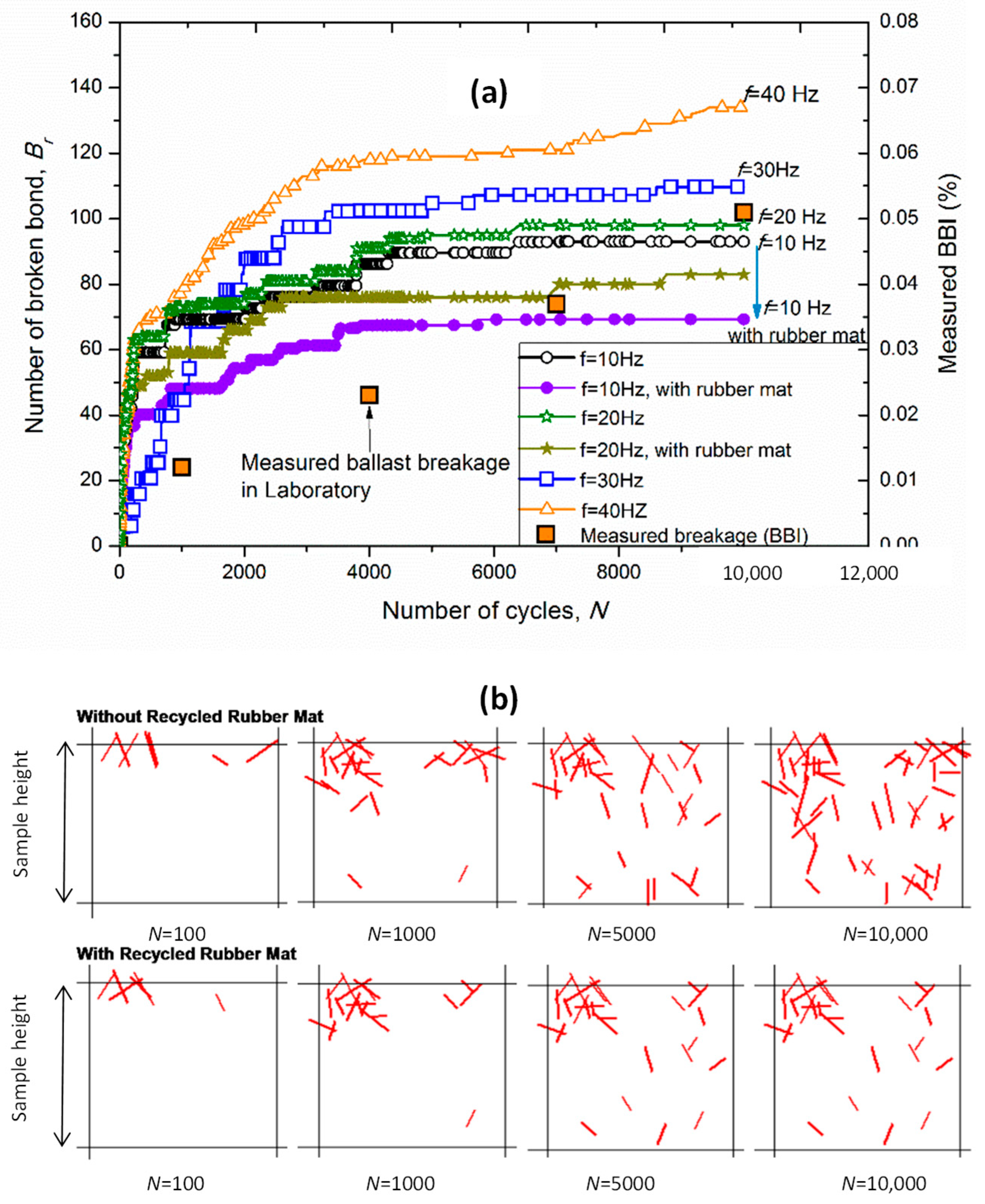
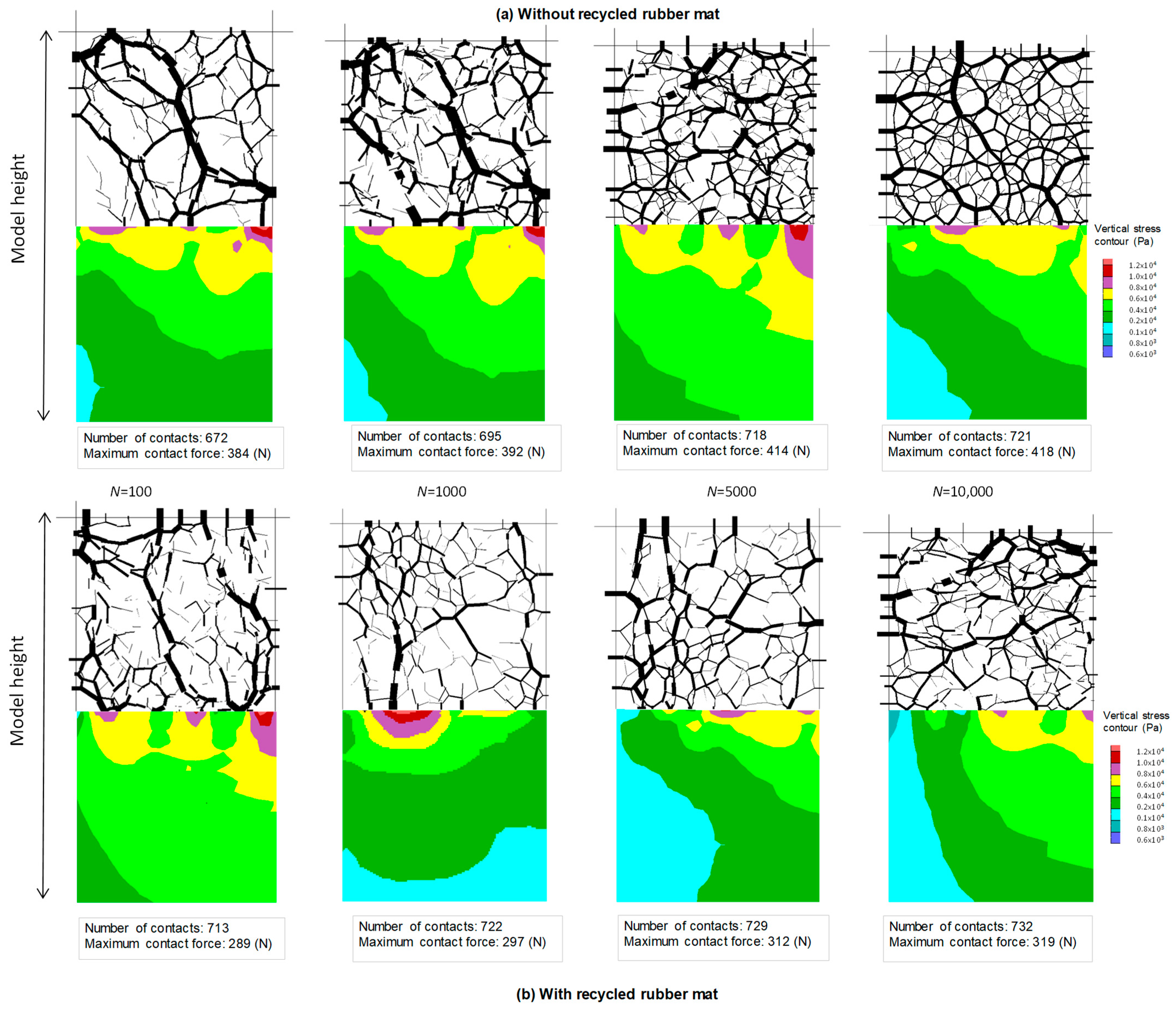
| Data Source | Mixtures | Effecive Confining Pressure | Critical State Ratio | Critical State Void Ratio | Critical State Parameters | |
|---|---|---|---|---|---|---|
| Qi et al. [38] | SFS:CW = 7:3, | 70 | 1.739 | 0.281 | 10.79 | |
| SFS:CW = 7:3, | 70 | 1.548 | 0.235 | 31.18 | ||
| SFS:CW = 7:3, | 70 | 1.51 | 0.198 | 33.82 | ||
| SFS:CW = 7:3, | 70 | 1.48 | 0.162 | 38.58 | ||
| SFS:CW = 7:3, | 10 | 1.8 | 0.390 | 5.81 | ||
| 40 | 1.5 | 0.216 | 23.28 | |||
| 70 | 1.43 | 0.148 | 42.74 | |||
| Tasalloti et al. [40] | SFS:CW = 75:25, | 30 | 1.65 | 0.601 | 10.0 | |
| 60 | 1.52 | 0.580 | 18.0 | |||
| 120 | 1.5 | 0.546 | 31.8 | |||
| Youwai and Bergado [26] | Sand:RC = 7:3 | 50 | 1.36 | 0.394 | 10.509 | |
| 100 | 1.3 | 0.374 | 37.408 | |||
| 200 | 1.29 | 0.353 | 56.59 |
| Data Source | Mixtures | |||
|---|---|---|---|---|
| Qi et al. [38] | SFS:RC = 7:3, = 0% | 4.0 | 0.0020 | 0.29 |
| SFS:RC = 7:3, = 10% | 2.5 | 0.0035 | 0.3 | |
| SFS:RC = 7:3, = 20% | 0.77 | 0.0048 | 0.31 | |
| SFS:RC = 7:3, = 30% | 0.88 | 0.0059 | 0.35 | |
| SFS:RC = 7:3, = 40% | 0.68 | 0.0063 | 0.35 | |
| Tasalloti et al. [59] | SFS:RC = 75:25, = 0% | 4.58 | 0.0018 | 0.25 |
| Youwai & Bergado [26] | Sand:RC = 7:3 | 0.6 | 0.0053 | 0.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Y.; Indraratna, B.; Ngo, T.; Ferreira, F.B. Advancements in Geo-Inclusions for Ballasted Track: Constitutive Modelling and Numerical Analysis. Sustainability 2021, 13, 9048. https://doi.org/10.3390/su13169048
Qi Y, Indraratna B, Ngo T, Ferreira FB. Advancements in Geo-Inclusions for Ballasted Track: Constitutive Modelling and Numerical Analysis. Sustainability. 2021; 13(16):9048. https://doi.org/10.3390/su13169048
Chicago/Turabian StyleQi, Yujie, Buddhima Indraratna, Trung Ngo, and Fernanda Bessa Ferreira. 2021. "Advancements in Geo-Inclusions for Ballasted Track: Constitutive Modelling and Numerical Analysis" Sustainability 13, no. 16: 9048. https://doi.org/10.3390/su13169048
APA StyleQi, Y., Indraratna, B., Ngo, T., & Ferreira, F. B. (2021). Advancements in Geo-Inclusions for Ballasted Track: Constitutive Modelling and Numerical Analysis. Sustainability, 13(16), 9048. https://doi.org/10.3390/su13169048









