Role of Model Predictive Control for Enhancing Eco-Driving of Electric Vehicles in Urban Transport System of Japan
Abstract
:1. Introduction
1.1. Research Background and Significance
1.2. Literature Review
- Freeway-based eco-driving considering the road gradient to minimize fuel consumption
- Urban roadway eco-driving considering traffic signal light information
- Urban roadway eco-driving under car-following driving scenario
1.3. What Will Be Elucidated in This Research
- A comprehensive PCC system for EVs eco-driving was proposed based on a tri-level MPC algorithm and an ANN-ICEM.
- A detailed DSSL is designed so that the proposed tri-level MPC-based PCC system can automatically handle synthetic daily driving scenarios.
- The performance of the overall PCC system is investigated based on a customized simulation platform using real urban road and transport data in Japan.
- The role of MPC for enhancing the eco-driving of EV is explored and exploited.
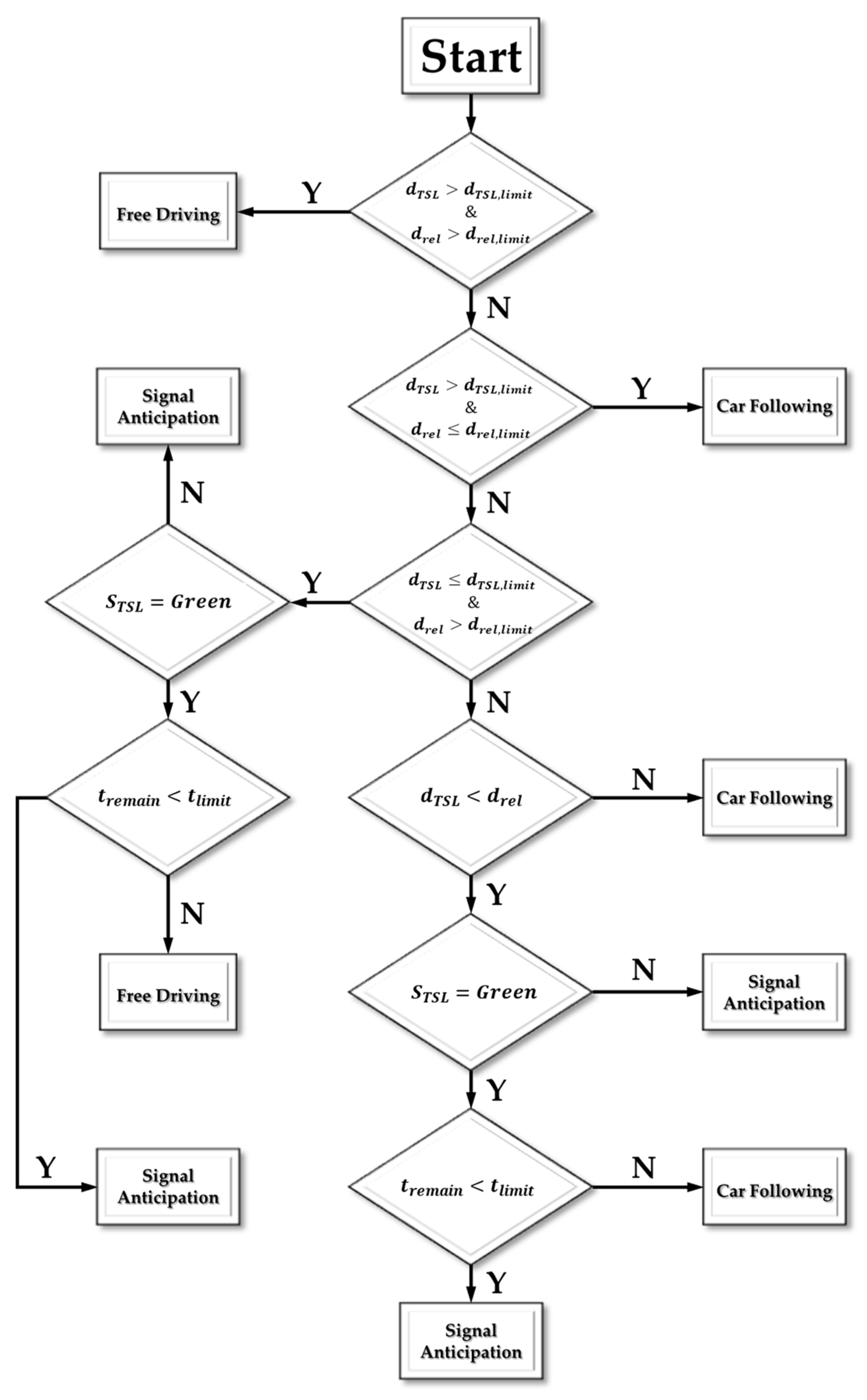
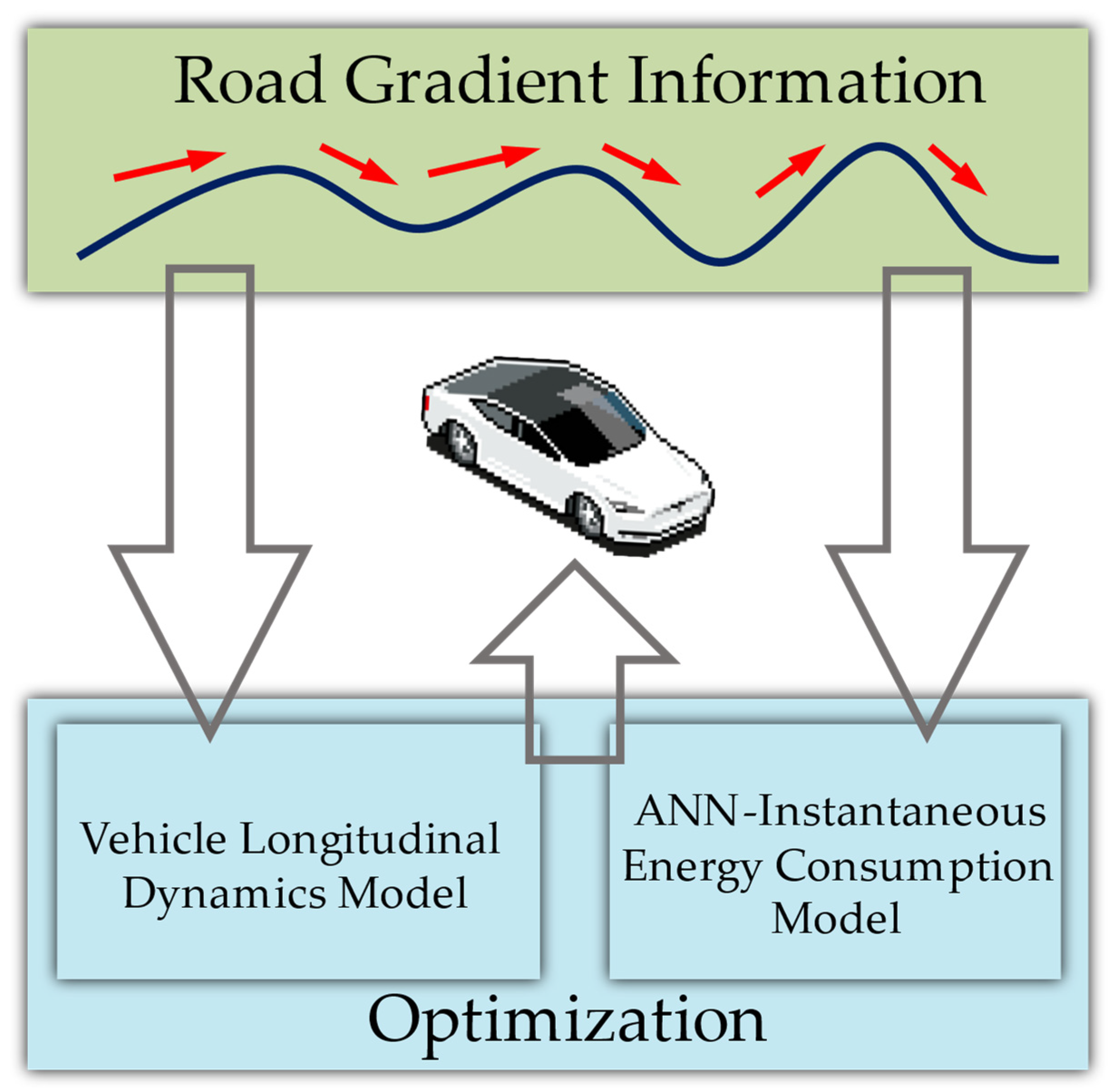
2. Problem Formulation
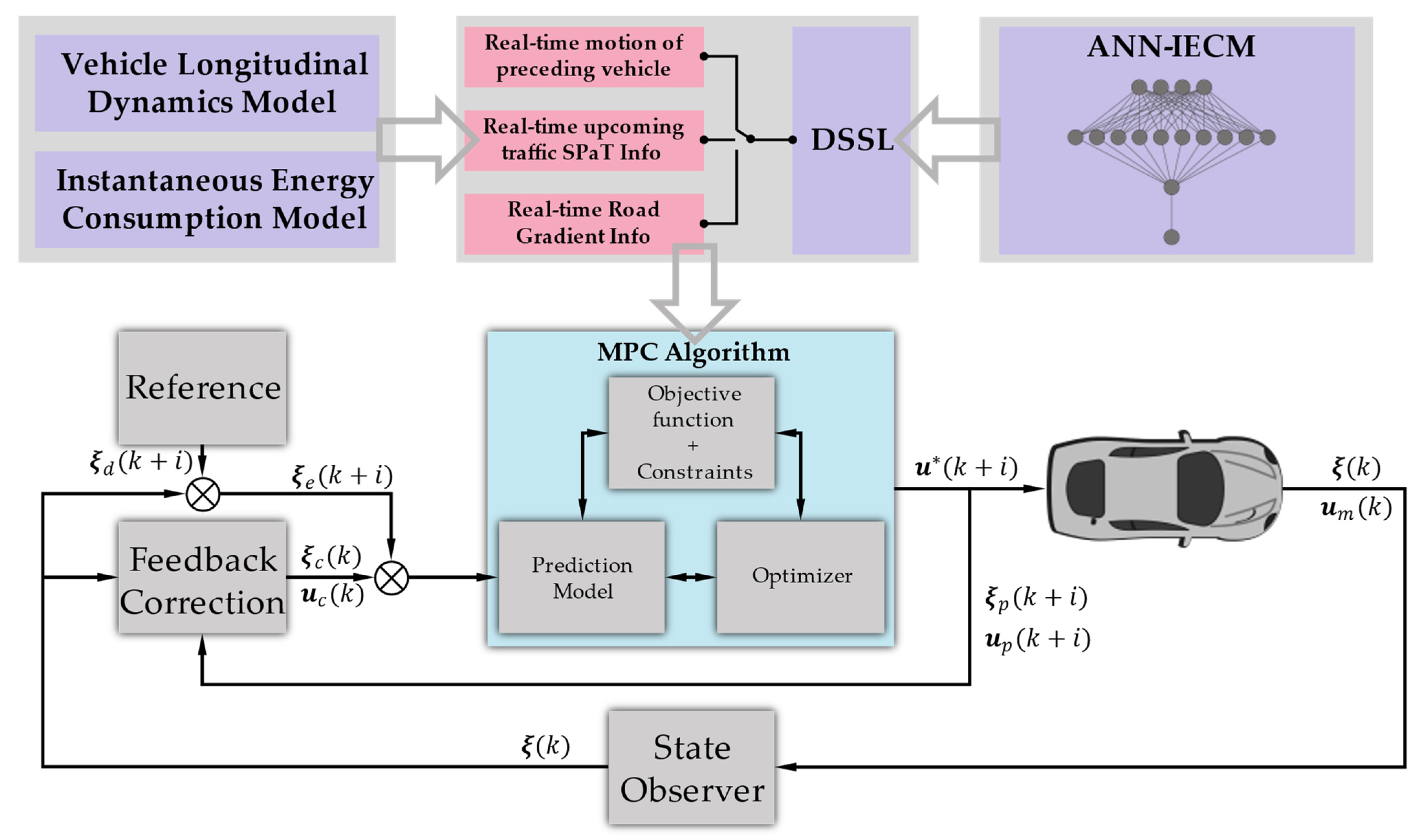
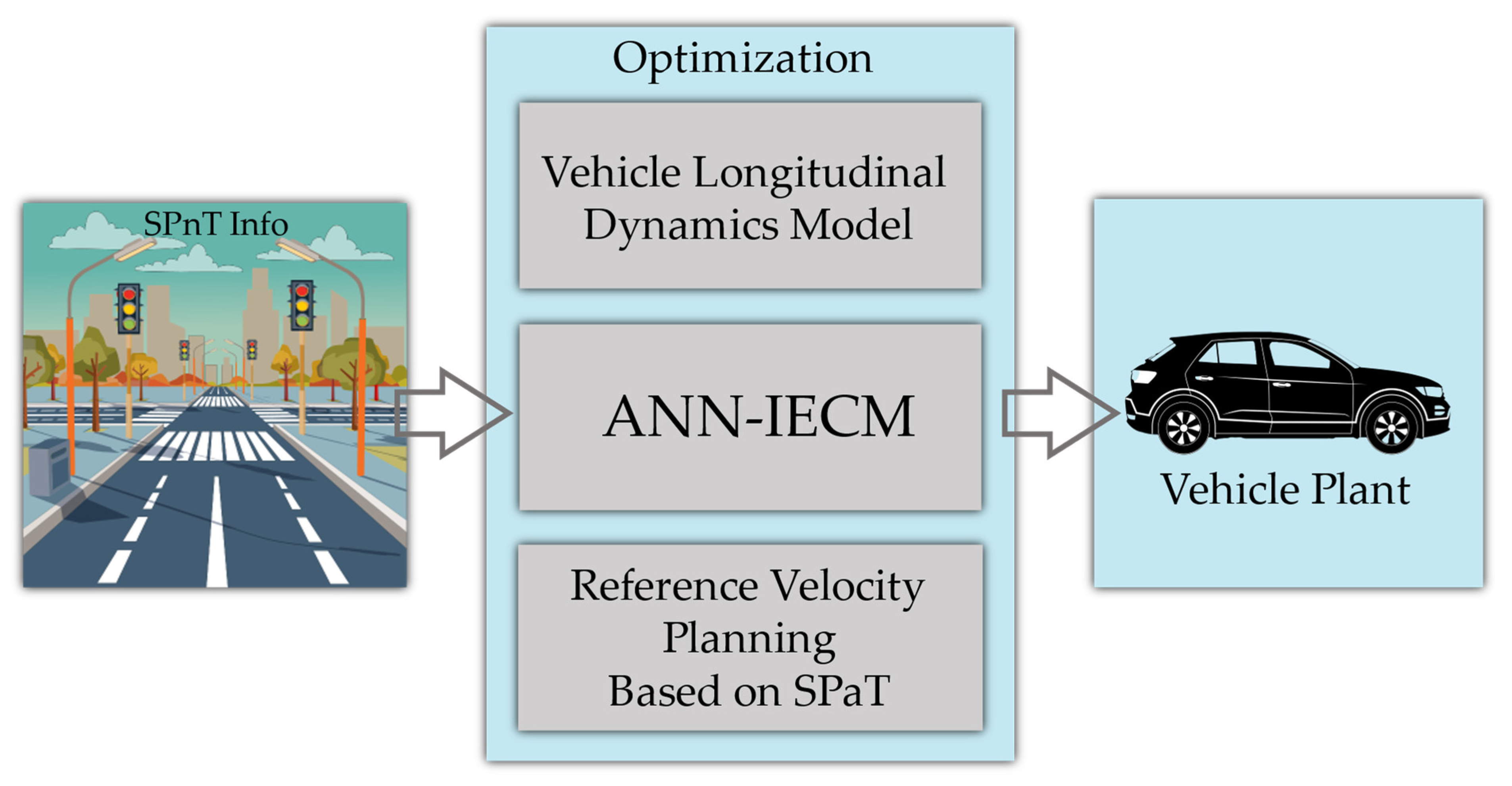
3. Proposed MPC-Based Predictive Cruise Control System
3.1. System Modeling
3.2. Tri-Level Model Predictive Controller
3.2.1. LMPC for Car-Following Scenario
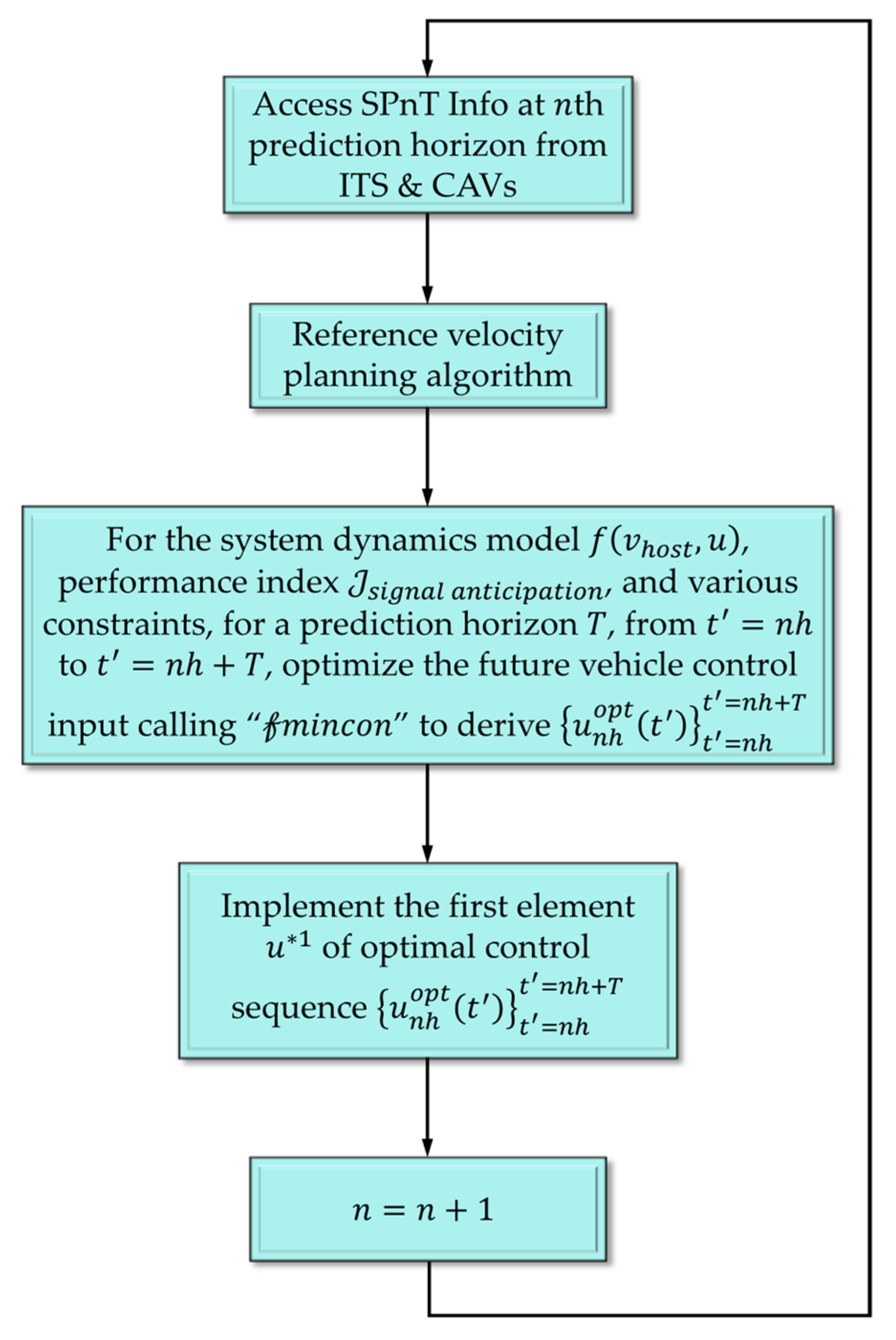
3.2.2. NLMPC for Signal Anticipation Scenario
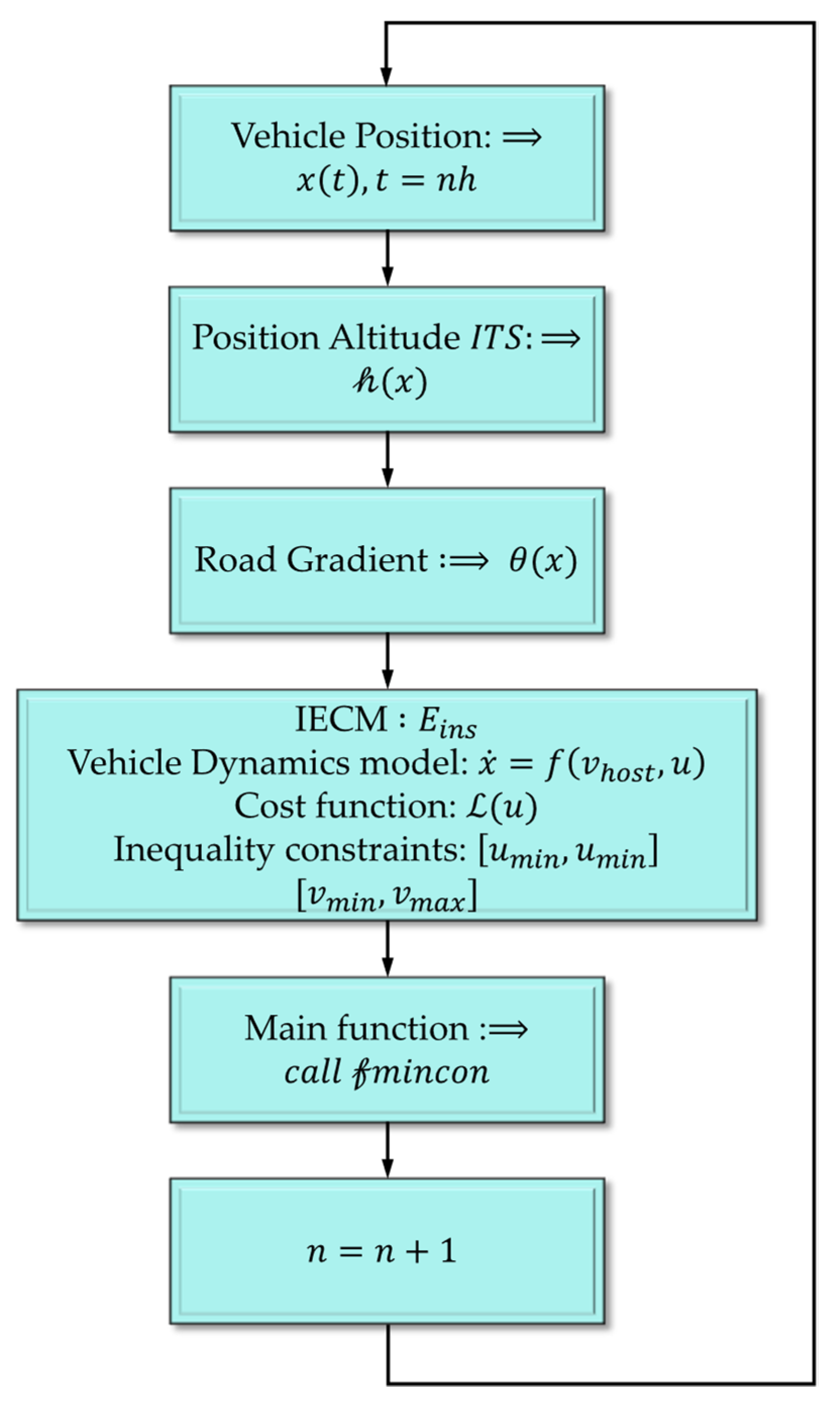
3.2.3. NLMPC for Free Driving Scenario
4. Results and Discussion of Case Studies
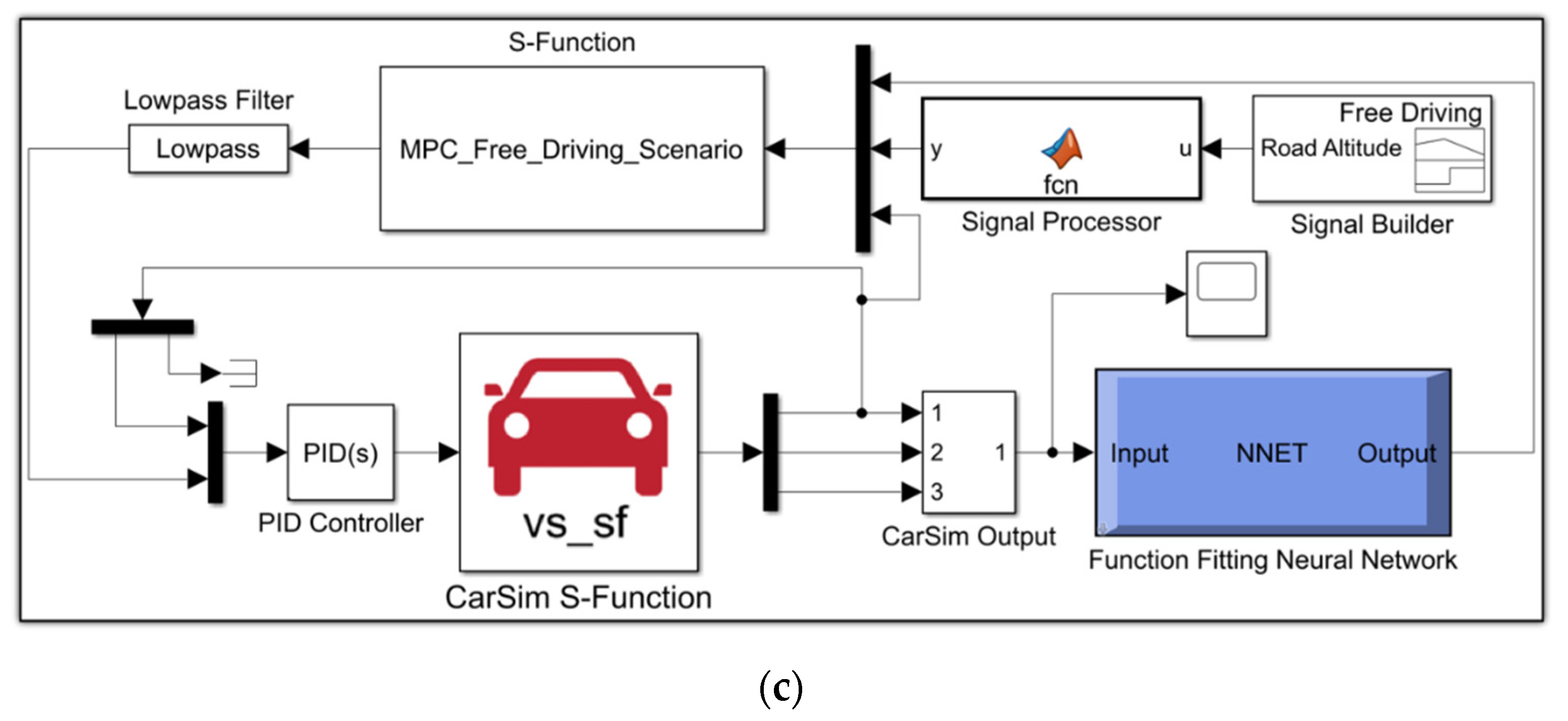
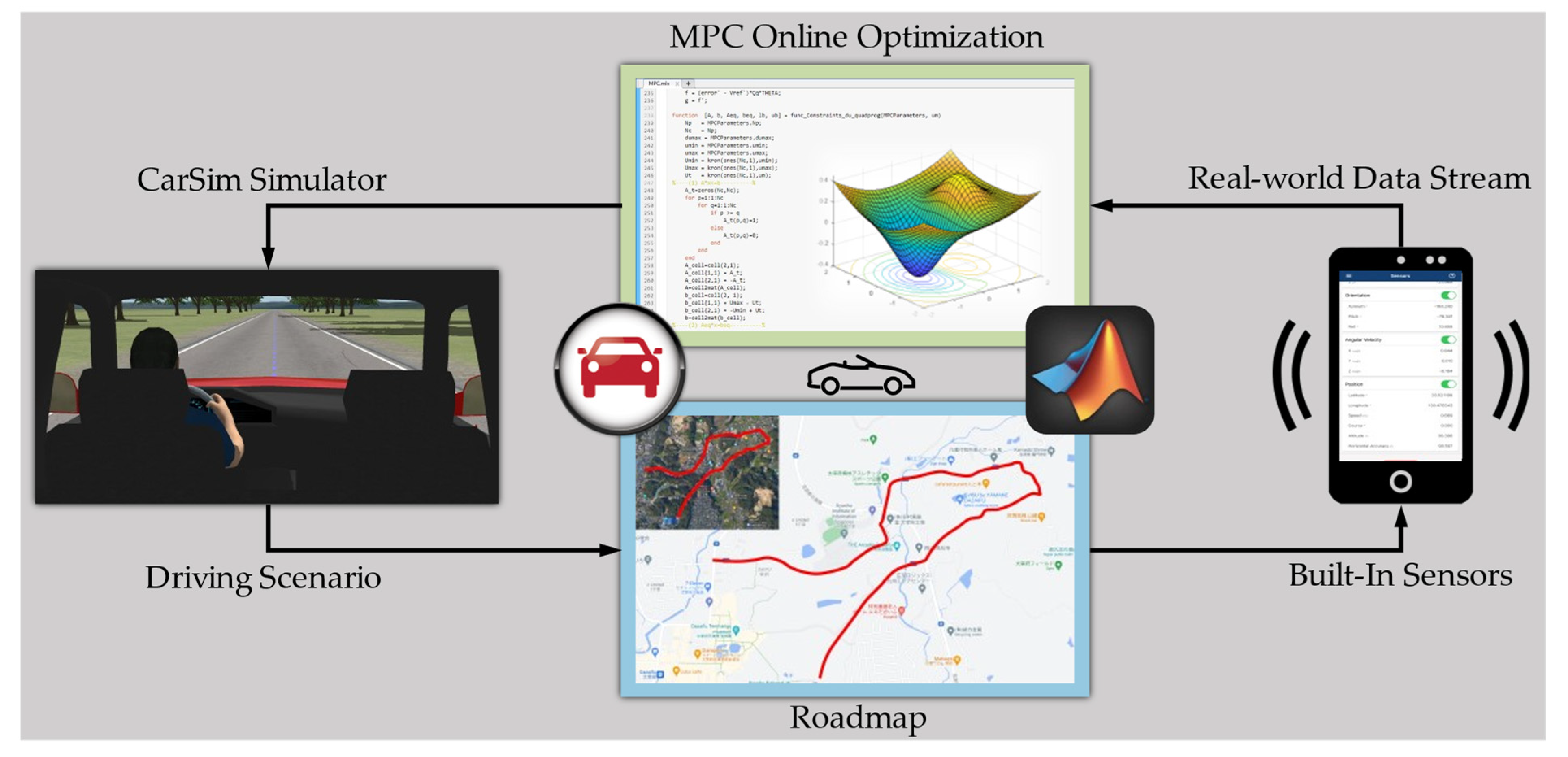
4.1. Establishment of Simulation Platform Based on CarSim and MATLAB/Simulink
4.2. Real Road and Transport Data Collection in Urban Area of Japan
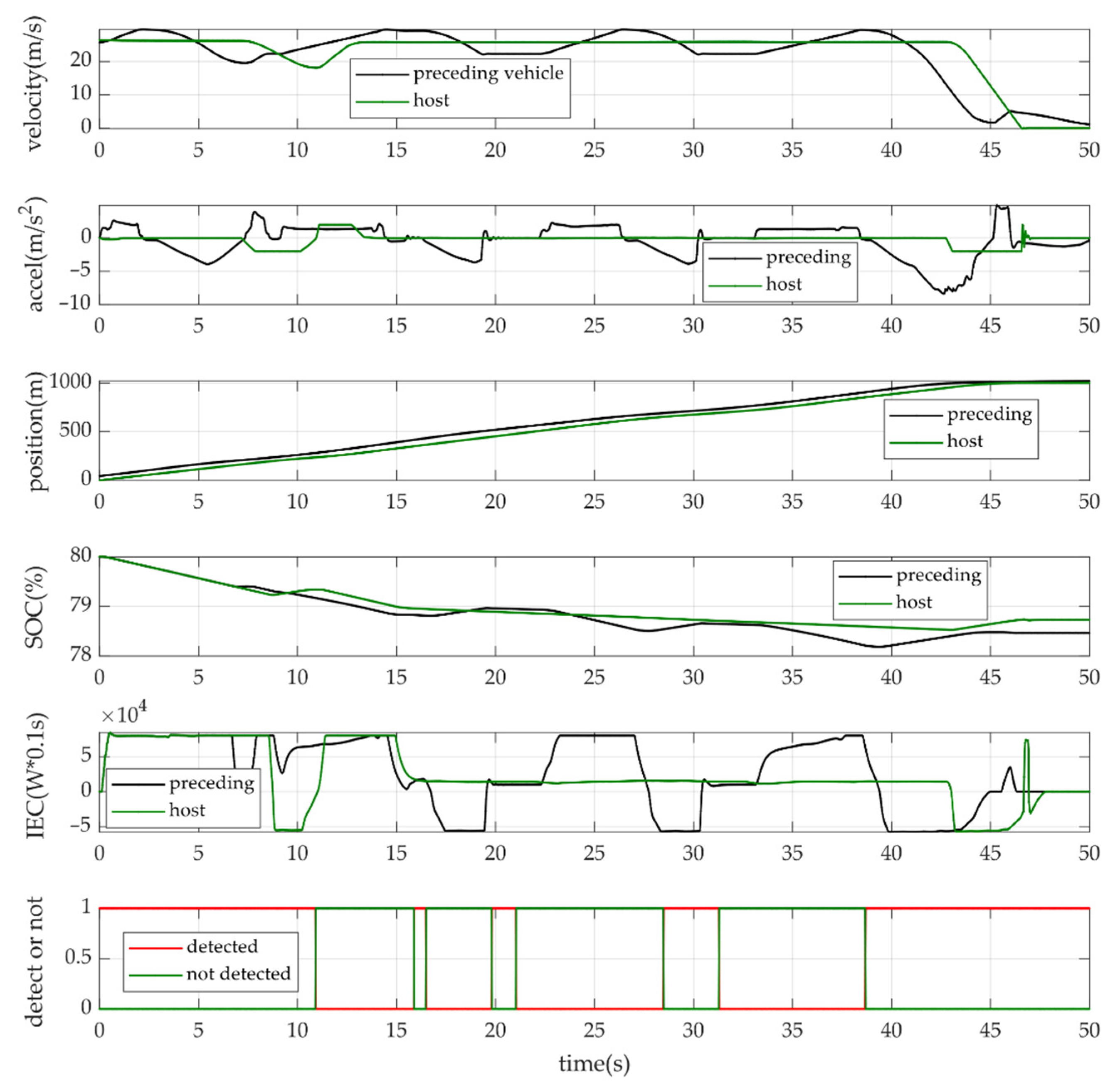
4.3. Real Case Study for Car-Following Driving Scenario
4.4. Real Case Study for Signal Anticipation Scenario
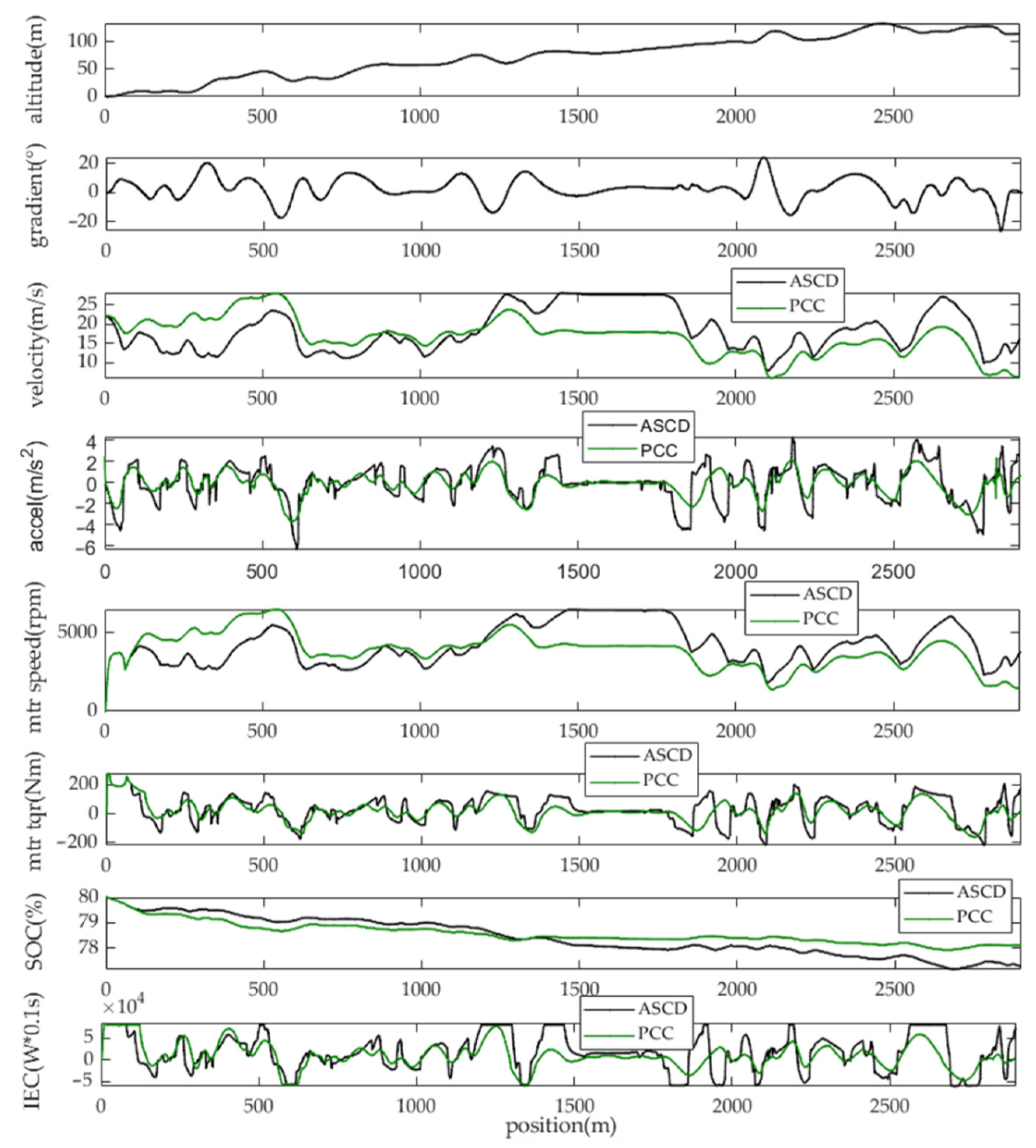
4.5. Real Case Study for Free Driving Scenario
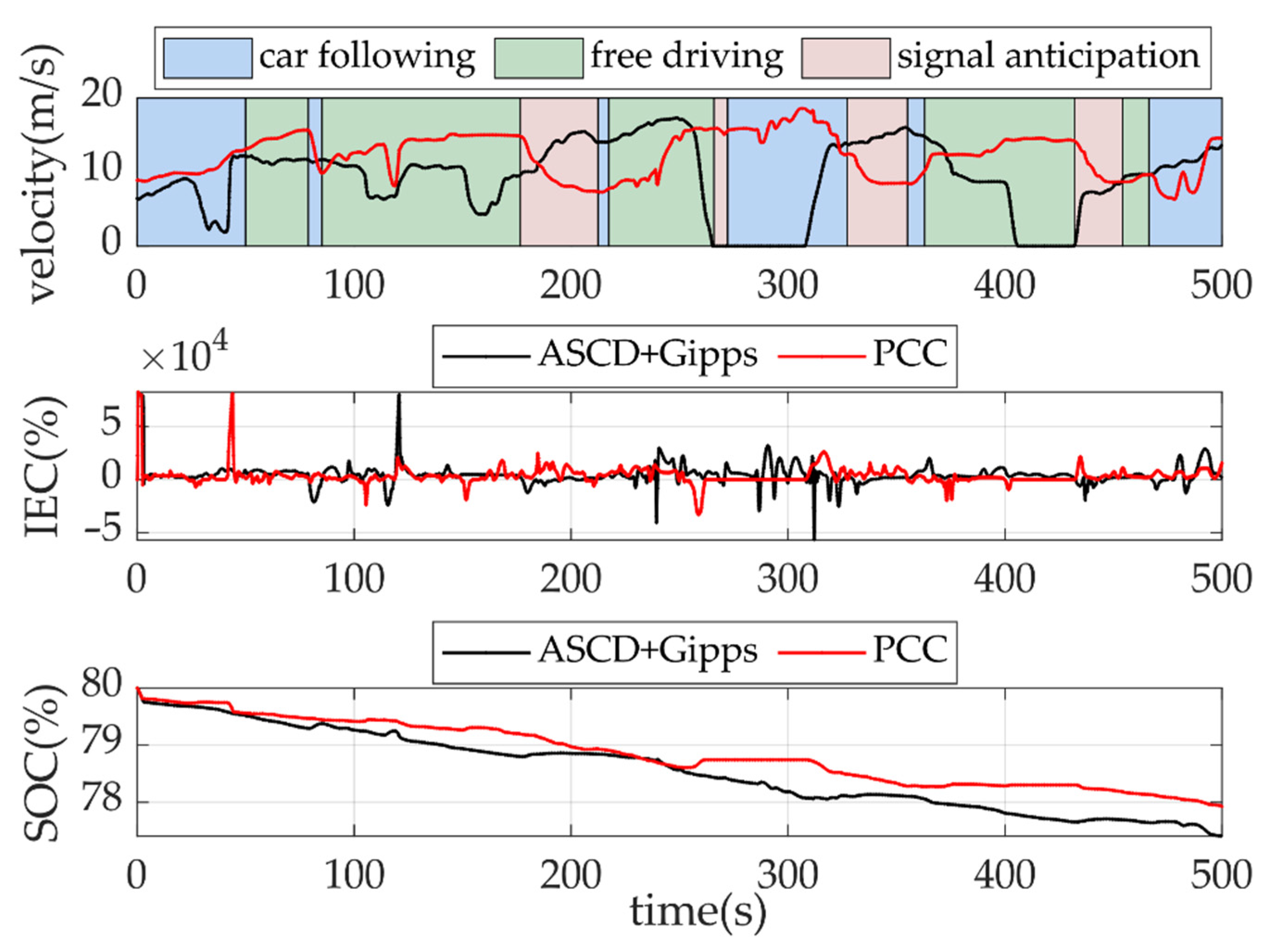
4.6. A Comprehensive Case Study in Synthetic Driving Scenario
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| EVs | Electric vehicles | - |
| MPC | Model predictive control | - |
| LMPC | Linear model predictive control | - |
| NLMPC | Nonlinear model predictive control | - |
| PCC | Predictive cruise control | - |
| DSSL | Driving scenario switching logic | - |
| SPnT | Signal phase and timing information | - |
| CAVs | Connected and autonomous vehicles | - |
| ITS | Intelligent transport system | - |
| ANN | Artificial neural network | - |
| IECM | Instantaneous energy consumption model | - |
| V2V | Vehicle-to-Vehicle | - |
| V2I | Vehicle-to-Infrastructure | - |
| The relative distance between the host and the preceding vehicle in the same lane | ||
| The real-time driving speed of the preceding vehicle | ||
| The distance to the upcoming signalized intersection | ||
| Allowable speed limitation on a given road section | ||
| Road altitude at a given position | ||
| The traffic signal lights state, including Green, Red, and Yellow | - | |
| The time left for the traffic light of the upcoming intersection | ||
| Braking distance | ||
| Minimum critical distance | ||
| Host vehicle velocity | ||
| Reaction time before braking | ||
| Deceleration during braking | ||
| Thresholds value for the distance to an upcoming signalized intersection | ||
| Thresholds value for the relative distance between the host and preceding vehicles in the same lane | ||
| Real-time estimated time length to pass the upcoming signalized intersection | ||
| Maximum physical allowable acceleration of the vehicle | ||
| Measured state values of the controlled vehicle | - | |
| Measured control values of the controlled vehicle | - | |
| Prediction state values | - | |
| Prediction control values | - | |
| , | Errors between measured values and prediction values | - |
| Electric motor efficiency | - | |
| Motor torque | ||
| Motor speed | ||
| Motor power | ||
| Equivalent internal resistance of the battery | ||
| Equivalent current in the circuit of the battery | ||
| Battery open-circuit voltage | ||
| SOC | Battery state of charge | % |
| Maximum battery capacity | ||
| Vehicle traction force | ||
| Battery maximum power | ||
| Air density | ||
| Aerodynamic drag coefficient | - | |
| Rolling resistance coefficient | - | |
| Frontal area of the vehicle | ||
| Effective radius of the vehicle wheel | ||
| Total mechanical efficiency of the driveline | - | |
| Gear ratio | - | |
| Equivalent total mass of the electric vehicle | ||
| Road gradient | ° | |
| Relative velocity between the host and preceding vehicle | ||
| Safe inter-distance between the host and preceding vehicle | ||
| Actual inter-distance between the host and preceding vehicle | ||
| Error of inter-vehicle distance | ||
| VTH | Variable time headway | - |
| Acceleration of the preceding vehicle | ||
| Acceleration of the host vehicle | ||
| System gain | - | |
| Time constant | ||
| Actual acceleration of the host vehicle | ||
| Optimal desired acceleration of the host vehicle | ||
| , | Start time of the th red and green interval of the upcoming traffic signal light | |
| Reference velocity optimized in signal anticipation scenario | ||
| Instantaneous energy consumption per 0.1 s | ||
| Jerk | ||
| Performance index of the energy economy | - | |
| Weight coefficient of desired acceleration | - | |
| Weight coefficient of the desired jerk | - | |
| Real-time safe distance | ||
| Time-to-collision | ||
| Performance index of driving safety | - | |
| Weight coefficient of the tracking distance error | - | |
| Weight coefficient of the relative velocity | - | |
| , | The lower and upper boundary of inter-distance error | |
| , | The extreme value of relative velocity | |
| , | Driver’s sensitivity to the and | - |
| , | The desired acceleration boundary condition | |
| , | The desired jerk boundary condition | |
| Performance index of driving comfortability | - | |
| Weight coefficient of the host vehicle longitudinal acceleration | - | |
| System cost function under car-following scenario | - | |
| System cost function under signal anticipation scenario | - | |
| Control input | ||
| Prediction horizon | ||
| Weight for the energy consumption under signal anticipation scenario | - | |
| Weight for tracking the reference velocity under signal anticipation | - | |
| Slack factor | - | |
| SQP | Sequential quadratic programming | - |
| Weight for tracking the desired velocity under free driving scenario | - | |
| Weight for acceleration command to avoid hard input because of tracking the desired velocity | - | |
| System cost function under free driving scenario | - | |
| ASCD | Automatic speed control drive | - |
Appendix A
| ANN-based IECM | 1.25 | |
| EV-MFECM | 3.20 |

References
- Alshehry, A.S.; Belloumi, M. Study of the environmental Kuznets curve for transport carbon dioxide emissions in Saudi Arabia. Renew. Sustain. Energy Rev. 2017, 75, 1339–1347. [Google Scholar] [CrossRef]
- NeV. Strategy for Diffusing the Next Generation Vehicles in Japan; Next Generation Vehicle Promotion Center: Tokyo, Japan, 2018. [Google Scholar]
- METI. Japan’s Energy 2020; Agency for Natural Resources and Energy: Tokyo, Japan, 2020.
- Motoko, H. Japan’s EV Shift to Boost Power Demand by 15pc: IEEJ; Commodity & Energy Price Benchmarks|Argus Media: Tokyo, Japan, 2021. [Google Scholar]
- Zhou, M.; Hui, J.; Wenshuo, W. A review of vehicle fuel consumption models to evaluate eco-driving and eco-routing. Transp. Res. Part D Transp. Environ. 2016, 49, 203–218. [Google Scholar] [CrossRef]
- Li, M.; Wu, X.; He, X.; Yu, G.; Wang, Y. An eco-driving system for electric vehicles with signal control under V2X environment. Transp. Res. Part C Emerg. Technol. 2018, 93, 335–350. [Google Scholar] [CrossRef]
- Maamria, D.; Gillet, K.; Colin, G.; Chamaillard, Y.; Nouillant, C. Optimal predictive eco-driving cycles for conventional, electric, and hybrid electric cars. IEEE Trans. Veh. Technol. 2019, 68, 6320–6330. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Q.; Nouveliére, L.; Orfila, O. A New Eco-driving Assistance System for a Light Vehicle: Energy Management and Speed Optimization. In Proceedings of the IEEE Intelligent Vehicles Symposium, Gold Coast, Australia, 23–26 June 2013; pp. 1434–1439. [Google Scholar]
- Gáspár, P.; Németh, B. Predictive Cruise Control for Road Vehicles Using Road and Traffic Information; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Lattemann, F.; Neiss, K.; Terwen, S.; Connolly, T. The predictive cruise control—A system to reduce fuel consumption of heavy-duty trucks. SAE Tech. Pap. Ser. 2004, 113, 139–146. [Google Scholar]
- Hellström, E.; Ivarsson, M.; Åslund, J.; Nielsen, L. Look-ahead control for heavy trucks to minimize trip time and fuel consumption. Control Eng. Pract. 2009, 17, 245–254. [Google Scholar] [CrossRef] [Green Version]
- Hellström, E. Explicit Use of Road Topography for Model Predictive Cruise Control in Heavy Trucks. Master’s Thesis, Linköping University, Linköping, Sweden, 2005. [Google Scholar]
- Hellström, E. Look-Ahead Control of Heavy Trucks Utilizing Road Topography. Ph.D. Thesis, Linköping University, Linköping, Sweden, 2007. [Google Scholar]
- Hellström, E.; Fröberg, A.; Nielsen, L. A real-time fuel-optimal cruise controller for heavy trucks using road topography information. SAE Tech. Pap. Ser. 2006. [Google Scholar] [CrossRef]
- Hellström, E.; Åslund, J.; Nielsen, L. Design of an efficient algorithm for fuel-optimal look-ahead control. Control Eng. Pract. 2010, 18, 1318–1327. [Google Scholar] [CrossRef] [Green Version]
- Kamal, M.A.; Mukai, M.; Murata, J.; Kawabe, T. Ecological vehicle control on roads with up-down slopes. IEEE Trans. Intell. Transp. Syst. 2011, 12, 783–794. [Google Scholar] [CrossRef]
- Yu, Q. Vehicular Speed Control of Eco-Driving Systems Based on Connected Vehicles. Master’s Thesis, Tsinghua University, Beijing, China, 2014. [Google Scholar]
- Markschläger, P.; Wahl, H.; Weberbauer, F.; Lederer, M. Assistance system for higher fuel efficiency. ATZ Worldw. 2012, 114, 8–13. [Google Scholar] [CrossRef]
- Asadi, B.; Vahidi, A. Predictive cruise control: Utilizing upcoming traffic signal information for improving fuel economy and reducing trip time. IEEE Trans. Control Syst. Technol. 2011, 19, 707–714. [Google Scholar] [CrossRef]
- Kamal, M.A.; Mukai, M.; Murata, J.; Kawabe, T. Model predictive control of vehicles on urban roads for improved fuel economy. IEEE Trans. Control Syst. Technol. 2013, 21, 831–841. [Google Scholar] [CrossRef]
- De Nunzio, G.; De Wit, C.C.; Moulin, P.; Di Domenico, D. Eco-driving in urban traffic networks using traffic signals information. Int. J. Robust Nonlinear Control 2015, 26, 1307–1324. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Cassandras, C.G. A real-time optimal eco-driving approach for autonomous vehicles crossing multiple signalized intersections. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019. [Google Scholar]
- Bae, S.; Kim, Y.; Guanetti, J.; Borrelli, F.; Moura, S. Design and implementation of ecological adaptive cruise control for autonomous driving with communication to traffic lights. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019. [Google Scholar]
- Zhang, J.; Ioannou, P. Longitudinal control of heavy trucks in mixed traffic: Environmental and fuel economy considerations. IEEE Trans. Intell. Transp. Syst. 2006, 7, 92–104. [Google Scholar] [CrossRef]
- Li, S.; Li, K.; Wang, J.; Zhang, L.; Lian, X.; Hiroshi, U.; Bai, D. MPC based vehicular following control considering both fuel economy and tracking capability. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008. [Google Scholar]
- Bakibillah, A.S.M.; Kamal, M.A.S.; Tan, C.P.; Hayakawa, T.; Imura, J. Eco-driving on Hilly Roads Using Model Predictive Control. In Proceedings of the 2018 Joint 7th International Conference on Informatics, Electronics & Vision (ICIEV) and 2018 2nd International Conference on Imaging, Vision & Pattern Recognition (icIVPR), Kitakyushu, Japan, 25–29 June 2018. [Google Scholar] [CrossRef]
- Ma, F.; Yang, Y.; Wang, J.; Liu, Z.; Li, J.; Nie, J.; Shen, Y.; Wu, L. Predictive energy-saving optimization based on nonlinear model predictive control for cooperative connected vehicles platoon with V2V communication. Energy 2019, 189, 116120. [Google Scholar] [CrossRef]
- Nie, Z.; Farzaneh, H. Adaptive Cruise Control for Eco-Driving Based on Model Predictive Control Algorithm. Appl. Sci. 2020, 10, 5271. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, X.; Tang, X.; Lin, X. Model predictive control of hybrid electric vehicles for fuel economy, emission reductions, and inter-vehicle safety in car-following scenarios. Energy 2020, 196, 117101. [Google Scholar] [CrossRef]
- Yang, C.; Wang, M.; Wang, W.; Pu, Z.; Ma, M. An efficient vehicle-following predictive energy management strategy for PHEV based on improved sequential quadratic programming algorithm. Energy 2021, 219, 119595. [Google Scholar] [CrossRef]
- Manzie, C.; Watson, H.; Halgamuge, S. Fuel economy improvements for urban driving: Hybrid vs. intelligent vehicles. Transp. Res. Part C Emerg. Technol. 2007, 15, 1–16. [Google Scholar] [CrossRef]
- Li, S.E.; Peng, H.; Li, K.; Wang, J. Minimum fuel control strategy in automated car-following scenarios. IEEE Trans. Veh. Technol. 2012, 61, 998–1007. [Google Scholar] [CrossRef]
- Li, L.; Wang, X.; Song, J. Fuel consumption optimization for smart hybrid electric vehicle during a car-following process. Mech. Syst. Signal Process. 2017, 87, 17–29. [Google Scholar] [CrossRef]
- Su, L.H.; Li, L.; Chu, J. Recent Advances on Predictive Control. Mech. Electr. Eng. Mag. 2011, 5, 4–8. [Google Scholar]
- Yi, C.; Epureanu, B.I.; Hong, S.; Ge, T.; Yang, X.G. Modeling, control, and performance of a novel architecture of hybrid electric powertrain system. Appl. Energy 2016, 178, 454–467. [Google Scholar] [CrossRef]
- Sun, C.; Moura, S.J.; Hu, X.; Hedrick, J.K.; Sun, F. Dynamic traffic feedback data enabled energy management in plug-in hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2015, 23, 1075–1086. [Google Scholar]
- Li, S. Vehicular Multi-Objective Coordinated Adaptive Cruise Control. Ph.D. Thesis, Tsinghua University, Beijing, China, 2009. [Google Scholar]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Treiber, M.; Kesting, A. Traffic Flow Dynamics: Data, Models and Simulation; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Yu, Y.; Li, Y.; Liang, Y.; Zhang, Z.; Liao, G. Modeling of Transient Energy Consumption Model of Electric Vehicle Based on Data Mining. In Proceedings of the Society of Automotive Engineers of Automotive Engineering Conference, Shanghai, China, 21–22 May 2019; pp. 277–283. [Google Scholar]












| Data | Explanation | Unit |
|---|---|---|
| The relative distance between the host and the preceding vehicle in the same lane | ||
| The real-time driving speed of the preceding vehicle | ||
| The distance to the upcoming signalized intersection | ||
| Allowable speed limitation on a given road section | ||
| Road altitude at a given position | ||
| The traffic signal lights state, including Green, Red, Yellow | - | |
| The time left for the traffic light of the upcoming intersection |
| Specification | Values |
|---|---|
| Equivalent total mass of the electric vehicle, | 1260 |
| Gear ratio, | 3.905 |
| Total mechanical efficiency of the driveline, | 0.95 |
| Effective radius of the vehicle wheel, | 287 |
| Frontal area of the vehicle, | 2.22 |
| Rolling resistance coefficient, | 0.028 |
| Aerodynamic drag coefficient, | 0.316 |
| Air density, | 1.206 |
| Motor | Maximum available power: = 55; Maximum output torque: 305; |
| Battery | Battery voltage: 6~9 V; Packs: 40; Initial charge level: 0.8; : 93 Ah |
| Parameter | Symbol | Values & Unit |
|---|---|---|
| System gain | 1.05 | |
| Time constant | 0.40 s | |
| Minimal stop distance | 5 m | |
| Sampling period | 0.1 s | |
| Prediction horizon | 30 | |
| Time-to-collision | −2.5 s | |
| Sensitivity first-order term coefficient of | 0.06 | |
| Sensitivity first-order term coefficient of | 0.005 | |
| Constant term of sensitivity of | −0.13 | |
| Constant term of sensitivity of | 0.92 | |
| Upper bound of acceleration | 1.5 m/s2 | |
| Lower bound of acceleration | −2 m/s2 | |
| Upper bound of jerk | () | 1.5 m/s3 |
| Lower bound of jerk | () | 2 m/s3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, Z.; Farzaneh, H. Role of Model Predictive Control for Enhancing Eco-Driving of Electric Vehicles in Urban Transport System of Japan. Sustainability 2021, 13, 9173. https://doi.org/10.3390/su13169173
Nie Z, Farzaneh H. Role of Model Predictive Control for Enhancing Eco-Driving of Electric Vehicles in Urban Transport System of Japan. Sustainability. 2021; 13(16):9173. https://doi.org/10.3390/su13169173
Chicago/Turabian StyleNie, Zifei, and Hooman Farzaneh. 2021. "Role of Model Predictive Control for Enhancing Eco-Driving of Electric Vehicles in Urban Transport System of Japan" Sustainability 13, no. 16: 9173. https://doi.org/10.3390/su13169173
APA StyleNie, Z., & Farzaneh, H. (2021). Role of Model Predictive Control for Enhancing Eco-Driving of Electric Vehicles in Urban Transport System of Japan. Sustainability, 13(16), 9173. https://doi.org/10.3390/su13169173







