Multi-Objective Fuzzy Tourist Trip Design Problem with Heterogeneous Preferences and Sustainable Itineraries
Abstract
:1. Introduction
- A model for group planning of sustainable tourism itineraries is presented and formulated, which articulates three objectives. These objectives are maximising the individual benefits of tourists (individual profit), maximisation of equity (equity in group profit), and minimising CO emissions derived from multi-modal transport. The problem modelled as TOP considers travel costs and budgets. Thus, all three dimensions of TBL are included;
- The social dimension is incorporated into the process of constructing itineraries under the concept of equity in the group profit. This dimension is measured based on the difference in personal benefits. The objective is to minimise the difference between the highest and lowest profit obtained by a tourist;
- The costs of CO emissions emitted by multi-modal transport in the itinerary are calculated. The only evidence of in the literature where this concept is applied is in [44];
- Uncertainty is considered in some of its components, and a fuzzy approximation is used to address it. Thus, fuzzy numbers are considered to quantify the heterogeneous preferences of tourists associated with the first and second objectives. Flexible (fuzzy) time window constraints, budget, and maximum travel time are also considered;
- The model also provides support for decision-making in tourism planning under COVID-19 scenarios. The maximum capacity of tourists on the route maintains the permissible occupancy at the sites of interest. This limitation helps to ensure the care and health of tourists.
2. Background
2.1. Transport and CO Emissions
2.2. Heterogeneous Preferences and Equity
2.3. Fuzzy Approach to TTDP
3. Mathematical Modelling
3.1. Model Formulation
3.2. Fuzzy Optimization
3.3. Consideration of CO Emissions
4. Experimentation
4.1. Case Study Area
4.1.1. Sustainability
4.1.2. Sustainability and Uncertainty
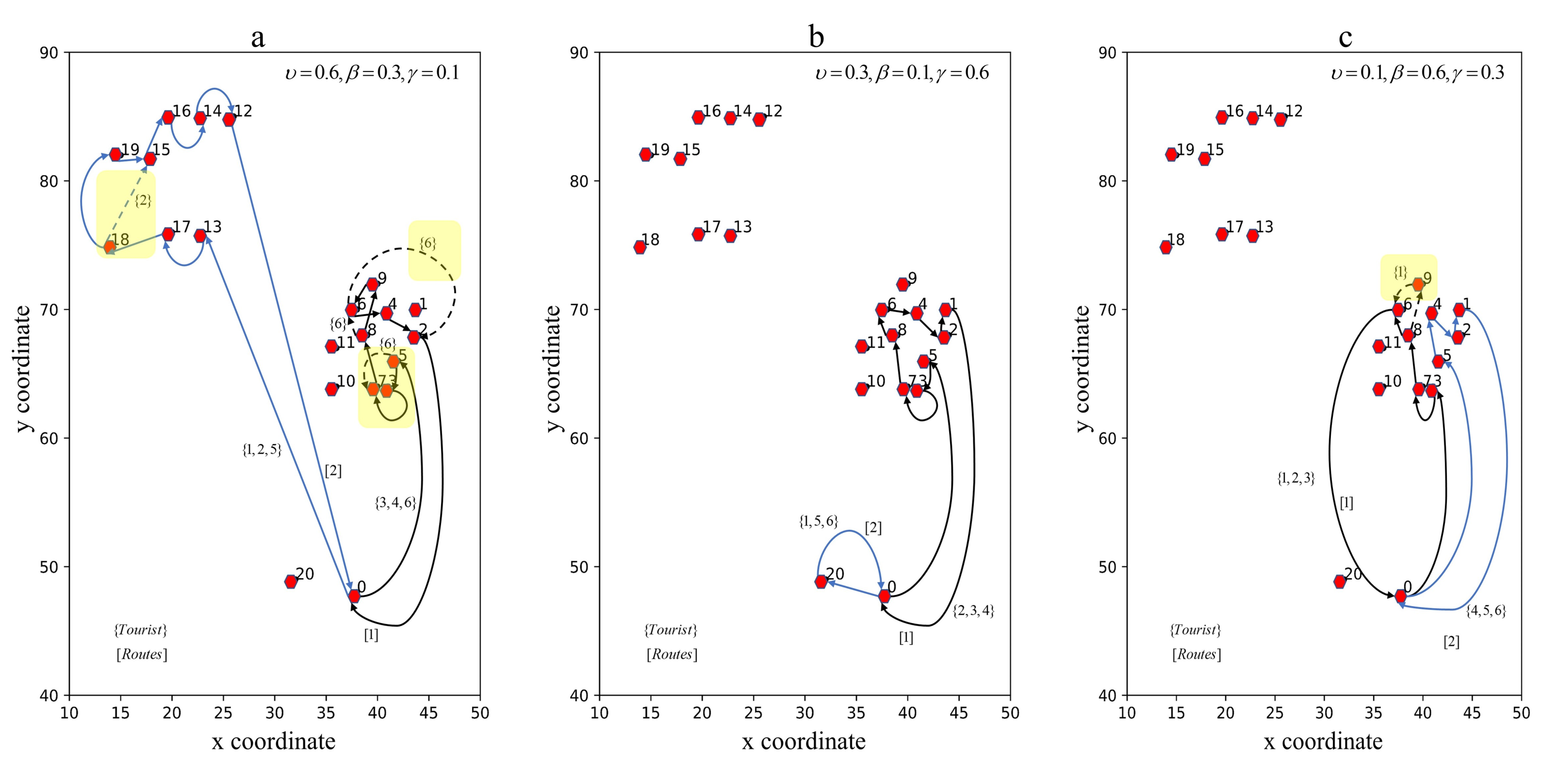
4.1.3. Variation of Preferences
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Delgado, M.; Mills, K.G. The supply chain economy: A new industry categorization for understanding innovation in services. Res. Policy 2020, 49, 104039. [Google Scholar] [CrossRef]
- The World Bank. World Development Indicators: Structure of Output; Technical Report; The World Bank: Washington, DC, USA, 2021. [Google Scholar]
- Lee, H.K.; Fernando, Y. The antecedents and outcomes of the medical tourism supply chain. Tour. Manag. 2015, 46, 148–157. [Google Scholar] [CrossRef]
- Daniel, A.D.; Costa, R.A.; Pita, M.; Costa, C. Tourism Education: What about entrepreneurial skills? J. Hosp. Tour. Manag. 2017, 30, 65–72. [Google Scholar] [CrossRef]
- Kanda, W.; Kivimaa, P. What opportunities could the COVID-19 outbreak offer for sustainability transitions research on electricity and mobility? Energy Res. Soc. Sci. 2020, 68, 101666. [Google Scholar] [CrossRef]
- Lokhandwala, S.; Gautam, P. Indirect impact of COVID-19 on environment: A brief study in Indian context. Environ. Res. 2020, 188, 109807. [Google Scholar] [CrossRef] [PubMed]
- Shakil, M.H.; Munim, Z.H.; Tasnia, M.; Sarowar, S. COVID-19 and the environment: A critical review and research agenda. Sci. Total Environ. 2020, 745, 141022. [Google Scholar] [CrossRef]
- Bertella, G. Re-thinking sustainability and food in tourism. Ann. Tour. Res. 2020, 84, 103005. [Google Scholar] [CrossRef] [PubMed]
- Higgins-Desbiolles, F. Socialising tourism for social and ecological justice after COVID-19. Tour. Geogr. 2020, 22, 610–623. [Google Scholar] [CrossRef] [Green Version]
- Hall, C.M. Constructing sustainable tourism development: The 2030 agenda and the managerial ecology of sustainable tourism. J. Sustain. Tour. 2019, 27, 1044–1060. [Google Scholar] [CrossRef]
- Nguyen, T.Q.T.; Young, T.; Johnson, P.; Wearing, S. Conceptualising networks in sustainable tourism development. Tour. Manag. Perspect. 2019, 32, 100575. [Google Scholar] [CrossRef]
- Gong, M.; Gao, Y.; Koh, L.; Sutcliffe, C.; Cullen, J. The role of customer awareness in promoting firm sustainability and sustainable supply chain management. Int. J. Prod. Econ. 2019, 217, 88–96. [Google Scholar] [CrossRef]
- Park, B.I.; Ghauri, P.N. Determinants influencing CSR practices in small and medium sized MNE subsidiaries: A stakeholder perspective. J. World Bus. 2015, 50, 192–204. [Google Scholar] [CrossRef]
- Scott, D.; Hall, C.M.; Gössling, S. Global tourism vulnerability to climate change. Ann. Tour. Res. 2019, 77, 49–61. [Google Scholar] [CrossRef]
- Wolf, F.; Filho, W.L.; Singh, P.; Scherle, N.; Reiser, D.; Telesford, J.; Miljković, I.B.; Havea, P.H.; Li, C.; Surroop, D.; et al. Influences of Climate Change on Tourism Development in Small Pacific Island States. Sustainability 2021, 13, 4223. [Google Scholar] [CrossRef]
- Scott, D.; Gössling, S.; Hall, C.M. International tourism and climate change. WIREs Clim. Chang. 2012, 3, 213–232. [Google Scholar] [CrossRef]
- Loehr, J.; Becken, S. The Tourism Climate Change Knowledge System. Ann. Tour. Res. 2021, 86, 103073. [Google Scholar] [CrossRef]
- Qian, J.; Eglese, R. Fuel emissions optimization in vehicle routing problems with time-varying speeds. Eur. J. Oper. Res. 2016, 248, 840–848. [Google Scholar] [CrossRef]
- Peeters, P.; Dubois, G. Tourism travel under climate change mitigation constraints. J. Transp. Geogr. 2010, 18, 447–457. [Google Scholar] [CrossRef]
- Le-Klähn, D.T.; Hall, C.M. Tourist use of public transport at destinations—A review. Curr. Issues Tour. 2014, 18, 785–803. [Google Scholar] [CrossRef]
- Sedarati, P.; Santos, S.; Pintassilgo, P. System Dynamics in Tourism Planning and Development. Tour. Plan. Dev. 2018, 16, 256–280. [Google Scholar] [CrossRef]
- Kotiloglu, S.; Lappas, T.; Pelechrinis, K.; Repoussis, P. Personalized multi-period tour recommendations. Tour. Manag. 2017, 62, 76–88. [Google Scholar] [CrossRef] [Green Version]
- Vansteenwegen, P.; Oudheusden, D.V. The Mobile Tourist Guide: An OR Opportunity. OR Insight 2007, 20, 21–27. [Google Scholar] [CrossRef]
- Brito, J.; Expósito, A.; Moreno, J.A. A fuzzy GRASP algorithm for solving a Tourist Trip Design Problem. In Proceedings of the 2017 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Naples, Italy, 9–12 July 2017. [Google Scholar] [CrossRef]
- Expósito, A.; Mancini, S.; Brito, J.; Moreno, J.A. A fuzzy GRASP for the tourist trip design with clustered POIs. Expert Syst. Appl. 2019, 127, 210–227. [Google Scholar] [CrossRef]
- Garcia, A.; Arbelaitz, O.; Linaza, M.T.; Vansteenwegen, P.; Souffriau, W. Personalized Tourist Route Generation. In Current Trends in Web Engineering; Springer: Berlin/Heidelberg, Germany, 2010; pp. 486–497. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Meza, J.; Montoya-Torres, J.R. A systematic literature review for the tourist trip design problem: Extensions, solution techniques and future research lines. Compt. Oper. Res. 2021. submitted for publication. [Google Scholar]
- Souffiau, W.; Maervoet, J.; Vansteenwegen, P.; Berghe, G.V.; Oudheusden, D.V. A Mobile Tourist Decision Support System for Small Footprint Devices. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1248–1255. [Google Scholar] [CrossRef]
- Zheng, W.; Liao, Z. Using a heuristic approach to design personalized tour routes for heterogeneous tourist groups. Tour. Manag. 2019, 72, 313–325. [Google Scholar] [CrossRef]
- Wang, W.; Liu, J.; Innes, J.L. Conservation equity for local communities in the process of tourism development in protected areas: A study of Jiuzhaigou Biosphere Reserve, China. World Dev. 2019, 124, 104637. [Google Scholar] [CrossRef]
- Arowoshegbe, A.O.; Uniamikogbo, E. Sustainability and Triple Bottom Line: An Overview of Two Interrelated Concepts. Igbinedion Univ. J. Account. 2016, 2, 88–126. [Google Scholar]
- D’Eusanio, M.; Serreli, M.; Zamagni, A.; Petti, L. Assessment of social dimension of a jar of honey: A methodological outline. J. Clean. Prod. 2018, 199, 503–517. [Google Scholar] [CrossRef]
- Kloepffer, W. Life cycle sustainability assessment of products. Int. J. Life Cycle Assess. 2008, 13, 89–95. [Google Scholar] [CrossRef]
- Vega-Mejía, C.A.; Montoya-Torres, J.R.; Islam, S.M.N. Consideration of triple bottom line objectives for sustainability in the optimization of vehicle routing and loading operations: A systematic literature review. Ann. Oper. Res. 2017, 273, 311–375. [Google Scholar] [CrossRef]
- Yeh, D.Y.; Cheng, C.H. Recommendation system for popular tourist attractions in Taiwan using Delphi panel and repertory grid techniques. Tour. Manag. 2015, 46, 164–176. [Google Scholar] [CrossRef]
- Zhang, X.; Song, H.; Huang, G.Q. Tourism supply chain management: A new research agenda. Tour. Manag. 2009, 30, 345–358. [Google Scholar] [CrossRef] [Green Version]
- Karunakaran, D.; Mei, Y.; Zhang, M. Multitasking Genetic Programming for Stochastic Team Orienteering Problem with Time Windows. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019. [Google Scholar] [CrossRef]
- Zheng, W.; Liao, Z.; Lin, Z. Navigating through the complex transport system: A heuristic approach for city tourism recommendation. Tour. Manag. 2020, 81, 104162. [Google Scholar] [CrossRef]
- Jaber, H.; Marle, F.; Vidal, L.A.; Sarigol, I.; Didiez, L. A Framework to Evaluate Project Complexity Using the Fuzzy TOPSIS Method. Sustainability 2021, 13, 3020. [Google Scholar] [CrossRef]
- Javanmardi, E.; Liu, S.; Xie, N. Exploring Grey Systems Theory-Based Methods and Applications in Sustainability Studies: A Systematic Review Approach. Sustainability 2020, 12, 4437. [Google Scholar] [CrossRef]
- Jiang, P.; Yang, H.; Li, R.; Li, C. Inbound tourism demand forecasting framework based on fuzzy time series and advanced optimization algorithm. Appl. Soft Comput. 2020, 92, 106320. [Google Scholar] [CrossRef]
- Lok, W.J.; Ng, L.Y.; Andiappan, V. Optimal decision-making for combined heat and power operations: A fuzzy optimisation approach considering system flexibility, environmental emissions, start-up and shutdown costs. Process Saf. Environ. Prot. 2020, 137, 312–327. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, M.; Zhang, W.; Zhuang, X. Fuzzy optimization model for electric vehicle routing problem with time windows and recharging stations. Expert Syst. Appl. 2020, 145, 113123. [Google Scholar] [CrossRef]
- Susanty, A.; Puspitasari, N.B.; Saptadi, S.; Prasetyo, S. Implementation of green tourism concept through a dynamic programming algorithm to select the best route of tourist travel. IOP Conf. Ser. Earth Environ. Sci. 2018, 195, 012035. [Google Scholar] [CrossRef]
- Gunawan, A.; Lau, H.C.; Vansteenwegen, P. Orienteering Problem: A survey of recent variants, solution approaches and applications. Eur. J. Oper. Res. 2016, 255, 315–332. [Google Scholar] [CrossRef]
- Kaushal, V.; Sharma, S.; Reddy, G.M. A structural analysis of destination brand equity in mountainous tourism destination in northern India. Tour. Hosp. Res. 2018, 19, 452–464. [Google Scholar] [CrossRef]
- Ravald, A.; Grönroos, C. The value concept and relationship marketing. Eur. J. Mark. 1996, 30, 19–30. [Google Scholar] [CrossRef]
- Michael, N.; Reisinger, Y.; Hayes, J.P. The UAE’s tourism competitiveness: A business perspective. Tour. Manag. Perspect. 2019, 30, 53–64. [Google Scholar] [CrossRef]
- Arbolino, R.; Yigitcanlar, T.; L’Abbate, P.; Ioppolo, G. Effective growth policymaking: Estimating provincial territorial development potentials. Land Use Policy 2019, 86, 313–321. [Google Scholar] [CrossRef]
- Truong, N.V.; Shimizu, T. The effect of transportation on tourism promotion: Literature review on application of the Computable General Equilibrium (CGE) Model. Transp. Res. Procedia 2017, 25, 3096–3115. [Google Scholar] [CrossRef]
- Belgin, O.; Karaoglan, I.; Altiparmak, F. Two-echelon vehicle routing problem with simultaneous pickup and delivery: Mathematical model and heuristic approach. Comput. Ind. Eng. 2018, 115, 1–16. [Google Scholar] [CrossRef]
- Bektaş, T.; Laporte, G. The Pollution-Routing Problem. Transp. Res. Part B Methodol. 2011, 45, 1232–1250. [Google Scholar] [CrossRef]
- Palmer, A. The Developement of an Integrated Routing and Carbon Dioxide Emissions Model for Goods Vehicle. Ph.D. Thesis, Cranfield University, Cranfield, UK, November 2007. [Google Scholar]
- Kara, İ.; Kara, B.Y.; Yetis, M.K. Energy Minimizing Vehicle Routing Problem. In Combinatorial Optimization and Applications; Springer: Berlin/Heidelberg, Germany, 2007; pp. 62–71. [Google Scholar] [CrossRef]
- Gavalas, D.; Konstantopoulos, C.; Mastakas, K.; Pantziou, G.; Vathis, N. Heuristics for the time dependent team orienteering problem: Application to tourist route planning. Comput. Oper. Res. 2015, 62, 36–50. [Google Scholar] [CrossRef]
- Gangoiti, A.G.; Arbelaitz, O.; Otaegui, O.; Vansteenwegen, P.; Linaza, M.T. Public Transportation Algorithm for an Intelligent Routing System. In Proceedings of the 16th ITS World Congress and Exhibition on Intelligent Transport Systems and Services, Stockholm, Sweden, 21–25 September 2009. [Google Scholar]
- Churchill, S.A.; Inekwe, J.; Ivanovski, K.; Smyth, R. Transport infrastructure and CO2 emissions in the OECD over the long run. Transp. Res. Part D Transp. Environ. 2021, 95, 102857. [Google Scholar] [CrossRef]
- Abbaspour, R.; Samadzadeg, F. Itinerary Planning in Multimodal Urban Transportation Network. J. Appl. Sci. 2009, 9, 1898–1906. [Google Scholar] [CrossRef]
- Garcia, A.; Arbelaitz, O.; Vansteenwegen, P.; Souffriau, W.; Linaza, M.T. Hybrid Approach for the Public Transportation Time Dependent Orienteering Problem with Time Windows. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; pp. 151–158. [Google Scholar] [CrossRef]
- Abbaspour, R.A.; Samadzadegan, F. Time-dependent personal tour planning and scheduling in metropolises. Expert Syst. Appl. 2011, 38, 12439–12452. [Google Scholar] [CrossRef]
- Garcia, A.; Vansteenwegen, P.; Arbelaitz, O.; Souffriau, W.; Linaza, M.T. Integrating public transportation in personalised electronic tourist guides. Comput. Oper. Res. 2013, 40, 758–774. [Google Scholar] [CrossRef]
- Gavalas, D.; Kasapakis, V.; Konstantopoulos, C.; Pantziou, G.; Vathis, N.; Zaroliagis, C. The eCOMPASS multimodal tourist tour planner. Expert Syst. Appl. 2015, 42, 7303–7316. [Google Scholar] [CrossRef]
- Wu, X.; Guan, H.; Han, Y.; Ma, J. A tour route planning model for tourism experience utility maximization. Adv. Mech. Eng. 2017, 9, 168781401773230. [Google Scholar] [CrossRef] [Green Version]
- Yu, V.F.; Jewpanya, P.; Ting, C.J.; Redi, A.P. Two-level particle swarm optimization for the multi-modal team orienteering problem with time windows. Appl. Soft Comput. 2017, 61, 1022–1040. [Google Scholar] [CrossRef]
- Liao, Z.; Zheng, W. Using a heuristic algorithm to design a personalized day tour route in a time-dependent stochastic environment. Tour. Manag. 2018, 68, 284–300. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, Z.; Feng, X. A novel flexible shuttle vehicle scheduling problem in scenic areas: Task-divided graph-based formulation and ALGORITHM. Comput. Ind. Eng. 2021, 156, 107295. [Google Scholar] [CrossRef]
- Kargar, M.; Lin, Z. A socially motivating and environmentally friendly tour recommendation framework for tourist groups. Expert Syst. Appl. 2021, 180, 115083. [Google Scholar] [CrossRef]
- Ntakolia, C.; Iakovidis, D.K. A swarm intelligence graph-based pathfinding algorithm (SIGPA) for multi-objective route planning. Comput. Oper. Res. 2021, 133, 105358. [Google Scholar] [CrossRef]
- Wang, Y.W.; Lin, C.C.; Lee, T.J. Electric vehicle tour planning. Transp. Res. Part D Transp. Environ. 2018, 63, 121–136. [Google Scholar] [CrossRef]
- Karbowska-Chilinska, J.; Chociej, K. Optimization of Multistage Tourist Route for Electric Vehicle. In Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2019; pp. 186–196. [Google Scholar] [CrossRef]
- Karbowska-Chilinska, J.; Chociej, K. Genetic Algorithm for Generation Multistage Tourist Route of Electrical Vehicle. In Computer Information Systems and Industrial Management; Saeed, K., Dvorský, J., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 366–376. [Google Scholar]
- Sylejmani, K.; Dorn, J.; Musliu, N. Planning the trip itinerary for tourist groups. Inf. Technol. Tour. 2017, 17, 275–314. [Google Scholar] [CrossRef]
- Malucelli, F.; Giovannini, A.; Nonato, M. Designing Single Origin-destination Itineraries for Several Classes of Cycle-tourists. Transp. Res. Procedia 2015, 10, 413–422. [Google Scholar] [CrossRef] [Green Version]
- Friedman, R.S.; Law, E.A.; Bennett, N.J.; Ives, C.D.; Thorn, J.P.R.; Wilson, K.A. How just and just how? A systematic review of social equity in conservation research. Environ. Res. Lett. 2018, 13, 053001. [Google Scholar] [CrossRef]
- İlhan, T.; Iravani, S.M.R.; Daskin, M.S. The orienteering problem with stochastic profits. IIE Trans. 2008, 40, 406–421. [Google Scholar] [CrossRef]
- Amghar, M.; Zoullouti, B.; Sbiti, N. Risk Analysis of Operating Room Using the Fuzzy Bayesian Network Model. Int. J. Eng. 2017, 30, 66–74. [Google Scholar]
- Zheng, W.; Huang, X.; Li, Y. Understanding the tourist mobility using GPS: Where is the next place? Tour. Manag. 2017, 59, 267–280. [Google Scholar] [CrossRef] [Green Version]
- Jackson, J.; Mei, Y. Genetic Programming Hyper-heuristic with Cluster Awareness for Stochastic Team Orienteering Problem with Time Windows. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020. [Google Scholar] [CrossRef]
- Matsuda, Y.; Nakamura, M.; Kang, D.; Miyagi, H. An optimal routing problem for sightseeing with fuzzy tilme-varying weights. In Proceedings of the 2004 IEEE International Conference on Systems, Man and Cybernetics (IEEE Cat. No.04CH37583), The Hague, The Netherlands, 10–13 October 2004. [Google Scholar] [CrossRef]
- Hasuike, T.; Katagiri, H.; Tsubaki, H. Tour route planning problem for sightseeing with the multiroute under several uncertain conditions. In Proceedings of the 2012 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Seoul, Korea, 14–17 October 2012. [Google Scholar] [CrossRef]
- Hasuike, T.; Katagiri, H.; Tsubaki, H.; Tsuda, H. Route planning problem under fuzzy sightseeing times and satisfaction values of sightseeing places. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013. [Google Scholar] [CrossRef]
- Hasuike, T.; Katagiri, H.; Tsubaki, H.; Tsuda, H. Flexible route planning for sightseeing with fuzzy random and fatigue-dependent satisfactions. J. Adv. Comput. Intell. Intell. Inform. 2014, 18, 190–196. [Google Scholar] [CrossRef]
- Expósito, A.; Mancini, S.; Brito, J.; Moreno, J.A. Uncertainty Management with Fuzzy and Rough Sets. In Chapter Solving a Fuzzy Tourist Trip Design Problem with Clustered Points of Interest; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Ariyarit, A.; Kanazaki, M.; Bureerat, S. An Approach Combining an Efficient and Global Evolutionary Algorithm with a Gradient-Based Method for Airfoil Design Problems. Smart Sci. 2020, 8, 14–23. [Google Scholar] [CrossRef]
- Trachanatzi, D.; Rigakis, M.; Marinaki, M.; Marinakis, Y. An interactive preference-guided firefly algorithm for personalized tourist itineraries. Expert Syst. Appl. 2020, 159, 113563. [Google Scholar] [CrossRef]
- Arbolino, R.; Boffardi, R.; Simone, L.D.; Ioppolo, G. Multi-objective optimization technique: A novel approach in tourism sustainability planning. J. Environ. Manag. 2021, 285, 112016. [Google Scholar] [CrossRef]
- Yan, L.; Gao, B.W.; Zhang, M. A mathematical model for tourism potential assessment. Tour. Manag. 2017, 63, 355–365. [Google Scholar] [CrossRef]
- Ishizaka, A.; Nemery, P.; Lidouh, K. Location selection for the construction of a casino in the Greater London region: A triple multi-criteria approach. Tour. Manag. 2013, 34, 211–220. [Google Scholar] [CrossRef] [Green Version]
- Bellman, R.E.; Zadeh, L.A. Decision-Making in a Fuzzy Environment. Manag. Sci. 1970, 17, B-141–B-164. [Google Scholar] [CrossRef]
- Verdegay, J.L. Fuzzy optimization: Models, methods and perspectives. In Proceedings of the 6th IFSA-95 World Congress, Sao Paulo, Brazil, 22–28 July 1995; pp. 39–71. [Google Scholar]
- Delgado, M.; Verdegay, J.; Vila, M. A general model for fuzzy linear programming. Fuzzy Sets Syst. 1989, 29, 21–29. [Google Scholar] [CrossRef]
- Ruiz-Meza, J.; Montoya-Torres, J.R. Tourist trip design with heterogeneous preferences, transport mode selection and environmental considerations. Ann. Oper. Res. 2021. [Google Scholar] [CrossRef] [PubMed]
- Jafari, R.; Yu, W.; Razvarz, S.; Gegov, A. Numerical methods for solving fuzzy equations: A survey. Fuzzy Sets Syst. 2021, 404, 1–22. [Google Scholar] [CrossRef]
- Kaufmann, A.; Gupta, M.M. Fuzzy Mathematical Models in Engineering and Management Science; Elsevier Science Inc.: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Adamo, J. Fuzzy decision trees. Fuzzy Sets Syst. 1980, 4, 207–219. [Google Scholar] [CrossRef]
- Herrera, F.; Verdegay, J. Fuzzy boolean programming problems with fuzzy costs: A general study. Fuzzy Sets Syst. 1996, 81, 57–76. [Google Scholar] [CrossRef]
- Hill, N.; Karagianni, E.; Jones, L.; MacCarthy, J.; Bonifazi, E.; Hinton, S.; Walker, C.; Harris, B. 2019 Government Greenhouse Gas Conversion Factors for Company Reporting. Methodologhy Paper for Emission Factors; Deparment for Business, Energy and Industrial Strategy: Kew, London, UK, 2019; Available online: https://www.gov.uk/government/publications/greenhouse-gas-reporting-conversion-factors-2019 (accessed on 16 February 2021)Technical Report.
- Fontaras, G.; Zacharof, N.G.; Ciuffo, B. Fuel consumption and CO2 emissions from passenger cars in Europe—Laboratory versus real-world emissions. Prog. Energy Combust. Sci. 2017, 60, 97–131. [Google Scholar] [CrossRef]
- Zacharof, N.; Fontaras, G.; Ciuffo, B.; Tsiakmakis, S.; Anagnostopoulos, K.; Marotta, A.; Pavlovic, J. Review of in Use Factors Affecting the Fuel Consumption and CO2 Emissions of Passenger Cars.; European Commission Joint Research Centre: Luxembourg, 2016. [Google Scholar] [CrossRef]
- SENDECO2. Precios de CO2. 2020. Available online: https://www.sendeco2.com/es/precios-co2 (accessed on 8 February 2021).
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Zeleny, M. The Attribute-Dynamic Attitude Model (Adam). Manag. Sci. 1976, 23, 12–26. [Google Scholar] [CrossRef]
- Gobernación de Sucre. Fondo de Promoción Turística-Colombia. Plan Estratégico de Desarrollo Turístico de Sucre 2011–2020. Technical Report, Gobernación de Sucre. 2011. Available online: https://www.citur.gov.co/upload/publications/documentos/184.Plan~_Estrategico_de_Turismo_de_Sucre.pdf (accessed on 3 February 2021).
- Viceministerio de Turismo. Listado de Atractivos Turísticos de Sucre. 2020. Available online: http://www.sucre.gov.co~/turismo/ruta-competitiva-turismo-vacacional (accessed on 15 February 2020).



| Notation | Description | Notation | Description |
|---|---|---|---|
| Set of POIs | Travel time matrix | ||
| Depot | Time windows | ||
| Set of routes | Transport cost | ||
| Set of transport mode | Unit cost per kilometre traveled | ||
| Set of tourist | Average speed | ||
| The profit of POIs | Profit-to-cost conversion parameter | ||
| Visit time | Alphas-cut | ||
| Maximum time of the tourist | Tolerance level vector | ||
| Maximum budget of the tourist | , , | Weights associated with the objectives | |
| Distance matrix | Emissions cost | ||
| CO2 | CO emissions by mode of transport | Preference factor | |
| Q | Maximum tourist capacity on the route | Minimum tourist capacity on the route |
| Notation | Description |
|---|---|
| Binary variable. 1 if the tourist u takes a trip on the arc of the route k, 0 otherwise | |
| Binary variable. 1 if the POI i is visited by tourist u on route k, 0 otherwise | |
| Binary variable. 1 if the route is enabled, 0 otherwise | |
| Binary variable. 1 if the mode of transport m is used to go from i to j, 0 otherwise | |
| Auxiliary binary variable. 1 if a trip is made on arc of route k, 0 otherwise | |
| Auxiliary binary variable. 1 if POI i is visited on route k, 0 otherwise | |
| Positive variable. Arrival time of tourist u at node i | |
| Positive variable. Tourist travel time u | |
| Positive variable. Use of private vehicles | |
| Positive variable. Number of tourists u using mode of transportation m in the arc | |
| Positive variable. Maximum profit | |
| Positive variable. Minimum profit |
| Weigths | Variation in Weights | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| 0 | 1 | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| 0 | 0 | 1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | |
| Test | POIs | Time (min) | Gap | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 37 | 0 | 1 | 0.6 | 0.3 | 0.1 | 711 | 44 | 1644.42 | 16 | 10.21 | 0% |
| 38 | 0.4 | 1 | 0.6 | 0.3 | 0.1 | 676.6 | 40.1 | 1644.42 | 16 | 9.32 | 0% |
| 39 | 0.6 | 1 | 0.6 | 0.3 | 0.1 | 659.4 | 38.15 | 1644.42 | 16 | 12.83 | 0% |
| 40 | 1 | 1 | 0.6 | 0.3 | 0.1 | 625 | 34.25 | 1644.42 | 16 | 15.1 | 0% |
| 41 | 0 | 0.6 | 0.6 | 0.3 | 0.1 | 717.5 | 44 | 1527.1 | 17 | 45.4 | 0% |
| 42 | 0.4 | 0.6 | 0.6 | 0.3 | 0.1 | 682.7 | 40.01 | 1539.11 | 17 | 90 | 1.5% |
| 43 | 0.6 | 0.6 | 0.6 | 0.3 | 0.1 | 631 | 22.65 | 1402.8 | 17 | 90 | 4.6% |
| 44 | 1 | 0.6 | 0.6 | 0.3 | 0.1 | 630.5 | 34.25 | 1558.08 | 17 | 90 | 10.8% |
| 45 | 0 | 0.2 | 0.6 | 0.3 | 0.1 | 704.5 | 59.5 | 1521.47 | 19 | 90 | 51.32% |
| 46 | 0.4 | 0.2 | 0.6 | 0.3 | 0.1 | 485.4 | 94 | 566.98 | 16 | 90 | 75.76% |
| 47 | 0.6 | 0.2 | 0.6 | 0.3 | 0.1 | 461.25 | 111.4 | 590.42 | 16 | 90 | 94.94% |
| 48 | 1 | 0.2 | 0.6 | 0.3 | 0.1 | 463.75 | 93.5 | 663.88 | 18 | 90 | 79.78% |
| 73 | 0 | 1 | 0.3 | 0.1 | 0.6 | 354.5 | 105.5 | 111.73 | 9 | 19.88 | 0% |
| 74 | 0.4 | 1 | 0.3 | 0.1 | 0.6 | 338.6 | 101.1 | 111.73 | 9 | 18.97 | 0% |
| 75 | 0.6 | 1 | 0.3 | 0.1 | 0.6 | 330.65 | 98.9 | 111.73 | 9 | 17.5 | 0% |
| 76 | 1 | 1 | 0.3 | 0.1 | 0.6 | 314.75 | 94.5 | 111.73 | 9 | 14.64 | 0% |
| 77 | 0 | 0.6 | 0.3 | 0.1 | 0.6 | 367 | 112.5 | 114.94 | 10 | 80.86 | 0% |
| 78 | 0.4 | 0.6 | 0.3 | 0.1 | 0.6 | 350.4 | 107.7 | 114.94 | 10 | 83.75 | 0% |
| 79 | 0.6 | 0.6 | 0.3 | 0.1 | 0.6 | 342.1 | 105.3 | 114.94 | 10 | 47.95 | 0% |
| 80 | 1 | 0.6 | 0.3 | 0.1 | 0.6 | 325.5 | 100.5 | 114.94 | 10 | 78.67 | 0% |
| 81 | 0 | 0.2 | 0.3 | 0.1 | 0.6 | 371 | 112.25 | 124.73 | 10 | 90 | 330.03% |
| 82 | 0.4 | 0.2 | 0.3 | 0.1 | 0.6 | 360.9 | 107.7 | 114.94 | 10 | 90 | 215.52% |
| 83 | 0.6 | 0.2 | 0.3 | 0.1 | 0.6 | 322.9 | 98.9 | 111.73 | 9 | 90 | 336.25% |
| 84 | 1 | 0.2 | 0.3 | 0.1 | 0.6 | 295 | 101.5 | 117.03 | 10 | 90 | 932.97% |
| 121 | 0 | 1 | 0.1 | 0.6 | 0.3 | 341.5 | 4.5 | 153.15 | 11 | 36.4 | 0% |
| 122 | 0.4 | 1 | 0.1 | 0.6 | 0.3 | 292.9 | 4.2 | 142.39 | 9 | 38.45 | 0% |
| 123 | 0.6 | 1 | 0.1 | 0.6 | 0.3 | 285.1 | 4.3 | 142.39 | 9 | 36.99 | 0% |
| 124 | 1 | 1 | 0.1 | 0.6 | 0.3 | 271.25 | 4.25 | 142.39 | 9 | 30.3 | 0% |
| 125 | 0 | 0.6 | 0.1 | 0.6 | 0.3 | 344.5 | 4.5 | 156.04 | 11 | 90 | 97.65% |
| 126 | 0.4 | 0.6 | 0.1 | 0.6 | 0.3 | 306.6 | 9 | 144.16 | 9 | 90 | 100.9% |
| 127 | 0.6 | 0.6 | 0.1 | 0.6 | 0.3 | 342.4 | 12.1 | 154.59 | 11 | 90 | 90.02% |
| 128 | 1 | 0.6 | 0.1 | 0.6 | 0.3 | 271.25 | 4.25 | 142.39 | 9 | 90 | 70.27% |
| 129 | 0 | 0.2 | 0.1 | 0.6 | 0.3 | 56.5 | 1.5 | 80.59 | 2 | 90 | 193.5% |
| 130 | 0.4 | 0.2 | 0.1 | 0.6 | 0.3 | 243.7 | 8.9 | 134.53 | 7 | 90 | 147.6% |
| 131 | 0.6 | 0.2 | 0.1 | 0.6 | 0.3 | 43.85 | 4.45 | 80.59 | 2 | 90 | 163.72% |
| 132 | 1 | 0.2 | 0.1 | 0.6 | 0.3 | 38.5 | 3.5 | 80.59 | 2 | 90 | 138.81% |
| POI | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.3 | 0.7 | 0.35 | 0.35 | 0.5 | 0.25 | 0.85 | 0.35 | 0.55 | 0.95 | 0.6 | 0.6 | 0.75 | 0.5 | 1 | 0.6 |
| 2 | 0.25 | 0.8 | 0.8 | 0.75 | 0.4 | 0.5 | 0.65 | 0.75 | 0.5 | 1 | 1 | 1 | 0.65 | 0.75 | 0.9 | 1 |
| 3 | 0.55 | 0.9 | 0.25 | 0.8 | 0.65 | 0.65 | 0.5 | 0.8 | 0.8 | 1 | 0.5 | 1 | 0.9 | 0.9 | 0.75 | 1 |
| 4 | 0.3 | 0.5 | 0.8 | 0.35 | 0.5 | 0.95 | 0.4 | 0.35 | 0.55 | 0.75 | 1 | 0.6 | 0.75 | 1 | 0.65 | 0.6 |
| 5 | 0.4 | 0.95 | 0.45 | 0.9 | 0.5 | 0.5 | 0.45 | 0.9 | 0.65 | 1 | 0.7 | 1 | 0.75 | 0.75 | 0.7 | 1 |
| 6 | 0.5 | 0.5 | 0.5 | 0.6 | 0.3 | 0.9 | 0.5 | 0.5 | 0.75 | 0.75 | 0.75 | 0.85 | 0.55 | 1 | 0.75 | 0.75 |
| 7 | 0.5 | 0.8 | 0.75 | 0.85 | 0.75 | 0.8 | 0.75 | 0.5 | 0.75 | 1 | 1 | 1 | 1 | 1 | 1 | 0.75 |
| 8 | 0.3 | 0.3 | 0.65 | 0.65 | 0.3 | 0.35 | 0.65 | 0.5 | 0.55 | 0.55 | 0.9 | 0.9 | 0.55 | 0.6 | 0.9 | 0.75 |
| 9 | 0.4 | 0.5 | 0.75 | 0.5 | 0.65 | 0.75 | 0.75 | 0.9 | 0.65 | 0.75 | 1 | 0.75 | 0.9 | 1 | 1 | 1 |
| 10 | 0.5 | 0.8 | 0.8 | 0.4 | 0.95 | 0.8 | 0.8 | 0.5 | 0.75 | 1 | 1 | 0.65 | 1 | 1 | 1 | 0.75 |
| 11 | 0.35 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.4 | 0.6 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.65 |
| 12 | 0.2 | 0.5 | 0.5 | 0.3 | 0.3 | 0.5 | 0.5 | 0.65 | 0.45 | 0.75 | 0.75 | 0.55 | 0.55 | 0.75 | 0.75 | 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-Meza, J.; Brito, J.; Montoya-Torres, J.R. Multi-Objective Fuzzy Tourist Trip Design Problem with Heterogeneous Preferences and Sustainable Itineraries. Sustainability 2021, 13, 9771. https://doi.org/10.3390/su13179771
Ruiz-Meza J, Brito J, Montoya-Torres JR. Multi-Objective Fuzzy Tourist Trip Design Problem with Heterogeneous Preferences and Sustainable Itineraries. Sustainability. 2021; 13(17):9771. https://doi.org/10.3390/su13179771
Chicago/Turabian StyleRuiz-Meza, José, Julio Brito, and Jairo R. Montoya-Torres. 2021. "Multi-Objective Fuzzy Tourist Trip Design Problem with Heterogeneous Preferences and Sustainable Itineraries" Sustainability 13, no. 17: 9771. https://doi.org/10.3390/su13179771
APA StyleRuiz-Meza, J., Brito, J., & Montoya-Torres, J. R. (2021). Multi-Objective Fuzzy Tourist Trip Design Problem with Heterogeneous Preferences and Sustainable Itineraries. Sustainability, 13(17), 9771. https://doi.org/10.3390/su13179771







