Global Optimization Algorithm Based on Kriging Using Multi-Point Infill Sampling Criterion and Its Application in Transportation System
Abstract
:1. Introduction
2. Literature Reviews about KGO Used in Traffic Area
3. Method
3.1. Kriging Model
3.2. Two Infill Sampling Criterions
3.2.1. Expected Improvement (EI)
3.2.2. A Multi-Point Infill Sampling Criterion Based on EI Criterion
Solution Algorithm
| Algorithm 1. MOEA/D. |
| Input: a multi-objective optimization problem. |
| A stop condition % the maximum number of iterations Gen. |
| Decompose into the number of subproblems N. |
| A set of weight vectors λ = (λ1, …, λN). |
| Number of neighbors T |
| Output: Approximate Pareto Frontier EP. |
| 1. Initialization |
| 2. suppose EP = ∅ (The ∅ represents a empty set). |
| 3. Calculate the distance between each weight vector and the ownership vector, take the nearest T weight vectors of each weight vector, and store their index in B. For each i = 1, 2, …, N, B(i) = {i1, i2, …, iT}. |
| 4. Randomly or by other methods to generate initial population: x1, x2, …, xN. |
| 5. For each i = 1, 2, …, N, set FVi= F(xi). |
| 6. Initialize reference point z. |
| 7. while the stop condition is not met |
| 8. for i = 1: N |
| 9. Generate offspring: randomly select two indexes k and l from B(i), and use analog binary crossover operator to generate offspring individuals x* from xk and xl. |
| 10. Adjustment: if necessary (out of bounds, etc.), then adjust x*. |
| 11. Calculate the objective function value F(x*). |
| 12. for j = 1: m |
| 13. if fj(x*)< zj |
| 14. zj = fj(x*) |
| 15. else |
| 16. zj = zj |
| 17. end |
| 18. end |
| 19. for j = 1: sum(B(i)) |
| 20. if gtch(x*|λj, z) ≤gtch(xj|λj, z) |
| 21. xj = x*, FVj = F(x*) |
| 22. else |
| 23. xj = xj, FVj = FVj |
| 24.end |
| 25. end |
| 26. Update EP: First delete all target vectors dominated by F(x*) in EP, then add the F(x*) to EP. |
| 27. end % corresponds to the for in line 8 |
| 28. end % corresponds to the while in line 7 |
| 29. END |
3.3. Kriging-Based Global Optimization Based on Multi-Point Infill Sampling Criterion
| Algorithm 2. Multi-point infill sampling criterion. Global Optimization BASED on Kriging Using Multi-Point Infill Sampling Criterion. |
| 1. Initialization |
| 2. Use design of experiment (DOE) to select a small number V of initial design points: {p1, p2, …, pV} %According to the literature [5], the selection number Vis generally 5d or 11d-1, where d is the number of design variables. |
| 3. for i = 1: V |
| 4. Evaluate the response values R(pi) of the design point pi |
| 5. end |
| 6. while the given algorithm termination condition is not met (in actual engineering problems, it is generally judged whether a certain number of iterations has been reached) |
| 7. Use all known design points and their corresponding objective function values to construct a Kriging model. |
| 8. Construct the MOP: min {EI1(x), EI2(x)} |
| 9. Solve the MOP through the decomposition-based multi-objective evolutionary algorithm (MOEA/D). |
| 10. Obtain the PS and its corresponded PF of the MOP with a number B of candidates: {ps1, ps2,…, psB} |
| 11. for i = 1: B |
| 12. calculate the Kriging predicted value kpv(psi) of the point psi |
| 13. end |
| 14. KPV = [] |
| 15. for i = 1: B |
| 16. KPV = [KPV, kpv(psi)] |
| 17. end |
| 18. KPV = sort(KPV, ‘ascend’) |
| 19. for i = 1: n |
| 20. find the corresponding point cpi of the KPV(i) |
| 21. end |
| 22. for i = 1: n |
| 23. Evaluate the response values R(cpi) of the design point cpi. |
| 24. end |
| 25. end % corresponds to the while in line 6. |
| 26. output the optimal solution. |
| 27. END |
4. Numerical and Engineering Examples Based on the Multi-Point Infill Sampling Criterion
4.1. Numerical Analysis
4.1.1. Six-Hump Camel Back Function (SC)
4.1.2. Hartman 6 Function (H6)
4.1.3. The Test of MOEA/D Parameters
4.2. Engineering Case
4.2.1. Optimization Model and Process
4.2.2. Data Description
4.2.3. Result Analysis
4.3. Implications
5. Conclusions and Discussion
- Considering the disadvantages of EGO and EGO-MO, this paper proposes a Kriging-based global optimization using multi-point infill sampling criterion. The characteristic of comparison to the already existing research is that the multi-point infill sampling criterion uses the method of EGO-MO to generate candidate sampling points, and the Kriging predicted values are employed as judgment standard. In this way, the extra parameters required are greatly reduced.
- At present, in the field of transportation, there are a few research studies on how to deal with simulation-based optimization problems. Therefore, the method proposed in this paper has certain reference significance for other time-consuming optimization problems in the transportation field.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pourhejazy, P.; Kwon, O.K. The new generation of operations research methods in supply chain optimization: A review. Sustainability 2016, 8, 1033. [Google Scholar] [CrossRef] [Green Version]
- Zheng, L.; Xue, X.; Xu, C.; Ran, B. A stochastic simulation-based optimization method for equitable and efficient network-wide signal timing under uncertainties. Transp. Res. Part B 2019, 122, 287–308. [Google Scholar] [CrossRef]
- Simpson, T.; Booker, A.; Ghosh, D.; Giunta, A.; Koch, P.; Yang, R.-J. Approximation methods in multidisciplinary analysis and optimization: A panel discussion. Struct. Multidiscip. Optim. 2004, 27, 302–313. [Google Scholar] [CrossRef] [Green Version]
- Han, Z.H. Kriging surrogate model and its application to design optimization: A review of recent progress. Acta Aeronaut. Astronaut. Sin. 2016, 37, 3197–3225. [Google Scholar]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Henkenjohann, N.; Kunert, J. An efficient sequential optimization approach based on the multivariate expected improvement criterion. Qual. Eng. 2007, 19, 267–280. [Google Scholar] [CrossRef]
- Kleijnen, J.P.; Van, B.W.; Van, N.I. Expected improvement in efficient global optimization through bootstrapped Kriging. J. Glob. Optim. 2012, 54, 59–73. [Google Scholar] [CrossRef]
- Picheny, V.; Wagner, T.; Ginsbourger, D. A benchmark of Kriging based infill criteria for noisy optimization. Struct. Multidiscip. Optim. 2013, 48, 607–626. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Gu, J.; Wang, X. Warpage optimization with dynamic injection molding technology and sequential optimization method. J. Adv. Manuf. Technol. 2015, 78, 177–187. [Google Scholar] [CrossRef]
- Jeong, S.; Murayama, M.; Yamamoto, K. Efficient Optimization Design Method Using Kriging Model. J. Aircr. 2004, 42, 1375. [Google Scholar] [CrossRef]
- Meunier, M. Simulation and Optimization of Flow Control Strategies for Novel High-Lift Configurations. AIAA J. 2009, 47, 1145–1157. [Google Scholar] [CrossRef]
- Wang, X.; Li, M.; Liu, Y.; Sun, W.; Song, X.; Zhang, J. Surrogate based multidisciplinary design optimization of lithium-ion battery thermal management system in electric vehicles. Struct. Multidiscip. Optim. 2017, 56, 1555–1570. [Google Scholar] [CrossRef]
- Song, X.; Sun, G.; Li, Q. Sensitivity analysis and reliability based design optimization for high-strength steel tailor welded thin-walled structures under crashworthiness. Thin-Walled Struct. 2016, 109, 132–142. [Google Scholar] [CrossRef]
- Song, J.; Yang, Y.; Wu, J.; Wu, J.; Sun, X.; Lin, J. Adaptive surrogate model based multiobjective optimization for coastal aquifer management. J. Hydrol. 2018, 561, 98–111. [Google Scholar] [CrossRef]
- Mastrippolito, F.; Aubert, S.; Ducros, F. Kriging metamodels-based multi-objective shape optimization applied a multi-scale heat exchanger. Comput. Fluids 2021, 221, 104899. [Google Scholar] [CrossRef]
- Li, Y.; Shi, J.; Cen, H. A Kriging-based adaptive global optimization method with generalized expected improvement and its application in numerical simulation and crop evapotranspiration. Agric. Water Manag. 2021, 245, 106623. [Google Scholar] [CrossRef]
- Li, Y.; Shen, J.; Cai, Z. A Kriging-assisted multi-objective constrained method for expensive black-box functions (dagger). Mathematics 2021, 9, 149. [Google Scholar] [CrossRef]
- Xia, B.; Liu, R.; He, Z. A single- and multi-objective optimization algorithm for electromagnetic devices assisted by adaptive Kriging based on parallel infilling strategy. J. Electr. Eng. Technol. 2021, 16, 301–308. [Google Scholar] [CrossRef]
- Kroetz, H.; Moustapha, M.; Beck, A. A two-level Kriging-based approach with active learning for solving time-variant risk optimization problems. Reliab. Eng. Syst. Saf. 2020, 203, 107033. [Google Scholar] [CrossRef]
- He, Y.; Sun, J.; Song, P. Dual Kriging assisted efficient global optimization of expensive problems with evaluation failures. Aerosp. Sci. Technol. 2020, 105, 106006. [Google Scholar] [CrossRef]
- Passos, A.; Luersen, M. Kriging-based multiobjective optimization using sequential reduction of the entropy of the predicted pareto front. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–17. [Google Scholar] [CrossRef]
- Ribaud, M.; Balchet-Scalliet, C.; Helbert, C. Robust optimization: A Kriging-based multi-objective optimization approach. Reliab. Eng. Syst. Saf. 2020, 200, 106913. [Google Scholar] [CrossRef] [Green Version]
- Yi, J.; Zhou, Q.; Cheng, Y. Efficient adaptive Kriging-based reliability analysis combining new learning function and error-based stopping criterion. Struct. Multidiscip. Optim. 2020, 62, 2517–2536. [Google Scholar] [CrossRef]
- Tao, T.; Zhao, G.; Ren, S. An efficient Kriging-based constrained optimization algorithm by global and local sampling in feasible region. J. Mech. Des. 2020, 142, 1–48. [Google Scholar] [CrossRef]
- Hong, L.; Li, H.; Peng, K. A novel Kriging based active learning method for for structural reliability analysis. J. Mech. Sci. Technol. 2020, 34, 1545–1556. [Google Scholar]
- Shi, R.; Liu, L.; Long, T. Multi-Fidelity modeling and adaptive Co-Kriging-based optimization for all-electric geostationary orbit satellite systems. J. Mech. Des. 2020, 142, 021404. [Google Scholar] [CrossRef]
- Sobester, A.; Leary, S.J.; Keane, A.J. On the design of optimization strategies based on global response surface approximation models. J. Glob. Optim. 2005, 33, 31–59. [Google Scholar] [CrossRef] [Green Version]
- Feng, Z.; Zhang, Q.B.; Zhang, Q.F. Amultiobjective optimizationbased framework to balance the global exploration and local exploitation in expensive optimization. J. Glob. Optim. 2015, 61, 677–694. [Google Scholar] [CrossRef]
- Li, M.; Li, S.; Jia, N. Simulation and optimization of bus schedule based on passenger flow big Data. China Transp. Rev. 2020, 42, 81–85. [Google Scholar]
- Lv, N.; Zhao, J. Research on Optimizing the Location of Logistics Park Based on Bayesian Probability Theory. China J. Highw. Transp. 2020, 33, 251–260. [Google Scholar]
- Zhang, K.; Zheng, L.; Liu, Z.; Jia, N. A deep learning based multitask model for network-wide traffic speed prediction. Neurocomputing 2020, 396, 438–450. [Google Scholar] [CrossRef]
- Wang, D.; Wang, C.; Xiao, J.; Xiao, Z.; Chen, W.; Havyarimana, V. Bayesian optimization of Support vector machine for regression prediction of short-term traffic flow. Intell. Data Anal. 2019, 23, 481–497. [Google Scholar] [CrossRef]
- Gu, X.; Han, Y.; Yu, J. Vehicle lane changing decision model based on decision mechanism and support vector machine. J. Harbin Inst. Technol. 2020, 52, 111–121. [Google Scholar]
- Tian, Z.; Zhang, S. Optimized empirical Bayesian accident black spot identification and sorting method. J. Chang’an Univ. 2019, 39, 115–126. [Google Scholar]
- Yu, Q. Hierarchical optimization OD estimation model based on Bayesian method. Highway 2014, 59, 123–127. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Tang, J.; Yang, Y.; Hao, W.; Liu, F.; Wang, Y. A data-driven timetable optimization of urban bus line based on multi-objective genetic algorithm. IEEE Trans. Intell. Transp. 2021, 22, 2417–2429. [Google Scholar] [CrossRef]


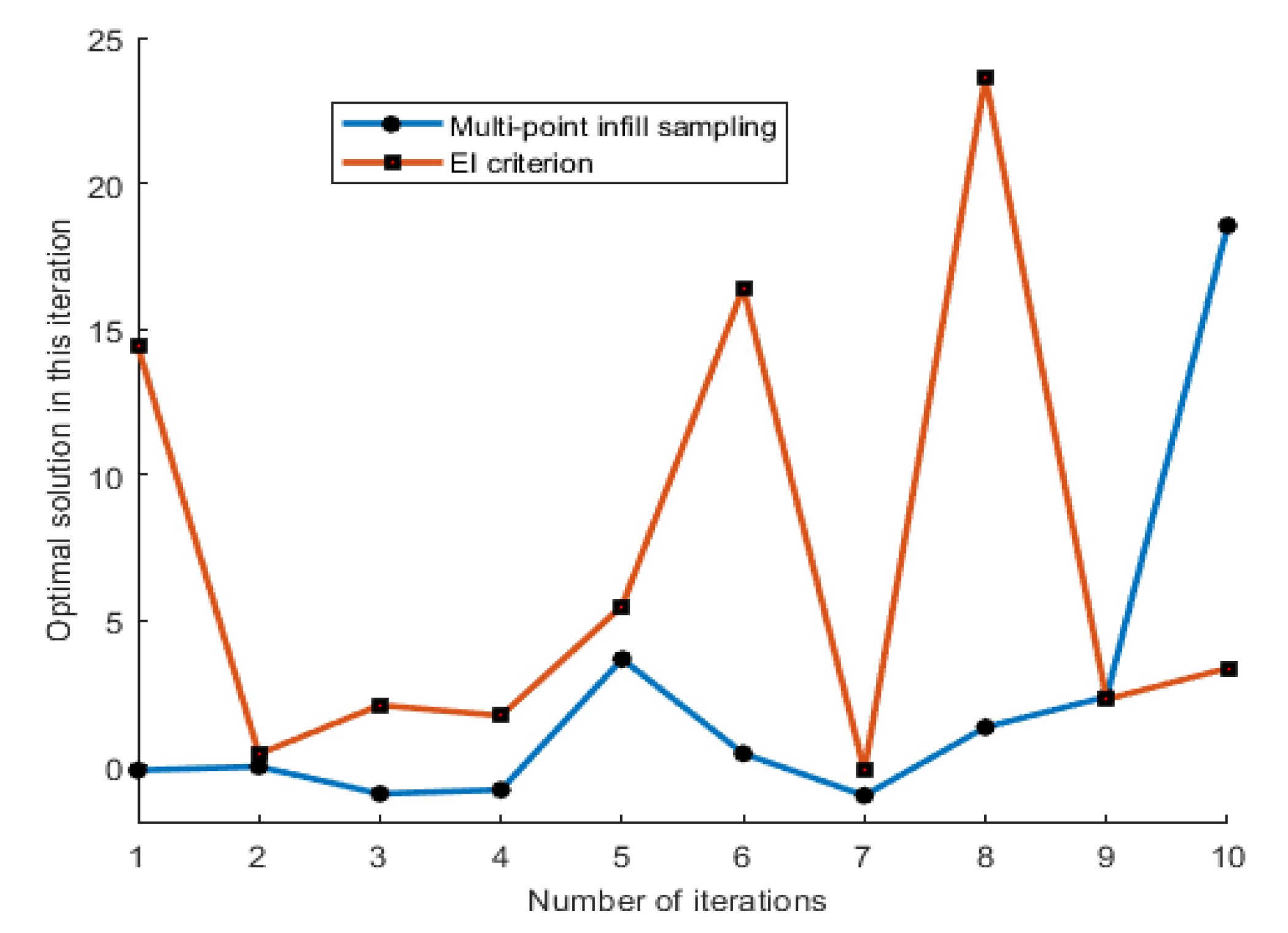




| Method | Multi-Point Infill Sampling | EI Criterion |
|---|---|---|
| Solution result | −1.0303 | −1.0127 |
| Number of iterations | 10 | 10 |
| Method | Multi-Point Infill Sampling | EI Criterion |
|---|---|---|
| Solution result | −3.2704 | −2.0399 |
| Number of iterations | 30 | 30 |
| Gen | Optimal Solution |
|---|---|
| 100 | −1.0299 |
| 200 | −1.0313 |
| 300 | −1.0152 |
| 400 | −1.0315 |
| 500 | −1.0314 |
| T | Opimal Solution |
|---|---|
| 5 | −1.0310 |
| 10 | −1.0310 |
| 15 | −1.0314 |
| 20 | −1.0313 |
| Time | Vehicle Number | Line | Longitude | Latitude | Speed |
|---|---|---|---|---|---|
| 2017/11/1 17:31 | 12301 | 445 | 116.4929 | 39.9629 | 7.9 |
| 2017/11/1 17:35 | 12301 | 445 | 116.497 | 39.9668 | 9.9 |
| 2017/11/1 17:50 | 12301 | 445 | 116.4837 | 39.9771 | 0.9 |
| 2017/11/1 17:59 | 12301 | 445 | 116.4836 | 39.9832 | 13.3 |
| … | … | … | … | … | |
| 2017/11/1 18:10 | 12301 | 445 | 116.4835 | 39.9863 | 0 |
| 2017/11/1 18:30 | 12301 | 445 | 116.4556 | 39.9845 | 29.9 |
| Smart Card Number | Drop off Time | Boardtime | Vehicle Number | Drop off Station Number | Boarding Station Number |
|---|---|---|---|---|---|
| C9FC4D76 | 20171129220144 | 20171129215400 | 12297 | 9 | 5 |
| 9D1F3E31 | 20171129220145 | 20171129215000 | 12297 | 11 | 5 |
| E420FD7C | 20171129220147 | 20171129215300 | 12297 | 10 | 5 |
| 627AEA05 | 20171129220148 | 20171129213900 | 12297 | 13 | 5 |
| … | … | … | … | … | |
| 22C69F45 | 20171129220150 | 20171129212900 | 12297 | 18 | 5 |
| 0144EB12 | 20171129220152 | 20171129215000 | 12297 | 11 | 5 |
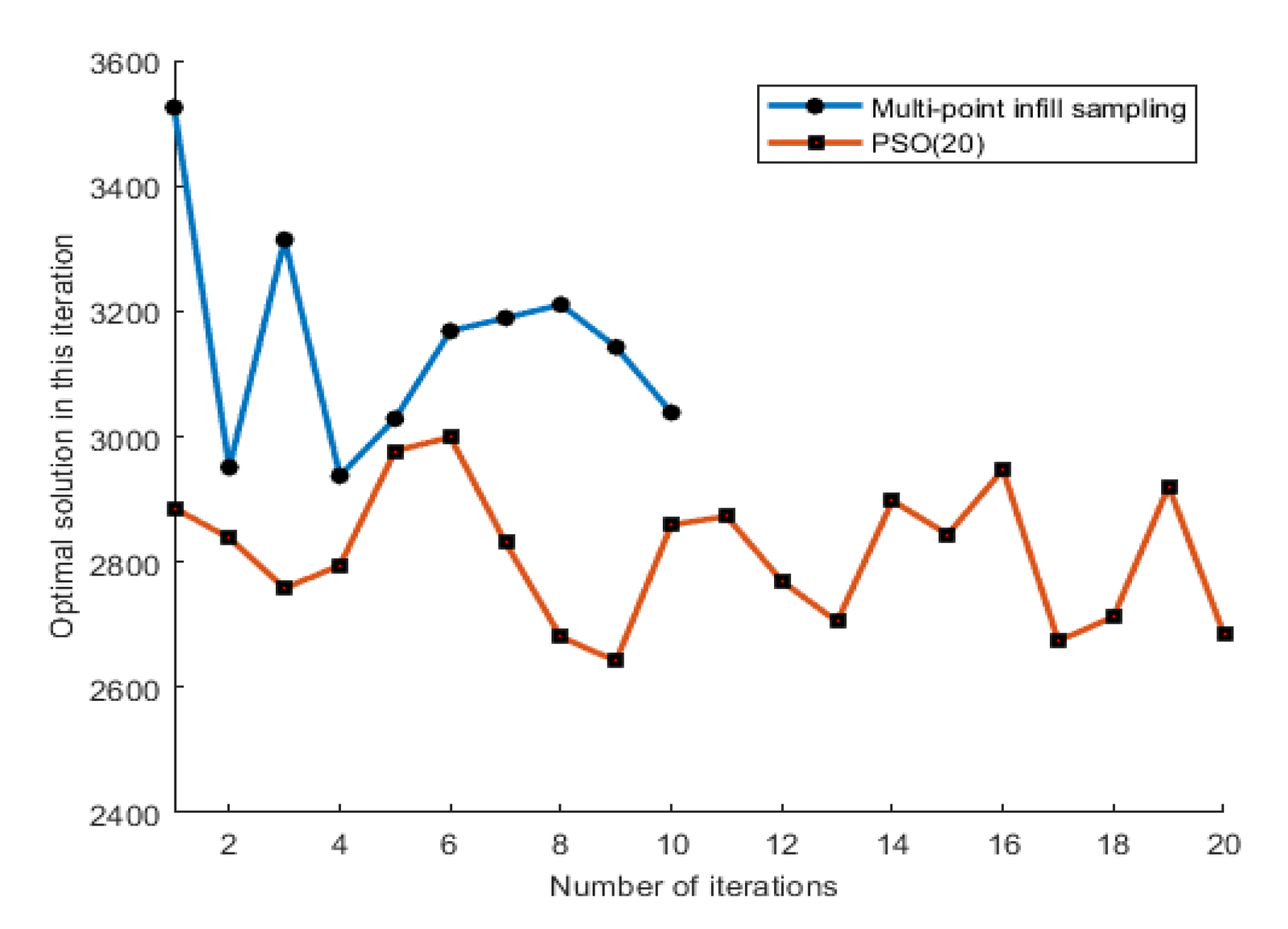
| Algorithm | Optimum | Number of Iterations | Number of Function Evaluations |
|---|---|---|---|
| PSO (population 80) | 3135.1 | 12 | 960 |
| PSO (population 20) | 2998.9 | 20 | 400 |
| PSO (population 50) | 3110 | 20 | 1000 |
| PSO (population 100) | 3287.5 | 10 | 1000 |
| Multi-point infill sampling | 3525.1 | 10 | 132 |
| Unoptimized value | 2431.1 | —— | —— |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Li, M.; Li, Z.; Liu, F. Global Optimization Algorithm Based on Kriging Using Multi-Point Infill Sampling Criterion and Its Application in Transportation System. Sustainability 2021, 13, 10645. https://doi.org/10.3390/su131910645
Song X, Li M, Li Z, Liu F. Global Optimization Algorithm Based on Kriging Using Multi-Point Infill Sampling Criterion and Its Application in Transportation System. Sustainability. 2021; 13(19):10645. https://doi.org/10.3390/su131910645
Chicago/Turabian StyleSong, Xiaodong, Mingyang Li, Zhitao Li, and Fang Liu. 2021. "Global Optimization Algorithm Based on Kriging Using Multi-Point Infill Sampling Criterion and Its Application in Transportation System" Sustainability 13, no. 19: 10645. https://doi.org/10.3390/su131910645
APA StyleSong, X., Li, M., Li, Z., & Liu, F. (2021). Global Optimization Algorithm Based on Kriging Using Multi-Point Infill Sampling Criterion and Its Application in Transportation System. Sustainability, 13(19), 10645. https://doi.org/10.3390/su131910645





