Investigating the Environmental Impacts of Construction Projects in Time-Cost Trade-Off Project Scheduling Problems with CoCoSo Multi-Criteria Decision-Making Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Leopold Matrix
2.2. Fuzzy Combined Compromise Solution (CoCoSo) Multi-Criteria Decision-Making Method
- (1)
- The CoCoSo model enables flexible decision making, taking into account the interaction between multi-input attributes;
- (2)
- The model considers the interactions between attributes and eliminates the impact of extreme/awkward data;
- (3)
- The model is characterized by flexibility, which is expressed by the parameters l, p, and q;
- (4)
- The model allows for checking the robustness of the results by varying the parameters l, p, and q and checking their influence on the final decision.
3. Results
- The first execution mode indicates that each project activity is performed with the least amount of resources (M1);
- The second execution mode is the most probable execution mode and is performed with the most available resources (M2);
- The third execution mode is the mode in which each activity is performed within the shortest possible duration (M3);
- The fourth execution mode is the mode in which each activity is performed at the lowest possible cost (M4);
- The fifth execution mode is the mode in which each activity is performed in the most pessimistic condition (M5).
- Soil texture and pollution, erosion, and sedimentation (EI1);
- Surface and groundwater pollution (EI2);
- Air pollution and dust (EI3);
- Noise pollution (EI4);
- Plant species, wildlife, and habitats (EI5).
- The indicators of the socio-economic environment are as follows:
- Increasing employment and reducing migration in the region (EI6);
- Increasing facilities and services in the region and improving people’s income levels (EI7).
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baptiste, P.; Demassey, S. Tight LP bounds for resource constrained project scheduling. OR Spectr. 2004, 26, 251–262. [Google Scholar] [CrossRef]
- Kelley, J.E., Jr. Critical-path planning and scheduling: Mathematical basis. Op. Res. 1961, 9, 296–320. [Google Scholar] [CrossRef]
- Eshtehardian, E.; Afshar, A.; Abbasnia, R. Fuzzy-based MOGA approach to stochastic time–cost trade-off problem. Autom. Constr. 2009, 18, 692–701. [Google Scholar] [CrossRef]
- Zhang, Y.; Thomas Ng, S. An ant colony system based decision support system for construction time-cost optimization. J. Civil Eng. Manag. 2012, 18, 580–589. [Google Scholar] [CrossRef]
- Xu, J.; Zheng, H.; Zeng, Z.; Wu, S.; Shen, M. Discrete time–cost–environment trade-off problem for large-scale construction systems with multiple modes under fuzzy uncertainty and its application to Jinping-II Hydroelectric Project. Int. J. Proj. Manag. 2012, 30, 950–966. [Google Scholar] [CrossRef]
- Zhong, Y.; Wu, P. Economic sustainability, environmental sustainability and constructability indicators related to concrete- and steel-projects. J. Clean. Prod. 2015, 108, 748–756. [Google Scholar] [CrossRef]
- Wang, T.; Gao, S.; Li, X.; Ning, X. A meta-network-based risk evaluation and control method for industrialized building construction projects. J. Clean. Prod. 2018, 205, 552–564. [Google Scholar] [CrossRef]
- Martens, M.L.; Carvalho, M.M. Key factors of sustainability in project management context: A survey exploring the project managers’ perspective. Int. J. Proj. Manag. 2017, 35, 1084–1102. [Google Scholar] [CrossRef]
- WCED. Our Common Future: The Bruntland Report; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Moldan, B.; Dahl, A.L. Challenges to sustainability indicators. Sustain. Indic. 2007, 67, 1–26. [Google Scholar]
- Stanitsas, M.; Kirytopoulos, K.; Leopoulos, V. Integrating sustainability indicators into project management: The case of construction industry. J. Clean. Prod. 2021, 279, 123774. [Google Scholar] [CrossRef]
- Yan, H.; Shen, Q.; Fan, L.C.; Wang, Y.; Zhang, L. Greenhouse gas emissions in building construction: A case study of One Peking in Hong Kong. Build. Environ. 2010, 45, 949–955. [Google Scholar] [CrossRef] [Green Version]
- Allett, E.J. Environmental impact assessment and decision analysis. J. Op. Res. Soc. 1986, 37, 901–910. [Google Scholar] [CrossRef]
- Morrison-Saunders, A. Advanced Introduction to Environmental Impact Assessment; Edward Elgar Publishing: Cheltenham, UK, 2018. [Google Scholar]
- Asadollahfardi, G.; Asadi, M. The comparison of a revised Leopold matrix and fuzzy methods in environmental impact assessment, a case study: The construction of Al-A’amiriya residential complex, Baghdad, Iraq. Environ. Qual. Manag. 2018, 27, 115–123. [Google Scholar] [CrossRef]
- Marzouk, M.; Madany, M.; Abou-Zied, A.; El-said, M. Handling construction pollutions using multi-objective optimization. Constr. Manag. Econ. 2008, 26, 1113–1125. [Google Scholar] [CrossRef]
- Ozcan-Deniz, G.; Zhu, Y.; Ceron, V. Time, cost, and environmental impact analysis on construction operation optimization using genetic algorithms. J. Manag. Eng. 2012, 28, 265–272. [Google Scholar] [CrossRef]
- Liu, S.; Tao, R.; Tam, C.M. Optimizing cost and CO2 emission for construction projects using particle swarm optimization. Habitat Int. 2013, 37, 155–162. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Tran, D.-H. Opposition-Based Multiple-Objective Differential Evolution to Solve the Time–Cost–Environment Impact Trade-Off Problem in Construction Projects. J. Comput. Civ. Eng. 2015, 29, 04014074. [Google Scholar] [CrossRef]
- Ozcan-Deniz, G.; Zhu, Y. Multi-objective optimization of greenhouse gas emissions in highway construction projects. Sustain. Cities Soc. 2017, 28, 162–171. [Google Scholar] [CrossRef] [Green Version]
- Lotfi, R.; Yadegari, Z.; Hosseini, S.H.; Khameneh, A.H.; Tirkolaee, E.B.; Weber, G.W. A robust time-cost-quality-energy-environment trade-off with resource-constrained in project management: A case study for a bridge construction project. J. Ind. Manag. Optim. 2020, 13, 1–22. [Google Scholar] [CrossRef]
- Yu, B.; Meng, X.; Liu, Q. Multi-objective optimisation of hot in-place recycling of asphalt pavement considering environmental impact, cost and construction quality. Int. J. Pavement Eng. 2020, 21, 1576–1584. [Google Scholar] [CrossRef]
- Santos, J.; Ferreira, A.; Flintsch, G. A life cycle assessment model for pavement management: Road pavement construction and management in Portugal. Int. J. Pavement Eng. 2015, 16, 315–336. [Google Scholar] [CrossRef]
- Vega, A.D.L.; Santos, J.; Martinez-Arguelles, G. Life cycle assessment of hot mix asphalt with recycled concrete aggregates for road pavements construction. Int. J. Pavement Eng. 2020, 1–14. [Google Scholar] [CrossRef]
- Stanujkic, D.; Popovic, G.; Zavadskas, E.K.; Karabasevic, D.; Binkyte-Veliene, A. Assessment of Progress towards Achieving Sustainable Development Goals of the “Agenda 2030” by Using the CoCoSo and the Shannon Entropy Methods: The Case of the EU Countries. Sustainability 2020, 12, 5717. [Google Scholar] [CrossRef]
- Raj Mishra, A.; Rani, P.; Krishankumar, R.; Zavadskas, E.K.; Cavallaro, F.; Ravichandran, K.S. A hesitant fuzzy combined compromise solution framework-based on discrimination measure for ranking sustainable third-party reverse logistic providers. Sustainability 2021, 13, 2064. [Google Scholar] [CrossRef]
- Huynh, V.H.; Nguyen, T.H.; Pham, H.C.; Nguyen, T.C.; Tran, D.H. Multiple Objective Social Group Optimization for Time–Cost–Quality–Carbon Dioxide in Generalized Construction Projects. Int. J. Civ. Eng. 2021, 19, 805–822. [Google Scholar] [CrossRef]
- Maceika, A.; Bugajev, A.; Šostak, O.R.; Vilutienė, T. Decision Tree and AHP Methods Application for Projects Assessment: A Case Study. Sustainability 2021, 13, 5502. [Google Scholar] [CrossRef]
- Wang, J.; Sekei, V.; Ganiyu, S.; Makwetta, J. Research on the Sustainability of the Standard Gauge Railway Construction Project in Tanzania. Sustainability 2021, 13, 5271. [Google Scholar] [CrossRef]
- Yazdani, M.; Wen, Z.; Liao, H.; Banaitis, A.; Turskis, Z. A grey combined compromise solution (COCOSO-G) method for supplier selection in construction management. J. Civ. Eng. Manag. 2019, 25, 858–874. [Google Scholar] [CrossRef] [Green Version]
- Yazdani, M.; Zarate, P.; Zavadskas, E.K.; Turskis, Z. A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar] [CrossRef]
- Zhang, Z.; Liao, H.; Al-Barakati, A.; Zavadskas, E.K.; Antuchevičienė, J. Supplier selection for housing development by an integrated method with interval rough boundaries. Int. J. Strat. Prop. Manag. 2020, 24, 269–284. [Google Scholar] [CrossRef]
- Wen, Z.; Liao, H.; Ren, R.; Bai, C.; Zavadskas, E.K.; Antucheviciene, J.; Al-Barakati, A. Cold chain logistics management of medicine with an integrated multi-criteria decision-making method. Int. J. Environ. Res. Public Health 2019, 16, 4843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leopold, L.B. A Procedure for Evaluating Environmental Impact; US Dept. of the Interior: Washington, DC, USA, 1971.
- Dehaghi, B.F.; Khoshfetrat, A. AHP-GP Approach by Considering the Leopold Matrix for Sustainable Water Reuse Allocation: Najafabad Case Study, Iran. Period. Polytech. Civ. Eng. 2020, 64, 485–499. [Google Scholar] [CrossRef]
- Lotfizadeh, A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar]
- Gupta, P.; Mehlawat, M.K. A new possibilistic programming approach for solving fuzzy multiobjective assignment problem. IEEE Trans. Fuzzy Syst. 2013, 22, 16–34. [Google Scholar] [CrossRef]
- Ecer, F.; Pamucar, D. Sustainable supplier selection: A novel integrated fuzzy best worst method (F-BWM) and fuzzy CoCoSo with Bonferroni (CoCoSo’B) multi-criteria model. J. Clean. Prod. 2020, 266, 121981. [Google Scholar] [CrossRef]
- Zhou, W.; He, J.-M. Intuitionistic Fuzzy Normalized Weighted Bonferroni Mean and Its Application in Multicriteria Decision Making. J. Appl. Math. 2012, 2012, 1–22. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, H. Fuzzy best-worst multi-criteria decision-making method and its applications. Knowl. Base Syst. 2017, 121, 23–31. [Google Scholar] [CrossRef]




| Triangular Fuzzy Number | Value | Linguistic Variable |
|---|---|---|
| (0,0.1,0.3) | 1 | Very low impact |
| (0.1,0.3,0.5) | 2 | Low impact |
| (0.3,0.5,0.7) | 3 | Medium impact |
| (0.5,0.7,0.9) | 4 | High impact |
| (0.7,0.9,1) | 5 | Very high impact |
| Code | Activity | Code | Activity |
|---|---|---|---|
| 1 | Dummy start activity | 9 | Leveling and regulating the tank floor |
| 2 | Lining and drilling the canal floor | 10 | Drilling and excavating the path |
| 3 | Spinning pipes | 11 | Drilling and underpinning the tank place |
| 4 | Regulating and leveling the canal floor | 12 | Concreting |
| 5 | Welding and transferring pipes to the floor of the canal | 13 | Preparing and reinforcing, form working, and concreting floor |
| 6 | Piping and screening operations | 14 | Reinforcing and molding walls and ceilings |
| 7 | Testing | 15 | Concreting roof and walls |
| 8 | Embanking the canal | 16 | Dummy finish activity |
| Activity Mode | EI1 | EI2 | EI3 | EI4 | EI5 | EI6 | EI7 |
|---|---|---|---|---|---|---|---|
| - | - | - | - | - | + | + | |
| M1 | (0.08,0.25,0.45) | (0.11,0.3,0.5) | (0.05,0.2,0.4) | (0.1,0.3,0.5) | (0.014,0.12,0.32) | (0,0.1,0.3) | (0,0.1,0.3) |
| M2 | (0.18,0.36,0.56) | (0.24,0.44,0.64) | (0.14,0.32,0.52) | (0.15,0.35,0.55) | (0.014,0.12,0.32) | (0.053,0.20,0.40) | (0.028,0.15,0.35) |
| M3 | (0.18,0.36,0.56) | (0.31,0.51,0.71) | (0.17,0.34,0.54) | (0.3,0.5,0.7) | (0.016,0.13,0.33) | (0.34,0.54,0.74) | (0.21,0.42,0.57) |
| M4 | (0.2,0.4,0.6) | (0.31,0.51,0.71) | (0.24,0.42,0.62) | (0.18,0.38,0.58) | (0.016,0.13,0.33) | (0.041,0.18,0.38) | (0.06,0.22,0.42) |
| M5 | (0.18,0.36,0.56) | (0.24,0.44,0.64) | (0.18,0.36,0.56) | (0.25,0.45,0.65) | (0.014,0.12,0.32) | (0.27,0.47,0.67) | (0.1,0.26,0.46) |
| Activity | Activity Mode | Duration | Cost | Environmental Impacts (Negative) | Environmental Impacts (Positive) |
|---|---|---|---|---|---|
| - | - | - | + | ||
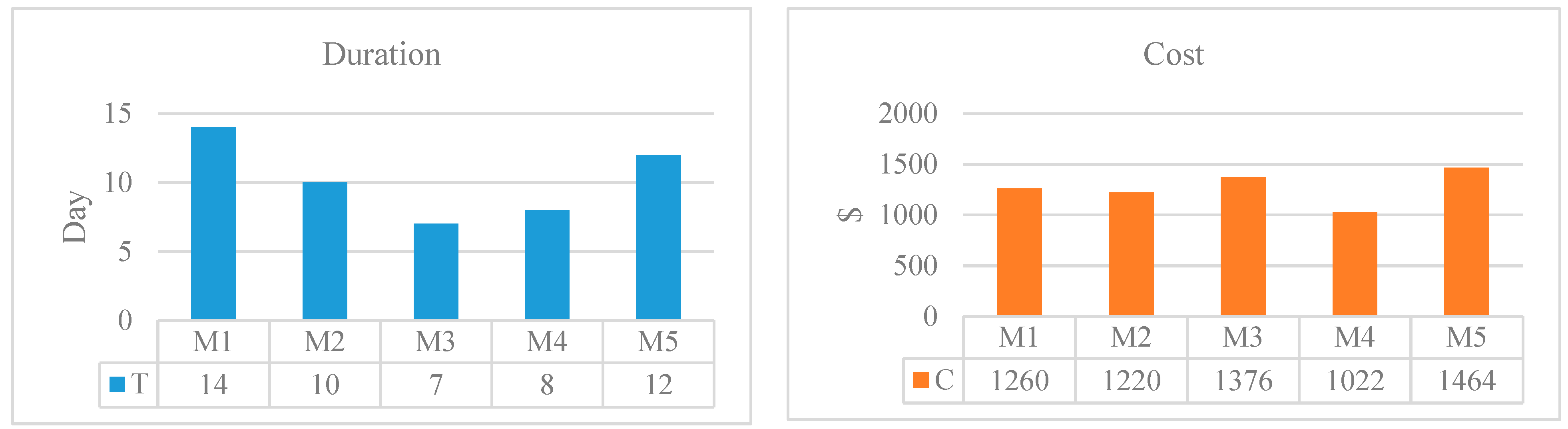
| 2 | M1 | (11,14,17) | (990,1260,1530) | (0.08,0.26,0.46) | (0,0.1,0.3) |
| M2 | (7,10,13) | (854,1220,1586) | (0.16,0.34,0.54) | (0,0.1,0.3) | |
| M3 | (4,7,10) | (860,1376,1892) | (0.36,0.54,0.74) | (0.3,0.5,0.7) | |
| M4 | (5,8,11) | (584,1022,1460) | (0.16,0.34,0.54) | (0,0.1,0.3) | |
| M5 | (9,12,15) | (1098,1464,1830) | (0.24,0.42,0.62) | (0.05,0.2,0.4) | |
| 3 | M1 | (21,25,29) | (640,960,1280) | (0,0.1,0.3) | (0,0.1,0.3) |
| M2 | (16,20,24) | (640,800,960) | (0.05,0.2,0.4) | (0.1,0.3,0.5) | |
| M3 | (8,12,16) | (672,896,1120) | (0.15,0.3,0.5) | (0.15,0.3,0.5) | |
| M4 | (12,16,20) | (336,400,464) | (0.25,0.4,0.6) | (0.1,0.3,0.5) | |
| M5 | (18,22,26) | (720,880,1040) | (0.15,0.3,0.5) | 0 | |
| 4 | M1 | (4,5,6) | (128,160,192) | (0.03,0.16,0.36) | (0,0.1,0.3) |
| M2 | (3,4,5) | (168,224,280) | (0.13,0.3,0.5) | (0,0.1,0.3) | |
| M3 | (2,3,4) | (160,240,320) | (0.2,0.36,0.56) | (0.3,0.5,0.7) | |
| M4 | (3,4,5) | (104,208,312) | (0.26,0.43,0.63) | (0.05,0.2,0.4) | |
| M5 | (4,5,6) | (224,280,336) | (0.13,0.3,0.5) | (0.2,0.4,0.6) | |
| 5 | M1 | (4,5,6) | 456,570,684) | (0.15,0.35,0.55) | (0,0.1,0.3) |
| M2 | (2,3,4) | (276,414,552) | (0.3,0.5,0.7) | (0,0.1,0.3) | |
| M3 | (1,2,3) | (366,488,610) | (0.15,0.35,0.55) | (0.3,0.5,0.7) | |
| M4 | (3,4,5) | (154,308,462) | (0.3,0.5,0.7) | (0.05,0.2,0.4) | |
| M5 | (4,5,6) | (448,610,732) | (0.3,0.5,0.7) | (0.3,0.5,0.7) | |
| 6 | M1 | (19,22,25) | (608,704,800) | (0.05,0.2,0.4) | (0,0.1,0.3) |
| M2 | (17,20,23) | (680,800,920) | (0.1,0.3,0.5) | (0.1,0.3,0.5) | |
| M3 | (12,15,18) | (672,840,1008) | (0.2,0.4,0.6) | (0.4,0.6,0.8) | |
| M4 | (14,17,20) | (672,816,960) | (0.3,0.5,0.7) | (0,0.1,0.3) | |
| M5 | (16,19,22) | (784,952,1120) | (0.1,0.3,0.5) | (0,0.1,0.3) | |
| 7 | M1 | (9,11,13) | (72,88,104) | (0.1,0.3,0.5) | 0 |
| M2 | (5,7,9) | (80,112,144) | (0.2,0.4,0.6) | (0.1,0.3,0.5) | |
| M3 | (1,2,3) | (48,96,144) | (0.2,0.4,0.6) | (0,0.1,0.3) | |
| M4 | (2,4,6) | (32,64,96) | (0.3,0.5,0.7) | 0 | |
| M5 | (6,8,10) | (96,128,160) | (0.2,0.4,0.6) | (0.1,0.3,0.5) | |
| 8 | M1 | (17,19,21) | (1088,1216,1344) | (0.05,0.2,0.4) | (0,0.1,0.3) |
| M2 | (13,15,17) | (1040,1200,1360) | (0.1,0.25,0.45) | (0.1,0.3,0.5) | |
| M3 | (3,5,7) | (456,684,912) | (0.2,0.4,0.6) | (0.15,0.3,0.5) | |
| M4 | (5,7,9) | (390,650,910) | (0.2,0.4,0.6) | (0,0.1,0.3) | |
| M5 | (14,16,18) | (1120,1280,1440) | (0.05,0.2,0.4) | (0.5,0.7,0.9) | |
| 9 | M1 | (5,7,9) | (280,392,504) | (0.03,0.16,0.43) | (0,0.1,0.3) |
| M2 | (5,6,7) | (490,588,686) | (0.25,0.45,0.65) | (0,0.1,0.3) | |
| M3 | (2,3,4) | (344,516,688) | (0.1,0.23,0.43) | (0.5,0.7,0.9) | |
| M4 | (3,4,5) | (160,240,320) | (0.35,0.55,0.75) | (0.1,0.3,0.5) | |
| M5 | (6,7,8) | (588,686,784) | (0.3,0.5,0.7) | (0.1,0.3,0.5) | |
| 10 | M1 | (11,13,15) | (990,1170,1350) | (0.08,0.26,0.46) | (0,0.1,0.3) |
| M2 | (7,9,11) | (854,1098,1342) | (0.16,0.34,0.54) | (0.1,0.3,0.5) | |
| M3 | (5,7,9) | (1032,1376,1720) | (0.36,0.54,0.74) | (0.3,0.5,0.7) | |
| M4 | (6,8,10) | (730,1022,1314) | (0.16,0.34,0.54) | (0.05,0.2,0.4) | |
| M5 | (8,10,12) | (976,1220,1464) | (0.24,0.42,0.62) | (0.1,0.3,0.5) | |
| 11 | M1 | (6,8,10) | (144,192,240) | (0,0.1,0.3) | (0,0.1,0.3) |
| M2 | (4,6,8) | (128,192,256) | (0.13,0.3,0.5) | (0,0.1,0.3) | |
| M3 | (1,2,3) | (120,160,200) | (0.06,0.23,0.43) | (0.3,0.5,0.7) | |
| M4 | (3,4,5) | (48,96,144) | (0.2,0.36,0.56) | (0,0.1,0.3) | |
| M5 | (5,7,9) | (160,224,288) | (0.06,0.23,0.43) | (0.3,0.5,0.7) | |
| 12 | M1 | (2,3,4) | (40,60,80) | (0.07,0.25,0.45) | (0,0.1,0.3) |
| M2 | (1,2,3) | (38,59,89) | (0.17,0.35,0.55) | (0.05,0.2,0.4) | |
| M3 | (1,1,2) | (38,38,89) | (0.17,0.35,0.55) | (0.5,0.7,0.9) | |
| M4 | (1,2,3) | (30,58,89) | (0.17,0.35,0.55) | (0.05,0.2,0.4) | |
| M5 | (2,3,4) | (60,90,120) | (0.17,0.35,0.55) | 0 | |
| 13 | M1 | (18,22,26) | (1872,2288,2704) | (0.06,0.23,0.43) | (0,0.1,0.3) |
| M2 | (16,20,24) | (1920,2400,2880) | (0.06,0.23,0.43) | (0.05,0.2,0.4) | |
| M3 | (13,17,21) | (2184,2856,3528) | (0.13,0.3,0.5) | (0.5,0.7,0.9) | |
| M4 | (16,21,24) | (1920,2550,2880) | (0.13,0.3,0.5) | (0.1,0.3,0.5) | |
| M5 | (18,22,26) | (2160,2640,3120) | (0.06,0.23,0.43) | (0.1,0.3,0.5) | |
| 14 | M1 | (22,26,30) | (2992,3536,4080) | (0.13,0.3,0.5) | (0,0.1,0.3) |
| M2 | (20,24,28) | (3040,3648,4256) | (0.13,0.3,0.5) | (0.1,0.3,0.5) | |
| M3 | (18,22,26) | (3168,3872,4576) | (0.2,0.36,0.56) | (0.3,0.5,0.7) | |
| M4 | (19,23,27) | (2888,3496,4104) | (0.13,0.3,0.5) | (0,0.1,0.3) | |
| M5 | (21,25,29) | (3192,3800,4408) | (0.13,0.3,0.5) | (0.5,0.7,0.9) | |
| 15 | M1 | (4,6,7) | (227,341,398) | (0.16,0.36,0.56) | (0,0.1,0.3) |
| M2 | (3,5,7) | (185,308,431) | (0.23,0.43,0.63) | (0,0.1,0.3) | |
| M3 | (1,2,3) | (156,234,312) | (0.23,0.43,0.63) | (0.3,0.5,0.7) | |
| M4 | (2,3,4) | (81,162,242) | (0.23,0.43,0.63) | (0.1,0.3,0.5) | |
| M5 | (4,6,8) | (246,370,493) | (0.23,0.43,0.63) | (0.3,0.5,0.7) |
| Activity | Activity Mode | Crisp SB | Crisp PB | K(ia) | K(ib) | K(ic) | K(i) |
|---|---|---|---|---|---|---|---|
| 2 | M1 | 0.3217 | 0.3214 | 0.1788 | 2.0852 | 0.6897 | 1.6208 |
| M2 | 0.3252 | 0.3245 | 0.1806 | 2.1065 | 0.2871 | 1.3365 | |
| M3 | 0.4664 | 0.4660 | 0.2593 | 3.0235 | 0.4120 | 1.9180 | |
| M4 | 0.3778 | 0.3763 | 0.2097 | 2.4451 | 0.3332 | 1.5512 | |
| M5 | 0.3085 | 0.3083 | 0.1715 | 2.0000 | 0.2726 | 1.2689 | |
| 3 | M1 | 0.2579 | 0.2510 | 0.1628 | 4.2322 | 0.5607 | 2.3805 |
| M2 | 0.3351 | 0.3343 | 0.2141 | 5.5819 | 0.3375 | 2.7837 | |
| M3 | 0.3946 | 0.3925 | 0.2518 | 6.5620 | 0.3969 | 3.2725 | |
| M4 | 0.4548 | 0.4529 | 0.2903 | 7.5674 | 0.4577 | 3.7737 | |
| M5 | 0.1553 | 0.0976 | 0.0809 | 2.0000 | 0.1276 | 1.0108 | |
| 4 | M1 | 0.3629 | 0.3600 | 0.1991 | 2.4430 | 0.7780 | 1.8635 |
| M2 | 0.2980 | 0.2938 | 0.1630 | 2.0000 | 0.2600 | 1.2473 | |
| M3 | 0.4650 | 0.4642 | 0.2559 | 3.1401 | 0.4083 | 1.9580 | |
| M4 | 0.3407 | 0.3391 | 0.1872 | 2.2970 | 0.2987 | 1.4325 | |
| M5 | 0.3541 | 0.3539 | 0.1949 | 2.3925 | 0.3111 | 1.4920 | |
| 5 | M1 | 0.2736 | 0.2734 | 0.1525 | 2.0000 | 0.5308 | 1.4397 |
| M2 | 0.3002 | 0.3001 | 0.1673 | 2.1948 | 0.2600 | 1.3314 | |
| M3 | 0.5153 | 0.5152 | 0.2872 | 3.7676 | 0.4463 | 2.2851 | |
| M4 | 0.3497 | 0.3497 | 0.1949 | 2.5571 | 0.3029 | 1.5511 | |
| M5 | 0.3556 | 0.3554 | 0.1981 | 2.5992 | 0.3079 | 1.5767 | |
| 6 | M1 | 0.4480 | 0.4434 | 0.1964 | 2.3374 | 0.7587 | 1.8013 |
| M2 | 0.4713 | 0.4697 | 0.2073 | 2.4677 | 0.3308 | 1.5554 | |
| M3 | 0.5875 | 0.5874 | 0.2588 | 3.0809 | 0.4130 | 1.9417 | |
| M4 | 0.3908 | 0.3781 | 0.1694 | 2.0160 | 0.2703 | 1.2708 | |
| M5 | 0.3846 | 0.3788 | 0.1682 | 2.0016 | 0.2683 | 1.2617 | |
| 7 | M1 | 0.1914 | 0.1831 | 0.1353 | 2.0000 | 0.5336 | 1.4146 |
| M2 | 0.3144 | 0.3142 | 0.2271 | 3.3588 | 0.3635 | 1.9688 | |
| M3 | 0.3510 | 0.3508 | 0.2535 | 3.7497 | 0.4058 | 2.1979 | |
| M4 | 0.2350 | 0.2331 | 0.1691 | 2.5012 | 0.2707 | 1.4663 | |
| M5 | 0.2977 | 0.2973 | 0.2150 | 3.1791 | 0.3440 | 1.8635 | |
| 8 | M1 | 0.2291 | 0.2288 | 0.1429 | 2.0000 | 0.5564 | 1.4418 |
| M2 | 0.2705 | 0.2704 | 0.1688 | 2.3625 | 0.2689 | 1.4089 | |
| M3 | 0.4120 | 0.4111 | 0.2568 | 3.5948 | 0.4092 | 2.1435 | |
| M4 | 0.3125 | 0.3085 | 0.1938 | 2.7122 | 0.3088 | 1.6173 | |
| M5 | 0.3815 | 0.3805 | 0.2377 | 3.3277 | 0.3788 | 1.9843 | |
| 9 | M1 | 0.2749 | 0.2738 | 0.1804 | 2.8729 | 0.5953 | 1.8922 |
| M2 | 0.1920 | 0.1899 | 0.1256 | 2.0000 | 0.1930 | 1.1379 | |
| M3 | 0.4620 | 0.4597 | 0.3031 | 4.8261 | 0.4658 | 2.7450 | |
| M4 | 0.3746 | 0.3726 | 0.2457 | 3.9123 | 0.3776 | 2.2254 | |
| M5 | 0.2210 | 0.2208 | 0.1453 | 2.3133 | 0.2233 | 1.3161 | |
| 10 | M1 | 0.3799 | 0.3791 | 0.1674 | 2.0000 | 0.7313 | 1.5922 |
| M2 | 0.4742 | 0.4737 | 0.2091 | 2.4977 | 0.3405 | 1.5785 | |
| M3 | 0.5191 | 0.5188 | 0.2290 | 2.7349 | 0.3728 | 1.7283 | |
| M4 | 0.4681 | 0.4666 | 0.2062 | 2.4629 | 0.3358 | 1.5565 | |
| M5 | 0.4268 | 0.4265 | 0.1883 | 2.2485 | 0.3065 | 1.4210 | |
| 11 | M1 | 0.1660 | 0.1629 | 0.1501 | 2.3953 | 0.4546 | 1.5471 |
| M2 | 0.1393 | 0.1354 | 0.1253 | 2.0000 | 0.1898 | 1.1344 | |
| M3 | 0.3635 | 0.3600 | 0.3302 | 5.2692 | 0.4999 | 2.9876 | |
| M4 | 0.2146 | 0.2050 | 0.1915 | 3.0547 | 0.2899 | 1.7324 | |
| M5 | 0.2241 | 0.2206 | 0.2029 | 3.2385 | 0.3072 | 1.8365 | |
| 12 | M1 | 0.3316 | 0.3311 | 0.1709 | 3.1011 | 0.5182 | 1.9137 |
| M2 | 0.3728 | 0.3720 | 0.1921 | 3.4860 | 0.2891 | 1.9013 | |
| M3 | 0.6394 | 0.6392 | 0.3298 | 5.9842 | 0.4963 | 3.2632 | |
| M4 | 0.3822 | 0.3813 | 0.1969 | 3.5733 | 0.2964 | 1.9489 | |
| M5 | 0.2141 | 0.2133 | 0.1102 | 2.0000 | 0.1659 | 1.0910 | |
| 13 | M1 | 0.4504 | 0.4460 | 0.1794 | 2.0000 | 0.7476 | 1.6208 |
| M2 | 0.4903 | 0.4877 | 0.1957 | 2.1822 | 0.3162 | 1.4115 | |
| M3 | 0.5995 | 0.5995 | 0.2399 | 2.6753 | 0.3876 | 1.7302 | |
| M4 | 0.4731 | 0.4714 | 0.1890 | 2.1073 | 0.3053 | 1.3630 | |
| M5 | 0.4901 | 0.4891 | 0.1959 | 2.1848 | 0.3166 | 1.4131 | |
| 14 | M1 | 0.5129 | 0.5110 | 0.1740 | 2.0000 | 0.7444 | 1.6105 |
| M2 | 0.5845 | 0.5838 | 0.1985 | 2.2822 | 0.3221 | 1.4611 | |
| M3 | 0.6228 | 0.6225 | 0.2116 | 2.4326 | 0.3433 | 1.5573 | |
| M4 | 0.5369 | 0.5345 | 0.1821 | 2.0928 | 0.2954 | 1.3399 | |
| M5 | 0.6878 | 0.6877 | 0.2338 | 2.6869 | 0.3792 | 1.7201 | |
| 15 | M1 | 0.2632 | 0.2629 | 0.1448 | 2.0224 | 0.5237 | 1.4326 |
| M2 | 0.2602 | 0.2601 | 0.1432 | 2.0000 | 0.2244 | 1.1901 | |
| M3 | 0.5024 | 0.5023 | 0.2764 | 3.8616 | 0.4333 | 2.2973 | |
| M4 | 0.4317 | 0.4316 | 0.2376 | 3.3183 | 0.3723 | 1.9742 | |
| M5 | 0.3603 | 0.3594 | 0.1980 | 2.7664 | 0.3104 | 1.6460 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banihashemi, S.A.; Khalilzadeh, M.; Zavadskas, E.K.; Antucheviciene, J. Investigating the Environmental Impacts of Construction Projects in Time-Cost Trade-Off Project Scheduling Problems with CoCoSo Multi-Criteria Decision-Making Method. Sustainability 2021, 13, 10922. https://doi.org/10.3390/su131910922
Banihashemi SA, Khalilzadeh M, Zavadskas EK, Antucheviciene J. Investigating the Environmental Impacts of Construction Projects in Time-Cost Trade-Off Project Scheduling Problems with CoCoSo Multi-Criteria Decision-Making Method. Sustainability. 2021; 13(19):10922. https://doi.org/10.3390/su131910922
Chicago/Turabian StyleBanihashemi, Sayyid Ali, Mohammad Khalilzadeh, Edmundas Kazimieras Zavadskas, and Jurgita Antucheviciene. 2021. "Investigating the Environmental Impacts of Construction Projects in Time-Cost Trade-Off Project Scheduling Problems with CoCoSo Multi-Criteria Decision-Making Method" Sustainability 13, no. 19: 10922. https://doi.org/10.3390/su131910922
APA StyleBanihashemi, S. A., Khalilzadeh, M., Zavadskas, E. K., & Antucheviciene, J. (2021). Investigating the Environmental Impacts of Construction Projects in Time-Cost Trade-Off Project Scheduling Problems with CoCoSo Multi-Criteria Decision-Making Method. Sustainability, 13(19), 10922. https://doi.org/10.3390/su131910922









