Abstract
The Brushless Doubly-Fed Reluctance Machine (BDFRM) has been widely investigated in numerous research studies since it is brushless and cageless and there is no winding on the rotor of this emerging machine. This feature leads to several advantages for this machine in comparison with its induction counterpart, i.e., Brushless Doubly-Fed Induction Machine (BDFIM). Less maintenance, less power losses, and also more reliability are the major advantages of BDFRM compared to BDFIM. The design complexity of its reluctance rotor, as well as flux patterns for indirect connection between the two windings mounted on the stator including power winding and control winding, have restricted the development of this machine technology. In the literature, there is not a comprehensive review of the research studies related to BDFRM. In this paper, the previous research studies are reviewed from different points of view, such as operation, design, control, transient model, dynamic model, power factor, Maximum Power Point Tracking (MPPT), and losses. It is revealed that the BDFRM is still evolving since the theoretical results have shown that this machine operates efficiently if it is well-designed.
1. Introduction
In recent decades, Doubly-Fed Machines (DFMs) [1,2,3] have been extensively used in different applications due to using partially-rated converters to control the machine, leading to lower converter cost [4]. Such machines are used in applications where the speed changes slightly with time, such as large wind turbines [5,6,7], as well as power drives [8] like pump drives [9] or even turbo-electric distributed propulsion systems [10]. The common type of DFMs is induction-rotor DFM so-called Doubly-Fed Induction Machine (DFIM). In this machine, two separate windings are mounted on the stator and rotor, in which the stator winding directly connects to power grids while the rotor winding indirectly connects to power grids via two back-to-back converters [11]. The main advantage of such machines is using partially-rated converters, which reduce the cost of power electronics converters compared to fully-rated converters in Permanent Magnet Synchronous Machines (PMSMs).
The presence of brush and slip-ring for connecting the rotor to the converters increases the need for maintenance, probability of failure, and power losses [12]. To tackle this issue, the brushless type of DFM, namely the Brushless Doubly-Fed Machine (BDFM), has been presented [13]. The main advantage of BDFM technology compared to DFM is the absence of brush and slip-ring, which reduces the need for maintenance services and additionally, improves the machine robustness. Different types of BDFM, such as wound-rotor, cage-rotor, dual-stator, and hybrid-rotor BDFMs, have been introduced in [13]. The widely-used type of BDFM is Brushless Doubly-Fed Induction Machine (BDFIM) type [14]. In BDFIM, the rotor is a short-circuit wound-rotor or a cage-rotor, whereas the stator has two windings. One winding is directly connected to power grids, while the other winding is connected to power grids via two back-to-back converters. Thus, both the windings are on the stator, while they have indirect coupling via the rotor and there is no direct coupling between them. BDFM is attractive for being used in many applications, such as variable-frequency speed regulation systems and variable-speed constant frequency generation systems. Therefore, the design and control of BDFM have been attracted much interest [13].
The significant rotor losses and poor efficiency caused by the cage or wound rotor make the machine considerably parameter-dependent and controller operation complicated. Such drawbacks make the BDFIM difficult to implement [15]. Accordingly, another promising BDFM technology has been proposed that has a reluctance-type rotor called Brushless Doubly-Fed Reluctance Machine (BDFRM). BDFRM was firstly introduced in the early 1970s [16]. In this machine, there is no wound-or cage-rotor. Hence, it has higher reliability and lower power losses compared to its induction counterpart, i.e., BDFIM [9]. Additionally, BDFRM is approximately maintenance-free due to the absence of rotor winding compared to wound-rotor BDFIM. Simpler structure, smaller size, higher power density, higher efficiency, and lower maintenance cost are the other advantages of BDFRM in comparison with traditional machines [17]. Furthermore, the BDFRM control is much easier due to its cageless rotor [18].
The BDFRM technology has a high potential to be used in large-power restricted-speed applications due to its manufacturing cost, as well as reliability and robustness criteria [19]. It also can be used in applications, such as turbomachinery, adjustable-speed constant-frequency wind, and hydro-power applications, air conditioning, commercial heating, and large pump drives [20,21]. The application of BDFRM in wind turbines especially offshore ones, has accelerated the research studies on BDFRM [22], due to the advantages of wind turbines in viewpoints of zero energy generation cost and environmental issues [23,24]. Due to the application and the importance of BDFRM, the requirements of BDFRM-based wind turbines are discussed in [6]. However, its complicated operation because of the coupling concept between the stator windings via the reluctance rotor is less investigated [15]. One implication of the unusual operating basics and improper design is the insignificant torque per volume for the constructed BDFRMs, and thus, a bigger and more expensive BDFRM is needed to achieve the torque of an equivalent synchronous reluctance or a cage induction machine [25]. However, recent advances have revealed that BDFRMs can be operated at high efficiency and torque density (torque per volume ratio) when properly designed [26]. Additionally, decreasing their mass per torque ratio has also been investigated in literature [27]. Furthermore, it is revealed that the BDFRM can achieve better torque density than a cage rotor induction machine using the same frame [28]. Due to the mentioned advantages of BDFRM compared to BDFIM, such as low manufacturing cost arising from its reluctance rotor, high reliability arising from the brushless structure, low losses, and lower maintenance needs, research studies have been conducted since the 1990s to analyze such machines [29]. For using low-capacity power converters, the BDFRM should operate in a narrow speed range around the synchronous speed, since it is a slip energy recovery machine [30]. For a typical speed range of 2:1 in wind turbines or pump drives, BDFRM allows to use of partially-rated converters with only 25% of the machine rating [31], which shows BDFRM is a slip power recovery machine. In recent years, some reports focusing on the performance of BDFRM have been released [32,33]. In [34], different aspects of BDFRM are discussed. The superiorities and deficiencies of the BDFRM technology compared with BDFIM are presented. Specific characteristics of BDFRM compared to BDFIM are addressed in the literature [35]. Simpler control and higher efficiency of BDFRM compared to BDFIM are achieved by the improvement of the reluctance rotor design. Such reasons made it necessary to conduct more research on the Brushless Doubly-Fed Reluctance Generator (BDFRG) [36]. In Table 1, the structure features of DFMs are compared.

Table 1.
Structure features of DFMs.
Figure 1 illustrates the main keywords of previous research studies in the field of BDFRM associated with the temporal relationship among them. As observed, in recent years, such research studies have notably increased.
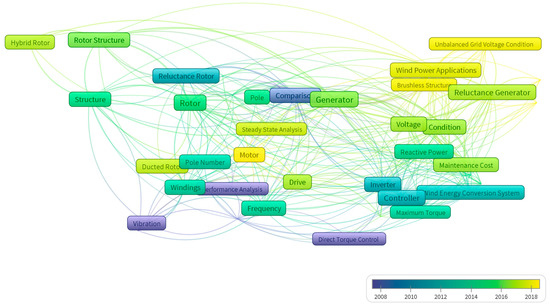
Figure 1.
Main keywords of previous research studies about Brushless BDFRM associated with temporal relationship among them.
In this paper, a comprehensive literature survey on BDFRM is performed. The publications are categorized into different points of view. The conducted study covers all the previous research studies on BDFRM design improvement, operation, dynamic modeling, power factor control, Maximum Power Point Tracking (MPPT), and power losses. The previous research studies have focused on one or more aspects of BDFRM, while this paper deals with the overview of all the previous research studies in different fields of this topic. The remarkable features of this paper are highlighted as:
- A comprehensive review is accomplished on all the previous works about BDFRM.
- Operation principle of BDFRM and its components are discussed.
- Detail characteristics of the previous research studies are presented.
- The research studies are compared in different aspects, such as machine type and machine size, etc.
- The conducted research studies in different fields, such as operation, design, and control of BDFRM, are reviewed.
2. BDFRM Principles
This topology is composed of a reluctance rotor, two-winding stator, two back-to-back power electronics circuits, which are inverters, forming Voltage-Sourced Inverter (VSI), with a capacitor in the intermediate circuit, called DC-link capacitor located in parallel between the converters. Indeed, the VSI-converter acts as an AC/DC/AC converter unit. One of the converters, namely the Machine-Side Converter (MSC), plays the role of controlling machine active and reactive power. Active power reference can be determined from Maximum Power Point Tracking (MPPT) in wind energy conversion systems [37]. On the other hand, the second converter, i.e., Grid-Side Converter (GSC), controls the DC-link voltage. Furthermore, it may absorb/inject reactive power from/into power grids [37], and thus, there is no need for reactive power compensation [38].
In some research studies, current source converters are used instead of voltage source ones [19,39]. The BDFRM structure is presented in Figure 2, where , , and are the angular velocities of the power winding, control winding, and rotor (rad./s), respectively, is the mechanical angular velocity of the rotor (mech.-rad./s), and shows the rotor pole numbers. Additionally, and are the pole-pair numbers of power and control windings, respectively. These parameters are used to analyze the operation of BDFRM.
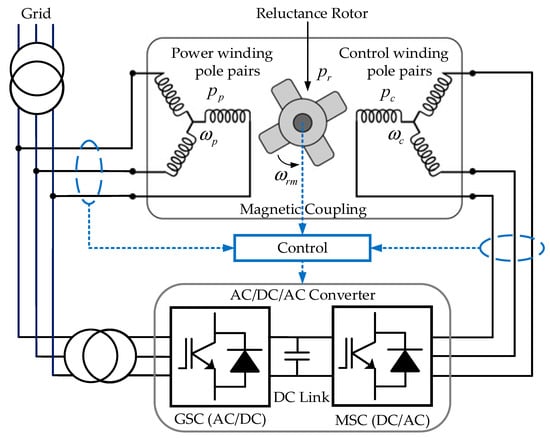
Figure 2.
Configuration of BDFRM (Combining the configurations used in [25,40,41]).
As previously mentioned, BDFRM has no winding on the rotor that is the superiority of this machine compared to BDFIM [40]. The operation of BDFRM is based on an indirect connection between the windings mounted on the stator. The windings are named as primary and secondary windings. The primary winding directly connects to power grids, whereas the control winding indirectly connects to power grids via a power electronics unit [42].
In BDFRM and other BDFM topologies, direct coupling between the windings must not be established. Because the power drained from power grids by the control winding can be reversed to power grids via the power winding. Hence, the machine cannot be controlled when there is a direct coupling between them. This is while the windings have indirect coupling via the rotor. In other words, both the windings have direct coupling with the reluctance rotor, separately [43]. Figure 3 shows the mentioned coupling concept in BDFRM.
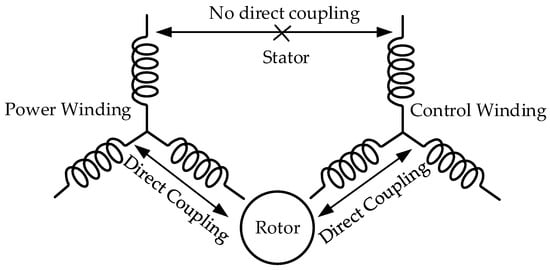
Figure 3.
Electromagnetic coupling in BDFRM [43].
Accordingly, the pole numbers mounted on the stator windings must be different [44]. Ideally, no coupling is created between the windings with a different number of pole pairs when the rotor has a round structure [45]. The key factor in this machine is its salient rotor, which is required for indirect coupling between the stator windings, and thus, for the desired operation of this machine technology. Formation of appropriate flux density harmonics for linking the windings needs a flux path with variable reluctance in the machine essentially for modulating the Magnetomotive Force (MMF) waveforms of the stator [45].
Generally, the stator has two sets of windings with three-phase including pole pairs, while the rotor has half of the summation of the stator winding poles, i.e., . For instance, for , the stator windings pole numbers are two and six, and thus, the rotor winding pole number is four. It seems that a higher number of pole numbers cannot result in effective operation [8]. In BDFIM, the number of poles for the windings mounted on the rotor is simultaneously equal to both the stator windings pole number by using a special rotor structure, while in BDFRM, the air gap permeance density is the key to modulate the MMFs for generating flux waves, and thus, generating cross-coupling [8].
The primary winding has a fixed-frequency voltage with roughly constant-magnitude (due to its connection to power grids) [25] while, the control winding is supplied from a converter with variable voltage and frequency [46], in which the frequency is changed by the MSC [47]. The power converter unit can absorb energy based on the machine’s condition. However, when BDFRM is used as pump drives, the power converter unit absorbs energy only during start-up [48] since for most of the pump applications, the range of the speed variation is roughly 70–100% of the nominal speed.
However, the V/f ratio may retain fixed [20,35], i.e., rotor speed, changes based on the load [8]. A bidirectional converter with 20% power rated of the machine rating can enable a 40% speed control range with constant average torque output [49]. The control winding must satisfy a synchronizing requirement, and thus, it is limited as Equation (1) [8,50] or Equation (2) [18,19,20,39,51,52,53].
Therefore, the power and control windings are 2-pole and 2-pole, respectively, while the rotor is -pole.
Firstly, some assumptions are described in order to make the analysis feasible [48]:
- The iron permeability of the machine is infinite.
- The stator windings of the machine are assumed to be adequately modeled as spatially sinusoidally distributed.
- The power and control windings are three phases.
- The three-phase temporal current of the stator windings is ideal.
- The air gap of the machine is modeled using a sinusoidal air gap function.
MMFs for a single phase of the power and control windings of a stator are illustrated in Figure 4 [54]. These MMFs are for a stator with two and six poles, respectively, for power and control windings.

Figure 4.
MMFs of a single phase of power and control windings.
The air gap function is as follows [55]:
where and are the fixed and variable parts of the air gap, respectively, so that . Additionally, and are the mechanical angle of the rotor and the mechanical angle around the machine with reference to phase , respectively. Therefore, the maximum and minimum air gap ( and ) are as follows:
The inverse air gap function is diagrammatically illustrated in Figure 5.
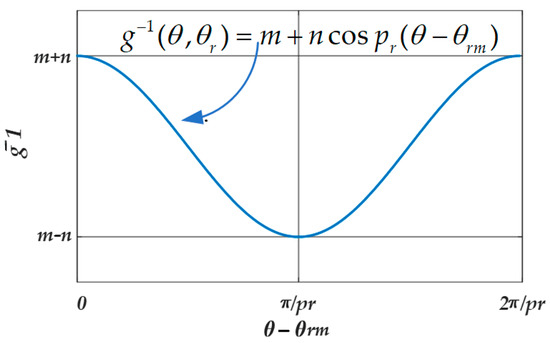
Figure 5.
The inverse air gap function with poles.
By assuming the sinusoidal three-phase current of the power and control windings as ideal, the current equations are as follows:
where and are current of phase for power and control windings, respectively. Additionally, is the angle difference of current for power and control windings, and and are the magnitudes of the mentioned current. It is worth mentioning that the current of phases and have and difference with the current of phase .
The resultant three-phase MMFs per air gap for the power and control windings, i.e., and , become as follows:
where and are the pole pair numbers of the power and control windings, respectively, is the periphery angle around machine (mech.-rad.). Moreover, the MMFs’ magnitude of power and control windings for phase , i.e., and , are as follows:
where and are obtained as follows:
where and represent the peak conductor density of the power and control windings in (conductors/rad.), respectively.
Based on the MMFs of the windings and the air gap function, the flux density distribution of power and control windings, i.e., and with respect to for each of the individual windings is obtained using the following expressions.
where represents the electromagnetism permeability.
In several research studies, it is assumed that and based on Equations (3)–(5), the following equation is derived [48,54,56,57].
Then,
One of the pre-requisites mentioned above is that the component field of one power winding must be rotating in the same direction as the fundamental field of the other stator winding, and the spatial pole numbers must be the same. This means that the two values including cosine terms of the secondary fundamental component and the primary harmonic component must be equal [45,58,59].
Hence, and .
Accordingly, for the positive sign, Equations (17) and (18) results in Equation (19).
In addition, for the positive sign (), Equations (20) and (21) results in Equation (22).
The negative case (), i.e., Equations (20)–(22), can be disregarded. This note is considered in problem formulation [2,7,48,50,60,61,62,63,64,65,66,67,68]. The electro-mechanical energy conversion occurs under the following conditions, and this shows the share of each winding [60].
where and are the power of the primary and secondary windings, i.e., the power and control windings, respectively, and and are the mechanical power and electromagnetic torque of the machine, respectively. Additionally, the synchronous speed () is as follows [44]:
It is worth mentioning that in BDFRM, the slip is as follows [50]:
In some research studies, the pole numbers of rotor () may be limited as follows [20,48,54,56,57,60,62]:
As mentioned, both the positive and negative signs are valid, only the positive sign () is considered in practice [63,69]. Further, the research studies have revealed that the negative sign () in Equation (27) does not give favorable couplings between the windings for some pole combinations [26], and thus, this case may result in impractical designs [45]. Therefore, unlike the conventional machines, the number of poles on the rotor can be an odd number [29,30,70]. For instance, for four and two pole numbers for stator windings, the number of poles on the rotor should be three [18,30]. The unusual operating principle of the BDFRM leads to this interesting design feature [30].
Unlike BDFM, the BDFRM rotor has no winding. However, the rotor design is more complicated in this machine technology [56,57,70]. The BDFRM rotor design is based on increasing its saliency to improve machine operation [47]. The BDFRM’s rotor is designed in different types according to its application. Figure 6 shows different types of BDFRM’s rotor. It should be noted that the rotor velocity is independent of the rotating field speed [8]. It is revealed that the axially-laminated rotor type results in high iron losses of the rotor, which have negative effects on the efficiency, as well as the thermal stability of BDFRM [8].
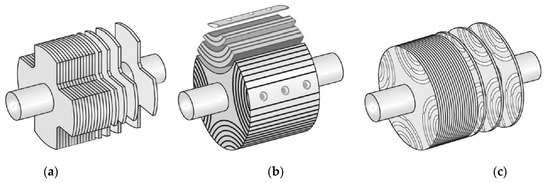
Figure 6.
Different rotor types used in BDFRM: (a) Salient-pole, (b) Axially-laminated, and (c) Radially-laminated ducted-rotor [35,44,50,65,71].
The flux density with air gap permeance of different rotor types is discussed in [72] while in [26], the flux density harmonics are calculated from the MMF and ideal coupling factors. The characteristics of different rotor types are compared in [13,56]. Moreover, in [26], the salient-rotor designs including simple salient-pole and ducted-rotor structures are studied. Different rotor configurations and their characteristics are discussed in [6,47]. Furthermore, designing two different rotor structures for wind-driven BDFRM including a salient-pole radially-laminated and axially-laminated rotor is performed in [73]. In [74], the characteristics of axially-laminated, as well as salient-pole radially-laminated reluctance rotors, are compared. A 2-D form of three rotor types including the traditional salient-pole, the segment, and the axially-laminated rotors are presented in [72]. A comparison between two rotor structures of BDFRM including axially-laminated and salient rotors is performed in [70]. Ideal and practical ducted rotors are discussed in [63].
As mentioned, in BDFRM, both windings are mounted on the stator. The circuit of stator windings is investigated in [43,45,75,76]. Additionally, the winding diagrams of the stator with six and two poles for power and control windings, respectively, are presented in [47].
Figure 7 illustrates a typical stator diagram with eight-pole and four-pole windings for the power and control windings, respectively [45]. Figure 8 depicts the winding connection diagrams of the stator for the one-pole pair (for power winding) and the three-pole pair (for control winding) on the inner and outer sides of it, respectively. In this figure, the number of slots is equal to . It is worth noting that Figure 8 and Figure 9 do not refer to an identical machine. The winding of the lower layer is wounded with the pitch 30, while the other winding in the upper layer is wounded with the pitch 10. BDFRM machines may operate in sub-synchronous or super-synchronous modes. The operation mode for BDFRG is shown in [60,62,63,77,78,79]. In [80], the operation mode for both the motor and generator in BDFMs is presented. The operation modes are illustrated in Figure 9.
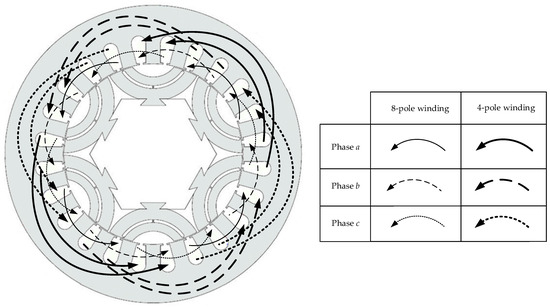
Figure 7.
Diagram of a BDFRM stator with two 8-pole and 4-pole windings [45] (The 8-pole winding is the power winding, which is wounded in the inner side of the stator, while the 4-pole winding is the control winding, which is wounded in the outer side of it).

Figure 8.
Winding connection diagrams of a typical stator: (a) Power winding, and (b) Control winding.
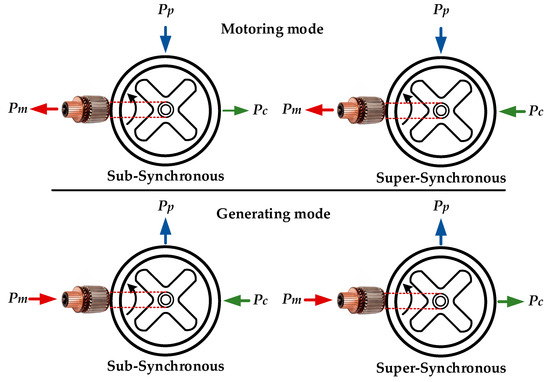
Figure 9.
The reference active power directions for motoring and generating modes and super-synchronous and sub-synchronous modes [80].
Electrical Equivalent Circuit (EEC) of BDFRM is presented in [6,17,34,48,50,54,56,57,73,81,82,83,84,85,86,87]. In [56], the equivalent electric circuit for both the case of considering and ignoring the rotor current is presented. A typical equivalent electric circuit of BDFRM ignoring rotor current is presented in Figure 10. The power and control induction voltage, i.e., and are as follows:
where is the mutual inductance between the windings, is the initial rotor position and it is equal to . This term is equivalent to the load angle in a conventional synchronous machine. is the initial position of and as mentioned, is the mechanical angular velocity of the rotor (mech.-rad./s). Different approaches are investigated to model the BDFRM with the aim of analyzing its operation. Classification of the BDFMs modeling approaches is performed in Figure 11.
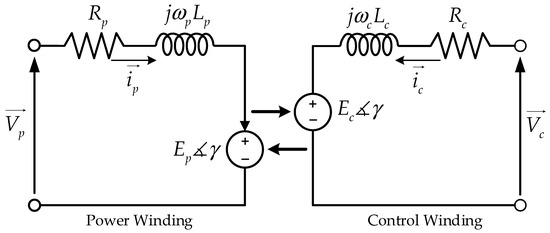
Figure 10.
EEC of BDFRM [34,54,57,82].
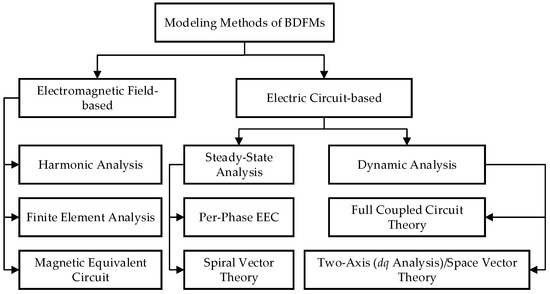
Figure 11.
The classification of the brushless doubly-fed machine (BDFM)’s modeling approaches [35].
In this study, the previous research works are compared from different points of view. Table 2 lists the main characteristics of the previous research studies in the field of BDFRM.

Table 2.
The main features of the previous research studies about BDFRM (Ψ: Unknown cases that have not been mentioned in the references).
3. Role of BDFRM in Decarbonization
BDFRM is one of the effective solutions for decarbonization. The high cost of existing wind turbines and probable maintenance costs are limiting factors for increasing the penetration of wind turbines. Such challenges can be solved by the development of BDFRM that can contribute to higher penetration of wind turbines. Additionally, lower energy losses of BDFRMs have been reported in the literature. However, the installing costs such as foundation cost and landing cost are required for all wind turbine types [141]. In addition to wind turbines, BDFRM is a potential solution for the development of Electric Vehicles (EVs), which are an alternative to conventional vehicles. EVs are developing due to the energy crisis and air pollution issues [142,143]. BDFRM can accelerate the development of EVs due to its advantages, such as lower maintenance and manufacturing cost, higher reliability, lower losses, and robustness feature. Furthermore, BDFRM can provide higher speeds. In [92], the application of BDFRM for EVs has been studied.
4. BDFRM Operation
The same as other machines, operation principles of BDFRM are essential for its reliable and efficient performance, which has been widely investigated in the literature. Several research studies are accomplished in the field of BDFRM operation. In [34,46,50,144], operation principles of BDFRM are described. A schematic of BDFRM operation by electric and electromagnetic circuits is presented in [55], in which some instructions are given to design the windings, torque generation principles, and electric power generation for the motoring mode, as well as the generating mode. The basic principles of BDFRM operation in synchronous mode and its mathematical modeling for a ducted-rotor one are described in [69], where an appropriate control scheme for operation with synchronous speed is investigated. In this research study, a prototype machine is manufactured and implemented as a motor drive. Finally, the BDFRM-based drive is examined in the synchronous operation mode at different load and speed levels. In another attempt, analysis of BDFIM and BDFRM using a developed Magnetic Circuit Modeling (MCM) strategy by calculating the flux density in both the rotor and stator considering the saturation is investigated in [145]. The Finite Element Analysis (FEA) is also used to validate the obtained results by MCM. The MCM approach is considered due to its rapid calculation compared to FEA since the model consists of simple circuit elements and expressions. In [81], a type of BDFRM is proposed, and the related model for analyzing the machine is presented. The stator has two sets of windings with sinusoidal distribution and a different number of poles. The pole number of the simple-saliencies rotor is dependent on the two stator windings. A d-q-n reference frame model, and accordingly, the machine EEC are developed for the machine. A comprehensive theoretical study of the BDFRM performance limitations when fed by an inverter is performed in [90,93,146]. The variable-speed operation of BDFRM is studied in [94]. Furthermore, the maximum torque per ampere in BDFRM is studied in [28]. A comparison between different BDFRM operating modes is performed in [91]. Moreover, the numerical FEA of a BDFRM machine is evaluated to cover the operation principles of the BDFRM with frequency sharing. Steady-state performance of a duel-stator BDFRM with different rotor structures is investigated in [71] by studying the impact of some external parameters including load, field current, and speed on the steady-state operation of such machines.
Some research studies examine the operation of different BDFMs, where BDFRM is a subcategory of them. In [35], a theoretical scheme for the BDFMs is presented. The characteristics of each BDFM topology and common features, such as the modeling strategies, operation modes, design insights, and control strategies, are discussed. Further, the current challenges of BDFRM in viewpoints of development ad opportunities are discussed according to the special structure of BDFM. Because of the structures’ diversity of stator windings, the existing criterion and generation mechanism of direct coupling between the windings of BDFRM mounted on the stator have not been fully revealed yet.
4.1. BDFRM Operation with Different Rotor Types
The main point in some research studies is the specific rotor types. In [44], a systematic analysis and performance specifications of the BDFRM with a multi-barrier rotor are introduced. Multi-barrier rotor is effective in applications that need high reliability and low maintenance applications, such as offshore wind turbines. The MMF distributions of the air gap under open-circuit and loaded conditions are explained to more effectively avoid the unbalanced magnetic pull in BDFRM, a more practical rule compared to the widely-accepted form, i.e., is derived. Analytical equations are also obtained to assess inductance parameters for circuit modeling and control purposes. In this research, both the FEA and real tests are conducted to validate the effectiveness of the proposed analysis. Investigation on different operating points of a BDFRM having a ducted rotor means hexagonal-based rotor with segment laminations in different speed regions including sub-synchronous, synchronous, and super-synchronous are accomplished in [45]. A model of the machine is proposed and evaluated by introducing a control strategy to increase the torque generation potential of the proposed structure, and the stages of power electronics drive implementation and machine assembly are presented. The results of analyzing the static structure of the understudy BDFRM are also discussed leading to the final laminations of the machine. The designed machine is experimentally examined in different speed regions. In [58], the optimal design of an axial-flux rotor of a BDFRM is investigated, which has higher power density and torque capability compared to a BDFRM with a radial-flux rotor. To improve the torque density, as well as the output power quality, optimization of the span and overhang lengths of the rotor are performed to reduce the torque ripple. Then, the obtained results for the optimal design are evaluated using the transient 3-D FEA and compared with the results of the diamond shape. Consequently, a sample prototype of a 1-hp is chosen for examination, taking into account the manufacturing cost and available examination facilities to validate the performance of the proposed topology. A comparison between two developed rotor structure types of BDFRM considering simple salient and axially-laminated rotors is accomplished in [70] from the viewpoint of performance evaluation. The performance of the complicated BDFRM is appropriately evaluated by calculating the self-flux linkage, as well as the mutual one of the two windings mounted on the stator as the function of the rotor position. Two rotor structures are also compared in this paper. The geometry of the BDFRM having a radially-laminated ducted rotor, which is the most appropriate choice for the reluctance rotor, is investigated in [87]. The reluctance ratio is low for the very thin ducts, and the intensity of the coupling is impressed. On the other hand, for very wide ducts, the machine saturation occurs since the reluctance path is high for the coupling flux between the stator windings. Using the FEA, it is revealed that 38% is appropriate for the duct ratio. Structure and operation modes of a BDFRM with axially-laminated anisotropy rotor are introduced in [95], in which the air gap magnetic field is analyzed using the theory of the field modulation. The coupling principle between the windings is assessed. The adjustable-speed operation of the BDFRM is also discussed in this research. It is claimed that the BDFRM with an adjustable-speed system requires a much smaller inverter size compared to the conventional AC motor-based variable-speed system.
4.2. Operation in Different Conditions
The operation of BDFRM under different conditions, such as the capability of generating reactive power for voltage drop considerations [79], open-circuit [82], and unbalanced grid voltage [83], is investigated. All grid-tied wind turbine generators must be compatible with locational system codes, as well as the reactive power considerations, and thus, need to be evaluated under grid-tied performance in the understudy zones. Therefore, in [79], design optimization and modeling of a 2-kW BDFRM are accomplished to evaluate the operation and reactive power capability of the machine in generator mode. The obtained results reveal that the capability curve of BDFRG seems to be V-shaped and hence, it is appropriate for wind energy conversion systems. Although the principle of BDFRM is similar to the BDFIM one, the machines’ magnetic fields barricades standard testing is more complicated. This complication in normal locked-rotor test is resulted from high leakage inductances and additionally non-sinusoidal air gap fluxes. Such issues have direct impacts on frequency-domain constant and time-domain testing, which is studied in [82]. In this research, the effectiveness of the combination of testing and analysis approaches, including open-circuit and pulse testing, which are consequently used to obtain the inductance parameters of BDFRM within a range of work points, is investigated. The accuracy of the results is justified by testing the machine and afterward compared with the FEA machine design. In [83], a mathematical model for a BDFRG under unbalanced grid voltage is introduced. Based on the sequence components, the machine EEC in the d-q reference frame is presented, and the torque, as well as the power formulations, are extracted. Furthermore, a real-time separation approach is introduced to separate the BDFRG positive sequences from its negative sequences.
4.3. Operation of Wind-Driven BDFRMs
The operation of wind-driven BDFRMs is studied in the literature. In [59], operation analysis and simulation for a BDFRM with related control strategies are accomplished, in which reasonable assumptions are made for the transient and steady-state analyses. A field-based speed control methodology is introduced, and digital simulation and tests are accomplished to extensively investigate the performance of the machine in start-up conditions. This paper also studies the impact of the voltage and frequency of the control winding on machine operational characteristics, such as rotor speed. The existing research studies regarding the BDFRG are mainly limited to the MPPT region. Accordingly, in [64], a power control scheme for the adjustable speed wind-driven BDFRG is introduced that covers all system operational regions including MPPT, constant speed, and constant power regions. This paper uses power feedback-based MPPT to track the maximum accessible wind power. In the fixed-speed region, the speed of BDFRG is preserved fixed, while the constant-power region is for high velocities of wind. Furthermore, an observer is proposed to determine the wind turbine power. In [96], the magnetic operation of a 2 MW wind-driven BDFRM is investigated. This research also assesses the impact of high-flux-density steels on the torque density, in which a 27% improvement in operation is achieved. In addition, this paper studies the unbalanced magnetic pull of the rotor in unbalanced conditions. It is revealed that a 4/6 pole combination may be appropriate for the effective operation of the machine for such an application, but it is demonstrated that the rotor experiences high radial forces and abrasion that may limit the use of this reluctance-type BDFM, i.e., BDFRM.
4.4. Parameter Determination of BDFRM
The parameter determination of BDFRM is investigated in some research studies. The explanations for asymmetric mutual inductances in BDFRM are given in [76]. Several techniques for determining the BDFRM parameters are examined in [82,97]. Despite the similarity of the BDFRM model to the BFIM, using the locked rotor/no-load rotor tests on BDFRM is prevented by its high leakage inductances. A comparison between the machine testing and FEA machine design is made to justify the accuracy of the derived parameters. The impact of winding and harmonics of gap flux density on the performance of BDFRM is highlighted in [98]. Additionally, the importance of pole numbers on the performance of this machine is discussed.
4.5. BDFRM Dynamic Model
The dynamic modeling of the BDFRM is investigated in some research studies. A mathematical formulation for the dynamic model of BDFRM using the d-q reference frame is presented in [17], in which the numerical simulations are accomplished in MATLAB/Simulink. Additionally, the dynamic model of BDFRM is studied in [46,50]. The fundamental modeling equations that are needed to research in dynamics and control of BDFRM are developed in [46]. The full dynamic model of a BDFRM is presented in this paper. The development of a novel strategy and its implementation aspects for fast control of the BDFRM power are investigated in [60], which is extracted from the dynamic principle comparison between the measurable and controllable features of the machine including the electrical power and electromagnetic torque, as well as the reactive power and flux. A predictive DPC strategy for the BDFRG is introduced in [61], in which fast dynamic response is achieved by the proposed control strategy. In [75], the dynamic performance of the BDFRMT is investigated. An adaptive control strategy is introduced in [99], in which the dynamics modeling of the generator is used to develop an indirect adaptive control scheme by a feedback controller.
4.6. BDFRM Transient Model
A BDFRM type called the AF-BDFRM is suggested in [49], which is appropriate for low-speed drive applications with high-torque features. Higher torque and power density are the main advantages of AF-BDFRM in comparison with RF-BDFRM. Additionally, the transient 3-D FEA results of the proposed design are presented. It is attempted in [56] to accomplish a comparison among different rotor types of BDFRM using 2-D transient FEA. In [58], transient 3-D FEA is used for the design optimization of the rotor pole in an AF-BDFRM. In [59], operation analysis and control strategy are adopted for a BDFRM with reasonable assumptions for transient and steady-state models of the machine. The simulation and experimental tests are compared in this research. A model predictive current control approach is presented in [68] for controlling the speed of a BDFRM drive, in which the primary field orientation strategy is included in the control strategy for the decoupled control of flux and torque/speed. The proposed approach is compared with the classical field-oriented approach of BDFRM drive concerning speed, torque ripple contents, and transient response. In [85], the transient model of a BDFRMT is studied using the winding function and the d-q transformation theory. By comparing the simulation and experimental results, it is revealed that the higher harmonics in the inductances of the machine are effective for forecasting the current waveform. The transient model of BDFRM in the abc reference frame is presented in [100] by using the winding function principles, in which comprehensive case studies are conducted to evaluate the BDFRM model for different modes of operation.
4.7. Comparison with Other Machines
In several research studies, a comparative study of BDFRG and Brushless Doubly-Fed Induction Generator (BDFIG) technologies is conducted. Two types of rotor structures including the cage-based and the reluctance-based types are common models of the BDFRM’s rotor. In [42], the experimental comparisons between two types of BDFM with a reluctance-rotor, i.e., axially-laminated anisotropic reluctance rotor and conventional cage rotor, is performed in viewpoints of parameters and performance by using a prototype machine that is specially designed and built. This study reveals that the understudy reluctance rotor improves the synchronous operation and doubly-fed variable-speed operation. However, a better starting performance is attained by the cage-rotor. Another similar work is also accomplished in [56] for comparison among different rotor structures of BDFRM, i.e., two reluctance-type rotors and one cage rotor with a common stator. A comparison among magnetizing features of the mentioned rotor structures is performed and their differences are mentioned. This comparative study is performed using 2-D transient FEA. In another attempt, analysis of BDFIM and BDFRM using a developed MCM strategy by calculating the flux density in both the rotor and stator is investigated in [145]. This is beneficial especially for the BDFIM because the saturation can be occurred arising from the generated current of the rotor or stator. This saturation can change the flux patterns and complicates the calculations in the design step. A flux-based coupling factor is introduced to calculate the coupling intensity between the teeth of the rotor and the stator of the BDFIM. The MCM analysis is accomplished considering the saturation of flux density caused by the windings’ current while the FEA is used to justify the obtained results. The existence of two field components for a different number of poles leads to vibration components [147]. Accordingly, investigation of vibration modes in BDFIM and BDFRM arising from the interaction of magnetic fields using the bending forces created in the back iron is accomplished in [101]. In this paper, it is revealed that choosing the pole numbers in the machine highly impacts the strength of the vibration components.
In some other research studies, a comparison between BDFRM and other machine types including synchronous reluctance machine [40] and DFIM [6,77] is accomplished. Accordingly, in [40], a comparison between the BDFRM and the reluctance synchronous machine is accomplished to cover the research gap of BDFRM operation principles since both machines have a reluctance rotor and identical copper losses. The analysis is carried out using machine-independent normalizations. In [6], a comparison between BDFRM and Doubly-Fed Induction Generator (DFIG) for wind applications is accomplished, where the similarities of them and also advantages of BDFRM are discussed. A comparison between a commercial wind-driven DFIG with slip-ring and an emerging wind-driven BDFRG with a two-stage gearbox with the aim of providing frequency support for ancillary service is accomplished in [77].
5. BDFRM Power Factor
Some research studies are conducted on the BDFRM power factor and its improvement for reactive power compensation. The power factor value as one of the BDFRM control properties is compared with the other control parameters of BDFRM in [15]. In [36], a control strategy based on indirect field-oriented control for the grid-connected wind-driven BDFRG is modeled, in which the active power is delivered at the rated value to power grids after reaching the steady-state condition, while the reactive power has a zero magnitude (reference value) to improve the power factor. The development of a novel strategy and its implementation aspects for fast control of the BDFRM power are investigated in [60], in which a variety of load, power factor, and speed states are supported by the proposed controller using a custom-designed generator prototype. The impacts of pole-numbers on the performance of BDFRM, as well as power factor correction, are investigated in [109]. An algorithm for shaft position sensorless independent active and reactive power control mechanism of the BDFRM is proposed and experimentally verified in [119], in which practical evaluations including the load response, power factor correction, and speed tracking, are performed to validate the effectiveness of the strategy on a 1.5-kW BDFRM prototype. The power factor value and inverter rating of BDFRM are studied in some other research studies [21,133]. Furthermore, in [57], the impact of rotor design on torque and power factor of BDFRM with two different rotor structures including the axially laminated rotor and radially laminated rotor is studied.
6. Maximum Power Point Tracking for Generation Mode of BDFRM
The MPPT is studied in some research studies for wind-driven BDFRM [64,111,117]. In [64], in addition to the MPPT region using a power observer, the constant speed and constant power regions are also covered that include all system operational regions. In the constant-speed region, the speed of BDFRG is preserved constant, while the constant-power region is for high velocities of wind. In [111], three strategies are used for the MPPT mechanism of a BDFRM summarized as minimum copper losses, minimum converter current, and unity power factor operation. Additionally, a soft starting approach is used to protect the converter against over-current. In [117], the MPPT with adjustable-speed constant-frequency for wind turbines is obtained by means of a proposed parameter-free control scheme.
A control method based on reactive power control for a variable-speed wind-driven BDFRM is presented in [39], in which the control objectives are MPPT and the reactive power exchange with power grids. A flux-and voltage-vector-based control of a partially-rated BDFRG for a variable-speed wind energy conversion system with MPPT are studied in [78]. The development of two parameter-independent controllers is examined for a BDFRG by using the maximum torque per inverter ampere approach for various loading and speed conditions that are widely used for wind energy conversion systems. The adjustable-speed generation controller in [134] uses a heuristic-based wind speed estimation-based MPPT system for optimizing the system power output of the wind power generator. A scalar V/f control scheme for MPPT of a grid-tied BDFRM-based wind energy conversion system is presented in [135], in which a soft starting strategy is introduced for protecting the bi-directional converter against over-current. Furthermore, its capability to estimate the generator speed is also investigated. The results reveal that the estimated and actual speeds of the generator are close to each other, which supports sensorless control capability. A vector-control strategy for the MPPT mechanism of a BDFRM is accomplished in [136] by two strategies summarized as minimum converter current and unity power factor operation, in which a soft-starting approach is proposed to protect the converter against over-current. The first approach is based on zero reactive power, i.e., the unity power factor of power-winding for operation under the unity power factor. On the other hand, the second strategy is based on retaining the d-axis control-winding current at zero for maximizing the ratio of the electromagnetic-torque of the machine per current of the converter. This enables the system to obtain a specific torque at the minimum current level of the converter. The MPPT of wind-driven BDFRM by means of a scalar control approach is investigated in [66]. Vector control strategies are investigated in [137] for MPPT of wind-driven BDFRM. The MPPT of wind-driven BDFRM using different vector control approaches is investigated in [138].
7. BDFRM Losses
The BDFIM has high rotor losses and low efficiency resulted from its cage rotor. On the other hand, the BDFRM has no rotor losses, and therefore, it has higher efficiency [15]. Some research studies are conducted on the investigation of the iron losses in BDFRM technology. The iron losses that occurred in a BDFRM are studied in [8]. It is demonstrated that the iron losses are large for a BDFRM with an axially-laminated rotor, which is commonly used for the synchronous reluctance machine. Simulations are conducted by the FEA, and losses of the rotor eddy-current are verified through experimental tests. The minimum copper losses as one of the BDFRM control properties associated with the other control properties of BDFRM are considered in [15]. In [40], an analysis is performed by machine-independent normalizations for comparison between the loss of BDFRM and the synchronous reluctance machine, in which both machines have identical reluctance rotor. In [111], a control technique for a grid-tied wind-driven BDFRG-based wind turbine for different purposes, such as minimizing the copper losses, is proposed. Furthermore, the loss considerations for BDFRM design are investigated in [139]. An adjustable structure robust controller for wind-driven BDFRM is proposed in [29]. Two control objectives, i.e., maximizing the wind turbine efficiency and minimizing the copper losses of the machine, are simultaneously considered. In [88], an MRAS control system based on active power is introduced for sensorless speed forecasting of the field of the power winding BDFRG. For this aim, the active power related to the control winding is utilized for speed forecasting. The obtained results present lower losses and higher efficiency in comparison with the equivalent BDFIM.
8. BDFRM Design
Although theoretical analysis shows the excellence of BDFRM compared to BDFIM, due to design restrictions, the BDFRM power density and efficiency are not yet satisfactory in comparison with the other machines. Recent advances on BDFRM reveal that this machine can operate at high efficiency and torque density if it is optimally designed. However, few research studies exist in the literature on how to design BDFRM. The design principles of BDFRM are described in [72]. Maximizing torque density of BDFRM using an approach for appropriate electrical excitations of two stator windings is investigated in [102]. A study on analytical strategies for design optimization of the BDFRM for favorable operation, in which the FEA is used to evaluate the obtained results for optimal design [26]. An analytical method for analyzing and designing a BDFRG by integrating both the equivalent and magnetic circuits is proposed in [84]. The proposed approach is effective to evaluate the BDFRG operation at the design step since the torque and terminal voltage can be assessed by the magnetic circuit and EEC, respectively. The proposed scheme provides a rapid analysis of a direct relationship between both the physical dimension and machine performance including mechanical power, electric power, torque, and efficiency. In [48], an approach for the steady-state operation analysis and design of the motor-based BDFRM, i.e., Brushless Doubly-Fed Reluctance Motor (BDFRMT), is introduced. This paper focuses on the linear modeling of the machine, but nonlinear characteristics of the magnetic modeling are also investigated. A 2-hp machine is designed, built, and compared with a conventional induction motor to comprehensively assess the machine’s performance. The design strategy, as well as the response analysis, of the BDFRM for practical implementation with the effective operation, is investigated in [103]. The operation principles of this machine are discussed, and a control approach is introduced for maximizing the performance of the motor torque. In this research, a BDFRM is designed and evaluated by simulation and then, it is built and experimentally tested. An electromagnetic model of BDFRM and its design principles are presented in [63]. In this paper, a semi-analytical model for size optimization of new machine designs is developed and the experimental tests are accomplished to confirm the effectiveness of the model for BDFRM. The semi-analytical model is a deterministic-optimization-based strategy for machine optimization, in which an objective function is iteratively solved, and different output constraints are satisfied.
8.1. Special Designs
Other research studies concentrate on BDFRM design for special applications. In [7], a design and performance evaluation of a BDFRM appropriate for wind applications has been investigated. A novel machine called the Axial-Flux BDFRM (AF-BDFRM) is suggested in [49], which is effective for drive applications with high-torque and low-speed characteristics. Higher torque and power density are the main advantages of AF-BDFRM in comparison with radial-flux BDFRM. The bidirectional power converter in this topology has a much lower capacity rating, which is another advantage of the proposed machine. However, the machine rating depends on the range of speed variations. The proposed axial-flux topology is composed of two stators and a reluctance iron rotor. The design theory of the proposed AF-BDFRM is studied in this research. Further, the transient 3-D FEA results of the proposed design are presented in this paper. The torque density of AF-BDFRM is greater than the Radial-Flux BDFRM (RF-BDFRM) making the proposed machine more appropriate for applications where constant torque over a variable speed range is needed. Design considerations of wind-driven BDFRM are presented in [73]. Sizing and designing of a 2 MW wind-driven BDFRG are investigated in [74]. In [75], a wound BDFM based on a reluctance rotor is introduced using FEA, which combines the flexible connection impact of the wound rotor and the magnetic flux-oriented impact of the reluctance rotor. This combination results in lower harmonics and strong coupling capability. To evaluate the obtained results by FEA, a 30-kW machine is designed and built. In [104], a BDFRM is analyzed using FEA for renewable-based applications, which focuses on the rotor design. Additionally, the share of the two stator windings in the total MMF is discussed. The experimental tests show the capabilities of the proposed design for a small BDFRM. In [105], a two-converter-based operation of a BDFRM for the frequency sharing mode is proposed. Operation theory and frequency sharing between the primary and control windings of the stator are introduced. The BDFRM design principles, machine manufacturing, and drive implementation mechanism are explained. The control scheme for the frequency sharing mode of BDFRM operation for different load levels is evaluated. None of the previous works has explored the frequency sharing operation of the BDFRM drive, in which the total frequency is divided between the power and control windings. A new approach to design optimization of wind-driven BDFRG is introduced in [27]. By using this procedure, the torque is increased considerably, while the iron mass has been retained at a suitable level.
8.2. Rotor Design
The rotor design, which is critical for occurring magnetic coupling between stator windings, is also investigated in different research studies. A suitable rotor design should have high saliency, as well as being manufacturable. BDFRM can be designed for different pole configurations, as well as rotor configurations [106]. In this regard, the pole combination in BDFRM is studied in [65,73,106,107,148]. The rotor design in [65] is performed by investigating the impact of variations of geometric parameters on BDFRM performance using FEA. Different parameters, such as the ending’s geometry of flux barrier, the number of slots on the rotor, duct ratio, and slot arc angle of the rotor, are studied in this paper. Furthermore, designing different rotor structures for wind-driven BDFRM is concentrated in [73]. In [106], three different pole configurations of BDFRM based on the salient-pole rotor are designed using FEM in ANSYS Maxwell software and a comparison is made between the obtained results and the results deriving from FEM. The simulation results reveal that the 4-8-6 configuration depicts promising results for variable-speed applications. The effective factors on BDFRM rotor design are investigated in [107]. Both the desirable and undesirable factors on magnetic performance for appropriate magnetic coupling of BDFRM are investigated in this paper. A comparison is performed between the theoretical analysis and experiment results from a prefabricated BDFRM, which are used to design a new BDFRM, in which the design is evaluated by FEA. In [148], the Taguchi method is combined with the FEA in order to optimize the average electromagnetic torque, as well as the coupling ability of a salient-pole rotor of BDFRM. According to practical conditions, four controllable factors including the length of the air gap, arc coefficient of the rotor pole, lateral radius, and the shaft diameter, are examined by the orthogonal array. The salient-pole rotor of the machine is designed using the optimal combination of parameters, as well as the signal to noise ratio. It is mentioned that the Taguchi method can be also developed for designing the other rotor types of BDFRM.
8.3. Optimal Pole Combinations
Selecting an appropriate pole combination of BDFRM is investigated in some research studies. Some critical issues of BDFRM rotor design are examined in [47], in which two different pole combinations, i.e., 6-4-2 pole and 8-6-4 pole combinations, for the power and control windings and the rotor are tested. It is revealed that the first combination is more appropriate than the second one. Additionally, the optimal pole combination for the optimal performance of BDFRM is studied in [74]. In [106], three different types for pole configurations of the salient-pole rotor of BDFRM are designed using FEA and compared with FEA-based simulation. The simulation results reveal that four, eight, and six poles, for control winding, power winding, and rotor, respectively, results in promising performance for variable-speed conditions. The new design of the stator is investigated in [108]. This paper introduces a new partitioned-stator BDFRM, in which the control winding is accommodated in the outer side of the stator and the power winding is accommodated in the inner side of the stator, whereas the rotor rotates between the two stator parts with two air gaps and is held with a non-magnetic holder. It is revealed that the proposed topology has a high-power density with reduced weight. In [96], two pole combinations, i.e., 4-8-6 and 4-6-5, are compared in viewpoint of the BDFRM operation for wind applications. This study reveal that a 4/6 pole combination may be a better choice for such applications. However, it is shown that the rotor experiences high radial forces and abrasion that may limit the use of this machine.
9. BDFRM Control
The control of BDFRM and other machine technologies is important for their optimal operation. In this case, different control schemes have been investigated and examined. Various research studies regarding BDFRM control are presented. Both the MCS converter and GSC must be controlled by power electronics drives. In the common model, the rotor indirectly connects to power grids using two back-to-back converters. The MSC is a rectifier to convert the AC voltage of the machine to DC voltage for the DC-link, in which this voltage is fixed with a capacitor (DC-link capacitor). On the other hand, the GSC is a rectifier that transforms the DC-link voltage to the AC voltage for the power exchange of the machine with power grids [54].
Compared to BDFIM technology, BDFRM has been ignored because of the inability of the currently designed rotors to generate large enough saliency ratios. In [20], it is attempted to cover this gap by proposing a theoretical analysis of the major control features of BDFRM. In [13], different control strategies of BDFM are reviewed and compared. A comprehensive comparison between different control schemes for the BDFRM technology, which are appropriate for digital implementation, is provided in [109]. In this paper, some aspects including the impact of pole-numbers on the performance of BDFRM, as well as power factor regulation are discussed. Different control characteristics of the BDFRM including maximum torque per inverter ampere, maximum power factor, and minimum copper losses, are studied by evaluating the related trade-offs are investigated in [15]. A comprehensive assessment and comparative development of vector control approaches for a variable-speed wind-driven promising BDFRG are presented in [22]. Two parameter-independent control methodologies, i.e., flux (field) and voltage vector-oriented approaches, are examined and the obtained results for both control systems are compared for an assembled BDFRG supplied from an Insulated Gate Bipolar Transistor (IGBT)-based converter. The obtained results from the simulation are experimentally justified by a BDFRG under the voltage-oriented control conditions. In [46], the fundamental modeling equations for dynamics and control of this machine are developed. The scheme is somehow tutorial as it studies some well-known strategies presented by the previous research studies in the context of BDFRM. The space vector model is used to obtain the steady-state equations of BDFRM. Throughout the analysis, standard sinusoidal spatial variation is used, as well as linearity assumptions. A per-unit system is also proposed in this research to make the analysis machine-independent. A theoretical analysis by implementing control strategies to accomplish a compromise between the machine performance and inverter size for the BDFRM for variable-speed large pump drives and variable-speed fixed-frequency wind turbines is discussed in [110]. Different control strategies including V/f scalar, direct torque (and flux), and vector control approaches for BDFRM are derived, analyzed, and simulated in [53,149].
9.1. Scalar-Based Approaches
In some research studies, the scalar control approaches for BDFRM are investigated. The MPPT of wind-driven BDFRM by means of a scalar control approach is investigated in [66]. An improved scalar control approach to control a wind-driven BDFRM is used in [51]. In [50], a closed-loop scalar control approach is presented. Moreover, the V/f scalar approach is studied to control the BDFRM in [53,149].
9.2. Vector-Oriented Strategies
In some other research studies, the vector-oriented strategies for controlling the BDFRM are utilized [18]. In [52], a comparison between different vector and scalar control strategies for the BDFRM is performed. A flux vector oriented encoder-less strategy is proposed in [80] to control the speed and inherently decoupling torque and reactive power, which is experimentally proved on a machine having a small size by following the pattern of the torque-speed features of DFIG wind turbines. The results reveal the better response of the proposed control system and its noise elimination capability. A vector-based control strategy for a grid-tied BDFRG-based wind turbine for MPPT under three scenarios summarized as the minimum current of converter (for the ratio maximization for the electromagnetic-torque per converter current), unity power factor, and minimum copper losses, is introduced in [111], in which a soft starting method is utilized to avoid the over-current condition on the converter. The vector control of a promising BDFRM for generator applications, such as wind turbines, as well as drive applications, such as pump-alike applications, with finite variable-speed applications, are investigated in [112,113]. A comprehensive comparison between the operations of the two control strategies is accomplished. Simulation and experimental tests are performed to check the performance of the prototype BDFRM under the maximum torque per inverter ampere condition. The vector control schemes for BDFRM exclusively for wind applications are analyzed in [114].
9.3. Open-Winding-Based Strategies
Open-winding control strategies of BDFRM are used in the literature. An open-winding wind-driven BDFRM and its control system for power decoupling are introduced in [115]. To control the machine, a cascade bi-level inverter with a double-end power supply is used. Compared to the common BDFRM, the proposed topology has better performance, lower switching frequency, smaller inverter capacity, and more adaptable control modes. Furthermore, to implement MPPT for the proposed structure, the common vector-oriented control strategy is developed to control the active and reactive power of the system independently and to decouple. A new open-winding approach to control a BDFRG for off-grid wind turbine applications or ship generator is introduced in [116]. The control winding of the proposed topology is fed with three-phase dual bi-level converters, in which a vector-oriented control approach is designed based on the Space Vector Pulse Width Modulation (SVPWM). In comparison with common tri-level inverter systems, the voltage rating of power electronics devices and the DC-link voltage in the suggested topology are decreased by 50%. The reliability, fault tolerance, and redundancy are improved by increasing the modes of switching. The MATLAB/Simulink is utilized to assess its operation via simulation. In addition, a 42-kW prototype machine is used for experimental validation.
9.4. Direct Power Control-Based Strategies
Direct Power Control (DPC) is also used to control the BDFRM. A predictive DPC strategy for the BDFRG is introduced in [61]. In this paper, the active and reactive power formulations are presented and afterward, the variations of the two mentioned parameters are predicted for a specific sampling horizon. The forecasted power fluctuations are utilized to obtain the required voltage for the control winding to eliminate the errors associated with power at the end of that sampling time horizon. Switching pulses are generated using the SVPWM method, which results in a constant switching frequency. Simulation results in MATLAB/Simulink reveal the effectiveness of the proposed control system in tracking the reference values of the active power, as well as reactive power. Furthermore, rapid dynamic response and ripple improvement of output power are the other strengths of the suggested control strategy. In [117], the theoretical derivation and implementation of a suggested DPC for open-winding BDFRG are presented. The MPPT with adjustable-speed constant-frequency for wind turbines is obtained using a parameter-free control scheme. In comparison with the tri-level converter systems, the capacity ratings of the designed converter system, the DC-link voltage, and also AC-side voltage are considerably high while notable improvements in fault tolerance, redundancy, and reliability are observed. A DPC approach is used for an open-winding BDFRG with dual bi-level converters in [118] with the aim of decreasing the converter capacity, as well as reducing the switching frequency, for wind turbines on larger scales. The proposed converter system is equivalent to a tri-level converter, which is directly connected to the secondary winding of the stator, i.e., control winding. More flexible control mode, fault detection capability, and better performance are the other characteristics of the suggested control system. A new algorithm is proposed in [31] for independent shaft position sensor-less control of active and reactive power, and therefore, power factor, of BDFRM. The algorithm is on the basis of the dynamic and magnetizing principles of the machine and does not require the estimation of the parameters. The proposed approach only relies on the voltage and current information of the grid-connected winding.
9.5. Sensorless-Based Strategies
In some other research studies, sensorless strategies are utilized to control the BDFRM. A newly developed shaft position sensorless approach to control the reactive power and torque of the BDFRM is successfully proven through a prototyped machine in [2]. The experimental results confirm the feasibility of the proposed parameter-independent controller for doubly-excited topologies. In [41], a shaft-position sensorless strategy to control the reactive power and torque of DFMs, such as BDFIM and recently developed BDFRM, is presented and examined. The basic control principles are extracted from the first concepts of torque generation and magnetization of the machines. For this control strategy, only the measurements of power winding and its resistance value are needed. Low dependence on parameters causes the robustness of the proposed control scheme, fast execution, and easy implementation. Controller effectiveness is proved through case studies including computer simulations of custom-designed and laboratory experiments of a designed BDFRM prototype. A novel position sensorless control strategy for the recently developed DFRM drives is proposed in [54], which is robust and appropriate for the adjustable-speed pump-type applications. The controller uses 60 Hz variables for the terminal, which are easy to achieve and forecasts the torque angle and control them, whereas the system is preserved in an open-loop state. Using the proposed control strategy, the required VA capacity of the Pulse Width Modulation (PWM) converter is half of the DFRM motor, and the full load torque can be accessible when the motor is started. The proposed control strategy is examined on a DFRM-based 2-hp drive to justify its performance. An approach for BDFRM control without shaft position or speed sensor is introduced in [62]. A control strategy based on shaft position sensorless for independent active and reactive power control of the BDFRM is introduced and experimentally tested in [119], which is an emerging solution for limited adjustable-speed applications. This parameter-independent strategy is derived from the concepts of the BDFRM operation and does not have sensitivity issues and fluctuation of machine parameters inaccuracy. The suggested control strategy exclusively depends on the voltage and current signals of the primary winding. Experimental tests, such as power factor regulation, load response, and speed tracking, are evaluated for a 1.5-kW BDFRM prototype.
9.6. Model Reference Adaptive System-Based Strategies
Model Reference Adaptive System (MRAS)-based approaches are also used to control the BDFRM. Two advantages are mentioned for MRAS-based strategies summarized: (1) MRAS-based control systems are capable of avoiding the machine parameter fluctuations, and (2) the model is independent of stator resistance because of using the reactive power as a functional candidate [120]. In [88], an MRAS-based on active power is introduced for sensorless speed forecasting of power winding field-based BDFRG. For this purpose, the secondary field-based control is utilized for speed forecasting. The MATLAB/Simulink is utilized to prove the efficiency of the proposed control strategy for a 1.6-kW machine. The applicability of several MRAS-based sensorless speed estimators for a generator-based BDFRM used in wind turbines is investigated in [89], which are based on active and reactive power control and under power winding field basis using the control winding parameters as functional variables. Simulation and experimental results under the variable wind speed (in the range of cut-in and rated speed) are accomplished for the mentioned strategies to estimate the generator speed. Numerous MRAS-based strategies are notably developed for speed forecasting of AC drives due to clarity and direct hardware interpretation of such strategies. Accordingly, in [121], an MRAS-based approach is proposed for sensorless control of a motor-based BDFRM drive based on the field of the power winding for the maximum torque per ampere condition of the inverter. On the other hand, the flux vectors of the control winding are used as the control functional variables in the equations of the MRAS. The obtained results from the simulation in MATLAB/Simulink are validated using experimental tests. In [120], the concept of classical reactive power-oriented MRAS for drive control, as well as the speed forecasting of BDFRM, is proposed. The simulation in MATLAB/Simulink is proved using the experimental evaluation of a 1.6-kW BDFRM, which shows the drive stability for the studied range of speed. Furthermore, in [122], a new MRAS-based method for sensorless control of a grid-connected wind turbine is introduced. In this method, there is no need for electro-mechanical shaft sensors, which are prone to failures in harsh environments, like those encountered in off-shore wind turbines.
9.7. Direct Torque Control-Based Approaches
The Direct Torque Control (DTC) approach is an excellent technique to control the flux and torque of doubly-excited machines [86]. DTC strategies are utilized for controlling the BDFRM technology in the literature. Characteristics of various control methods for BDFRM including scalar V/f control, direct torque (and flux) control, and also vector control are studied in [25]. Additionally, sensorless speed control is investigated since it can appropriately accomplish zero supply frequency of the control winding. The conventional DTC-based scheme is subjected to flux estimation issues and can deteriorate the machine operation under the condition of maximum torque per inverter ampere. Accordingly, this issue at low torque and current levels for BDFRM is solved in [67] by flux-oriented approaches using sliding mode observer and Kalman filter. A DTC strategy appropriate for the low-adjustable-frequency operation of the BDFRM is presented in [123]. The obtained results from numerical simulation and machine tests reveal that by using DTC, unlike most of the existing alternating machines, BDFRM has promising performance in zero supply frequency of the control winding. This research also claims that this advantage of BDFRM is resultant from using a flux forecasting scheme that does not depend on the voltage of the control winding. This advantage prevents some important problems, such as the influence of adverse resistance fluctuations on the forecasting accuracy at low applied voltage. While the DTC method is successfully applied to almost all conventional AC machines, its applications for controlling doubly-fed systems is investigated in [124]. In this research, the concepts and practical implementation aspects of DTC for the BDFRM are investigated. The presented results prove the effectiveness of the control system over the entire range of supply frequency for the maximum torque per inverter ampere. Furthermore, in [125], a DTC strategy is used to control a low variable-frequency limited-speed BDFRMT, which can effectively operate in a zero-supply frequency of the control winding. This achievement is the result of using a flux forecasting strategy, which is independent of the voltage of the control winding and therefore, can prevent the well-known issues at low frequencies of the same winding that are common for BDFRM. An improved DTC method is introduced in [86,126] for improving the performance of the conventional DTC strategy for wind-driven BDFRM. A real-time digital controller based on the suggested improved DTC method for the BDFRM is described and also explanations on the hardware arrangement are given. A real-time DTC strategy for the BDFRM is introduced in [127]. The simulation and experimental results reveal that the machine has an effective performance for zero supply frequency of the control winding, unlike most of the other alternative AC machines with DTC. A sliding mode observer is introduced in [128] to improve the prediction quality and the control operation of the DTC by solving the intrinsic flux forecasting issues that spread along with the algorithm. It is revealed that the proposed approach is reliable for the entire operating range of the BDFRM. Moreover, an observer-based scheme for speed, as well as direct torque (and flux), control of such machines is presented in [129], in which there is no need for a shaft position sensor. In [30], a sensorless DTC-based procedure to control the BDFRM is proposed, in which the obtained results from the simulation show the promising performance of the proposed approach for different loading conditions over the desired speed range.
9.8. Reactive Power Control-Based Approaches
Some strategies based on reactive power control of BDFRM are utilized in the literature. A decoupled control based on active and reactive power for an adjustable-speed fixed-frequency BDFRM is designed in [19]. The design strategy is based on multi-input second-order sliding strategies that are specific to systems with nonlinear models expose to external noise, as well as errors associated with the model. The proposed closed-loop system controller presents high robustness characteristics, fast convergence, and also low vibration. The operation of the system is evaluated by numerical simulations. The control strategy of an adjustable-speed wind-driven BDFRM is presented in [39]. Using this control approach, the MPPT is attained, while the injected reactive power into power grids is maximized. The proposed controller is based on multi-input second-order sliding methods that are specific for systems with nonlinear models under noisy conditions and considering the inaccuracies of the model. The simulation is presented to evaluate the performance of the suggested system. The development of a novel strategy and its implementation aspects for fast control of the BDFRM power with a partially-rated converter at low cost, and a promising candidate among brushless types for wind turbines with narrow speed ranges, are investigated in [60]. The concept of the method is derived from the principles of dynamic analogies between electromagnetic torque and electrical power, as well as flux and reactive power. The strategy is utilized on a stationary reference frame without any data about the BDFRM characteristics, including the velocity or angular position of the rotor, which is structurally simpler and to recognize in real-time. A variety of speed, load, and/or power factor states are supported by the proposed controller using a custom-designed generator prototype.
9.9. Flux-and Voltage-Vector-Based Strategies
Flux-and voltage-vector-based strategies are also utilized to control the BDFRM. In [9], the flux-and voltage-vector-based control methods for a BDFRM with limited variable-speed ranges, are investigated. The experimental studies are used to assess the performance of the control strategies on a custom-built BDFRM in both generating and motoring operation modes under the maximum torque per inverter ampere condition. The theoretical analysis, numerical and experimental evaluations, and validation of the flux-and voltage-vector-based control of a variable-speed wind-driven BDFRG with MPPT are accomplished in [78]. The development of two parameter-independent controllers is examined on a BDFRG by means of maximum torque per inverter ampere approach for different loading and speed conditions. Investigation on the flux-and voltage-vector-based control of a wind-driven grid-connected BDFRG is accomplished in [130]. The experimental results of testing a custom-built machine for the two algorithms including parameter-independent reactive power and speed control strategies prove the obtained results from the numerical simulation.
9.10. Multi-Input Controllers
Multi-input controllers are utilized in some research studies including multiple-input multiple-output robust controllers [29] and multi-input second-order sliding strategies [19,39]. A robust adjustable-structure controller for wind-driven BDFRM is proposed in [29]. Two control objectives as maximizing the wind turbine efficiency and minimizing the copper loss of the machine are simultaneously considered. The proposed multiple-input multiple-output controller is developed based on a common design approach for multiple-input multiple-output nonlinear dependent systems. A theoretical scheme based on the combined adjustable-structure strategies and Lyapunov’s theory is used to complete the design. Noise and vibration improvement are achieved by the model implementation. A decoupled closed-loop control based on active and reactive power for an adjustable-speed fixed-frequency BDFRM is investigated in [19]. The design of the proposed control is developed by multi-input second-order sliding strategies that are specific to systems with nonlinear models subject to external noises, as well as approximations of the model. The controller presents robust performance, fast convergence, and also low vibration. The operation of the control system is evaluated by numerical simulation. A control approach based on multi-input second-order sliding methods, which are proper for nonlinear systems, is proposed for variable-speed wind-driven BDFRM in [39].
9.11. Field-Oriented Approaches
Field-oriented approaches are also utilized to control the BDFRM. In [36], a control strategy based on indirect field-oriented control is modeled for the grid-tied wind-driven BDFRGs. It is revealed that all results approximately reach the steady-state condition after 0.4 sec. from the starting point. A model predictive current control approach is introduced in [68] for speed control of BDFRM drive, in which for the decoupled control of flux and torque/speed, the primary field orientation strategy is included in the control strategy. The suggested approach is compared with the classical field-oriented approach for BDFRM drive concerning speed, torque ripple contents, and transient response. In [131], the development of a field-oriented control strategy based on the angular velocity observer for a partially-rated wind-driven BDFRG is presented. The controller performance is validated on a BDFRG for different speed and loading conditions. In [140], the implementation of a field-oriented control approach to control the BDFRM in variable-speed applications is investigated. Simulation of the machine performance is validated by experimental results of the decoupled control of torque and reactive power.
9.12. Other Approaches
There are some other approaches to control the BDFRM in the literature. A study is performed in [132] to overcome the tediousness of BDFRM drive tuning to adequately track the speed. To attain proper operation of the system in speed tracking, an improved particle swarm optimization is utilized. The BDFRM drive intricacies are taken into account in order to accelerate the convergence in obtaining the gain parameters of the proportional-integral controller. An adaptive control strategy is introduced in [99] to control a BDFRM by using a feedback controller, which has several advantages, such as the capability of covering the uncertainty in the model, variations in the BDFRM parameters, and also the lack of measurements of the state vector elements. Furthermore, a supplementary control term is calculated using the H-∞ control approach for the robustness of the control loop. The Lyapunov analysis is accomplished to evaluate the stability of the proposed observer-oriented adaptive control strategy.
10. Future Directions
An overview of BDFRMs is presented in the previous sections by analyzing the previous research studies on such machines. The following notes are obtained by the conducted literature review.
- (a)
- The operation principles of BDFRM can be more clarified and different operation modes can be more discussed.
- (b)
- Most of the research studies on BDFRM are accomplished in the field of BDFRM control, while other fields, such as design and operation have been somewhat ignored.
- (c)
- The provided results in the literature clearly show the excellence of BDFRM compared to BDFIM, while due to the design limits, development of BDFRM and its commercialization for practical application need more analyses.
- (d)
- Due to the lower maintenance requirement of BDFRM and other advantages of it, such as higher reliability, lower losses, and capability of attaining to higher speeds due to its robustness feature, the penetration level of such machines can increase in future.
- (e)
- Most of the previous research have been conducted for generating mode of BDFRM, i.e., BDFRG. The motoring mode of BDFRM, i.e., BDFRMT, needs to be thoroughly investigated since the application of BDFRM for pump drives has been widely stated in the literature.
11. Conclusions
A comprehensive literature survey on BDFRM is accomplished in this paper. Most of the previous research studies in this field are categorized and reviewed. The main body of literature is categorized from different points of view including operation, design improvement, control, dynamic modeling, power factor control, and MPPT. The importance of using BDFRM for special applications especially offshore wind turbines due to its advantages, such as easy maintenance, are discussed, but as mentioned, BDFRM has not been fully developed. Therefore, further developments on BDFRM especially BDFRM designing need to be accomplished in the future.
Author Contributions
O.S.: Writing—original draft; S.T.: Investigation and validation, resources, conceptualization, writing—review and editing; B.M.-I.: Formal analysis, investigation and validation, conceptualization, writing—review and editing; F.M.: conceptualization, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
The study does not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, L.; Cheng, W. Torque and Reactive Power Control of a Doubly Fed Induction Machine by Position Sensorless Scheme. IEEE Trans. Ind. Appl. 1995, 31, 636–642. [Google Scholar] [CrossRef]
- Chaal, H.; Jovanovic, M. Practical implementation of sensorless torque and reactive power control of doubly fed machines. IEEE Trans. Ind. Electron. 2012, 59, 2645–2653. [Google Scholar] [CrossRef]
- Wu, H. Performance Comparisons of Doubly-Fed Machines. Ph.D. Thesis, University of Northumbria, Newcastle, UK, 2013. [Google Scholar]
- Stefani, A.; Yazidi, A.; Rossi, C.; Filippetti, F.; Casadei, D.; Capolino, G.A. Doubly fed induction machines diagnosis based on signature analysis of rotor modulating signals. IEEE Trans. Ind. Appl. 2008, 44, 1711–1721. [Google Scholar] [CrossRef]
- Pena, R.; Clare, J.C.; Asher, G.M. Doubly fed induction generator using back-to-back PWM converters and its application to variablespeed wind-energy generation. IEE Proc. Electr. Power Appl. 1996, 143, 231–241. [Google Scholar] [CrossRef]
- Schulz, E.M.; Betz, R.E. Use of Doubly Fed Reluctance Machines in Wind Power Generation. In Proceedings of the 12th International Power Electronics and Motion Control Conference, Portoroz, Slovenia, 20 August–1 September 2006; pp. 1901–1906. [Google Scholar]
- Kunte, S.; Bhawalkar, M.P.; Gopalakrishnan, N.; Nerkar, Y.P. Design and analysis of brushless doubly fed reluctance machine suitable for wind generation applications. In Proceedings of the 18th International Conference on Electrical Machines and Systems, Pattaya, Thailand, 25–28 October 2015; pp. 2082–2088. [Google Scholar]
- Scian, I.; Dorrell, D.G.; Holik, P.J. Assessment of losses in a brushless doubly-fed reluctance machine. IEEE Trans. Magn. 2006, 42, 3425–3427. [Google Scholar] [CrossRef]
- Ademi, S.; Jovanović, M.G. Vector control methods for brushless doubly fed reluctance machines. IEEE Trans. Ind. Electron. 2015, 62, 96–104. [Google Scholar] [CrossRef]
- Agrawal, S.; Banerjee, A.; Beach, R.F. Brushless Doubly-Fed Reluctance Machine Drive for Turbo- Electric Distributed Propulsion Systems. In Proceedings of the AIAA/IEEE Electric Aircraft Technologies Symposium, Cincinnati, OH, USA, 12–14 July 2018; pp. 1–17. [Google Scholar]
- Tapia, A.; Tapia, G.; Ostolaza, J.X.; Saenz, J.R. Modeling and control of a wind turbine driven doubly fed induction generator. IEEE Trans. Energy Convers. 2003, 18, 194–204. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z. Overview of different wind generator systems and their comparisons. IET Renew. Power Gener. 2008, 2, 123–138. [Google Scholar] [CrossRef]
- Zhang, F.; Yu, S.; Wang, H.; Wang, Y.; Wang, D. Overview of research and development status of brushless doubly-fed machine system. Chin. J. Electr. Eng. 2016, 2, 1–13. [Google Scholar] [CrossRef]
- Li, R.; Wallace, A.; Spee, R. Dynamic simulation of brushless doubly-fed machines. IEEE Trans. Energy Convers. 1991, 6, 445–452. [Google Scholar] [CrossRef]
- Jovanović, M.G. A Comparative Study of Control Strategies for Performance Optimisation of Brushless Doubly-Fed Reluctance Machines. J. Electr. Syst. 2006, 2, 208–255. [Google Scholar]
- Broadway, A.R.W. Cageless induction machine. Proc. Inst. Electr. Eng. 1971, 118, 1593–1600. [Google Scholar] [CrossRef]
- Song, W.K.; Dorrell, D.G. Modeling and simulation study for dynamic model of brushless doubly fed reluctance machine using matlab simulink. In Proceedings of the 3rd International Conference on Artificial Intelligence, Modelling and Simulation, Kota Kinabalu, Malaysia, 2–4 December 2016; pp. 382–386. [Google Scholar]
- Jovanović, M.G.; Betz, R.E. Slip power recovery systems based on brushless doubly fed reluctance machines. In Proceedings of the Power Conversion Conference—Osaka 2002, Osaka, Japan, 2–5 April 2002; Volume 3, pp. 987–992. [Google Scholar]
- Valenciaga, F. Second order sliding power control for a variable speed-constant frequency energy conversion system. Energy Convers. Manag. 2010, 51, 3000–3008. [Google Scholar] [CrossRef]
- Betz, R.E.; Jovanović, M.G. Theoretical analysis of control properties for the brushless doubly fed reluctance machine. IEEE Trans. Energy Convers. 2002, 17, 332–339. [Google Scholar] [CrossRef]
- Jovanovic, M.G. Power factor and inverter rating—A compromise in doubly fed reluctance machine drives. In Proceedings of the 8th International Conference on Power Electronics and Variable Speed Drives, London, UK, 18–19 September 2000; pp. 311–316. [Google Scholar]
- Jovanović, M.; Ademi, S.; Obichere, J.K. Comparisons of vector control algorithms for doubly-fed reluctance wind generators. In Transactions on Engineering Technologies: World Congress on Engineering and Computer Science 2014; Springer: Berlin/Heidelberg, Germany, 2015; pp. 85–99. ISBN 9789401772365. [Google Scholar]
- Sadeghian, O.; Oshnoei, A.; Khezri, R.; Hagh, M.T. Data clustering-based approach for optimal capacitor allocation in distribution systems including wind farms. IET Gener. Transm. Distrib. 2019, 13, 3397–3408. [Google Scholar] [CrossRef]
- Sadeghian, O.; Oshnoei, A.; Kheradmandi, M.; Khezri, R.; Mohammadi-Ivatloo, B. A robust data clustering method for probabilistic load flow in wind integrated radial distribution networks. Int. J. Electr. Power Energy Syst. 2020, 115, 105392. [Google Scholar] [CrossRef]
- Jovanovic, M. Sensored and sensorless speed control methods for brushless doubly fed reluctance motors. IET Electr. Power Appl. 2009, 3, 503–513. [Google Scholar] [CrossRef]
- Knight, A.M.; Betz, R.E.; Dorrell, D.G. Design and analysis of brushless doubly fed reluctance machines. IEEE Trans. Ind. Appl. 2013, 49, 50–58. [Google Scholar] [CrossRef]
- Staudt, T.; Wurtz, F.; Gerbaud, L.; Batistela, N.J.; Kuo-Peng, P. A New Approach on the Design and Optimization of Brushless Doubly-Fed Reluctance Machines. In Proceedings of the SGE 2014—Symposium de Génie Electrique, Cachan, France, 8–10 July 2014. [Google Scholar]
- Schulz, E.M.; Betz, R.E. Optimal torque per amp for brushless doubly fed reluctance machines. In Proceedings of the 14th IAS Annual Meeting, Conference Record of the 2005 Industry Applications Conference, Kowloon, Hong Kong, China, 2–6 October 2005; Volume 3, pp. 1749–1753. [Google Scholar]
- Valenciaga, F.; Puleston, P.F. Variable structure control of a wind energy conversion system based on a brushless doubly fed reluctance generator. IEEE Trans. Energy Convers. 2007, 22, 499–506. [Google Scholar] [CrossRef]
- Jovanović, M.G.; Yu, J.; Levi, E. A doubly-fed reluctance motor drive with sensorless direct torque control. In Proceedings of the IEEE International Electric Machines and Drives Conference, Madison, WI, USA, 1–4 June 2003; Volume 3, pp. 1518–1524. [Google Scholar]
- Chaal, H.; Jovanovic, M. Direct power control of brushless Doubly-Fed Reluctance Machines. In Proceedings of the 5th IET International Conference on Power Electronics, Machines and Drives, Brighton, UK, 19–21 April 2010; pp. 3–8. [Google Scholar]
- A Project Sponsored by The Engineering and Physical Sciences Research Council (EPSRC). Available online: https://www.ncl.ac.uk/engineering/research/eee/projects/performancecomparisonoftraditionalandemergingdoubly-fedgeneratortopologi.html (accessed on 16 November 2021).
- A Project Organized by The University of Newcastle. Available online: https://textarchive.ru/c-2497883-pall.html (accessed on 16 November 2021).
- Betz, R.E.; Jovanovic, M.G. Introduction to Brushless Doubly Fed Reluctance Machines—The Basic Equations; Aalborg University: Aalborg, Denmark, 1998. [Google Scholar]
- Han, P.; Cheng, M.; Ademi, S.; Jovanovic, M.G. Brushless doubly-fed machines: Opportunities and challenges. Chin. J. Electr. Eng. 2018, 4, 1–17. [Google Scholar] [CrossRef]
- Rihan, M.; Nasrallah, M.; Hasanin, B. Performance analysis of grid-integrated brushless doubly fed reluctance generator-based wind turbine: Modelling, control and simulation. SN Appl. Sci. 2020, 2, 1–9. [Google Scholar] [CrossRef]
- Tohidi, S.; Mohammadi Ivatloo, B. A comprehensive review of low voltage ride through of doubly fed induction wind generators. Renew. Sustain. Energy Rev. 2016, 57, 412–419. [Google Scholar] [CrossRef]
- Sadeghian, O.; Oshnoei, A.; Kheradmandi, M.; Mohammadi-Ivatloo, B. Optimal placement of multi-period-based switched capacitor in radial distribution systems. Comput. Electr. Eng. 2020, 82, 106549. [Google Scholar] [CrossRef]
- Valenciaga, F.; Evangelista, C.A. 2-Sliding active and reactive power control of a wind energy conversion system. IET Control Theory Appl. 2010, 4, 2479–2490. [Google Scholar] [CrossRef]
- Betz, R.E.; Jovanovic, M.G. The brushless doubly fed reluctance machine and the synchronous reluctance machine—A comparison. IEEE Trans. Ind. Appl. 2000, 36, 1103–1110. [Google Scholar] [CrossRef]
- Chaal, H.; Jovanovic, M. Toward a generic torque and reactive power controller for doubly fed machines. IEEE Trans. Power Electron. 2012, 27, 113–121. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, F.; Xu, L. Parameter and performance comparison of doubly fed brushless machine with cage and reluctance rotors. IEEE Trans. Ind. Appl. 2002, 38, 1237–1243. [Google Scholar] [CrossRef]
- Han, L.; Ou, X.; Du, J.; Han, X.; Guo, Y. Study of Direct Coupling in Stator Dual Windings of a Brushless Doubly Fed Machine. IEEE Trans. Energy Convers. 2017, 32, 974–982. [Google Scholar] [CrossRef]
- Han, P.; Zhang, J.; Cheng, M. Analytical Analysis and Performance Characterization of Brushless Doubly-Fed Machines with Multi-Barrier Rotors. IEEE Trans. Ind. Appl. 2019, 55, 5758–5767. [Google Scholar] [CrossRef]
- Rebeiro, R.S.; Knight, A.M. Characterization of a ducted rotor brushless doubly fed reluctance machine. IEEE Trans. Energy Convers. 2019, 34, 79–87. [Google Scholar] [CrossRef]
- Betz, R.E.; Jovanović, M.G. Introduction to the space vector modeling of the brushless doubly fed reluctance machine. Electr. Power Compon. Syst. 2003, 31, 729–755. [Google Scholar] [CrossRef]
- Kunte, S.; Bhawalkar, M.; Gopalakrishnan, N.; Nerkar, Y. Optimal design and comparative analysis of different configurations of brushless doubly fed reluctance machine. IEEJ J. Ind. Appl. 2017, 6, 370–380. [Google Scholar] [CrossRef][Green Version]
- Liao, Y.; Xu, L.; Zhen, L. Design of a doubly fed reluctance motor for adjustable-speed drives. IEEE Trans. Ind. Appl. 1996, 32, 1195–1203. [Google Scholar] [CrossRef]
- Khaliq, S.; Modarres, M.; Lipo, T.A.; Kwon, B. Design of Novel Axial-Flux Dual Stator Doubly Fed Reluctance Machine. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Taluo, T.; Ristic, L.; Jovanovic, M. Performance Analysis of Brushless Doubly Fed Reluctance Machines. In Proceedings of the 20th International Symposium on Power Electronics, Novi Sad, Serbia, 23–26 October 2019; pp. 1–6. [Google Scholar]
- Hassan, M.; Jovanovic, M. Improved scalar control using flexible DC-link voltage in Brushless Doubly-Fed Reluctance Machines for wind applications. In Proceedings of the 2nd International Symposium on Environment Friendly Energies and Applications, Newcastle upon Tyne, UK, 25–27 June 2012; pp. 482–487. [Google Scholar]
- Jovanović, M.G.; Betz, R.E.; Yu, J.; Levi, E. Aspects of vector and scalar control of brushless doubly fed reluctance machines. In Proceedings of the International Conference on Power Electronics and Drive Systems, Denpasar, Indonesia, 25 October 2001; Volume 2, pp. 461–467. [Google Scholar]
- Jovanović, M. Control of brushless doubly-fed reluctance motors. In Proceedings of the IEEE International Symposium on Industrial Electronics, Dubrovnik, Croatia, 20–23 June 2005; Volume 4, pp. 1667–1672. [Google Scholar]
- Liao, L.; Sun, C. A Novel Position Sensorless Control Scheme for Dyoubly Fed Reluctance Motor Drives. IEEE Trans. Ind. Appl. 1994, 30, 1210–1218. [Google Scholar] [CrossRef]
- Ojo, O.; Dong, G.; Omoigui, O. Analysis of a synchronous reluctance machine with an auxiliary single-phase winding. IEEE Trans. Ind. Appl. 2003, 39, 1307–1313. [Google Scholar] [CrossRef]
- Xu, L.; Wang, F. Comparative study of magnetic coupling for a doubly fed brushless machine with reluctance and cage rotors. In Proceedings of the Conference Record of the IEEE Industry Applications Conference Thirty-Second IAS Annual Meeting, New Orleans, LA, USA, 5–9 October 1997; Volume 1, pp. 326–332. [Google Scholar]
- Schulz, E.M.; Betz, R.E. Optimal Rotor Design for Brushless Doubly Fed Reluctance Machines. In Proceedings of the 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, Salt Lake City, UT, USA, 12–16 October 2003; Volume 1, pp. 256–261. [Google Scholar]
- Khaliq, S.; Atiq, S.; Lipo, T.A.; Kwon, B. Rotor Pole Optimization of Novel Axial-Flux Brushless Doubly Fed Reluctance Machine for Torque Enhancement. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- El-Sayed, H.S.; El-Khouly, F.M.; Osheiba, A.M. Performance analysis and control of a brushless doubly fed reluctance machine. Electr. Power Compon. Syst. 2005, 33, 1105–1122. [Google Scholar] [CrossRef]
- Jovanović, M.; Chaal, H. Wind power applications of doubly-fed reluctance generators with parameter-free hysteresis control. Energy Convers. Manag. 2017, 134, 399–409. [Google Scholar] [CrossRef]
- Moazen, M.; Kazemzadeh, R.; Azizian, M.R. Model-based predictive direct power control of brushless doubly fed reluctance generator for wind power applications. Alex. Eng. J. 2016, 55, 2497–2507. [Google Scholar] [CrossRef]
- Jovanovic, M.; Ademi, S.; Llano, D.X. Control of Doubly-Fed Reluctance Machines without a Shaft Position or Speed Sensor. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Amalfi, Italy, 20–22 June 2018; pp. 1245–1250. [Google Scholar]
- Staudt, T.; Wurtz, F.; Gerbaud, L.; Batistela, N.J.; Kuo-Peng, P. An optimization-oriented sizing model for brushless doubly fed reluctance machines: Development and experimental validation. Electr. Power Syst. Res. 2016, 132, 125–131. [Google Scholar] [CrossRef]
- Moazen, M.; Kazemzadeh, R.; Azizian, M.R. Power control of BDFRG variable-speed wind turbine system covering all wind velocity ranges. Int. J. Renew. Energy Res. 2016, 6, 477–486. [Google Scholar]
- Staudt, T.; Wurtz, F.; Batistela, N.J.; Kuo-Peng, P. Influence of rotor design and geometric parameter variation on global performance of Brushless Doubly-Fed Reluctance Machines. In Proceedings of the International Conference on Electrical Machines, Berlin, Germany, 2–5 September 2014; pp. 537–543. [Google Scholar]
- Mousa, M.G.; Allam, S.M.; Rashad, E.M. Maximum power tracking of a grid-connected wind-driven Brushless Doubly-Fed Reluctance Generator using scalar control. In Proceedings of the 8th GCC Conference and Exhibition, Muscat, Oman, 1–4 February 2015; pp. 1–6. [Google Scholar]
- Chaal, H.; Jovanovic, M. Flux observer algorithms for direct torque control of brushless doubly-fed reluctance machines. In Proceedings of the 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009; pp. 4440–4445. [Google Scholar]
- Kiran, K.; Das, S.; Singh, D. Model predictive field oriented speed control of brushless doubly-fed reluctance motor drive. In Proceedings of the IEEE International Conference on Power, Instrumentation, Control and Computing, Thrissur, India, 18–20 January 2018; pp. 1–6. [Google Scholar]
- Rebeiro, R.S.; Knight, A.M. Two-converters-based synchronous operation and control of a brushless doubly fed reluctance machine. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Xu, L.; Tang, Y.; Ye, L. Comparison Study of Rotor Structures of Doubly Excited Brushless Reluctance Machine by Finite Element Analysis. IEEE Trans. Energy Convers. 1994, 9, 165–172. [Google Scholar] [CrossRef]
- Fukami, T.; Momiyama, M.; Shima, K.; Hanaoka, R.; Takata, S. Steady-state analysis of a dual-winding reluctance generator with a multiple-barrier rotor. IEEE Trans. Energy Convers. 2008, 23, 492–498. [Google Scholar] [CrossRef]
- Knight, A.M.; Betz, R.E.; Dorrell, D. Design principles for brushless doubly fed reluctance machines. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 3602–3607. [Google Scholar]
- Dorrell, D.G.; Betz, R.E.; Jovanovic, M. Analysis of design variations in brushless double-fed reluctance generators for wind turbine applications. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC, Ohrid, Macedonia, 6–8 September 2010; pp. 9–14. [Google Scholar]
- Dorrell, D.G.; Jovanovic, M. On the possibilities of using a brushless doubly-fed reluctance generator in a 2 MW wind turbine. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 5–9 October 2008; pp. 1–8. [Google Scholar]
- Kan, C.; Ren, T.; Hu, Y. Design and experimental analysis of a wound brushless doubly Fed machine based on a rotor with the reluctance effect. IET Electr. Power Appl. 2019, 13, 551–558. [Google Scholar] [CrossRef]
- Gay, D.; Betz, R.E.; Knight, A.; Dorrell, D. An explanation of asymmetric mutual inductances in brushless doubly fed reluctance machines. In Proceedings of the 21st European Conference on Power Electronics and Applications, Genova, Italy, 3–5 September 2019. [Google Scholar]
- Attya, A.B.; Ademi, S.; Jovanović, M.; Anaya-Lara, O. Frequency support using doubly fed induction and reluctance wind turbine generators. Int. J. Electr. Power Energy Syst. 2018, 101, 403–414. [Google Scholar] [CrossRef]
- Ademi, S.; Jovanovic, M.G.; Hasan, M. Control of Brushless Doubly-Fed Reluctance Generators for Wind Energy Conversion Systems. IEEE Trans. Energy Convers. 2015, 30, 596–604. [Google Scholar] [CrossRef]
- Bhawalkar, M.; Gopalakrishnan, N.; Nerkar, Y. Reactive power capability curve of brushless doubly fed reluctance generator. Wind Eng. 2019. [Google Scholar] [CrossRef]
- Ademi, S.; Jovanović, M. A novel sensorless speed controller design for doubly-fed reluctance wind turbine generators. Energy Convers. Manag. 2016, 120, 229–237. [Google Scholar] [CrossRef]
- Liang, F.; Xu, L.; Lipo, T.A. D-q analysis of a variable speed doubly ac excited reluctance motor. Electr. Mach. Power Syst. 1991, 19, 125–138. [Google Scholar] [CrossRef]
- Gay, D.; Betz, R.E.; Dorrell, D.; Knight, A. Brushless doubly fed reluctance machine testing for parameter determination. IEEE Trans. Ind. Appl. 2019, 55, 2611–2619. [Google Scholar] [CrossRef]
- Moazen, M.; Kazemzadeh, R.; Azizian, M.R. Mathematical modeling and analysis of brushless doubly fed reluctance generator under unbalanced grid voltage condition. Int. J. Electr. Power Energy Syst. 2016, 83, 547–559. [Google Scholar] [CrossRef]
- Hsieh, M.F.; Lin, I.H.; Dorrell, D.G. An analytical method combining equivalent circuit and magnetic circuit for BDFRG. IEEE Trans. Magn. 2014, 50, 1–5. [Google Scholar] [CrossRef]
- Xu, L.; Liang, F.; Lipo, T.A. Transient model of a doubly excited reluctance motor. IEEE Trans. Energy Convers. 1991, 6, 126–133. [Google Scholar] [CrossRef]
- Song, W.K.; Dorrell, D.G. Implementation of improved direct torque control method of brushless doubly-fed reluctance machines for wind turbine. In Proceedings of the IEEE International Conference on Industrial Technology, Busan, Korea, 26 February–1 March 2014; pp. 509–513. [Google Scholar]
- Dorrell, D.G.; Knight, A.M.; Song, W.K.; Betz, R.E. Saturation and ducting effects in a brushless doubly-fed reluctance machine. IEEE Trans. Magn. 2013, 49, 3933–3936. [Google Scholar] [CrossRef]
- Kumar, M.; Das, S.; Kiran, K. Sensorless Speed Estimation of Brushless Doubly-Fed Reluctance Generator Using Active Power Based MRAS. IEEE Trans. Power Electron. 2019, 34, 7878–7886. [Google Scholar] [CrossRef]
- Kumar, M.; Das, S. Model reference adaptive system based sensorless speed estimation of brushless doubly-fed reluctance generator for wind power application. IET Power Electron. 2018, 11, 2355–2366. [Google Scholar] [CrossRef]
- Rebeiro, R.S.; Knight, A.M. Operating limits of a Brushless Doubly Fed Reluctance Machine driven by two converters. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 20–24 September 2015; pp. 3872–3877. [Google Scholar]
- Rebeiro, R.S.; Knight, A.M. Comparison of operating modes for a brushless doubly fed reluctance motor drive. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Cincinnati, OH, USA, 1–5 October 2017; pp. 1323–1330. [Google Scholar]
- Guo, X.; Wu, S.; Fu, W.; Liu, Y.; Wang, Y.; Zeng, P. Control of a Dual-Stator Flux-Modulated Motor for Electric Vehicles. Energies 2016, 9, 517. [Google Scholar] [CrossRef]
- Song, W.K.; Dorrell, D.G.; Knight, A.M.; Betz, R.E.; Gay, D. Operating limits and practical operation of a brushless doubly-fed reluctance machine. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Cincinnati, OH, USA, 1–5 October 2017; pp. 5846–5852. [Google Scholar]
- Kiran, K.; Das, S. Variable Speed Operation of Brushless Doubly Fed Reluctance Machine Drive Using Model Predictive Current Control Technique. IEEE Trans. Power Electron. 2020, 35, 8396–8404. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, F.; Grünberger, H.P.; Nolle, E. The structure and adjusting speed characteristics of new type of Doubly-fed brushless machine with ALA rotor. Eur. Trans. Electr. Power 2006, 16, 409–421. [Google Scholar] [CrossRef]
- Dorrell, D.G.; Knight, A.M.; Betz, R.E. Improvements in brushless doubly fed reluctance generators using high-flux-density steels and selection of the correct pole numbers. IEEE Trans. Magn. 2011, 47, 4092–4095. [Google Scholar] [CrossRef]
- Gay, D.; Betz, R.; Dorrell, D.; Knight, A. Brushless Doubly Fed Reluctance Machine Parameter Determination. In Proceedings of the 20th International Conference on Electrical Machines and Systems, Sydney, NSW, Australia, 11–14 August 2017; pp. 1–6. [Google Scholar]
- Schulz, E.M.; Betz, R.E. Impact of winding and gap flux density harmonics on Brushless Doubly Fed Reluctance machines. In Proceedings of the Second International Conference on Power Electronics, Machines and Drives, Edinburgh, UK, 31 March–2 April 2004; Volume 2, pp. 487–491. [Google Scholar]
- Rigatos, G.; Siano, P.; Ademi, S. Flatness-based adaptive fuzzy control of brushless doubly-fed reluctance machines. In Proceedings of the IEEE 26th International Symposium on Industrial Electronics, Edinburgh, UK, 19–21 June 2017; pp. 1913–1920. [Google Scholar]
- Ibrahim, A.K.; Marei, M.I.; El-goharey, H.S. Transient Model of Brushless Doubly Fed Reluctance Machine using ABC Reference Frame. Int. J. Recent Trends Eng. Res. 2018, 4, 26–32. [Google Scholar] [CrossRef]
- Logan, T.; McMahon, R.; Seffen, K. Noise and vibration in brushless doubly fed machine and brushless doubly fed reluctance machine. IET Electr. Power Appl. 2014, 8, 50–59. [Google Scholar] [CrossRef]
- Agrawal, S.; Province, A.; Banerjee, A. An Approach to Maximize Torque Density in a Brushless Doubly-fed Reluctance Machine. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Baltimore, MD, USA, 29 September–3 October 2019; pp. 298–305. [Google Scholar]
- Rebeiro, R.S.; Knight, A.M. Design and torque capability of a ducted rotor brushless doubly fed reluctance machine. IET Electr. Power Appl. 2018, 12, 1058–1064. [Google Scholar] [CrossRef]
- Hsieh, M.F.; Chang, Y.H.; Dorrell, D.G. Design and Analysis of Brushless Doubly Fed Reluctance Machine for Renewable Energy Applications. IEEE Trans. Magn. 2016, 52. [Google Scholar] [CrossRef]
- Rebeiro, R.S.; Knight, A.M. Two-Converter-Based Frequency-Sharing Operation and Control of a Brushless Doubly Fed Reluctance Motor Drive. IEEE Trans. Ind. Appl. 2019, 55, 5873–5880. [Google Scholar] [CrossRef]
- Kunte, S.; Bhawalkar, M.P.; Gopalakrishnan, N.; Nerkar, Y.P.; Vaidya, G.A. Selection of suitable pole configuration of BDFRM for variable speed applications. In Proceedings of the IEEE International WIE Conference on Electrical and Computer Engineering, Pune, India, 19–21 December 2017; pp. 208–211. [Google Scholar]
- Knight, A.M.; Betz, R.E.; Song, W.K.; Dorrell, D.G. Brushless doubly-fed reluctance machine rotor design. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Raleigh, NC, USA, 15–20 September 2012; pp. 2308–2315. [Google Scholar]
- Saeed, M.S.R.; Mohamed, E.E.M. Partitioned stator doubly-fed brushless reluctance machine for wind generating systems. In Proceedings of the 19th International Middle-East Power Systems Conference, Cairo, Egypt, 19–21 December 2018; pp. 864–869. [Google Scholar]
- Jovanovic, M. Brushless doubly fed reluctance machines: An emerging technology. Int. J. Emerg. Electr. Power Syst. 2007, 8. [Google Scholar] [CrossRef]
- Jovanović, M.G.; Betz, R.E.; Yu, J. The use of doubly fed reluctance machines for large pumps and wind turbines. IEEE Trans. Ind. Appl. 2002, 38, 1508–1516. [Google Scholar] [CrossRef]
- Mousa, M.G.; Allam, S.M.; Rashad, E.M. A comparative study of vector-control strategies for maximum wind-power extraction of a grid-connected wind-driven brushless doubly-fed reluctance generator. Aust. J. Electr. Electron. Eng. 2017, 14, 1–11. [Google Scholar] [CrossRef]
- Ademi, S.; Jovanovic, M. High-efficiency control of brushless doubly-fed machines for wind turbines and pump drives. Energy Convers. Manag. 2014, 81, 120–132. [Google Scholar] [CrossRef]
- Hargreaves, N.B.; Pantea, S.M.; Taylor, G.A. Control of Emerging Brushless Doubly-Fed Reluctance Wind Turbine Generators. In Large Scale Renewable Power Generation; Springer: Singapore, 2014; pp. 395–411. ISBN 978-981-4585-29-3. [Google Scholar]
- Ademi, S.; Jovanovic, M. Vector control strategies for brushless doubly-fed reluctance wind generators. In Proceedings of the 2nd International Symposium on Environment Friendly Energies and Applications, Newcastle upon Tyne, UK, 25–27 June 2012; pp. 44–49. [Google Scholar]
- Jin, S.; Zhang, F.; Fan, S.; Zhu, L.; Cao, W. Power decoupling control of open-winding brushless doubly-fed reluctance machine for wind power generator application. Int. J. Control. Autom. 2015, 8, 173–182. [Google Scholar] [CrossRef][Green Version]
- Zhang, F.; Zhu, L.; Jin, S.; Cao, W.; Wang, D.; Kirtley, J.L. Developing a new SVPWM control strategy for open-winding brushless doubly-fed reluctance generators. IEEE Trans. Ind. Appl. 2015, 51, 4567–4574. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, L.; Jin, S.; Su, X.; Ademi, S.; Cao, W. Controller Strategy for Open-Winding Brushless Doubly Fed Wind Power Generator with Common Mode Voltage Elimination. IEEE Trans. Ind. Electron. 2019, 66, 1098–1107. [Google Scholar] [CrossRef]
- Jin, S.; Shi, L.; Zhu, L.; Cao, W.; Dong, T.; Zhang, F. Dual Two-Level Converters Based on Direct Power Control for an Open-Winding Brushless Doubly-Fed Reluctance Generator. IEEE Trans. Ind. Appl. 2017, 53, 3898–3906. [Google Scholar] [CrossRef]
- Chaal, H.; Jovanovic, M. Power control of brushless doubly-fed reluctance drive and generator systems. Renew. Energy 2012, 37, 419–425. [Google Scholar] [CrossRef]
- Kiran, K.; Das, S. Implementation of reactive power-based MRAS for sensorless speed control of brushless doubly fed reluctance motor drive. IET Power Electron. 2018, 11, 192–201. [Google Scholar] [CrossRef]
- Kiran, K.; Das, S.; Kumar, M.; Sahu, A. Sensorless Speed Control of Brushless Doubly-Fed Reluctance Motor Drive using Secondary Flux based MRAS. Electr. Power Compon. Syst. 2018, 46, 701–715. [Google Scholar] [CrossRef]
- Agha Kashkooli, M.R.; Jovanovic, M.G.; Ademi, S. Sensorless power control of doubly-fed reluctance wind turbine generators using a current-based MRAS estimator. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 24–26 June 2020; pp. 65–70. [Google Scholar]
- Jovanović, M.G.; Yu, J.; Levi, E. Encoderless direct torque controller for limited speed range applications of brushless doubly fed reluctance motors. IEEE Trans. Ind. Appl. 2006, 42, 712–722. [Google Scholar] [CrossRef]
- Jovanovic, M.G.; Yu, J.; Levi, E. Direct torque control of brushless doubly fed reluctance machines. Electr. Power Compon. Syst. 2004, 32, 941–958. [Google Scholar] [CrossRef]
- Jovanović, M.; Yu, J.; Levi, E. A direct torque controller for limited speed range applications of brushless doubly-fed reluctance motors. In Proceedings of the Conference Record of the 2004 IEEE Industry Applications Conference, 39th IAS Annual Meeting, Seattle, WA, USA, 3–7 October 2004; Volume 4, pp. 2403–2410. [Google Scholar]
- Song, W.K.; Dorrell, D.G. Improved direct torque control method of brushless doubly-fed reluctance machines for wind turbine. In Proceedings of the IEEE International Symposium on Industrial Electronics, Taipei, Taiwan, 28–31 May 2013; pp. 1–5. [Google Scholar]
- Jovanović, M.G.; Yu, J.; Levi, E. Real-time implementation of direct torque control scheme for brushless doubly-fed reluctance motors. In Proceedings of the Second International Conference on Power Electronics, Machines and Drives, Edinburgh, UK, 31 March–2 April 2004; Volume 2, pp. 752–757. [Google Scholar]
- Chaal, H.; Jovanovic, M.; Busawon, K. Sliding mode observer based direct torque control of a brushless doubly-fed reluctance machine. In Proceedings of the IEEE Symposium on Industrial Electronics and Applications, Kuala Lumpur, Malaysia, 4–6 October 2009; Volume 2, pp. 866–871. [Google Scholar]
- Jovanović, M.G.; Dorrell, D.G. Sensorless control of brushless doubly-fed reluctance machines using an angular velocity observer. In Proceedings of the International Conference on Power Electronics and Drive Systems, Bangkok, Thailand, 27–30 November 2007; pp. 717–724. [Google Scholar]
- Ademi, S.; Jovanovic, M. Control of doubly-fed reluctance generators for wind power applications. Renew. Energy 2016, 85, 171–180. [Google Scholar] [CrossRef]
- Ademi, S.; Jovanovic, M.G.; Chaal, H.; Cao, W. A New Sensorless Speed Control Scheme for Doubly Fed Reluctance Generators. IEEE Trans. Energy Convers. 2016, 31, 993–1001. [Google Scholar] [CrossRef]
- Sahu, A.; Kiran, K.; Das, S. Particle Swarm Optimization based tuning of brushless doubly-fed reluctance machine drive for speed control applications. In Proceedings of the 1st IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems, Delhi, India, 4–6 July 2017; pp. 1–6. [Google Scholar]
- Jovanović, M.G.; Betz, R.E. Power factor control using brushless doubly fed reluctance machines. In Proceedings of the Thirty-Fifth IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy, Rome, Italy, 8–12 October 2000; Volume 1, pp. 523–530. [Google Scholar]
- Bhowmik, S.; Spec, R.; Enslin, J.H.R. Performance optimization for doubly fed wind power generation systems. IEEE Trans. Ind. Appl. 1999, 35, 949–958. [Google Scholar] [CrossRef]
- Mousa, M.G.; Allam, S.M.; Rashad, E.M. Sensored and sensorless scalar-control strategy of a wind-driven BDFRG for maximum wind-power extraction. J. Control. Decis. 2018, 5, 209–227. [Google Scholar] [CrossRef]
- Mousa, M.G.; Allam, S.M.; Rashad, E.M. Maximum power extraction under different vector-control schemes and grid-synchronization strategy of a wind-driven Brushless Doubly-Fed Reluctance Generator. ISA Trans. 2018, 72, 287–297. [Google Scholar] [CrossRef] [PubMed]
- Mousa, M.G.; Allam, S.M.; Rashad, E.M. Vector control strategy for maximum wind-power extraction of a grid-connected wind-driven Brushless Doubly-Fed Reluctance Generator. In Proceedings of the 4th International Conference on Electric Power and Energy Conversion Systems, Sharjah, UAE, 24–26 November 2015; pp. 1–6. [Google Scholar]
- Mousa, M.G.; Allam, S.M.; Rashad, E.M. Maximum wind-power extraction of a grid-connected wind-driven brushless Doubly-Fed Reluctance Generator under different vector-control strategies. In Proceedings of the 22nd International Conference on Electrical Machines, Lausanne, Switzerland, 4–7 September 2016; pp. 1105–1111. [Google Scholar]
- Dorrell, D.G.; Knight, A.M.; Betz, R.E. Issues with the design of brushless doubly-fed reluctance machines: Unbalanced magnetic pull, skew and iron losses. In Proceedings of the IEEE International Electric Machines and Drives Conference, Niagara Falls, ON, Canada, 15–18 May 2011; pp. 663–668. [Google Scholar]
- Xu, L.; Zhen, L.; Kim, E.H. Field orientation control of a doubly excited brushless reluctance machine. In Proceedings of the Conference Record of the IEEE Industry Applications Conference Thirty-First IAS Annual Meeting, San Diego, CA, USA, 6–10 October 1996; Volume 1, pp. 319–325. [Google Scholar]
- Sadeghian, O.; Oshnoei, A.; Tarafdar-Hagh, M.; Khezri, R. A clustering-based technoeconomic analysis for wind farm and shunt capacitor allocation in radial distribution systems. Int. Trans. Electr. Energy Syst. 2020, e12708. [Google Scholar] [CrossRef]
- Sadeghian, O.; Nazari-Heris, M.; Abapour, M.; Taheri, S.S.; Zare, K. Improving reliability of distribution networks using plug-in electric vehicles and demand response. J. Mod. Power Syst. Clean Energy 2019, 7, 1189–1199. [Google Scholar] [CrossRef]
- Ahrabi, M.; Abedi, M.; Nafisi, H.; Mirzaei, M.A.; Mohammadi-Ivatloo, B.; Marzband, M. Evaluating the effect of electric vehicle parking lots in transmission-constrained AC unit commitment under a hybrid IGDT-stochastic approach. Int. J. Electr. Power Energy Syst. 2021, 125, 106546. [Google Scholar] [CrossRef]
- Betz, R.E.; Jovanovic, M.G. Brushless Doubly Fed Reluctance Machines—A Tutorial. Available online: http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=A3A97ADF20F08F33FBE4EC88F8BB5029?doi=10.1.1.565.8777&rep=rep1&type=pdf (accessed on 16 November 2021).
- Hsieh, M.F.; Lin, I.H.; Dorrell, D. Magnetic circuit modeling of brushless doubly-fed machines with induction and reluctance rotors. IEEE Trans. Magn. 2013, 49, 2359–2362. [Google Scholar] [CrossRef]
- Jovanovic, M.; Betz, R.E. Optimal performance of brushless doubly fed reluctance machines. In Proceedings of the 9th International Conference on Electrical Machines and Drives, Canterbury, UK, 1–3 September 1999; pp. 386–390. [Google Scholar]
- Mehdipour, C.; Mohammadi, F.; Mehdipour, I. Analytical Approach to Nonlinear Behavior Study of an Electric Vehicle. In Proceedings of the 6th International Conference on Control, Instrumentation and Automation, Sanandaj, Iran, 30–31 October 2020; pp. 1–7. [Google Scholar]
- Liangzhou, J.; Xiangyu, Y. Optimization design on salient pole rotor of BDFRM using the Taguchi method. In Proceedings of the 4th International Conference on Power Electronics Systems and Applications, Hong Kong, China, 8–10 June 2011; pp. 1–4. [Google Scholar]
- Jovanović, M.G.; Yu, J.; Levi, E. A review of control methods for brushless doubly-fed reluctance machines. In Proceedings of the International Conference on Power Electronics, Machines and Drives, Sante Fe, NM, USA, 4–7 June 2002; pp. 528–533. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).