LSTM-Based Model Predictive Control for Optimal Temperature Set-Point Planning
Abstract
1. Introduction
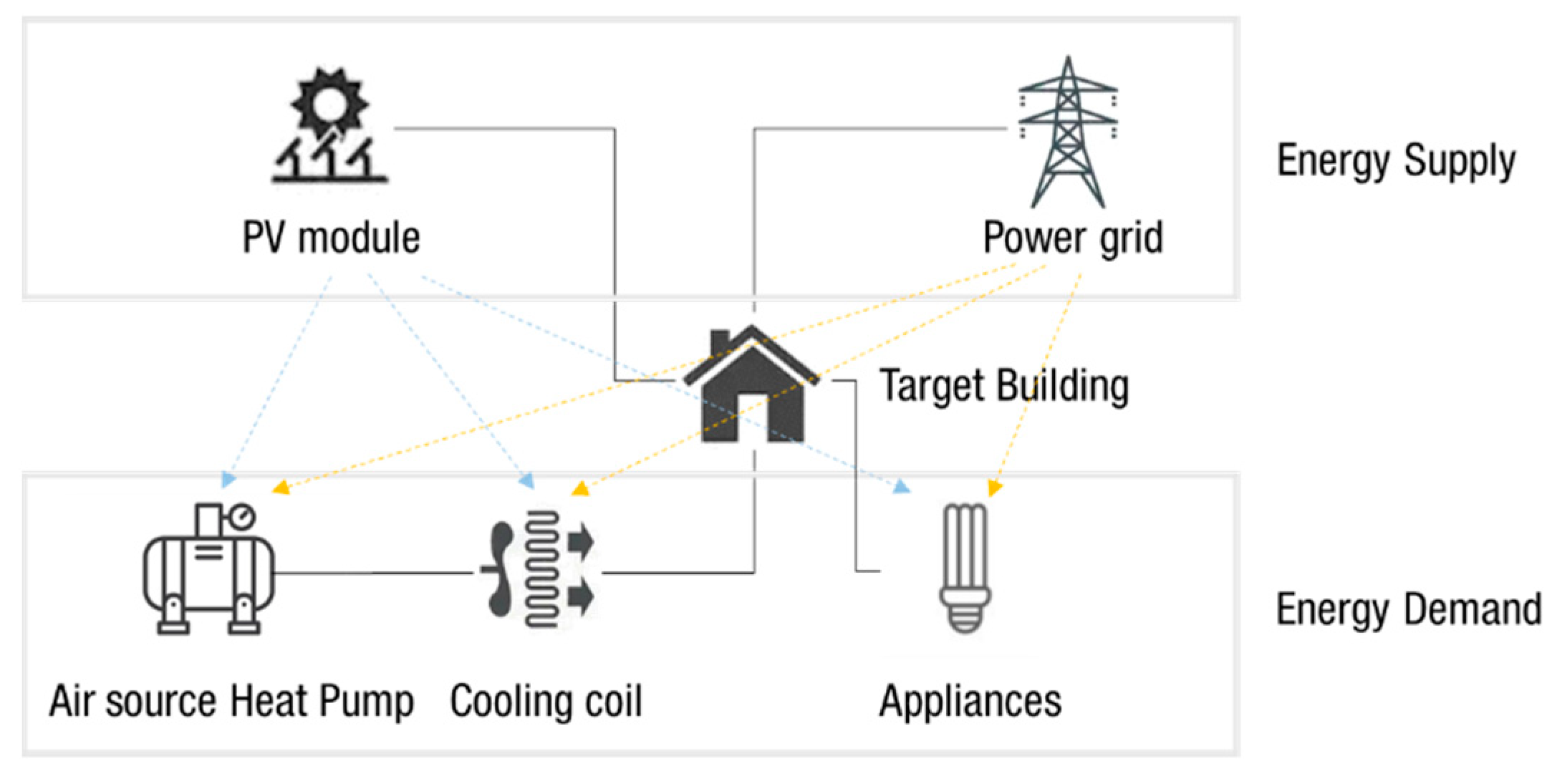
2. Simulation Model
3. Deep Learning-Based Building Energy Model (Proposed Model)
3.1. LSTM Network
3.2. Data-Driven LSTM Model
4. MPC Simulation
5. Simulation Results
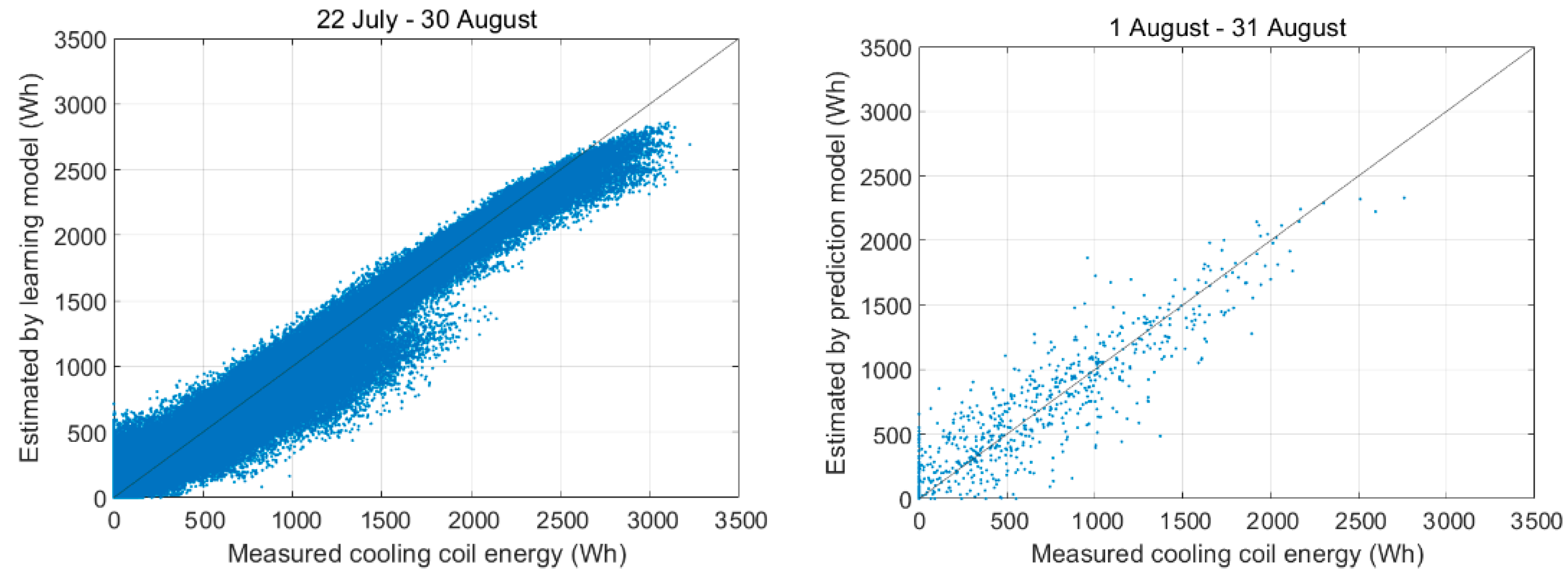
5.1. LSTM Model Verification
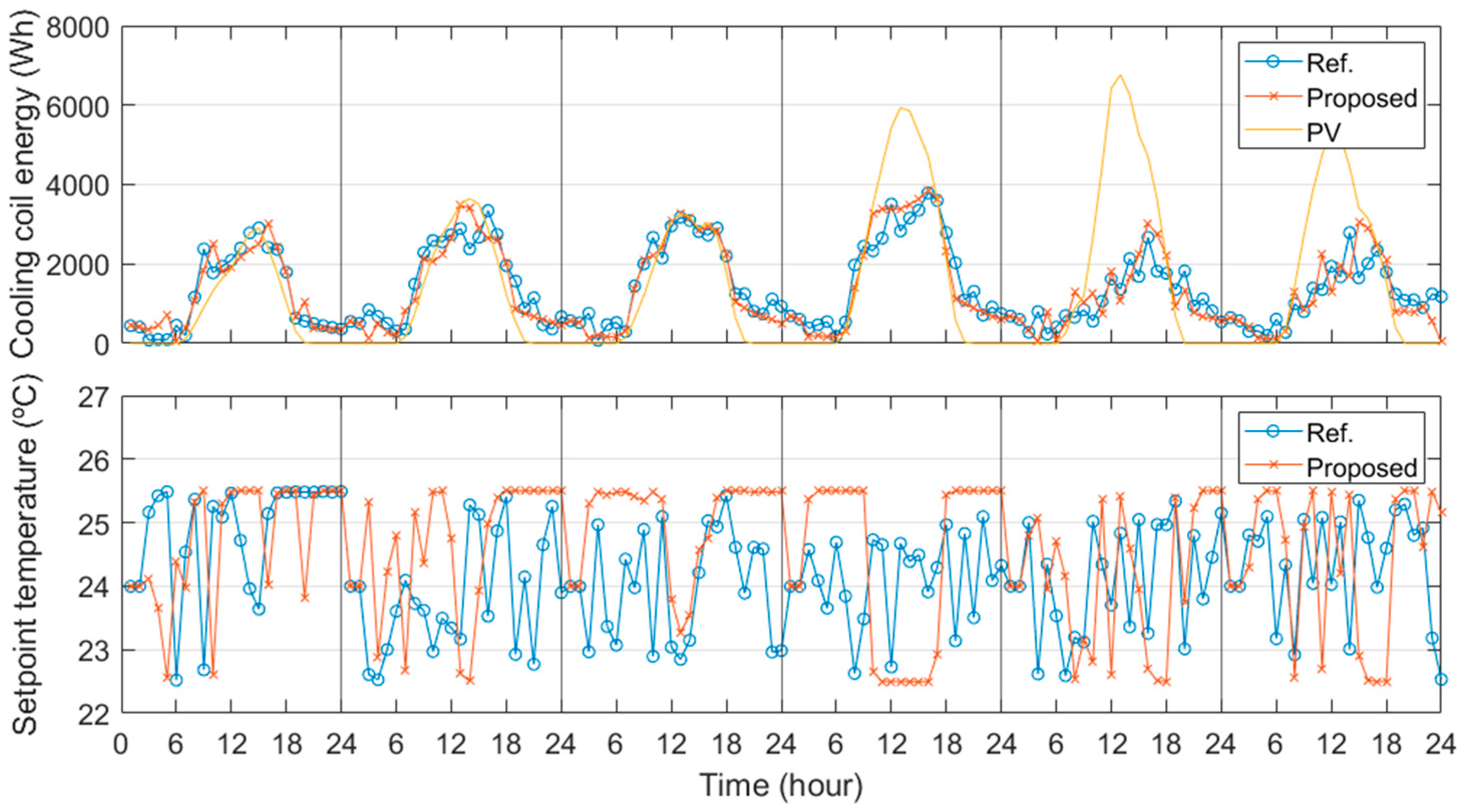
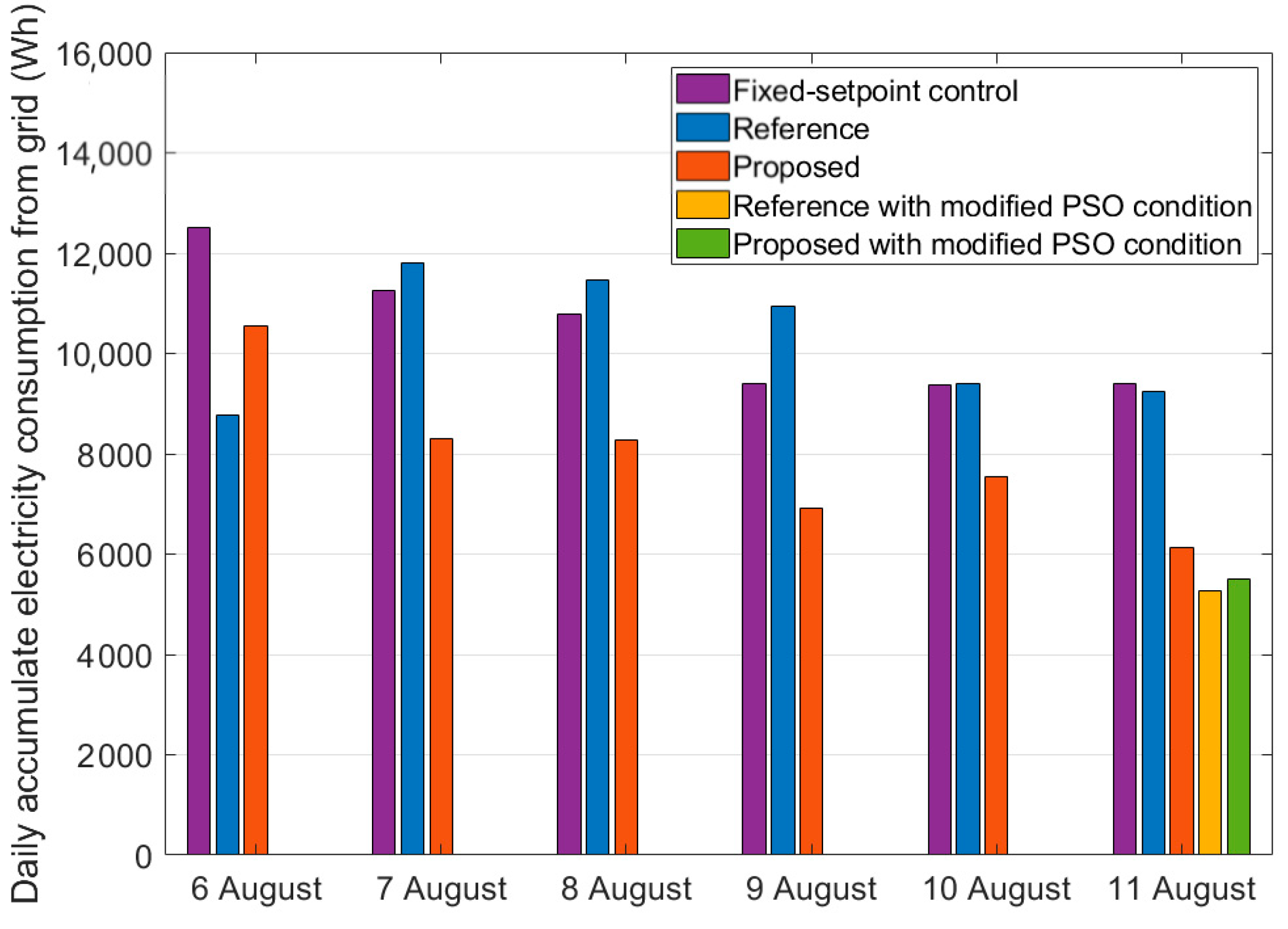
5.2. Optimization Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Subscript |
| f | function |
| Econsumption | Electricity consumption (Wh) |
| Egrid | Grid electricity consumption (Wh) |
| EPV | PV electricity production (Wh) |
| T | temperature (°C) |
| t | time (s) |
| v | value |
| obj | object |
| ref. | reference |
| t | time (hour) |
References
- Zhuang, J.; Chen, Y.; Chen, X. A new simplified modeling method for model predictive control in a medi-um-sized commercial building: A case study. Build. Environ. 2018, 127, 1–12. [Google Scholar] [CrossRef]
- Henze, G.P.; Felsmann, C.; Knabe, G. Evaluation of optimal control for active and passive building thermal storage. Int. J. Therm. Sci. 2004, 43, 173–183. [Google Scholar] [CrossRef]
- Verhelst, C.; Logist, F.; Van Impe, J.; Helsen, L. Study of the optimal control problem formulation for modulat-ing air-to-water heat pumps connected to a residential floor heating system. Energy Build. 2012, 45, 43–53. [Google Scholar] [CrossRef]
- Mbungu, N.T.; Naidoo, R.M.; Bansal, R.C. Real-time electricity pricing: TOU-MPC based energy manage-ment for commercial buildings. Energy Procedia 2017, 105, 3419–3424. [Google Scholar] [CrossRef]
- Joe, J.; Im, P.; Dong, J. Empirical modeling of direct expansion (DX) cooling system for multiple research use cases. Sustainability 2020, 12, 8738. [Google Scholar] [CrossRef]
- Ma, Y.; Borrelli, F.; Hencey, B.; Coffey, B.; Bengea, S.; Haves, P. Model Predictive Control for the Operation of Building Cooling Systems. IEEE Trans. Control. Syst. Technol. 2012, 20, 796–803. [Google Scholar]
- Prívara, S.; Široký, J.; Ferkl, L.; Cigler, J. Model predictive control of a building heating system: The first expe-rience. Energy Build. 2011, 43, 564–572. [Google Scholar] [CrossRef]
- Široký, J.; Oldewurtel, F.; Cigler, J.; Prívara, S. Experimental analysis of model predictive control for an energy efficient building heating system. Appl. Energy 2011, 88, 3079–3087. [Google Scholar] [CrossRef]
- Gyalistras, D.; Gwerder, M. Use of Weather and Occupancy Forecasts for Optimal Building Climate Control (Op-tiControl): Two Years Progress Report; Terrestrial Systems Ecology; ETH Zürich: Zürich, Switzerland; Building Technologies Division, Siemens Switzerland Ltd.: Zug, Switzerland, 2010. [Google Scholar]
- Nguyen, T.-T.; Yoo, H.-J.; Kim, H.-M. Analyzing the Impacts of System Parameters on MPC-Based Frequency Control for a Stand-Alone Microgrid. Energies 2017, 10, 417. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Theory and applications of HVAC control systems—A review of model predictive control (MPC). Build. Environ. 2014, 72, 343–355. [Google Scholar] [CrossRef]
- Khanmirza, E.; Esmaeilzadeh, A.; Markazi, A.H.D. Predictive control of a building hybrid heating system for energy cost reduction. Appl. Soft Comput. 2016, 46, 407–423. [Google Scholar] [CrossRef]
- Prívara, S.; Váňa, Z.; Žáčeková, E.; Cigler, J. Building modeling: Selection of the most appropriate model for predictive control. Energy Build. 2012, 55, 341–350. [Google Scholar] [CrossRef]
- Hoes, P.; Loonen, R.C.G.M.; Trcka, M.; Hensen, J. Performance Prediction of Advanced Building Controls in the Design Phase Using ESP-r, BCVTB and MATLAB; BSO12 (IBPSA-England): Loughborough, UK, 2012. [Google Scholar]
- Zhao, J.; Lam, K.P.; Ydstie, B.E.; Loftness, V. Occupant-oriented mixed-mode EnergyPlus predictive control simulation. Energy Build. 2016, 117, 362–371. [Google Scholar] [CrossRef]
- Hilliard, T.; Swan, L.; Kavgic, M.; Qin, Z. Applying model predictive control to a LEED silver-certified build-ing. Energy Procedia 2015, 78, 1817–1822. [Google Scholar] [CrossRef]
- Bruni, G.; Cordiner, S.; Mulone, V.; Rocco, V.; Spagnolo, F. A study of energy management in domestic mi-cro-grids based on model predictive control strategies. Energy Procedia 2014, 61, 1012–1016. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F.; Fung, A.S.; Raahemifar, K. Artificial neural network (ANN) based model predic-tive control (MPC) and optimization of HVAC systems: A state of the art review and case study of a residential HVAC system. Energy Build. 2017, 141, 96–113. [Google Scholar] [CrossRef]
- Dounis, A.; Caraiscos, C. Advanced control systems engineering for energy and comfort management in a building environment—A review. Renew. Sustain. Energy Rev. 2009, 13, 1246–1261. [Google Scholar] [CrossRef]
- Huang, H.; Chen, L.; Hu, E. A new model predictive control scheme for energy and cost savings in commercial buildings: An airport terminal building case study. Build. Environ. 2015, 89, 203–216. [Google Scholar] [CrossRef]
- Lu, L.; Cai, W.; Xie, L.; Li, S.; Soh, Y.C. HVAC system optimization—In-building section. Energy Build. 2005, 37, 11–22. [Google Scholar] [CrossRef]
- Ning, M.; Zaheeruddin, M. Neuro-optimal operation of a variable air volume HVAC&R system. Appl. Therm. Eng. 2010, 30, 385–399. [Google Scholar]
- Kusiak, A.; Xu, G.; Tang, F. Optimization of an HVAC system with a strength multi-objective particle-swarm algorithm. Energy 2011, 36, 5935–5943. [Google Scholar] [CrossRef]
- Kusiak, A.; Xu, G.; Zhang, Z. Minimization of energy consumption in HVAC systems with data-driven models and an interior-point method. Energy Convers. Manag. 2014, 85, 146–153. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Kim, M.; Hong, C. The Artificial Neural Network based Electric Power Demand Forecast using a Season and Weather Informations. J. Inst. Electron. Inf. Eng. 2016, 53, 71–78. [Google Scholar]
- Li, X.; Wen, J. Review of building energy modeling for control and operation. Renew. Sustain. Energy Rev. 2014, 37, 517–537. [Google Scholar] [CrossRef]
- Fabrizio, E.; Monetti, V. Methodologies and advancements in the calibration of building energy mod-els. Energies 2015, 8, 2548–2574. [Google Scholar] [CrossRef]
- Taheri, M.; Tahmasebi, F.; Mahdavi, A. A case study of optimization-aided thermal building performance sim-ulation calibration. Optimization 2012, 4, 603–607. [Google Scholar]
- Kim, W.; Jeon, Y.; Kim, Y. Simulation-based optimization of an integrated daylighting and HVAC system using the design of experiments method. Appl. Energy 2016, 162, 666–674. [Google Scholar] [CrossRef]
- Shin, Y.; Kim, E.-J.; Lee, K.-H. Optimal Cooling Operation of a Single Family House Model Equipped with Renewable Energy Facility by Linear Programming. Korean J. Air Cond. Refrig. Eng. 2017, 29, 638–644. [Google Scholar]
- Jeon, B.-K.; Kim, E.-J.; Shin, Y.; Lee, K.-H. Learning-Based Predictive Building Energy Model Using Weather Forecasts for Optimal Control of Domestic Energy Systems. Sustainability 2018, 11, 147. [Google Scholar] [CrossRef]
- Dobos, A.P. PVWatts Version 5 Manual; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014.
- Schuster, M.; Paliwal, K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Somu, N.; MR, G.R.; Ramamritham, K. A hybrid model for building energy consumption forecasting us-ing long short term memory networks. Appl. Energy 2020, 261, 114131. [Google Scholar] [CrossRef]
- Muzaffar, S.; Afshari, A. Short-Term Load Forecasts Using LSTM Networks. Energy Procedia 2019, 158, 2922–2927. [Google Scholar] [CrossRef]
- Kim, T.-Y.; Cho, S.-B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Documentation, M.A.T.L.A.B. Matlab Documentation. Matlab, R2012b. 2012. Available online: https://www.mathworks.com/help/matlab/ (accessed on 17 January 2021).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference Learn, Represent, (ICLR), San Diego, CA, USA, 5–8 May 2015. [Google Scholar]
- Guide, A. Guide for Using EnergyPlus with External Interface (s); US Department of Energy: Washington, DC, USA, 2011.
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Zhang, Y.; Wang, S.; Ji, G. A comprehensive survey on particle swarm optimization algorithm and its applica-tions. Math. Probl. Eng. 2015, 2015, 1–38. [Google Scholar]
- Wu, X.; Dai, J.; Zhao, Y.; Zhuo, Z.; Yang, J.; Zeng, X.C. Two-Dimensional Boron Monolayer Sheets. ACS Nano 2012, 6, 7443–7453. [Google Scholar] [CrossRef]
- Tambouratzis, G. Using Particle Swarm Optimization to Accurately Identify Syntactic Phrases in Free Text. J. Artif. Intell. Soft Comput. Res. 2018, 8, 63–77. [Google Scholar] [CrossRef]
- Jeon, B.-K.; Kim, E.-J. Next-Day Prediction of Hourly Solar Irradiance Using Local Weather Forecasts and LSTM Trained with Non-Local Data. Energies 2020, 13, 5258. [Google Scholar] [CrossRef]
- Lu, H.; Chang, G.W. A Hybrid Approach for Day-Ahead Forecast of PV Power Generation. IFAC PapersOnLine 2018, 51, 634–638. [Google Scholar] [CrossRef]
- Ashrae, A. ANSI/ASHRAE 55–2010 Thermal Environmental Conditions for Human Occupancy; American Society of Heating, Refrigerating and Air-Conditioning Engineering: Atlanta, GA, USA, 2010. [Google Scholar]





| Parameter | Value | ||
|---|---|---|---|
| PV-1 | PV-2 | PV-3 | |
| DC System Capacity (kW) | 4 | 3 | 3 |
| Tilt Angle (°) | 20 | 37 | 37 |
| Inverter Efficiency (%) | 96 | 96 | 96 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Optimization Algorithm | Adam | Hidden layer | 3 |
| Initial Learn Rate | 0.001 | Hidden unit | 300 (×3) |
| Execution Environment | GPU (RTX 2080ti) | Max epochs | 200 |
| Parameter | Data (Learning/Prediction) | |
|---|---|---|
| Input | Solar irradiance, outdoor temperature, setpoint temperature (random), humidity, time of day (1–24 h) | 240 h/24 h |
| Output | Energy consumption of cooling coil |
| Parameter | 6 August | 7 August | 8 August | 9 August | 10 August | 11 August |
|---|---|---|---|---|---|---|
| Learning performance (CVRMSE/%) | 4.15 | 5.32 | 3.55 | 3.21 | 2.85 | 4.55 |
| Prediction performance-Day (CVRMSE/%) | 26.80 | 10.57 | 9.64 | 9.75 | 16.96 | 14.52 |
| Prediction performance—7 to 18 h (CVRMSE/%) | 19.92 | 4.46 | 5.14 | 8.97 | 11.01 | 12.80 |
| Day | Model | Grid Energy Consumption (Wh) | Average Indoor Temp (°C) | Unused PV Energy (Wh) | Simulation Time (min) |
|---|---|---|---|---|---|
| 6 August | Fixed setpoint | 12,497.1 | 24 | 0 | - |
| Reference | 8762.4 | 24.8 | 0 | 111.1 | |
| Proposed | 13,170.1 | 24.7 | 1057.6 | 20.9 | |
| 7 August | Fixed setpoint | 11,245.3 | 24 | 2508.0 | - |
| Reference | 11,808.8 | 23.8 | 3258.5 | 122.5 | |
| Proposed | 10,597.0 | 24.6 | 2213.5 | 20.3 | |
| 8 August | Fixed setpoint | 10,778.7 | 24 | 1047.3 | - |
| Reference | 11,467.7 | 24.0 | 1092.0 | 102.5 | |
| Proposed | 8121.3 | 25.0 | 281.5 | 53.0 | |
| 9 August | Fixed setpoint | 9406.2 | 24 | 26,676.7 | - |
| Reference | 10,935.0 | 24.1 | 13,627.8 | 125.7 | |
| Proposed | 6209.4 | 24.3 | 10,879.9 | 51.7 | |
| 10 August | Fixed setpoint | 9368.8 | 24 | 27,443.1 | - |
| Reference | 9389.8 | 24.1 | 28,173.5 | 126.9 | |
| Proposed | 4375.8 | 24.1 | 25,805.2 | 22.6 | |
| 11 August | Fixed setpoint | 9398.1 | 24 | 19,583.4 | - |
| Reference | 9228.8 | 24.3 | 19,969.2 | 127.3 | |
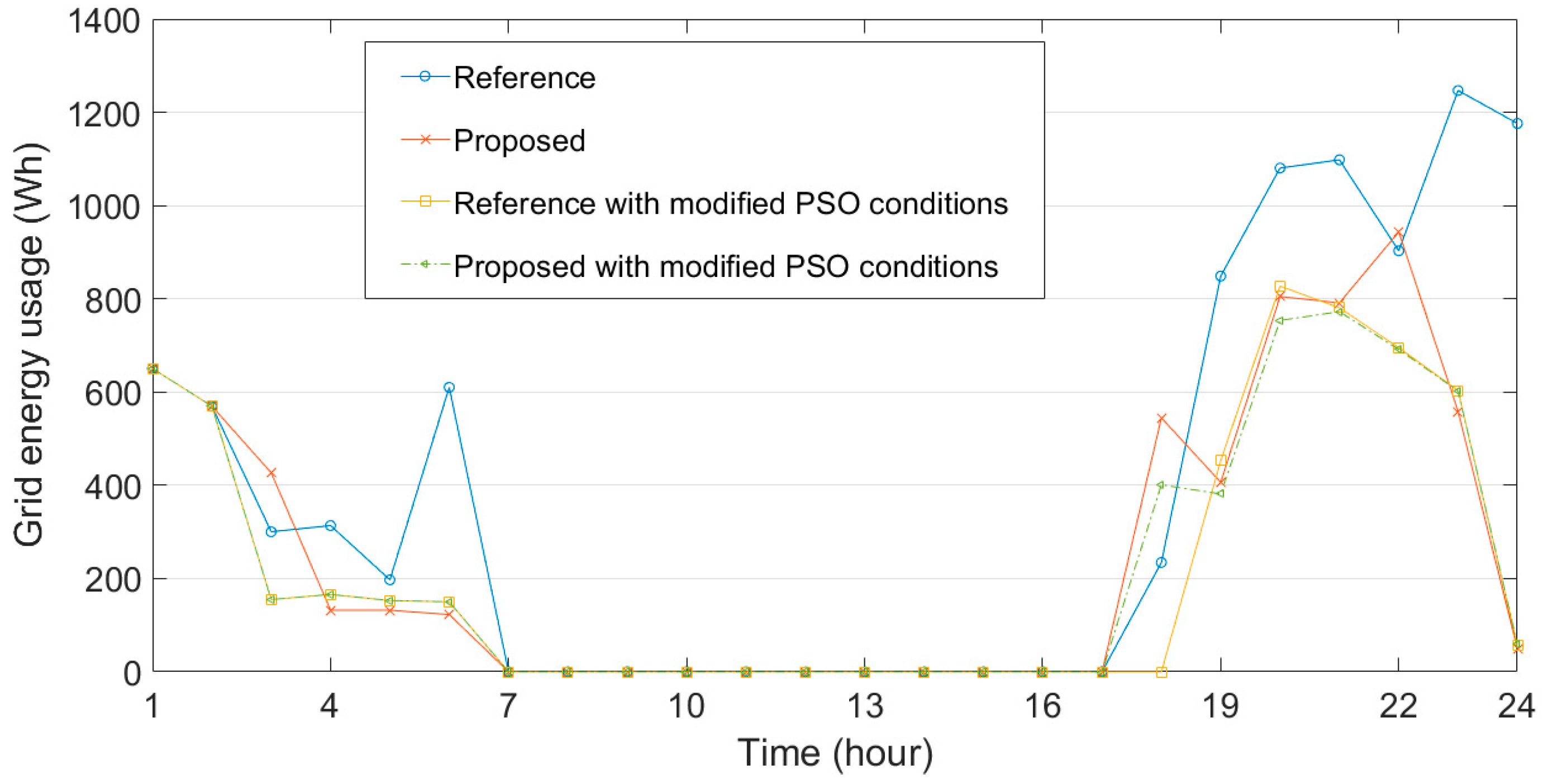
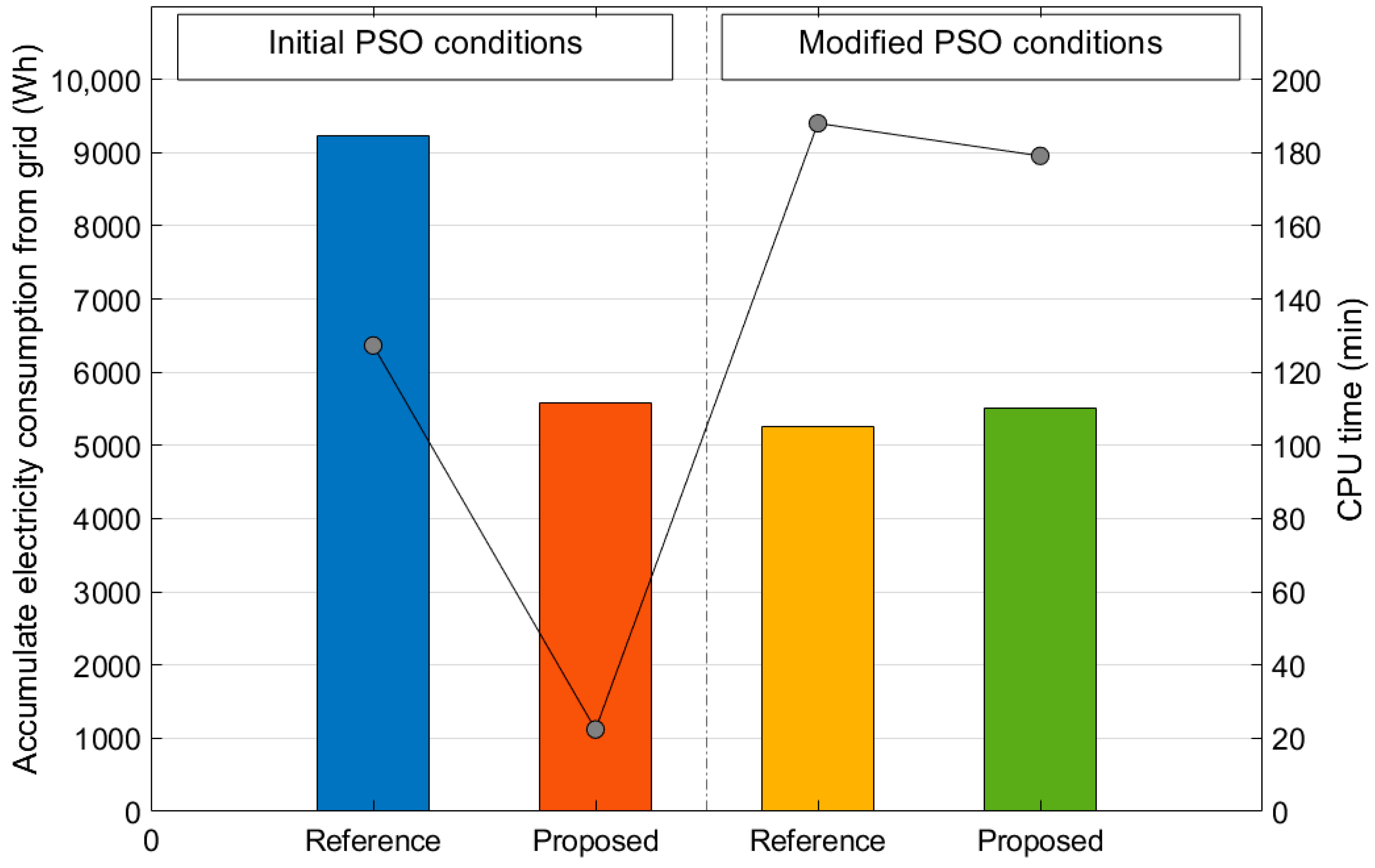
| Proposed | 5585.7 | 24.4 | 18,119.4 | 22.4 | |
| Reference (modified PSO conditions) | 5259.0 | 23.9 | 17,148.4 | 188.0 | |
| Proposed (modified PSO conditions) | 5504.9 | 24.3 | 17,436.7 | 179.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, B.-K.; Kim, E.-J. LSTM-Based Model Predictive Control for Optimal Temperature Set-Point Planning. Sustainability 2021, 13, 894. https://doi.org/10.3390/su13020894
Jeon B-K, Kim E-J. LSTM-Based Model Predictive Control for Optimal Temperature Set-Point Planning. Sustainability. 2021; 13(2):894. https://doi.org/10.3390/su13020894
Chicago/Turabian StyleJeon, Byung-Ki, and Eui-Jong Kim. 2021. "LSTM-Based Model Predictive Control for Optimal Temperature Set-Point Planning" Sustainability 13, no. 2: 894. https://doi.org/10.3390/su13020894
APA StyleJeon, B.-K., & Kim, E.-J. (2021). LSTM-Based Model Predictive Control for Optimal Temperature Set-Point Planning. Sustainability, 13(2), 894. https://doi.org/10.3390/su13020894





