Eco-Efficiency for the G18: Trends and Future Outlook

Abstract

Eco-efficiency is an important ecological indicator for tracking the progress of how countries’ environmental-adjusted economic activity changes over time. The objective of this research is to calculate country-level eco-efficiency for a group of 18 major countries (G18) that are part of the G20. First, the data envelope analysis (DEA) method is used to calculate eco-efficiency scores. Second, the Malmquist productivity index (MPI) is used to examine how eco-efficiency changes over time. Eco-efficiency is forecast to the year 2040 using automated forecasting methods under a business-as-usual (BAU) scenario. Over the period 1997 to 2040, eco-efficiency varies widely between these countries with some countries reporting positive growth in eco-efficiency and other countries reporting negative growth. Eco-efficiency leaders over the period 1997 to 2019 and 2019 to 2040 include Australia, Brazil, France, Germany, Great Britain, Italy, Japan, Russia, and the United States. Laggards include Canada, China, India, and Indonesia. These laggard countries recorded negative growth rates in eco-efficiency over the period 1997 to 2019 and 2019 to 2040. Negative eco-efficiency growth points to a worsening of environmental sustainability. Large variations in eco-efficiency between countries make it more difficult to negotiate international agreements on energy efficiency and climate change. For the G18 countries, the average annual change in MPI over the period 1997 to 2019 was 0.5%, while the forecasted average annual change over the period 2019 to 2040 was a 0.1% decrease. For the G18 countries, there has been little change in eco-efficiency. The G18 are an important group of developed and developing countries that need to show leadership when it comes to increasing eco-efficiency.

1. Introduction

Ecological efficiency (eco-efficiency) at the country level is an important ecological indicator for tracking the progress of how countries’ environmental-adjusted economic activity changes over time [1,2]. The basic idea of eco-efficiency is to produce more goods and services while using fewer material inputs and generating less waste and pollution. In 1992, the World Business Council for Sustainable Development released their landmark publication “Changing Course”, which introduced the terminology of eco-efficiency [2]. In the context of climate change at the country level, the eco in eco-efficiency often refers to CO₂ emissions, and this is the definition used in this paper. CO₂ emissions is an important indicator in discussions on climate change and transitioning to a low-carbon economy [1,3,4,5]. A positive trend in eco-efficiency indicates that eco-efficiency is increasing over time, while a negative trend indicates that eco-efficiency is decreasing over time. Eco-efficiency can be calculated using either non-parametric techniques such as data envelope analysis (DEA) or parametric methods such as stochastic frontier analysis (SFA) [6]. As discussed below, each method has its advantages and disadvantages. Changes in eco-efficiency over time can be analyzed using a Malmquist productivity index (MPI) [1,5,7]. The existing literature on eco-efficiency MPI at the country level reveals there is much room for improving eco-efficiency [1,5,7].

While the existing literature has calculated eco-efficiency at the country level, there are still some important unanswered questions. How does eco-efficiency compare across a large group of CO₂-emitting countries? Which countries are experiencing improvements in eco-efficiency over time, and which countries are experiencing decreases? What does the future trend in eco-efficiency look like?

The purpose of this present paper is to estimate and forecast changes in eco-efficiency over time using the Malmquist productivity index (MPI) for a group of 18 large polluting countries. These 18 countries along with Saudi Arabia and the European Union form the group of countries known collectively as the G20. The G20 is an important group of countries that accounts for 85% of global economic output, two-thirds of the world’s population, and 75% of international trade [8]. Comprised of important developed and developing countries that span the world, participation and leadership from the G20 is vital for international energy and climate change policy [9]. DEA is used to calculate eco-efficiency, and MPI used to calculate eco-efficiency over time. DEA is a non-parametric approach that does not specify a parametric functional form between the inputs and outputs nor does it consider noise in the data [10,11]. SFA is an alternative approach to estimating eco-efficiency and energy efficiency that requires an explicit parametric functional form and allows for noise in the data [12,13,14,15]. Many existing studies of eco-efficiency use DEA because it is a more flexible approach, and this is the method used in this paper [10]. The DEA provides efficiency values for each year. Efficiency is a level concept, and measures of efficiency can be used to compare the performance of countries at a given point in time. Efficiency changes (or productivity changes) refer to movements in the efficiency or productivity of a country over time. To see how efficiency changes across time, these efficiency values are chained together using MPI [1,5,7]. The MPI is the product of an efficiency change component and a technical change component. The efficiency change component measures how a country’s efficiency changes between time periods, and the technical change component refers to the movement of the efficient frontier between time periods. The analysis is conducted for the period 1996 to 2040. Actual data are used for the period 1996 to 2019, and forecasts are used for the period 2020 to 2040. Forecasts of eco-efficiency are made under a business as usual (BAU) scenario that assumes no major changes in economic structural or policy changes.

The analysis from this paper reveals some interesting results. Over the period 1997 to 2040, eco-efficiency varies widely between these countries with some countries reporting positive growth in eco-efficiency and other countries reporting negative growth. Eco-efficiency leaders over the sub-periods (1997 to 2019 and 2019 to 2040) include Australia, Brazil, France, Germany, Great Britain, Italy, Japan, Russia, and the United States. Laggards include Canada, China, India, and Indonesia. These laggard countries recorded negative growth rates in over the period 1997 to 2019 and 2019 to 2040. Negative eco-efficiency growth is particularly troublesome because it reflects a worsening of environmental sustainability. Large variations in eco-efficiency between countries make it more difficult to negotiate international agreements on energy efficiency and climate change.

This paper is organized as follows. The following sections of the paper set out the literature review, the methods and data, results, and discussion. The last section of the paper provides the conclusions and some policy implications.

2. Literature Review

This section presents a brief review of the literature on using DEA to estimate eco-efficiency at the country level. Bianchi et al. [16] use DEA and metafrontier analysis to measure eco-efficiency in 282 European regions for the period 2006 to 2014. For inputs, they use the employment rate and domestic material consumption per capita. The output variable is GDP per capita. They find evidence of an upward trend in eco-efficiency across European regions, although there is no evidence that regions are converging to similar levels of eco-efficiency. Halkos and Tzeremes [17] use DEA to calculate environmental efficiency for 17 OECD countries over the period 1980 to 2002. The main focus of their research is to test whether a Kuznet’s-like hypothesis exists between environmental efficiency and income. The capital stock and labor are used as inputs to the DEA model, GDP is the desirable output, and sulfur emissions is the undesirable output. They do not find evidence of such a relationship. Hsieh et al. [18] use DEA to estimate the energy and environmental efficiency of 29 EU countries for the period 2006 to 2013. In their DEA analysis, labor, capital, and energy consumption are inputs. GDP is the desirable output and greenhouse gas emissions and sulfur oxide emission are undesirable outputs. About half of the countries have room for environmental performance improvements. Environmental performance is higher in the latter part of the sample period. Somewhat surprising in this study is that Great Britain, Germany, France, and Italy have relatively low environmental efficiency scores due to their greenhouse gas emissions and SO₂ emissions. Iftikhar et al. [19] use slacks-based (SBM) DEA to estimate energy and CO₂ emissions efficiency for 26 major countries for the years 2013 and 2014. The inputs are capital, labor, and energy consumption, while the desirable and undesirable outputs are GDP and carbon dioxide emissions, respectively. Larger countries with raw material intense production, and weak carbon laws are the least efficient. In particular, China, India, and Russia have much room for improvement in eco-efficiency. Lacko and Hajduova [20] study environmental efficiency among 26 EU countries covering the years 2008 to 2016. CO₂ per capita, methane per capita, and nitrous oxide per capita are the inputs and the output is GDP per capita. Eastern European countries tend to have low environmental efficiency and England and Sweden have high environmental efficiency. Climate change and socioeconomic factors are important drivers of environmental efficiency. Lozowicka [7] uses SBM DEA to analyze ecological efficiency and MPI in selected EU member states for the years 2005, 2010, and 2015. The input variables include the share of non-renewable energy, the percentage of the population not connected to wastewater treatment systems, the non-forested land ratio, and the unprotected area relative to the area of the country. The output variables include biochemical oxygen demand, the balance of nutrients, index of clean energy, and population exposed to PM2.5 air pollution. Northern Europe states have the highest eco-efficiency, while Central and Eastern Europe states have the least. Marti and Puertas [21] study the efficiency of the ecological footprint and biocapacity of 45 African countries. They use a variable returns DEA model with ecological footprint and population as the inputs and GDP as the output. Countries are divided into two groups. One group has a biocapacity surplus while the other has a deficit. Among the deficit countries, Gambia, South Africa, Swaziland, Mauritius, and Nigeria are efficient. Angola, Gabon, and Guinea-Bissau are surplus countries with high efficiency. Moutinho and Madaleno [22] use DEA to study eco-efficiency for 27 European Union (EU) countries over the period 2008 to 2018. They use a two-step estimation approach where in the first step, eco-efficiency scores are estimated, and in the second step, a fractional regression is used to estimate the impact of pollutants per area on eco-efficiency. The output variable is the ratio of GDP per capita to greenhouse gas emissions per area. The input variables are capital per capita, labor per capita, energy use per area, electricity use per area, and a temperature variable. From the second step regression, increases in CO₂/area and CH₄/area decrease eco-efficiency. Moutinho et al. [4] use constant returns to scale (CRS) and variable returns to scale (VRS) DEA to study environmental efficiency for 26 European countries. The DEA input variables include labor productivity, capital productivity, and non-fossil fuel energy share. The output variable is GDP per greenhouse gas emissions. The shares of renewable energy and non-renewable energy sources are important factors explaining differences in country-level environmental efficiency. Moutinho et al. [5] use CRS and VRS DEA and MPI to study eco-efficiency in 16 Latin American countries for the time period 1994 to 2013. The input variables include energy use, population density, labor productivity, renewable energy consumption share, and capital productivity. The output variable is the ratio of GDP to CO₂ emissions. For most countries, the degree of technical efficiency is lower than the degree of technological efficiency, indicating that some of the overall inefficiency is due to producing below the production frontier. Sarkhosh-Sara et al. [23] use network DEA to measure the sustainability of three groups of countries (high, middle, and low income). In total, 97 developed and developing countries are studied for the year 2011. The first stage DEA uses labor, capital, and energy as inputs. GDP is the desirable output, and CO₂ emissions is the undesirable output. For the second stage of the network analysis, GDP and population are used as inputs and income class is used as the output variable. Countries with high and low incomes perform well in the sustainable production stage but are weak performers in the sustainable distribution stage. Middle-income countries rank low on sustainable production but are strong performance in the sustainable distribution stage. Tsai et al. [24] use DEA-based meta frontier analysis to compare environmental efficiency between 37 European and 36 Asian countries. The input variables include the labor force, energy consumption, and government expenditures. The desirable output is GDP, and the undesirable output is CO₂ emissions. Mean meta-efficiency tends to be higher in European countries. Twum et al. [3] use DEA to calculate environmental efficiency for three Asia-Pacific regions. The desirable output is GDP and the undesirable output is CO₂ emissions. The input variables are the share of renewable energy and total patent applications. They find that East Asia is highly efficient, while South East Asia is the least efficient. They find evidence of an inverted U-shaped relationship between environmental efficiency and technological innovation. Wang et al. [1] use slacks-based DEA and MPI to investigate eco-efficiency for 17 European countries for the years 2013 to 2017. The desirable output variable is GDP per capita and the undesirable output is CO₂ emissions per capita. The input variables are energy consumption per capita, labor productivity, share of renewable energy consumption, and capital formation productivity. Nine of the 17 countries were found to have an eco-efficiency score of 1. As a group, the countries lacked eco-efficiency over the period 2013 to 2017. The lack of eco-efficiency comes mostly from a lack of technological progress.

In summary, while there is literature studying eco-efficiency at the country level for various groups of countries, there is no study that explicitly focuses on G18 eco-efficiency and how G18 eco-efficiency will evolve into the future.

3. Methods and Data

3.1. The DEA Method

DEA is a popular approach for analyzing eco-efficiency [6]. In order to account for non-radial adjustments in the inputs and outputs, a DEA slack-based model (SBM) is used [25]. The output variable is production-based CO₂ productivity as measured by the ratio of output to CO₂ emissions [5,26] and the four inputs are the capital to labor ratio, the output to labor ratio, the capital to energy ratio, and the share of non-fossil fuels in energy consumption. This choice of variables is based on related work that estimates ecological efficiency at the country level [4,5].

The basic set up of the model is as follows. The four inputs and output are represented by $x\in R^m$ and $y\in R^{s1}$, respectively. For a collection of n DMUs, define the following matrices: $X=\left[x_1,\dots ,x_n\right]\in R^{m x n}$ and $Y=\left[y_1,\dots ,y_n\right]\in R^{s x n}$. Assume that X > 0 and Y > 0.

The production possibility set, P, is:

$$P=\left\{\left(x,y\right)\right|x\ge X\lambda , y \le Y\lambda ,\lambda \ge 0\}.$$

(1)

In Equation (1), the intensity vector is λ, and P corresponds to constant returns to scale (CRS) technology. Variable returns to scale can be obtained by adding the constraint that the sum of the elements in λ equal unity. A DMU $\left(x_0,y_0\right)$ is efficiency if there is no vector $\left(x,y \right)\in P$ such that $x_0\ge x$ and $y_0\le y$ and there is at least one strict inequality. The SBM is:

$$\left[SBM\right] \epsilon =min\frac{1-\frac{1}{m}{\sum }_{i=1}^m\frac{s_i^{-}}{x_{i0}}}{1+\frac{1}{s} {\sum }_{i=1}^S\frac{s_r^{+}}{y_{i0}^{}}}.$$

(2)

Subject to:

$$x_0=X\lambda +s^{-}$$

(3)

$$y_0=Y\lambda -s^{+}$$

(4)

$$s^{-}\ge 0, s^{+}\ge 0,\lambda \ge 0.$$

(5)

The vectors $s^{-}$ and s⁺ refer to the excess in inputs and the shortage of output, respectively. The objective function in (2) satisfies $0<\mathsf{\epsilon }\le 1$. Eco-efficiency is represented by ε with higher values indicating a higher level of eco-efficiency.

Changes in eco-efficiency over time can be estimated using the Malmquist productivity index (MPI) [27,28]. The MPI is the product of a catch-up effect and a frontier-shift effect [7]. The catch-up effect refers to how much a DMU improves or worsens its efficiency over time and is sometimes referred to as the efficiency change component (EFFCH). The frontier-shift effect is the change in the efficient frontier over time and is sometimes referred to as the technical change component (TECH).

$$MPI=\left(Catch-up\right)\left(Fronter-shift\right)$$

(6)

$$Catch-up=\frac{\epsilon of DM{U}_0^{t+1} wrt period t+1 frontier}{\epsilon of DM{U}_0^t wrt period t frontier}{ }^{}$$

(7)

$$\begin{gathered} Frontier-shift= \\ =\sqrt{\frac{\epsilon of DM{U}_0^t wrt period t frontier}{\epsilon of DM{U}_0^t wrt period t+1 frontier}·\frac{\epsilon of DM{U}_0^{t+1} wrt period t frontier}{\epsilon of DM{U}_0^{t+1} wrt period t+1 frontier}} \end{gathered}$$

(8)

In Equations (7) and (8), the combination of letters wrt denotes “with respect to”. A change in catch-up greater than unity means that the efficiency of a DMU in period t + 1 is greater than the efficiency in period t. Thus, there has been a relative improvement in efficiency. A change in frontier shift greater than unity means that the efficient frontier in period t + 1 is higher than in period t. This indicates technological innovation. Total productivity change is the product of catch-up and frontier-shift. The DEA estimations in this paper were done using the R programing language [29] and the DJL package [30].

3.2. Forecasting

In order to provide forecasts of eco-efficiency to the year 2040, forecasts of the DEA inputs and output need to be made. Since the data have a relatively short time span (annual data from 1996 to 2019), methods suited to forecasting short time series data sets are used. These methods include ETS, ARIMA, TBATS, and THETA [31]. ETS, which is based on exponential smoothing, is a state-space model with error (E), trend (T), and seasonal (S) components. The tradeoff between these components is controlled by smoothing parameters, and the optimal smoothing parameters can be determined using an automatic search algorithm. ARIMA is the acronym for autoregressive integrated moving average. While ETS models describe the trend and seasonality in the data, ARIMA models describe the autocorrelations in the data. The selection of the best-fitting ARIMA model can be easily achieved through a search algorithm. ETS and ARMA models are widely used in forecasting. The TBATS refers to an exponential smoothing state space model with Box-Cox transformations, ARMA error, trend and seasonal components. TBATS is estimated using a fully automatic modeling approach. The THETA model is equivalent to simple exponential smoothing with drift. The ETS, ARIMA, TBATS, and THETA models can be considered as examples of machine learning, since for each model, a fully automated search algorithm is used to find the best-fitting model. In order to reduce the dependence on forecasts from any one model, an average forecast is computed. Averaging forecasts often works well in practice [31]. The average forecast from these methods is referred to as the business as usual (BAU) scenario. Forecasting was done using the R package fpp2 [32].

The approach taken to forecasting in this paper is similar to the approach taken by international agencies such as the International Energy Agency (IEA) in their World Energy Outlook [33] and the US Energy Information Agency (EIA) in their Annual Energy Outlook [34] where they make long-term projections (20–30 years or so) for energy demand. A reference case, base case, or business as usual (BAU) scenario is taken as the benchmark where past data trends are assumed to continue into the future, and policy assumptions are assumed to be fixed. The forecasting methods used in this paper are useful for creating forecasts under a BAU scenario.

3.3. Data

Country-level data on CO₂ emissions, GDP, labor, capital, energy consumption, and non-fossil fuel energy consumption are required for the analysis. Data on GDP (real GDP in millions of 2011 US dollars: gdpna), capital (capital stock in millions of 2011 US dollars: rnna), and labor force (number of persons employed in millions: emp) come from the Penn World Tables (PWT 9.1) [35]. Data on CO₂ emissions (millions of tonnes) from the consumption of energy, energy (fossil fuel and non-fossil fuel) consumption (Exajoules), and non-fossil fuel energy consumption (Exajoules) come from the BP Statistical Review [36]. CO₂ emissions from the consumption of energy include emissions that result from the consumption of petroleum, natural gas, and coal and from natural gas flaring. Total energy consumption includes coal, natural gas, petroleum and other liquids, nuclear, renewables, and other. The 18 countries included in this study include Argentina (ARG), Australia (AUS), Brazil (BRA), Canada (CAN), China (CHN), France (FRA), Germany (DEU), India (IND), Indonesia (IDN), Italy (ITA), Japan (JPN), South Korea (KOR), Mexico (MEX), Russia (RUS), South Africa (ZAF), Turkey (TUR), Great Britain (GBR), and the United States of America (USA). These 18 countries along with the European Union and Saudi Arabia form the group of countries known as the G20. The dataset covers the years 1996 to 2019. Saudi Arabia is not included in the analysis because the share of non-fossil fuel energy is very low (close to zero). The dataset starts in 1996 to accommodate the breakup of the Former Soviet Union in 1991 and the turmoil that followed for those countries involved.

The inputs to the DEA analysis are the capital to labor ratio (klratio), output to labor ratio (ylratio), capital to energy ratio (keratio), and non-fossil fuel share of energy (nffshare). The output variable in the DEA analysis is labeled eco and is measured by GDP/CO₂ emissions.

The time-series pattern of production-based CO₂ productivity varies considerably between countries (Figure 1, Figure 2 and Figure 3). Actual data are recorded up to and including 2019, after which time forecasts are shown (Figure 1, Figure 2 and Figure 3;

Table 1. Summary statistics for GDP/CO₂ (US dollars per tonne of CO₂ emissions).

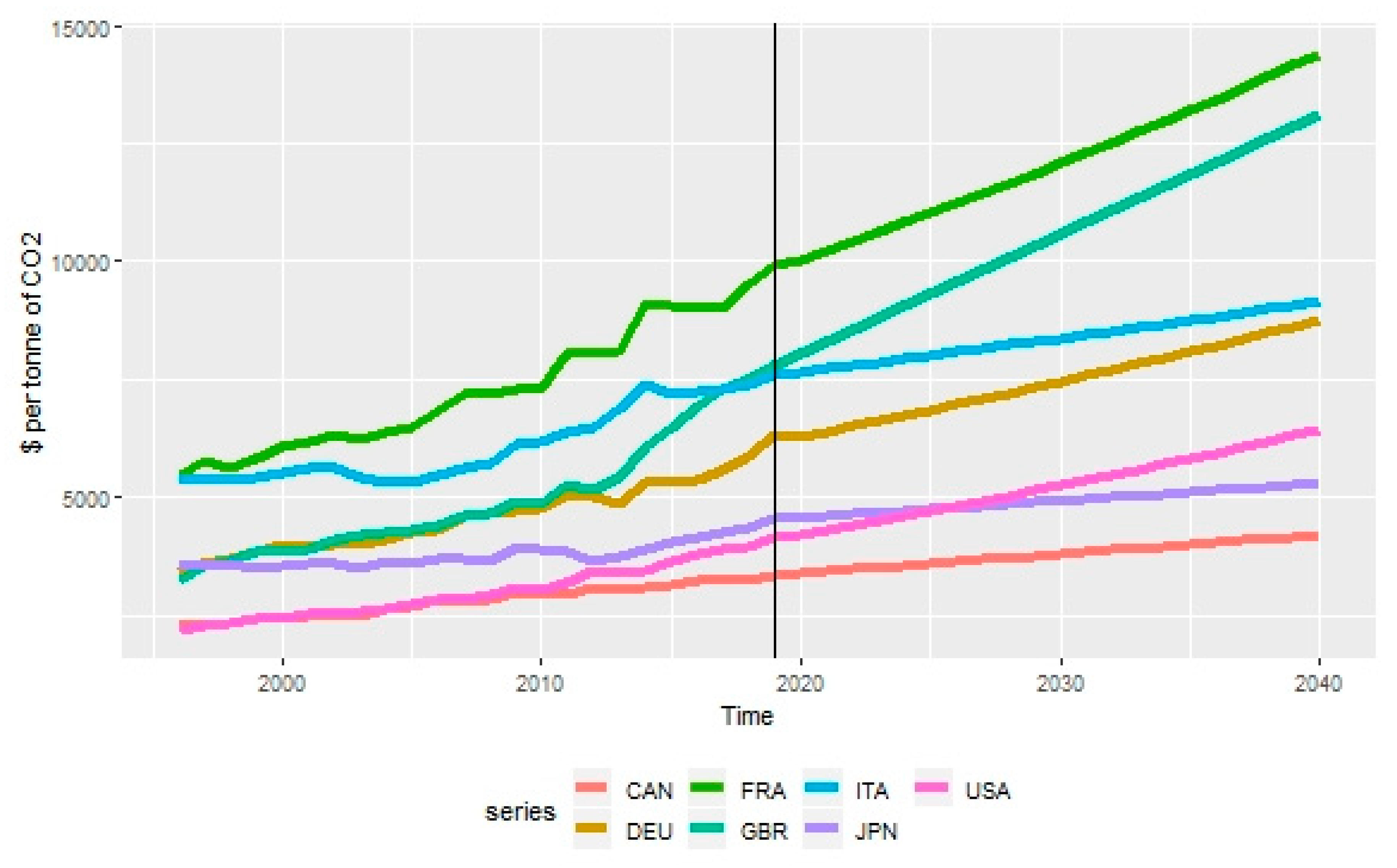
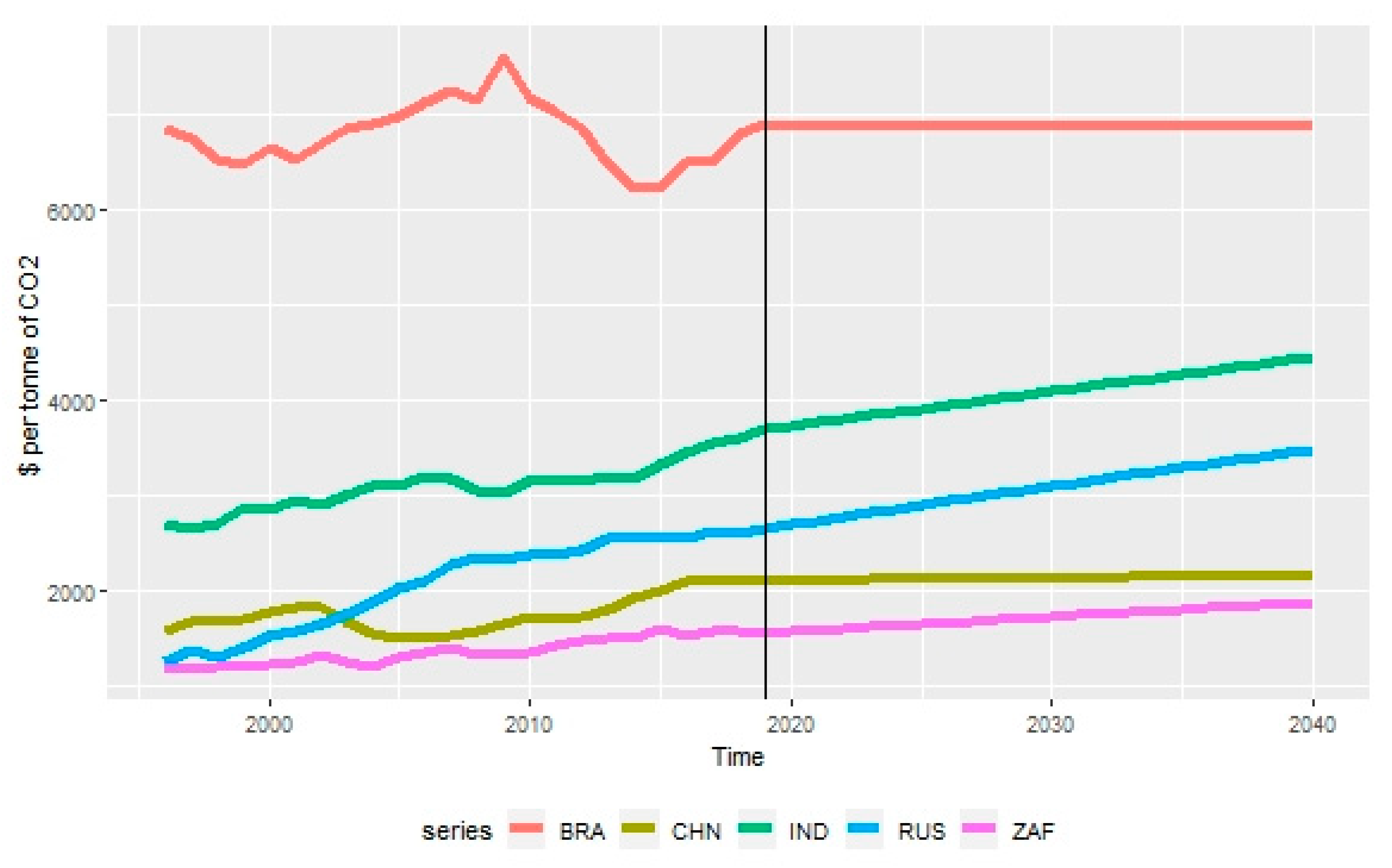
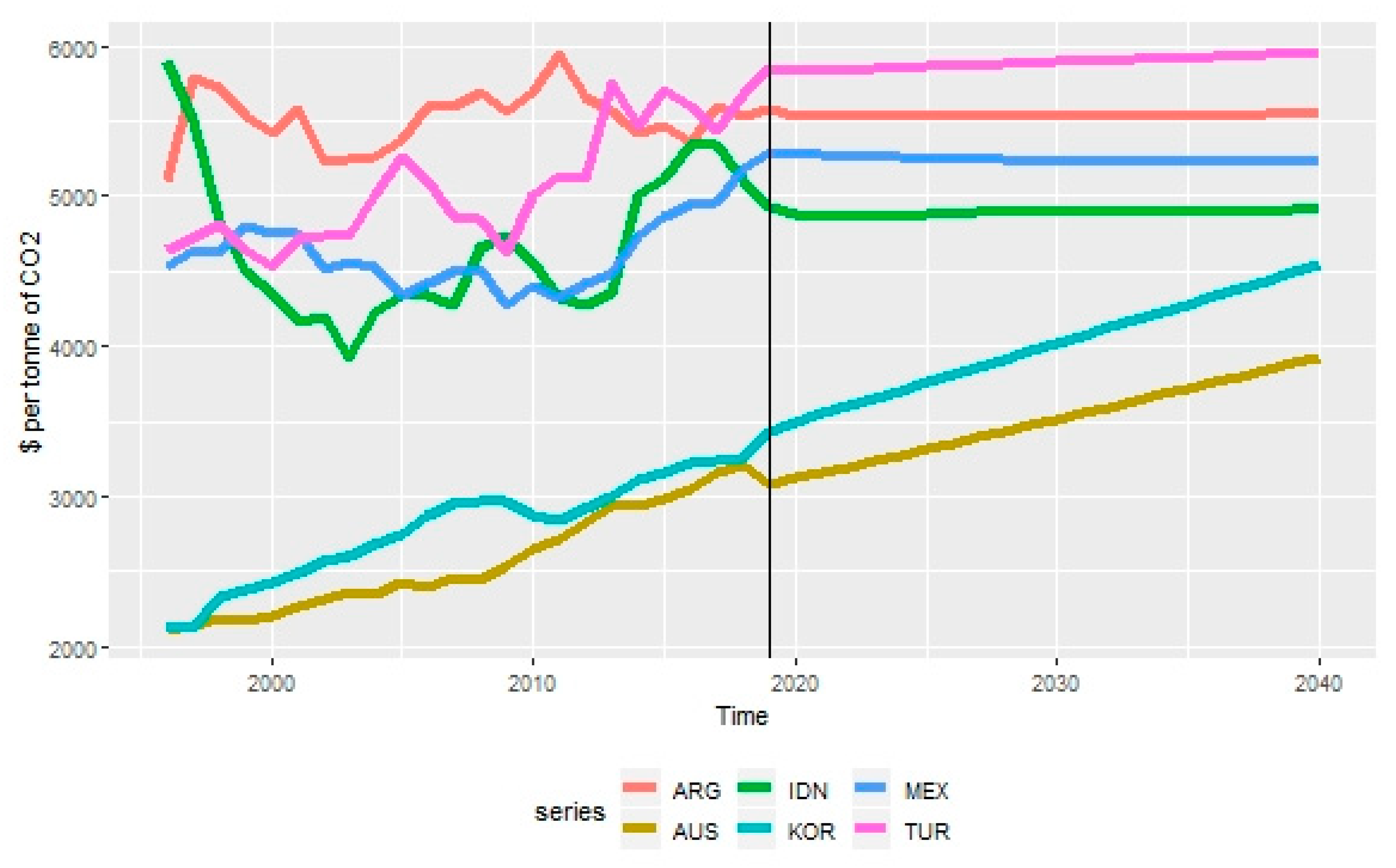
	2000	2010	2020	2030	2040	GR1	Rank	GR2	Rank
ARG	5422.53	5694.28	5533.80	5534.30	5541.13	0.39	16	−0.03	17
AUS	2197.85	2653.32	3119.50	3513.58	3926.51	1.64	8	1.17	7
BRA	6648.00	7187.09	6889.25	6870.16	6865.03	0.03	17	−0.02	16
CAN	2445.83	2927.63	3405.59	3809.89	4213.27	1.69	7	1.06	8
CHN	1774.02	1712.71	2098.46	2123.93	2147.78	1.25	11	0.12	13
DEU	3992.10	4743.18	6286.36	7461.81	8772.57	2.66	4	1.57	4
FRA	6103.18	7316.91	10038.14	12078.57	14397.68	2.57	5	1.78	3
GBR	3875.79	4852.46	8055.22	10591.27	13127.32	3.80	1	2.48	1
IDN	4348.61	4555.83	4885.15	4893.71	4904.26	−0.78	18	−0.02	15
IND	2836.82	3143.15	3727.49	4087.08	4446.67	1.39	10	0.88	11
ITA	5508.29	6174.88	7656.65	8379.11	9152.01	1.48	9	0.89	10
JPN	3554.71	3893.36	4568.16	4932.84	5297.52	1.09	13	0.73	12
KOR	2432.16	2863.68	3495.61	4018.35	4541.09	2.11	6	1.33	5
MEX	4755.46	4394.05	5281.04	5232.37	5222.25	0.67	15	−0.06	18
RUS	1510.82	2357.20	2686.68	3091.27	3470.76	3.26	2	1.30	6
TUR	4523.68	4998.02	5826.36	5889.67	5952.98	1.02	14	0.08	14
USA	2463.67	3062.75	4225.92	5257.28	6444.34	2.76	3	2.10	2
ZAF	1223.90	1341.53	1561.66	1714.58	1867.85	1.22	12	0.95	9

GR1 and GR2 are the average annual growth rates from 1996 to 2019 and 2019 to 2040, respectively.

). In order for production-based CO₂ productivity to be increasing over time, GDP must grow faster than CO₂ emissions.

In 2020, the countries with the highest values of GDP per unit of CO₂ were France, Great Britain, Italy, Brazil, and Germany. The countries with the lowest values were South Africa, China, Russia, Australia, and Canada. Notice that the economics of four of these countries (South Africa, Russia, Australia, and Canada) are heavily reliant on natural resource extraction. These rankings are mostly unchanged in 2040. In 2040, the countries with the highest values of GDP per unit of CO₂ are France, Great Britain, Italy, Germany, and Brazil. As in the case of 2020, the countries with the lowest values of GDP per unit of CO₂ in 2040 are South Africa, China, Russia, Australia, and Canada. In general, production-based CO₂ productivity tends to be low in countries that have a large amount of mineral or fossil fuel resource extraction (Australia, Canada, South Africa, Russia). Canada, Australia, Russia, and South Africa are sometimes referred to as the CARS group of countries.

Great Britain, Russia, the United States, Germany, and France have recorded the highest growth rates in GDP per unit of CO₂ over the period 1996 to 2019 (Table 1). The lowest growth rates were recorded for Indonesia, Brazil, Argentina, Mexico, and Turkey. Over the period 2019 to 2040, the countries with the highest growth rates are Great Britain, United States, France, Germany, and South Korea. The countries with the lowest growth rates are Mexico, Argentina, Indonesia, Brazil, and Turkey. Four of these countries (Mexico, Argentina, Indonesia, Brazil) recorded negative growth rates, indicating that production-based CO₂ productivity is expected to decline over the period 2019 to 2040.

Each country in the G7 has experienced an increase in production-based CO₂ productivity, but the rate of increase varies considerably (Figure 1). Great Britain has the highest growth in production-based CO₂ productivity over both periods (1996 to 2009 and 2009 to 2040). France has the highest production-based CO₂ productivity and one of the highest growth rates of the countries studied. Japan has the lowest growth rate of production-based CO₂ productivity in the G7 over the period 2019 to 2040.

Among the BRICS, Brazil has the highest production-based CO₂ productivity (Figure 2). Over the period 2019 to 2040, Russia and South Africa experience the fastest growth. Brazil recorded the slowest growth in production-based CO₂ productivity.

For the remaining group of countries, Australia and South Korea have low values of production-based CO₂ productivity (Figure 3). Notice that over the period 2019 to 2040, Australia and South Korea also have the highest growth rates of production-based CO₂ productivity in this group of countries.

Summary statistics for the inputs and output to the DEA analysis are shown in

Table 2. Summary statistics.

2000	klratio	ylratio	keratio	nffshare	eco
mean	277,076.531	56,563.527	964,298.382	0.148	3645.413
min	21,421.861	6647.760	371,245.827	0.034	1223.902
max	685,330.501	103,538.244	2,096,226.960	0.440	6648.001
sd	181,172.821	32,356.395	444,240.280	0.126	1633.171
CV	0.654	0.572	0.461	0.853	0.448
2010	klratio	ylratio	keratio	nffshare	eco
mean	312,698.881	63,813.004	1,083,100.190	0.155	4104.001
min	42,319.065	11,167.207	405,927.151	0.027	1341.533
max	743,960.972	119,401.134	2,532,021.912	0.456	7316.906
sd	195,609.458	32,417.909	529,437.749	0.128	1751.996
CV	0.626	0.508	0.489	0.824	0.427
2020	klratio	ylratio	keratio	nffshare	eco
mean	338,651.529	69,381.077	1,276,345.426	0.181	4963.391
min	73,993.932	19,033.970	537,705.879	0.045	1561.656
max	739,140.772	131,053.041	2,992,167.107	0.486	10,038.137
sd	190,770.768	33,649.249	647,702.338	0.126	2227.819
CV	0.563	0.485	0.507	0.697	0.449
2030	klratio	ylratio	keratio	nffshare	eco
mean	363,826.895	74,172.020	1,388,752.686	0.190	5526.655
min	105,706.833	26,265.436	558,296.433	0.044	1714.577
max	756,740.844	141,610.885	3,224,594.427	0.489	12,078.572
sd	194,533.247	34,807.152	719,988.070	0.128	2729.977
CV	0.535	0.469	0.518	0.672	0.494
BAU
2040	klratio	ylratio	keratio	nffshare	eco
mean	392,150.585	78,910.716	1,504,329.735	0.201	6127.279
min	147,150.042	29,204.619	578,886.988	0.044	1867.851
max	774,340.915	150,934.140	3,457,021.748	0.492	14,397.679
sd	200,686.796	36,051.050	805,171.877	0.134	3364.628
CV	0.512	0.457	0.535	0.666	0.549
GR1	1.003	1.021	1.402	1.006	1.543
GR2	0.733	0.644	0.822	0.507	1.053

Klratio (US dollars per worker), ylratio (US dollars per worker), keratio (millions of US dollars per Exajoules), nffshare (a ratio between 0 and 1), and eco (US dollars per tonne of CO₂ emissions). BAU is the business-as-usual scenario. GR1 and GR2 are the average annual growth rates from 2000 to 2020 and 2020 to 2040. CV is the coefficient of variation.

. Each variable is increasing over time. Between 2000 and 2020, production-based CO₂ productivity grew the greatest followed by the capital to energy ratio. The slowest growth was observed for the share of non-fossil fuels. In the BAU scenario, each variable grows less over the period 2020 to 2040 than it did over the 2000 to 2020 period. For each of the years shown, the coefficient of variation (CV) shows that the non-fossil fuel share has the greatest amount of variability. For most of the years shown, eco has the least variability.

4. Results

The eco-efficiency MPI for the G18 in the BAU scenario shows the highest average value in 2000 (1.020) and lowest value in 2010 (0.973) (

Table 3. Eco-efficiency MPI for the BAU scenario.

	2000	2010	2020	2030	2040	Geom1	Rank	Geom2	Rank	Geom3	Rank
ARG	0.974	1.030	0.997	1.001	1.000	1.003	11	1.000	11	1.002	10
AUS	1.002	0.944	1.003	1.003	1.003	1.012	7	1.002	8	1.008	7
BRA	1.031	0.970	1.001	1.000	1.000	1.001	12	1.001	10	1.000	12
CAN	1.019	0.678	0.988	0.970	0.983	0.940	18	0.964	17	0.951	17
CHN	0.969	0.912	0.954	0.910	0.963	0.957	17	0.916	18	0.936	18
DEU	1.023	1.016	0.996	1.013	1.009	1.021	4	1.017	5	1.017	5
FRA	1.050	0.999	1.014	1.018	1.016	1.050	1	1.019	3	1.035	2
GBR	1.028	1.010	1.031	1.020	1.015	1.050	2	1.022	2	1.036	1
IDN	0.987	0.921	1.006	0.992	0.993	0.977	16	0.990	14	0.985	15
IND	0.994	0.977	1.007	0.988	0.986	0.980	15	0.988	16	0.984	16
ITA	1.044	0.992	1.014	1.029	1.005	1.014	5	1.036	1	1.024	4
JPN	1.004	1.009	0.999	1.006	1.006	1.005	9	1.005	7	1.005	8
KOR	1.016	0.999	1.015	1.003	1.004	0.998	13	1.001	9	1.000	11
MEX	1.170	0.999	1.010	0.999	1.000	1.007	8	1.000	12	1.004	9
RUS	1.098	1.049	1.041	1.012	1.007	1.031	3	1.019	4	1.026	3
TUR	0.989	1.009	1.003	0.991	0.991	1.004	10	0.990	15	0.998	13
USA	1.014	1.008	1.000	1.010	1.014	1.014	6	1.008	6	1.011	6
ZAF	0.954	0.986	1.004	1.000	1.000	0.990	14	1.000	13	0.995	14
mean	1.020	0.973	1.005	0.998	1.000	1.005		0.999		1.002

Geometric mean computed for the periods 1997 to 2019, 2019 to 2040, and 1997 to 2040 denoted by geom1, geom2, and geom3, respectively. Rank refers to the ranking of the geomean.

). The drop in the average value of the MPI between 2000 and 2010 was likely due to the global financial crisis (2008–2009). The G18 mean value recovers after 2010 and records a value of 1.00 in 2040. Table 3 presents country-specific geometric mean values for the complete sample period (1997 to 2040) as well as two sub-periods. Calculations for the first sub-period (1997 to 2019) use the actual data to calculate MPI. Calculations for the second sub-period (2019 to 2040) use the forecasted values to calculate MPI. For the G18 countries, the average annual change in MPI over the period 1997 to 2019 was 0.5%, while the forecasted average annual change over the period 2019 to 2040 was a 0.1% decrease. Over the complete sample (1997 to 2040), the average annual change in MPI was 0.2%. For the G18 countries, there has been little change in eco-efficiency.

Over the period 1997 to 2019, countries that recorded geometric mean values of MPI greater than unity include Argentina, Australia, Brazil, Germany, France, Great Britain, Italy, Japan, Mexico, Russia, Turkey, and the USA. France, Great Britain, and Russia record the three highest geometric mean values. Canada, China, India, Indonesia, Korea, and South Africa recorded negative average growth over this time period. Notice that the ranking of geometric mean values does not separate clearly on country income grouping. Russia, an emerging economy, has a high geometric mean value, while Canada, a developed G7 country, has a low value. The results change slightly over the second sub-period 2019 to 2040, as most countries experience lower MPI growth. One of the biggest differences is that South Korea now has a geometric mean value greater than one. For the period 1997 to 2040, Argentina, Australia, Germany, France, Great Britain, Italy, Japan, Mexico, Russia, and the United States each have improved their MPI. Over the period 1997 to 2040, the highest MPI growth is observed for Great Britain, France, and Russia, while the lowest growth is observed for Canada, China, India, Indonesia, Turkey, and South Africa. Notice that China and India, the two largest countries in the world by population, are experiencing a decline in MPI over the time period 1997 to 2040.

The G18 average catch-up value is highest in 2010 and lowest in 2040 (

Table 4. Eco-efficiency catch-up for the BAU scenario.

	2000	2010	2020	2030	2040	Geom1	Rank	Geom2	Rank	Geom3	Rank
ARG	1.000	1.000	1.000	1.000	1.000	1.000	15	1.000	9	1.000	14
AUS	1.018	0.968	0.964	1.005	1.002	1.009	10	1.005	4	1.006	10
BRA	1.000	1.000	1.000	1.000	1.000	1.000	12	1.000	6	1.000	11
CAN	1.000	1.000	1.000	0.949	0.982	1.000	13	0.970	17	0.985	17
CHN	1.000	1.000	1.000	1.000	0.963	1.000	13	0.961	18	0.980	18
DEU	1.026	1.034	0.998	1.003	1.003	1.034	6	1.007	3	1.019	4
FRA	1.046	1.811	1.000	1.000	1.000	1.036	5	1.000	10	1.019	5
GBR	1.026	1.063	1.000	1.000	1.000	1.051	2	1.000	14	1.026	2
IDN	1.000	1.000	1.000	1.000	1.000	1.000	17	1.000	12	1.000	15
IND	1.000	1.000	1.000	1.000	1.000	1.000	16	1.000	11	1.000	13
ITA	1.000	1.000	1.000	1.000	0.997	1.048	3	0.984	16	1.017	7
JPN	1.002	1.030	0.978	1.007	1.006	1.026	8	1.007	2	1.016	8
KOR	1.017	0.983	1.012	1.004	1.003	1.015	9	1.003	5	1.010	9
MEX	1.261	1.000	1.000	1.000	1.000	1.033	7	1.000	7	1.017	6
RUS	1.092	1.054	1.084	1.000	1.000	1.061	1	1.014	1	1.038	1
TUR	1.026	1.018	1.007	0.988	0.989	0.998	18	0.986	15	0.994	16
USA	1.045	0.994	1.000	1.000	1.000	1.041	4	1.000	8	1.021	3
ZAF	1.000	1.000	1.000	1.000	1.000	1.000	11	1.000	12	1.000	12
mean	1.031	1.053	1.002	0.998	0.997	1.025		0.997		1.012

Geometric mean computed for the periods 1997 to 2019, 2019 to 2040, and 1997 to 2040 denoted by geom1, geom2, and geom3, respectively. Rank refers to the ranking of the geomean.

). The G18 experienced an increase in catch-up over the periods 1997–2019 and 1997–2040. The average catch-up effect is positive over the period 1997 to 2019 but negative over the period 2019 to 2040.

Countries that have an increase in catch-up over all three sub-periods include Australia, Germany, Japan, Korea, and Russia. In other words, only five of the 18 countries studied improved their eco-efficiency catch-up over all three sub-periods.

The G18 average frontier-shift value is highest in 2020 and 2040 and lowest in 2010 (

Table 5. Eco-efficiency frontier shift for the BAU scenario.

	2000	2010	2020	2030	2040	Geom1	Rank	Geom2	Rank	Geom3	Rank
ARG	0.974	1.030	0.997	1.001	1.000	1.003	4	1.000	9	1.002	6
AUS	0.985	0.976	1.040	0.997	1.001	1.004	3	0.997	14	1.002	5
BRA	1.031	0.970	1.001	1.000	1.000	1.001	5	1.001	8	1.000	7
CAN	1.019	0.678	0.988	1.022	1.000	0.940	18	0.994	15	0.965	17
CHN	0.969	0.912	0.954	0.910	1.000	0.957	17	0.953	18	0.955	18
DEU	0.997	0.982	0.999	1.010	1.007	0.987	8	1.010	4	0.998	8
FRA	1.004	0.551	1.014	1.018	1.016	1.013	1	1.019	3	1.016	1
GBR	1.002	0.950	1.031	1.020	1.015	0.999	6	1.022	2	1.009	2
IDN	0.987	0.921	1.006	0.992	0.993	0.977	12	0.990	16	0.985	15
IND	0.994	0.977	1.007	0.988	0.986	0.980	10	0.988	17	0.984	16
ITA	1.044	0.992	1.014	1.029	1.008	0.967	16	1.053	1	1.007	3
JPN	1.002	0.980	1.022	0.999	1.000	0.980	11	0.998	13	0.990	12
KOR	0.999	1.016	1.004	0.999	1.001	0.983	9	0.999	12	0.991	10
MEX	0.928	0.999	1.010	0.999	1.000	0.976	13	1.000	10	0.987	14
RUS	1.006	0.995	0.961	1.012	1.007	0.972	15	1.005	6	0.988	13
TUR	0.964	0.991	0.996	1.003	1.002	1.006	2	1.003	7	1.005	4
USA	0.970	1.014	1.000	1.010	1.014	0.974	14	1.008	5	0.990	11
ZAF	0.954	0.986	1.004	1.000	1.000	0.990	7	1.000	11	0.995	9
mean	0.990	0.940	1.003	1.000	1.003	0.988		1.002		0.995

Geometric mean computed for the period 1997 to 2019, 2019 to 2040, and 1997 to 2040 denoted by geom1, geom2, and geom3 respectively. Rank refers to the ranking of the geometric mean.

). As a group, the G18 recorded an increase in frontier-shift in the 2019 to 2040 sub-period but not in the 1997 to 2019 or 1997 to 2040 periods. Countries that showed an increase in frontier-shift growth over the period 2019 to 2040 are Brazil, Germany, France, Great Britain, Italy, Russia, Turkey, and the United States. Eight out of eighteen countries report an increase in frontier-shift over the period 2019 to 2040.

5. Discussion

The analysis in the previous section shows that twelve out of eighteen countries recorded average annual changes in eco-efficiency MPI greater than unity over the period 1997 to 2020 (Table 3). The average eco-efficiency MPI over this period for the G18 was, at 0.5%, low. Eco-efficiency leaders over this period include France, Great Britain, Russia, Germany, Italy, and the United States. Germany, France, Great Britain, and Italy benefited from the European Union’s 2020 Climate and Energy Package, which aims to reduce greenhouse gas emissions 20% from 1990 levels, target 20% of EU energy from renewables, and accomplish a 20% improvement in energy efficiency by the year 2020 [37]. Great Britain’s performance is partly due to fuel switching and reduced fuel consumption. Great Britain has moved to a cleaner fuel mix in electricity generation as coal was switched for natural gas and renewables [38]. Reduced fuel consumption by business and industry also contributed to the reduction in carbon dioxide emissions. However, Great Britain’s decision to exit the European Union (BREXIT) may weaken the stimulus and incentive for further eco-efficiency improvements. In addition, Germany’s success comes from cross-partisan policy consistency, shared goals between political leaders and renewable energy advocates, a strong social movement for renewable energy, and decentralized energy policies [39]. These results are consistent with the results of Midova et al. [40], who study low-carbon scenarios of six northwest European countries (Netherlands, Germany, France, Denmark, the UK, and Belgium). In ranking these countries on ten criteria regarding low-carbon energy scenario design, Germany comes out on top followed by the UK. France’s reliance on nuclear energy for electricity generation has helped to reduce carbon emissions but has also reduced technological innovation for other renewable energy sources. [41]. Russia’s growth in eco-efficiency is related to the modernizing of the economy after the breakup of the Soviet Union. The United States benefits from economy-wide technical progress and, at times, environmentally favorable US presidency.

The eco-efficiency laggards over the period 1997 to 2019 include Canada, China, India, and Indonesia. Canada is a developed country with a large resource extraction sector. China, India, and Indonesia are populous fast-growing countries where economic growth has taken priority over environmental stewardship.

Predicting eco-efficiency into the future under a BAU scenario shows that between 2019 and 2040, the average annual rate of change in MPI, catch-up, and frontier shift is forecast at −0.1%, −0.3%, and 0.2%, respectively. A slowdown in technical efficiency is predicted to be the main reason for the decline in MPI. However, these numbers are small, indicating that even for countries where eco-efficiency MPI growth is positive, the practical impact on eco-efficiency is likely to be insignificant.

There are some limitations to this research. The forecasts for the period 2020 to 2040 were conducted under a BAU scenario, which assumes existing data trends continue into the future and there are no major changes in policy or economic structure. Small changes in the growth rate (1% or 2%) of the DEA input variables and output will have a small impact on the efficiency scores and the MPI calculations. Large changes in energy policy, the energy mix, and CO₂ emissions reductions could lead to higher eco-efficiency than those reported in the BAU scenario. Then, the question becomes, how likely is it that these large changes occur? Recent research by the IPCC indicates that climate change is widespread, rapid, and intensifying [42]. A substantial increase in eco-efficiency would require the G18 to quickly enact long-term energy policy aimed at greatly reducing fossil fuel consumption. Future research could look into conducting further scenario analysis to account for major changes in clean energy policy. Additional analysis could also be conducted on the choice of DEA model.

6. Conclusions and Policy Implications

Since the 1992 World Business Council for Sustainable Development publication “Changing Course”, eco-efficiency has been an important indicator for the discussion on environmental sustainability. The focus of this research is to study how eco-efficiency has changed over time and is likely to change in the future for a group of 18 major countries (G18) that are part of the G20. DEA is used to estimate eco-efficiency, and these values are used in constructing an eco-efficiency Malmquist productivity index, which is a useful ecological indicator. Analysis is conducted over the period 1996 to 2040 with actual data being used for the period 1996 to 2019 and forecasted data for the years 2020 to 2040.

For the G18, the average annual growth in MPI over the period 1997 to 2019 was 0.5%. Over this same time period, catch-up and frontier shift average annual growth rates were 2.5% and −0.2%, respectively, indicating that efficiency change was growing positively while technical change was regressing. Over the forecast period, 2019 to 2040, the average annual rate of change in MPI, catch-up, and frontier shift is forecast at −0.1%, −0.3%, and 0.2%, respectively. These values indicate that a slowdown in efficiency change is forecast to be the main reason for the decline in MPI. However, the small magnitude of these numbers indicates that even when eco-efficiency MPI growth is positive, the practical impact on eco-efficiency is likely to be slight.

Eco-efficiency leaders over the period 1997 to 2019 and 2019 to 2040 include Australia, Brazil, France, Germany, Great Britain, Italy, Japan, Russia, and the United States. Laggards include Canada, China, India, and Indonesia. These laggard countries recorded negative growth rates in eco-efficiency over the period 1997 to 2019 and 2019 to 2040. These results are important in establishing not only what country-level eco-efficiency currently looks like but also what eco-efficiency is likely to look like in the future.

There are several policy implications stemming from this research. First, increasing eco-efficiency should be a top priority for all G18 countries. A positive trend in eco-efficiency is desirable from an environmental sustainability perspective, but it does not mean that substantial increases in eco-efficiency are being realized or that there is no room for further improvement. It could be that eco-efficiency is increasing but at such a slow rate that improvements are only marginal. This is consistent with the current values of G18 eco-efficiency and future predictions as presented in this paper. In such cases, even countries with positive eco-efficiency growth could still fall well short of meeting their nationally determined contributions (NDCs) targets, as specified under the Paris climate change agreement [43]. Countries need to prioritize increasing eco-efficiency to the forefront of economic policy making. One way to do this is to incorporate environmental sustainability into industrial policy so that future economic growth embodies environmental quality. For example, industrial policy could be focused on developing composite materials that are more lightweight and less energy intensive to construct, and there could be a greater emphasis on life-cycle analysis. The transportation sector should move away from fossil fuel-powered engines to electric motors that use electricity generated from renewable energy sources. Second, the large variations in eco-efficiency between countries make it more difficult to negotiate international agreements on energy efficiency and climate change. In general, it is easier to gain consensus on policy matters when the members share a common ground. Third, the G18 are an important group of developed and developing countries that need to show leadership when it comes to increasing eco-efficiency. The G20 countries need to establish a non-partisan environment ministry that is focused on designing and implementing aggressive goals on increasing eco-efficiency, which are consistent with the UN’s SDGs. Under the current G20 structure, the chair of the G20 rotates on a yearly basis, and this offers little in the way of substantial long-term commitment to environmental policy [44]. Hopefully, the impact of COVID, record hot temperatures in 2021, and the latest IPCC research on the effects of climate change will provide the appropriate stimulus for the G20 to take environmental sustainability more seriously.