Teaching Multiplication to Students with Mathematical Learning Disabilities (MLD): Analysis of Preservice Teachers’ Lesson Design
Abstract
:1. Introduction
2. Review of the Literature
2.1. Teaching Mathematics for All
2.2. Teaching Mathematics to Students with Mathematical Learning Disabilities (MLD)
2.3. Teaching Multiplication
2.3.1. Conceptual Understanding of Multiplication
2.3.2. Mathematical Representations for Teaching and Learning Multiplication
2.4. Research Questions
- How do preservice teachers accommodate and modify mathematics strategies to teach multiplication to students with mathematical learning disabilities (MLD)?
- What instructional strategies do preservice teachers use for teaching multiplication in their lesson design for students with mathematical learning disabilities (MLD)?
- Mathematical approaches including multiplicative concepts and its representation are categorized as mathematics strategies; general instructional approaches including lesson goals, structure, flow, and task are categorized as instructional strategies.
3. Method
3.1. Setting and Participants
3.2. Data Source
3.3. Data Analysis
4. Results
4.1. Accommodations and Modification in Mathematical Strategies
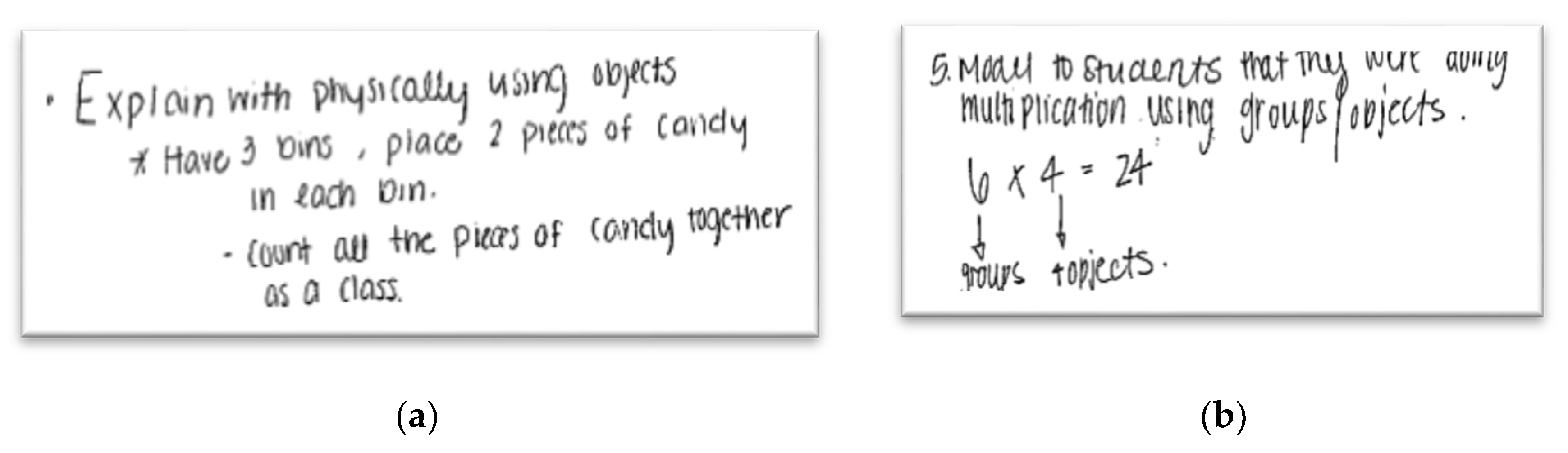
4.1.1. Introduction of the Multiplication Concept
4.1.2. Experiencing the Multiplicative Concept
4.2. Accommodations and Modification in Lesson Design
4.2.1. Articulation of Expectations
- I can multiply single digit numbers.
- I can recognize multiplication problems.
4.2.2. Orchestration of Instructional Activity
- Task Management: Content Modification
- 2.
- Instructional Structures
- For Jose: teach multiplication to the whole group and have students (such as Jose) engage in a group activity;
- For Liam: provide individual support separately.
- 3.
- Instructional Flow
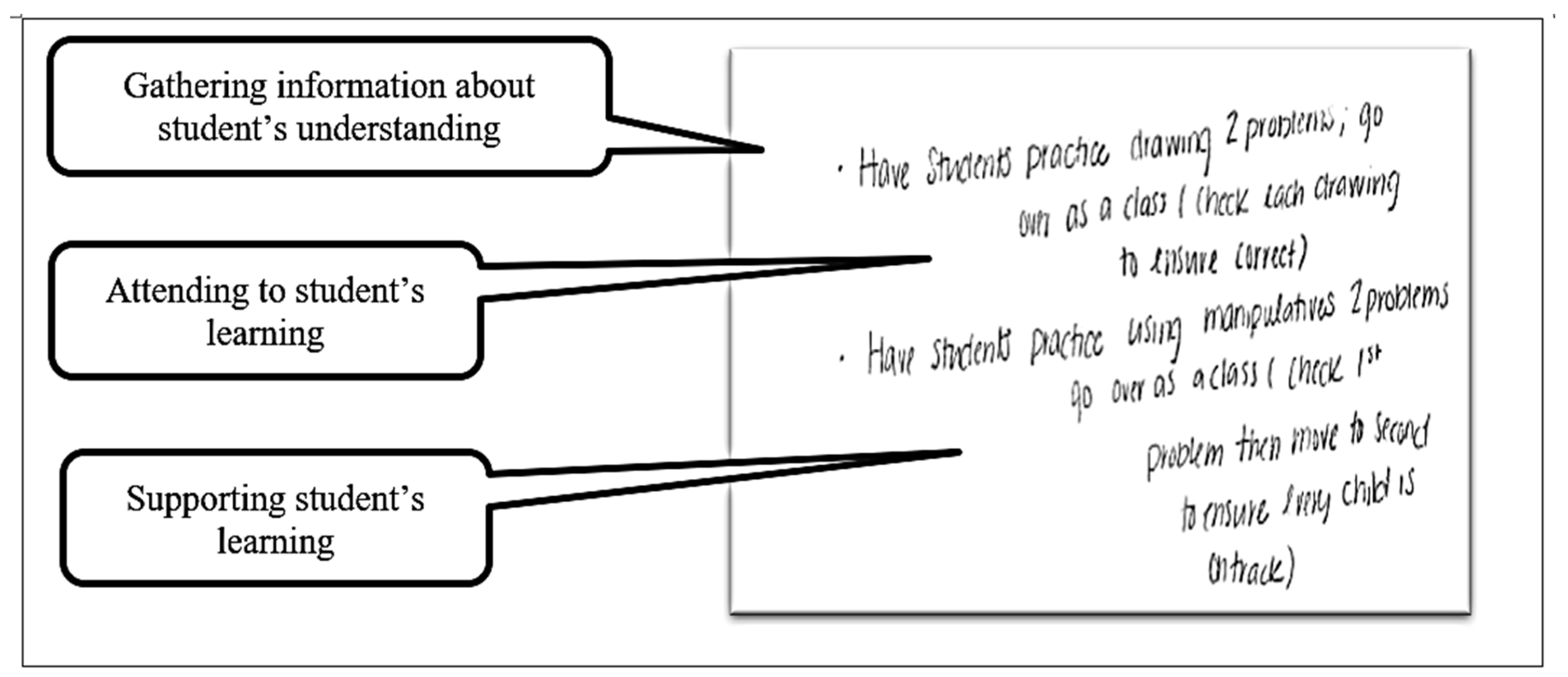
4.2.3. Assessment of Students’ Mathematical Thinking
5. Discussion
5.1. Content-Oriented Alternation for Equitable Responsive Teaching
5.2. Modification and Accommodations for Responsive Teaching
5.3. From Band-Aid Solutions to Sustainable Support
6. Implications
7. Limitations of the Study
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, C.; Navarro, V. An examination of student mathematics learning in elementary and middle schools: A longitudinal look from the US. Stud. Educ. Eval. 2004, 30, 237–253. [Google Scholar] [CrossRef]
- Jackson, K.; Wilson, J. Supporting African American students’ learning of mathematics: A problem of practice. Urban Educ. 2012, 47, 354–398. [Google Scholar] [CrossRef] [Green Version]
- National Council of Teachers of Mathematics. Principles to Actions: Ensuring Mathematical Success for All; National Council of Teachers of Mathematics: Reston, VA, USA, 2014. [Google Scholar]
- Urick, A.; Wilson, A.S.P.; Ford, T.G.; Frick, W.C.; Wronowski, M.L. Testing a framework of math progress indicators for ESSA: How opportunity to learn and instructional leadership matter. Educ. Adm. Q. 2018, 54, 396–438. [Google Scholar] [CrossRef]
- Riley, K.; Solic, K. “Change happens beyond the comfort zone”: Brining undergraduate teacher-candidates into activist teacher communities. J. Teach. Educ. 2017, 68, 179–192. [Google Scholar] [CrossRef]
- Foegen, A.; Dougherty, B. Instruction that meets the needs of students with mathematics disabilities and difficulties. In Compendium for Research in Mathematics Education; Cai, J., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2017; pp. 893–907. [Google Scholar]
- Congress of the United States. Elementary and Secondary Education Act of 1965: Public Law 89-10; Congress of the United States: Washington, DC, USA, 1965.
- U.S. Department of Education. No Child Left Behind; U.S. Department of Education, Office of the Secretary: Washington, DC, USA, 2001.
- Congress of the United States. Every Student Succeeds Act [ESSA]. Public Law No: 114-95. A Reauthorization of the Elementary and Secondary School Act, 1965; Congress of the United States: Washington, DC, USA, 2015.
- Norwich, B. Changing policy and legislation and its effects on inclusive and special education: A perspective from England. Br. J. Spec. Educ. 2014, 41, 403–425. [Google Scholar] [CrossRef]
- Department of Education and Training. Disability Standards for Education 2005. 2005. Available online: https://www.dese.gov.au/disability-standards-education-2005 (accessed on 28 December 2020).
- Department of Education and Training. Disability Standards for Education 2005: 2020 Review. 2020. Available online: https://www.dese.gov.au/disability-standards-education-2005/resources/final-report-2020-review-disability-standards-education-2005 (accessed on 28 December 2020).
- Kilpatrick, J.; Swafford, J.; Findell, B. (Eds.) Adding It up: Helping Children Learn Mathematics; National Academy Press: Washington, DC, USA, 2001. [Google Scholar]
- Trani, J.-F.; Fowler, P.; Bakhshi, P.; Kumar, P. Assessment of progress in education for children and youth with disabilities in Afghanistan: A multilevel analysis of repeated cross-sectional surveys. PLoS ONE 2019, 14, e0217677. [Google Scholar] [CrossRef] [PubMed]
- Jobling, A.; Moni, K.B. “I never imagined I’d have to teach these children”: Providing authentic learning experiences for secondary pre-service teachers in teaching students with special needs. Asia-Pac. J. Teach. Educ. 2004, 32, 5–22. [Google Scholar] [CrossRef]
- Lewis, K.E. Understanding mathematical learning disabilities: A case study of errors and explanations. Learn. Disabil. A Contemp. J. 2010, 8, 9–18. [Google Scholar]
- Raja, B.W.D.; Kumar, S.P. Findings of studies on dyscalculia—A synthesis. J. Educ. Psychol. 2012, 5, 41–51. [Google Scholar]
- Lewis, K. Difference not deficit: Reconceptualizing mathematical learning disabilities. J. Res. Math. Educ. 2014, 45, 351–396. [Google Scholar] [CrossRef]
- Artut, P.D. Experimental evaluation of the effects of cooperative learning on kindergarten children’s mathematics ability. Int. J. Educ. Res. 2009, 48, 370–380. [Google Scholar] [CrossRef]
- Cai, J.; Chen, T.; Li, X.; Xu, R.; Zhang, S.; Hu, Y.; Zhang, L.; Song, N. Exploring the impact of a problem-posing workshop on elementary school mathematics teachers’ conceptions on problem posing and lesson design. Int. J. Educ. Res. 2020, 102, 101404. [Google Scholar] [CrossRef]
- Munter, C.; Stein, M.K.; Smith, M.A. Dialogic and Direct Instruction: Two Distinct Models of Mathematics Instruction and the Debate(s) Surrounding Them. Teach. Coll. Rec. 2015, 117, 1–32. [Google Scholar]
- Baker, S.; Gersten, R.; Lee, D. A synthesis of empirical research on teaching mathematics to low-achieving students. Elem. Sch. J. 2002, 103, 51–73. [Google Scholar] [CrossRef]
- Evans, D. Developing mathematical proficiency in the Australian context: Implications for students with learning difficulties. J. Learn. Disabil. 2007, 40, 420–426. [Google Scholar] [CrossRef]
- Fuchs, L.S.; Vaughn, S. Responsiveness-to-intervention: A decade later. J. Learn. Disabil. 2012, 45, 195–203. [Google Scholar] [CrossRef] [PubMed]
- Kroesbergen, E.H.; Van Luit, J.E.H. Mathematics interventions for children with special educational needs: A meta-analysis. Remedial Spec. Educ. 2003, 24, 97–114. [Google Scholar] [CrossRef]
- Leach, D. Using high-probability instructional sequences and explicit instruction to teach multiplication facts. Interv. Sch. Clin. 2016, 52, 102–107. [Google Scholar] [CrossRef]
- Stein, M.; Carnine, D.; Dixon, R. Direct instruction: Integrating curriculum design and effective teaching practice. Interv. Sch. Clin. 1998, 33, 227–233. [Google Scholar] [CrossRef]
- Van Garderen, D.; Scheuermann, A.; Jackson, C. Developing representational ability in mathematics for students with learning disabilities: A content analysis of grades 6 and 7 textbooks. Learn. Disabil. Q. 2012, 35, 24–38. [Google Scholar] [CrossRef]
- Fyfe, E.; Nathan, M. Making “concreteness fading” more concrete as a theory of instruction for promoting transfer. Educ. Rev. 2019, 71, 403–422. [Google Scholar] [CrossRef]
- Gibbs, A.S.; Hinton, V.M.; Flores, M.M. A case study using CRA to teach students with disabilities to count using flexible numbers: Applying skip counting to multiplication. Prev. Sch. Fail. 2018, 62, 49–57. [Google Scholar] [CrossRef]
- Hawkins, R.; Musti-Rao, S.; Hughes, C.; Berry, L.; McGuire, S. Applying a randomized interdependent group contingency component to classwide peer tutoring for multiplication fact fluency. J. Behav. Educ. 2009, 18, 300–318. [Google Scholar] [CrossRef]
- Wood, M.B.; Kalinec, C.A. Student talk and opportunities for mathematical learning in small group interactions. Int. J. Educ. Res. 2012, 51–52, 109–127. [Google Scholar] [CrossRef]
- Smith, T. Discrete trial training in the treatment of autism. Focus Autism Other Dev. Disabil. 2001, 16, 86–92. [Google Scholar] [CrossRef]
- Kim, H. Concreteness fading strategy: A promising and sustainable instructional model in mathematics classrooms. Sustainability 2020, 12, 2211. [Google Scholar] [CrossRef] [Green Version]
- Miller, S.P.; Hudson, P.J. Helping students with disabilities understand what mathematics means. Teach. Except. Child. 2006, 39, 28–35. [Google Scholar] [CrossRef]
- Miller, S.P.; Stringfellow, J.L.; Kaffar, B.J.; Ferreira, D.; Mancl, D.B. Developing computation competence among students who struggle with mathematics. Teach. Except. Child. 2011, 44, 38–46. [Google Scholar] [CrossRef]
- Flores, M.M.; Hinton, V.M.; Meyer, J.M. Teaching fraction concepts using the concrete-representational-abstract sequence. Remedial Spec. Educ. 2020, 41, 165–175. [Google Scholar] [CrossRef]
- Fyfe, E.R.; McNeil, N.M.; Borjas, S. Benefits of “concreteness fading” for children’s mathematics understanding. Learn. Instr. 2015, 35, 104–120. [Google Scholar] [CrossRef]
- Fuson, K.C.; Murata, A. Integrating NRC principles and the NCTM process standards to form a class learning path model that individualizes within whole-class activities. Natl. Counc. Superv. Math. J. Math. Educ. Leadersh. 2007, 10, 72–91. [Google Scholar]
- Swanson, H.L.; Lussier, C.; Orosco, M. Effects of cognitive strategy interventions and cognitive moderators on word problem solving in children at risk for problem solving difficulties. Learn. Disabil. Res. Pract. 2013, 28, 170–183. [Google Scholar] [CrossRef]
- Dexter, D.D.; Hughes, C.A. Graphic organizers and students with learning disabilities: A meta-analysis. Learn. Disabil. Q. 2011, 34, 51–72. [Google Scholar] [CrossRef]
- Ives, B. Graphics organizers applied to secondary algebra instruction for students with learning disorders. Learn. Disabil. Res. Pract. 2007, 22, 110–118. [Google Scholar] [CrossRef]
- Van Garderen, D. Teaching students with LD to use diagrams to solve mathematical word problems. J. Learn. Disabil. 2007, 40, 540–553. [Google Scholar] [CrossRef]
- Matheson, I.; Hutchinson, N. Visual Representation in Mathematics. LD@School. 2014. Available online: https://www.ldatschool.ca/visual-representation/ (accessed on 21 June 2021).
- Zhang, D.; Ding, Y.; Stegall, J.; Mo, L. The effect of visual-chunking-representation accommodation on geometry testing for students with math disabilities. Learn. Disabil. Res. Pract. 2012, 27, 167–177. [Google Scholar] [CrossRef]
- Krawec, J.; Huang, J.; Montague, M.; Kressler, B.; Melia de Alba, A. The effects of cognitive strategy instruction on knowledge of math problem-solving processes of middle school students with learning disabilities. Learn. Disabil. Q. 2012, 36, 80–92. [Google Scholar] [CrossRef] [Green Version]
- Fuchs, L.S.; Fuchs, D.; Phillips, N.B.; Hamlett, C.L.; Karns, K. Acquisition and transfer effects of classwide peer-assisted learning strategies in mathematics for students with varying learning histories. Sch. Psychol. Rev. 1995, 24, 604–620. [Google Scholar] [CrossRef]
- Maheady, L.; Mallette, B.; Harper, G.F. Four classwide peer tutoring models: Similarities, differences, and implications for research and practice. Read. Writ. Q. 2006, 22, 65–89. [Google Scholar] [CrossRef]
- Kinzer, C.; Stanford, T. The distributive property: The core of multiplication. Teach. Child. Math. 2014, 20, 302–309. [Google Scholar] [CrossRef]
- Anghileri, J.; Johnson, D.C. Arithmetic operations on whole numbers: Multiplication and division. In Teaching Mathematics in Grades K-8 Research Based Methods; Post, T.R., Ed.; Allyn and Bacon: Boston, MA, USA, 1992; pp. 157–200. [Google Scholar]
- Otto, A.; Caldwell, J.; Hancock, S.W.; Zbiek, R.M. Developing Essential Understanding of Multiplication and Division for Teaching Mathematics in Grades 3–5; National Council of Teachers of Mathematics: Reston, VA, USA, 2011. [Google Scholar]
- Biddlecomb, B.; Carr, M. A longitudinal study of the development of mathematics strategies and underlying counting schemes. Int. J. Sci. Math. Educ. 2011, 9, 1–24. [Google Scholar] [CrossRef]
- Burns, M.K.; Ysseldyke, J.; Nelson, P.M.; Kanive, R. Number of repetitions required to retain single-digit multiplication math facts for elementary students. Sch. Psychol. Q. 2014, 30, 398–405. [Google Scholar] [CrossRef]
- Robinson, K.; LeFevre, J. The inverse relationship between multiplication and division: Concepts, procedures and a cognitive framework. Educ. Stud. Math. 2012, 79, 409–428. [Google Scholar] [CrossRef]
- Carpenter, T.P.; Fennema, E.; Franke, M.L.; Levi, L.; Empson, S.B. Children’s Mathematics: Cognitively Guided Instruction, 2nd ed.; Heinemann: Portsmouth, NH, USA, 2015. [Google Scholar]
- Greer, B. Multiplication and division as models of situations. In Handbook of Research on Mathematics Teaching and Learning a Project of the National Council of Teachers of Mathematics; Grouws, D.A., Ed.; Macmillan Publishing Company: New York, NY, USA, 1992; pp. 276–295. [Google Scholar]
- Reys, R.; Lindquist, M.; Lambdin, D.V.; Smith, N.L. Helping Children Learn Mathematics; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Van de Walle JAKarp, K.S.; Bay-Williams, J.M. Elementary and Middle School Mathematics Teaching Developmentally, 10th ed.; Pearson: New York, NY, USA, 2019. [Google Scholar]
- Izsák, A. “We want a statement that is always true”: Criteria for good algebraic representations and the development of modeling knowledge. J. Res. Math. Educ. 2003, 34, 191–227. [Google Scholar] [CrossRef]
- Freudenthal, H. Didactical Phenomenology of Mathematical Structures; D. Reidel Publishing Company: Dodlerk, The Netherlands, 1983. [Google Scholar]
- National Council of Teachers of Mathematics. Principles and Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 2000. [Google Scholar]
- National Governors Association Center for Best Practices and the Council of Chief State School Officers. Common Core State Standards for Mathematics; National Governors Association Center for Best Practices and the Council of Chief State School Officers: Washington, DC, USA, 2010. [Google Scholar]
- Lesh, R.A.; Cramer, K.; Doerr, H.; Post, T.; Zawojewski, J. Model development sequences. In Beyond Constructivism: A Models and Modeling Perspective on Mathematics Teaching, Learning, and Problem Solving; Lesh, R.A., Doerr, H., Eds.; Erlbaum: Mahwah, NJ, USA, 2003; pp. 35–58. [Google Scholar]
- Fuson, K.C.; Kalchman, M.; Bransford, J.D. Mathematical understanding: An introduction. In How Students Learn Mathematics in the Classroom; Donovan, M.S., Bransford, J., Eds.; National Research Council: Washington, DC, USA, 2005; pp. 217–256. [Google Scholar]
- Lesh, R.; Post, T.; Behr, M. Representations and translations among representations in mathematics learning and problem solving. In Problems of Representation in the Teaching and Learning of Mathematics; Janvier, C., Ed.; Erlbaum: Mahwah, NJ, USA, 1987; pp. 33–40. [Google Scholar]
- Creswell, J.; Creswell, J.D. Research Design: Qualitative, Quantitative, and Mixed Methods Approaches, 5th ed.; SAGE Publications: Thousand Oaks, CA, USA, 2018. [Google Scholar]
- Kennedy, M.M. Approximations to indicators of student outcomes. Educ. Eval. Policy Anal. 1999, 21, 345–363. [Google Scholar] [CrossRef]
- Strauss, A.L. Qualitative Analysis for Social Scientists; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Strauss, A.; Corbin, J. Grounded Theory Methodology: An Overview. In Handbook of Qualitative Research; Denzin, N.K., Lincoln, Y.S., Eds.; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 1994; pp. 273–285. [Google Scholar]
- Stein, M.K.; Grover, B.W.; Henningsen, M. Building student capacity for mathematical thinking and reasoning: An analysis of mathematical tasks used in reform classrooms. Am. Educ. Res. J. 1996, 33, 455–488. [Google Scholar] [CrossRef]
- Van den Heuvel-Panhuizen, M. (Ed.) Children Learn Mathematics. A Learning-Teaching Trajectory with Intermediate Attainment Targets for Calculation with Whole Numbers in Primary School; Freudenthal Institute Utrecht University & National Institute for Curriculum Development: Utrecht, The Netherlands, 2001. [Google Scholar]
- Golding, J. Reviews of fundamental constructs in mathematics education. Math. Gaz. 2005, 89, 123. [Google Scholar] [CrossRef]
- Cai, J.; Morris, A.; Hohensee, C.; Hwang, S.; Robison, V.; Cirillo, M.; Bakker, A. Maximizing the quality of learning opportunities for every student. J. Res. Math. Educ. 2020, 51, 12–25. [Google Scholar] [CrossRef]
- Jitendra, A.K.; Dupuis, D.N.; Star, J.R.; Rodriguez, M.C. The effect of schema-based instruction on the proportional thinking of students with mathematics difficulties with and without reading difficulties. J. Learn. Disabil. 2016, 49, 354–367. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Xin, Y.P. A follow-up meta-analysis for word-problem-solving interventions for students with mathematics difficulties. J. Educ. Res. 2012, 105, 303–318. [Google Scholar] [CrossRef]
- Fuchs, D.; Fuchs, L.; Mathes, P.; Simmons, D. Peer-assisted learning strategies: Making classrooms more responsive to diversity. Am. Educ. Res. J. 1997, 34, 174–206. [Google Scholar] [CrossRef]
- Haydon, T.; Maheady, L.; Hunter, W. Effects of numbered heads together on the daily quiz scores and on-task behavior of students with disabilities. J. Behav. Educ. 2010, 19, 222–238. [Google Scholar] [CrossRef]

| External Representations of Multiplications | Multiplicative Situations and Structure | ||||
|---|---|---|---|---|---|
| Equal Groups | Multiplicative Comparison | Rectangular Array Rectangular Area | Cartesian Product | ||
| Grouping model | A model of grouping of objects having the same number in each group. | Can be represented | Can be represented | ||
| Number-line model | A number line model equally divided by constant intervals and drawing regular arcs of each interval. | Can be represented | Can be represented | ||
| Array model | A model that uniformly arranges several objects in a rectangular shape of rows and columns. | Can be represented | Can be represented | Can be represented | Can be represented |
| Combinations | A model that identifies possible ordered pairs made between two or more sets. | Can be represented | |||
| Purpose | Description in the Lesson Design Activity |
|---|---|
| Understand objectives of the lesson (A state standard for 3rd grade math was provided) | You want to teach a math lesson on multiplication 3.OA.1 Interpret products of whole numbers, e.g., interpret 5 × 7 as the total number of objects in five groups of seven objects each. (Note: These standards are written with the convention that a × b means a groups of b objects each; however, because of the commutative property, students may also interpret 5 × 7 as the total number of objects in seven groups of five objects each). |
| Understand learners and plan a lesson for a typically performing student | Jose is a typically performing 3rd grade student in terms of grade level scores on mathematical assessments. |
| Understand learners and modify/accommodate a lesson for students with MLD | Liam is a 3rd grade student with MLD. He has difficulty counting backwards, difficulty remembering ‘basic’ facts, is slow to perform calculations, has weak mental arithmetic skills, finds Addition is often the default operation and has high levels of mathematics anxiety. Liam’s strengths include a strong work ethic, the desire to please the teachers, and the ability to work well with classmates. |
| Categories | Properties | Codes and Sub-Codes | Description | |
|---|---|---|---|---|
| Mathematical strategies | Multiplicative concept | Situation modeled |
| The distinguishable cases of situations that the multiplication modeled |
| External representation |
| External representations reflect the diversity of situations | ||
| Types of representing the multiplicative concept | Visual aid | Draw a diagram, pictorial representation | ||
| Physical experience | Hands-on activity, using manipulatives | |||
| Symbolic objectification | Symbol ×, multiplication expressions or equations | |||
| Verbal expression | Focus on the meaning of specific words, such as “groups” for multiplier and “objects” for multiplicand | |||
| Contextual transition | Storytelling using the real-life context: historical, cultural, and artificial examples | |||
| Lesson design elements | Articulation of expectations | Mentioned the standard | Revisited standard/key concept | |
| Stated learning objectives | Stated observable and measurable learning objectives | |||
| None | No discussion of goals/objectives | |||
| Instructional activity | Task selection and development |
| Low: Immediate/not complicated task, simply using a number, procedural—a product of multiplication is a single-digit number Intermediate: Procedural—a product of multiplication greater than 10; conceptual–easily convertible to multiplication expressions High: Challenging task, open-ended, conceptual—not easily convertible to multiplication expressions | |
| Contextualized: Changing the number or formula Abstract: Changing the story or material of the task | |||
| Instructional structures |
| Whole group instruction; Peer tutor, Group work–centers; Independent work | ||
| Time for individualized support | |||
| Instructional progress |
| Begin with teacher directed modeling/demonstrating/explaining; “I do/You do/We do”; explicit; conventional Begin with student-directed discovery/project-based + group discussion | ||
| Concrete  Concreteness fading Concreteness fading  Abstract Abstract | |||
| Formative assessment | Gathering/sharing | Have students share/present their solutions/work | ||
| Attending/interpreting | Looking into patterns or analyzing students’ work | |||
| Supporting/feedback | Discuss ideas to use the interpretation of students’ work for instruction or to support students learning | |||
| External Representations of Equal Group Situation | Jose | Liam |
|---|---|---|
| Grouping model | 11 | 2 |
| Number-line model | 1 | 2 |
| Array model | 6 | 2 |
| Combination model | 0 | 0 |
| Sub-total | 18 | 6 |
| Student Profile | Type of Representations | Sub-Total | ||||
|---|---|---|---|---|---|---|
| Visual Aid | Physical Experience | Symbolic Objectification | Verbal Expression | Contextual Transition | ||
| Typical | 16 (30.77%) | 15 (28.85%) | 11 (21.15%) | 5 (9.62%) | 5 (9.62%) | 52 |
| MLD | 7 (28%) | 15 (60%) | 0 | 0 | 3 (12%) | 25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.-J.; Han, C.; Kim, H.-j.; Herner-Patnode, L. Teaching Multiplication to Students with Mathematical Learning Disabilities (MLD): Analysis of Preservice Teachers’ Lesson Design. Sustainability 2021, 13, 11813. https://doi.org/10.3390/su132111813
Lee H-J, Han C, Kim H-j, Herner-Patnode L. Teaching Multiplication to Students with Mathematical Learning Disabilities (MLD): Analysis of Preservice Teachers’ Lesson Design. Sustainability. 2021; 13(21):11813. https://doi.org/10.3390/su132111813
Chicago/Turabian StyleLee, Hea-Jin, Chaereen Han, Hee-jeong Kim, and Leah Herner-Patnode. 2021. "Teaching Multiplication to Students with Mathematical Learning Disabilities (MLD): Analysis of Preservice Teachers’ Lesson Design" Sustainability 13, no. 21: 11813. https://doi.org/10.3390/su132111813
APA StyleLee, H.-J., Han, C., Kim, H.-j., & Herner-Patnode, L. (2021). Teaching Multiplication to Students with Mathematical Learning Disabilities (MLD): Analysis of Preservice Teachers’ Lesson Design. Sustainability, 13(21), 11813. https://doi.org/10.3390/su132111813





