An Integrated Model of Train Re-Scheduling and Control for High-Speed Railway
Abstract
:1. Introduction
2. Literature Review
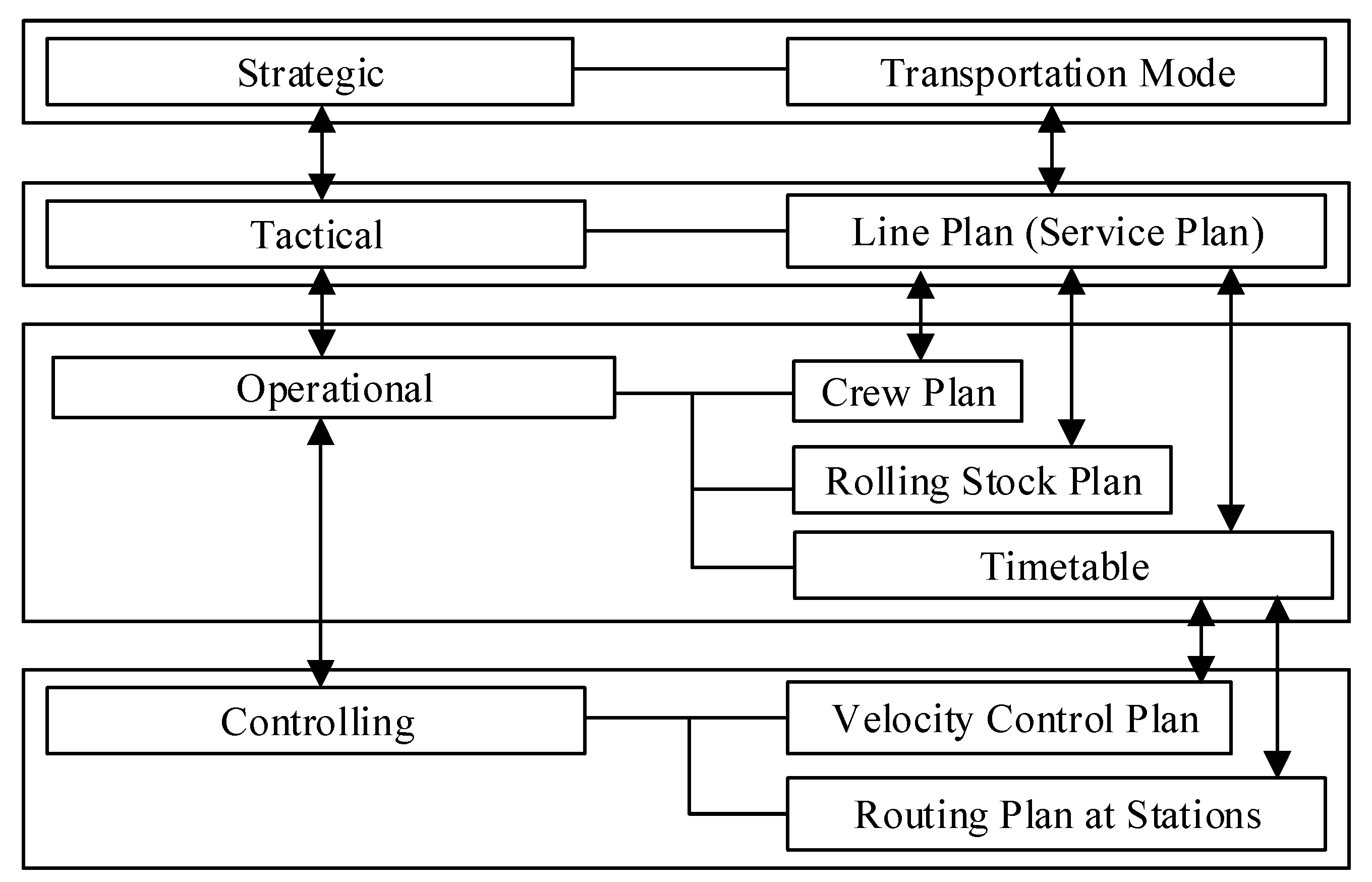
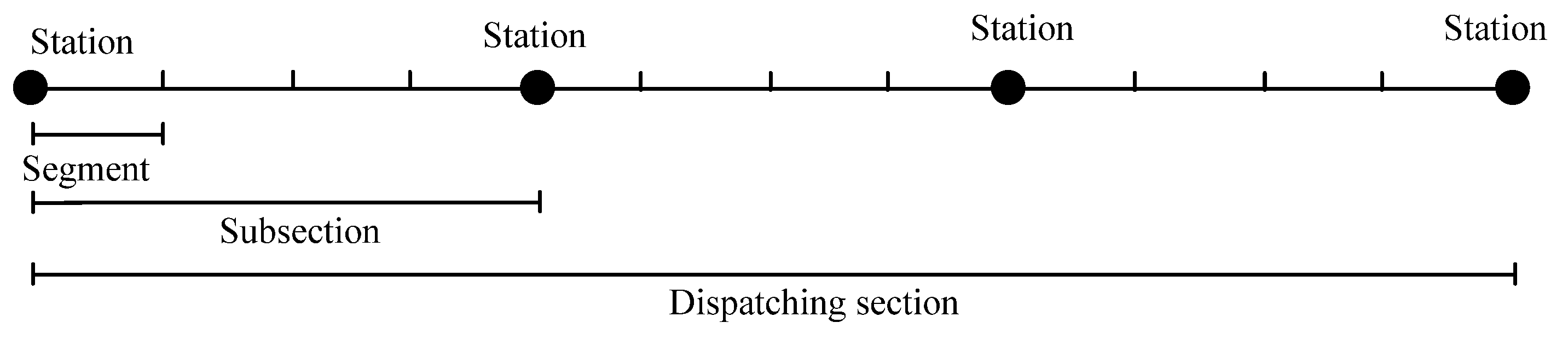
3. Integrated Model for Re-Scheduling and Control
- Intervals of the trains,
- Minimum running time at each segment,
- Minimum dwelling time at all the stations of each train.
3.1. Variables and Parameters of the Model
3.2. First Stage-Train Re-Scheduling Problem
3.2.1. Objective of Train Re-Scheduling Model
3.2.2. Constraints for Train Re-Scheduling Model
3.2.3. Mathematical Model
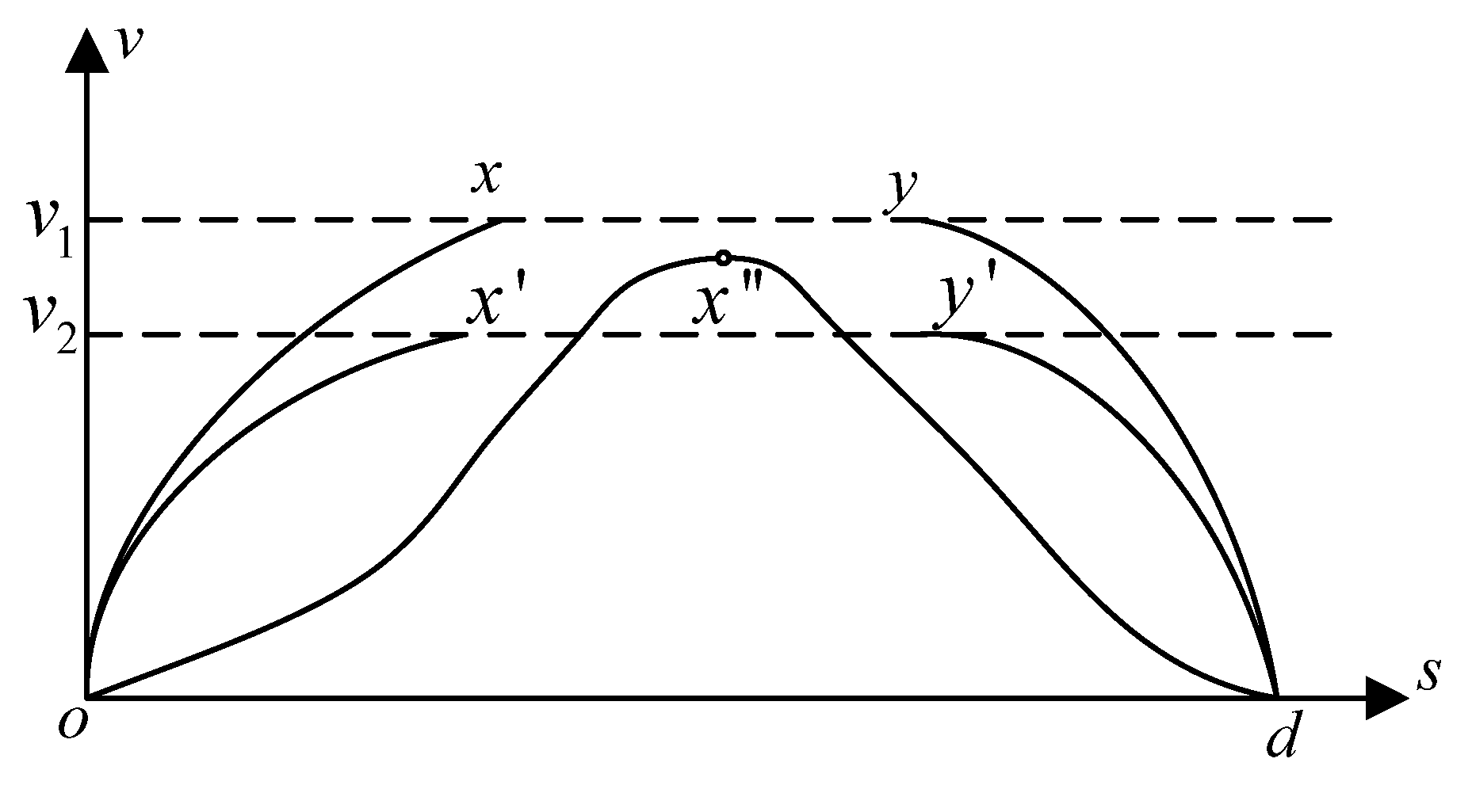
3.3. Second Stage-Train Control Problem
4. Quantum-Inspired PSO for the Integrated Model
4.1. Particle Swarm Optimization Algorithm
4.2. Quantum Particle Swarm Optimization Algorithm
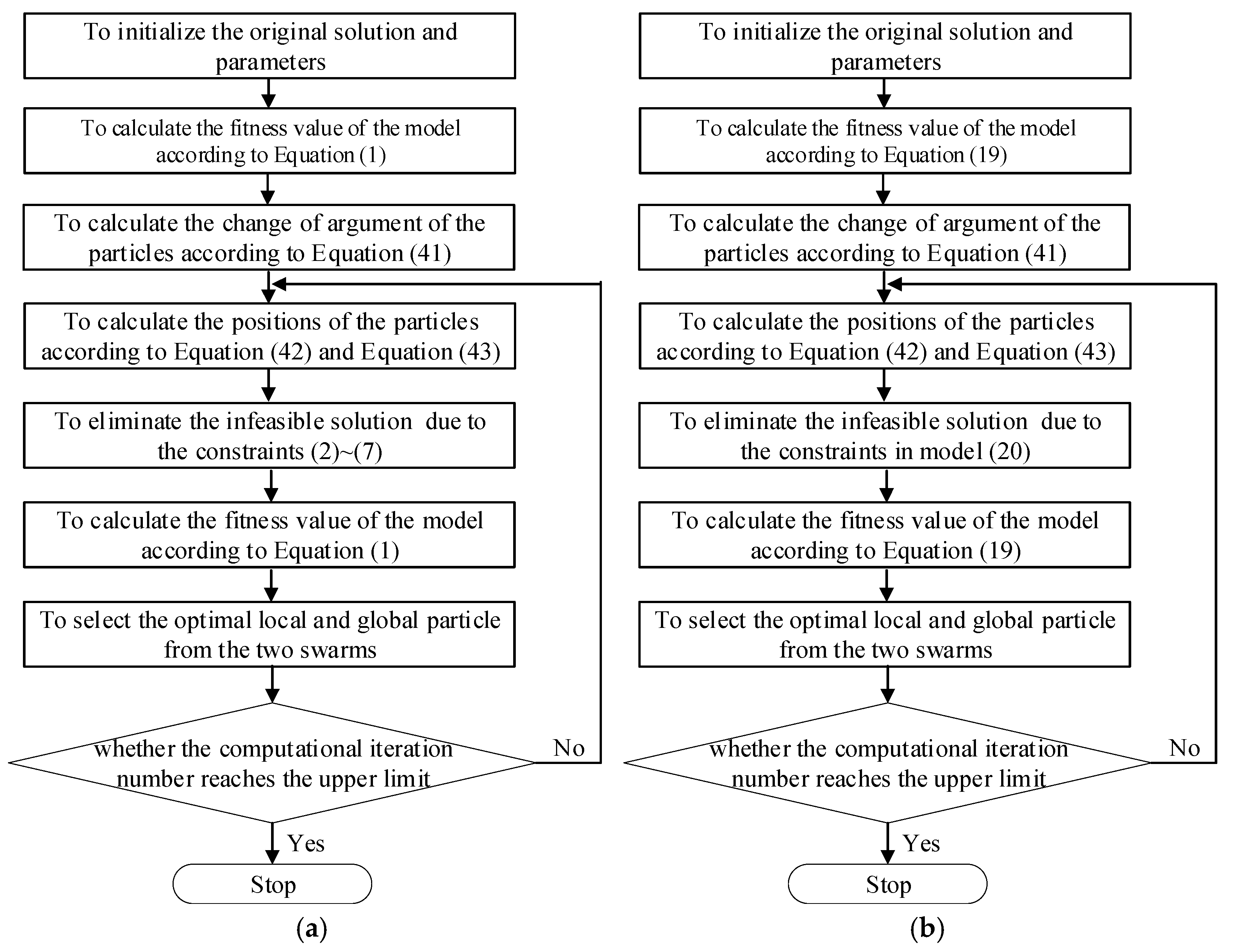
4.3. QPSO for Resolving Train Re-Scheduling and Control Problem
- Step 1: To initiate all the original solution and parameters of the model;
- Step 2: To calculate the fitness value of the model according to Equation (1) when solving train re-scheduling problem (Equation (19) when solving train control problem);
- Step 3: To calculate the change of argument of the particles according to Equation (30);
- Step 4: To calculate the positions of the particles according to Equation (35) and Equation (36);
- Step 5: To calculate the fitness value of the model according to Equation (1) when solving train re-scheduling problem (Equation (19) when solving train control problem);
- Step 6: To select the optimal local and global particle from the two swarms;
- Step 7: To check if the computational accuracy satisfies the requirements. If yes, stop; otherwise, go to step 3.
5. Computation Case and Results Analysis
5.1. Basic Data of the Computing Case
5.2. Computation Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carey, M. A model and strategy for train pathing with choice of lines, platforms and routes. Transp. Res. B Methodol. 1994, 28, 333–353. [Google Scholar] [CrossRef]
- D’Ariano, A.; Corman, F.; Pacciarelli, D.; Pranzo, M. Reordering and local rerouting strategies to manage train traffic in real time. Transp. Sci. 2008, 42, 405–419. [Google Scholar] [CrossRef]
- Michaelis, M.; Schöbel, A. Integrating line planning, timetabling, and vehicle scheduling: A customer-oriented heuristic. J. Public Transp. 2009, 1, 211–232. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.; Chen, C.Y. A heuristic for the train pathing and timetabling problem. Transp. Res. B Methodol. 2009, 43, 837–851. [Google Scholar] [CrossRef]
- Sun, Y.; Cao, C.; Wu, C. Multi-objective optimization of train routing problem combined with train scheduling on a high-speed railway network. Transp. Res. C Emerg. Technol. 2014, 44, 1–20. [Google Scholar] [CrossRef]
- Groves, G.; Roux, L.J.; Vuuren, J.H.V. Network service scheduling and routing. Int. Trans. Oper. Res. 2004, 11, 613–643. [Google Scholar] [CrossRef]
- Schöbel, A. A model for the delay management problem based on mixed-integer-programming. Electron. Notes Theor. Comput. Sci. 2001, 50, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Tőrnquist, J.; Persson, J.A. N-tracked railway traffic re-scheduling during disturbances. Transp. Res. B Methodol. 2007, 41, 342–362. [Google Scholar] [CrossRef]
- D’Ariano, A.; Pacciarelli, D.; Pranzo, M. A branch and bound algorithm for scheduling trains in a railway network. Eur. J. Oper. Res. 2007, 183, 643–657. [Google Scholar] [CrossRef]
- Dundar, S.; Şahin, I. Train re-scheduling with genetic algorithms and artificial neural networks for single-track railways. Transp. Res. C Emerg. Technol. 2013, 27, 1–15. [Google Scholar] [CrossRef]
- Meng, L.; Zhou, X. Robust single-track train dispatching model under a dynamic and stochastic environment: A scenario-based rolling horizon solution approach. Transp. Res. B Methodol. 2011, 45, 1080–1102. [Google Scholar] [CrossRef]
- Chen, D.; Ni, S.; Xu, C.; Jiang, X. Optimizing the draft passenger train timetable based on node importance in a railway network. Transp. Lett. 2019, 11, 20–32. [Google Scholar] [CrossRef]
- Chen, D.; Ni, S.; Lv, H.; Li, H. Genetic algorithm based on conflict detecting for solving departure time domains of passenger trains. Transp. Lett. 2015, 7, 181–187. [Google Scholar] [CrossRef]
- Yang, X.; Chen, A.; Wu, J.; Gao, Z.; Tang, T. An energy-efficient rescheduling approach under delay perturbations for metro systems. Transp. B Trans. Dyn. 2018, 7, 386–400. [Google Scholar] [CrossRef]
- Wen, C.; Li, Z.; Huang, P.; Lessan, J.; Fu, L.; Jiang, C. Cause-specific investigation of primary delays of Wuhan–Guangzhou HSR. Transp. Lett. 2019, 12, 451–464. [Google Scholar] [CrossRef]
- Chang, Y.; Zhu, X.; Yan, B.; Wang, L. Integrated scheduling of handling operations in railway container terminals. Transp. Lett. 2019, 11, 402–412. [Google Scholar] [CrossRef]
- Chen, S.; Sun, D. A multistate-based travel time schedule model for fixed transit route. Transp. Lett. 2019, 11, 33–42. [Google Scholar] [CrossRef]
- Corman, F. Interactions and equilibrium between rescheduling train traffic and routing passengers in microscopic delay management: A game theoretical study. Transp. Sci. 2020, 54, 758–822. [Google Scholar] [CrossRef]
- Zhu, Y.; Goverde, R.M.P. Dynamic and robust timetable rescheduling for uncertain railway disruptions. J. Rail Transp. Plan. Manag. 2020, 15, 100196. [Google Scholar] [CrossRef]
- Zinder, Y.; Lazarev, A.; Musatova, E. Rescheduling traffic on a partially blocked segment of railway with a siding. Automat. Remote Control 2020, 81, 955–966. [Google Scholar] [CrossRef]
- Mazzarello, M.; Ottaviani, E. A traffic management system for real-time traffic optimization in railways. Transp. Res. B Methodol. 2007, 41, 246–274. [Google Scholar] [CrossRef]
- Rodriguez, J. Constraint programming model for real-time trains scheduling at junctions. Transp. Res. B Methodol. 2007, 41, 231–245. [Google Scholar] [CrossRef]
- Cacchiani, V.; Caprara, A.; Toth, P. Scheduling extra freight trains on railway networks. Transp. Res. B Methodol. 2010, 44, 215–231. [Google Scholar] [CrossRef]
- Acuna-Agost, R.; Michelon, P.; Feillet, D.; Gueye, S. A MIP-based local search method for the railway re-scheduling problem. Networks 2011, 57, 69–86. [Google Scholar] [CrossRef]
- Acuna-Agost, R.; Michelon, P.; Feillet, D.; Gueye, S. SAPI: Statical analysis of propagation of incidents. A new approach for re-scheduling trains after disruptions. Eur. J. Oper. Res. 2011, 215, 227–243. [Google Scholar] [CrossRef]
- Krasemann, J.T. Design of an effective algorithm for fast response to the re-scheduling of railway traffic during disturbances. Transp. Res. C Emerg. Technol. 2012, 20, 62–78. [Google Scholar] [CrossRef]
- Almodóvar, M.; García-Ródenas, R. On-line reschedule optimization for passenger railways in case of emergencies. Comput. Oper. Res. 2013, 40, 725–736. [Google Scholar] [CrossRef]
- Dalapati, P.; Padhy, A.; Mishra, B.; Dutta, A.; Bhattacharya, S. Real-time collision handling in railway transport network: An agent-based modeling and simulation approach. Transp. Lett. 2019, 11, 458–468. [Google Scholar] [CrossRef]
- Altazinab, E.; Dauzère-Pérèsbc, S.; Ramond, F.; Trefond, S. A multi-objective optimization-simulation approach for real time rescheduling in dense railway systems. Eur. J. Oper. Res. 2020, 286, 662–672. [Google Scholar] [CrossRef]
- Huang, Y.; Mannino, C.; Yang, L.; Tang, T. Coupling time-indexed and big-M formulations for real-time train scheduling during metro service disruptions. Transp. Res. B Methodol. 2020, 133, 38–61. [Google Scholar] [CrossRef]
- Dong, H.R.; Ning, B.; Cai, B.; Hou, Z. Automatic train control system development and simulation for high-speed railways. IEEE Circuits Syst. Mag. 2010, 10, 6–18. [Google Scholar] [CrossRef]
- Song, Q.; Song, Y.D.; Tang, T.; Ning, B. Computationally inexpensive tracking control of high-speed trains with traction/braking saturation. IEEE Intell. Transp. Syst. 2011, 12, 1116–1125. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Wang, Y.P. Coordinated control among high-speed trains based on model predictive control. Key Eng. Mater. 2011, 467, 2143–2148. [Google Scholar] [CrossRef]
- Yang, L.X.; Li, K.P.; Gao, Z.Y.; Li, X. Optimizing trains movement on a railway network. Omega 2012, 40, 619–633. [Google Scholar] [CrossRef]
- Wang, Y.H.; Schutter, B.D.; van den Boom, T.J.J.; Ning, B. Optimal trajectory planning for trains—A pseudospectral method and a mixed integer linear programming approach. Transp. Res. C Emerg. Technol. 2013, 29, 97–144. [Google Scholar] [CrossRef]
- Faieghi, M.; Jalali, A.; Mashhadi, S.K.M. Robust adaptive cruise control of high-speed trains. ISA Trans. 2014, 53, 533–541. [Google Scholar] [CrossRef]
- Li, S.K.; Yang, L.X.; Li, K.P.; Gao, Z. Robust sampled-data cruise control scheduling of high-speed train. Transp. Res. Emerg. Technol. 2014, 46, 274–283. [Google Scholar] [CrossRef]
- Su, S.; Tang, T.; Roberts, C. A cooperative train control model for energy saving. IEEE Trans. Intell. Transp. 2015, 16, 622–631. [Google Scholar] [CrossRef]
- Bersani, C.; Qiu, A.; Sacile, R.; Sallak, M.; Schon, W. Rapid, robust, distributed evaluation and control of train scheduling on a single line track. Control Eng. Pract. 2015, 35, 12–21. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Gao, Z. Coordinated cruise control for high-speed train movements based on a multi-agent model. Transp. Res. C Emerg. Technol. 2015, 56, 281–292. [Google Scholar] [CrossRef]
- Xu, P.; Corman, F.; Peng, Q.; Luan, X. A train rescheduling model integrating speed management during disruptions of high-speed traffic under a quasi-moving block system. Transp. Res. B Methodol. 2017, 104, 638–666. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the CNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Meng, X.; Jia, L.; Xiang, W.; Xu, J. Train re-scheduling based on an improved fuzzy linear programming model. Kybernetes 2015, 44, 1472–1503. [Google Scholar] [CrossRef]
- Meng, X.; Jia, L.; Qin, Y. Train timetable optimizing and rescheduling based on improved particle swarm algorithm. Transp. Res. Rec. 2010, 2197, 71–79. [Google Scholar] [CrossRef]
- Meng, X.; Wang, Y.; Xiang, W.; Jia, L. An integrated model for train rescheduling and station track assignment. IET Intell. Transp. Syst. 2021, 15, 17–30. [Google Scholar] [CrossRef]

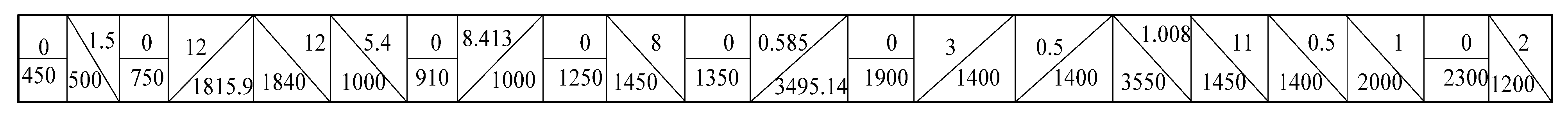
| Variables and Parameters | Description | Role |
|---|---|---|
| arrival time of train i at station k | decision variable | |
| departure time of train i at station k | decision variable | |
| acceleration of train i at the kth segment of section j in the accelerating process | decision variable | |
| acceleration of train i at the kth segment of section j in the decelerating process (negative) | decision variable | |
| time consumed at the kth segment of section j in the accelerating process by train i | decision variable | |
| time consumed at the kth segment of section j in the decelerating process by train i | decision variable | |
| time consumed at the kth segment of section j when it runs at a constant speed by train i | decision variable | |
| original planned arrival time | parameter | |
| original planned departure time | parameter | |
| interval between two arrivals station j | parameter | |
| interval between two departures station j | parameter | |
| minimum interval between a train’s leaving and another train’s arrival at a station from the same direction | parameter | |
| minimum running time of train i on the section between station j and j + 1 | parameter | |
| minimum dwelling time of train i at station j | parameter | |
| energy consumed of train i at the kth segment of section j | intermediate variable | |
| tractive force of train i at the kth segment of section j in the accelerating process | intermediate variable | |
| braking force of train i at the kth segment of section j in the decelerating process | intermediate variable | |
| tractive force of train i at the kth segment of section j when the train runs at a constant speed | intermediate variable | |
| resistance force put on train i at the kth segment of section j | intermediate variable | |
| distance of kth segment of section j | parameter | |
| distance train i runs at the kth segment of section j in the accelerating process | intermediate variable | |
| distance train i runs at the kth segment of section j in the decelerating process | intermediate variable | |
| distance train i runs at the kth segment of section j when it runs at a constant speed | intermediate variable |
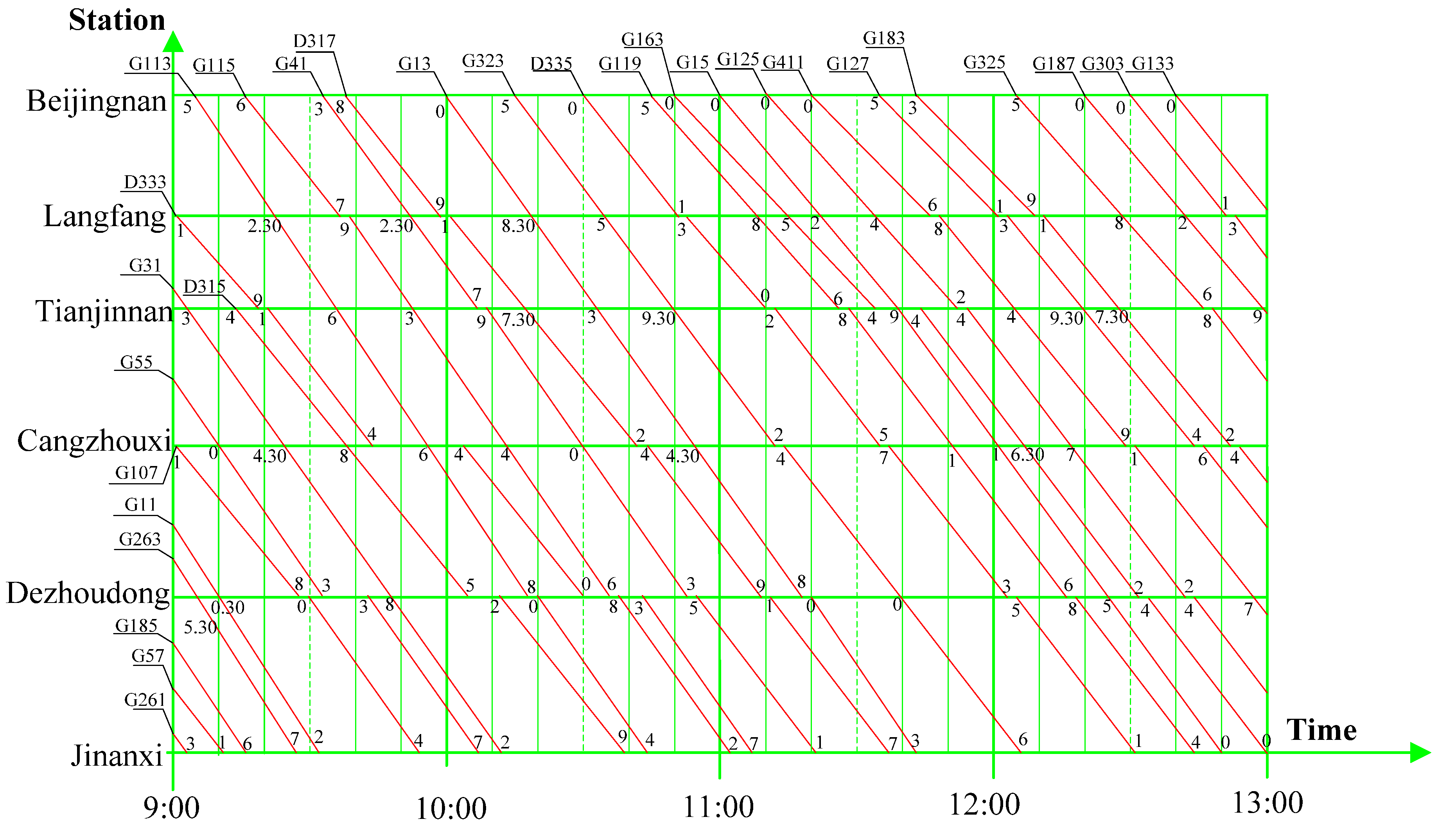
| Train ID | Beijingnan | Langfang | Tianjinnan | Cangzhouxi | Dezhoudong | Jinanxi | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Departure | Arrival | Departure | Arrival | Departure | Arrival | Departure | Arrival | Departure | Arrival | |
| G261 | - | - | - | - | - | - | - | - | - | 9:03:00 |
| G57 | - | - | - | - | - | - | - | - | - | 9:11:00 |
| G185 | - | - | - | - | - | - | - | - | - | 9:16:00 |
| G263 | - | - | - | - | - | - | - | 9:05:30 | 9:05:30 | 9:27:00 |
| G11 | - | - | - | - | - | - | - | 9:10:30 | 9:10:30 | 9:32:00 |
| G107 | - | - | - | - | - | - | 9:01:00 | 9:28:00 | 9:30:00 | 9:54:00 |
| G55 | - | - | - | - | - | 9:10:00 | 9:10:00 | 9:33:00 | 9:43:00 | 10:07:00 |
| D315 | - | - | - | - | 9:14:00 | 9:38:00 | 9:38:00 | 10:05:00 | 10:12:00 | 10:39:00 |
| D333 | - | - | 9:01:00 | 9:19:00 | 9:21:00 | 9:44:00 | 10:04:00 | 10:30:00 | 10:43:00 | 11:07:00 |
| G31 | - | - | - | 9:03:00 | 9:03:00 | 9:24:30 | 9:24:30 | 9:48:00 | 9:48:00 | 10:02:00 |
| G113 | 9:05:00 | 9:22:30 | 9:22:30 | 9:36:00 | 9:36:00 | 9:56:00 | 9:56:00 | 10:18:00 | 10:20:00 | 10:44:00 |
| G115 | 9:16:00 | 9:37:00 | 9:39:00 | 9:53:00 | 9:53:00 | 10:14:00 | 10:14:00 | 10:36:00 | 10:38:00 | 11:02:00 |
| G41 | 9:33:00 | 9:52:30 | 9:52:30 | 10:07:00 | 10:09:00 | 10:30:00 | 10:30:00 | 10:53:00 | 10:55:00 | 11:19:00 |
| D317 | 9:38:00 | 9:59:00 | 10:01:00 | 10:17:30 | 10:17:30 | 10:42:00 | 10:44:00 | 11:09:00 | 11:11:00 | 11:37:00 |
| G13 | 10:00:00 | 10:18:30 | 10:18:30 | 10:33:00 | 10:33:00 | 10:54:30 | 10:54:30 | 11:18:00 | 11:18:00 | 11:43:00 |
| G323 | 10:15:00 | 10:35:00 | 10:35:00 | 10:49:30 | 10:49:30 | 11:12:00 | 11:14:00 | 11:40:00 | 11:40:00 | 12:06:00 |
| D335 | 10:30:00 | 10:51:00 | 10:53:00 | 11:10:00 | 11:12:00 | 11:35:00 | 11:37:00 | 12:03:00 | 12:05:00 | 12:31:00 |
| G119 | 10:45:00 | 11:08:00 | 11:08:00 | 11:26:00 | 11:28:00 | 11:51:00 | 11:51:00 | 12:16:00 | 12:18:00 | 12:44:00 |
| G163 | 10:50:00 | 11:15:00 | 11:15:00 | 11:34:00 | 11:44:00 | 12:06:30 | 12:06:30 | 12:32:00 | 12:34:00 | 13:00:00 |
| G15 | 11:00:00 | 11:22:00 | 11:22:00 | 11:39:00 | 11:39:00 | 12:01:00 | 12:01:00 | 12:25:00 | 12:25:00 | - |
| G125 | 11:10:00 | 11:34:00 | 11:34:00 | 11:52:00 | 11:54:00 | 12:17:00 | 12:17:00 | 12:42:00 | 12:44:00 | - |
| G411 | 11:20:00 | 11:46:00 | 11:48:00 | 12:04 | 12:04:00 | 12:29:00 | 12:31:00 | 12:57:00 | 12:57:00 | - |
| G127 | 11:35:00 | 12:01:00 | 12:03:00 | 12:19:30 | 12:19:30 | 12:44:00 | 12:46:00 | - | - | - |
| G183 | 11:43:00 | 12:09:00 | 12:11:00 | 12:27:30 | 12:27:30 | 12:52:00 | 12:54:00 | - | - | - |
| G325 | 12:05:00 | 12:28:00 | 12:28:00 | 12:46:00 | 12:48:00 | - | - | - | - | - |
| G187 | 12:20:00 | 12:42:00 | 12:42:00 | 12:59:00 | 12:59:00 | - | - | - | - | - |
| G303 | 12:30:00 | 12:51:00 | 12:53:00 | - | - | - | - | - | - | - |
| G133 | 12:40:00 | - | - | - | - | - | - | - | - | - |
| Segment | Minimal Running Time (Measurement Unit: Minutes) | |
|---|---|---|
| “G” Trains | “D” Trains | |
| Beijingnan-Langfang | 18 | 21.5 |
| Langfang-Tianjinnan | 11.5 | 14.5 |
| Tianjinnan-Cangzhouxi | 16 | 18 |
| Cangzhouxi-Dezhoudong | 18 | 21 |
| Dezhoudong-Jinanxi | 23 | 26 |
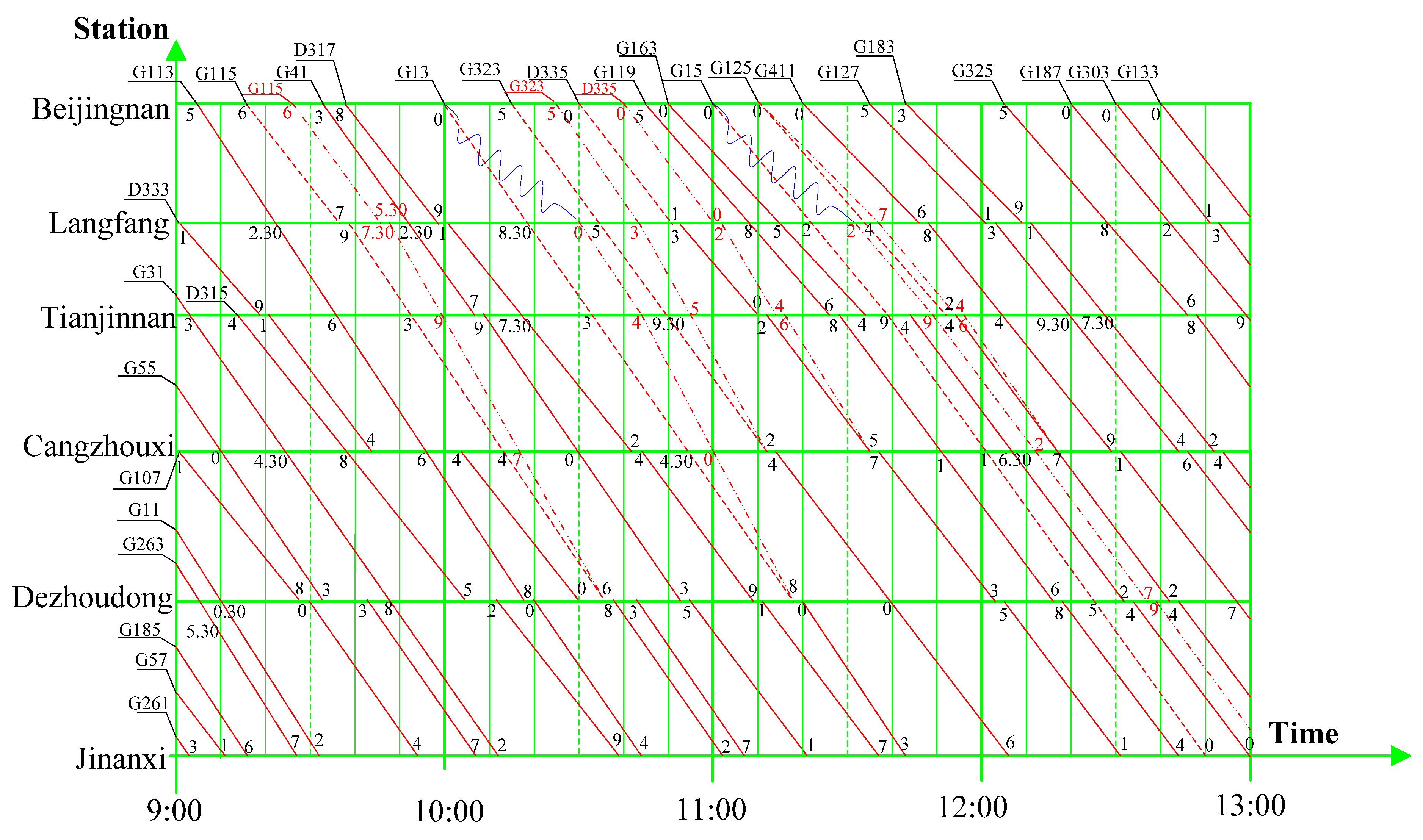
| Train ID | Beijingnan | Langfang | Tianjinnan | Cangzhouxi | Dezhoudong | Jinanxi | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Departure | Arrival | Departure | Arrival | Departure | Arrival | Departure | Arrival | Departure | Arrival | |
| G115 | 9:26:00 | 9:45:30 | 9:47:30 | 9:59:00 | 9:59:00 | 10:17:00 | 10:17:00 | 10:36:00 | 10:38:00 | 11:02:00 |
| G13 | 10:00:00 | 10:30:00 | 10:30:00 | 10:44:00 | 10:44:00 | 11:00:00 | 11:00:00 | 11:18:00 | 11:18:00 | 11:43:00 |
| G323 | 10:25:00 | 10:43:00 | 10:43:00 | 10:55:00 | 10:55:00 | 11:12:00 | 11:14:00 | 11:40:00 | 11:40:00 | 12:06:00 |
| D335 | 10:40:00 | 11:00:00 | 11:00:00 | 11:14:00 | 11:16:00 | 11:35:00 | 11:37:00 | 12:03:00 | 12:05:00 | 12:31:00 |
| G15 | 11:00:00 | 11:32:00 | 11:32:00 | 11:49:00 | 11:49:00 | 12:12:00 | 12:12:00 | 12:37:00 | 12:37:00 | - |
| G125 | 11:10:00 | 11:37:00 | 11:37:00 | 11:54:00 | 11:56:00 | 12:17:00 | 12:17:00 | 12:42:00 | 12:44:00 | - |
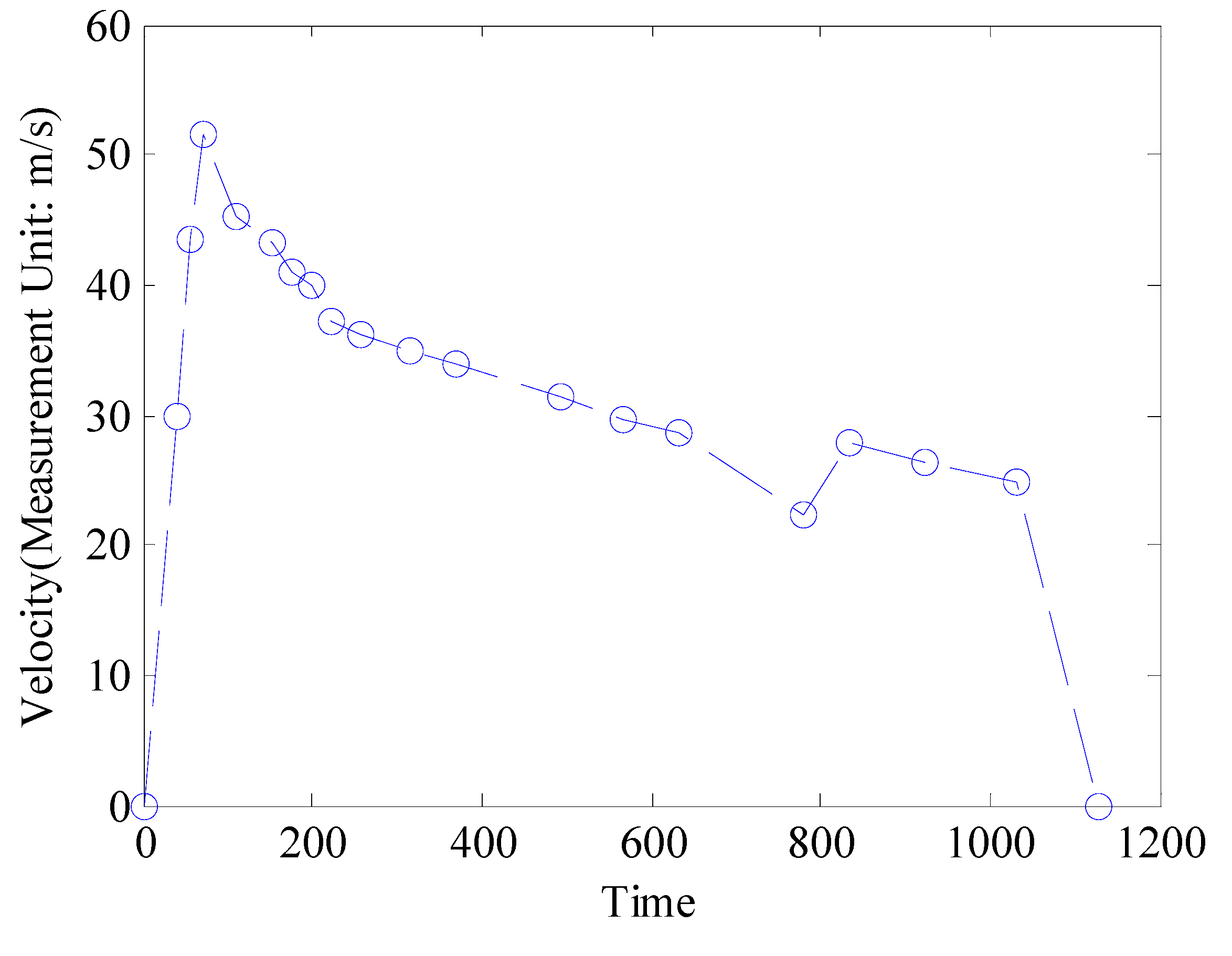
| Segments | Operating Mode | Acceleration (m/s2) | Running Distance (m) | T (s) | Error (m) | E (109J) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Accelerating | 0.5 | 450.000 | 0 | 0 | 0 | 42.426 | 21.213 | 450.000 | 0 | 1.8208 |
| 2 | Accelerating | 0.5 | 500.000 | 0 | −1.500 | 30 | 14.833 | 37.417 | 500.000 | 0 | 0.2274 |
| 3 | Accelerating | 0.5 | 750.000 | 0 | 0 | 43.58899 | 15.778 | 51.478 | 750.000 | 0 | 0.3062 |
| 4 | Coasting | Variable | 1815.864 | 0.000 | 12.000 | 51.478 | 37.553 | 45.240 | 1815.900 | −0.036 | 0 |
| 5 | Coasting | Variable | 1839.140 | 0.000 | 1.000 | 45.240 | 41.582 | 43.185 | 1840.000 | −0.860 | 0 |
| 6 | Coasting | Variable | 1000.805 | 0.000 | 5.400 | 43.185 | 23.752 | 41.041 | 1000.000 | 0.805 | 0 |
| 7 | Coasting | Variable | 910.365 | 0.900 | 0.000 | 41.041 | 22.432 | 40.076 | 910.000 | 0.365 | 0 |
| 8 | Coasting | Variable | 1000.377 | 0.000 | 8.413 | 40.076 | 25.916 | 37.085 | 1000.000 | 0.377 | 0 |
| 9 | Coasting | Variable | 1250.959 | 0.000 | 0.000 | 37.085 | 34.161 | 36.106 | 1250.000 | 0.959 | 0 |
| 10 | Coasting | Variable | 1450.053 | 0.000 | 0.000 | 36.106 | 55.983 | 34.991 | 1450.000 | 0.053 | 0 |
| 11 | Coasting | Variable | 1350.412 | 0.000 | 0.000 | 34.991 | 54.657 | 33.972 | 1350.000 | 0.412 | 0 |
| 12 | Coasting | Variable | 3495.152 | 0.000 | 0.000 | 33.972 | 122.768 | 31.417 | 3495.140 | 0.012 | 0 |
| 13 | Coasting | Variable | 1900.591 | 0.000 | 0.585 | 31.417 | 75.322 | 29.715 | 1900.000 | 0.591 | 0 |
| 14 | Coasting | Variable | 1400.511 | 0.050 | 0.000 | 29.715 | 64.550 | 28.728 | 1400.000 | 0.511 | 0 |
| 15 | Coasting | Variable | 3550.377 | 0.000 | 3.000 | 28.728 | 157.574 | 22.240 | 3550.000 | 0.377 | 0 |
| 16 | Accelerating | 0.10 | 1400.000 | 0.000 | 0.500 | 22.240 | 65.920 | 27.832 | 1400.000 | 0.000 | 0.2407 |
| 17 | Coasting | Variable | 2000.202 | 0.080 | 0.000 | 27.832 | 100.597 | 26.446 | 2000.000 | 0.202 | 0 |
| 18 | Coasting | Variable | 2300.374 | 0.000 | 0.000 | 26.446 | 117.553 | 24.956 | 2300.000 | 0.374 | 0 |
| 19 | Braking | −0.26 | 1200.000 | 0.090 | 0.000 | 24.956 | 96.169 | 0.000 | 1200.000 | 0.000 | 0 |
| Summary | - | - | 29,560.728 | - | - | - | 1169.527 | - | 29,561.040 | −0.312 | 2.5951 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Wang, Y.; Lin, L.; Li, L.; Jia, L. An Integrated Model of Train Re-Scheduling and Control for High-Speed Railway. Sustainability 2021, 13, 11933. https://doi.org/10.3390/su132111933
Meng X, Wang Y, Lin L, Li L, Jia L. An Integrated Model of Train Re-Scheduling and Control for High-Speed Railway. Sustainability. 2021; 13(21):11933. https://doi.org/10.3390/su132111933
Chicago/Turabian StyleMeng, Xuelei, Yahui Wang, Li Lin, Lei Li, and Limin Jia. 2021. "An Integrated Model of Train Re-Scheduling and Control for High-Speed Railway" Sustainability 13, no. 21: 11933. https://doi.org/10.3390/su132111933
APA StyleMeng, X., Wang, Y., Lin, L., Li, L., & Jia, L. (2021). An Integrated Model of Train Re-Scheduling and Control for High-Speed Railway. Sustainability, 13(21), 11933. https://doi.org/10.3390/su132111933






