What Factors Affect the RMB Carry Trade Return for Sustainability? An Empirical Analysis by Using an ARDL Model
Abstract
:1. Introduction
2. Literature Review
3. Realization of the Carry Trade
3.1. Interest Differential and Exchange-Rate Movement
3.2. Capital Mobility
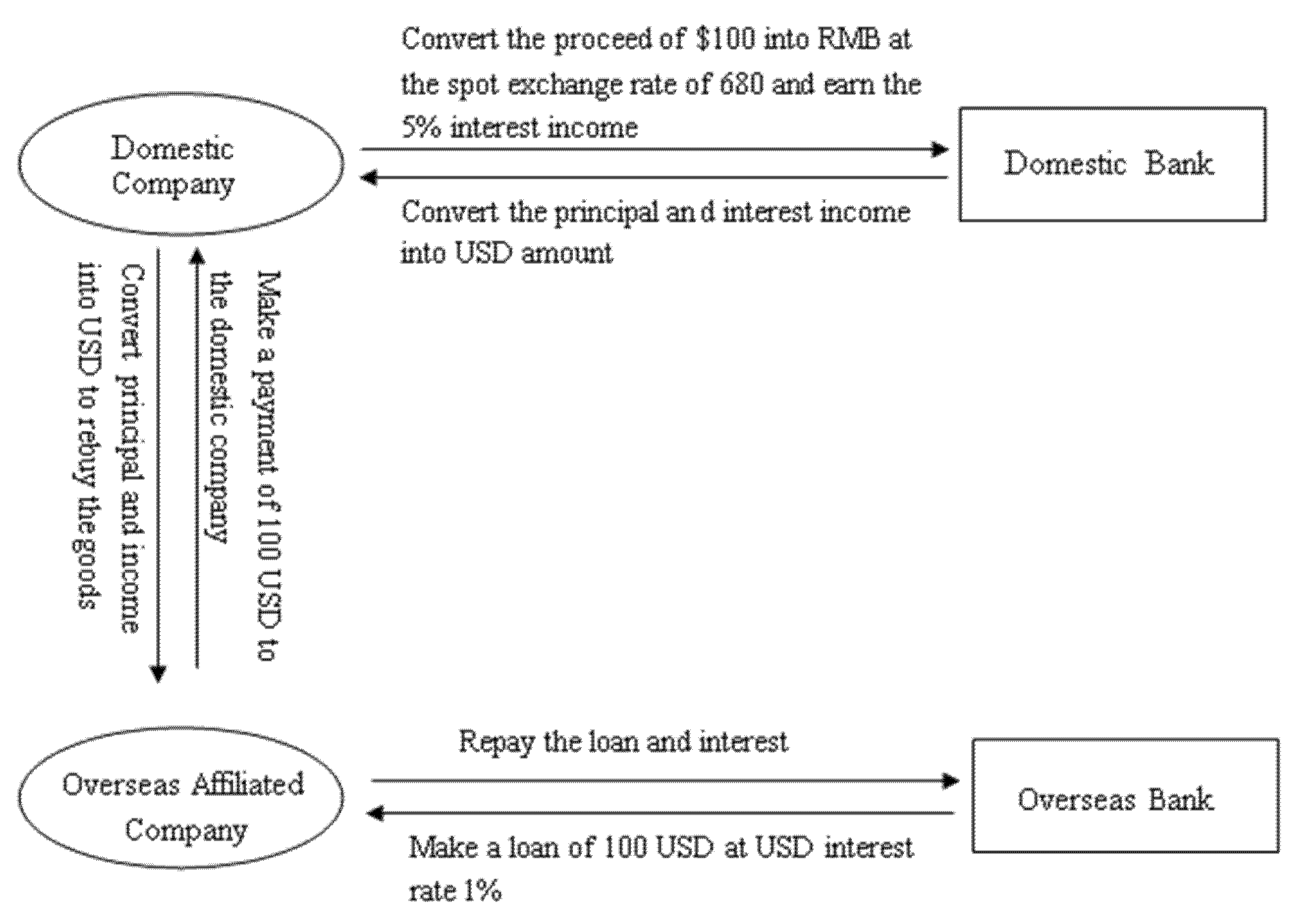
3.3. Realization of the RMB Carry Trade
4. Model Design
4.1. Constructing the Carry Trade
4.2. Explanatory Variables
4.3. Model Specification
5. Empirical Results
5.1. Data
5.2. Stationary Test
5.3. RMB/USD UIP Test
5.4. Model Estimation
5.4.1. Bounds Test
5.4.2. Parameter Estimation
5.5. Robustness Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berg, K.A.; Mark, N.C. Global macro risks in currency excess returns. J. Empir. Financ. 2018, 45, 300–315. [Google Scholar] [CrossRef] [Green Version]
- Berg, K.A.; Mark, N.C. Measures of global uncertainty and carry-trade excess returns. J. Int. Money Financ. 2018, 88, 212–227. [Google Scholar] [CrossRef]
- Engel, C.; Lee, D.; Liu, C.; Liu, C.; Wu, S.P.Y. The uncovered interest parity puzzle, exchange rate forecasting, and Taylor rules. J. Int. Money Financ. 2019, 95, 317–331. [Google Scholar] [CrossRef] [Green Version]
- Galí, J. Uncovered interest parity, forward guidance and the exchange rate. J. Money Credit. Bank. 2020, 52, 465–496. [Google Scholar] [CrossRef]
- Menkhoff, L.; Sarno, L.; Schmeling, M.; Schrimpf, A. Carry trades and global foreign exchange volatility. J. Financ. 2012, 67, 681–718. [Google Scholar] [CrossRef] [Green Version]
- Ilut, C. Ambiguity aversion: Implications for the uncovered interest rate parity puzzle. Am. Econ. J. Macroecon. 2012, 4, 33–65. [Google Scholar] [CrossRef] [Green Version]
- Colacito, R.; Croce, M.M. International asset pricing with recursive preferences. J. Financ. 2013, 68, 2651–2686. [Google Scholar] [CrossRef] [Green Version]
- Brunnermeier, M.K.; Pedersen, L.H. Market liquidity and funding liquidity. Rev. Financ. Stud. 2009, 22, 2201–2238. [Google Scholar] [CrossRef] [Green Version]
- Farhi, E.; Fraiberger, S.P.; Gabaix, X.; Ranciere, R.; Verdelhan, A. Crash Risk in Currency Markets; National Bureau of Economic Research: Cambridge, MA, USA, 2009; pp. 898–2937. [Google Scholar]
- Ismailov, A.; Rossi, B. Uncertainty and deviations from uncovered interest rate parity. J. Int. Money Financ. 2018, 88, 242–259. [Google Scholar] [CrossRef]
- Fama, E.F. Forward and spot exchange rates. J. Monet. Econ. 1984, 14, 319–338. [Google Scholar] [CrossRef]
- Li, D.; Ghoshray, A.; Morley, B. Uncovered Interest Parity and the Risk Premium; Working Paper; University of Bath, Department of Economics: Bath, UK, 2011. [Google Scholar]
- McCallum, B.T. A reconsideration of the uncovered interest parity relationship. J. Monet. Econ. 1994, 33, 105–132. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.; Xiao, J.; Ye, H. Disguised carry trade and the transmission of global liquidity shocks: Evidence from China’s goods trade data. J. Int. Money Financ. 2020, 104, 102180. [Google Scholar] [CrossRef]
- Zhang, M.; Balding, C. Carry Trade Dynamics under Capital Controls: The Case of China. 2015. Available online: https://ssrn.com/abstract=2623794 (accessed on 7 November 2021).
- Zhao, W. RMB Carry Trade, Commodity Carry and Trade Imbalance of China. Ph.D. Thesis, Central University of Finance and Economics, Beijing, China, 2017. (In Chinese). [Google Scholar]
- Brunnermeier, M.K.; Nagel, S.; Pedersen, L.H. Carry trades and currency crashes. NBER Macroecon. Annu. 2008, 23, 313–348. [Google Scholar] [CrossRef] [Green Version]
- Plantin, G.; Shin, H.S. Carry Trades, Monetary Policy and Speculative Dynamics. 2011. Available online: https://ssrn.com/abstract=1758433 (accessed on 7 November 2021).
- Fratzscher, M. What explains global exchange rate movements during the financial crisis? J. Int. Money Financ. 2009, 28, 1390–1407. [Google Scholar] [CrossRef] [Green Version]
- Gagnon, J.; Chaboud, A. What can the data tell us about carry trades in Japanese yen? 2007. Available online: https://ssrn.com/abstract=1006193 (accessed on 7 November 2021).
- Melvin, M.; Taylor, M.P. The crisis in the foreign exchange market. J. Int. Money Financ. 2009, 28, 1317–1330. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, S.; Zlate, A. Capital flows to emerging market economies: A brave new world? J. Int. Money Financ. 2014, 48, 221–248. [Google Scholar] [CrossRef] [Green Version]
- Aizenman, J.; Binici, M.; Hutchison, M.M. The Transmission of Federal Reserve Tapering News to Emerging Financial Markets. Int. J. Cent. Bank. 2016, 12, 317–356. [Google Scholar]
- Korinek, A. Regulating capital flows to emerging markets: An externality view. J. Int. Econ. 2018, 111, 61–80. [Google Scholar] [CrossRef] [Green Version]
- Pesaran, M.H.; Shin, Y.; Smith, R.J. Bounds testing approaches to the analysis of level relationships. J. Appl. Econom. 2001, 16, 289–326. [Google Scholar] [CrossRef]
- Nkoro, E.; Uko, A.K. Autoregressive Distributed Lag (ARDL) cointegration technique: Application and interpretation. J. Stat. Econom. Methods 2016, 5, 63–91. [Google Scholar]
- Zheng, L. Does 811 Exchange Rate Reform Enhance the Market-Orientation and Benchmark Status of the Central Parity Rate? J. Financ. Res. 2017, 4, 1–16. [Google Scholar]
- Londono, J.M.; Zhou, H. Variance risk premiums and the forward premium puzzle. J. Financ. Econ. 2017, 124, 415–440. [Google Scholar] [CrossRef] [Green Version]
- Yung, J. Can interest rate factors explain exchange rate fluctuations? J. Empir. Financ. 2021, 61, 34–56. [Google Scholar] [CrossRef]
- Ready, R.; Roussanov, N.; Ward, C. Commodity trade and the carry trade: A tale of two countries. J. Financ. 2017, 72, 2629–2684. [Google Scholar] [CrossRef]
- Lustig, H.; Roussanov, N.; Verdelhan, A. Countercyclical currency risk premia. J. Financ. Econ. 2014, 111, 527–553. [Google Scholar] [CrossRef] [Green Version]
- Lustig, H.; Roussanov, N.; Verdelhan, A. Common risk factors in currency markets. Rev. Financ. Stud. 2011, 24, 3731–3777. [Google Scholar] [CrossRef]
- Shen, J.; Sun, X.; Chen, H. Who is the protagonist of explaining the excess returns of carry trade?--Based on the empirical evidence of decomposing volatility risk. Int. Financ. Res. 2020, 7, 77–86. (In Chinese) [Google Scholar]
- Della Corte, P.; Ramadorai, T.; Sarno, L. Volatility risk premia and exchange rate predictability. J. Financ. Econ. 2016, 120, 21–40. [Google Scholar] [CrossRef]
- Schmitt-Grohé, S.; Uribe, M.; Ramos, A. International Macroeconomics; Duke University: Durham, NC, USA, 2008. [Google Scholar]
- Jurek, J.W. Crash-neutral currency carry trades. J. Financ. Econ. 2014, 113, 325–347. [Google Scholar] [CrossRef] [Green Version]
- Burnside, C.; Eichenbaum, M.; Kleshchelski, I.; Rebelo, S. Do peso problems explain the returns to the carry trade? Rev. Financ. Stud. 2011, 24, 853–891. [Google Scholar] [CrossRef]
- Burnside, C. Carry Trades and Risk. In Handbook of Exchange Rates; James, J., Marsh, I.W., Sarno, L., Eds.; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Rafferty, B. Currency Returns, Skewness and Crash Risk; Duke University, 2012; Available online: https://ssrn.com/abstract=2022920 (accessed on 7 November 2021). [CrossRef] [Green Version]
- Atanasov, V.; Nitschka, T. Currency excess returns and global downside market risk. J. Int. Money Financ. 2014, 47, 268–285. [Google Scholar] [CrossRef] [Green Version]
- Mancini, L.; Ranaldo, A.; Wrampelmeyer, J. Liquidity in the Foreign Exchange Market: Measurement, Commonality, and Risk Premiums. J. Financ. 2013, 68, 1805–1841. [Google Scholar] [CrossRef] [Green Version]
- MacDonald, R.; Nagayasu, J. Currency forecast errors and carry trades at times of low interest rates: Evidence from survey data on the yen/dollar exchange rate. J. Int. Money Financ. 2015, 53, 1–19. [Google Scholar] [CrossRef]
- Abankwa, S.; Blenman, L.P. Measuring liquidity risk effects on carry trades across currencies and regimes. J. Multinatl. Financ. Manag. 2021, 60, 100683. [Google Scholar] [CrossRef]
- Serdengeçti, S.; Sensoy, A.; Nguyen, D.K. Dynamics of return and liquidity (co) jumps in emerging foreign exchange markets. J. Int. Financ. Mark. Inst. Money 2021, 73, 101377. [Google Scholar] [CrossRef]
- Lustig, H.; Verdelhan, A. The cross section of foreign currency risk premia and consumption growth risk. Am. Econ. Rev. 2007, 97, 89–117. [Google Scholar] [CrossRef] [Green Version]
- Cao, G. Time-varying effects of changes in the interest rate and the RMB exchange rate on the stock market of China: Evidence from the long-memory TVP-VAR model. Emerg. Mark. Financ. Trade 2012, 48 (Suppl. S2), 230–248. [Google Scholar] [CrossRef]
- Qin, J. Relationship between onshore and offshore renminbi exchange markets: Evidence from multiscale cross-correlation and nonlinear causal effect analyses. Phys. A Stat. Mech. Its Appl. 2019, 527, 121183. [Google Scholar] [CrossRef]
- Xing, W.; Xueping, N.; Fuyou, L. Empirical Test of the Relationship between Renminbi NDF and Onshore Renminbi Exchange Rate. Manag. Rev. 2020, 32, 81. [Google Scholar]


| Variables | ADF Test | Stationary | PP Test | Stationary | Results |
|---|---|---|---|---|---|
| −5.702 ** | Stationary | −31.736 *** | Stationary | I(0) | |
| −2.578 * | Non-stationary | −6.742 | Non-stationary | I(1) | |
| −5.670 *** | Stationary | −32.917 *** | Stationary | I(0) | |
| −11.232 *** | Stationary | −3275.681 *** | Stationary | I(0) | |
| −4.017 *** | Stationary | −12.147 * | Non-stationary | I(1) | |
| −12.484 *** | Stationary | −3684.156 *** | Stationary | I(0) | |
| −5.749 *** | Stationary | −15.558 ** | Non-stationary | I(1) | |
| −4.737 *** | Stationary | −56.039 *** | Stationary | I(0) | |
| −3.936 *** | Stationary | −17.551 ** | Stationary | I(0) | |
| FXcrash | −6.050 *** | Stationary | −92.174 *** | Stationary | I(0) |
| PD | −6.864 *** | Stationary | −507.787 *** | Stationary | I(0) |
| ARDL(1,0) | Δst Coefficient | γ | α |
|---|---|---|---|
| Δst + 1 | 0.991 *** | 0.010 | −0.008 |
| (0.002) | (0.009) | (0.007) |
| Time Period | F Statistic | p Value | Conclusion |
|---|---|---|---|
| Global financial crisis | 5.557 *** | 0.003 | Level relationship exists |
| Before 811-exchange-rate reform | 3.569 *** | 0.003 | Level relationship exists |
| After 811-exchange-rate reform | 10.842 *** | 0.000 | Level relationship exists |
| Global Financial Crisis | |||||
|---|---|---|---|---|---|
| Long-Term Level | Short-Term Dynamic | ||||
| Variables | Coefficients | Std. Err. | Variables | Coefficients | Std. Err. |
| ARDL (3,0,0,0,0,1,4) | −0.136 *** | (0.038) | |||
| Adjustment θ | −0.010 * | (0.006) | −0.081 | (0.037) | |
| −0.145 | (0.317) | −0.001 | (0.003) | ||
| 0.128 | (0.244) | 0.002 | (0.002) | ||
| 0.048 | (0.073) | 0.00003 | (0.001) | ||
| −99.357 | (147.316) | −0.952 | (1.053) | ||
| −0.077 | (0.685) | 0.113 *** | (0.027) | ||
| 0.897 * | (0.532) | 0.001 | (0.003) | ||
| −0.005 * | (0.003) | ||||
| −0.012 *** | (0.003) | ||||
| −0.006 ** | (0.003) | ||||
| Breusch–Godfrey LM test | 0 (0.993) | No serial correlation | |||
| Breusch–Pagan test | 4.21 (0.0402) | Heteroscedasticity exists | |||
| Ramsey RESET test | 8.88 (0.000) | Omitted variables exist | |||
| Jarque–Bera test | 14.15 (0.001) | Not normality | |||
| Before 811-Exchange-Rate Reform | |||||
|---|---|---|---|---|---|
| Long-Term Level | Short-Term Dynamic | ||||
| Variables | Coefficients | Std. Err. | Variables | Coefficients | Std. Err. |
| ARDL (4,0,2,0,4,4,0) | −0.035 | (0.031) | |||
| −0.01 ** | (0.005) | −0.02 | (0.03) | ||
| 0.059 ** | (0.03) | ||||
| 17.802 * | (10.192) | 0.169 *** | (0.047) | ||
| −10.875 | (12.912) | −0.088 | (0.082) | ||
| 0.174 ** | (0.08) | ||||
| 0.071 | (0.089) | 0.001 | (0.001) | ||
| 1.687 | (64.287) | −13.995 ** | (7.122) | ||
| −2.303 | (7.194) | ||||
| 7.005 | (7.212) | ||||
| 17.516 ** | (7.478) | ||||
| 1.531 | (1.076) | 0.106 *** | (0.017) | ||
| −0.049 *** | (0.018) | ||||
| −0.032 ** | (0.018) | ||||
| −0.033 ** | (0.018) | ||||
| −0.059 | (0.312) | −0.00027 | (0.003) | ||
| Breusch–Godfrey LM test | 0.329 (0.566) | No serial correlation | |||
| Breusch–Pagan test | 1.36 (0.243) | No heteroscedasticity | |||
| Ramsey RESET test | 2.65 (0.0476) | Omitted variables exist | |||
| Jarque–Bera test | 6.84 (0.033) | Normality | |||
| After 811-Exchange-Rate Reform | |||||
|---|---|---|---|---|---|
| Long-Term Level | Short-Term Dynamic | ||||
| Variables | Coefficients | Std. Err. | Variables | Coefficients | Std. Err. |
| ARDL (1,0,0,0,2) | |||||
| −0.009 ** | (0.004) | ||||
| −4.965 ** | (2.15) | −0.046 *** | (0.007) | ||
| −1.296 * | (0.737) | −0.012 ** | (0.005) | ||
| 0.265 * | (0.15) | 0.002 ** | (0.001) | ||
| 0.892 | (0.991) | 0.212 *** | (0.039) | ||
| −0.111 *** | (0.038) | ||||
| Breusch–Godfrey LM test | 0.523 (0.470) | No serial correlation | |||
| Breusch–Pagan test | 0.12 (0.731) | No heteroscedasticity | |||
| Ramsey RESET test | 0.56 (0.6388) | No omitted variables | |||
| Jarque–Bera test | 0.55 (0.759) | Normality | |||
| Sub Period | Global Financial Crisis | Before Reform | After Reform | |||
|---|---|---|---|---|---|---|
| ARDL (1,4,1,4,4,1,4) | ARDL (3,0,1,1,4,4,3) | ARDL (2,0,0,0,2) | ||||
| Estimation | Variables | Coefficients | Variables | Coefficients | Variables | Coefficients |
| Level relationship | −0.019 | 18.041 | −3.5 ** | |||
| −0.593 * | −5.881 | −1.238 * | ||||
| 0.039 *** | 0.044 | 0.227 * | ||||
| −9.412 | 22.575 | 0.548 | ||||
| −0.033 | 1.004 | |||||
| 0.156 *** | −0.543 | |||||
| Short-term dynamic | −0.067 *** | −0.007 * | −0.01 *** | |||
| 0.156 *** | −0.021 | −0.075 *** | ||||
| 0.004 | −0.074 ** | −0.039 *** | ||||
| 0.029 * | 0.139 *** | −0.014 ** | ||||
| 0.009 | −0.205 ** | 0.018 *** | ||||
| −0.009 * | 0.022 *** | 0.195 *** | ||||
| 0.023 *** | −5.748 | −0.120 *** | ||||
| −0.002 | −12.655 | |||||
| −0.015 ** | 12.944 | |||||
| −0.013 ** | 21.134 ** | |||||
| 21.315 | 0.101 *** | |||||
| 39.305 *** | −0.051 ** | |||||
| 1.273 | −0.029 | |||||
| 30.633 ** | −0.034 * | |||||
| 0.131 ** | −0.007 | |||||
| 0.002 | 0.011 ** | |||||
| −0.008 * | 0.012 ** | |||||
| −0.010 ** | ||||||
| −0.011 ** | ||||||
| Bounds test | 0.000 | Level relationship exists | 0.174 | No level relationship | 0.0 | Level relationship exists |
| Correlation test | 0.484 | No serial correlation | 0.344 | No serial correlation | 0.074 | No serial correlation |
| Hetero test | 0.000 | Heteroscedasticity | 0.149 | No heteroscedasticity | 0.165 | No heteroscedasticity |
| Model test | 0.003 | Omitted variables exist | 0.014 | Omitted variables exist | 0.953 | No omitted variables |
| Normality test | 0.006 | Not normality | 0.704 | Normality | 0.328 | Normality |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Guo, S. What Factors Affect the RMB Carry Trade Return for Sustainability? An Empirical Analysis by Using an ARDL Model. Sustainability 2021, 13, 13533. https://doi.org/10.3390/su132413533
Zhang Z, Guo S. What Factors Affect the RMB Carry Trade Return for Sustainability? An Empirical Analysis by Using an ARDL Model. Sustainability. 2021; 13(24):13533. https://doi.org/10.3390/su132413533
Chicago/Turabian StyleZhang, Ziyun, and Sen Guo. 2021. "What Factors Affect the RMB Carry Trade Return for Sustainability? An Empirical Analysis by Using an ARDL Model" Sustainability 13, no. 24: 13533. https://doi.org/10.3390/su132413533
APA StyleZhang, Z., & Guo, S. (2021). What Factors Affect the RMB Carry Trade Return for Sustainability? An Empirical Analysis by Using an ARDL Model. Sustainability, 13(24), 13533. https://doi.org/10.3390/su132413533





