Re-Allocation of Distributed Generations Using Available Renewable Potential Based Multi-Criterion-Multi-Objective Hybrid Technique
Abstract
:1. Introduction
2. Literature Surveys
- DGs with unity power factor (UPF) alone has been considered in few approaches.
- In a few cases, CBs and/or DGs locations were fixed.
- Economic and environmental implications and a few network constraints have been ignored.
- The simulation time and the results have been non-optimal in few existing techniques.
- Re-allocation of DGs based on available renewable energy potential (AREP) has not been considered.
- To enhance the technical objectives, viz., power loss and voltage deviation reduction and voltage stability index improvement.
- To minimize costs of CBs and generated power.
- To resolve the environmental implications by reducing emissions from the generated units.
3. Problem Statement
3.1. Objective Functions
3.1.1. Technical Objectives
- The distribution network power losses (obj1) can be minimized [29] by
- The voltage deviation index (obj2) can be minimized [30] using Equation (2).
3.1.2. Economic Objective
3.1.3. Environmental Objective
3.2. Constraints
3.2.1. Power Balance
3.2.2. Inequality Constraints
- Generator performance [16]:
- Sizing of DGs [33]:
- Reactive power from DG and CB resources:
- Bus voltage:
3.3. LSF Based Optimal Location of DGs and CBs
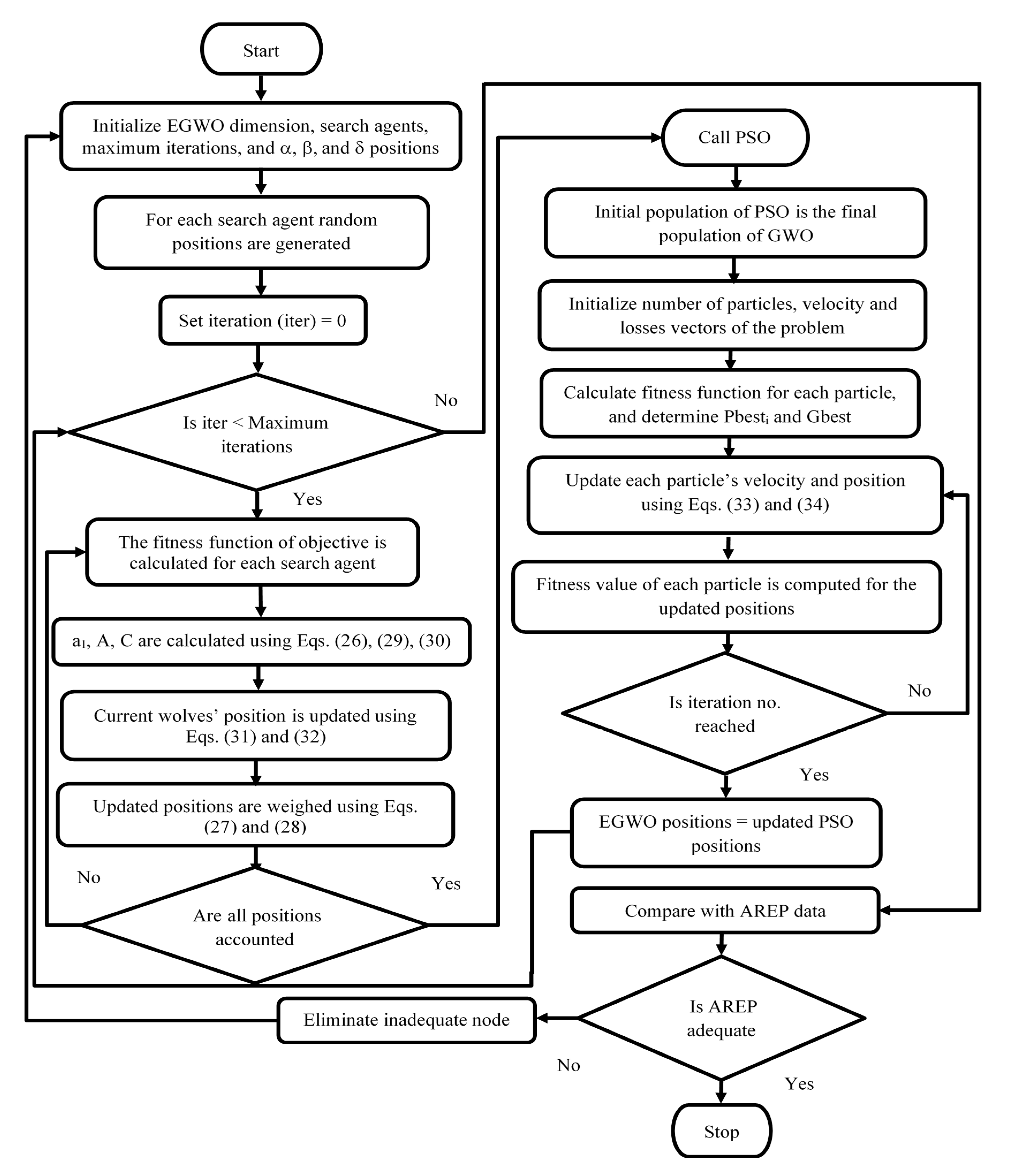
4. AREP-Based Hybrid EGWO-PSO Optimization Algorithm
5. Case Study
- Case 1: Optimal allocation of DGs at UPF
- Case 2: Optimal allocation of DGs at UPF with fixed CBs
- Case 3: Optimal allocation of DGs at Lagging/leading power factor (LPF)
- Case 4: Optimal allocation of DGs at LPF with fixed CBs
- Case 5: Optimal allocation of multi-DGs with fixed CBs
6. Results and Discussions
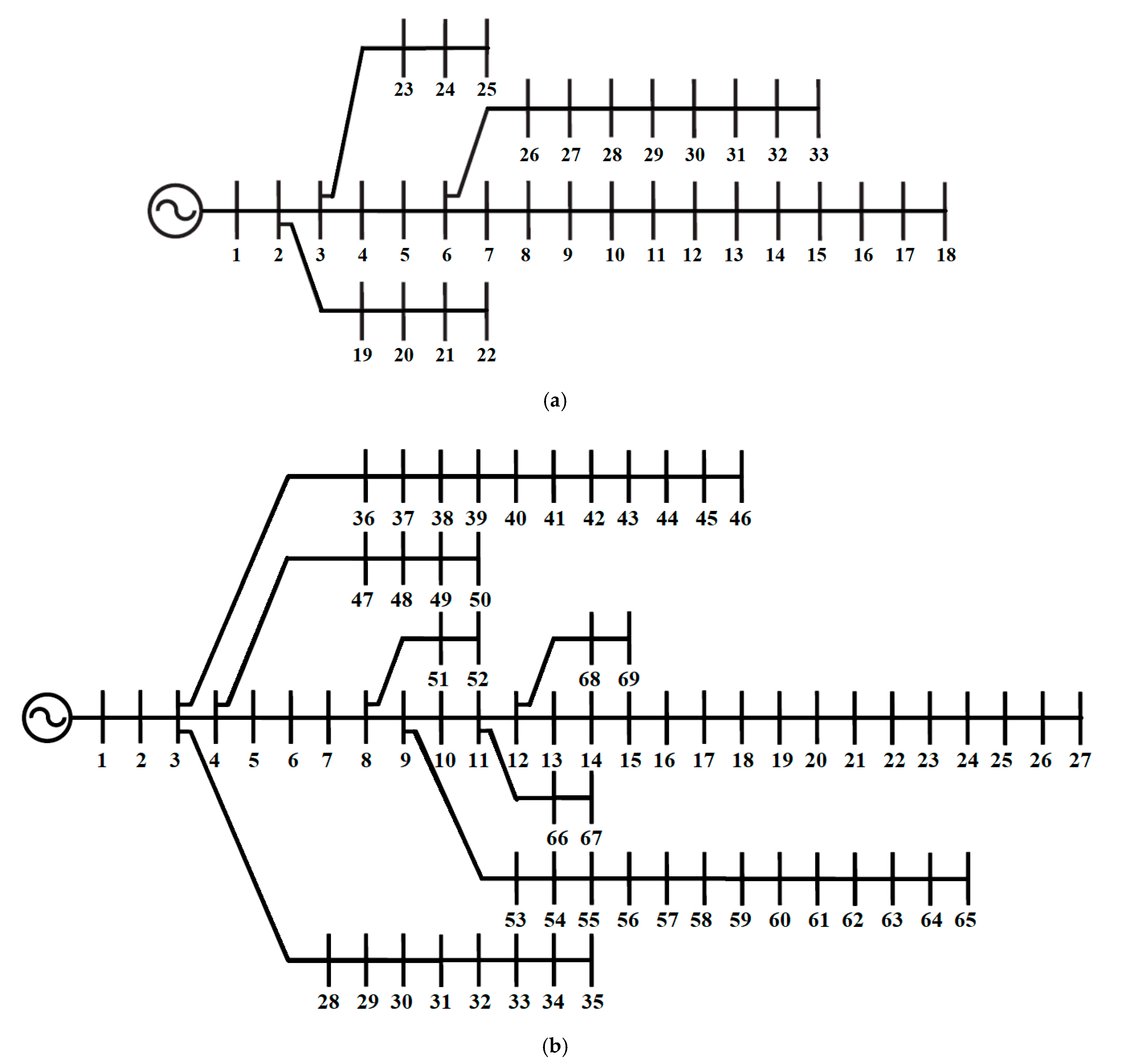
6.1. IEEE 33-Bus System
6.1.1. Case 1
6.1.2. Case 2
6.1.3. Case 3
6.1.4. Case 4
6.1.5. Case 5
6.2. IEEE 69-Bus System
6.2.1. Case 1
6.2.2. Case 2
6.2.3. Case 3
6.2.4. Case 4
6.2.5. Case 5
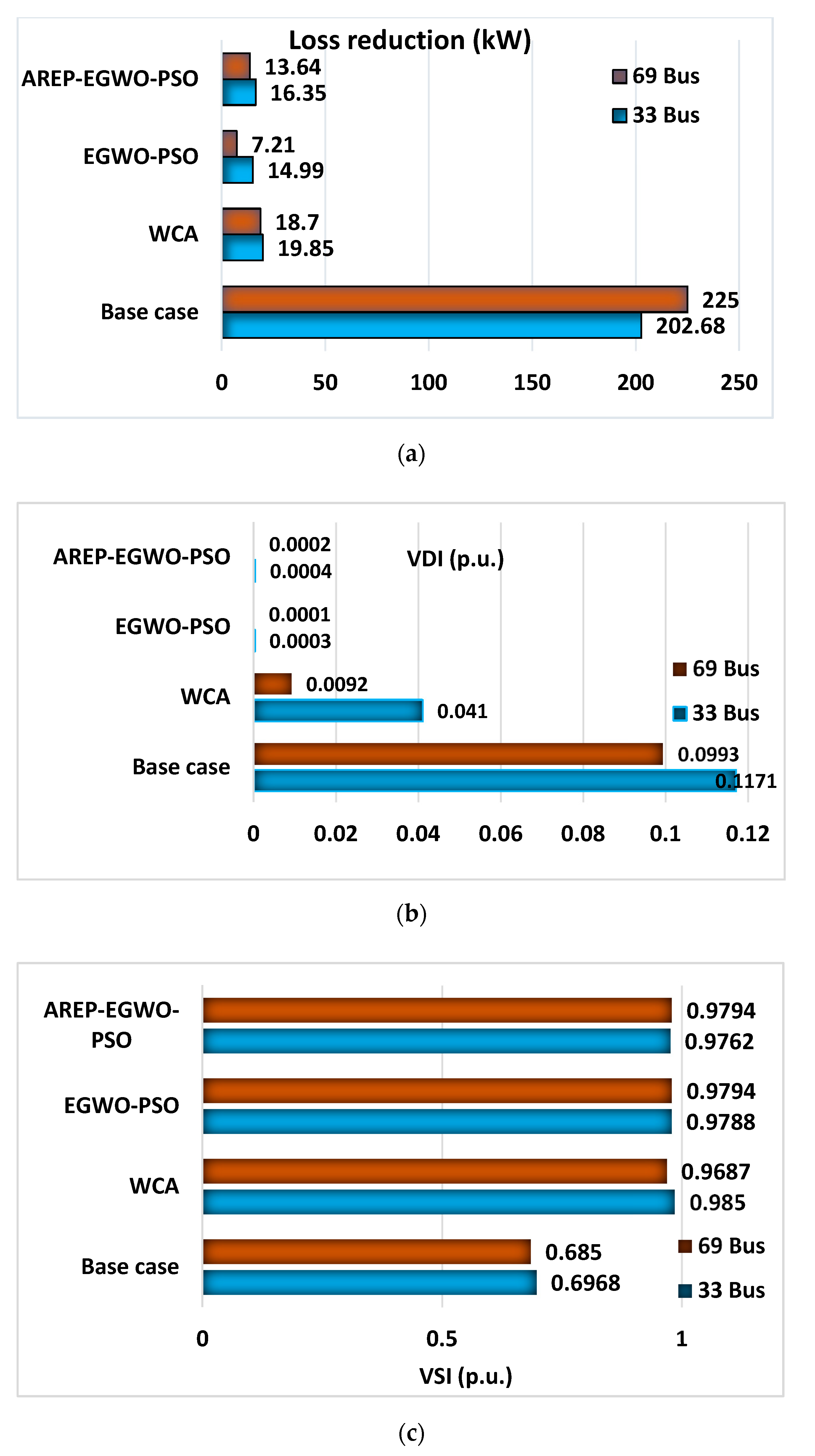
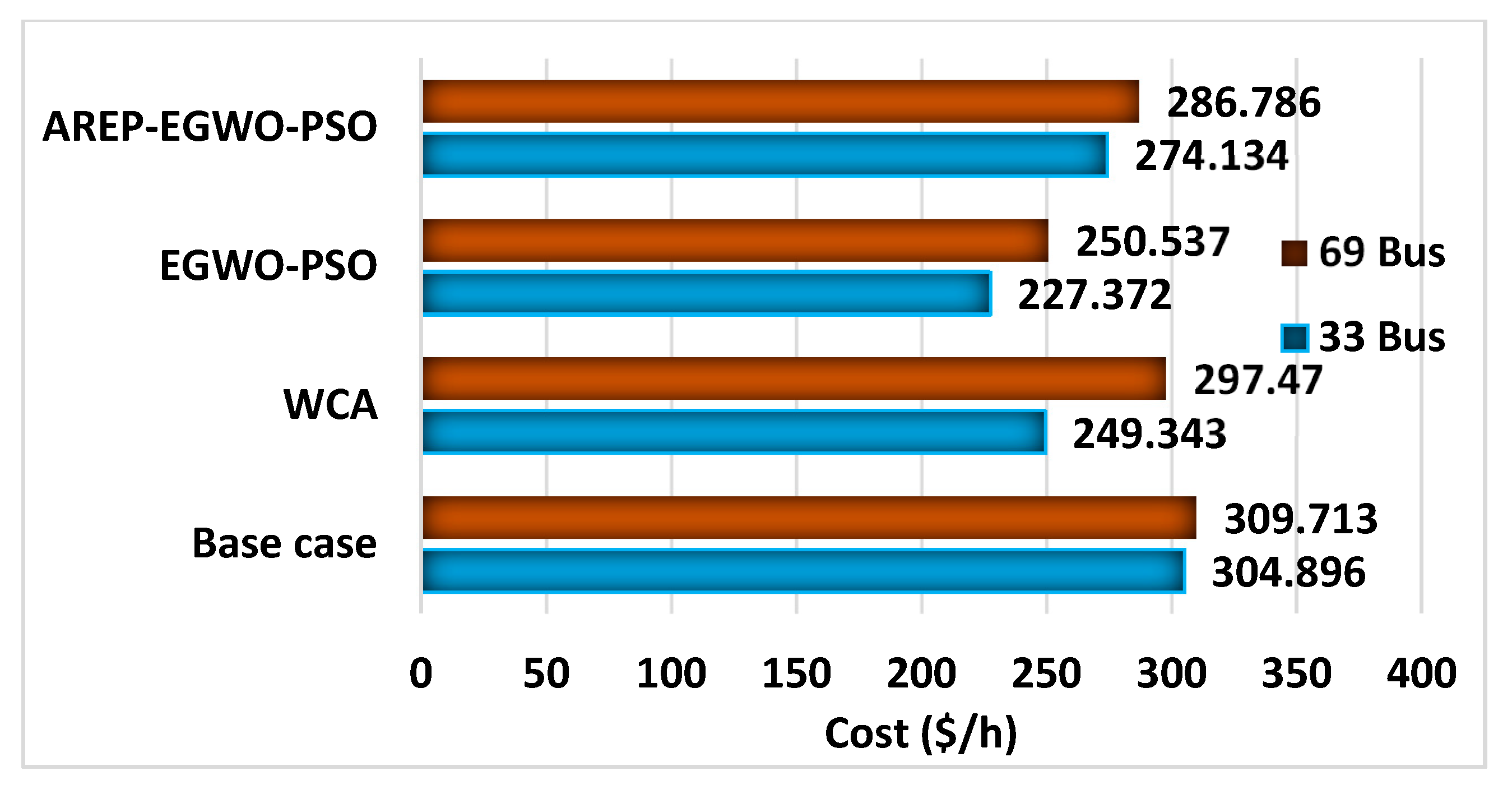
6.3. Comparative Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| ‘Bus No’ | ‘PV’ | ‘WT’ | ‘GT’ |
|---|---|---|---|
| 2 | 1.416811 | 0.14859 | 0.725957 |
| 3 | 1.618209 | 1.831352 | 1.649998 |
| 4 | 0.968719 | 1.950474 | 1.617671 |
| 5 | 0.778194 | 1.353325 | 0.112631 |
| 5 | 0.928099 | 1.358976 | 0.094402 |
| 7 | 1.385327 | 1.779761 | 1.034487 |
| 8 | 0.461034 | 0.818609 | 0.223704 |
| 9 | 0.34476 | 1.779539 | 1.088131 |
| 10 | 1.523637 | 1.368845 | 1.283628 |
| 11 | 0.911622 | 1.140432 | 0.23583 |
| 12 | 1.150228 | 0.460206 | 0.498481 |
| 13 | 0.1256 | 0.1514 | 0.2128 |
| 14 | 0.1147 | 0.2136 | 0.3249 |
| 15 | 1.114726 | 0.125897 | 1.83734 |
| 16 | 1.368482 | 1.946823 | 0.161324 |
| 17 | 0.214187 | 1.024223 | 1.804306 |
| 18 | 0.774483 | 1.159366 | 1.385843 |
| 19 | 0.631677 | 0.332454 | 0.447655 |
| 20 | 0.358377 | 1.828926 | 1.542147 |
| 21 | 0.090268 | 0.633536 | 1.580214 |
| 22 | 1.724825 | 0.607015 | 1.556447 |
| 23 | 1.958863 | 0.057297 | 1.668655 |
| 24 | 1.464163 | 1.552195 | 1.160197 |
| 25 | 0.1626 | 1.2106 | 0.8399 |
| 26 | 0.571004 | 1.286817 | 1.964925 |
| 27 | 0.404072 | 0.284293 | 0.304324 |
| 28 | 1.118003 | 1.741504 | 0.114022 |
| 29 | 0.8989 | 1.5806 | 1.4299 |
| 30 | 0.1432 | 0.2658 | 0.3146 |
| 31 | 0.74843 | 0.397773 | 0.080544 |
| 32 | 1.154837 | 1.006679 | 0.660426 |
| 33 | 1.244935 | 0.933108 | 1.390878 |
Appendix B
| ‘Bus No’ | ‘PV’ | ‘WT’ | ‘GT’ |
|---|---|---|---|
| 2 | 0.2986 | 1.7386 | 0.7015 |
| 3 | 0.515 | 1.1594 | 1.878 |
| 4 | 1.6814 | 1.0997 | 1.7519 |
| 5 | 0.5086 | 0.2899 | 1.1003 |
| 5 | 1.6286 | 1.7061 | 1.245 |
| 7 | 0.487 | 1.2441 | 1.1741 |
| 8 | 1.8585 | 0.7019 | 0.4155 |
| 9 | 0.723 | 1.0265 | 0.6025 |
| 10 | 0.3932 | 0.8036 | 0.9418 |
| 11 | 0.1215 | 0.1532 | 0.2146 |
| 12 | 1.2321 | 0.4798 | 1.6886 |
| 13 | 0.9466 | 0.2466 | 0.3895 |
| 14 | 0.7033 | 0.3678 | 0.4518 |
| 15 | 1.6617 | 0.4799 | 0.3414 |
| 16 | 1.1705 | 0.8345 | 0.4553 |
| 17 | 1.0994 | 0.0993 | 0.8714 |
| 18 | 1.8344 | 1.8054 | 0.6222 |
| 19 | 0.5717 | 1.8896 | 1.8468 |
| 20 | 1.5144 | 0.9817 | 0.8604 |
| 21 | 1.5075 | 0.9785 | 0.3696 |
| 22 | 0.7609 | 0.6754 | 1.8098 |
| 23 | 1.1356 | 1.8001 | 1.9595 |
| 24 | 0.1517 | 0.7385 | 0.8777 |
| 25 | 0.1079 | 0.2224 | 0.2222 |
| 26 | 1.0616 | 1.5605 | 0.5161 |
| 27 | 1.5583 | 0.7795 | 0.8174 |
| 28 | 1.868 | 0.4834 | 1.1898 |
| 29 | 0.2598 | 0.8078 | 0.5244 |
| 30 | 1.1376 | 0.1929 | 1.2057 |
| 31 | 0.9388 | 0.2639 | 1.4224 |
| 32 | 0.0238 | 1.8841 | 0.4435 |
| 33 | 0.6742 | 1.9123 | 0.2348 |
| 34 | 0.3244 | 1.1504 | 0.5934 |
| 35 | 1.5886 | 0.1196 | 0.6376 |
| 36 | 0.6224 | 0.4696 | 0.8483 |
| 37 | 1.0571 | 0.7063 | 1.0157 |
| 38 | 0.3313 | 1.6424 | 0.171 |
| 39 | 1.204 | 0.0308 | 0.525 |
| 40 | 0.5259 | 0.086 | 1.602 |
| 41 | 1.3082 | 0.338 | 0.0584 |
| 42 | 1.3784 | 1.2982 | 1.8577 |
| 43 | 1.4963 | 1.4634 | 1.4607 |
| 44 | 0.9011 | 1.2955 | 0.9772 |
| 45 | 0.1676 | 0.9018 | 1.1571 |
| 46 | 0.458 | 1.094 | 0.4746 |
| 47 | 1.8267 | 0.5926 | 0.9177 |
| 48 | 0.3048 | 1.4894 | 1.9262 |
| 49 | 1.6516 | 0.3779 | 1.0936 |
| 50 | 1.0767 | 1.3736 | 1.0423 |
| 51 | 1.9923 | 0.367 | 0.4632 |
| 52 | 0.1564 | 0.737 | 0.9778 |
| 53 | 0.8854 | 1.2512 | 1.2481 |
| 54 | 0.2133 | 1.5605 | 1.3583 |
| 55 | 1.9238 | 0.1623 | 0.791 |
| 56 | 0.0093 | 1.8588 | 0.7349 |
| 57 | 1.5498 | 1.5514 | 1.976 |
| 58 | 1.6346 | 0.9736 | 0.0755 |
| 59 | 1.7374 | 0.8717 | 1.7703 |
| 60 | 0.922 | 0.6564 | 0.7402 |
| 61 | 0.1321 | 0.2021 | 0.3211 |
| 62 | 0.5197 | 1.017 | 0.1974 |
| 63 | 0.1232 | 0.2123 | 0.3135 |
| 64 | 0.8628 | 1.6353 | 0.6707 |
| 65 | 1.8213 | 1.5897 | 1.3595 |
| 66 | 0.3637 | 1.2886 | 0.2731 |
| 67 | 0.5276 | 0.7572 | 1.4425 |
| 68 | 0.2911 | 1.6232 | 0.2135 |
| 69 | 0.2721 | 1.0657 | 1.3075 |
References
- HA, M.P.; Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Seyedi, H. A hybrid genetic particle swarm optimization for distributed generation allocation in power distribution networks. Energy 2020, 209, 118218. [Google Scholar] [CrossRef]
- Rao, R.S.; Ravindra, K.; Satish, K.; Narasimham, S.V.L. Power Loss Minimization in Distribution System Using Network Reconfiguration in the Presence of Distributed Generation. IEEE Trans. Power Syst. 2013, 28, 317–325. [Google Scholar] [CrossRef]
- Pereira, B.R.; Da Costa, G.R.M.M.; Contreras, J.; Mantovani, J.R.S. Optimal Distributed Generation and Reactive Power Allocation in Electrical Distribution Systems. IEEE Trans. Sustain. Energy 2016, 7, 975–984. [Google Scholar] [CrossRef] [Green Version]
- Bawazir, R.O.; Cetin, N.S. Comprehensive overview of optimizing PV-DG allocation in power system and solar energy resource potential assessments. Energy Rep. 2020, 6, 173–208. [Google Scholar] [CrossRef]
- Morsali, R.; Ghadimi, N.; Karimi, M.; Mohajeryami, S. Solving a novel multiobjective placement problem of recloser and distributed generation sources in simultaneous mode by improved harmony search algorithm. Complexity 2015, 21, 328–339. [Google Scholar] [CrossRef]
- Sheng, W.; Liu, K.; Liu, Y.; Ye, X.; He, K. Reactive power coordinated optimisation method with renewable distributed generation based on improved harmony search. IET Gener. Transm. Distrib. 2016, 10, 3152–3162. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A. Optimal Coordinated Allocation of Distributed Generation Units/Capacitor Banks/Voltage Regulators by EGWA. IEEE Syst. J. 2021, 15, 257–264. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Rezk, H. Optimal Sizing and Placement of Capacitors in Radial Distribution Systems Based on Grey Wolf, Dragonfly and Moth–Flame Optimization Algorithms. Iran J. Sci. Technol. Trans. Electr. Eng. 2019, 43, 77–96. [Google Scholar] [CrossRef]
- Rajendran, A.; Narayanan, K. Multi-Objective Hybrid WIPSO–GSA Algorithm-Based DG and Capacitor Planning for Reduction of Power Loss and Voltage Deviation in Distribution System. Smart Sci. 2018, 6, 295–307. [Google Scholar] [CrossRef]
- Montazeri, M.; Askarzadeh, A. Capacitor placement in radial distribution networks based on identification of high potential busses. Int. Trans. Electr. Energy Syst. 2019, 29, e2754. [Google Scholar] [CrossRef]
- Sanjay, R.; Jayabarathi, T.; Raghunathan, T.; Ramesh, V.; Mithulananthan, N. Optimal Allocation of Distributed Generation Using Hybrid Grey Wolf Optimizer. IEEE Access 2017, 5, 14807–14818. [Google Scholar] [CrossRef]
- Quadri, I.A.; Bhowmick, S.; Joshi, D. A hybrid teaching–learning-based optimization technique for optimal DG sizing and placement in radial distribution systems. Soft Comput. 2019, 23, 9899–9917. [Google Scholar] [CrossRef]
- Bayat, S.A.; Davoudkhani, I.F.; Moghaddam, M.J.H.; Najmi, E.S.; Abdelaziz, A.Y.; Ahmadi, A.; Razavi, S.E.; Gandoman, F.H. Fuzzy multi-objective placement of renewable energy sources in distribution system with objective of loss reduction and reliability improvement using a novel hybrid method. Appl. Soft Comput. 2019, 77, 761–779. [Google Scholar]
- Arif, S.M.; Hussain, A.; Lie, T.T.; Ahsan, S.M.; Khan, H.A. Analytical Hybrid Particle Swarm Optimization Algorithm for Optimal Siting and Sizing of Distributed Generation in Smart Grid. J. Mod. Power Syst. Clean Energy 2020, 8, 1221–1230. [Google Scholar] [CrossRef]
- Yang, B.; Yu, L.; Chen, Y.; Ye, H.; Shao, R.; Shu, H.; Yu, T.; Zhang, X.; Sun, L. Modelling, applications, and evaluations of optimal sizing and placement of distributed generations: A critical state-of-the-art survey. Int. J. Energy Res. 2020, 45, 3615–3642. [Google Scholar] [CrossRef]
- Venkatesan, C.; Kannadasan, R.; Alsharif, M.; Kim, M.-K.; Nebhen, J. A Novel Multiobjective Hybrid Technique for Siting and Sizing of Distributed Generation and Capacitor Banks in Radial Distribution Systems. Sustainability 2021, 13, 3308. [Google Scholar] [CrossRef]
- Taha, I.B.M.; Elattar, E.E. Optimal reactive power resources sizing for power system operations enhancement based on improved grey wolf optimiser. IET Gener. Transm. Distrib. 2018, 12, 3421–3434. [Google Scholar] [CrossRef]
- Das, S.; Das, D.; Patra, A. Operation of distribution network with optimal placement and sizing of dispatchable DGs and shunt capacitors. Renew. Sustain. Energy Rev. 2019, 113, 109219. [Google Scholar] [CrossRef]
- Suresh, M.; Edward, J.B. A hybrid algorithm based optimal placement of DG units for loss reduction in the distribution system. Appl. Soft Comput. 2020, 91, 106191. [Google Scholar] [CrossRef]
- Muthukumar, K.; Jayalalitha, M. Integrated approach of network reconfiguration with distributed generation and shunt capacitors placement for power loss minimization in radial distribution networks. Appl. Soft Comput. 2017, 52, 1262–1284. [Google Scholar] [CrossRef]
- El-Salam, M.F.A.; Beshr, E.; Eteiba, M. A New Hybrid Technique for Minimizing Power Losses in a Distribution System by Optimal Sizing and Siting of Distributed Generators with Network Reconfiguration. Energies 2018, 11, 3351. [Google Scholar] [CrossRef] [Green Version]
- Alzaidi, K.M.S.; Bayat, O.; Uçan, O.N. Multiple DGs for Reducing Total Power Losses in Radial Distribution Systems Using Hybrid WOA-SSA Algorithm. Int. J. Photoenergy 2019, 2019, 2426538. [Google Scholar] [CrossRef]
- Arulraj, R.; Kumarappan, N. Optimal economic-driven planning of multiple DG and capacitor in distribution network considering different compensation coefficients in feeder’s failure rate evaluation. Eng. Sci. Technol. Int. J. 2019, 22, 67–77. [Google Scholar] [CrossRef]
- Angalaeswari, S.; Sanjeevikumar, P.; Jamuna, K.; Leonowicz, Z. Hybrid PIPSO-SQP Algorithm for Real Power Loss Minimization in Radial Distribution Systems with Optimal Placement of Distributed Generation. Sustainability 2020, 12, 5787. [Google Scholar] [CrossRef]
- Milovanović, M.; Tasić, D.; Radosavljević, J.; Perović, B. Optimal Placement and Sizing of Inverter-Based Distributed Generation Units and Shunt Capacitors in Distorted Distribution Systems Using a Hybrid Phasor Particle Swarm Optimization and Gravitational Search Algorithm. Electr. Power Compon. Syst. 2020, 48, 543–557. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Orozco-Henao, C. Vortex search and Chu-Beasley genetic algorithms for optimal location and sizing of distributed generators in distribution networks: A novel hybrid approach. Eng. Sci. Technol. Int. J. 2020, 23, 1351–1363. [Google Scholar] [CrossRef]
- Coelho, F.C.R.; Junior, I.C.D.S.; Dias, B.H.; Peres, W.; Ferreira, V.H.; Marcato, A.L.M. Optimal distributed generation allocation in unbalanced radial distribution networks via empirical discrete metaheuristic and steepest descent method. Electr. Eng. 2021, 103, 633–646. [Google Scholar] [CrossRef]
- Venkatesan, C.; Kannadasan, R.; Alsharif, M.; Kim, M.-K.; Nebhen, J. Assessment and Integration of Renewable Energy Resources Installations with Reactive Power Compensator in Indian Utility Power System Network. Electronics 2021, 10, 912. [Google Scholar] [CrossRef]
- El-Ela, A.A.A.; El-Sehiemy, R.A.; Abbas, A.S. Optimal Placement and Sizing of Distributed Generation and Capacitor Banks in Distribution Systems Using Water Cycle Algorithm. IEEE Syst. J. 2018, 12, 3629–3636. [Google Scholar] [CrossRef]
- Ali, A.U.; Keerio, M.U.; Laghari, J.A. Optimal Site and Size of Distributed Generation Allocation in Radial Distribution Network Using Multi-objective Optimization. J. Mod. Power Syst. Clean Energy 2021, 9, 404–415. [Google Scholar] [CrossRef]
- Palanisamy, R.; Muthusamy, S.K. Optimal Siting and Sizing of Multiple Distributed Generation Units in Radial Distribution System Using Ant Lion Optimization Algorithm. J. Electr. Eng. Technol. 2021, 16, 79–89. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Ali, E.; Elazim, S.A. Flower Pollination Algorithm and Loss Sensitivity Factors for optimal sizing and placement of capacitors in radial distribution systems. Int. J. Electr. Power Energy Syst. 2016, 78, 207–214. [Google Scholar] [CrossRef]
- Oliveira, V.Y.M.; Oliveira, R.M.S.; Affonso, C.M. Cuckoo Search approach enhanced with genetic replacement of abandoned nests applied to optimal allocation of distributed generation units. IET Gener. Transm. Distrib. 2018, 12, 3353–3362. [Google Scholar] [CrossRef]
- Quadri, I.A.; Bhowmick, S.; Joshi, D. A comprehensive technique for optimal allocation of distributed energy resources in radial distribution systems. Appl. Energy 2018, 211, 1245–1260. [Google Scholar] [CrossRef]
- Pasha, A.M.; Zeineldin, H.H.; El-Saadany, E.F.; Alkaabi, S.S. Optimal allocation of distributed generation for planning master–slave controlled microgrids. IET Gener. Transm. Distrib. 2019, 13, 3704–3712. [Google Scholar] [CrossRef]
- Muthukumar, K.; Jayalalitha, S. Optimal placement and sizing of distributed generators and shunt capacitors for power loss minimization in radial distribution networks using hybrid heuristic search optimization technique. Int. J. Electr. Power Energy Syst. 2016, 78, 299–319. [Google Scholar] [CrossRef]
- Murthy, V.; Kumar, A. Comparison of optimal DG allocation methods in radial distribution systems based on sensitivity approaches. Int. J. Electr. Power Energy Syst. 2013, 53, 450–467. [Google Scholar] [CrossRef]
- Sadiq, A.; Adamu, S.; Buhari, M. Optimal distributed generation planning in distribution networks: A comparison of transmission network models with FACTS. Eng. Sci. Technol. Int. J. 2019, 22, 33–46. [Google Scholar] [CrossRef]
- Poornazaryan, B.; Karimyan, P.; Gharehpetian, G.; Abedi, M. Optimal allocation and sizing of DG units considering voltage stability, losses and load variations. Int. J. Electr. Power Energy Syst. 2016, 79, 42–52. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Şenel, F.A.; Gökçe, F.; Yüksel, A.S.; Yiğit, T. A novel hybrid PSO–GWO algorithm for optimization problems. Eng. Comput. 2019, 35, 1359–1373. [Google Scholar] [CrossRef]
- Abdelshafy, A.M.; Hassan, H.; Jurasz, J. Optimal design of a grid-connected desalination plant powered by renewable energy resources using a hybrid PSO–GWO approach. Energy Convers. Manag. 2018, 173, 331–347. [Google Scholar] [CrossRef]
- Ramadan, H.; Bendary, A.; Nagy, S. Particle swarm optimization algorithm for capacitor allocation problem in distribution systems with wind turbine generators. Int. J. Electr. Power Energy Syst. 2017, 84, 143–152. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E. Matpower [Software]. Available online: https://matpower.org (accessed on 20 September 2021). [CrossRef]
- Kumar, S.; Mandal, K.; Chakraborty, N. Optimal DG placement by multi-objective opposition based chaotic differential evolution for techno-economic analysis. Appl. Soft Comput. 2019, 78, 70–83. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P. Multi-objective quasi-oppositional teaching learning based optimization for optimal location of distributed generator in radial distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 534–545. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M. A combination of genetic algorithm and particle swarm optimization for optimal DG location and sizing in distribution systems. Int. J. Electr. Power Energy Syst. 2012, 34, 66–74. [Google Scholar] [CrossRef]
- Mohamed Imran, A.; Kowsalya, M.; Kothari, D.P. A novel integration technique for optimal network reconfiguration and distributed generation placement in power distribution networks. Int. J. Electr. Power Energy Syst. 2014, 63, 461–472. [Google Scholar] [CrossRef]
- Kefayat, M.; Ara, A.L.; Niaki, S.N. A hybrid of ant colony optimization and artificial bee colony algorithm for probabilistic optimal placement and sizing of distributed energy resources. Energy Convers. Manag. 2015, 92, 149–161. [Google Scholar] [CrossRef]
- Injeti, S.K.; Kumar, N.P. A novel approach to identify optimal access point and capacity of multiple DGs in a small, medium and large scale radial distribution systems. Int. J. Electr. Power Energy Syst. 2013, 45, 142–151. [Google Scholar] [CrossRef]


| Ref. No. | Year | Optimization Algorithm | Objectives | Constraints | Allocation | Inferences | Limitations | |
|---|---|---|---|---|---|---|---|---|
| DG | CB | |||||||
| [17] | 2018 | Improved grey wolf optimizer (IGWO) | Minimizing generation cost, power loss, and voltage deviation | Equality, generator, transformer, bus voltage, line loading, and installed reactive power resource constraints | √ | Improved rate of convergence with quality solution | Voltage stability and power factor constraints are neglected | |
| [10] | 2018 | Modified power loss index + Crow search (MPLI + CS) | Minimize active power loss and cost | Bus voltage, reactive power injected, complex power, capacitor size and power factor | √ | Reduced search space, accurate and quick convergence | Voltage stability is not considered | |
| [18] | 2019 | Voltage stability index + Genetic algorithm (VSI + GA) | Minimize feeder current, voltage deviation and power losses | Voltage and branch current carrying capacity | √ | √ | Hourly variation of load demand is modelled | Relaxed network constraints and single test system |
| [7] | 2020 | Enhance grey wolf algorithm (EGWA) | Minimize total investment costs, maximize voltage profile, loading capacity, and benefits from the reduction of losses and purchased power | Equality constraints, DG penetration level, power factor limit, CB size, node voltage, and branch current limits | √ | √ | Improved performance, highly stable and superior capabilities | Voltage stability and emission perspectives are ignored |
| [3] | 2016 | Tabu search + Chu–Beasley genetic algorithm (TS + CBGA) | Minimize investment and operation costs | Technical and operational constraints | √ | √ | Very efficient and used for planning the system | Single test system and stability constraint is ignored |
| [19] | 2017 | Grasshopper optimization algorithm + Cuckoo search algorithm (GOA + CSA) | Minimize voltage deviation, line losses, and cost | Equality, load bus voltage and DG capacity | √ | Less complexity with reduced computational time | Limited type of DGs, voltage stability, and emission analysis are ignored | |
| [11] | 2017 | Hybrid grey wolf optimizer (HGWO) | Minimizing total real power losses | Equality, Bus voltage, DG unit size, and power factor | √ | Algorithm performance is enhanced without tuning | Demand uncertainties and reliability are not considered | |
| [20] | 2017 | Harmony search algorithm + Particle artificial bee colony (HSA + PABC) | Minimize real power loss, line loading, and voltage deviation | Bus voltage, thermal limit of the lines, maximum power injection from DGs and CBs | √ | √ | Enhanced performance with fast convergence | Economic and voltage stability constraints are ignored |
| [21] | 2018 | HGWO-PSO | Minimizing power losses | Equality, bus voltage, line current, total generated power, and DG size | √ | Optimal solution with less iteration. | Power factor and voltage stability constraints are ignored | |
| [13] | 2019 | Multi-objective hybrid teaching learning-based optimization-grey wolf optimizer (MOHTLBOGWO) | Minimizing power losses and improving reliability | Equilibrium, bus voltage, DG size, and line capacity | √ | Improved speed of convergence and no local trapping | Solar PV and wind resources are only considered | |
| [12] | 2019 | Hybrid teaching-learning based optimization | Minimize power losses, voltage deviation and maximize voltage stability index | Equality, active and reactive power balance, voltage and thermal limits, and DG penetration | √ | Avoidance of local minima/maxima trappings and improved convergence | Tuning of algorithm parameters are required; limited type of DGs | |
| [22] | 2019 | Hybrid Whale optimization algorithm—Salp swarm algorithm (WOA-SSA) | Minimize power losses and voltage deviation | Bus voltage magnitude, DG number, and capacity | √ | More effective and better execution time | Convergence is ignored, and limited types of DGs | |
| [23] | 2019 | Hybrid weight improved particle swarm optimization + gravitational search algorithm (WIPSO + GSA) | Maximize total cost benefit | DG and capacitor power limits, voltage limits of bus | √ | √ | Feeder’s failure rate is evaluated through compensation coefficients, greater convergence speed | DGs with reactive power capabilities and stability are ignored |
| [1] | 2020 | Hybrid GA + PSO | Minimize active, reactive power losses and voltage deviation | Active and reactive power balance, voltage, line, and DG power limits | √ | More realistic, accurate, improved performance, and easy to apply | Cost analysis, stability, and environmental factors are ignored | |
| [14] | 2020 | Analytical hybrid PSO (AHPSO) | Minimize total cost | Real power of DG, angle deviation limit, and line current flow | √ | Modified 2/3rd rule is used, faster convergence | No power factor and voltage stability assessment | |
| [24] | 2020 | Hybrid Parameter improved PSO—Sequential quadratic programming (PIPSO-SQP) | Minimize real power loss | Net power flow, DG limit and node voltage | √ | Highly stable, rapid convergence and less computation time | No power factor, cost analysis, and voltage stability assessment | |
| [25] | 2020 | Hybrid Phasor PSO and GSA (PPSOGSA) | Minimize active power losses | Equality, bus voltage, THD of voltage, branch flow, DG and capacitor capacity, and positions | √ | √ | Different constraints are used, solutions are effective, robust with high-quality and less no. of iterations | Limited type of DGs, power factor constraint, stability, and economic issues are ignored |
| [26] | 2020 | Hybrid CBGA—Vortex search algorithm (CBGA- VSA) | Minimize power loss | Complex power and network voltage | √ | Successive approximation power flow is used. More efficient and better solution with low computational times | Limited type of DGs, emission, and stability investigations are ignored | |
| [27] | 2021 | Hybrid empirical discrete metaheuristic—Steepest descent method (EDM-SDM) | Minimize power losses | Active and reactive power balance, DG status and limits, and voltage | √ | High-quality and straightforward solutions with low tuning parameters | Stability and economic evaluations are ignored | |
| DG Type | Life Time (Year) | Rated Capacity (MW) | Capital Cost ($/kW) | Fuel Cost ($/kWh) | O&M Costs ($/kWh) | Emission Factors (lb/MWh) | ||
|---|---|---|---|---|---|---|---|---|
| NOx | SO2 | CO2 | ||||||
| Grid | 25 | 25 | - | 0.044 | - | 5.06 | 11.6 | 2031 |
| PV | 20 | 1 | 3985 | - | 0.01207 | - | - | - |
| WT | 20 | 5 | 1822 | - | 0.00952 | - | - | - |
| GT | 12 | 3 | 1224 | 0.0667 | 0.06481 | 0.279 | 0.93 | 1239.2 |
| Methods | Power Loss (KW) | DGs Size (MW)/Position | Min. Voltage (p.u.)/Bus | VDI (p.u.) | VSI (p.u.) |
|---|---|---|---|---|---|
| Base case | 202.68 | -- | 0.913/18 | 0.1171 | 0.6968 |
| Water cycle algorithm (WCA) [29] | 71.05 | 0.855/14, 1.102/24, 1.181/29 | 0.973/33 | -- | -- |
| Improved decomposition-based evolutionary algorithm (I-DBEA) [30] | 94.85 | 1.098/13, 1.097/24, 1.715/30 | -- | 0.0007 | 0.9650 |
| Comprehensive teaching learning-based optimization (CTLBO) [34] | 85.96 | 1.036/13, 1.163/24, 1.522/30 | -- | 0.0026 | 0.9481 |
| CTLBO ε-method [34] | 96.17 | 1.193/13, 0.871/25, 1.629/30 | -- | 0.0009 | 0.9638 |
| Teaching learning-based optimization (TLBO) [46] | 124.69 | 1.183/12, 1.191/28, 1.186/30 | -- | 0.0011 | 0.9503 |
| Quasi-oppositional TLBO (QOTLBO) [46] | 103.40 | 1.083/13, 1.188/26, 1.199/30 | -- | 0.0011 | 0.9530 |
| GA [47] | 106.30 | 1.500/11, 0.423/29, 1.071/30 | 0.981/25 | 0.0407 | 0.9497 |
| PSO [47] | 105.30 | 1.177/8, 0.982/13, 0.829/32 | 0.980/30 | 0.0335 | 0.9256 |
| GA/PSO [47] | 103.40 | 0.925/11, 0.863/16, 1.200/32 | 0.980/25 | 0.0124 | 0.9508 |
| Fireworks algorithm (FWA) [48] | 88.68 | 0.589/14, 0.189/18, 1.015/32 | 0.968 | -- | -- |
| HSA [49] | 96.76 | 0.572/17, 0.107/18, 1.046/33 | 0.967/29 | -- | -- |
| Ant colony optimization and artificial bee colony (ACO-ABC) [49] | 71.40 | 0.755/14, 1.099/24, 1.071/30 | -- | -- | -- |
| EGWO-PSO [16] | 71.46 | 0.754/14, 1.099/24, 1.071/30 | 0.969/33 | 0.0135 | 0.8813 |
| AREP-EGWO-PSO | 72.53 | 0.823/13, 1.121/24, 0.934/31 | 0.970/30 | 0.0140 | 0.8871 |
| Methods | Power Loss (KW) | DGs Size (MW)/Position | CBs Size (MVAR)/Position | Min. Voltage (p.u.)/Bus | VDI (p.u.) | VSI (p.u.) |
|---|---|---|---|---|---|---|
| Base case | 202.68 | -- | -- | 0.913/18 | 0.1171 | 0.6968 |
| WCA [29] | 24.69 | 0.563/11, 0.973/25, 1.04/29 | 0.535/14, 0.465/23, 0.565/30 | 0.980/33 | -- | -- |
| EGWO-PSO [16] | 15.16 | 0.746/14, 1.078/24, 1.048/30 | 0.528/11, 0.712/23, 1.000/29 | 0.994/22 | 0.0003 | 0.9786 |
| AREP-EGWO-PSO | 16.00 | 0.811/13, 1.098/24, 0.921/31 | 0.528/11, 0.712/23, 1.000/29 | 0.994/22 | 0.0004 | 0.9767 |
| Methods | Power Loss (KW) | DGs Size (MW)/Position/Power Factor | Min. Voltage (p.u.)/Bus | VDI (p.u.) | VSI (p.u.) |
|---|---|---|---|---|---|
| Base case | 202.68 | -- | 0.913/18 | 0.1171 | 0.6968 |
| I-DBEA [30] | 14.57 | 0.749/13/0.85, 1.042/24/0.85, 1.239/30/0.85 | -- | 0.0002 | 0.9733 |
| Loss sensitivity factor simulated annealing (LSFSA) [50] | 26.70 | 1.383/6/0.85, 0.552/18/0.85, 1.063/30/0.85 | -- | 0.0013 | 0.9323 |
| EGWO-PSO [16] | 11.68 | 0.779/13/0.91, 1.072/24/0.89, 1.036/30/0.72 | 0.993/8 | 0.0006 | 0.9707 |
| AREP-EGWO-PSO | 15.50 | 0.780/14/0.89, 1.103/24/0.89, 0.937/31/0.73 | 0.991/8 | 0.0009 | 0.9626 |
| Methods | Power Loss (KW) | DGs Size (MW)/Position/Power Factor | CBs Size (MVAR)/Position | Min. Voltage (p.u.)/Bus | VDI (p.u.) | VSI (p.u.) |
|---|---|---|---|---|---|---|
| Base case | 202.68 | - | 0.913/18 | 0.1171 | 0.6968 | |
| WCA [29] | 19.85 | 0.992/11/0.91 0.982/31/0.98 1.650/24/0.96 | 0.325/19, 0.312/23, 0.543/30 | 0.989/18 | 0.0410 | 0.9850 |
| EGWO-PSO [16] | 14.99 | 0.778/13/1 1.072/24/0.99 1.035/30/0.99 | 0.524/11, 0.693/23, 1.000/29 | 0.994/22 | 0.0003 | 0.9788 |
| AREP-EGWO-PSO | 16.35 | 0.782/14/1 1.109/24/0.99 0.909/32/0.99 | 0.524/11, 0.693/23, 1.000/29 | 0.994/8 | 0.0004 | 0.9762 |
| Methods | Power Loss (KW) | Grid Real Power (MW)/Reactive Power (MVAR)/Position | CBs Reactive Power (MVAR)/Position | WT Real Power (MW)/Reactive Power (MVAR)/Position | PV Real Power (MW)/Reactive Power (MVAR)/Position | GT Real Power (MW)/Reactive Power (MVAR)/ Position | Cost ($/h) | Emission (lb/h) |
|---|---|---|---|---|---|---|---|---|
| Base case | 202.68 | -- | -- | -- | -- | -- | 304.896 | 8.027 × 106 |
| WCA [29] | 28.96 | 1.541/0.657/1 | 0.30/15 0.45/19 0/26 | 0.648/0.147/25 | 0.715/0.439/32 0.639/0.278/27 | 0.201/0.052/18 | 249.343 | 3.405 × 106 |
| EGWO-PSO [16] | 19.22 | 1.014/ 0.243/1 | 0.30/15 0.45/19 0/26 | 0.775/0.422/25 | 0.173/0.836/32 1.301/0.074/27 | 0.472/ 0.021/13 | 227.372 | 2.290 × 106 |
| AREP-EGWO-PSO | 21.49 | 0.842/ 0.026/1 | 0.30/15 0.45/19 0/26 | 1.064/ 0.429/24 | 0.723/ 0.186/28 0.598/ 0.882/30 | 0.501/ 0.0429/18 | 274.134 | 2.467 × 106 |
| Methods | Power Loss (KW) | DGs Size (MW)/Position | Min. Voltage (p.u.)/Bus | VDI (p.u.) | VSI (p.u.) |
|---|---|---|---|---|---|
| Base case | 225 | -- | 0.909/65 | 0.0993 | 0.6850 |
| WCA [29] | 71.50 | 0.775/61, 1.105/62, 0.438/23 | 0.987/65 | -- | -- |
| I-DBEA [30] | 78.35 | 2.149/61, 0.472/19, 0.713/11 | -- | 0.0002 | 0.9772 |
| CTLBO [34] | 76.37 | 0.560/11, 0.427/18, 2.153/61 | -- | 0.0008 | 0.9770 |
| CTLBO ε-method [34] | 79.66 | 0.966/12, 0.231/25, 2.134/61 | -- | 0.0003 | 0.9770 |
| TLBO [46] | 82.17 | 1.013/13, 0.990/61, 1.160/62 | -- | 0.0008 | 0.9745 |
| QOTLBO [46] | 80.59 | 0.811/15, 1.147/61, 1.002/63 | -- | 0.0007 | 0.9769 |
| GA [47] | 89.00 | 0.929/21, 1.075/62, 0.984/64 | -- | 0.0012 | 0.9706 |
| PSO [47] | 83.20 | 1.199/61, 0.796/63, 0.993/17 | -- | 0.0049 | 0.9676 |
| GA/PSO [47] | 81.10 | 0.885/63, 1.193/61, 0.911/21 | -- | 0.0031 | 0.9768 |
| FWA [48] | 77.85 | 0.226/27, 1.199/61, 0.409/65 | 0.974/62 | -- | -- |
| HSA [49] | 86.77 | 0.102/65, 0.369/64, 1.302/63 | 0.968 | -- | -- |
| ACO-ABC [49] | 69.43 | 0.559/11, 0.346/21, 1.715/61 | -- | -- | -- |
| EGWO-PSO [16] | 69.43 | 0.527/11, 0.380/18, 1.719/61 | 0.979/65 | 0.0052 | 0.9205 |
| AREP-EGWO-PSO | 76.50 | 0.528/18, 1.361/60, 0.454/65 | 0.978/61 | 0.0063 | 0.9164 |
| Methods | Power Loss (KW) | DGs Size (MW)/Position | CBs Size (MVAR)/Position | Min. Voltage (p.u.)/Bus | VDI (p.u.) | VSI (p.u.) |
|---|---|---|---|---|---|---|
| Base case | 225 | -- | -- | 0.909/65 | 0.0993 | 0.6850 |
| WCA [29] | 33.34 | 0.541/17, 2.000/61, 1.159/69 | 1.188/2, 1.237/62, 0.269/69 | 0.994/50 | -- | -- |
| EGWO-PSO [16] | 7.86 | 0.496/11, 0.380/17, 1.655/61 | 1.000/61, 0.413/64, 0.476/69 | 0.994/50 | 0.0002 | 0.9794 |
| AREP-EGWO-PSO | 14.12 | 0.521/17, 1.295/60, 0.449/65 | 1.000/61, 0.413/64, 0.476/69 | 0.994/50 | 0.0003 | 0.9794 |
| Methods | Power Loss (KW) | DGs Size (MW)/Position/Power Factor | Min. Voltage (p.u.)/Bus | VDI (p.u.) | VSI (p.u.) |
|---|---|---|---|---|---|
| Base case | 225 | -- | 0.909/65 | 0.0993 | 0.6850 |
| I-DBEA [30] | 7.97 | 1.500/61/0.85, 0.370/59/0.85, 0.575/16/0.85 | -- | 0.0003 | 0.9774 |
| LSFSA [50] | 16.26 | 0.549/18/0.85, 1.195/60/0.85, 0.312/65/0.85 | -- | 0.0023 | 0.9678 |
| EGWO-PSO [16] | 4.27 | 0.495/11/0.81, 0.379/18/0.83, 1.674/61/0.81 | 0.994/50 | 0.0001 | 0.9794 |
| AREP-EGWO-PSO | 13.98 | 0.516/18/0.83, 1.312/60/0.81, 0.455/65/0.82 | 0.994/50 | 0.0005 | 0.9778 |
| Methods | Power Loss (KW) | DGs Size (MW)/Position/Power Factor | CBs Size (MVAR)/Position | Min. Voltage (p.u.)/Bus | VDI (p.u.) | VSI (p.u.) |
|---|---|---|---|---|---|---|
| Base case | 225 | -- | -- | 0.909/65 | 0.0993 | 0.6850 |
| WCA [29] | 18.70 | 1.825/61/0.88, 1.041/36/0.92, 0.106/19/0.90 | 0.019/15, 0.458/33, 0.559/22 | 0.994/50 | 0.0092 | 0.9687 |
| EGWO-PSO [16] | 7.21 | 0.494/11/1, 0.379/18/0.95, 1.653/61/1 | 1.000/61, 0.413/64, 0.476/69 | 0.994/50 | 0.0001 | 0.9794 |
| AREP-EGWO-PSO | 13.64 | 0.492/20/0.97 1.304/60/1 0.444/65/1 | 1.000/61, 0.413/64, 0.476/69 | 0.994/50 | 0.0002 | 0.9794 |
| Methods | Power Loss (KW) | Grid Real Power (MW)/Reactive Power (MVAR)/Position | CBs Reactive Power (MVAR)/Position | WT Real Power (MW)/Reactive Power (MVAR)/Position | PV Real Power (MW)/Reactive Power (MVAR)/Position | GT Real Power (MW)/Reactive Power (MVAR)/Position | Cost ($/h) | Emission (lb/h) |
|---|---|---|---|---|---|---|---|---|
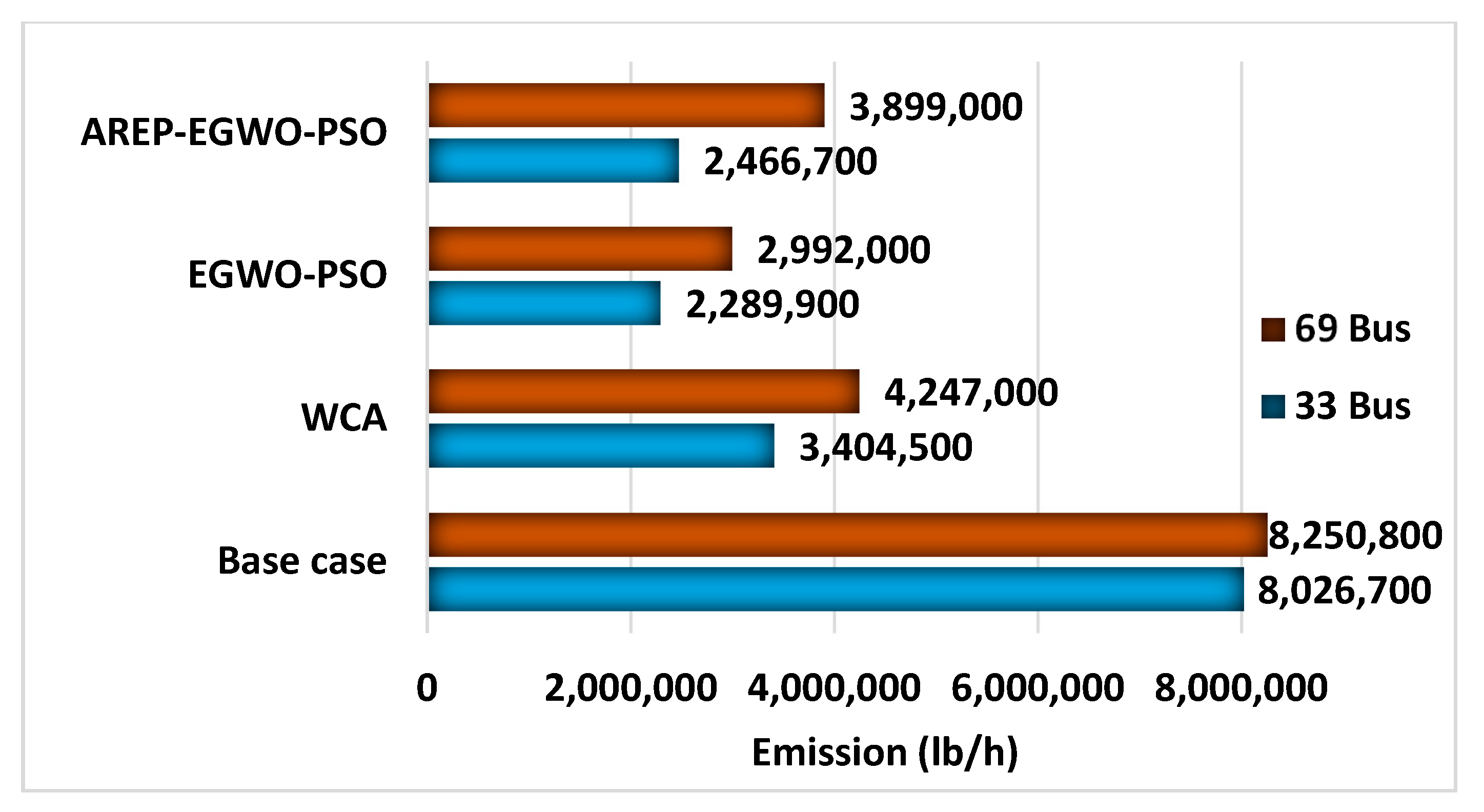
| Base case | 225 | -- | -- | -- | -- | -- | 309.713 | 8.251 |
| WCA [29] | 22.36 | 1.747/0.295/1 | 0.60/23 0.60/62 0.30/42 | 0.703/0.274/63 | 0.102/0.035/58 0.731/0.291/66 | 0.5405/0.3130/64 | 297.470 | 4.247 |
| EGWO-PSO [16] | 8.84 | 1.289/0.507/1 | 0.30/23 0.45/42 0.60/62 | 1.334/0.028/63 | 0.547/0.355/11 0.356/0.005/20 | 0.2851/0.4603/64 | 250.537 | 2.992 |
| AREP-EGWO-PSO | 12.78 | 1.603/0.765/1 | 0.30/23 0.45/42 0.60/62 | 1.046/0.809/61 | 0.451/0/23 0.217/0.080/60 | 0.49798/0.29762/64 | 286.786 | 3.899 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Venkatesan, C.; Kannadasan, R.; Ravikumar, D.; Loganathan, V.; Alsharif, M.H.; Choi, D.; Hong, J.; Geem, Z.W. Re-Allocation of Distributed Generations Using Available Renewable Potential Based Multi-Criterion-Multi-Objective Hybrid Technique. Sustainability 2021, 13, 13709. https://doi.org/10.3390/su132413709
Venkatesan C, Kannadasan R, Ravikumar D, Loganathan V, Alsharif MH, Choi D, Hong J, Geem ZW. Re-Allocation of Distributed Generations Using Available Renewable Potential Based Multi-Criterion-Multi-Objective Hybrid Technique. Sustainability. 2021; 13(24):13709. https://doi.org/10.3390/su132413709
Chicago/Turabian StyleVenkatesan, Chandrasekaran, Raju Kannadasan, Dhanasekar Ravikumar, Vijayaraja Loganathan, Mohammed H. Alsharif, Daeyong Choi, Junhee Hong, and Zong Woo Geem. 2021. "Re-Allocation of Distributed Generations Using Available Renewable Potential Based Multi-Criterion-Multi-Objective Hybrid Technique" Sustainability 13, no. 24: 13709. https://doi.org/10.3390/su132413709
APA StyleVenkatesan, C., Kannadasan, R., Ravikumar, D., Loganathan, V., Alsharif, M. H., Choi, D., Hong, J., & Geem, Z. W. (2021). Re-Allocation of Distributed Generations Using Available Renewable Potential Based Multi-Criterion-Multi-Objective Hybrid Technique. Sustainability, 13(24), 13709. https://doi.org/10.3390/su132413709









