Evaluation of Road Safety Performance Based on Self-Reported Behaviour Data Set

Abstract

Self-reported behavioural data, being often linguistic variables that represent a qualitative measure of respondents’ opinions/attitudes, are vague, uncertain, and fuzzy in nature. A road safety performance index, based on these fuzzy data, should consider this uncertainty. In this study, fuzzy numbers were used to describe self-reported behaviour on Montenegrin roads, which was further integrated into the data envelopment analysis (DEA), a technique for measuring the relative performance of decision-making units (DMUs). The vagueness of the performance scores obtained in this way was treated with grey relational analysis (GRA). GRA was applied to the cross-efficiency (CE) matrix constructed by the DEA to distinguish Montenegrin municipalities’ performance, with the main goal of describing road safety in the observed territories in the environment of uncertain/grey data. It is concluded that the proposed DEA–GRA model, based on fuzzy data, provides a more reasonable and encompassing measure of performance, and with which the overall ranking position of municipalities can be obtained.

1. Introduction

Traffic accidents are a global problem, and injuries and the material damage caused by traffic accidents have a huge impact on both the individual and the community as a whole. At the national level, accidents result in high financial costs, which particularly affect developing countries. According to the WHO [1], two of the leading causes of death by injury in the world are road deaths and traffic injuries.

Traffic safety risk-management is a complex problem and is based, above all, on defining the current situation in a certain territory and comparing it with different entities (e.g., countries, local regions, municipalities). All territories are specific from the point of view of safety management, the state of road infrastructure, the behaviour of traffic participants, and the number and equipment of medical services, and that is why cross-comparison is very important. In addition, assessing the road safety of a territory and describing it with a single performance index is a complicated task since there are a large number of factors and causes (indicators) that need to be integrated. Usually, all indicators selected for describing traffic safety are classified into a few main road-safety domains: speed, alcohol, protective systems, vehicles, roads, and trauma management [2,3].

The reliability of the final performance score depends on the data from which it is constructed. Therefore, its quality should improve in parallel with the improvement of the quality of the collected data. The majority of safety performance indicators (SPIs) are collected from international and/or national databases based on methodologically established measurements, and are presented quantitatively (such as the number of fatalities, number of accidents, risk exposures, etc.). However, some indicators, such as those related to driver behaviours, are more subjective and imprecise. They rely primarily on the data collected by the survey method, i.e., on self-reported behavioural practices [4]. These data indicate the extent of agreement (or disagreement) on a scale with multiple response categories and are described with linguistic terms representing qualitative (and subjective) measures of opinion about road-user behaviours. Due to the interplay between cognitive, affective, and contextual factors, they can be barely captured by standard (crisp) rating responses. They are uncertain in nature [5], and the accuracy and precision of these subjective measures is unlikely. Existing road safety evaluation models, based on multi-criteria decision-making (MCDM) techniques, commonly consider data uncertainty regarding the subjective opinion of safety experts/evaluators, as in [6,7], using a fuzzy-oriented analytic hierarchy process (AHP), in [8,9], using a Pythagorean fuzzy AHP, and in [10], via an analytic network process. On the other hand, when constructing a traffic safety index, extended DEA-oriented MCDM approaches allow subjectivity to be reduced only to the uncertainty of road users’ self-reported behaviour, as shown in this paper. The indicators used here are data on Montenegrin driver behaviours collected through a questionnaire designed for this particular study, and a fuzzy number approach, which has already been successfully applied in both road safety [6,7] and other fields [11,12], was used to describe self-reported behaviour. After defuzzification, these behavioural indicators were integrated into the DEA for weighting and performance index construction. The vagueness of the performance scores obtained in this way was further treated with a grey relational analysis (GRA). The GRA was applied on the cross-efficiency (CE) matrix constructed by the DEA to distinguish the performance of Montenegrin municipalities and to rank them. The main aim of this approach was to provide a set of robust road safety indexes for each analysed territory in the environment of uncertain/grey data. The proposed algorithm is not complex; it is a convenient methodology that is easy to solve, allows for the full ranking of all territories under analysis without implementing subjective information from the outside, and also handles the uncertainty of road safety DEA scores, similar to some other extended DEA methods (e.g., imprecise DEA, fuzzy DEA, robust DEA).

The rest of the paper is organized as follows: the next section provides a literature review; an overview of the applied methodologies is briefly presented in Section 3; the identification of the SPIs for a case study are given in Section 4. In Section 5, the results of the implemented methodology are presented. In Section 6, the results and findings of the proposed method are discussed. Finally, the last section concludes the paper and represents the direction of future research.

2. Literature Review

There is no universal approach for obtaining an exact uniform assessment of road safety. Various techniques and mathematical and statistical tools are used to aggregate a number of SPIs into one composite index. Different types of input/output data and criteria, which should be included in the final assessment, are also a problem. The technique of mathematical linear programming, i.e., data envelopment analysis (DEA), enables the combination of diverse criteria with the aim of calculating the relative efficiency of an entity. Consequently, quite a lot of interest in measuring relative performance in terms of efficiency is focused on DEA.

DEA measures the efficiency of entities based on weights that are not previously known. Entities in DEA are called decision-making units (DMUs), and the way in which they are classified depends on their location relative to the efficient frontier. DEA has been used by many authors to create road safety performance indexes and benchmarks, from the national [13,14] to the micro level [15,16], and more recently, to solve the problem of evaluating the layered hierarchy of indicators with a common set of weights [17]. In addition, with the given freedom for selecting inputs and outputs, it has been used to rank road sections [18], to measure the performance of public transport organizations [19], and to evaluate older drivers’ performance [20].

When input and output data are numerical, their application in the DEA methodology is relatively easy, and the issue of the accuracy and reliability of these data is often neglected. In the case of qualitative, linguistic data, however, their natural vagueness and ambiguity must be taken into account. When collecting self-reported data on behaviour, the main focus is on their final presentation, since, in many cases, respondents are not able to clearly express their judgments, and it is assumed that all final values derived from such data are uncertain [21]. Recently, in an uncertain DEA framework, imprecise DEA approaches [22], fuzzy DEA methods [23], and robust DEA methods [24] have been used. In [25,26], it was shown that both imprecise DEA and fuzzy DEA models can give robust composite index scores, which implies the effectiveness and reliability of these two approaches for modelling qualitative data. Furthermore, in [23], it is illustrated that each fuzzy number can be converted into an interval number, thus reducing the issue of the DMUs’ efficiency assessment to an imprecise DEA problem. In addition to the above, rough set theory, probability theory, Shannon’s entropy, and grey theory have been put forward to deal with imprecise and ambiguous data. It is proven that, despite the differences, all existing models for addressing uncertainties are related to one another [27].

Fuzzy theory is the most-applied methodology for processing imprecise and inaccurate data, most notably when they are described in human language [28]. Apart from the one mentioned above (in [23]), there are two ways to implement fuzzy numbers (usually triangular or trapezoidal) for modelling linguistic variables. The first approach concerns the introduction of alternative scales—for example, the fuzzy Likert scale [29,30,31]. Another approach, known as the fuzzy linguistic approach, is more common in the literature and considers the process of coding the already-collected survey answers with fuzzy numbers, i.e., assigning a fuzzy number to each answer from the Likert scale [32,33,34]. The question is raised about the implementation of such data into the DEA. One of the ways that should be mentioned is based on the previous defuzzification process of the values of the input and output variables in order to apply the conventional DEA model [35]. The reliability of the efficiency score obtained from such data is questionable, and can be addressed with a grey relational analysis (GRA), as in this paper.

GRA is part of the grey system theory proposed by Deng [36], and it is suitable for solving a variety of multiple-attribute decision-making problems. Many authors have used the grey system theory for this purpose: Kuang et al. [37] dealt with a combination of GRA and PROMETHEE II; Thakur and Ramesh [38] used a combination of it and the analytic hierarchy process (AHP); Sakthivel et al. [39] combined it with the technique for order preference by similarity to ideal solution (TOPSIS); Xue et al. [40] combined it with the fuzzy theory; and Wang [41] combined it with the network nodes. Other ways of applying GRA are given in [42,43], including its combination with DEA in the form of the evaluation and selection of efficient suppliers [44], evaluating the effect of the conditions of both feeding and climate in poultry houses on production performance in a commercial poultry enterprise [45], ranking the efficiency of DMUs [46], and assessing the performance of exchange-traded funds [47].

According to these studies, where GRA has been successfully integrated with DEA, the main purpose of this paper was to implement a corresponding methodology to address the road safety performance of a territory based on uncertain data, taking Montenegrin municipalities as DMUs. The proposed methodology is easy to solve, allows for a full ranking of all analysed territories, and also handles the uncertainty of road safety DEA scores similar to an imprecise DEA. Here, however, instead of interval efficiencies for DMUs, the vagueness of the DEA efficiencies is treated with a GRA. In this way, the contributing factors that have the most influence on the road accidents are targeted, which can serve policy makers in planning future measures and prevention.

3. Materials and Methods

3.1. Questionnaire

For improving road safety, road-user behaviours should be considered and investigated carefully. Inappropriate behaviour is always present and proves to be a contributing factor in most accidents [48,49,50]. As stated in [51,52], in countries that do not have established databases of behaviour-related indicators, the assessment of traffic safety can be performed on the basis of data collected through a survey method—namely, through self-reported behaviour. This method is appropriate, because decision makers, even without quality databases, have the opportunity to conduct a relatively simple assessment of the situation and rank the region in terms of traffic safety. Since one of the goals of this study was to identify the most influential road safety behaviour, the driver was chosen to represent the unit of the analysis, rather than any users involved in the road traffic. To address driver behaviour, a national survey was conducted among 780 drivers from all Montenegrin cities (sample size with 3% error bounds and 95% confidence limits).

Due to its suitability for measuring abstract attitudes and behaviours, psychometric testing has been developed based on questions with multidimensional answers where the respondent shows his degree of agreement for each question. One of the most commonly used psychometric scales is the Likert scale [53,54], which offers several categories of answers and requires respondents to rank their position with one of the offered options. These categories can cover any range, but are usually up to 5 or 7 points (e.g., from the smallest (“strongly disagree”) to the largest (“strongly agree”)) and reliability is satisfied when more than four answer options are used [55].

In the conducted national survey, the questionnaire was compiled in accordance with the ESRA and SARTRE methodology, which means the drivers were asked to confirm how often they behave as indicated in the question (

Table 1. Survey questions.

Survey Questions	Mark
Driving above the speed limit
How often do you drive over the speed limit?
(On main roads)	V1
(On regional roads)	V2
(On local/urban roads)	V3
Do you exceed the prescribed speed on roads with higher permitted speeds (60–80 km/h)?
(By more than 30 km/h)	V4
(By less than 30 km/h)	V5
Do you exceed the prescribed speed on roads with lower permitted speeds (50–60 km/h)?
(By more than 20 km/h)	V6
(By less than 20 km/h)	V7
Do you exceed the prescribed speed on local/urban roads?
(By more than 10 km/h)	V8
(By less than 10 km/h)	V9
Driving under the influence of alcohol
Do you drive under the influence of alcohol?
(On main roads)	A1
(On regional roads)	A2
(On local/urban roads)	A3
Not wearing a seatbelt
How often do you wear your seat belt while driving?
(On main roads)	P1
(On regional roads)	P2
(On local/urban roads)	P3
Using a mobile phone while driving
Do you use a hands-free device to talk on a mobile phone while driving?
(On main or regional roads)	T1
(On local/urban roads)	T2
Do you use a mobile phone while driving to write messages and visit social networks?
(On main or regional roads)	T3
(On local/urban roads)	T4

) in the previous three years, using one of the following values of language variables: never, rarely, sometimes, often, very often, and always.

Six-option answers are offered for each question in order to address the frequency of the particular behaviour. All questions are divided into those related to main roads, regional roads, and local/urban roads. Finally, participants (drivers) answered up to 19 questions grouped into four main domains (V1–V9, A1–A3, P1–P3, T1–T4). The processing of data obtained in this way can be diverse, and it is possible to use both parametric and non-parametric methods. To obtain the final result, the aggregate score, and the mean value of the coded attitudes (or modes, medians, etc.), are most often used. Depending on the method of data collection, it is possible to make a comparison between pairs of questions and their mutual importance. In relation to the level of dominance between questions, quantitative values are assigned to each answer. In addition to the many geometric or constructed scales (for example, the Salo–Hämäläinen scale) that are used to compare pairs of attitudes, the smallest error occurs using the Saaty scale [56,57]. Moreover, the processing of the survey data can be performed using the theory of fuzzy number sets [58,59], and this particular method was used in this paper, rather than simply averaging the Likert scores. Processing with fuzzy theory is based on modelling uncertain and subjective data in such a way that each category of responses on the Likert scale is coded as a fuzzy number. In addition to applying this methodology, more appropriate and reasonable values are assigned for qualitative data. The following section presents the basics of creating fuzzy numbers.

3.2. Fuzzy Numbers

Fuzzy theory refers to addressing the uncertainty and imprecision of data; it relies on possibility and neglects probability. The degree of relevance for a particular observed element is described by the membership function, with values from the interval (0–1). In this paper, all input indicator calculations were made based on the trapezoidal fuzzy numbers (i.e., a₁, a₂, a₃, a₄) with the following membership function:

$$\begin{gathered} {\mu }_{a\left(x\right)}=\frac{x-a_1}{a_2-a_1};x\in \left[a_1,a_2\right], \\ {\mu }_{a\left(x\right)}=1;x\in \left[a_2,a_3\right], \\ {\mu }_{a\left(x\right)}=\frac{a_4-x}{a_4-a_3};x\in \left[a_3,a_4\right], \\ {\mu }_{a\left(x\right)}=0;\mathrm{Otherwise}. \end{gathered}$$

(1)

To obtain a final crisp value to serve as the input data in the DEA, normalisation of the obtained fuzzy numbers was performed, and defuzzification was conducted as follows:

$$\begin{array}{cc}\hfill i_{ij}=Defuzz \left(x_{ij}\right)& \\ \hfill =& \frac{\left(\frac{1}{3}\right){\left(x_{ij4}-x_{ij3}\right)}^2+\left(\frac{1}{3}\right){\left(x_{ij2}-x_{ij1}\right)}^2-x_{ij1}{x}_{ij2}+x_{ij3}{x}_{ij4}}{-x_{ij1}-x_{ij2}+x_{ij3}+x_{ij4}}\hfill \end{array}$$

(2)

3.3. Data Envelopment Analysis with Cross-Evaluation

When indicators are defined, the next step is their implementation in the DEA. DEA defines the efficiency of DMU_j as the ratio of the sum of the weighted outputs and the sum of the weighted inputs, and it is efficient when the ratio is equal to 1. The simplified, linear formulation is given as follows:

$$\begin{gathered} maxE{f}_j={{\displaystyle \sum }}_{r=1}^s{u}_r{y}_{rj}, \\ \mathrm{subject\; to:} \\ {{\displaystyle \sum }}_{i=1}^m{v}_i{x}_{ij}=1, \\ {{\displaystyle \sum }}_{r=1}^s{u}_r{y}_{rj}\le {{\displaystyle \sum }}_{i=1}^m{v}_i{x}_{ij},j=1,\dots ,n, \\ {u}_r\ge 0;r=1,\dots ,s, \\ {v}_i\ge 0;i=1,\dots ,m \end{gathered}$$

(3)

where y_rj stands for rth output and x_ij stands for ith input of the jth decision-making unit, u_r is the weight of the output r, and v_i is the weight for the input i. The efficiency of DMU_j, calculated with (3), is called simple efficiency and is based on self-evaluation. In addition, the efficiency of DMU_j can be also calculated taking into account the set of the optimal weights of DMU_k ($u_r^k, v_i^k,$ k = 1, …, n):

$$E{f}_{jk}=\frac{{{\displaystyle \sum }}_{r=1}^s{u}_r^k{y}_{rj}}{{{\displaystyle \sum }}_{i=1}^m{v}_i^k{x}_{ij}}$$

(4)

Such efficiency is called cross efficiency. The efficiencies thus obtained (known in the literature as peer efficiencies) form a cross-efficiency matrix, where simple DEA efficiency (self-evaluated) is placed in the matrix diagonal. The value of the final cross efficiency of a DMU_j is obtained by calculating the arithmetic mean (averaging) of all corresponding peer efficiencies:

$$\overline{E{f}_j}=\frac{1}{n}{\displaystyle \sum }_{k=1}^{n}E{f}_{jk}$$

(5)

In this paper, instead of averaging, a grey relational analysis is suggested in order to obtain the final efficiency, i.e., the final road safety performance index.

3.4. Grey Relational Analysis

Grey relational analysis is a useful method for solving multiple-attribute problems in an uncertain environment. Here, GRA was applied on the cross-efficiency matrix obtained with DEA (DEA-CE matrix). Normalisation, as the first step, was conducted with:

$$g_i\left(j\right)=\frac{x_i\left(j\right)-mi{n}_{j=1}^n{x}_i\left(j\right)}{ma{x}_{i=1}^n{x}_i\left(j\right)-mi{n}_{j=1}^n{x}_i\left(j\right)},$$

(6)

with n data sequences (i = 1…n), and m attributes (j = 1…m), in the general case. In this study, the reference sequence was selected from the normalised matrix, which refers to the best performance for each territory under evaluation. All obtained normalised efficiencies from the DEA-CE matrix were compared to the reference sequence, and the grey relational coefficient was calculated as:

$${\zeta }_{0i}\left(j\right)=\frac{mi{n}_{i=1}^{n}mi{n}_{j=1}^m\left|g_i\left(j\right)-g_0\left(j\right)\right|+\rho ma{x}_{i=1}^{n}ma{x}_{j=1}^m\left|g_i\left(j\right)-g_0\left(j\right)\right|}{\left|g_i\left(j\right)-g_0\left(j\right)\right|+\rho ma{x}_{i=1}^{n}ma{x}_{j=1}^m\left|g_i\left(j\right)-g_0\left(j\right)\right|}$$

(7)

where ρ is the distinguishing coefficient (0, 1) s and, in most situations, this value is 0.5 because it offers moderate distinguishing effects. The final grade of the relation was derived as follows:

$${\mathrm{\Gamma }}_{0i}\left(j\right)=\frac{1}{n}{{\displaystyle \sum }}_{j=1}^m{\zeta }_{0i}\left(j\right),$$

(8)

$${\mathrm{\Gamma }}_{DEA}=\frac{{\mathrm{\Gamma }}_{0i}\left(j\right)}{{\mathrm{\Gamma }}_{0i}{\left(j\right)}^{+}},$$

(9)

The final grades were normalised with (9), and based on this, the territories with the highest degree of relation were identified as those with the highest safety level. A graphical presentation of the proposed methodology is given in Figure 1.

As can be seen, after the selection of indicators (first step), their classification into two groups (inputs and outputs; second step), and data collection (here via a questionnaire and referring to self-reported behaviour), data processing is performed. Related to input indicators, fuzzy numbers were proposed to describe drivers’ self-reported behaviours, and defuzzification needs to be obtained. Both inputs and outputs need to be normalised before incorporation into the DEA. In the fifth step, DEA is proposed for aggregation, as it is the most reliable method for index construction. The extension of the DEA produces evaluation scores in the form of a cross-efficiency matrix, and GRA was used to aggregate cross efficiencies into one final index score.

All of the mentioned methods represent an effort to build an appropriate method for evaluating road safety and provide reliable efficiency scores consistent with qualitative data.

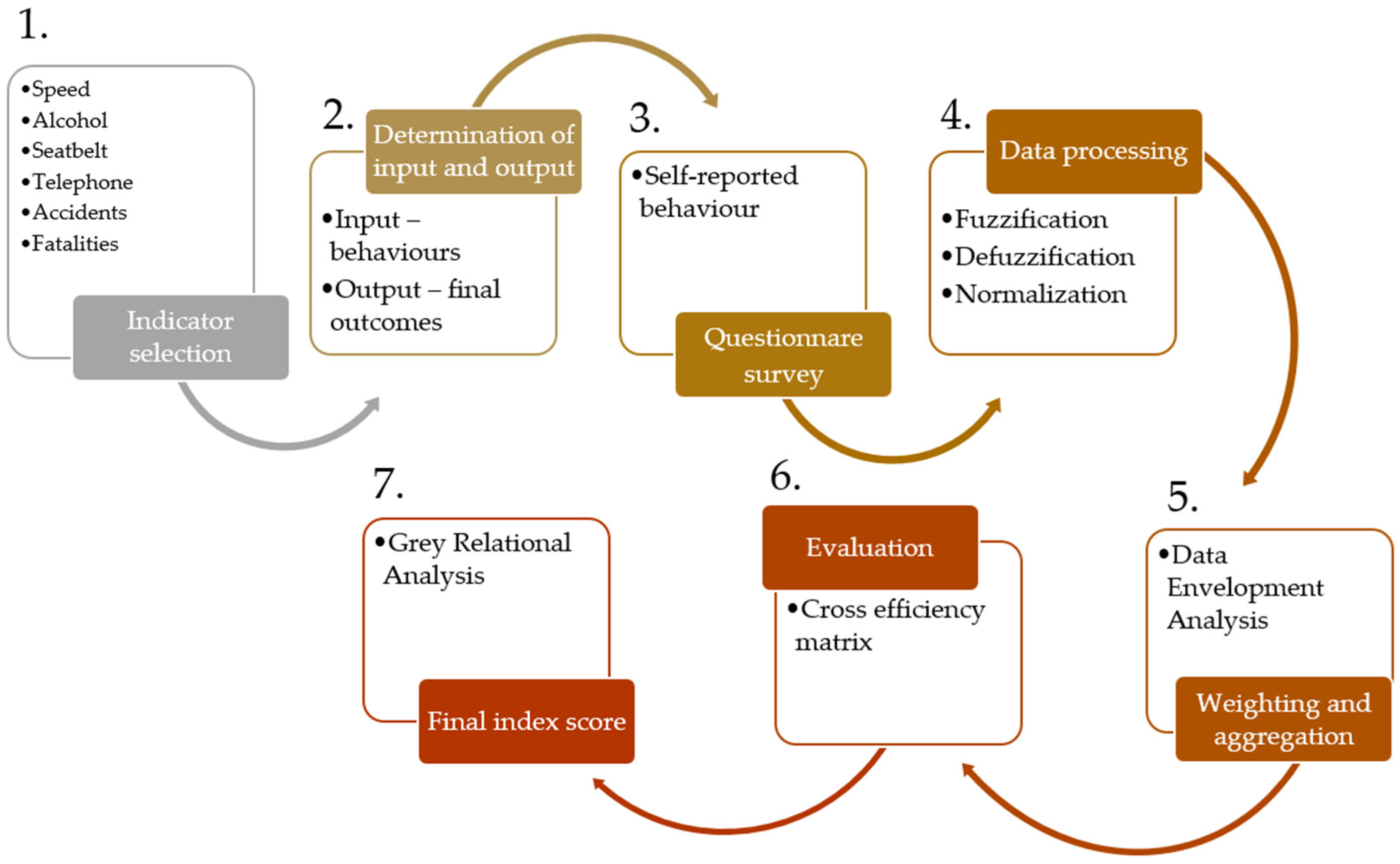
4. Data

With the final composite index, the complexity of road safety can be captured. It is very important to choose indicators properly because the final assessment depends mostly on them [3]. Respecting the rule that the number of DMUs should be three times larger than the number of inputs and outputs [15], four road safety indicators were selected as inputs, and two outcomes as outputs, to calculate the safety performance of 21 municipalities in Montenegro. Road safety behaviours related to speeding, driving under the influence of alcohol, not wearing a seatbelt, and using a telephone while driving (for calls, text messages, or visiting social networks) were chosen as the inputs, and the number of accidents and the number of fatalities as the outputs (Figure 2).

Given the lack of availability of road safety data in Montenegro, the authors conducted a survey using a self-reported questionnaire to address the real situation on the roads of Montenegro. The case study was conducted in the period from July to October 2019. Data were collected by conducting random face-to-face and online questionnaire surveys with participants from each municipality of Montenegro. A total of 780 drivers answered the selected behaviour-related questions (descriptive statistics are given in

Table 2. Descriptive statistics.

Variables	Choices	%
Gender	Male	45.64
	Female	54.36
Age	17–24	25.13
	25–35	33.97
	35–44	19.49
	45–54	11.41
	55–64	6.67
	65+	3.33
Employment status	Student	19.36
	Unemployed	28.33
	Employed	52.31
Frequency of driving	Everyday	76.03
	1–3 times per week	15.13
	1–3 times per month	4.36
	Less than once per month	4.49
Years with driving licence	0–5	30.26
	6–10	20.00
	11–20	29.49
	21–30	10.13
	30–40	8.08
	40+	4.62

).

To answer the 19 questions related to behaviour, the following linguistic variables were offered in each question: never, rarely, sometimes, often, very often, and always. The answers were converted to trapezoidal fuzzy numbers, as given in

Table 3. Linguistic variables and the corresponding fuzzy numbers.

Linguistic Variable	Fuzzy Number
Never	(0.0, 0.0, 0.1, 0.2)
Rarely	(0.1, 0.2, 0.3, 0.4)
Sometimes	(0.3, 0.4, 0.4, 0.5)
Often	(0.4, 0.5, 0.6, 0.7)
Very often	(0.6, 0.7, 0.8, 0.9)
Always	(0.8, 0.9, 1.0, 1.0)

.

The source of output data on the number of accidents and fatalities was the Ministry of Internal Affairs of Montenegro, and they represent a three-year average for the period 2017–2019. Considering that the outputs should be as low as possible, the output data included in the DEA model were taken as reciprocal values.

5. Results

The fuzzy numbers were used to convert the questionnaire answers into numerical values.

Table 4. Crisp values of input and output data for the DEA model.

Municipality	Inputs				Outputs
	I1	I2	I3	I4	O1	O2
AN	0.8944	0.8303	0.8262	0.6667	0.0588	1.0000
BA	0.4875	0.9177	0.4926	0.4959	0.0167	0.5000
BD	0.7322	0.8303	0.4555	0.5148	0.0022	0.2500
BP	0.7335	0.9079	0.7199	0.5528	0.0053	0.3333
BR	0.8078	0.9217	0.7672	0.5210	0.0019	0.2500
CT	0.7563	0.8148	0.5102	0.4955	0.0068	0.5000
DG	0.9196	0.9196	0.7250	0.4968	0.0066	0.5000
HN	0.4875	0.8216	0.7038	0.4228	0.0022	0.3333
KL	0.8132	0.9444	0.7045	0.5605	0.0091	0.1111
KO	0.5923	0.8015	0.8133	0.5074	0.0024	0.3333
MK	0.6235	0.9444	0.3774	0.6116	0.0185	1.0000
NK	0.7454	0.8468	0.7507	0.4812	0.0013	0.1667
PG	0.7188	0.8956	0.6805	0.5357	0.0004	0.0769
PL	0.7371	0.8548	0.0778	0.5705	0.0625	1.0000
PV	0.7747	0.9329	0.6861	0.5548	0.0104	1.0000
PŽ	0.4875	0.9225	0.5997	0.5274	0.0625	0.5000
RO	0.6901	0.9444	0.4187	0.4003	0.0141	0.3333
ŠA	0.8086	0.9189	0.7108	0.5527	0.0417	0.5000
TV	0.6979	0.8271	0.8262	0.4620	0.0047	0.5000
UL	0.9143	0.5569	0.7661	0.5569	0.0038	0.5000
ŽB	0.8944	0.8844	0.9444	0.7863	0.0500	1.0000

illustrates the final crisp values obtained for each answer after defuzzification. The final input value for the particular indicators (for example, speeding in municipality AN) was derived as an average of all the calculated fuzzy numbers related to the three categories of roads. On the right side of Table 4, the output data, in the form of reciprocal values of the number of accidents and the number of fatalities, are given.

DEA was run 21 times (in Excel Solver) and the best possible efficiency score was calculated for a given municipality to represent its performance in the best light (compared to all other municipalities). Additionally, a cross-efficiency matrix was derived (see

Table A1. Cross-efficiency matrix derived by Data Envelopment Analysis (DEA-CE).

Decision Making Unit	Target DMU
	KO	BP	PG	CT	NK	TV	BD	HN	PŽ	BA	BR	PV	ŽB	DG	KL	RO	UL	MK	PL	AN	ŠA
KO	0.386	0.386	0.386	0.370	0.364	0.364	0.370	0.386	0.297	0.335	0.364	0.364	0.362	0.364	0.094	0.364	0.345	0.337	0.305	0.362	0.094
BP	0.340	0.340	0.340	0.337	0.335	0.335	0.337	0.340	0.255	0.280	0.335	0.335	0.316	0.336	0.127	0.336	0.305	0.280	0.270	0.316	0.127
PG	0.081	0.081	0.081	0.080	0.080	0.080	0.080	0.081	0.055	0.063	0.080	0.080	0.074	0.079	0.018	0.079	0.071	0.066	0.064	0.074	0.018
CT	0.543	0.543	0.542	0.563	0.560	0.560	0.563	0.542	0.365	0.404	0.560	0.561	0.520	0.561	0.194	0.561	0.509	0.416	0.428	0.520	0.194
NK	0.185	0.185	0.185	0.190	0.192	0.192	0.190	0.185	0.118	0.133	0.192	0.190	0.168	0.192	0.050	0.192	0.163	0.138	0.134	0.168	0.050
TV	0.583	0.583	0.584	0.591	0.600	0.600	0.591	0.584	0.383	0.430	0.600	0.591	0.518	0.600	0.172	0.600	0.502	0.437	0.411	0.518	0.172
BD	0.268	0.268	0.268	0.272	0.269	0.269	0.272	0.268	0.182	0.204	0.269	0.272	0.257	0.269	0.075	0.269	0.250	0.215	0.222	0.257	0.075
HN	0.463	0.463	0.465	0.421	0.437	0.437	0.421	0.465	0.359	0.405	0.437	0.434	0.360	0.437	0.109	0.437	0.337	0.408	0.354	0.360	0.109
PŽ	0.593	0.593	0.595	0.521	0.526	0.526	0.521	0.595	1.000	0.922	0.526	0.531	0.486	0.559	1.000	0.559	0.450	0.615	0.543	0.486	1.000
BA	0.620	0.620	0.623	0.546	0.559	0.559	0.546	0.623	0.642	0.679	0.559	0.565	0.488	0.566	0.347	0.566	0.452	0.624	0.565	0.488	0.347
BR	0.256	0.256	0.256	0.263	0.266	0.266	0.263	0.256	0.163	0.184	0.266	0.264	0.231	0.266	0.069	0.266	0.225	0.191	0.187	0.231	0.069
PV	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0.696	0.778	1.000	1.000	0.920	1.000	0.301	1.000	0.890	0.800	0.786	0.920	0.301
ŽB	0.758	0.758	0.754	0.770	0.706	0.706	0.770	0.754	0.771	0.788	0.706	0.718	0.947	0.721	0.602	0.721	0.939	0.682	0.674	0.947	0.602
DG	0.502	0.502	0.502	0.545	0.558	0.558	0.545	0.502	0.299	0.331	0.558	0.549	0.456	0.559	0.189	0.559	0.451	0.341	0.347	0.456	0.189
KL	0.109	0.109	0.109	0.110	0.110	0.110	0.110	0.109	0.111	0.108	0.110	0.110	0.101	0.114	0.143	0.114	0.098	0.085	0.084	0.101	0.143
RO	0.425	0.425	0.427	0.419	0.462	0.462	0.419	0.427	0.319	0.331	0.462	0.455	0.307	0.470	0.344	0.470	0.293	0.306	0.307	0.307	0.344
UL	0.474	0.474	0.470	0.555	0.498	0.498	0.555	0.470	0.289	0.326	0.498	0.501	0.693	0.497	0.131	0.497	0.745	0.341	0.362	0.693	0.131
MK	1.000	1.000	1.000	0.926	0.907	0.907	0.926	1.000	0.914	1.000	0.907	0.928	0.931	0.911	0.376	0.911	0.879	1.000	1.000	0.931	0.376
PL	1.000	1.000	0.998	1.000	0.973	0.973	1.000	0.998	1.000	1.000	0.973	1.000	1.000	1.000	1.000	1.000	0.971	0.878	1.000	1.000	1.000
AN	0.848	0.848	0.844	0.890	0.832	0.832	0.890	0.844	0.809	0.814	0.832	0.840	1.000	0.854	0.813	0.854	1.000	0.691	0.699	1.000	0.813
ŠA	0.494	0.494	0.494	0.503	0.502	0.502	0.503	0.494	0.505	0.489	0.502	0.501	0.464	0.522	0.662	0.522	0.452	0.384	0.381	0.464	0.662
Reference set	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000

in Appendix A), where the values on the diagonal represent the self-evaluated DEA scores. Standard DEA cannot distinguish between efficient territories. Likewise, when calculating the DEA-CE score by averaging peer efficiencies, the uncertainty of results is not considered, and the final index loses its connections to its peers. To overcome this, GRA was applied to examine the positions of the municipalities and to rank them. Normalisation of the DEA-CE matrix was performed, and grey relational coefficients were calculated in relation to the reference set, using Equation (7) (it is assumed that each municipality tended to be efficient, so the ideal reference set is made of efficiencies equal to 1; the reference set is given at the bottom of Table A1 in Appendix A).

After averaging the grey coefficients (see

Table A2. Grey correlation coefficient.

Decision Making Unit	KO	BP	PG	CT	NK	TV	BD	HN	PŽ	BA	BR	PV	ŽB	DG	KL	RO	UL	MK	PL	AN	ŠA
KO	0.409	0.411	0.418	0.421	0.403	0.417	0.428	0.428	0.394	0.423	0.420	0.421	0.427	0.407	0.372	0.418	0.401	0.400	0.406	0.407	0.350
BP	0.411	0.411	0.411	0.409	0.409	0.409	0.409	0.411	0.388	0.394	0.409	0.409	0.404	0.409	0.360	0.409	0.400	0.393	0.391	0.404	0.360
PG	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333	0.333
CT	0.501	0.501	0.501	0.513	0.511	0.511	0.513	0.501	0.426	0.440	0.511	0.512	0.491	0.512	0.379	0.512	0.486	0.444	0.450	0.491	0.379
NK	0.361	0.361	0.361	0.362	0.363	0.363	0.362	0.361	0.349	0.351	0.363	0.362	0.357	0.363	0.341	0.363	0.357	0.351	0.351	0.357	0.341
TV	0.525	0.525	0.525	0.529	0.535	0.535	0.529	0.525	0.434	0.451	0.535	0.530	0.490	0.535	0.372	0.535	0.482	0.453	0.443	0.490	0.372
BD	0.386	0.386	0.386	0.387	0.386	0.386	0.387	0.386	0.366	0.371	0.386	0.387	0.384	0.386	0.347	0.386	0.382	0.373	0.376	0.384	0.347
HN	0.461	0.461	0.462	0.443	0.450	0.450	0.443	0.462	0.424	0.441	0.450	0.448	0.420	0.450	0.355	0.450	0.412	0.441	0.420	0.420	0.355
PŽ	0.530	0.530	0.532	0.490	0.493	0.493	0.490	0.532	1.000	0.857	0.493	0.495	0.474	0.511	1.000	0.511	0.458	0.548	0.506	0.474	1.000
BA	0.547	0.547	0.549	0.503	0.511	0.511	0.503	0.549	0.569	0.593	0.511	0.514	0.475	0.515	0.429	0.515	0.459	0.554	0.518	0.475	0.429
BR	0.382	0.382	0.382	0.384	0.385	0.385	0.384	0.382	0.361	0.365	0.385	0.385	0.376	0.385	0.345	0.385	0.375	0.366	0.365	0.376	0.345
PV	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0.608	0.678	1.000	1.000	0.853	1.000	0.413	1.000	0.808	0.700	0.686	0.853	0.413
ŽB	0.655	0.655	0.651	0.667	0.610	0.610	0.667	0.651	0.673	0.689	0.610	0.620	0.897	0.622	0.553	0.622	0.883	0.595	0.590	0.897	0.553
DG	0.480	0.480	0.480	0.503	0.510	0.510	0.503	0.480	0.402	0.412	0.510	0.505	0.460	0.511	0.377	0.511	0.458	0.415	0.417	0.460	0.377
KL	0.340	0.340	0.340	0.341	0.341	0.341	0.341	0.340	0.347	0.344	0.341	0.341	0.340	0.342	0.364	0.342	0.340	0.338	0.338	0.340	0.364
RO	0.444	0.444	0.445	0.442	0.461	0.461	0.442	0.445	0.409	0.412	0.461	0.458	0.401	0.465	0.428	0.465	0.396	0.402	0.403	0.401	0.428
UL	0.466	0.466	0.464	0.508	0.478	0.478	0.508	0.464	0.399	0.410	0.478	0.480	0.602	0.478	0.361	0.478	0.646	0.415	0.423	0.602	0.361
MK	1.000	1.000	1.000	0.862	0.832	0.832	0.862	1.000	0.846	1.000	0.832	0.865	0.870	0.838	0.440	0.838	0.793	1.000	1.000	0.870	0.440
PL	1.000	1.000	0.996	1.000	0.944	0.944	1.000	0.996	1.000	1.000	0.944	1.000	1.000	1.000	1.000	1.000	0.942	0.793	1.000	1.000	1.000
AN	0.752	0.752	0.746	0.808	0.733	0.733	0.808	0.746	0.712	0.715	0.733	0.742	1.000	0.759	0.724	0.759	1.000	0.601	0.609	1.000	0.724
ŠA	0.476	0.476	0.476	0.481	0.480	0.480	0.481	0.476	0.488	0.478	0.480	0.480	0.463	0.490	0.593	0.490	0.459	0.431	0.431	0.463	0.593

in Appendix A), the grey relational grade was derived and the results were normalised with Equations (8) and (9), respectively, to obtain the DEA–GRA score (Γ_DEA).

The efficiencies and the corresponding ranking based on the Γ_DEA scores are given in

Table 5. Efficiency scores and corresponding rankings.

Municipality	Standard DEA Score	Rank	DEA-CE Score	Rank	ΓDEA Score	Rank	Public Risk Score	Rank
PV	1.000	1	0.876	3	0.8762	3	122	4
AN	1.000	1	0.850	4	0.7859	4	176	5
MK	1.000	1	0.892	2	0.8766	2	309	9
PŽ	1.000	1	0.626	6	0.6039	6	312	7
PL	1.000	1	0.989	1	1.0000	1	335	1
ŽB	0.947	6	0.752	5	0.6796	5	406	8
UL	0.745	7	0.462	11	0.4848	11	492	15
BA	0.679	8	0.552	7	0.5243	7	565	2
ŠA	0.662	9	0.500	9	0.4945	9	626	13
TV	0.600	10	0.507	8	0.5035	8	822	19
CT	0.563	11	0.486	10	0.4906	10	876	11
DG	0.559	12	0.452	12	0.4749	12	1083	10
RO	0.470	13	0.390	13	0.4433	14	1158	3
HN	0.465	14	0.387	14	0.4435	13	1283	17
KO	0.386	15	0.333	15	0.4174	15	1309	20
BP	0.340	16	0.301	16	0.4091	16	1311	6
BD	0.272	17	0.237	17	0.3875	17	1457	21
BR	0.266	18	0.224	18	0.3834	18	1504	14
NK	0.192	19	0.162	19	0.3648	19	1524	12
KL	0.143	20	0.109	20	0.3505	20	1808	16
PG	0.081	21	0.070	21	0.3405	21	2334	18

. At the same time, for comparison, the scores obtained according to the standard (self-evaluated) DEA and DEA-CE models are given, as well as the scores of public risks, derived as the number of accidents per 100,000 populations.

6. Discussion

To verify the proposed methodology, and to grasp insight into the relationship among the rankings related to the different methods, Spearman’s test was performed. The results are presented in

Table 6. Correlations between the ranks related to the different methods.

Ranking	DEA-GRA	DEA	DEA-CE	Public Risk
DEA-GRA	1	0.960 *	0.998 *	0.603
DEA		1	0.961 *	0.590
DEA-CE			1	0.621 *
Public risk				1

* The correlation is significant at the p < 0.01 level (2-tailed), N = 21.

(all negative correlations were changed to positive correlations). The DEA-CE ranking was obtained as an average of the municipality scores derived from the weights of every other municipality.

The very high degree of correlation between the proposed fuzzy-number DEA-GRA and DEA-CE methods shows that both methods (which otherwise work on a similar basis) are suitable for ranking territories. Nevertheless, these methods provide some differences

In the ranking of municipalities of close efficiency, as seen in Figure 3 in the middle of the range. The largest deviations and the smallest degree of correlation occur in public risk ranking, due to different basic methodologies.

Municipalities with high road safety levels are all small municipalities with low populations and motorization levels, and with no main roads in their territories; therefore, it is not surprising that their safety situation is defined as satisfactory. Additionally, it was noticed that municipalities at the bottom half of the scale have consistent positions, which is an important insight into the road safety situation for policy makers, and may provide guidance in the right direction in terms of where to put more effort in addressing road safety.

Using the standard DEA model, five municipalities were identified as having the best performance, namely, PV, AN, MK, PŽ, and PL. One of the shortcomings of DEA is its inability to further rank entities with the same efficiency, especially those that are on the efficient frontier (efficiency equal to 1). This can be overcome with the proposed DEA–GRA methodology, which appears to have more distinguished power among municipalities, and with this, the higher-scaled ones can be further re-ranked. Based on the DEA-GRA, only PL is an efficient territory, remaining efficient in the other models as well. Therefore, the proposed approach provides a more reasonable and encompassing measure of performance, which, among others, clearly verifies the robustness of the DEA-GRA model results. An additional sensitivity analysis could support this assertion.

Further, the DEA calculates target values that will make a municipality efficient. Priorities for each municipality can be set because the required proportionate movement is known for each indicator in order for the municipality to become efficient (see

Table 7. Target values of road safety indicators and their proportionate movement.

Municipality	Target Values (Projection)				Proportionate Movement
	I1	I2	I3	I4	I1	I2	I3	I4
ŽB	0.847	0.838	0.601	0.638	–0.047	–0.047	–0.050	–0.042
UL	0.447	0.415	0.413	0.333	–0.233	–0.142	–0.195	–0.142
BA	0.331	0.457	0.138	0.299	–0.157	–0.295	–0.158	–0.159
ŠA	0.408	0.592	0.226	0.366	–0.273	–0.310	–0.240	–0.187
TV	0.387	0.466	0.343	0.277	–0.279	–0.331	–0.330	–0.185
CT	0.384	0.459	0.283	0.279	–0.331	–0.356	–0.223	–0.217
DG	0.386	0.464	0.327	0.278	–0.405	–0.405	–0.320	–0.219
RO	0.251	0.295	0.105	0.188	–0.366	–0.501	–0.222	–0.212
HN	0.227	0.313	0.165	0.197	–0.261	–0.439	–0.376	–0.226
KO	0.229	0.310	0.145	0.196	–0.363	–0.492	–0.499	–0.311
BP	0.250	0.309	0.194	0.188	–0.484	–0.599	–0.475	–0.365
BD	0.190	0.226	0.116	0.140	–0.533	–0.604	–0.332	–0.375
BR	0.194	0.233	0.172	0.139	–0.593	–0.676	–0.563	–0.382
NK	0.129	0.155	0.114	0.092	–0.602	–0.684	–0.606	–0.389
KL	0.090	0.129	0.047	0.080	–0.697	–0.810	–0.604	–0.480
PG	0.058	0.072	0.050	0.043	–0.661	–0.823	–0.626	–0.492

). However, these targets, defined with DEA, are sometimes impossible to achieve, so it is important to compare it with current values in order to quantify the effort that needs to be made.

If the set of optimal weights of one efficient municipality in DEA moves another municipality up to the efficiency frontier, that municipality is called the benchmark and can provide useful guidance for and insight into the best practice. The choice of the benchmark depends on the characteristics of the territory under study. To find benchmarks, it is more realistic to determine a set of comparable territories and target the best-performing territory among them than it is to make a comparison between territories placed into a single group.

Since differences between road safety backgrounds always exist, cluster analysis is performed, and a connection tree (the so-called dendrogram) using Ward’s technique is constructed (Figure 4). From the dendrogram, it can be seen how the cluster of territories was merged, and which territories are similar to each other (for example, MK-PV, KO-BP, DG-TV-UL-ŠA-CT).

7. Conclusions

When applying MCDM techniques to measure the performance of a territory, many road safety variables (indicators) can be taken into consideration. The proposed methodology makes it possible to combine those input/output variables that are vague and/or uncertain in nature. In this study, the uncertainty of self-reported driver behaviours was addressed with fuzzy theory, presenting the questionnaire results as fuzzy trapezoidal numbers. DEA was then conducted with defuzzificated and normalised data as inputs and final outcomes as outputs. DEA results in a cross-efficiency matrix that is further extended, with the GRA providing the reliable, objective, and fair final road safety performance for each of the 21 Montenegrin municipalities. In doing so, the integrated DEA-GRA model allowed for crisp DEA efficiency values to be treated as uncertain/grey data. Based on the results, a final ranking was derived and compared with the selected methods.

The proposed methodology overcomes the inability of the DEA model to rank municipalities of equal efficiency, and GRA enables the avoidance of the loss of important information by averaging the cross-efficiency matrix scores. Thus, policy makers and road safety experts can evaluate the efficiency of territories and make important decisions to improve the current safety situation. Insights into the target values of each indicator are presented, which offers a broader picture to the experts to conduct measures and campaigns in order to increase awareness of recognised deficiencies. Since the characteristics of the territories differ in relation to road safety backgrounds, a derived dendrogram can aid with identifying the best practice.

Despite all of the above, the proposed approach can potentially suffer from some limitations. Firstly, as it is based on a psychometric model for rating responses, the sample size or the number of respondents should be as large as possible to provide more reliable results for the behavioural assessment survey. Next, since the DEA model assigns weights if they are not previously known, in future work, experts should be involved to introduce restrictions or relations in regard to the share of weights for each input and output data Moreover, more inputs and outputs considering road safety could be involved (helmet wearing, trauma management, etc.), and a sensitivity analysis could be performed to investigate how changes in the dataset affect the results and, also, how different membership functions of the fuzzy numbers influence the final scores. Considering that GRA is a normalisation-based technique, the impact of different normalisation methods should be investigated. Furthermore, the proposed GRA has encountered the sensitivity problem arising from the parameter setup of the distinguished coefficient. The different distinguished coefficients may lead to different solution results, so in future work, researchers should try several different distinguishing coefficients and analyse the impact on the results.