Polylactic Acid and Its Cellulose Based Composite as a Significant Tool for the Production of Optimized Models Modified for Additive Manufacturing
Abstract
:1. Introduction
2. Methodology
- Step-determination of printing operating parameters. Clear definition of software limitations of model processing software. Analysis of the construction and method of production of models, determination of median limits of the device.
- Step-the selection of model material suitable for the goal of sustainable development in this area. Research and possibilities of production of alternative composites on the biological basis and study of their mechanical properties. Implementation of mechanical properties of these materials into a separate library used in optimization.
- Step-the selection of suitable software and method of the optimization process. We are taking into account the mechanical and software limitations of FDM devices in the optimization process.
- Step-analysis of the selected structure, its parameters, and forces are acting on the system. The subsequent release of the system and implementation of the results of this analysis into the optimization software.
- Step-comparison of the results of analyses with a sample non-composite material PLA and evaluate the effects connected with the change of volume, the time required for the production of models made from unique composites.
2.1. Fused Deposition Modeling Technology
2.2. Material Selection
2.3. Topology Optimization
2.3.1. Discrediting
2.3.2. Solid Isotropic Microstructure with Penalization Method (SIMP)
2.4. Choosing a Software
2.5. Preparation of the Optimization Module
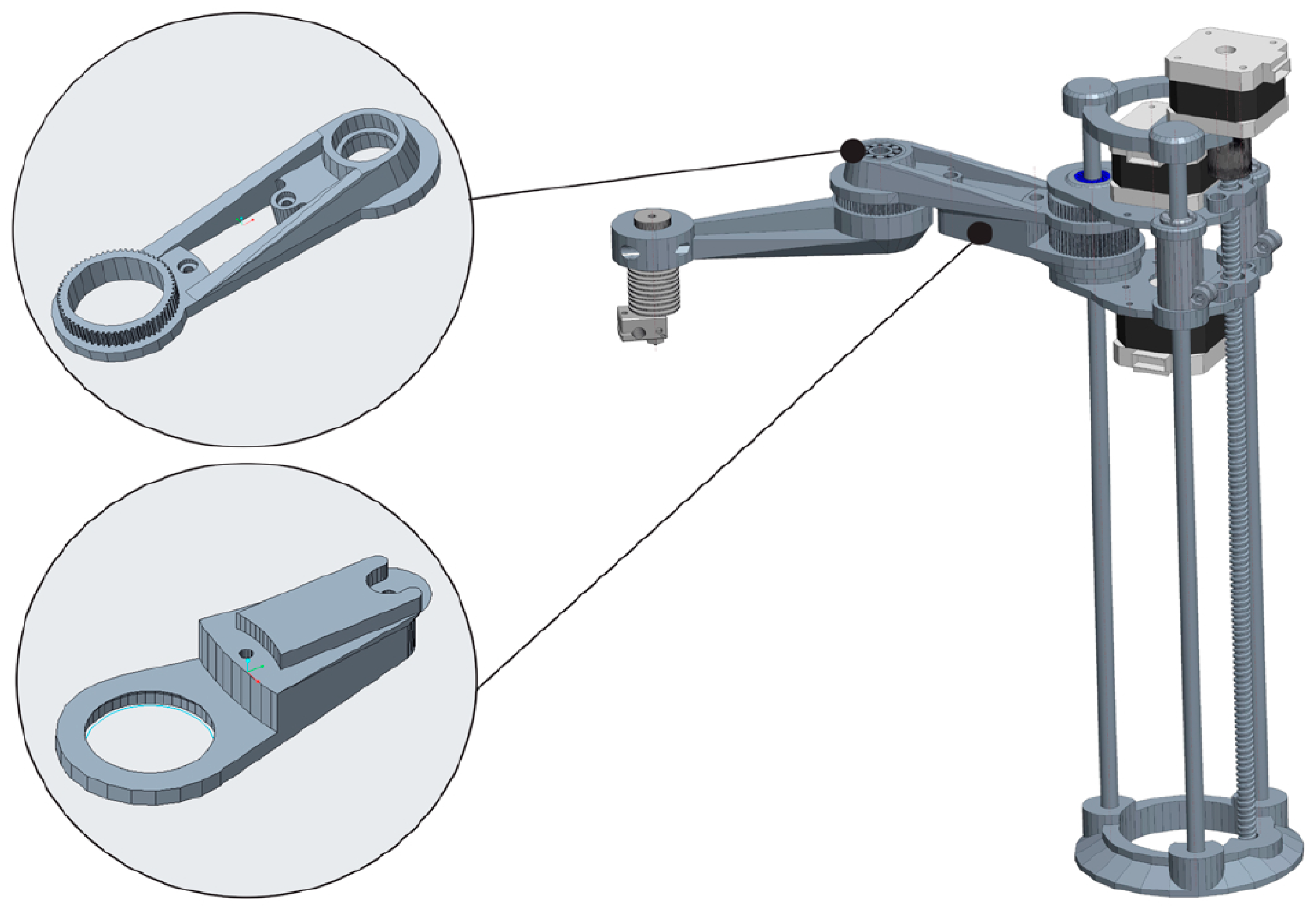
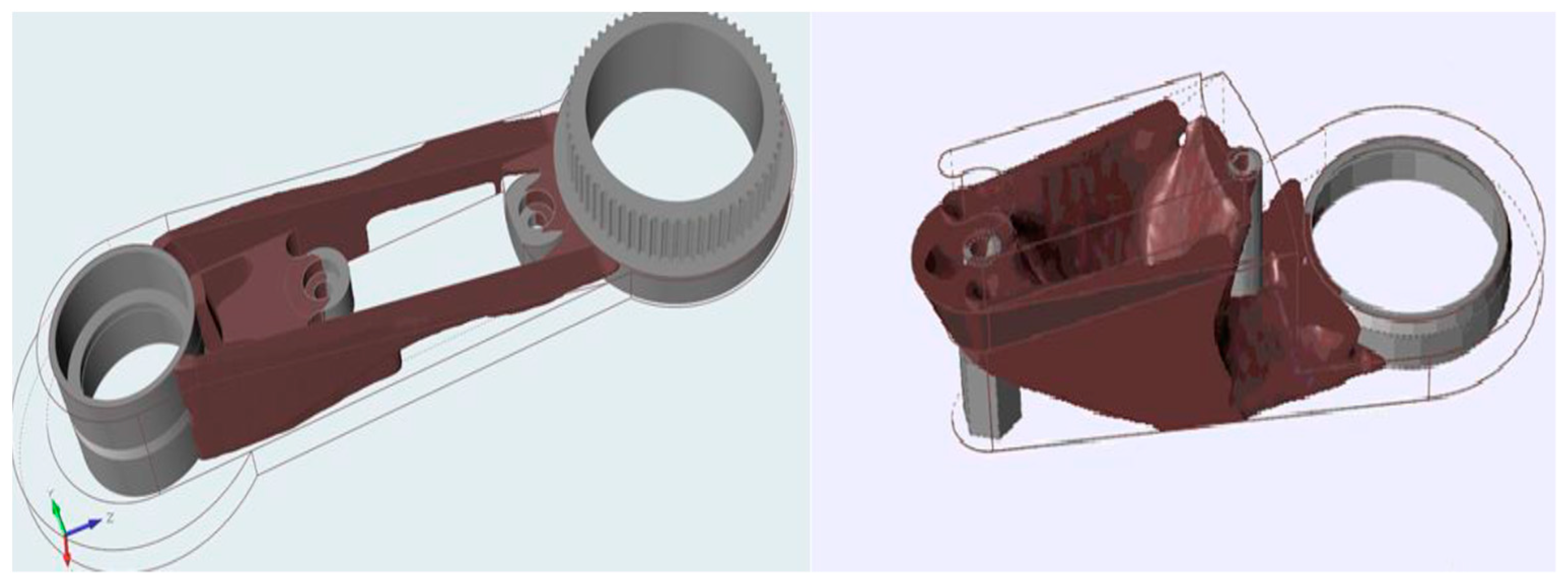
3. Results of Optimization of Individual Parts of the Subsystem
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Bioplastics Market Size, Share & Trends Analysis Report by Product (Biodegradable, Non-Biodegradable), by Application (Packaging, Automotive & Transportation, Textile), by Region, And Segment Forecasts, 2020–2027. Available online: https://www.grandviewresearch.com/industry-analysis/bioplastics-industry (accessed on 23 December 2020).
- Dey, A.; Yodo, N. A Systematic survey of FDM process parameter optimization and their influence on part characteristics. J. Manuf. Mater. Process. 2019, 3, 64. [Google Scholar] [CrossRef] [Green Version]
- Khademhosseini, A.; Gulden, C.-U. 3D Bioprinting in Regenerative Engineering; CRC Press series: Boca Raton, FL, USA, 2018; p. 401. [Google Scholar]
- Calì, M.; Pascoletti, G.; Gaeta, M.; Milazzo, G.; Ambu, R. A New Generation of Bio-Composite Thermoplastic Filaments for a More Sustainable Design of Parts Manufactured by FDM. Appl. Sci. 2020, 10, 5852. [Google Scholar] [CrossRef]
- Ahlers, D. 3D Printing of Nonplanar Layers for Smooth Surface Generation. Master’s Thesis, MIN- Fakultät, University of Hamburg, Hamburg, Germany, 2018; pp. 13–19. [Google Scholar]
- Harrison, I.; Huttenhuis, P.J.G.; Heesink, A.B.M.; Enschede, P.T.B. BIOCA—Biomass Streams to Produce Cellulose Acetate; Department of Chemical Engineering, Twente University, Enschede, Procede Twente B.V.: Enschede, The Netherlands; Available online: https://www.researchgate.net/publication/237673369_BIOCA_-_Biomass_Streams_to_Produce_Cellulose_Acetate (accessed on 21 December 2020).
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies; Springer: New York, NY, USA, 2015; p. 498. [Google Scholar]
- Qiu, G.Y.; Hu, P.; Zhou, W. Two-dimensional structural topology optimization based on isogeometric analysis. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2014; Volume 472, pp. 475–479. [Google Scholar]
- Stoneman, S.; Lampariello, R. Embedding nonlinear optimization in RRT* for optimal kinodynamic planning. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 3737–3744. [Google Scholar]
- Guo, X.; Cheng, G.D. Recent development in structural design and optimization. Acta Mech. Sin. 2010, 26, 807–823. [Google Scholar] [CrossRef]
- Key Design Considerations for 3D Printing. Available online: https://www.3dhubs.com/knowledge-base/key-design-considerations-3d-printing/ (accessed on 25 December 2020).
- Pollák, M.; Kaščák, J.; Telišková, M.; Tkáč, J. Design of the 3D Printhead with Extruder for the Implementation of 3D Printing from Plastic and Recycling by Industrial Robot. TEM J. 2019, 8, 709–713. [Google Scholar]
- Degradation of PLA in a Simulated Marine Environment after 600 Days. Available online: https://www.longdom.org/conference-abstracts-files/2252–5211-C1-006-005.pdf (accessed on 23 December 2020).
- Scopigno, R.; Cignoni, P.; Pietroni, N.; Callieri, M.; Dellepiane, M. Digital Fabrication Techniques for Cultural Heritage: A Survey. Comput. Graph. Forum 2015, 36, 6–21. [Google Scholar] [CrossRef]
- Kuznetsov, V.E.; Tavitov, A.G.; Urzhumtsev, O.D.; Mikhalin, M.V.; Moiseev, A.I. Hardware Factors Influencing Strength of Parts Obtained by Fused Filament Fabrication. Polymers 2019, 11, 1870. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meggiorin, M. Fused Deposition Modeling of 3D Porous Structures and Their Characterization. Master’s Thesis, University of Padua, Padua, Italy, 2018. [Google Scholar]
- UPM Formi 3D Data Sheet. Available online: https://www.upmformi.com/siteassets/documents/formi-3d/upm-formi-3d-product-data-sheet-en.pdf (accessed on 23 December 2020).
- Smith, J. Redesigning a Bicycle Crank Arm for Metal Additive Manufacturing by Applying DFMAM Guidelines to the Topology Optimization Process; Western Carolina University: Cullowhee, NC, USA, 2019. [Google Scholar]
- Pollak, M.; Kascak, J.; Torokova, M.; Kocisko, M.; Dobransky, J. Topological Optimization of a Supporting Part of a 3D Printer Pad. Manuf. Technol. 2020, 20, 492–499. [Google Scholar]
- Liu, J.; Gaynor, A.T.; Chen, S.; Kang, Z.; Suresh, K.; Takezawa, A.; Li, L.; Kato, J.; Tang, J.; Wang, C.C.L.; et al. Current and future trends in topology optimization for additive manufacturing. Struct. Multidiscip. Optim. 2018, 57, 2457–2483. [Google Scholar] [CrossRef] [Green Version]
- Olason, A.; Tidman, D. Methodology for Topology and Shape Optimization in the Design Process. Applied Mechanics. Master’s Thesis, Chalmers University of Technology, Goteborg, Sweden, 2011. [Google Scholar]
- Marck, G.; Nemer, M.; Harion, J.-L.; Russeil, S.; Bougeard, D. Topology Optimization Using the SIMP Method for Multiobjective Conductive Problems. Numer. Heat Transfer Part B Fundam. 2012, 61, 439–470. [Google Scholar] [CrossRef]
- Parameters for Standard Linear Static Topology Optimization. Available online: https://abaqus-docs.mit.edu/2017/English/TsoUserMap/tso-c-user-TopOpt-Sett-LStaTop.htm (accessed on 21 December 2020).
- Fiebig, S.; Sellschopp, J.; Manz, H.; Vietor, T.; Axmann, K.; Schumacher, A. Future challenges for topology optimization for the usage in automotive lightweight design technologies. In Proceedings of the 11th world congress on structural and multidisciplinary optimization, Sydney, Australia, 7–12 June 2015; Volume 142, pp. 1–8. [Google Scholar]
- Polak, R.; Sedlacek, F.; Raz, K.; Katalinic, B. Determination of FDM printer settings with regard to geometrical accuracy. In Proceedings of the 28th DAAAM International Symposium, Zadar, Croatia, 8–11 November 2017; pp. 0561–0566. [Google Scholar]
- Židek, K.; Maxim, V.; Pitel, J.; Hosovsky, A. Embedded vision equipment of industrial robot for inline detection of product errors by clustering-classification algorithms. Int. J. Adv. Robot. Syst. 2016, 13, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Michalik, P.; Hatala, M.; Straka, L.; Petrus, M.; Macej, J.; Jusko, J.; Tirpak, P. Optimizing Component Production with Multi-axis Turning Technology. In 4th EAI International Conference on Management of Manufacturing Systems; Springer Nature: Cham, Switzerland, 2020; pp. 273–283. [Google Scholar]
- Dilyova, M.; Hatala, M.; Radchenko, S.; Botko, F.; Mitaľová, Z. Optimalization of parameters for measurement of the tribological properties of coating for machine parts. In Proceedings of the International Conference on Social and Technological Development; University PIM: Banja Luka, Bosnia and Herzegovina, 2019; pp. 357–361. [Google Scholar]
- Janáčová, D.; Pitel, J.; Vasek, V.; Mokrejs, P.; Viteckova, M.; Drga, R.; Krenek, J. Simulation of printed circuit boards recycling process. In Proceedings of the International Conference on Circuits, Systems, Communications and Computers, Athens, Greece, 14–17 July 2019; Édition Diffusion Presse Sciences: London, UK, 2019; pp. 1–4. [Google Scholar]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar]
- Leary, M. Design for Additive Manufacturing; Elsevier: Amsterdam, The Netherlands, 2020; p. 358. [Google Scholar]
- Yuang, S.; Shen, F.; Chua, C.K.; Zhou, K. Polymeric composites for powder-based additive manufacturing: Materials and applications. Prog. Polym. Sci. 2019, 91, 141–168. [Google Scholar] [CrossRef]
- Singh, R.; Davim, J.P. Additive Manufacturing: Applications and Innovations, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018; p. 280. [Google Scholar]
- Li, N.; Huang, S.; Zhang, G.; Qin, R.; Liu, W.; Xiong, H.; Shi, G.; Blackburn, J. Progress in additive manufacturing on new materials: A review. J. Mater. Sci. Technol. 2019, 35, 242–269. [Google Scholar] [CrossRef]
- Zhang, J.; Jung, Y.G. Additive Manufacturing: Materials, Processes, Quantifications and Applications; Butterworth-Heinemann: Oxford, UK, 2018; p. 362. [Google Scholar]
- Babu, S.S.; Love, L.; Dehoff, R.R.; Peter, W.; Watkins, T.; Pannala, S. Additive manufacturing of materials: Opportunities and challenges. MRS Bull. 2015, 40, 1154–1161. [Google Scholar] [CrossRef] [Green Version]

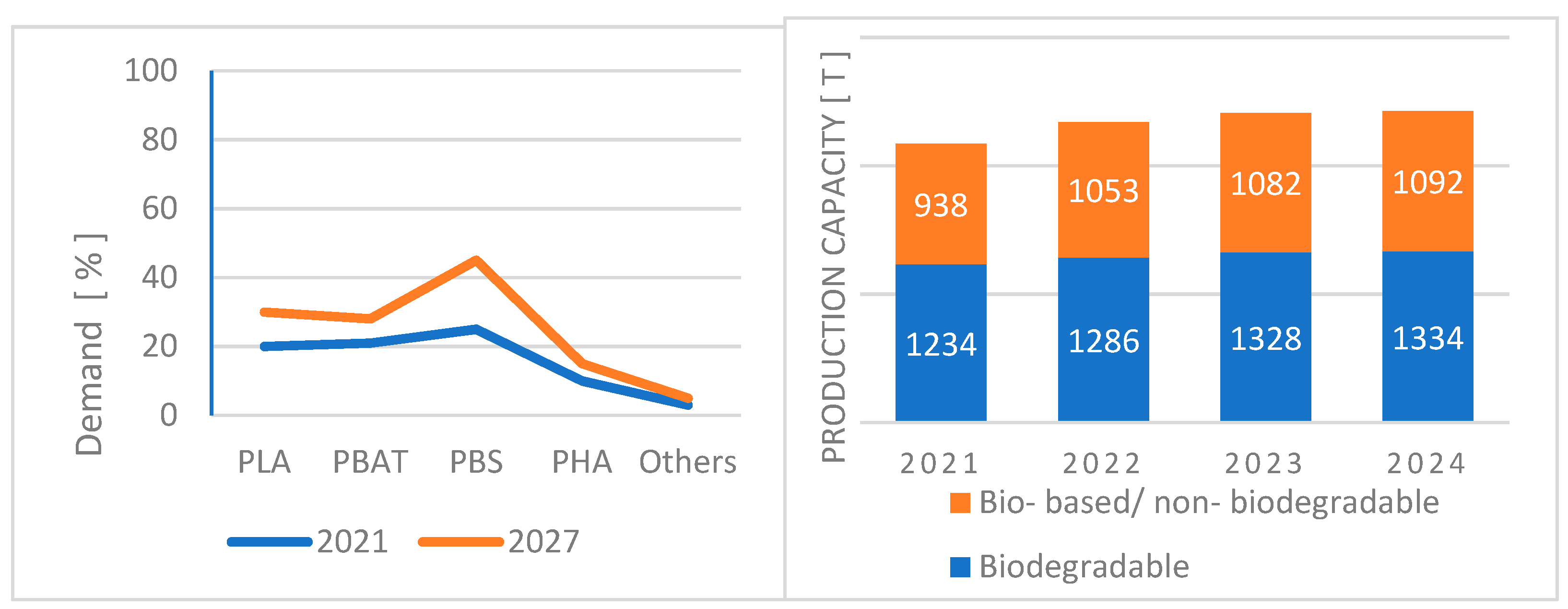
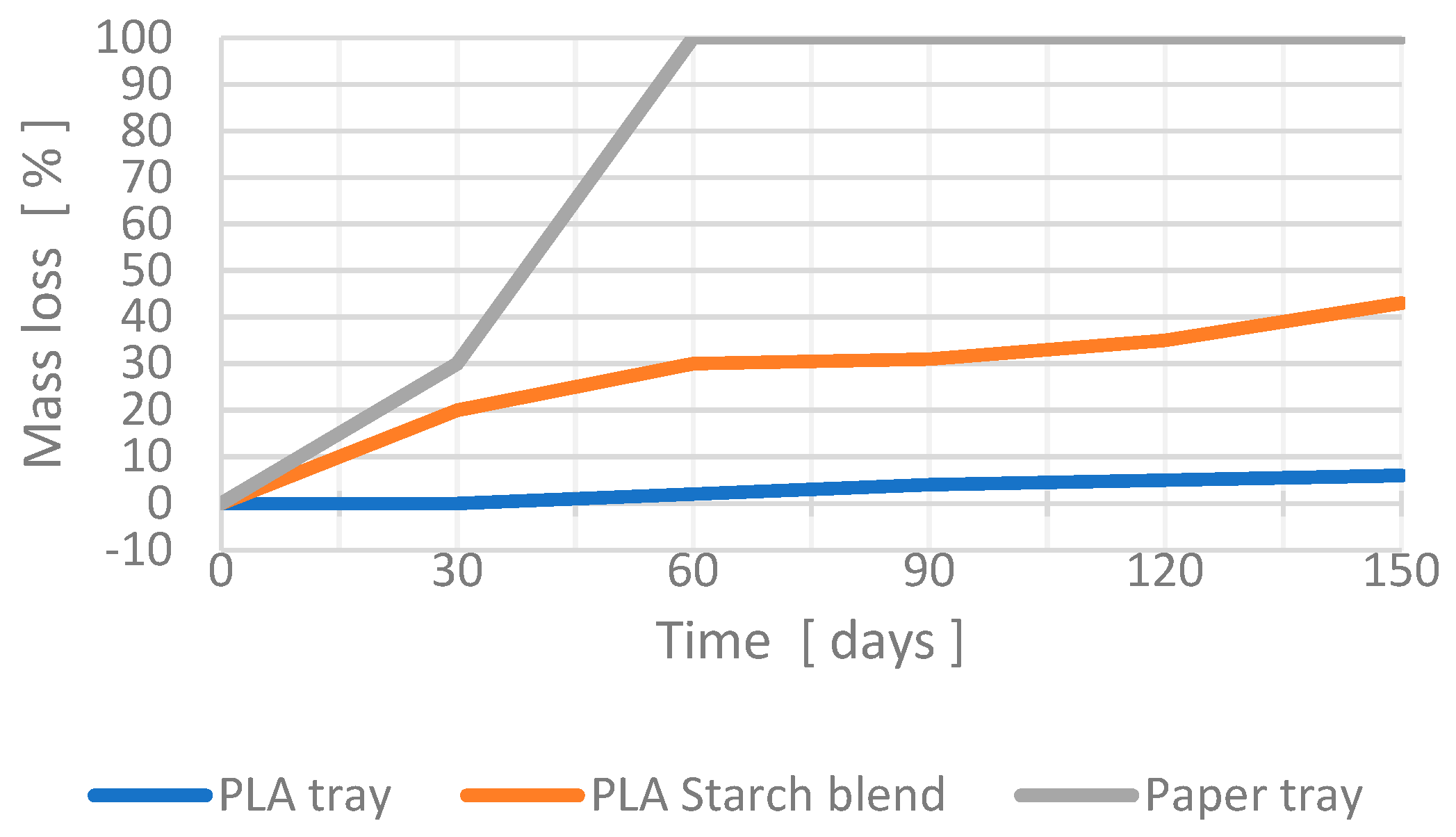
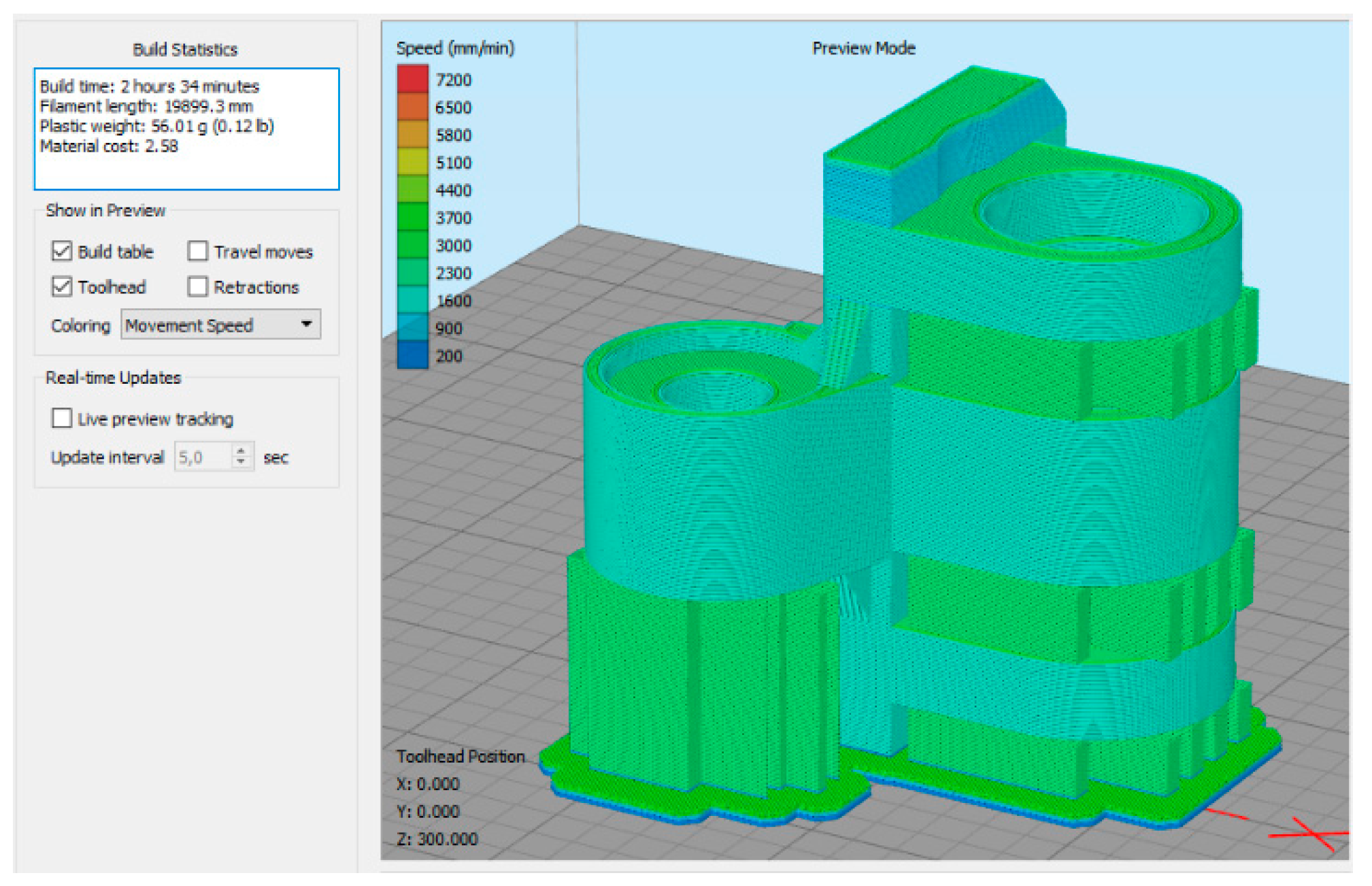






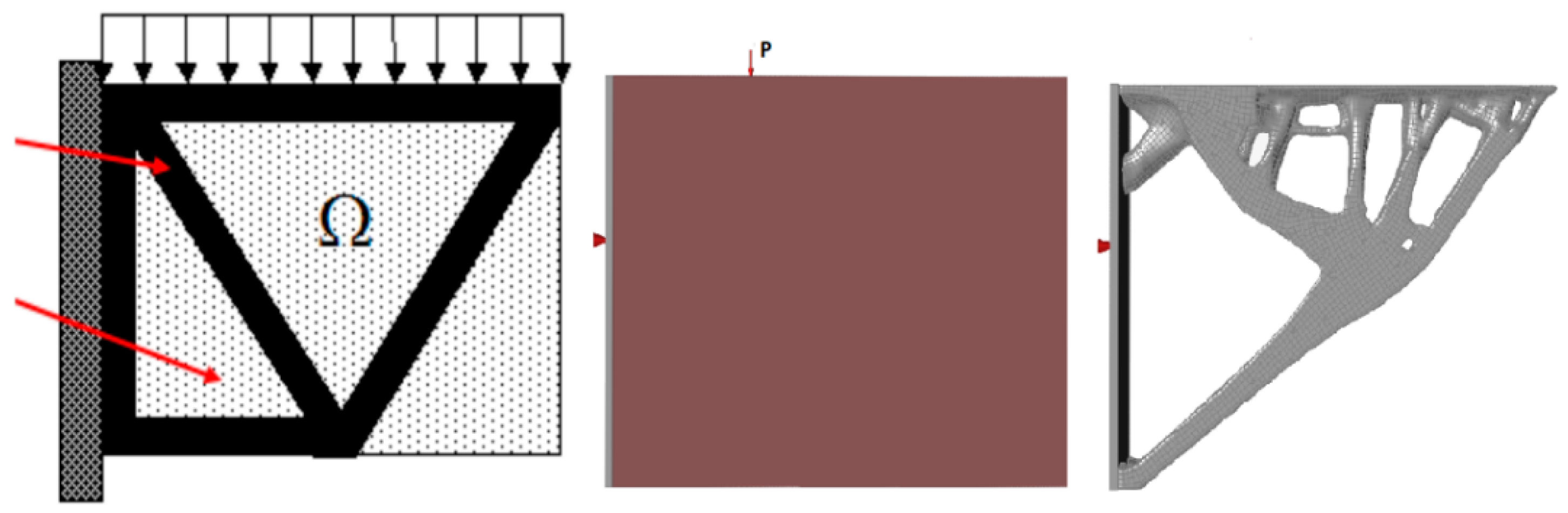











| Property | Test Method | 3D 20 | 3D 20/19 | 3D 40 |
|---|---|---|---|---|
| Density [g/cm3] | EN ISO 1183 | 1.2 | 1.2 | 1.2 |
| Tensile strength [N/mm2] | ISO 527 | 28 | 39 | 48 |
| Tensile modulus [N/mm2] | ISO 527 | 2600 | 3600 | 5400 |
| Strain (tensile) [%] | ISO 527 | 5 | 4 | 2 |
| Impact Strength, Charpy [kJ/m2] | ISO 179/1eU | 24 | 20 | 14 |
| Peak melt temperature [°C] | ISO 11357 | 140–180 | 140–180 | 135–180 |
| Glass transition temperature [°C] | ISO 11357 | 62 | 65 | 60 |
| Melt flow index (granulates) * | ISO 1133 | 12 | 16 | 7 |
| Fibre content [%] | 20 | 20 | 40 |
| PLA 100% Shape | PLA Optimized | cPLA 20% Cellulose | cPLA 40% Cellulose | cPLA 20/19 Cellulose | ||
|---|---|---|---|---|---|---|
| Arm A1 [min] | 124.35 | 100.59 | 95.04 | 84.00 | 89.25 | |
| Arm A2 [min] | 97.31 | 73.45 | 82.01 | 79.13 | 72.25 | |
| Print time reduction * A1/A2 [%] | / | 18.45/24.31 | 23.69/17.95 | 28.23/18.76 | 32.58/25.74 |
| PLA 100% Shape | PLA Optimized | cPLA 20% Cellulose | cPLA 40% Cellulose | cPLA 20/19 Cellulose | ||
|---|---|---|---|---|---|---|
| Arm A1 [g] | 44.27 | 25.58 | 24.15 | 29.26 | 24.31 | |
| Arm A2 [g] | 42.22 | 21.73 | 22.59 | 26.98 | 21.57 | |
| Mass reduction * A1/A2 [%] | / | 42.22/48.54 | 45.45/46.50 | 33.91/36.10 | 42.09/48.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaščak, J.; Gašpár, Š.; Paško, J.; Husár, J.; Knapčíková, L. Polylactic Acid and Its Cellulose Based Composite as a Significant Tool for the Production of Optimized Models Modified for Additive Manufacturing. Sustainability 2021, 13, 1256. https://doi.org/10.3390/su13031256
Kaščak J, Gašpár Š, Paško J, Husár J, Knapčíková L. Polylactic Acid and Its Cellulose Based Composite as a Significant Tool for the Production of Optimized Models Modified for Additive Manufacturing. Sustainability. 2021; 13(3):1256. https://doi.org/10.3390/su13031256
Chicago/Turabian StyleKaščak, Jakub, Štefan Gašpár, Ján Paško, Jozef Husár, and Lucia Knapčíková. 2021. "Polylactic Acid and Its Cellulose Based Composite as a Significant Tool for the Production of Optimized Models Modified for Additive Manufacturing" Sustainability 13, no. 3: 1256. https://doi.org/10.3390/su13031256
APA StyleKaščak, J., Gašpár, Š., Paško, J., Husár, J., & Knapčíková, L. (2021). Polylactic Acid and Its Cellulose Based Composite as a Significant Tool for the Production of Optimized Models Modified for Additive Manufacturing. Sustainability, 13(3), 1256. https://doi.org/10.3390/su13031256









