Identify Optimal Traffic Condition and Speed Limit for Hard Shoulder Running Strategy
Abstract
1. Introduction
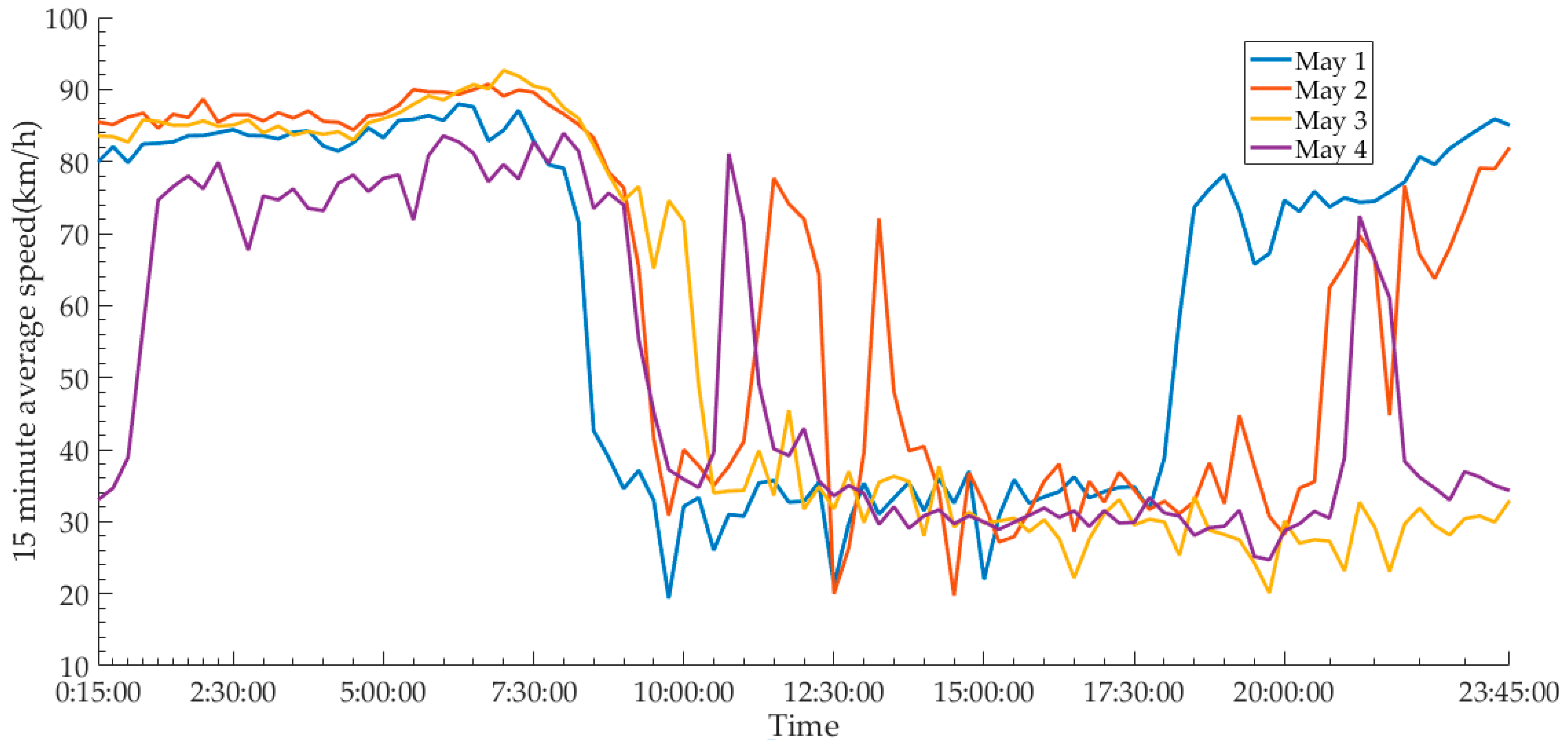
2. Research Data
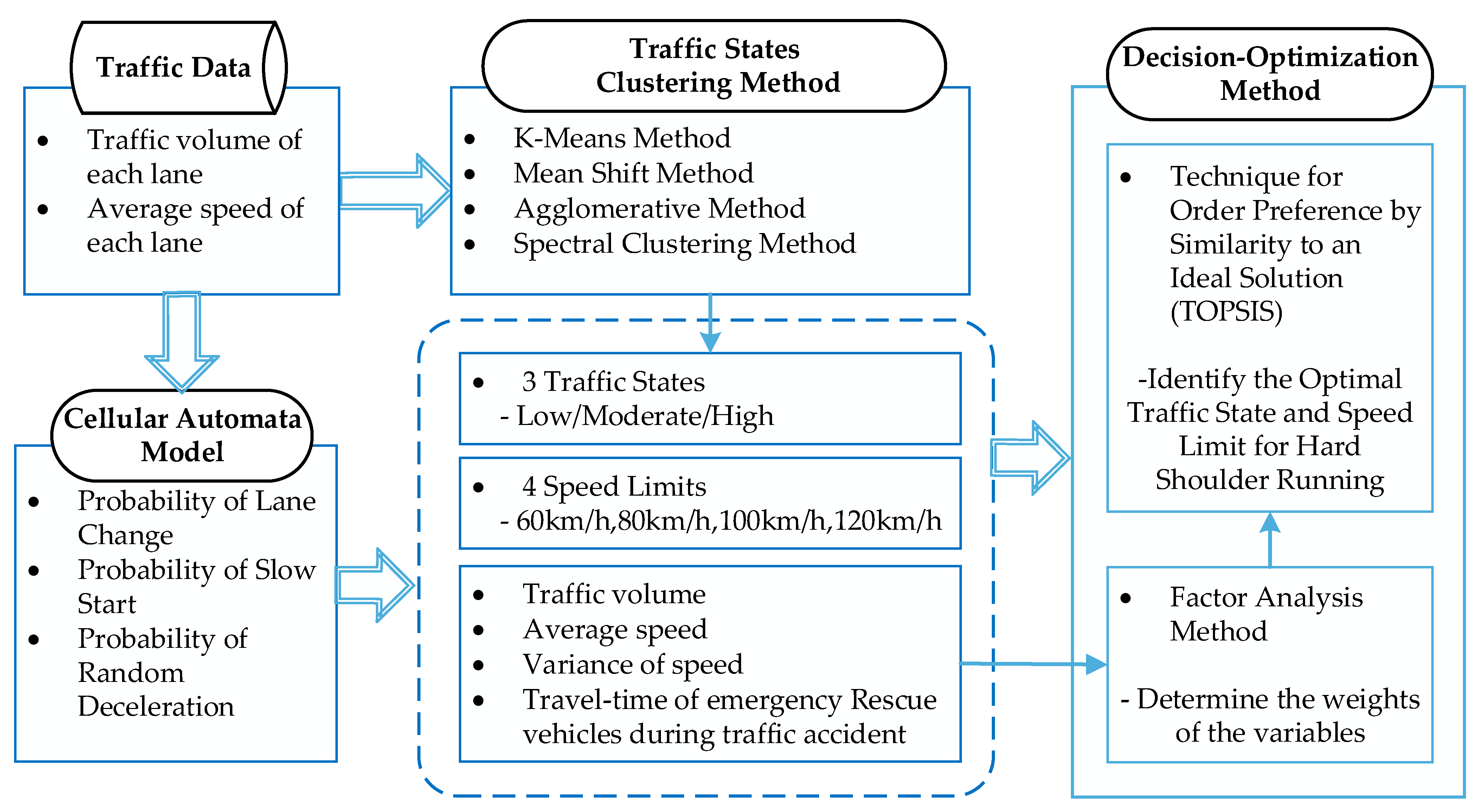
3. Methods
3.1. Clustering Traffic States
3.2. Cellular Automata Model
- Acceleration rule: . This rule described the drivers are expected to drive at the maximum speed.
- Random deceleration rule: with probability , , the speed of vehicles would slow down due to various uncertain reasons.
- Lane change rule: with probability , and , the vehicle would change the lane.
- Slow start rule: with probability , and = 0, instead of accelerating, the vehicle would keep the original position.
- Deceleration rule:. This rule described the measures taken by the driver to avoid a collision with other cars.
3.3. Decision-Optimization Methods
4. Results
4.1. Results of Clustering Traffic States
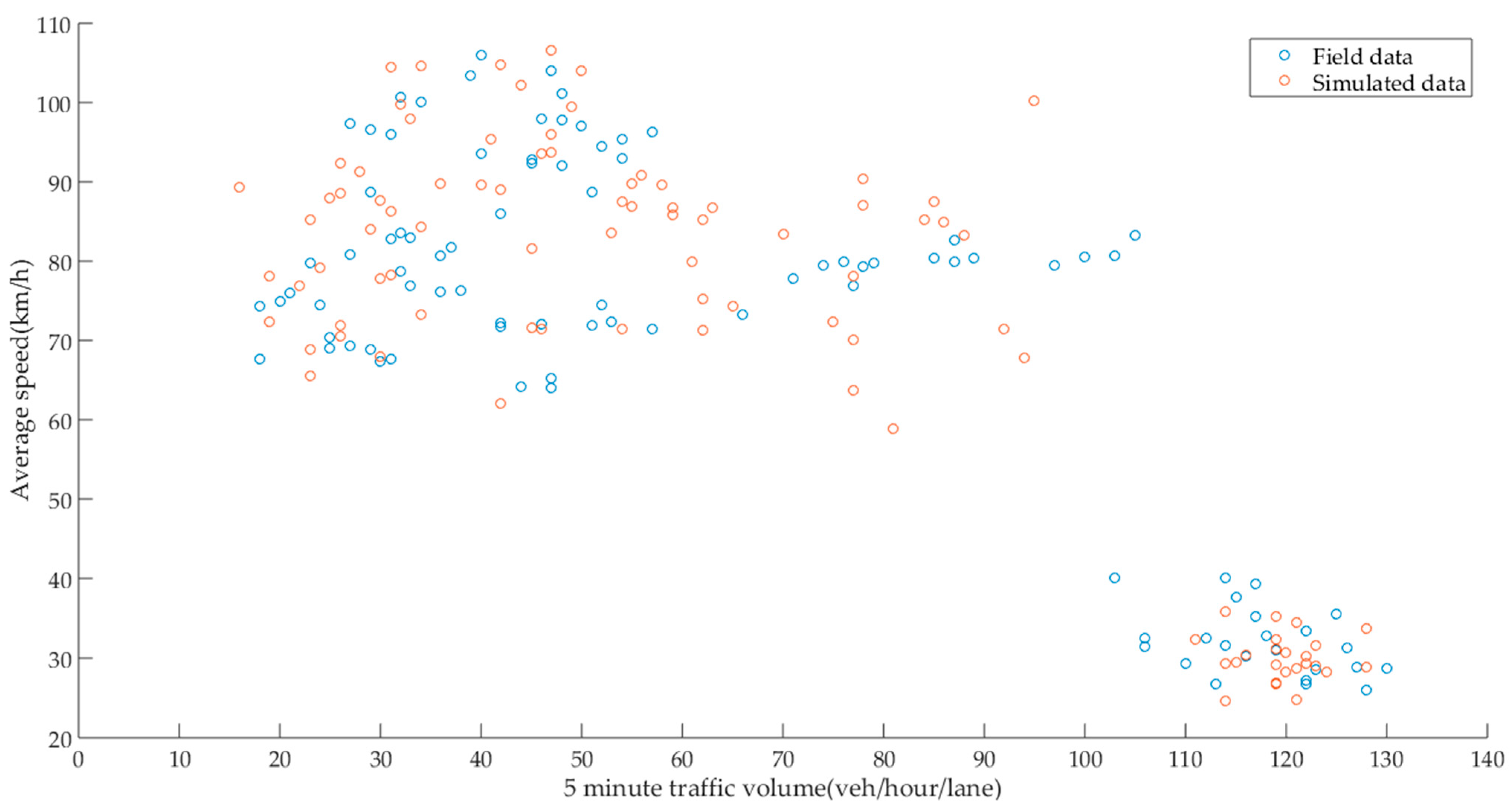
4.2. Validation of the Cellular Automata Model
4.3. Application of the Cellular Automata Model
4.4. Results of Decision Optimization Method
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Djahel, S.; Zhang, Z.; McManis, J. Next Road Rerouting: A Multiagent System for Mitigating Unexpected Urban Traffic Congestion. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2888–2899. [Google Scholar] [CrossRef]
- Schrank, D.; Eisele, B.; Lomax, T. TTI’s 2012 Urban Mobility Report Powered by INRIX Traffic Data; Texas A&M Transportation Institute Texas, A&M University System: College Station, TX, USA, 2011. [Google Scholar]
- Jiang, P.; Liu, L.; Cui, L.; Li, H.; Shi, Y. Congestion prediction of urban traffic employing SRBDP. In Proceedings of the 2017 IEEE International Symposium on Parallel and Distributed Processing with Applications and 2017 IEEE International Conference on Ubiquitous Computing and Communications (ISPA/IUCC), Guangzhou, China, 12–15 December 2018; pp. 1099–1106. [Google Scholar]
- Dutta, N.; Boateng, R.A.; Fontaine, M.D. Safety and Operational Effects of the Interstate 66 Active Traffic Management System. J. Transp. Eng. Part A Syst. 2019, 145, 4018089. [Google Scholar] [CrossRef]
- Lemke, K. Hard Shoulder Running as a Short-Term Measure to Reduce Congestion. In Proceedings of the Interntional Symposium on Highway Geometric Design, Valencia, Spain, 1–5 June 2010. [Google Scholar]
- Geistefeldt, J. Operational Experience with Temporary Hard Shoulder Running in Germany. Transp. Res. Rec. 2012, 2278, 67–73. [Google Scholar] [CrossRef]
- Brilon, W.; Lippold, C. Country Report--Germany: A New Concept for Highway Design Guidelines in Germany. In Proceedings of the International Symposium on Highway Geometric Design, Chicago, IL, USA, 29 June–1 July 2005. [Google Scholar]
- Guerrieri, M.; Mauro, R. Capacity and safety analysis of hard-shoulder running (HSR). A motorway case study. Transp. Res. Part A Policy Pract. 2016, 92, 162–183. [Google Scholar] [CrossRef]
- Lemke, K.; Irzik, M. Temporary Use of Hard Shoulders—Experiences and Economic Assessment; Traffic Planning Highway Disaster Safety Analytical Section, Federal Highway Research Institute: Bergisch Gladbach, Germany, 2016. [Google Scholar]
- Gitelman, V.; Hakkert, S.; Zilberstein, R.; Grof, T. Bus Operations on Hard Shoulders during Congested Morning Hours—A Pilot Evaluation in Israel. Transp. Res. Procedia 2016, 14, 1144–1153. [Google Scholar] [CrossRef]
- Kellermann, G. Experience of Using the Hard Shoulder to Improve Traffic Flows. Traffic Eng. Control 2000, 41, 412–414. [Google Scholar]
- Chase, P.; Avineri, E. Maximizing Motorway Capacity Through Hard Shoulder Running: UK Perspective. Open Transp. J. 2008, 2, 7–18. [Google Scholar] [CrossRef]
- Farrag, S.G.; Outay, F.; Yasar, A.U.H.; El-Hansali, M.Y. Evaluating active traffc management (ATM) strategies under non-recurring congestion: Simulation-based with benefit cost analysis case study. Sustainability 2020, 12, 6027. [Google Scholar] [CrossRef]
- Berger, W.J.; Maurer, P. Emergency bays versus emergency lanes on motorways-A cost benefit analysis. In Proceedings of the 10th International Conference-Traffic Safety on Two Continents, Malmo, Sweden, 20–22 September 1999; pp. 1–12. [Google Scholar]
- Bergmeister, K.; Benesperi, C.; Cavestro, R.; Mauro, R. New Information technologies on the Brenner Freeway. In Proceedings of the 2nd Int. SIIV Congress on New Technologies and Modelling Tools for Roads: Applications to Design and Management (CD-ROM), Italian Society of Road Railway Airport, Ancona, Italy, 27–29 October 2004. [Google Scholar]
- Zhou, W.; Yang, M.; Lee, M.; Zhang, L. Q-Learning-Based Coordinated Variable Speed Limit and Hard Shoulder Running Control Strategy to Reduce Travel Time at Freeway Corridor. Transp. Res. Rec. 2020, 2674, 915–925. [Google Scholar] [CrossRef]
- Karan, A. An Integrated Variable Speed Limit with Dynamic Hard Shoulder Running for Urban Freeway Traffic Control. Schulich Sch. Eng. 2018. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, Y.; Sun, D. Discrimination and Prediction of Traffic Congestion States of Urban Road Network Based on Spatio-Temporal Correlation. IEEE Access 2020, 8, 3330–3342. [Google Scholar] [CrossRef]
- Shen, X.; Chen, J. Study on prediction of traffic congestion based on LVQ neural network. 2009 Int. Conf. Meas. Technol. Mechatronics Autom. ICMTMA 2009 2009, 3, 318–321. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Yamasaki, R.; Tanaka, T. Properties of Mean Shift. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2273–2286. [Google Scholar] [CrossRef]
- Huang, D.; Wang, C.D.; Wu, J.S.; Lai, J.H.; Kwoh, C.K. Ultra-scalable spectral clustering and ensemble clustering. IEEE Trans. Knowl. Data Eng. 2020, 32, 1212–1226. [Google Scholar] [CrossRef]
- Kakkavas, G.; Karyotis, V.; Papavassiliou, S. A Distance-based Agglomerative Clustering Algorithm for Multicast Network Tomography. In Proceedings of the ICC 2020–2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Hua, W.; Yue, Y.; Wei, Z.; Chen, J.; Wang, W. A cellular automata traffic flow model with spatial variation in the cell width. Physica A 2020, 556, 124777. [Google Scholar] [CrossRef]
- Ad, V.; Networks, H.; Cheng, S.; Horng, G.; Chou, C. Using Cellular Automata to Form Car Society in Vehicular Ad Hoc Networks. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1374–1384. [Google Scholar] [CrossRef]
- Mamei, M.; Roli, A.; Zambonelli, F.; Università, I. Emergence and Control of Macro-Spatial Structures in Perturbed Cellular Automata, and Implications for Pervasive Computing Systems. IEEE Trans. Syst. Man, Cybern. Part A Syst. Hum. 2005, 35, 337–348. [Google Scholar] [CrossRef]
- Hamurcu, M.; Eren, T. Strategic planning based on sustainability for urban transportation: An application to decision-making. Sustainability 2020, 12, 3589. [Google Scholar] [CrossRef]
- Gong, Y. Business performance evaluation of sports industry listed-companies based on factor analysis. In Proceedings of the 2017 International Conference on Smart Grid and Electrical Automation (ICSGEA), Changsha, China, 27–28 May 2017; pp. 450–453. [Google Scholar] [CrossRef]
- Han, D.; Ren, X. Financial risk assessment based on factor analysis model. J. Phys. Conf. Ser. 2020, 1616. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K.; Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making. Lect. Notes Econ. Math. Syst. 1981, 404, 287–288. [Google Scholar]
- Shih, H.; Shyur, H.; Lee, E.S. An extension of TOPSIS for group decision making. Math. Comput. Model. 2007, 45, 801–813. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.; Liu, L.; Guo, H.; Liu, G.; Li, Y.; Deng, S. Science of the Total Environment Investigation of carbon dioxide emission in China by primary component analysis. Sci. Total Environ. 2014, 472, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.C.; Chang, T.H. Application of TOPSIS in evaluating initial training aircraft under a fuzzy environment. Expert Syst. Appl. 2007, 33, 870–880. [Google Scholar] [CrossRef]
- Chen, S.; Fan, Y.; Cao, Y.; Khattak, A. Assessing the relative importance of factors influencing travel happiness. Travel Behav. Soc. 2019, 16, 185–191. [Google Scholar] [CrossRef]






| Cluster Number | Silhouette Score (K-Means) | DBI (K-Means) | Caliski-Harabaz Score (K-Means) |
|---|---|---|---|
| 2 | 0.6046 | 0.6012 | 4824.4674 |
| 3 | 0.6014 | 0.5814 | 6235.6981 |
| 4 | 0.4484 | 0.7787 | 5554.2090 |
| 5 | 0.4253 | 0.8242 | 5925.4492 |
| 6 | 0.4202 | 0.8200 | 5826.7358 |
| 7 | 0.3946 | 0.8727 | 5920.5752 |
| 8 | 0.3713 | 0.8955 | 5712.3713 |
| 9 | 0.3361 | 0.9454 | 5578.5043 |
| Cluster Number | Silhouette Score (Agglomerative) | DBI (Agglomerative) | Caliski-Harabaz Score (Agglomerative) |
|---|---|---|---|
| 2 | 0.6037 | 0.5998 | 4584.4790 |
| 3 | 0.5935 | 0.5735 | 5786.7530 |
| 4 | 0.5345 | 0.7359 | 5200.3829 |
| 5 | 0.4622 | 0.7560 | 5384.5324 |
| 6 | 0.4308 | 0.7848 | 5197.1510 |
| 7 | 0.3944 | 0.8863 | 5060.2791 |
| 8 | 0.3263 | 0.9981 | 4972.6302 |
| 9 | 0.3056 | 0.9902 | 5014.4874 |
| Cluster Number | Silhouette Score (Spectral Clustering) | DBI (Spectral Clustering) | Caliski-Harabaz Score (Spectral Clustering) |
|---|---|---|---|
| 2 | 0.6034 | 0.6000 | 4566.6627 |
| 3 | 0.6010 | 0.5813 | 6190.4380 |
| 4 | 0.5483 | 0.7000 | 5458.8068 |
| 5 | 0.4908 | 0.6659 | 5314.5480 |
| 6 | 0.4608 | 0.7511 | 5033.8106 |
| 7 | 0.3963 | 0.8103 | 5139.0803 |
| 8 | 0.3674 | 0.8488 | 4952.6232 |
| 9 | 0.3593 | 0.8641 | 4756.4975 |
| KERRYPNX | Silhouette Score (Mean shift) | DBI (Mean shift) | Caliski-Harabaz Score (Mean shift) |
|---|---|---|---|
| 0.5 | 0.1448 | 1.1194 | 1349.0838 |
| 0.8 | 0.3978 | 0.8621 | 4003.6231 |
| 1.1 | 0.5497 | 0.7003 | 5364.1282 |
| 1.4 | 0.5128 | 0.7454 | 5198.6654 |
| 1.7 | 0.5994 | 0.5731 | 6006.6977 |
| 2 | 0.6013 | 0.5787 | 6179.0463 |
| 2.3 | 0.6060 | 0.5992 | 4802.9241 |
| 2.6 | 0.6010 | 0.6048 | 4805.8280 |
| Low Density | ||||
|---|---|---|---|---|
| Speed Limit | Traffic Volume | Average Speed | Variance of Speed | Travel time of emergency rescue vehicles during traffic accidents |
| 60 km/h | 0.10 | −2.59 | −9. 40 | 6.20 |
| 80 km/h | 1.33 | −1.70 | −8.45 | 2.02 |
| 100 km/h | 0.71 | −0.84 | −1.34 | 0.08 |
| 120 km/h | 0.09 | 2.10 | −7.78 | 5.07 |
| Moderate density | ||||
| Speed limit | Traffic volume | Average speed | Variance of speed | Travel time of emergency rescue vehicles during traffic accidents |
| 60 km/h | 1.57 | −6.81 | −11.39 | −1.02 |
| 80 km/h | 0.05 | −0.73 | −12.99 | −3.10 |
| 100 km/h | −0.71 | 6.15 | −13.95 | 0.08 |
| 120 km/h | 0.25 | 10.19 | −17.67 | 3.31 |
| High density | ||||
| Speed limit | Traffic volume | Average speed | Variance of speed | Travel time of emergency rescue vehicles during traffic accidents |
| 60 km/h | 23.06 | 5.58 | 2.96 | 34.07 |
| 80 km/h | 24.09 | 10.07 | 9.74 | 74.93 |
| 100 km/h | 24.65 | 19.43 | 17.38 | 125.67 |
| 120 km/h | 24.46 | 12.49 | 13.25 | 154.77 |
| Cluster Label | Speed Limit of Hard Shoulder | Rank of TOPSIS | |
|---|---|---|---|
| 1 | 60 km/h | 0.1602 | 10 |
| 1 | 80 km/h | 0.1815 | 9 |
| 1 | 100 km/h | 0.2723 | 6 |
| 1 | 120 km/h | 0.2348 | 8 |
| 2 | 60 km/h | 0.1042 | 12 |
| 2 | 80 km/h | 0.1417 | 11 |
| 2 | 100 km/h | 0.2451 | 7 |
| 2 | 120 km/h | 0.2923 | 5 |
| 0 | 60 km/h | 0.5099 | 4 |
| 0 | 80 kn/h | 0.6759 | 3 |
| 0 | 100 km/h | 0.9122 | 1 |
| 0 | 120 km/h | 0.8495 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Wang, F.; Ding, F.; Tan, H.; Ran, B. Identify Optimal Traffic Condition and Speed Limit for Hard Shoulder Running Strategy. Sustainability 2021, 13, 1822. https://doi.org/10.3390/su13041822
Yang F, Wang F, Ding F, Tan H, Ran B. Identify Optimal Traffic Condition and Speed Limit for Hard Shoulder Running Strategy. Sustainability. 2021; 13(4):1822. https://doi.org/10.3390/su13041822
Chicago/Turabian StyleYang, Fan, Fan Wang, Fan Ding, Huachun Tan, and Bin Ran. 2021. "Identify Optimal Traffic Condition and Speed Limit for Hard Shoulder Running Strategy" Sustainability 13, no. 4: 1822. https://doi.org/10.3390/su13041822
APA StyleYang, F., Wang, F., Ding, F., Tan, H., & Ran, B. (2021). Identify Optimal Traffic Condition and Speed Limit for Hard Shoulder Running Strategy. Sustainability, 13(4), 1822. https://doi.org/10.3390/su13041822








