Optimal Electric Bus Scheduling Based on the Combination of All-Stop and Short-Turning Strategies
Abstract
1. Introduction
1.1. Background
1.2. Related Works
1.3. Contributions
2. Methods
2.1. Scheduling Strategy of EBs
- (1)
- The combinational scheduling strategies
- (2)
- Charging strategy
- (3)
- Optimization objectives and variables
2.2. Description of the Bus Route
2.3. Description of EBs Operation
2.4. Description of Charging and Discharging Process of EBs
2.5. Optimization Model
2.5.1. Passenger-Related Travel Time Costs
- (1)
- The passenger-related waiting time costs
- (a)
- The passenger-related waiting time costs inside the overlapping segmentWe assume that the arrival rate of passengers follows a uniform distribution; thus, the average waiting time of each passenger is half of the headway.Equation (26) illustrates the passengers waiting times, consisting of the waiting times of arriving passengers and residual passengers due to the limitation of the bus capacity.where denotes the unit value of passengers, CNY/min; and denote respectively the passenger arrival rates at stop n in Type 1 and Type 2, pax/min; denotes the waiting times of residual passengers at stop n, min.The first term in Equation (27) indicates the waiting times of passengers in Type 2 when the bus is all-stop scheduling and its leading vehicle is short-turning strategy. The second term refers to the waiting times of residual passengers from the previous bus, and they can take the following bus regardless of scheduling strategy.
- (b)
- The passenger-related waiting time costs outside the overlapping segmentOnly the all-stop strategy is adopted outside the overlapping segment, and the waiting time cost is represented by Equation (28).
- (2)
- The passenger-related in-vehicle travel time costsThe passenger-related in-vehicle travel time is equal to the sum of dwell times at the entire stops and inter-stop travel times.
- (a)
- The passenger-related in-vehicle travel time costs inside the overlapping segmentwhere denotes the number of in-vehicle passengers before arriving at stop n, pax.
- (b)
- The passenger-related in-vehicle travel time costs outside the overlapping segmentTherefore, the total passenger-related travel time cost is expressed by Equation (31)
2.5.2. Charging Costs
2.5.3. Depreciation Costs
3. Solution Algorithm
3.1. Column Generation
3.2. Branch-And-Price Algorithm
4. Numerical Example
4.1. Data Collection
4.2. Optimization Results
- (1)
- Determine the overlapping segments and timetable
- (2)
- Vehicles scheduling
- (3)
- Vehicle charging scheme
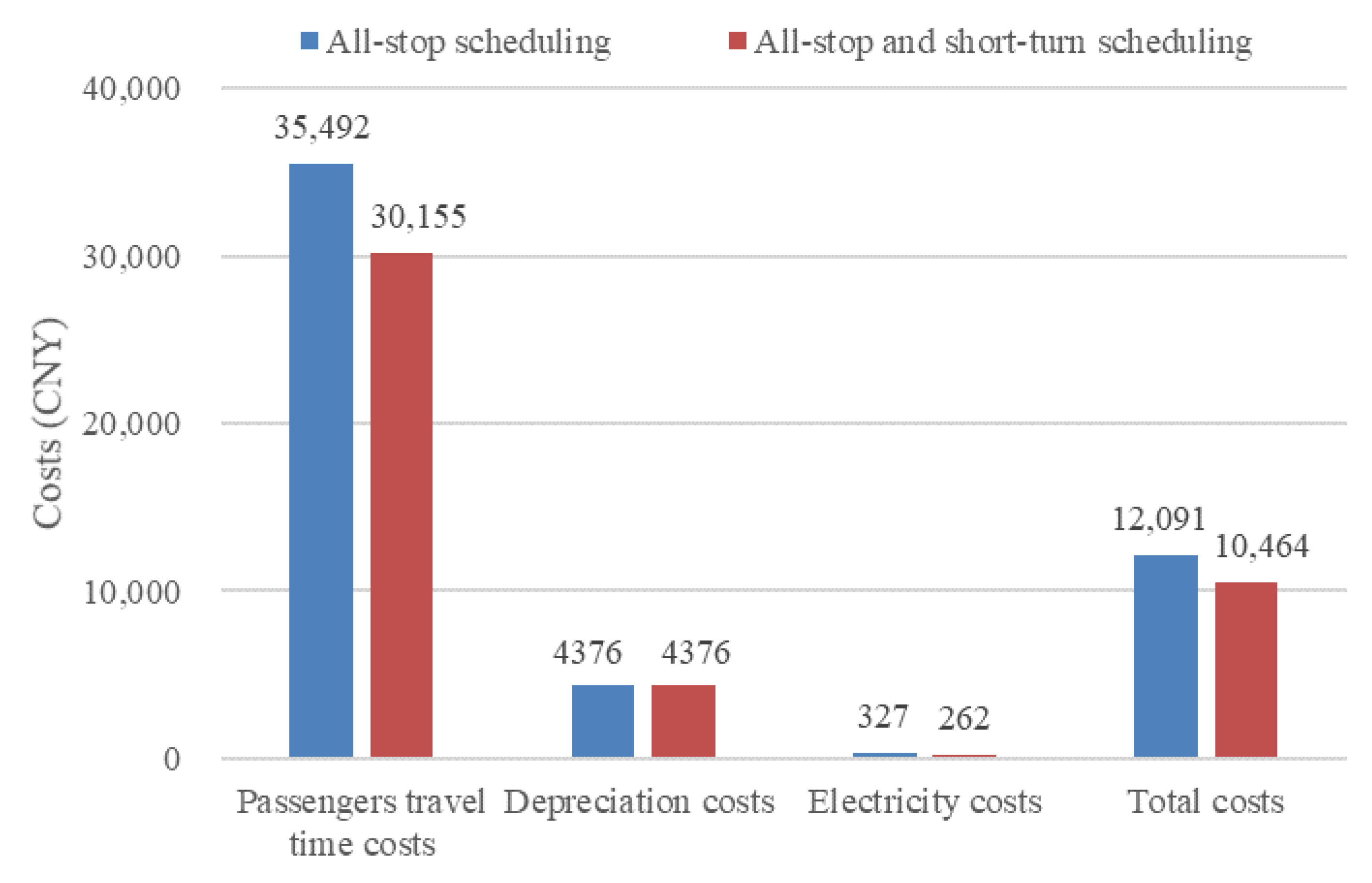
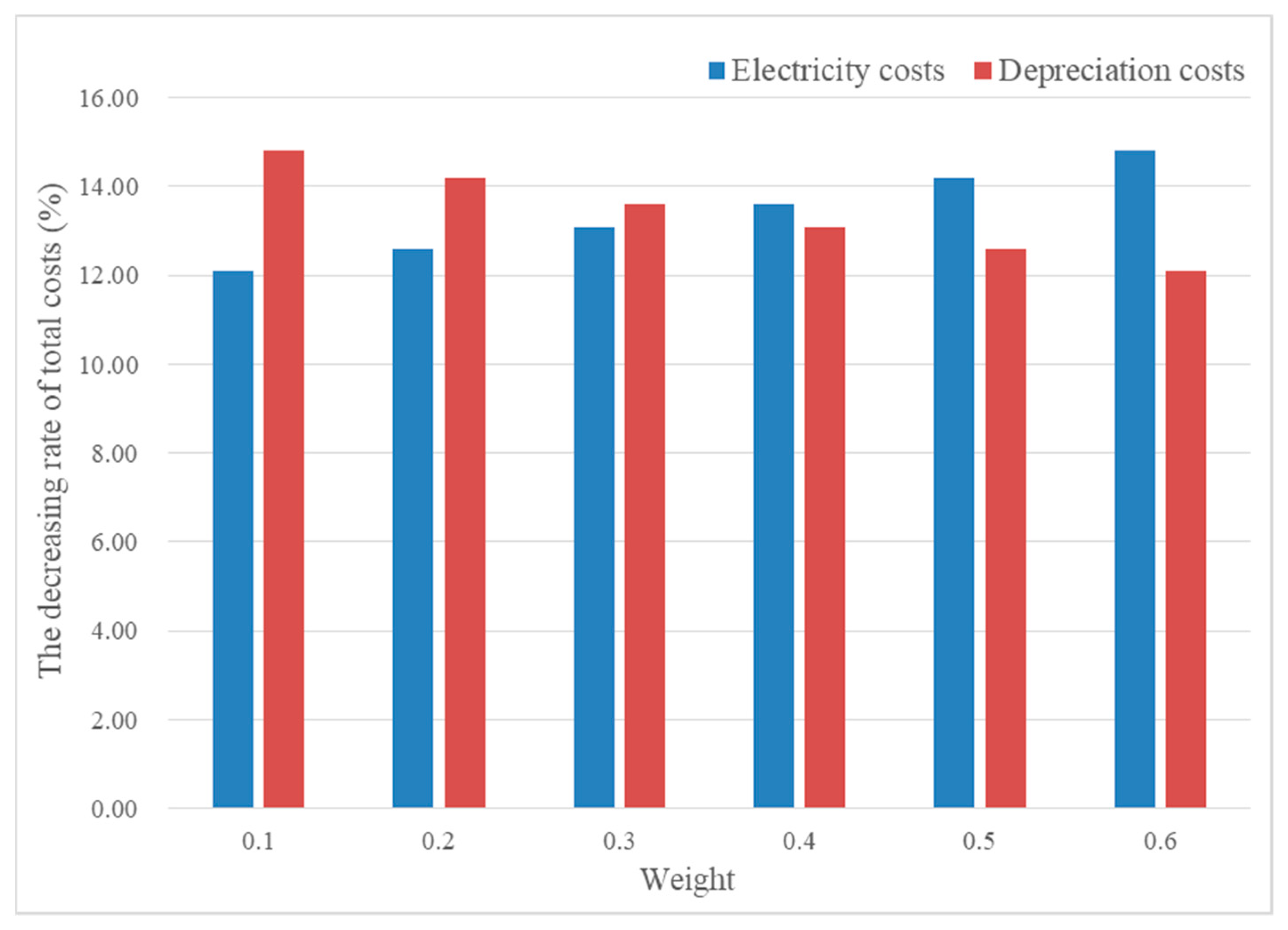
4.3. Schemes Comparison
- (1)
- Total costs comparison
- (2)
- Weight analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Kang, L.; Liu, Y. Optimal scheduling for electric bus fleets based on dynamic programming approach by considering battery capacity fade. Renew. Sustain. Energy Rev. 2020, 130, 9978. [Google Scholar] [CrossRef]
- Quttineh, N.H.; Häll, C.H.; Ekström, J.; Ceder, A. Combined Timetabling and Vehicle Scheduling for Electric Buses. In Proceedings of the 22nd International Conference of Hong Kong Society for Transportation Studies (HKSTS), Hong Kong, China, 9–11 December 2017. [Google Scholar]
- Wang, Y.; Huang, Y.; Xu, J.; Barclay, N. Optimal recharging scheduling for urban electric buses: A case study in Davis. Transp. Res. Part E Logist. Transp. Rev. 2017, 100, 115–132. [Google Scholar] [CrossRef]
- Guedes, P.C.; Borenstein, D. Column generation based heuristic framework for the multiple-depot vehicle type scheduling problem. Comput. Ind. Eng. 2015, 90, 361–370. [Google Scholar] [CrossRef]
- Gong, L.; Li, Y.; Xu, D. Combinational Scheduling Model Considering Multiple Vehicle Sizes. Sustainability 2019, 11, 5144. [Google Scholar] [CrossRef]
- Perumal, S.; Dollevoet, T.; Huisman, D.; Lusby, R.; Larsen, J.; Riis, M. Solution Approaches for Vehicle and Crew Scheduling with Electric Buses. Econometric Institute Research Papers. Available online: https://repub.eur.nl/pub/123963 (accessed on 4 January 2021).
- Gao, L. Research and application of vehicle bus combined scheduling model for urban public interval bus. Dalian Maritime University. 2017. Available online: http://cdmd.cnki.com.cn/Article/CDMD-10151-1017196186.htm (accessed on 4 January 2021).
- Cortés, C.E.; Díaz, J.S.; Tirachini, A. Integrating short turning and deadheading in the optimization of transit services. Transp. Res. Part A Policy Pract. 2011, 45, 419–434. [Google Scholar] [CrossRef]
- Ke, B.R.; Chung, C.Y.; Chen, Y.C. Minimizing the costs of constructing an all plug-in electric bus transportation system: A case study in Penghu. Appl. Energy 2016, 177, 649–660. [Google Scholar] [CrossRef]
- Bellei, G.; Gkoumas, K. Transit vehicles’ headway distribution and service irregularity. Public Transp. 2010, 2, 269–289. [Google Scholar] [CrossRef]
- Borndörfer, R.; Grötschel, M.; Pfetsch, M.E. A column-generation approach to line planning in public transport. Transp. Sci. 2007, 41, 123–132. [Google Scholar] [CrossRef]
- Ghaemi, N.; Cats, O.; Goverde, R.M.P. A microscopic model for optimal train short-turnings during complete blockages. Transp. Res. Part B Methodol. 2017, 105, 423–437. [Google Scholar] [CrossRef]
- Ji, Y.; Yang, X.; Du, Y. Optimal design of a short-turning strategy considering seat availability. J. Adv. Transp. 2016, 50, 1554–1571. [Google Scholar] [CrossRef]
- Canca, D.; Barrena, E.; Laporte, G.; Ortega, F.A. A short-turning policy for the management of demand disruptions in rapid transit systems. Ann. Oper. Res. 2016, 246, 145–166. [Google Scholar] [CrossRef]
- Carosi, S.; Frangioni, A.; Galli, L.; Girardi, L.; Vallese, G. A matheuristic for integrated timetabling and vehicle scheduling. Transp. Res. Part B Methodol. 2019, 127, 99–124. [Google Scholar] [CrossRef]
- Shang, H.Y.; Huang, H.J.; Wu, W.X. Bus timetabling considering passenger satisfaction: An empirical study in Beijing. Comput. Ind. Eng. 2019, 135, 1155–1166. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, Q.; Meng, Z.; Ralescu, A. Fuzzy dynamic timetable scheduling for public transit. Fuzzy Sets Syst. 2020, 395, 235–253. [Google Scholar] [CrossRef]
- Zhang, S.; Ceder, A.A.; Cao, Z. Integrated optimization for feeder bus timetabling and procurement scheme with consideration of environmental impact. Comput. Ind. Eng. 2020, 145, 6501. [Google Scholar] [CrossRef]
- Peña, D.; Tchernykh, A.; Nesmachnow, S.; Massobrio, R.; Feoktistov, A.; Bychkov, I.; Garichev, S.N. Operating cost and quality of service optimization for multi-vehicle-type timetabling for urban bus systems. J. Parallel Distrib. Comput. 2019, 133, 272–285. [Google Scholar] [CrossRef]
- Gkiotsalitis, K.; Alesiani, F. Robust timetable optimization for bus lines subject to resource and regulatory constraints. Transp. Res. Part E Logist. Transp. Rev. 2019, 128, 30–51. [Google Scholar] [CrossRef]
- Wang, C.; Shi, H.; Zuo, X. A multi-objective genetic algorithm based approach for dynamical bus vehicles scheduling under traffic congestion. Swarm Evol. Comput. 2020, 54, 667. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, P. Economic benefit analysis of battery charging and swapping station for pure electric bus based on differential power purchase policy: A new power trading model. Sustain. Cities Soc. 2021, 64, 2570. [Google Scholar] [CrossRef]
- Gao, K.; Yang, Y.; Li, A.; Li, J.; Yu, B. Quantifying economic benefits from free-floating bike-sharing systems: A trip-level inference approach and city-scale analysis. Transp. Res. Part A Policy Pract. 2021, 144, 89–103. [Google Scholar] [CrossRef]
- Xu, Y.; Zheng, Y.; Yang, Y. On the movement simulations of electric vehicles: A behavioral model-based approach. Appl. Energy 2020, 6356. [Google Scholar] [CrossRef]
- Gao, K.; Yang, Y.; Sun, L.; Qu, X. Revealing psychological inertia in mode shift behavior and its quantitative influences on commuting trips. Transp. Res. Part F Traffic Psychol. Behav. 2020, 71, 272–287. [Google Scholar] [CrossRef]
- Teng, J.; Chen, T.; Fan, W.D. Integrated Approach to Vehicle Scheduling and Bus Timetabling for an Electric Bus Line. J. Transp. Eng. Part A Syst. 2020, 146, 9073. [Google Scholar] [CrossRef]
- Ke, B.R.; Lin, Y.H.; Chen, H.Z.; Fang, S.C. Battery charging and discharging scheduling with demand response for an electric bus public transportation system. Sustain. Energy Technol. Assess. 2020, 40, 741. [Google Scholar] [CrossRef]
- Tang, X.; Lin, X.; He, F. Robust scheduling strategies of electric buses under stochastic traffic conditions. Transp. Res. Part C Emerg. Technol. 2019, 105, 163–182. [Google Scholar] [CrossRef]
- Alwesabi, Y.; Wang, Y.; Avalos, R.; Liu, Z. Electric bus scheduling under single depot dynamic wireless charging infrastructure planning. Energy 2020, 213, 8855. [Google Scholar] [CrossRef]
- Häll, C.H.; Ceder, A.; Ekström, J.; Quttineh, N.H. Adjustments of public transit operations planning process for the use of electric buses. J. Intell. Transp. Syst. 2019, 23, 216–230. [Google Scholar] [CrossRef]
- Rinaldi, M.; Parisi, F.; Laskaris, G.; Ariano, D.A.; Viti, F. Optimal dispatching of electric and hybrid buses subject to scheduling and charging constraints. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 41–46. [Google Scholar]
- Zhang, L.; Zeng, Z.; Qu, X. On the Role of Battery Capacity Fading Mechanism in the Lifecycle Cost of Electric Bus Fleet. IEEE Trans. Intell. Transp. Syst. 2020. [Google Scholar] [CrossRef]
- Bie, Y.; Xiong, X.; Yan, Y.; Qu, X. Dynamic headway control for high-frequency bus line based on speed guidance and intersection signal adjustment. Comput. Aided Civil Infrastruct. Eng. 2020, 35, 4–25. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, W.; Bie, Y.; Wang, K.; Diabat, A. Mixed-integer second-order cone programming model for bus route clustering problem. Transp. Res. Part C Emerg. Technol. 2019, 102, 351–369. [Google Scholar] [CrossRef]
- Ma, D.; Xiao, J.; Song, X.; Ma, X.; Jin, S. A back-pressure-based model with fixed phase sequences for traffic signal optimization under oversaturated networks. IEEE Trans. Intell. Transp. Syst. 2020. [Google Scholar] [CrossRef]
- Gkiotsalitis, K.; Wu, Z.; Cats, O. A cost-minimization model for bus fleet allocation featuring the tactical generation of short-turning and interlining options. Transp. Res. Part C Emerg. Technol. 2019, 98, 14–36. [Google Scholar] [CrossRef]
- Cao, Z.; Ceder, A.A. Autonomous short-turning bus service timetabling and vehicle scheduling using skip-stop tactic. Transp. Res. Part C Emerg. Technol. 2019, 102, 370–395. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Z.; Wang, S.; Chen, X. Continuum approximation modeling of transit network design considering local route service and short-turn strategy. Transp. Res. Part E Logist. Transp. Rev. 2018, 119, 165–188. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, S.; Liu, H.; Liang, S. Design of integrated limited-stop and short-turn services for a bus route. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Tirachini, A.; Cortés, C.E.; Díaz, J.S.R. Optimal design and benefits of a short-turning strategy for a bus corridor. Transportation 2011, 38, 169–189. [Google Scholar] [CrossRef]
- Ma, D.; Song, X.; Li, P. Daily traffic flow forecasting through a contextual convolutional recurrent neural network modeling inter-and intra-day traffic patterns. IEEE Trans. Intell. Transp. Syst. 2020. [Google Scholar] [CrossRef]
- Ma, D.; Xiao, J.; Ma, X. A decentralized model predictive traffic signal control method with fixed phase sequence for urban networks. J. Intell. Transp. Syst. 2020. [Google Scholar] [CrossRef]
- Wolbertus, R.; Van den Hoed, R. Electric vehicle fast charging needs in cities and along corridors. World Electr. Veh. J. 2019, 10, 45. [Google Scholar] [CrossRef]
- Rogge, M.; van der Hurk, E.; Larsen, A.; Sauer, D.U. Electric bus fleet size and mix problem with optimization of charging infrastructure. Appl. Energy 2018, 211, 282–295. [Google Scholar] [CrossRef]
- Rupp, M.; Rieke, C.; Handschuh, N.; Kuperjans, I. Economic and ecological optimization of electric bus charging considering variable electricity prices and CO2eq intensities. Transp. Res. Part D Transp. Environ. 2020, 81, 2293. [Google Scholar] [CrossRef]
- Yang, Y.; Yao, E.; Yang, Z.; Zhang, R. Modeling the charging and route choice behavior of BEV drivers. Transp. Res. Part C Emerg. Technol. 2016, 65, 190–204. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, K.; Shen, Z.J.M.; Ye, B.; Miao, L. Multistage large-scale charging station planning for electric buses considering transportation network and power grid. Transp. Res. Part C Emerg. Technol. 2019, 107, 423–443. [Google Scholar] [CrossRef]
- An, K. Battery electric bus infrastructure planning under demand uncertainty. Transp. Res. Part C Emerg. Technol. 2020, 111, 572–587. [Google Scholar] [CrossRef]
- He, Y.; Song, Z.; Liu, Z. Fast-charging station deployment for battery electric bus systems considering electricity demand charges. Sustain. Cities Soc. 2019, 48, 1530. [Google Scholar] [CrossRef]
- Chen, L.; Qian, K.; Qin, M.; Xu, X.; Xia, Y. A Configuration-Control Integrated Strategy for Electric Bus Charging Station With Echelon Battery System. IEEE Trans. Ind. Appl. 2020, 56, 6019–6028. [Google Scholar] [CrossRef]
- Chen, G.; Hu, D.; Chien, S. Optimizing battery-electric-feeder service and wireless charging locations with nested genetic algorithm. IEEE Access 2020, 8, 67166–67178. [Google Scholar] [CrossRef]
- Xu, M.; Yang, H.; Wang, S. Mitigate the range anxiety: Siting battery charging stations for electric vehicle drivers. Transp. Res. Part C Emerg. Technol. 2020, 114, 164–188. [Google Scholar] [CrossRef]
- Qin, N.; Gusrialdi, A.; Brooker, R.P.; Ali, T. Numerical analysis of electric bus fast charging strategies for demand charge reduction. Transp. Res. Part A Policy Pract. 2016, 94, 386–396. [Google Scholar] [CrossRef]
- He, Y.; Liu, Z.; Song, Z. Optimal charging scheduling and management for a fast-charging battery electric bus system. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 2056. [Google Scholar] [CrossRef]
- Wang, G.; Xie, X.; Zhang, F.; Liu, Y.; Zhang, D. bCharge: Data-driven real-time charging scheduling for large-scale electric bus fleets. In Proceedings of the 2018 IEEE Real-Time Systems Symposium (RTSS), Nashville, TN, USA, 11–14 December 2018; pp. 45–55. [Google Scholar]
- Barnhart, C.; Johnson, E.L.; Nemhauser, G.L.; Savelsbergh, M.W.P.; Vance, P.H. Branch-and-price: Column generation for solving huge integer programs. Oper. Res. 1998, 46, 316–329. [Google Scholar] [CrossRef]
- Tian, S. Study on Multi-Mode Bus Frequency Allocation Based on Stop Demand Elasticity; Chang’an University: Xi’an, China, 2017. [Google Scholar]
- Guo, C.; Wang, C.; Zuo, X. A genetic algorithm based column generation method for multi-depot electric bus vehicle scheduling. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, New York, NY, USA, 9–13 July 2019; pp. 367–368. [Google Scholar]

| NO. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Coefficient of nonuniformity | 0.2 | 0.3 | 0.6 | 0.9 | 1.0 | 1.2 | 1.3 | 1.5 | 1.4 | 1.5 | 1.5 | 1.5 |
| NO. | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Coefficient of nonuniformity | 1.5 | 1.4 | 1.3 | 1.2 | 1.1 | 1.0 | 0.9 | 0.8 | 0.8 | 0.7 | 0.4 | 0.2 |
| NO. | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| Coefficient of nonuniformity | 0.4 | 0.6 | 0.8 | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.4 | 1.4 | 1.5 | 1.5 |
| NO. | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| Coefficient of nonuniformity | 1.4 | 1.4 | 1.4 | 1.3 | 1.3 | 1.2 | 1.0 | 0.9 | 0.7 | 0.5 | 0.3 | 0.2 |
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Boarding rates(pax/min) | 0.0 | 0.3 | 0.3 | 0.4 | 0.5 | 0.5 | 0.6 | 1.2 | 1.5 | 1.2 | 1.0 | 1.0 |
| Alighting rates(pax/min) | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.3 | 0.2 | 0.0 | 0.1 | 0.3 | 0.8 | 0.9 |
| No. | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Boarding rates(pax/min) | 0.5 | 0.4 | 0.3 | 0.1 | 0.0 | 0.3 | 0.2 | 0.3 | 0.0 | 0.0 | 0.0 | 0.0 |
| Alighting rates(pax/min) | 0.8 | 1.3 | 0.9 | 0.1 | 0.6 | 0.3 | 0.6 | 0.6 | 0.4 | 0.5 | 0.3 | 0.5 |
| No. | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| Boarding rates(pax/min) | 0.0 | 0.5 | 0.6 | 0.7 | 0.0 | 0.3 | 0.6 | 0.5 | 0.2 | 1.0 | 1.1 | 1.2 |
| Alighting rates(pax/min) | 0.9 | 0.0 | 0.0 | 0.3 | 0.0 | 0.3 | 0.0 | 0.2 | 0.0 | 0.0 | 0.2 | 0.3 |
| No. | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| Boarding rates(pax/min) | 0.8 | 0.9 | 0.0 | 0.3 | 0.3 | 0.2 | 0.3 | 0.0 | 0.2 | 0.0 | 0.0 | 0.1 |
| Alighting rates(pax/min) | 0.2 | 0.5 | 0.7 | 1.2 | 0.6 | 1.1 | 0.7 | 0.5 | 0.4 | 0.6 | 0.5 | 0.6 |
| Scheduling Mode | Parameters | Period 1 | Period 2 | Period 3 | Period 4 |
|---|---|---|---|---|---|
| All-stop bus | Departure interval (min) | 15 | 10 | 15 | 10 |
| Average of travel time (min) | 25.4 | 29.1 | 25.9 | 28 | |
| Short-turning bus | Departure interval (min) | 20 | 12 | 20 | 11 |
| Average of travel time (min) | 8.9 | 9.4 | 8.4 | 10.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bie, Y.; Hao, M.; Guo, M. Optimal Electric Bus Scheduling Based on the Combination of All-Stop and Short-Turning Strategies. Sustainability 2021, 13, 1827. https://doi.org/10.3390/su13041827
Bie Y, Hao M, Guo M. Optimal Electric Bus Scheduling Based on the Combination of All-Stop and Short-Turning Strategies. Sustainability. 2021; 13(4):1827. https://doi.org/10.3390/su13041827
Chicago/Turabian StyleBie, Yiming, Mingjie Hao, and Mengzhu Guo. 2021. "Optimal Electric Bus Scheduling Based on the Combination of All-Stop and Short-Turning Strategies" Sustainability 13, no. 4: 1827. https://doi.org/10.3390/su13041827
APA StyleBie, Y., Hao, M., & Guo, M. (2021). Optimal Electric Bus Scheduling Based on the Combination of All-Stop and Short-Turning Strategies. Sustainability, 13(4), 1827. https://doi.org/10.3390/su13041827







