The High-Performance Dissipating Frame (HPDF) System for the Seismic Strengthening of RC Existing Buildings
Abstract
:1. Introduction
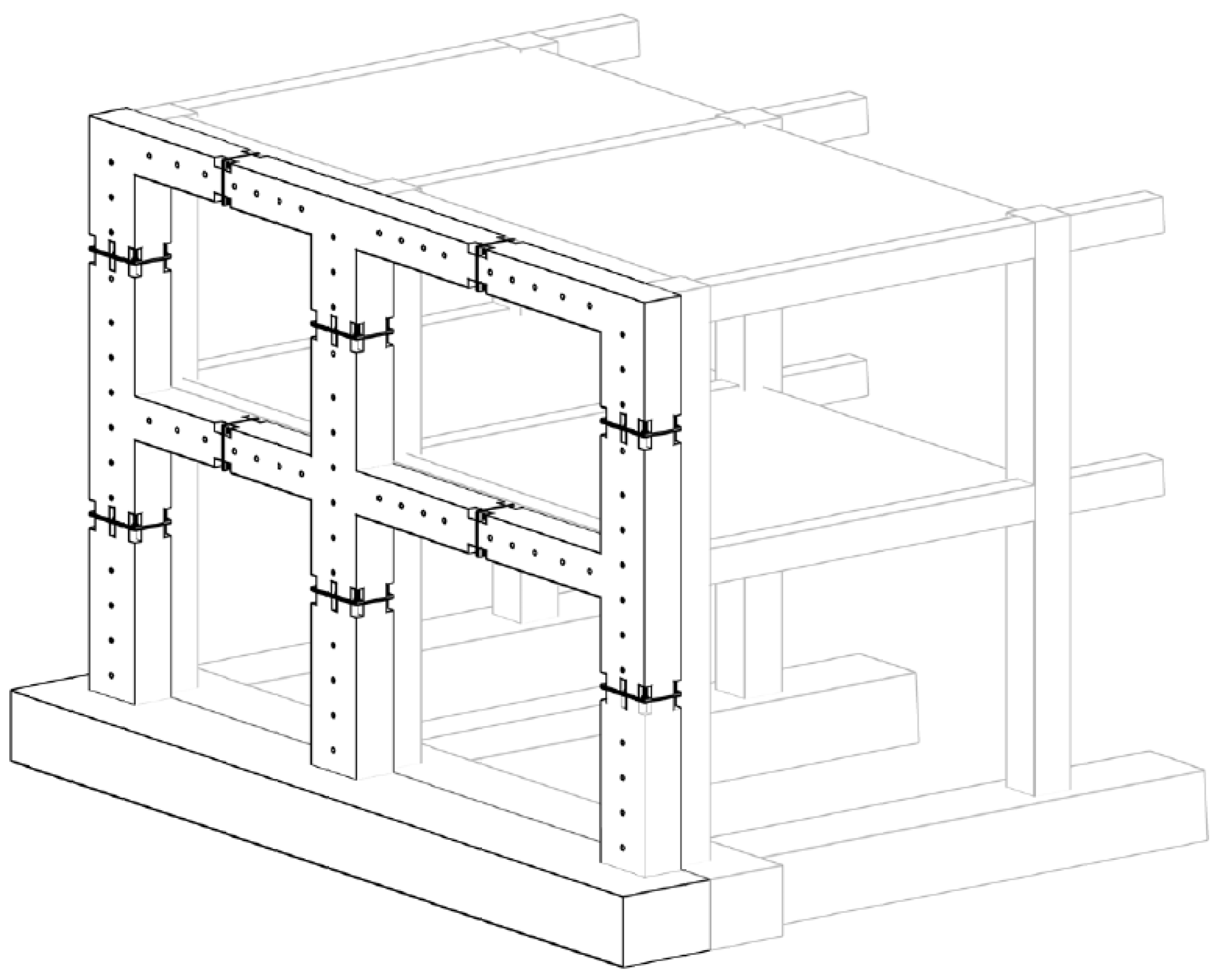
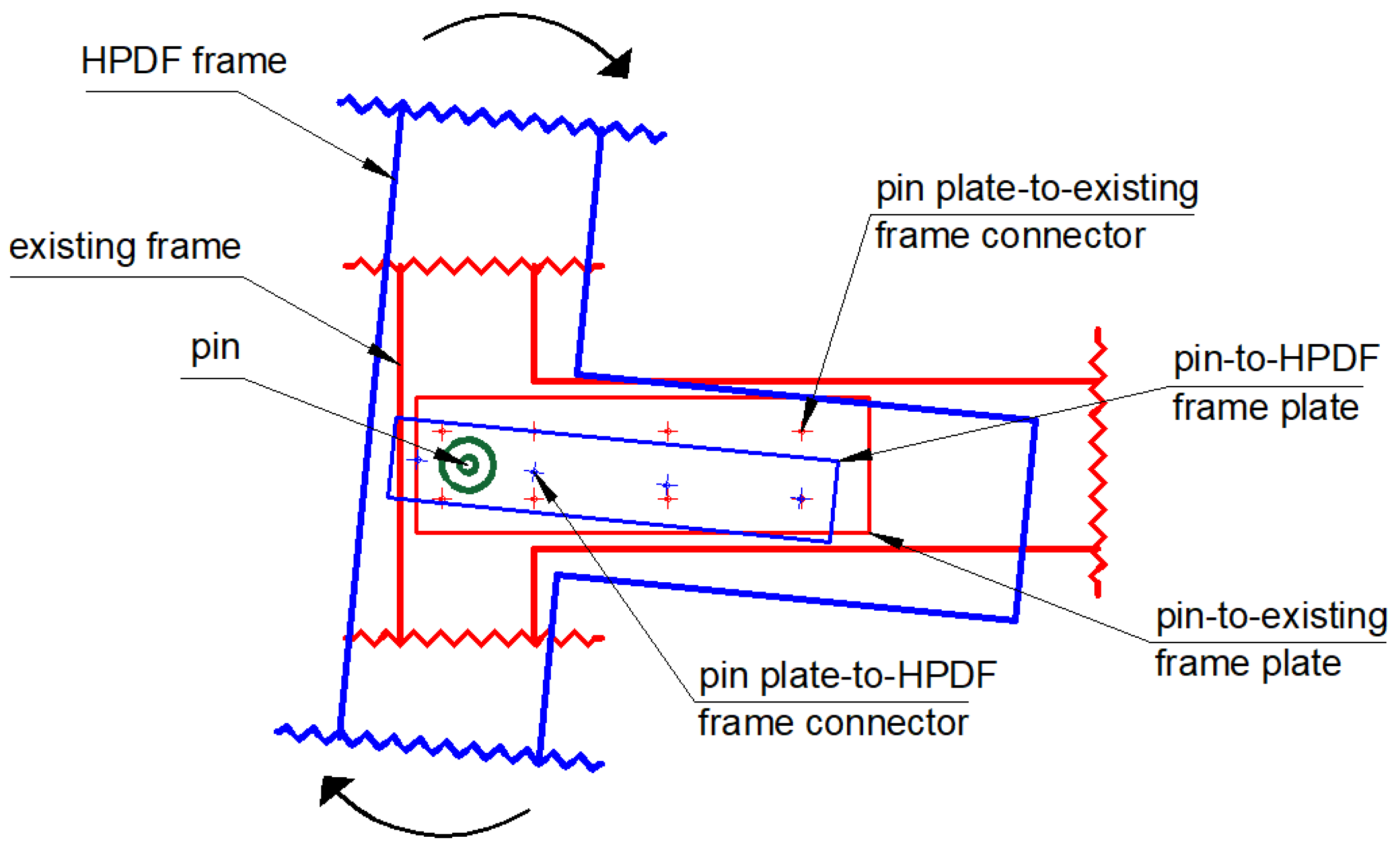
2. The High-Performance Dissipating Frame (HPDF) System
2.1. Background and Description of the System
- I.
- for low- and mid-seismic intensity values, the new frames’ response is elastic, counteracting seismic actions by proper stiffness and strength values, duly designed in order to convey most lateral loads on them thus protecting the existing deficient structure;
- II.
- for high-seismic intensity values, dissipative devices simultaneously yield dissipating energy through hysteretic loops.
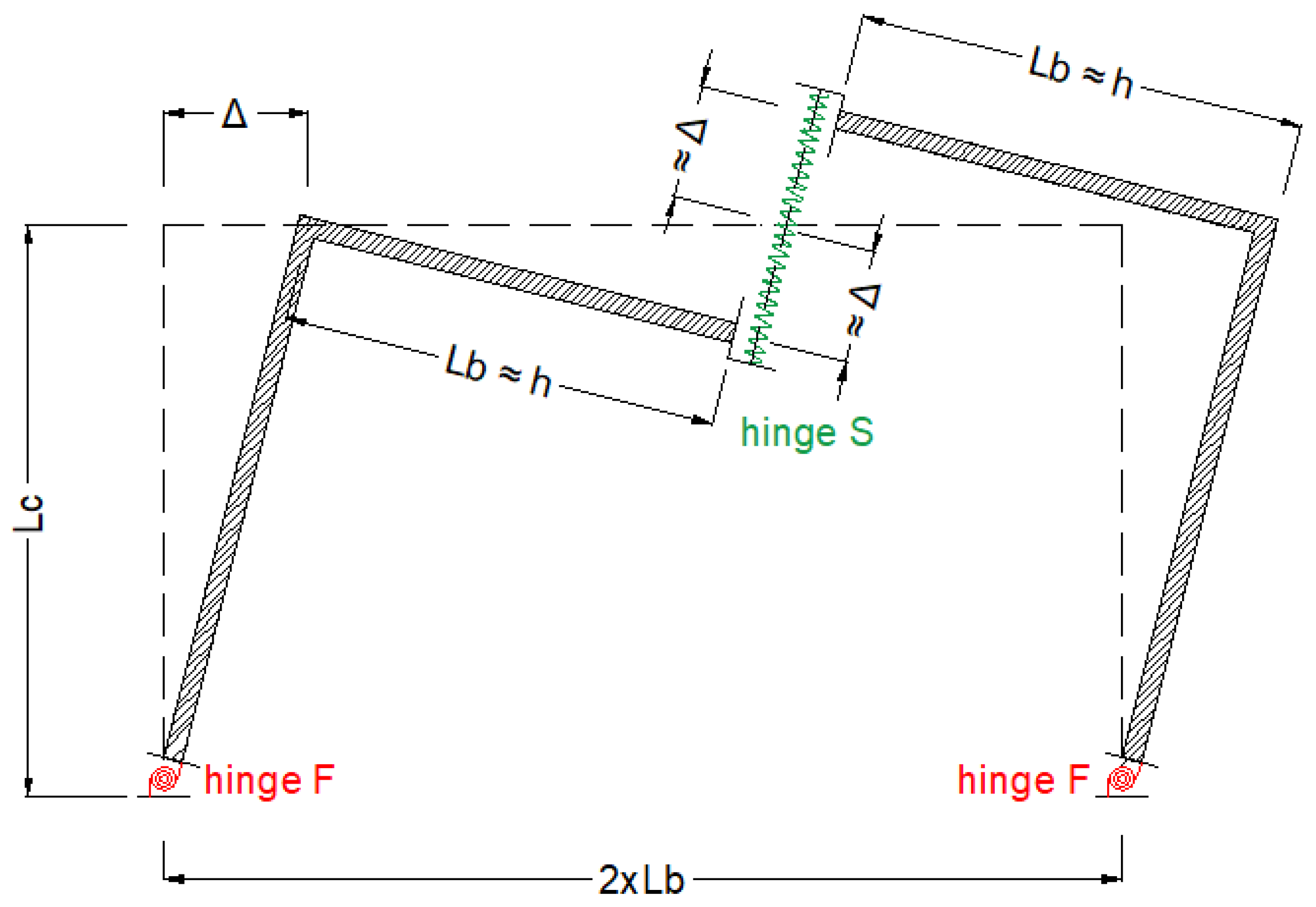
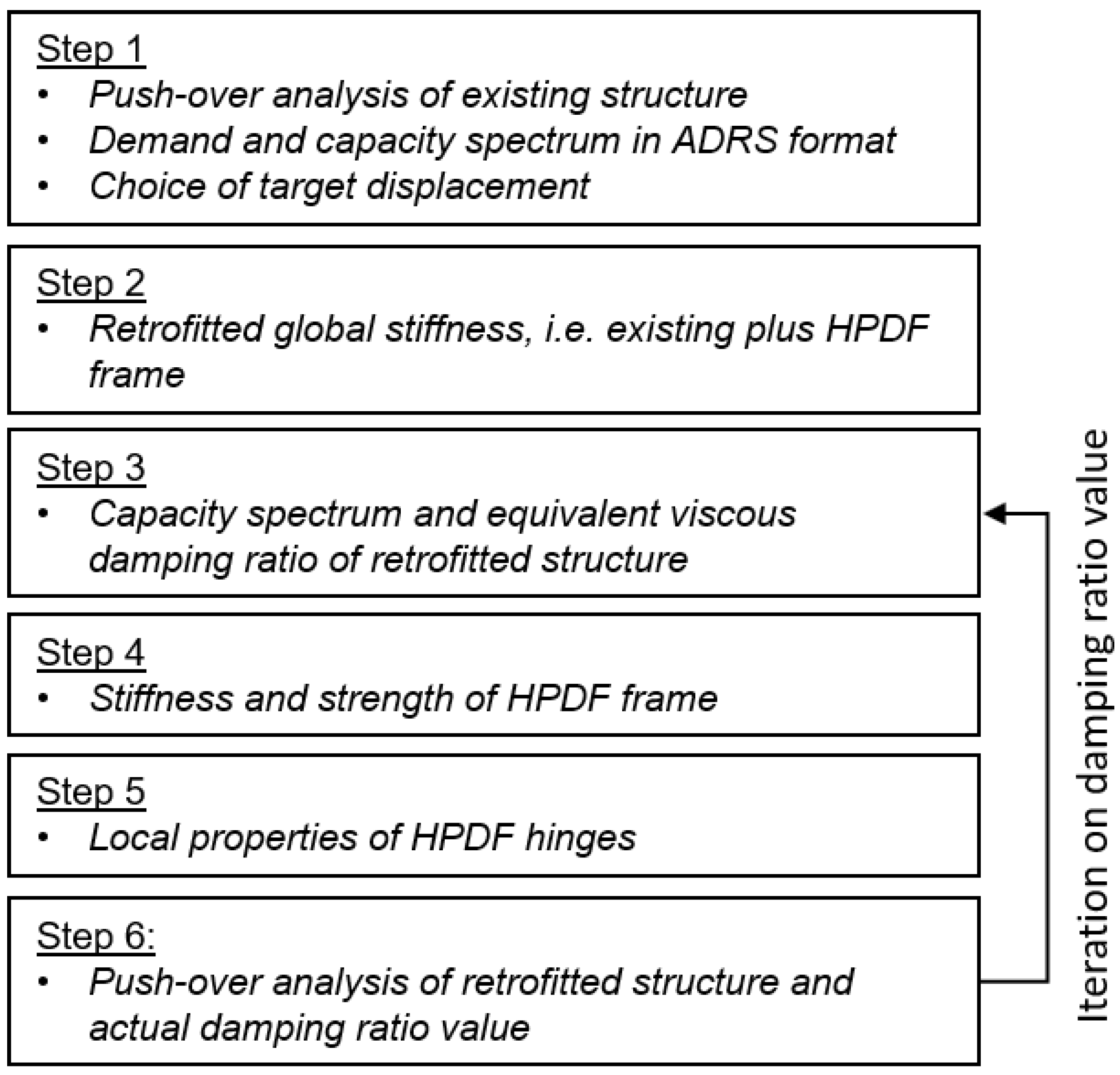
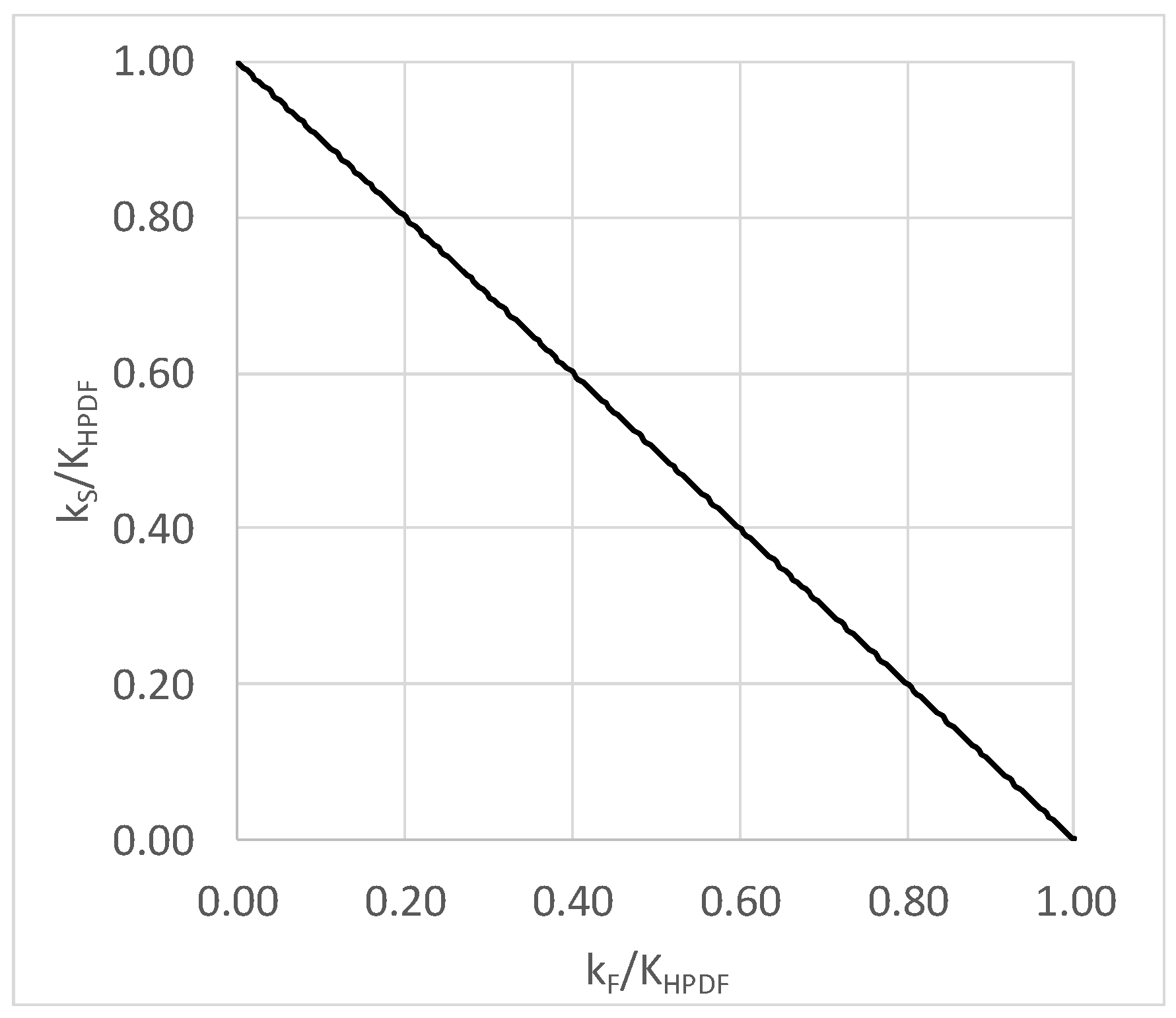
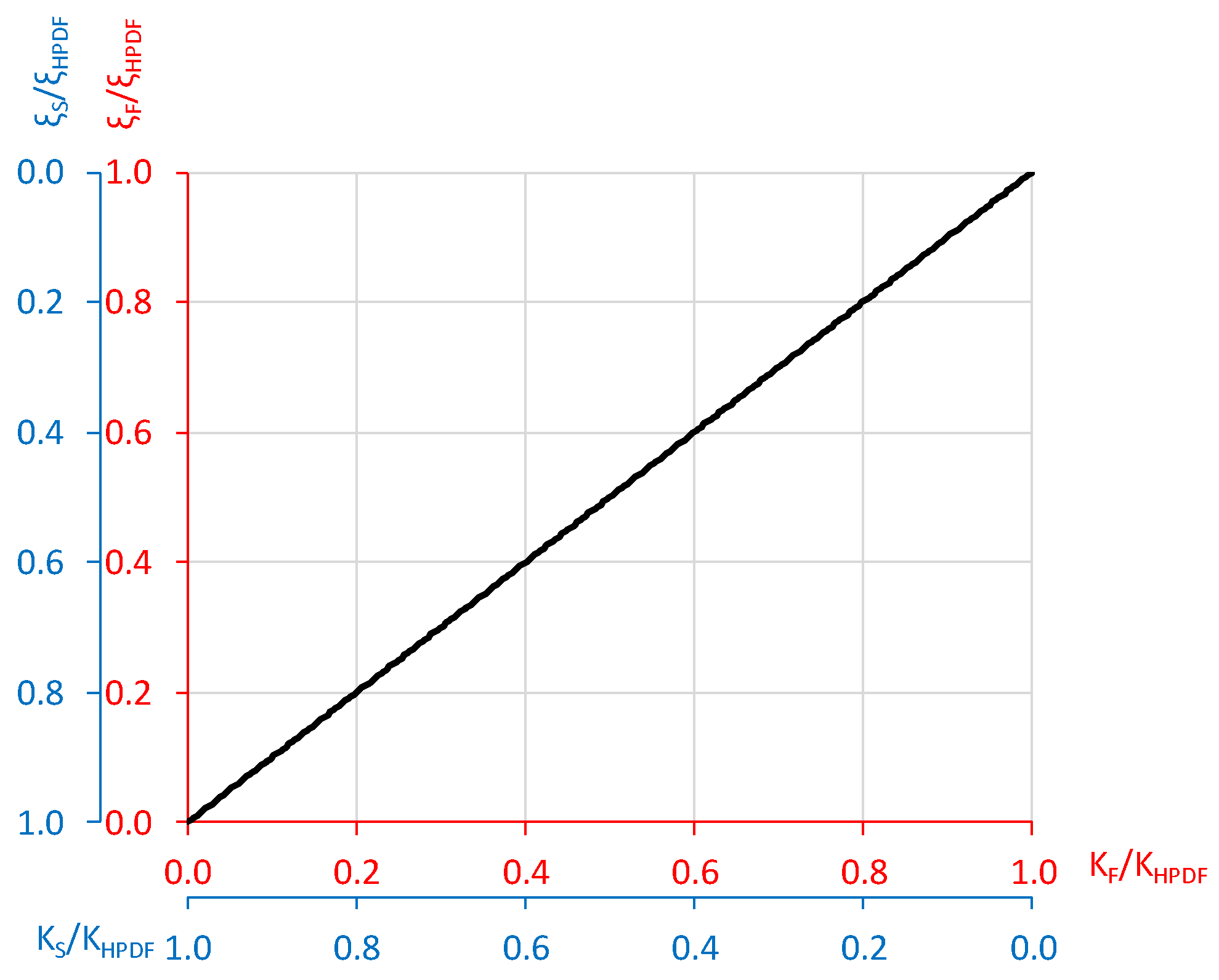
2.2. Design Procedure of the HPDF System
- -
- flexural stiffness value is the same for all columns, i.e., KF,i,j = constant;
- -
- for a given shear hinge, KS value is the same for each beam at different storeys;
- -
- for a given beam between the j-th and j + 1-th columns, the shear hinges of the two part of beams (i.e., right and left) have the same stiffness value, i.e., KSL,j = KSR,j+1;
- -
- for the j-th column member, the following relationships between the shear stiffness of the dampers at the right and left side can be drawn:
3. Numerical Application
3.1. Prototype Structure and Modeling
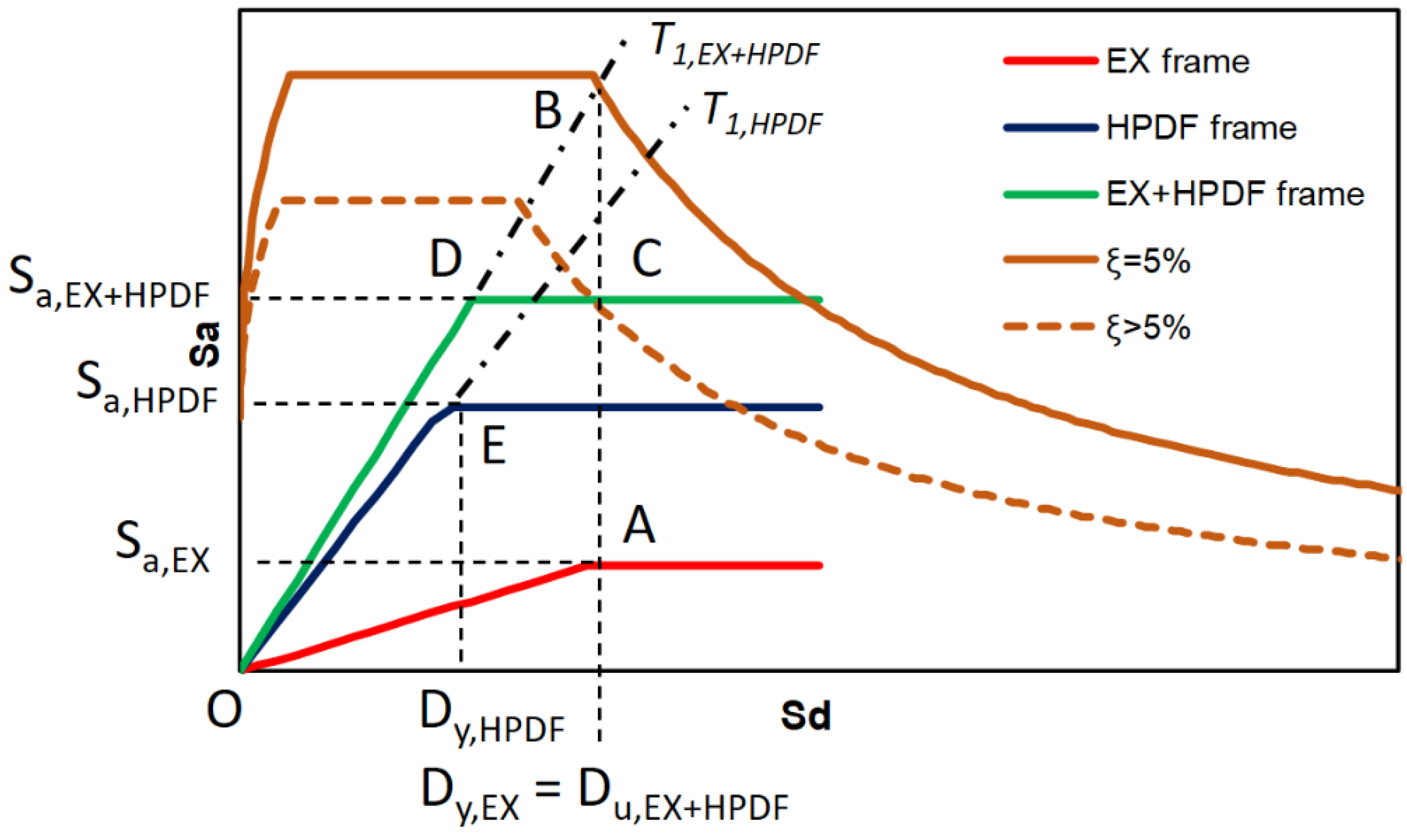
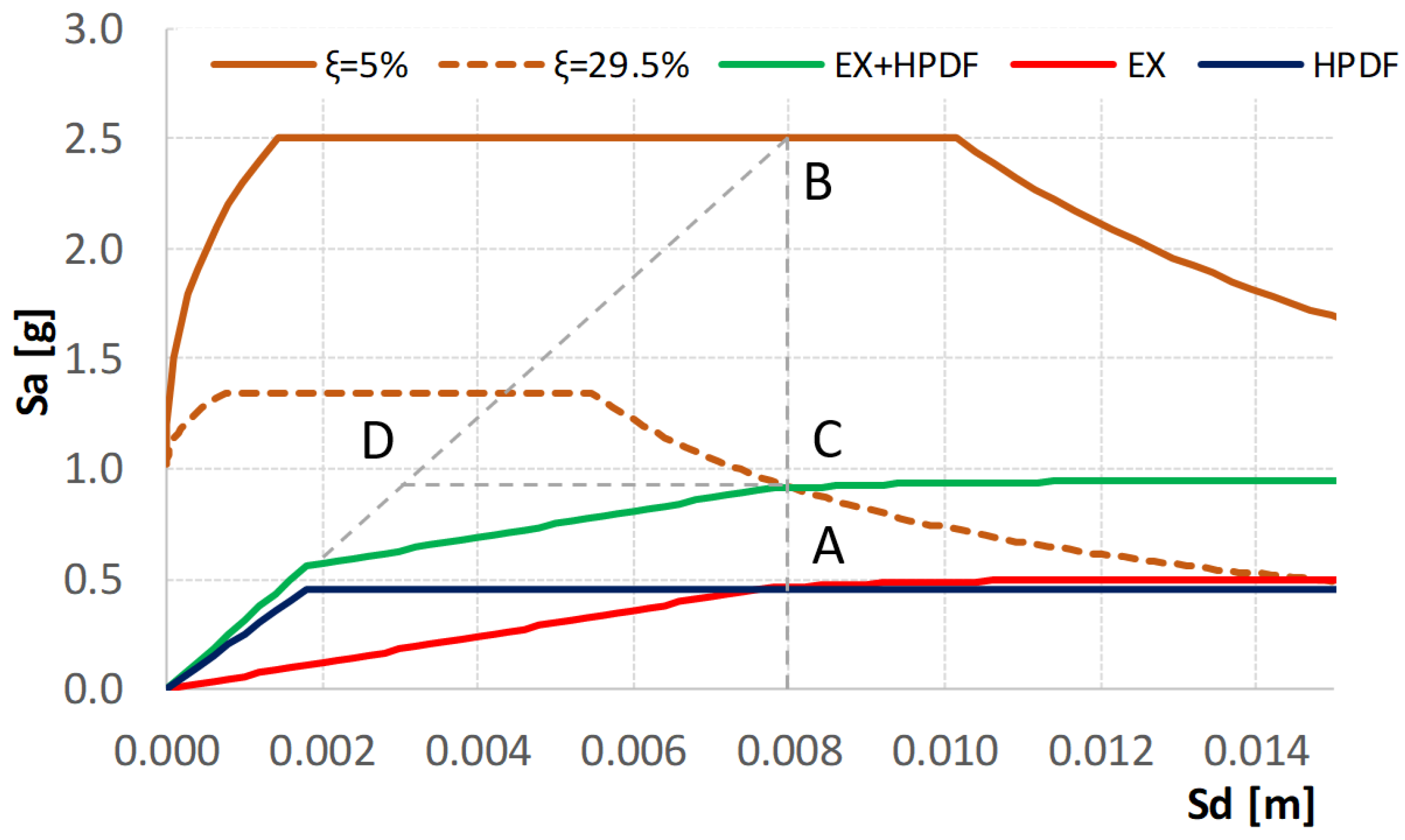
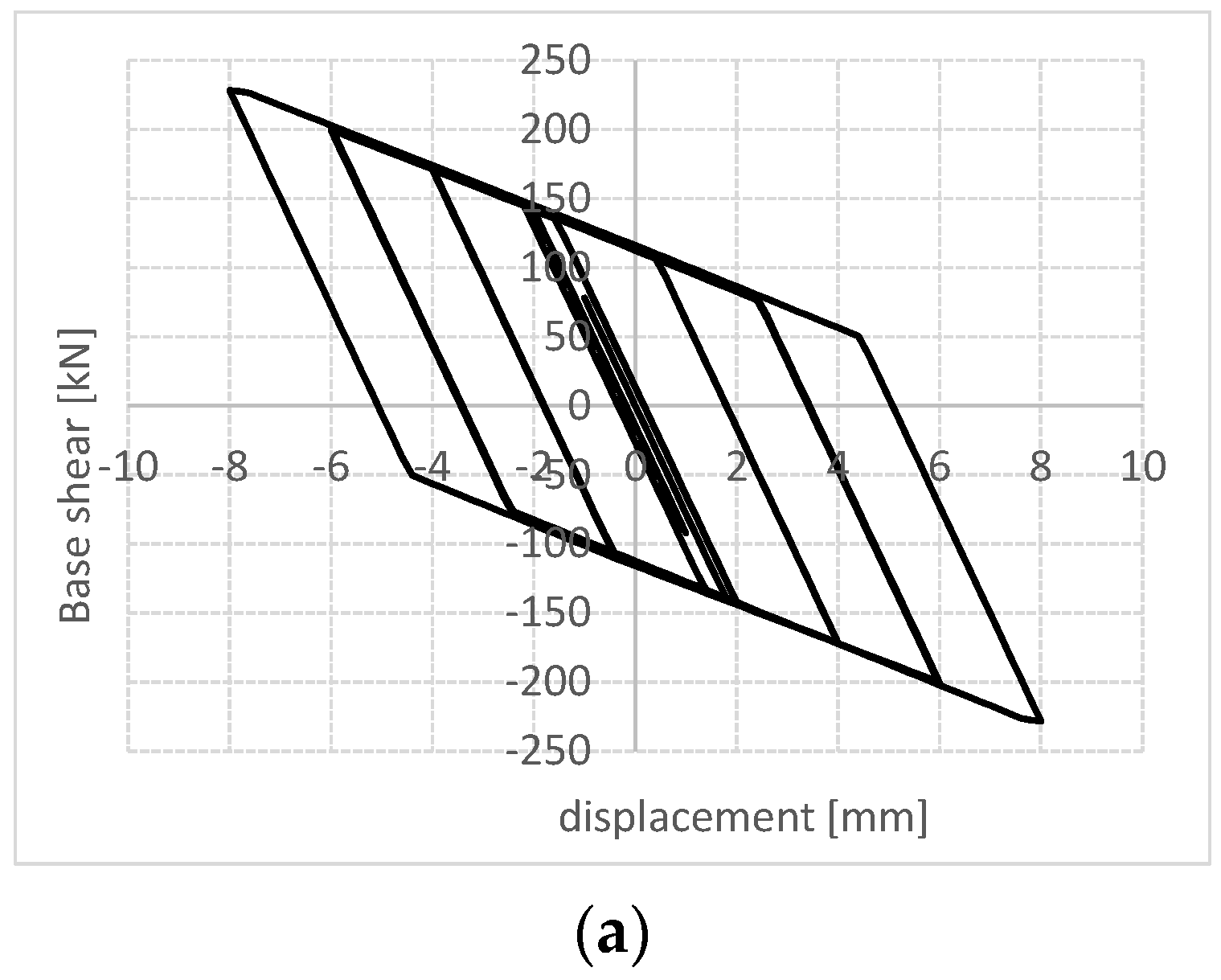
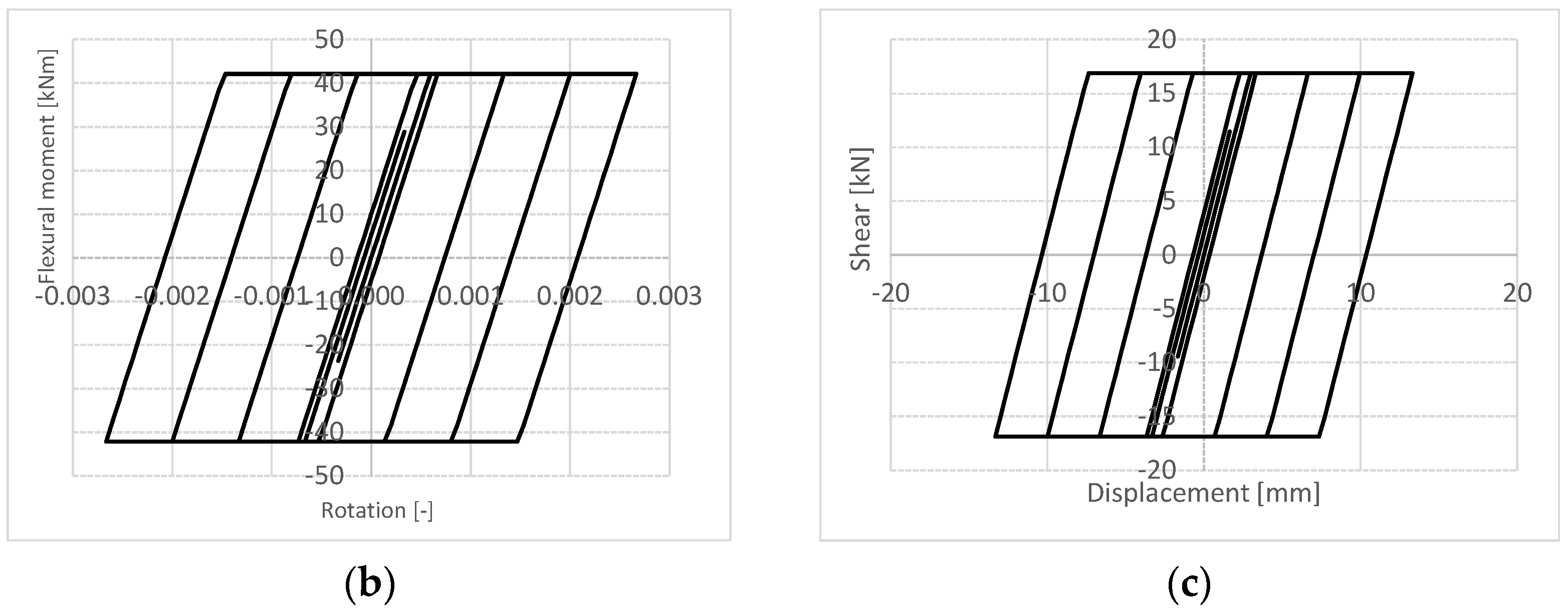
3.2. Design and Non-Linear Analysis Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ISTAT. 2011: XV Censimento Generale Della Popolazione e Delle Abitazioni. Available online: www.istat.it.
- Masi, A.; Chiauzzi, L.; Santarsiero, G.; Manfredi, G.; Biondi, S.; Spacone, E.; Del Gaudio, C.; Ricci, P.; Manfredi, G.; Verderame, G.M. Seismic response of RC buildings during the Mw 6.0 August 24, 2016 Central Italy earthquake: The Amatrice case study. Bull. Earthq. Eng. 2019, 17, 5631–5654. [Google Scholar] [CrossRef]
- BPIE (Building Performance Institute Europe). Europe’s Buildings under the Microscope—A Country-By-Country Review of the Energy Performance of the Buildings. Brussel. 2011. Available online: http://www.bpie.eu/eu_buildings_under_microscope.html.
- Bournas, D. Innovative Materials for Seismic and Energy Retrofitting of the Existing EU Buildings; EUR 29184 EN.; Publications Office of the European Union: Luxembourg, 2018. [Google Scholar]
- UNDRR and CRED. The human cost of disasters: An overview of the last 20 years (2000–2019), Centre for Research on the Epidemiology of Disasters, 2020, UN Office for Disaster Reduction. Available online: https://reliefweb.int/.
- Calvi, G.M. Choices and Criteria for Seismic Strengthening. J. Earthq. Eng. 2013, 17, 769–802. [Google Scholar] [CrossRef]
- FIB. Seismic Assessment and Retrofit of Reinforced Concrete Buildings; Bulletin No. 24; International Federation for Structural Concrete: Lausanne, Switzerland, 2003. [Google Scholar] [CrossRef]
- Fardis, M.N. Seismic Design, Assessment and Retrofitting of Concrete Buildings: Based on EN-Eurocode 8; Springer Science & Business Media: Cham, The Netherlands, 2009. [Google Scholar]
- Santarsiero, G.; Manfredi, V.; Masi, A. Numerical evaluation of the Steel Plate Energy Absorption Device (SPEAD) for Seismic Strengthening of RC Frame Structures. Int. J. Civ. Eng. 2020, 18, 835–850. [Google Scholar] [CrossRef]
- Masi, A.; Manfredi, V.; D’Angola, A.; Laguardia, A. Seismic and thermal rehabilitation of existing RC buildings through an integrated approach: An application case study. In Proceedings of the XVII Convegno ANIDIS-L’ingegneria Sismica in Italia, Pistoia, Italy, 17–21 September 2017. [Google Scholar]
- Pertile, V.; Stella, A.; De Stefania, L.; Scotta, R. Experimental tests on full-scale specimens for the characterization of an integrated retrofitting system for existing buildings. In Proceedings of the XVIII Convegno ANIDIS-L’ingegneria Sismica in Italia, Ascoli Piceno, Italy, 15–19 September 2019. [Google Scholar]
- Gkournelos, P.D.; Bournas, D.A.; Triantafillou, T.C. Combined seismic and energy upgrading of existing reinforced concrete buildings using TRM jacketing and thermal insulation. Earthq. Struct. 2019, 16, 625–639. [Google Scholar]
- Labò, S.; Passoni, C.; Marini, A.; Belleri, A. Design of diagrid exoskeletons for the retrofit of existing RC buildings. Eng. Struct. 2020, 220, 110899. [Google Scholar] [CrossRef]
- Sustersic, I.; Dujic, B. Seismic Strengthening of Existing Concrete and Masonry Buildings with Crosslam Timber Panels. RILEM Bookseries 2014, 9, 713–723. [Google Scholar] [CrossRef]
- Manfredi, V.; Masi, A. Seismic strengthening and energy efficiency: Towards an integrated approach for the rehabilitation of existing RC buildings. Buildings 2018, 8, 36. [Google Scholar] [CrossRef] [Green Version]
- Manfredi, V.; Masi, A.; Ventura, G.; Chiauzzi, L.; Digrisolo, A.; Santarsiero, G. Rafforzamento sismico degli edifici esistenti in c.a. una soluzione innovativa per interventi integrati e sostenibili. Structural 2018, 215. [Google Scholar] [CrossRef]
- Zanni, J.; Marini, A.; Belleri, A.; Riva, P.; Simonetti, F. Integrated rehabilitation with exoskeleton under a life cycle thinking approach: Application to an existing building. In Proceedings of the XXVII Congresso, C.T.A., Bologna, Italy, 3–5 October 2019. [Google Scholar]
- Whittaker, A.; Bertero, V.; Alonso, J.; Thompson, C. Earthquake Simulator Testing of Steel Plate Added Damping and Stiffness Elements; Report Number: UCB/EERC 89/02; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1988. [Google Scholar] [CrossRef]
- Constantinou, M.C.; Soong, T.T.; Dargush, G.F. Passive Energy Dissipation Systems for Structural Design and Retrofit, MCEER Monograph No.1; Multidisciplinary Center for Earthquake Engineering Research: Buffalo, NY, USA, 1998.
- Ye, Q.; Wang, Z.; Wang, Y. Numerical study on seismic performance of prefabricated steel frames with recentering energy dissipative braces. Eng. Struct. 2020, 207, 110223. [Google Scholar] [CrossRef]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C.; Kircher, C.A.; Johnson, M.W.; McNamara, R.J. Energy dissipation systems for seismic applications: Current practice and recent developments. J. Struct. Eng. 2008, 134, 3–21. [Google Scholar] [CrossRef] [Green Version]
- Nuzzo, I.; Losanno, D.; Caterino, N.; Serino, G.; Bozzo, L.M. Experimental and analytical characterization of steel shear links for seismic energy dissipation. Eng. Struct. 2017, 172, 405–418. [Google Scholar] [CrossRef]
- Ponzo, F.C.; Di Cesare, A.; Nigro, D.; Vulcano, A.; Mazza, F.; Dolce, M.; Moroni, C. Jet-Pacs Project: Dynamic Experimental Tests and Numerical Results Obtained for a Steel Frame Equipped with Hysteretic Damped Chevron Braces. J. Earthq. Eng. 2012, 16, 662–685. [Google Scholar] [CrossRef]
- Fajfar, P. A nonlinear analysis method for performance based seismic design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- Antoniou, S.; Pinho, R. Development and verification of a displacement-based adaptive pushover procedure. J. Earthq. Eng. 2004, 8, 643–661. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 561–582. [Google Scholar] [CrossRef] [Green Version]
- Bommer, J.J.; Mendis, R. Scaling of spectral displacement ordinates with damping ratios. Earthq. Eng. Struct. Dyn. 2005, 34, 145–165. [Google Scholar] [CrossRef]
- Rezaeian, S.; Bozorgnia, Y.; Idriss, I.M.; Abrahamson, N.; Campbell, K.; Silva, W. Damping Scaling Factors for Elastic Response Spectra for Shallow Crustal Earthquakes in Active Tectonic Regions: “Average” Horizontal Component. Earthq. Spectra 2014, 30, 939–963. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineer, 4th ed.; Hall, J.W., Ed.; Series in Civil Engineering and Engineering Mechanics; Prentice-Hall International: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Mazza, F.; Vulcano, A. Displacement-based design procedure of damped braces for the seismic retrofitting of R.C. framed buildings. Bull. Earthq. Eng. 2015, 13, 2121–2143. [Google Scholar] [CrossRef]
- Priestley, M.J.N.; Grant, D.N. Viscous damping in seismic design and analysis. J. Earthq. Eng. 2005, 9 (Suppl. S2), 229–255. [Google Scholar] [CrossRef]
- Nuzzo, I.; Losanno, D.; Caterino, N. Seismic design and retrofit of frame structures with hysteretic dampers: A simplified displacement-based procedure. Bull. Earthq. Eng. 2019, 17, 2787–2819. [Google Scholar] [CrossRef]
- McKenna, F. OpenSees: A framework for earthquake engineering simulation. Comput. Sci. Eng. 2011, 13, 58–66. [Google Scholar] [CrossRef]
- Ibarra, L.F.; Medina, R.A.; Krawinkler, H. Hysteretic models that incorporate strength and stiffness deterioration. Earthq. Eng. Struct. Dyn. 2005, 34, 1489–1511. [Google Scholar] [CrossRef]
- Haselton, C.B.; Deierlein, G.G. Assessing Seismic Collapse Safety of Modern Reinforced Concrete Moment Frame Buildings. Ph.D. Thesis, Stanford University, Stanford, CA, USA, February 2007. [Google Scholar]
- Comité Européen de Normalisation. CEN-European Standard ENV 1998-1-1/2/3, Eurocode 8: Design Provisions for Earthquake Resistance of Structures—Part I: General Rules; Technical Committee 250/SC8; Comité Européen de Normalisation: Brussels, Belgium, 2004. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manfredi, V.; Santarsiero, G.; Masi, A.; Ventura, G. The High-Performance Dissipating Frame (HPDF) System for the Seismic Strengthening of RC Existing Buildings. Sustainability 2021, 13, 1864. https://doi.org/10.3390/su13041864
Manfredi V, Santarsiero G, Masi A, Ventura G. The High-Performance Dissipating Frame (HPDF) System for the Seismic Strengthening of RC Existing Buildings. Sustainability. 2021; 13(4):1864. https://doi.org/10.3390/su13041864
Chicago/Turabian StyleManfredi, Vincenzo, Giuseppe Santarsiero, Angelo Masi, and Giuseppe Ventura. 2021. "The High-Performance Dissipating Frame (HPDF) System for the Seismic Strengthening of RC Existing Buildings" Sustainability 13, no. 4: 1864. https://doi.org/10.3390/su13041864
APA StyleManfredi, V., Santarsiero, G., Masi, A., & Ventura, G. (2021). The High-Performance Dissipating Frame (HPDF) System for the Seismic Strengthening of RC Existing Buildings. Sustainability, 13(4), 1864. https://doi.org/10.3390/su13041864








