Utility of Remotely Sensed Evapotranspiration Products to Assess an Improved Model Structure
Abstract
1. Introduction
2. Materials and Methods
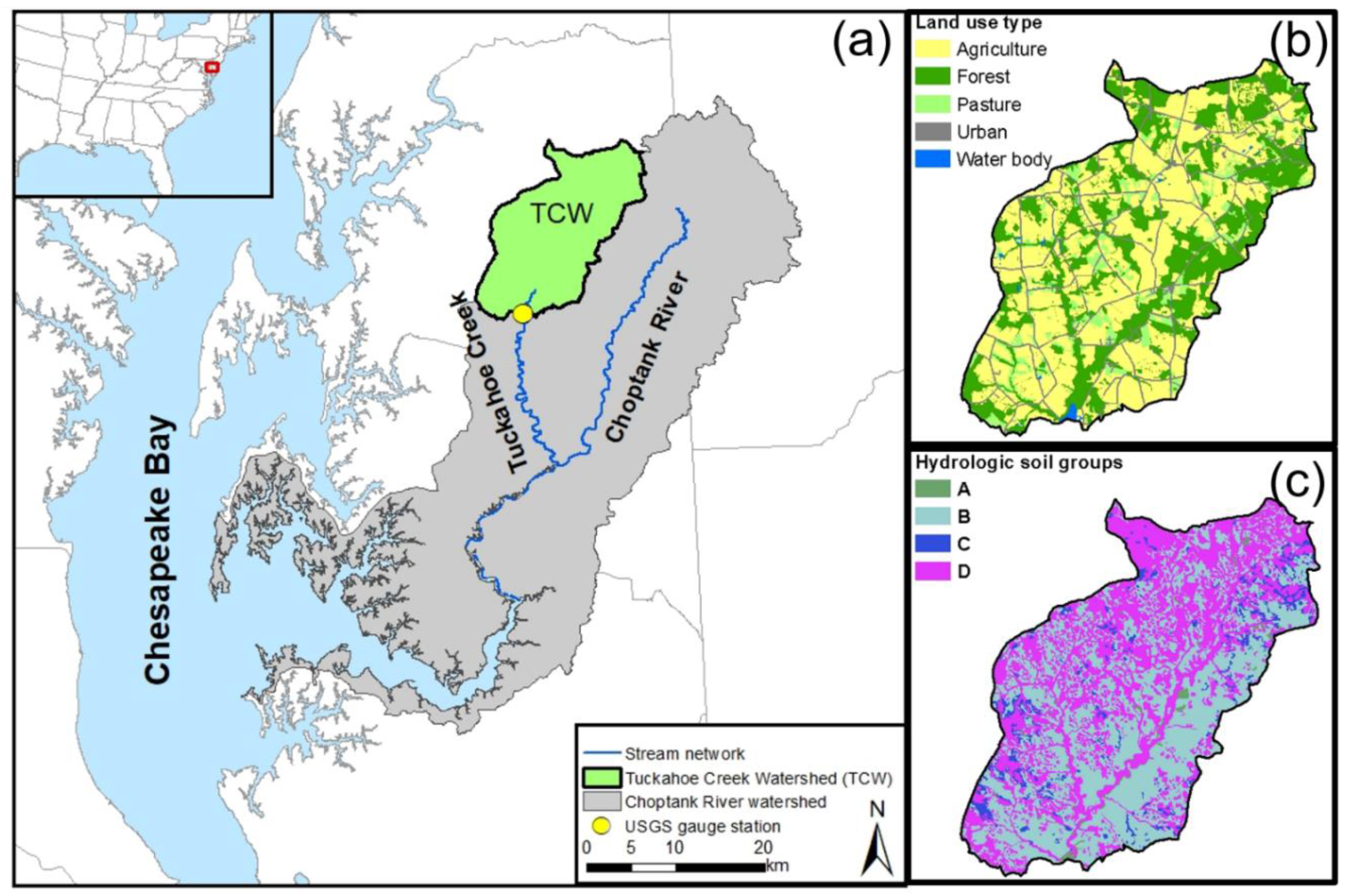
2.1. Study Area
2.2. Description of SWAT
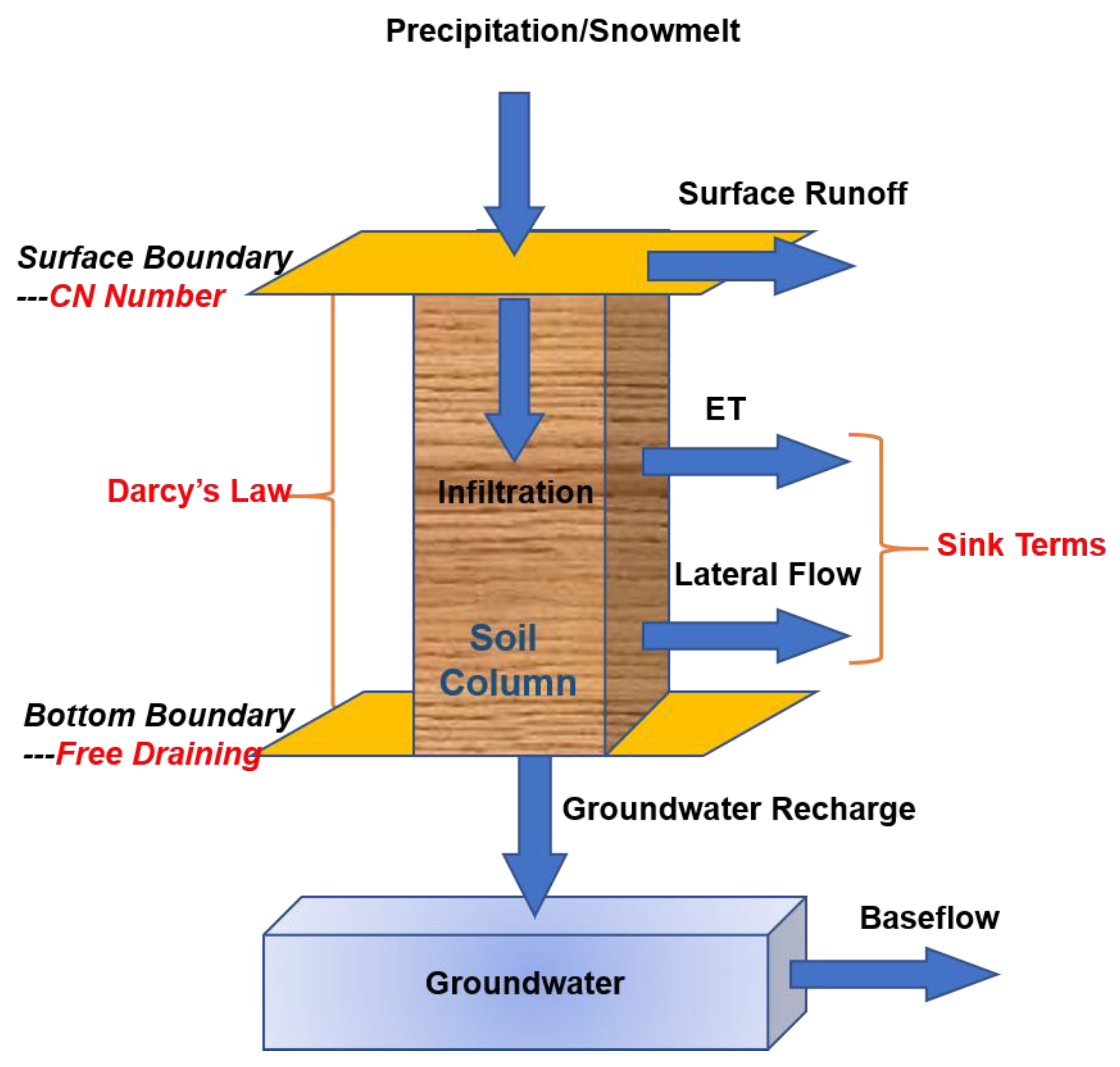
2.3. RSWAT
2.4. SWAT Input Data and Model Constraints
2.5. Model Calibration
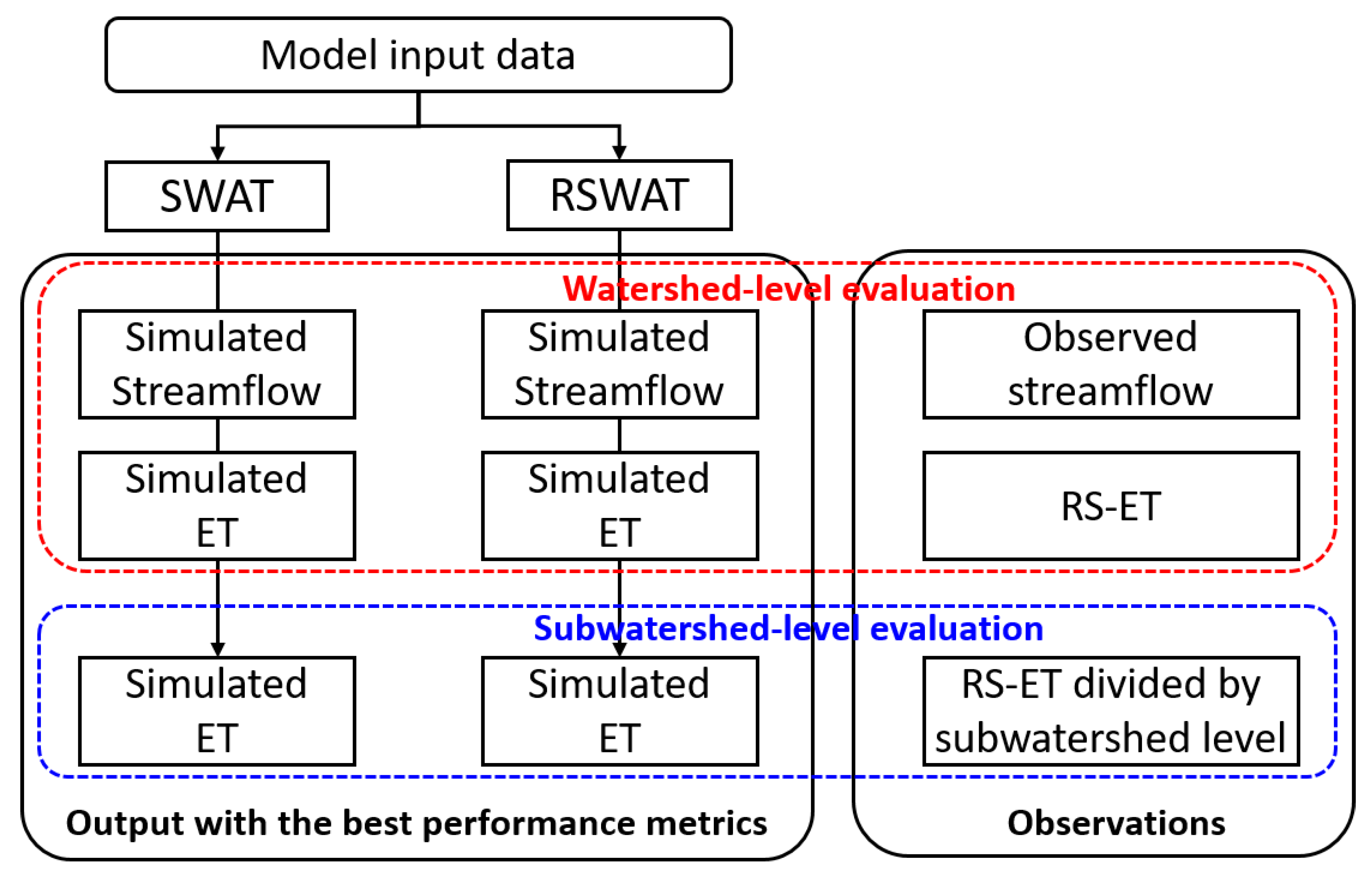
2.6. Comparing the Prediction Capacity of SWAT and RSWAT
3. Results and Discussion
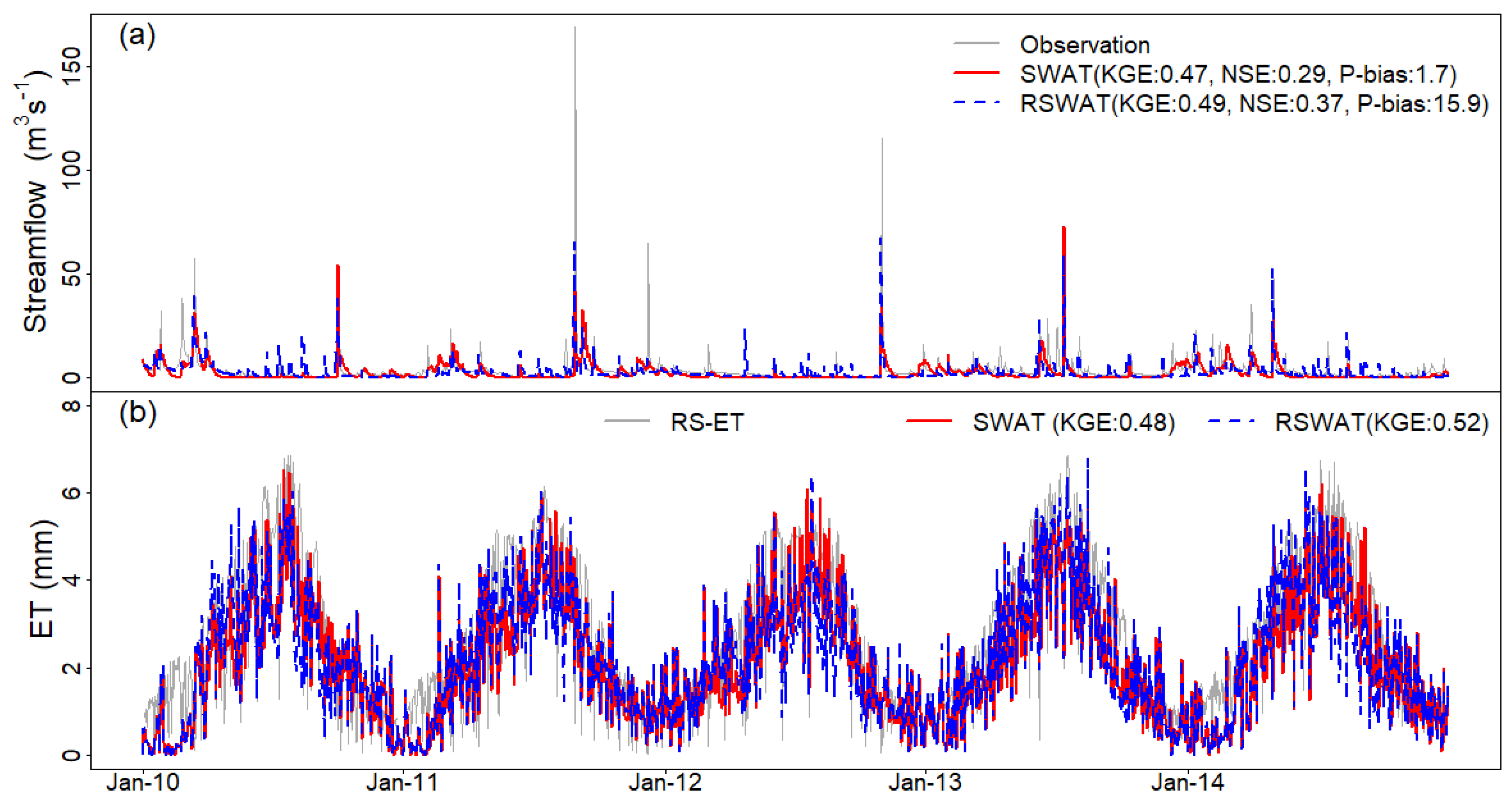
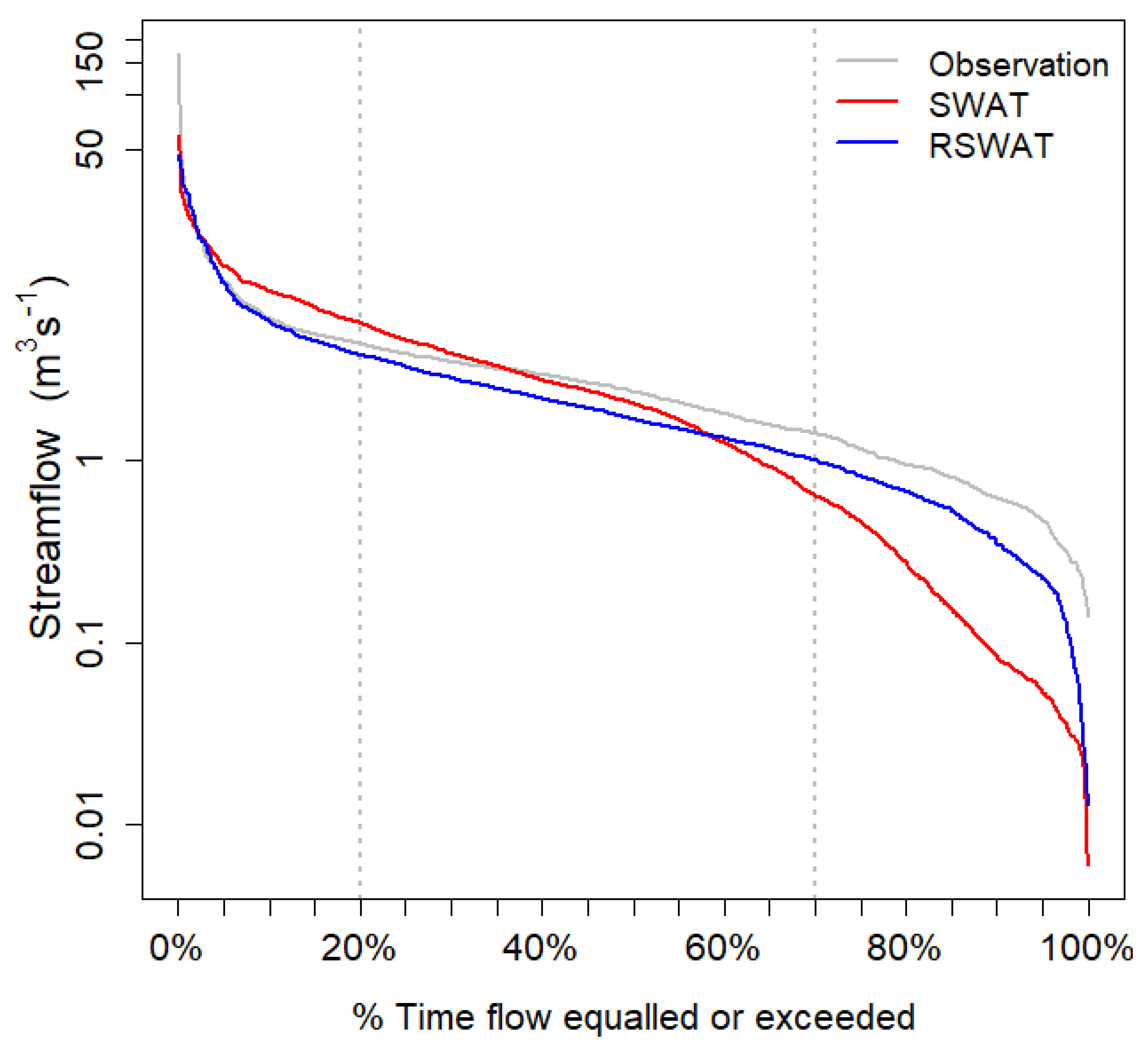
3.1. Streamflow and ET Predictions at the Watershed Level
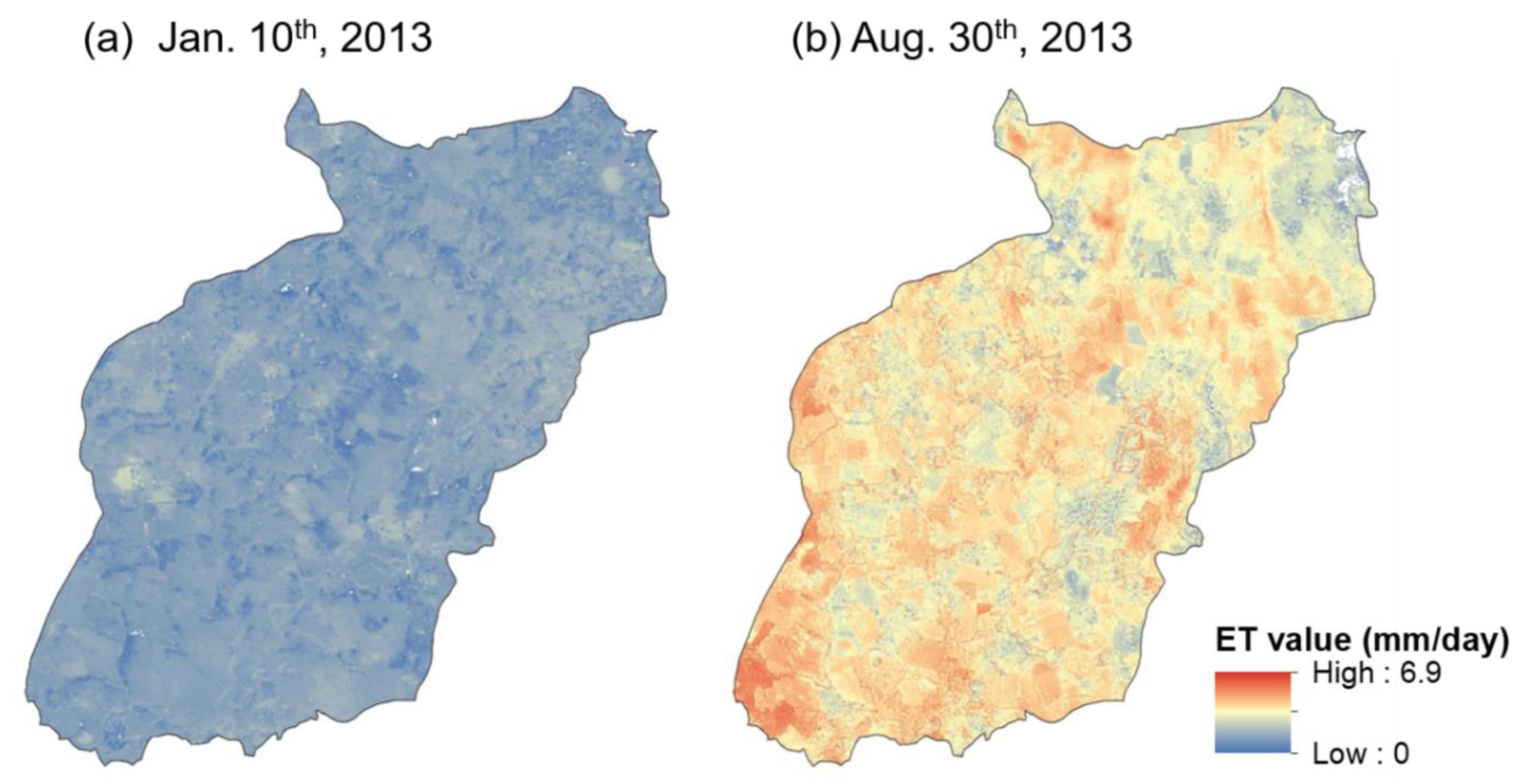
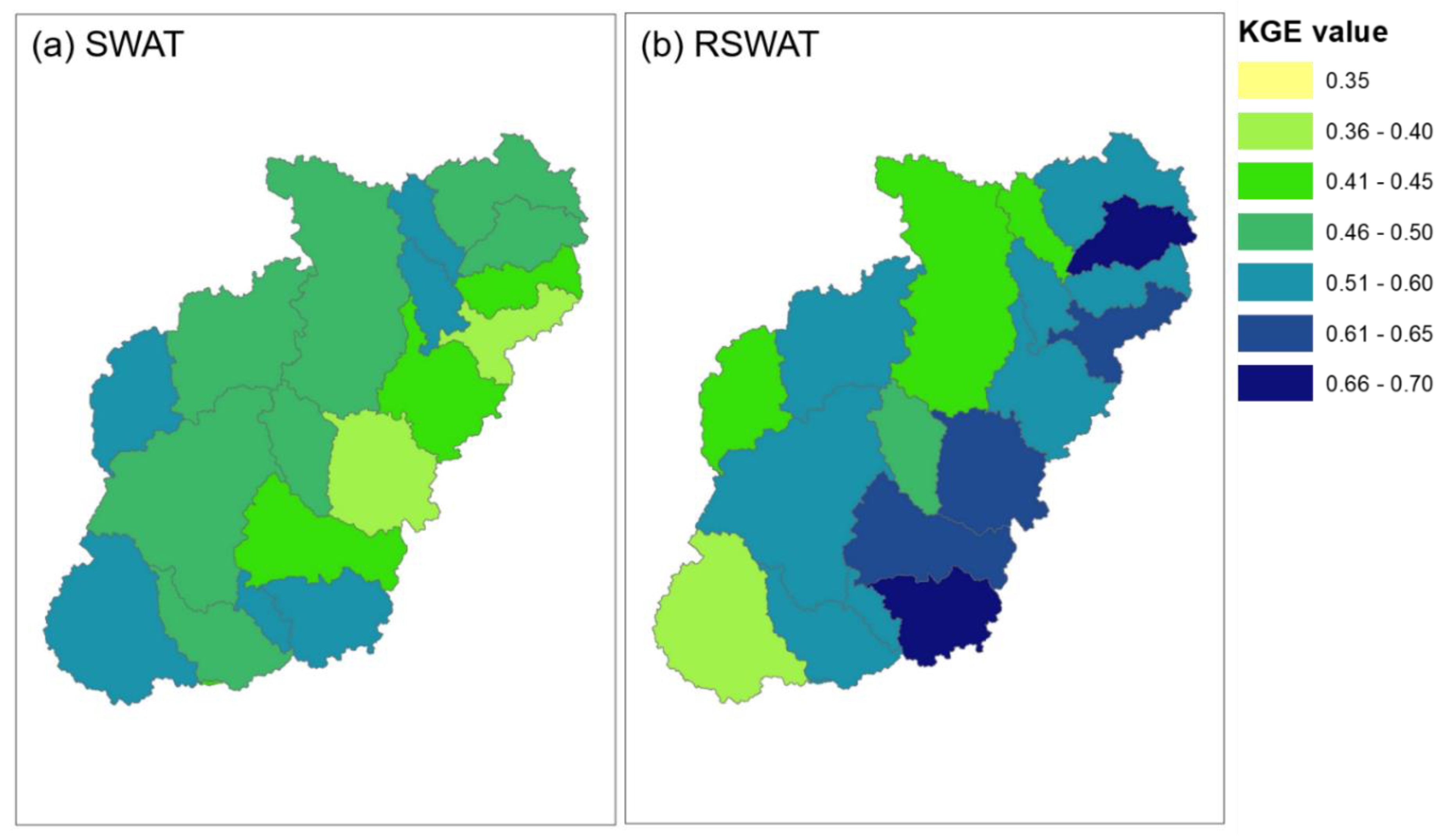
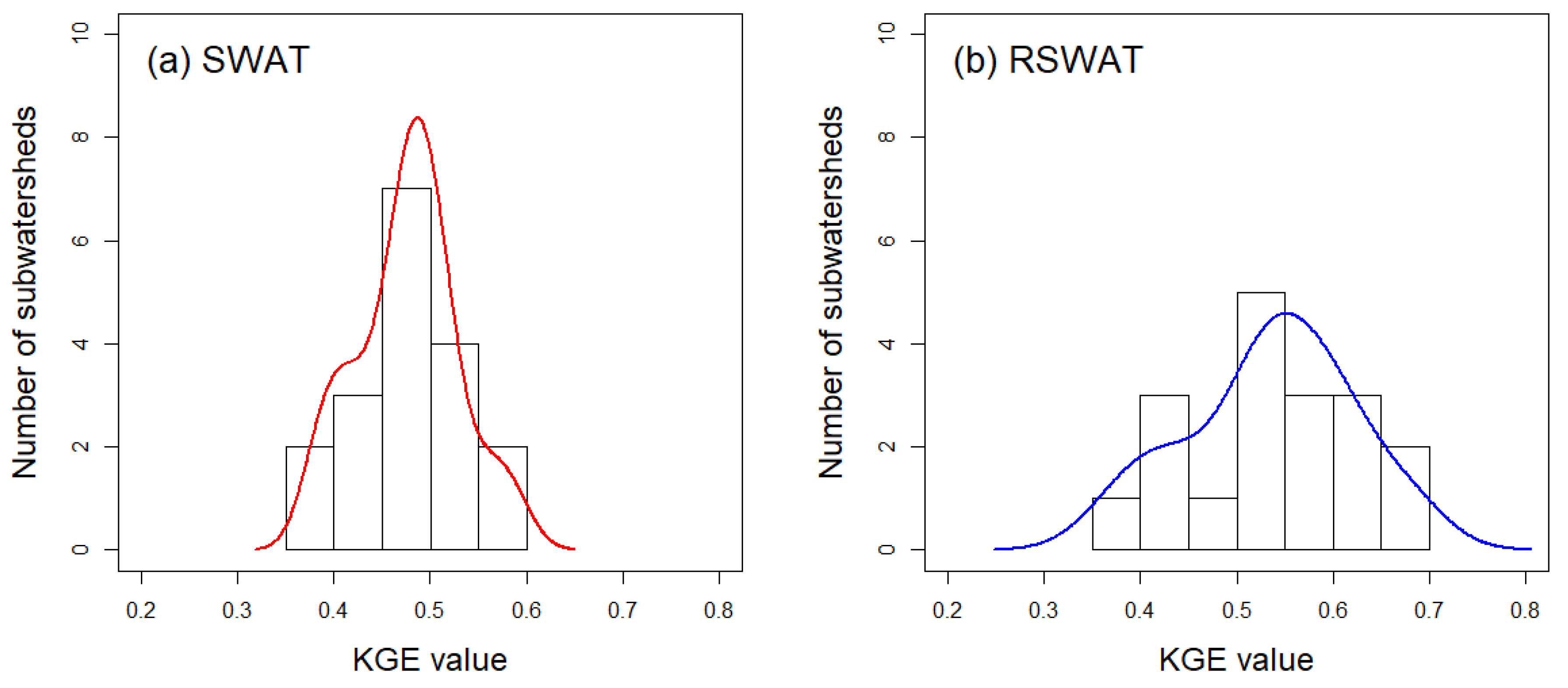
3.2. ET Predictions at the Subwatershed Level
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cosgrove, W.J.; Loucks, D.P. Water management: Current and future challenges and research directions. Water Resour. Res. 2015, 4823–4839. [Google Scholar] [CrossRef]
- Brown, C.M.; Lund, J.R.; Cai, X.; Reed, P.M.; Zagona, E.A.; Ostfeld, A.; Hall, J.; Characklis, G.W.; Yu, W.; Brekke, L. The future of water resources systems analysis: Toward a scientific framework for sustainable water management. Water Resour. Res. 2015, 51, 6110–6124. [Google Scholar] [CrossRef]
- Poff, N.L.; Brown, C.M.; Grantham, T.E.; Matthews, J.H.; Palmer, M.A.; Spence, C.M.; Wilby, R.L.; Haasnoot, M.; Mendoza, G.F.; Dominique, K.C.; et al. Sustainable water management under future uncertainty with eco-engineering decision scaling. Nat. Clim. Chang. 2016, 25–34. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Kirchner, J.W. Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology. Water Resour. Res. 2006, 42, W03S04. [Google Scholar] [CrossRef]
- Farmer, W.H.; Vogel, R.M. On the deterministic and stochastic use of hydrologic models. Water Resour. Res. 2016, 52, 5619–5633. [Google Scholar] [CrossRef]
- Whittaker, G.; Confesor, R.; Di Luzio, M.; Arnold, J.G. Detection of overparameterization and overfitting in an automatic calibration of SWAT. Trans. ASABE 2010, 53, 1487–1499. [Google Scholar] [CrossRef]
- Beven, K. Towards an alternative blueprint for a physically based digitally simulated hydrologic response modelling system. Hydrol. Process. 2002, 16, 189–206. [Google Scholar] [CrossRef]
- Yan, B.; Fang, N.F.; Zhang, P.C.; Shi, Z.H. Impacts of land use change on watershed streamflow and sediment yield: An assessment using hydrologic modelling and partial least squares regression. J. Hydrol. 2013, 484, 26–37. [Google Scholar] [CrossRef]
- Yen, H.; Bailey, R.T.; Arabi, M.; Ahmadi, M.; White, M.J.; Arnold, J.G. The Role of Interior Watershed Processes in Improving Parameter Estimation and Performance of Watershed Models. J. Environ. Qual. 2014, 43, 1601–1613. [Google Scholar] [CrossRef] [PubMed]
- Seibert, J.; McDonnell, J.J. On the dialog between experimentalist and modeler in catchment hydrology: Use of soft data for multicriteria model calibration. Water Resour. Res. 2002, 38, 1241. [Google Scholar] [CrossRef]
- Arnold, J.G.; Youssef, M.A.; Yen, H.; White, M.J.; Sheshukov, A.Y.; Sadeghi, A.M.; Moriasi, D.N.; Steiner, J.L.; Amatya, D.M.; Skaggs, R.W.; et al. Hydrological processes and model representation: Impact of soft data on calibration. Trans. ASABE 2015, 58, 1637–1660. [Google Scholar] [CrossRef]
- Wambura, F.J.; Dietrich, O.; Lischeid, G. Improving a distributed hydrological model using evapotranspiration-related boundary conditions as additional constraints in a data-scarce river basin. Hydrol. Process. 2018, 32, 759–775. [Google Scholar] [CrossRef]
- Lee, S.; Yeo, I.-Y.; Lang, M.W.; McCarty, G.W.; Sadeghi, A.M.; Sharifi, A.; Jin, H.; Liu, Y. Improving the catchment scale wetland modeling using remotely sensed data. Environ. Model. Softw. 2019, 122, 104069. [Google Scholar] [CrossRef]
- Sharifi, A.; Lang, M.W.; McCarty, G.W.; Sadeghi, A.M.; Lee, S.; Yen, H.; Rabenhorst, M.C.; Jeong, J.; Yeo, I.-Y. Improving model prediction reliability through enhanced representation of wetland soil processes and constrained model auto calibration—A paired watershed study. J. Hydrol. 2016, 541, 1088–1103. [Google Scholar] [CrossRef]
- Rajib, A.; Kim, I.L.; Golden, H.E.; Lane, C.R.; Kumar, S.V.; Yu, Z.; Jeyalakshmi, S. Watershed modeling with remotely sensed big data: Modis leaf area index improves hydrology and water quality predictions. Remote Sens. 2020, 12, 2148. [Google Scholar] [CrossRef] [PubMed]
- Carvalho-Santos, C.; Marcos, B.; Nunes, J.P.; Regos, A.; Palazzi, E.; Terzago, S.; Monteiro, A.T.; Honrado, J.P. Hydrological impacts of large fires and future climate: Modeling approach supported by satellite data. Remote Sens. 2019, 11, 2823. [Google Scholar] [CrossRef]
- Tobin, K.J.; Bennett, M.E. Improving SWAT model calibration using soil MERGE (SMERGE). Water 2020, 12, 2039. [Google Scholar] [CrossRef]
- Khatami, S.; Peel, M.C.; Peterson, T.J.; Western, A.W. Equifinality and Flux Mapping: A New Approach to Model Evaluation and Process Representation Under Uncertainty. Water Resour. Res. 2019, 55, 8922–8941. [Google Scholar] [CrossRef]
- Cho, K.H.; Pachepsky, Y.A.; Kim, J.H.; Kim, J.W.; Park, M.H. The modified SWAT model for predicting fecal coliforms in the Wachusett Reservoir Watershed, USA. Water Res. 2012, 46, 4750–4760. [Google Scholar] [CrossRef] [PubMed]
- Qi, J.; Li, S.; Li, Q.; Xing, Z.; Bourque, C.P.A.; Meng, F.R. A new soil-temperature module for SWAT application in regions with seasonal snow cover. J. Hydrol. 2016, 538, 863–877. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Dietrich, J. Modification of the SWAT model to simulate regional groundwater flow using a multicell aquifer. Hydrol. Process. 2018, 32, 939–953. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, X.; Lee, S.; Moglen, G.E.; Sadeghi, A.M.; McCarty, G.W. A coupled surface water storage and subsurface water dynamics model in SWAT for characterizing hydroperiod of geographically isolated wetlands. Adv. Water Resour. 2019, 131, 103380. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, W.; Wang, X. Development of a SWAT extension module to simulate riparian wetland hydrologic processes at a watershed scale. Hydrol. Process. 2008, 22, 2901–2915. [Google Scholar] [CrossRef]
- Qi, J.; Du, X.; Zhang, X.; Lee, S.; Wu, Y.; Deng, J.; Moglen, G.E.; Sadeghi, A.M.; McCarty, G.W. Modeling riverine dissolved and particulate organic carbon fluxes from two small watersheds in the northeastern United States. Environ. Model. Softw. 2020, 124, 104601. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, X.; Lee, S.; Wu, Y.; Moglen, G.E.; McCarty, G.W. Modeling sediment diagenesis processes on riverbed to better quantify aquatic carbon fluxes and stocks in a small watershed of the Mid-Atlantic region. Carbon Balance Manag. 2020, 15, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Du, X.; Luo, W. Incorporation of the simplified equilibrium temperature approach in a hydrodynamic and water quality model—CE-QUAL-W2. Water Sci. Technol. Water Supply 2019, 19, 156–164. [Google Scholar] [CrossRef]
- Evenson, G.R.; Golden, H.E.; Lane, C.R.; D’Amico, E. Geographically isolated wetlands and watershed hydrology: A modified model analysis. J. Hydrol. 2015, 529, 240–256. [Google Scholar] [CrossRef]
- Qi, J.; Lee, S.; Zhang, X.; Yang, Q.; McCarty, G.W.; Moglen, G.E. Effects of surface runoff and infiltration partition methods on hydrological modeling: A comparison of four schemes in two watersheds in the Northeastern US. J. Hydrol. 2020, 581, 124415. [Google Scholar] [CrossRef]
- Kuczera, G.; Mroczkowski, M. Assessment of hydrologic parameter uncertainty and the worth of multiresponse data. Water Resour. Res. 1998, 34, 1481–1489. [Google Scholar] [CrossRef]
- Lee, S.; McCarty, W.G.; Lang, W.M.; Li, X. Overview of the USDA Mid-Atlantic regional wetland conservation effects assessment project. J. Soil Water Conserv. 2020, 75, 684–694. [Google Scholar] [CrossRef]
- Hively, W.D.; Lee, S.; Sadeghi, A.M.; McCarty, G.W.; Lamb, B.T.; Soroka, A.; Keppler, J.; Yeo, I.Y.; Moglen, G.E. Estimating the effect of winter cover crops on nitrogen leaching using cost-share enrollment data, satellite remote sensing, and Soil and Water Assessment Tool (SWAT) modeling. J. Soil Water Conserv. 2020, 75, 362–375. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, X.; McCarty, G.W.; Sadeghi, A.M.; Cosh, M.H.; Zeng, X.; Gao, F.; Daughtry, C.S.T.; Huang, C.; Lang, M.W.; et al. Assessing the performance of a physically-based soil moisture module integrated within the Soil and Water Assessment Tool. Environ. Model. Softw. 2018, 109, 329–341. [Google Scholar] [CrossRef]
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Wagener, T.; Sivapalan, M.; Troch, P.; Woods, R. Catchment Classification and Hydrologic Similarity. Geogr. Compass 2007, 1, 901–931. [Google Scholar] [CrossRef]
- Yeo, I.-Y.; Lee, S.; Sadeghi, A.M.; Beeson, P.C.; Hively, W.D.; McCarty, G.W.; Lang, M.W. Assessing winter cover crop nutrient uptake efficiency using a water quality simulation model. Hydrol. Earth Syst. Sci. 2014, 18, 5239–5253. [Google Scholar] [CrossRef]
- Lee, S.; McCarty, G.W.; Moglen, G.E.; Lang, M.W.; Nathan Jones, C.; Palmer, M.; Yeo, I.-Y.; Anderson, M.; Sadeghi, A.M.; Rabenhorst, M.C. Seasonal drivers of geographically isolated wetland hydrology in a low-gradient, Coastal Plain landscape. J. Hydrol. 2020, 583, 124608. [Google Scholar] [CrossRef]
- Wolman, M.G. Water for Maryland’s Future: What We Must Do Today; Maryland Department of the Environment: Baltimore, MD, USA, 2008.
- Lee, S.; Sadeghi, A.M.; McCarty, G.W.; Baffaut, C.; Lohani, S.; Duriancik, L.F.; Thompson, A.; Yeo, I.-Y.; Wallace, C. Assessing the suitability of the Soil Vulnerability Index (SVI) on identifying croplands vulnerable to nitrogen loss using the SWAT model. Catena 2018, 167. [Google Scholar] [CrossRef]
- Neitsch, S.; Arnold, J.; Kiniry, J.; Williams, J. Soil & Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011.
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Oleson, K.; Bonan, G.B.; Levis, S.; Thornton, P.; Vertenstein, M.; Yang, Z. Technical Description of the Community Land Model (CLM); National Center for Atmospheric Research: Boulder, CO, USA, 2004. [Google Scholar]
- Clapp, R.B.; Hornberger, G.M. Empirical equations for some soil hydraulic properties. Water Resour. Res. 1978, 14, 601–604. [Google Scholar] [CrossRef]
- Cosby, B.J.; Hornberger, G.M.; Clapp, R.B.; Ginn, T.R. A Statistical Exploration of the Relationships of Soil Moisture Characteristics to the Physical Properties of Soils. Water Resour. Res. 1984, 20, 682–690. [Google Scholar] [CrossRef]
- Zeng, X.; Decker, M. Improving the numerical solution of soil moisture-based Richards equation for land models with a deep or shallow water table. J. Hydrometeorol. 2009, 10, 308–319. [Google Scholar] [CrossRef]
- Xia, Y.; Mitchell, K.; Ek, M.; Cosgrove, B.; Sheffield, J.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; Livneh, B.; et al. Continental-scale water and energy flux analysis and validation for North American Land Data Assimilation System project phase 2 (NLDAS-2): 2. Validation of model-simulated streamflow. J. Geophys. Res. Atmos. 2012, 117, 1–27. [Google Scholar] [CrossRef]
- Lee, S.; Yeo, I.-Y.; Sadeghi, A.M.; McCarty, G.W.; Hively, W.D.; Lang, M.W. Impacts of watershed characteristics and crop rotations on winter cover crop nitrate-nitrogen uptake capacity within agricultural watersheds in the Chesapeake Bay region. PLoS ONE 2016, 11, e0157637. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Anderson, M.C.; Gao, F.; Hain, C.; Alfieri, J.G.; Sharifi, A.; McCarty, G.W.; Yang, Y.; Yang, Y.; Kustas, W.P.; et al. Investigating water use over the Choptank River Watershed using a multisatellite data fusion approach. Water Resour. Res. 2017, 53, 5298–5319. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. J. Geophys. Res. Atmos. 2007, 112, D10117. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Yeo, I.-Y.; Lee, S.; Lang, M.W.; Yetemen, O.; McCarty, G.W.; Sadeghi, A.M.; Evenson, G. Mapping landscape-level hydrological connectivity of headwater wetlands to downstream waters: A catchment modeling approach—Part 2. Sci. Total Environ. 2019, 653, 1557–1570. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Barnhart, B.L. SWAT hydrologic model parameter uncertainty and its implications for hydroclimatic projections in snowmelt-dependent watersheds. J. Hydrol. 2014, 519, 2081–2090. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Records, R.M.; Arabi, M.; Fassnacht, S.R.; Duffy, W.G.; Ahmadi, M.; Hegewisch, K.C. Climate change and wetland loss impacts on a western river’s water quality. Hydrol. Earth Syst. Sci. 2014, 18, 4509–4527. [Google Scholar] [CrossRef]
- Zambrano, M.B. Package “hydroGOF”: Goodness-of-Fit Functions for Comparison of Simulated and Observed Hydrological Time Series. R Packag. version 0.3-8. 2017. Available online: http://www.rforge.net/hydroGOF/ (accessed on 23 February 2021).
- Winchell, M.; Srinivasan, R.; Di Luzio, M.; Arnold, J. ArcSWAT Interface for SWAT 2005: User’s Guide; Texas Agricultural Experiment Station and Agricultural Research Service-US Department of Agriculture: Temple, TX, USA, 2007.
- Poméon, T.; Diekkrüger, B.; Springer, A.; Kusche, J.; Eicker, A. Multi-objective validation of SWAT for sparsely-gaugedWest African river basins—A remote sensing approach. Water 2018, 10, 451. [Google Scholar] [CrossRef]
- Becker, R.; Koppa, A.; Schulz, S.; Usman, M.; Aus der Beek, T.; Schüth, C. Spatially distributed model calibration of a highly managed hydrological system using remote sensing-derived ET data. J. Hydrol. 2019, 577, 123944. [Google Scholar] [CrossRef]
- Rajib, A.; Evenson, G.R.; Golden, H.E.; Lane, C.R. Hydrologic model predictability improves with spatially explicit calibration using remotely sensed evapotranspiration and biophysical parameters. J. Hydrol. 2018, 567, 668–683. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Zhang, X. Improving SWAT for simulating water and carbon fluxes of forest ecosystems. Sci. Total Environ. 2016, 569–570, 1478–1488. [Google Scholar] [CrossRef] [PubMed]
- Sinnathamby, S.; Douglas-Mankin, K.R.; Craige, C. Field-scale calibration of crop-yield parameters in the Soil and Water Assessment Tool (SWAT). Agric. Water Manag. 2017, 180, 61–69. [Google Scholar] [CrossRef]
- Tasdighi, A.; Arabi, M.; Harmel, D. A probabilistic appraisal of rainfall-runoff modeling approaches within SWAT in mixed land use watersheds. J. Hydrol. 2018, 564, 476–489. [Google Scholar] [CrossRef]
- Qi, J.; Wang, Q.; Zhang, X. On the use of NLDAS2 weather data for hydrologic modeling in the Upper Mississippi River Basin. Water 2019, 11, 960. [Google Scholar] [CrossRef]
- Shahrban, M.; Walker, J.P.; Wang, Q.J.; Robertson, D.E. On the importance of soil moisture in calibration of rainfall–runoff models: Two case studies. Hydrol. Sci. J. 2018, 63, 1292–1312. [Google Scholar] [CrossRef]
- Yeo, I.-Y.; Lang, M.W.; Lee, S.; McCarty, G.W.; Sadeghi, A.M.; Yetemen, O.; Huang, C. Mapping landscape-level hydrological connectivity of headwater wetlands to downstream waters: A geospatial modeling approach—Part 1. Sci. Total Environ. 2019, 653, 1546–1556. [Google Scholar] [CrossRef] [PubMed]
- Tobin, K.J.; Bennett, M.E. Improving alpine summertime streamflow simulations by the incorporation of evapotranspiration data. Water 2019, 11, 112. [Google Scholar] [CrossRef]
- Abiodun, O.O.; Guan, H.; Post, V.E.A.; Batelaan, O. Comparison of MODIS and SWAT evapotranspiration over a complex terrain at different spatial scales. Hydrol. Earth Syst. Sci. 2018, 22, 2775–2794. [Google Scholar] [CrossRef]
- Mendiguren, G.; Koch, J.; Stisen, S. Spatial pattern evaluation of a calibrated national hydrological model—A remote-sensing-based diagnostic approach. Hydrol. Earth Syst. Sci. 2017, 21, 5987–6005. [Google Scholar] [CrossRef]
- Zou, M.; Kang, S.; Niu, J.; Lu, H. Untangling the effects of future climate change and human activity on evapotranspiration in the Heihe agricultural region, Northwest China. J. Hydrol. 2020, 585, 124323. [Google Scholar] [CrossRef]
- Aouissi, J.; Benabdallah, S.; Lili Chabaâne, Z.; Cudennec, C. Evaluation of potential evapotranspiration assessment methods for hydrological modelling with SWAT—Application in data-scarce rural Tunisia. Agric. Water Manag. 2016, 174, 39–51. [Google Scholar] [CrossRef]
- Chen, M.; Gassman, P.W.; Srinivasan, R.; Cui, Y.; Arritt, R. Analysis of alternative climate datasets and evapotranspiration methods for the Upper Mississippi River Basin using SWAT within HAWQS. Sci. Total Environ. 2020, 720, 137562. [Google Scholar] [CrossRef] [PubMed]
- Herman, M.R.; Nejadhashemi, A.P.; Abouali, M.; Hernandez-Suarez, J.S.; Daneshvar, F.; Zhang, Z.; Anderson, M.C.; Sadeghi, A.M.; Hain, C.R.; Sharifi, A. Evaluating the role of evapotranspiration remote sensing data in improving hydrological modeling predictability. J. Hydrol. 2018, 556, 39–49. [Google Scholar] [CrossRef]
- Parajuli, P.B.; Jayakody, P.; Ouyang, Y. Evaluation of Using Remote Sensing Evapotranspiration Data in SWAT. Water Resour. Manag. 2018, 32, 985–996. [Google Scholar] [CrossRef]
- Kim, H.; Parinussa, R.; Konings, A.G.; Wagner, W.; Cosh, M.H.; Lakshmi, V.; Zohaib, M.; Choi, M. Global-scale assessment and combination of SMAP with ASCAT (active) and AMSR2 (passive) soil moisture products. Remote Sens. Environ. 2018, 204, 260–275. [Google Scholar] [CrossRef]
| Data Type | Source | Description | Year |
|---|---|---|---|
| Climatic | NLDAS2 | Hourly precipitation, temperature, solar radiation, wind speed, and humidity | 2008–2014 |
| DEM | MD-DNR | LiDAR-based 1-m resolution | 2006 |
| Land use | USDA-NASS | Cropland Data Layer (CDL) | 2008–2012 |
| MRLC | National Land Cover Database (NLCD) | 2006 | |
| USDA-FSA-APFO | National Agricultural Imagery Program digital Orthophoto quad imagery | 1998 | |
| US Census Bureau | TIGER road map | 2010 | |
| Soils | USDA-NRCS | Soil Survey Geographical Database (SSURGO) | 2012 |
| Streamflow | USGS | Daily streamflow | 2010–2014 |
| ET | Sun et al. [48] | Daily ET | 2010–2014 |
| Parameter | Description (Units) | Range | SWAT | RSWAT |
|---|---|---|---|---|
| CN | SCS runoff curve number | −20–20% | 0% | −3% |
| GW_DELAY | Groundwater delay (days) | 0–100 | 0.14 | 88.63 |
| ALPHA_BF | Baseflow alpha factor (days−1) | 0–1 | 0.43 | 0.83 |
| GWQMN | Threshold depth of water in the shallow aquifer required for return flow to occur (mm H2O) | 0–5000 | 13.85 | 1226.97 |
| GW_REVAP | Groundwater “revap” coefficient | 0.02–0.2 | 0.17 | 0.15 |
| REVAPMN | Threshold depth of water in the shallow aquifer for “revap” to occur (mm H2O) | 0–500 | 450.95 | 68.69 |
| SOL_AWC | Available water capacity of the soil layer (mm H2O ·mm soil−1) | −50–50% | −26% | −43% |
| CH_K2 | Manning’s “n” value for the main channel | 0–150 | 92.07 | 145.11 |
| CH_N2 | Manning’s “n” value for the tributary channels | 0.01–0.3 | 0.17 | 0.03 |
| SURLAG | Surface runoff lag coefficient | 0.5–24 | 22.48 | 0.85 |
| ESCO | Soil evaporation compensation factor | 0–1 | 0.92 | 0.69 |
| EPCO | Plant uptake compensation factor | 0–1 | 0.21 | 0.40 |
| CANM# | Maximum canopy storage (mm H2O) | 0–1 | 0.72 | 0.42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Qi, J.; Kim, H.; McCarty, G.W.; Moglen, G.E.; Anderson, M.; Zhang, X.; Du, L. Utility of Remotely Sensed Evapotranspiration Products to Assess an Improved Model Structure. Sustainability 2021, 13, 2375. https://doi.org/10.3390/su13042375
Lee S, Qi J, Kim H, McCarty GW, Moglen GE, Anderson M, Zhang X, Du L. Utility of Remotely Sensed Evapotranspiration Products to Assess an Improved Model Structure. Sustainability. 2021; 13(4):2375. https://doi.org/10.3390/su13042375
Chicago/Turabian StyleLee, Sangchul, Junyu Qi, Hyunglok Kim, Gregory W. McCarty, Glenn E. Moglen, Martha Anderson, Xuesong Zhang, and Ling Du. 2021. "Utility of Remotely Sensed Evapotranspiration Products to Assess an Improved Model Structure" Sustainability 13, no. 4: 2375. https://doi.org/10.3390/su13042375
APA StyleLee, S., Qi, J., Kim, H., McCarty, G. W., Moglen, G. E., Anderson, M., Zhang, X., & Du, L. (2021). Utility of Remotely Sensed Evapotranspiration Products to Assess an Improved Model Structure. Sustainability, 13(4), 2375. https://doi.org/10.3390/su13042375






