Latent Heat Phase Change Heat Transfer of a Nanoliquid with Nano–Encapsulated Phase Change Materials in a Wavy-Wall Enclosure with an Active Rotating Cylinder
Abstract
1. Introduction
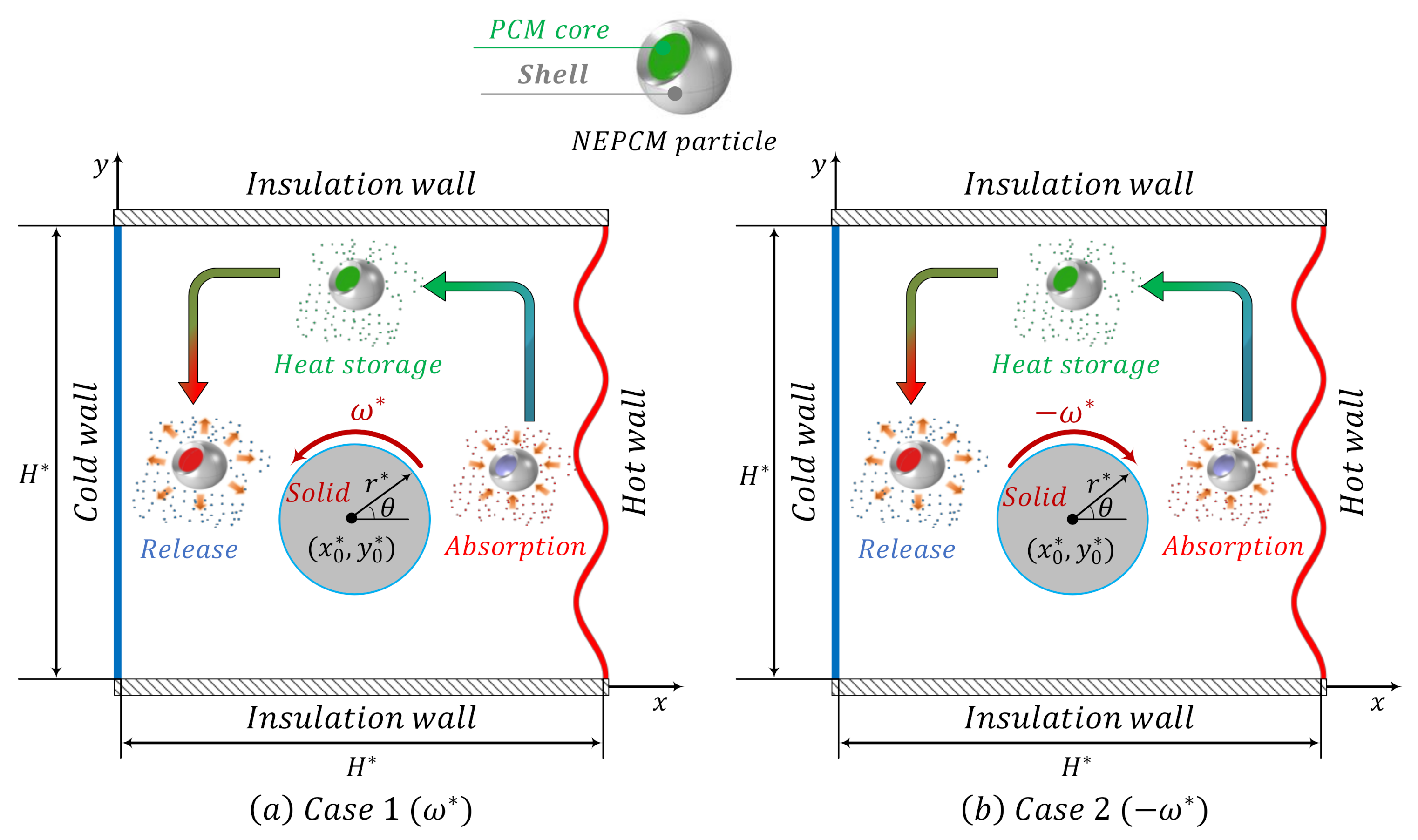
2. Problem Physics and Modeling
2.1. Problem Physics
2.2. Conservation Equations and Boundary Conditions
2.3. Bulk Properties of the Nanoliquid
2.4. Normalized Conservation Equations
2.5. Heat Transfer Rate
3. Solution Method
3.1. Numerical Method
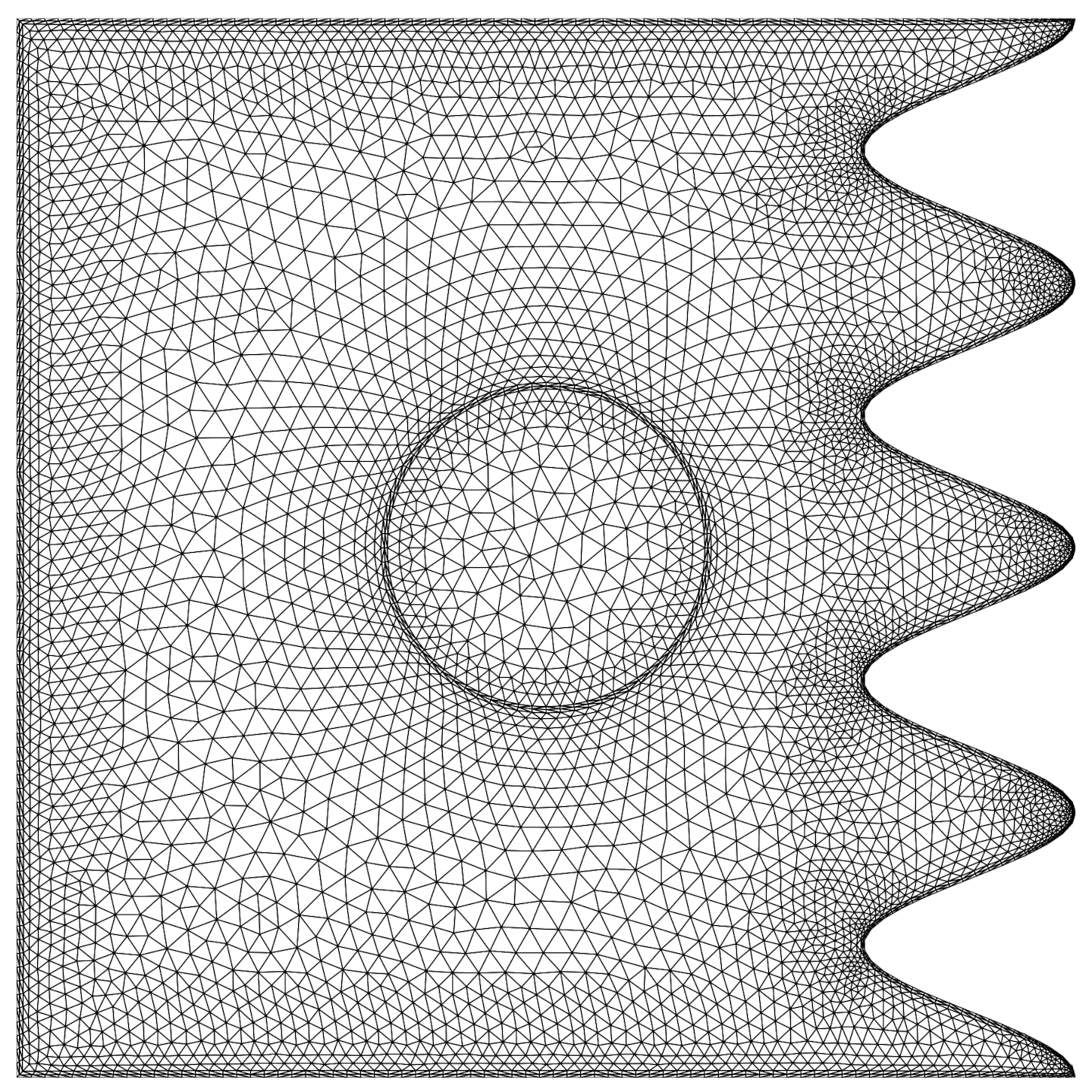
3.2. Mesh Study
3.3. Validations
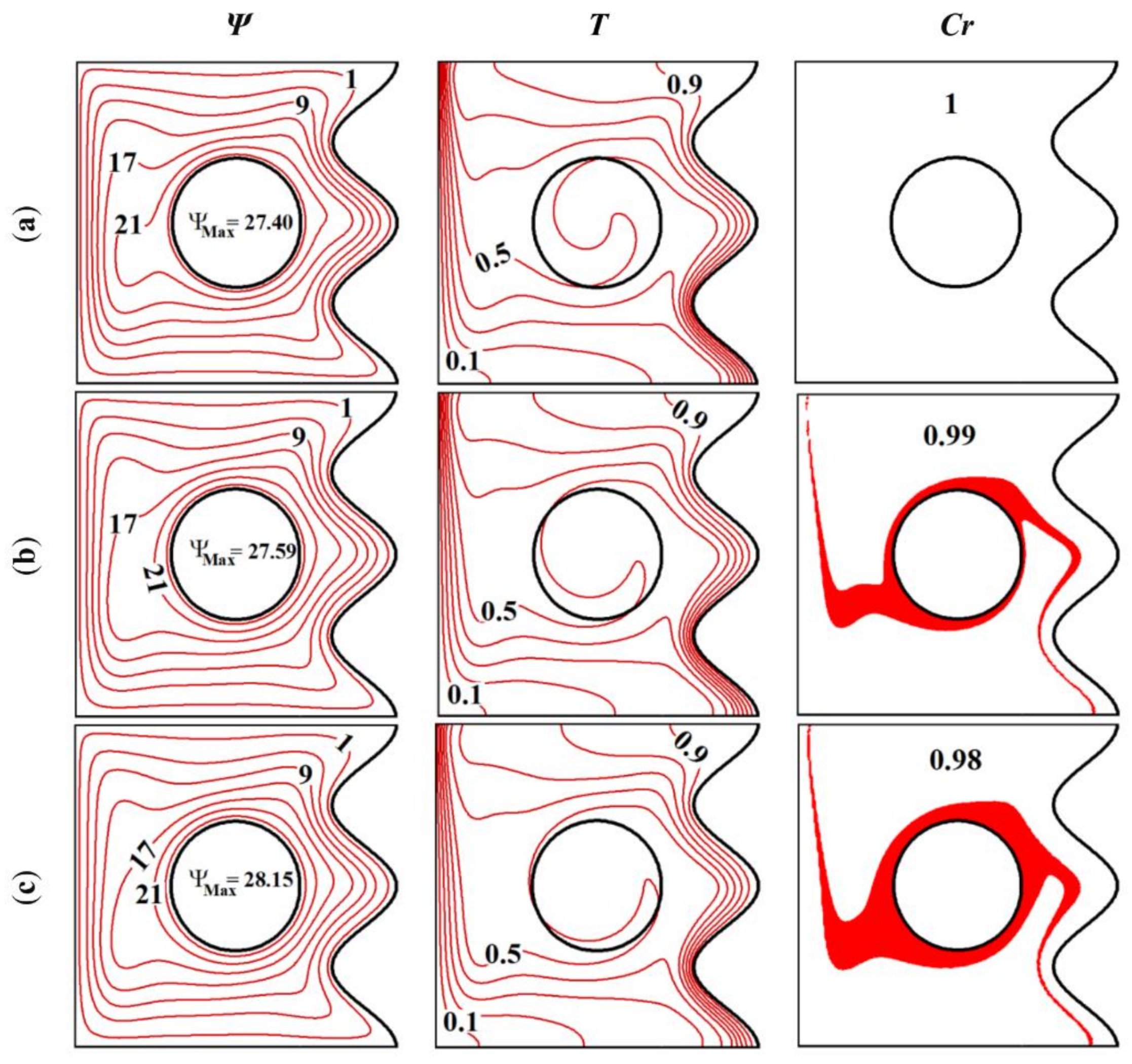
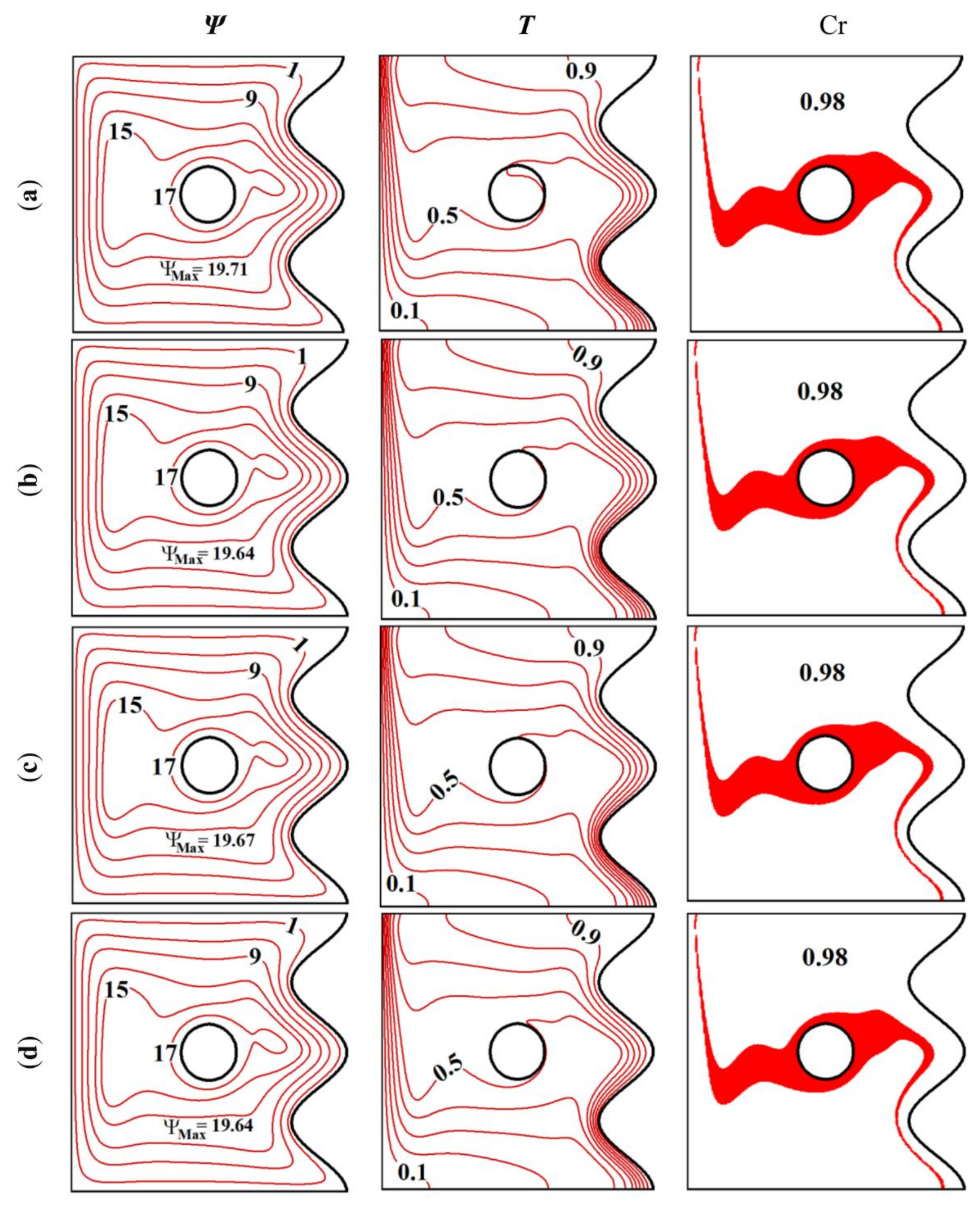
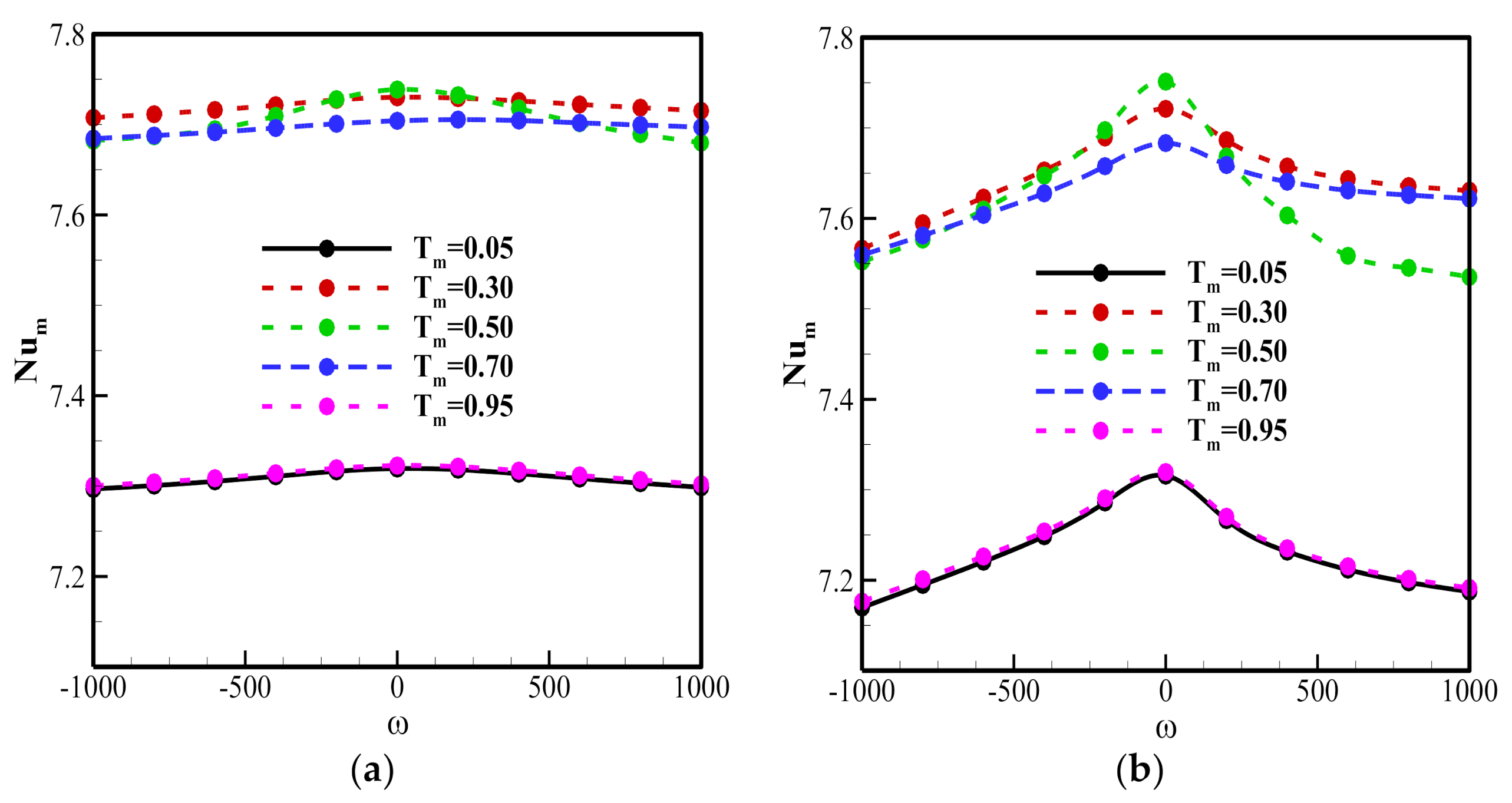
4. Simulation Results
5. Conclusions
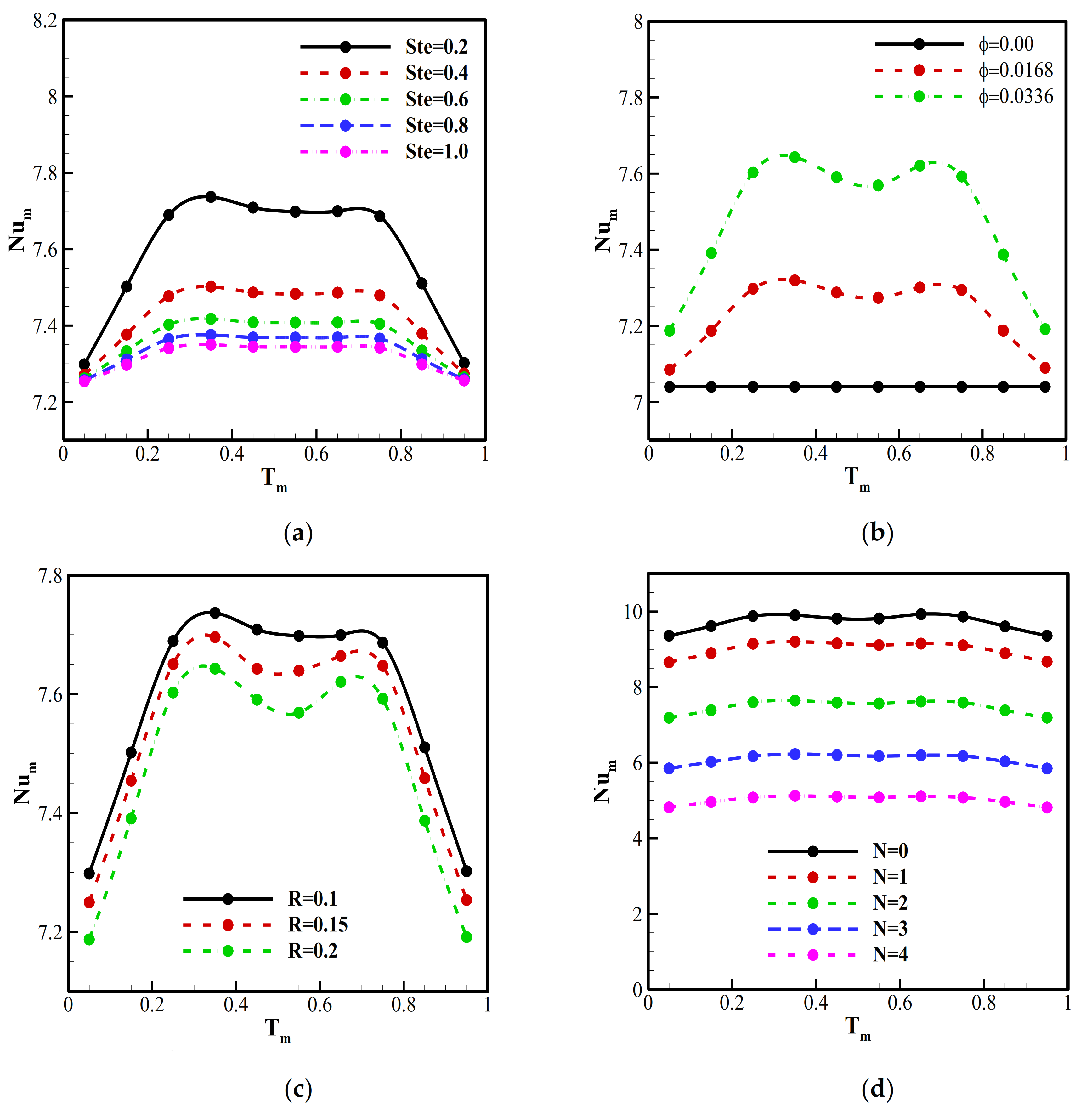
- Dispersing NEPCM particles in the base fluid enhances heat transfer. This enhancement increases with the volume fraction of the nanoparticles. A 10% increase in heat transfer can be observed when a 3.36% volume particle is used compared to the base fluid. The latent heat involved when the PCM undergoes phase change contributes to the overall heat transfer.
- The fusion temperature Tm of the NEPCM core affects the contribution of the nanoparticles to the overall heat transfer. When Tm is close to the temperature of the hot wall or the cold wall, the zone in which the core, undergoes the phase-change, is reduced. The number of NEPCM particles experiencing melting decreases and heat transfer is diminished.
- Using a larger cylinder inhibits heat transfer by reducing the space in which the fluid can flow and, consequently, the convective effects. Heat transfer is also slightly higher when the cylinder rotational velocity is close to zero. On the other hand, the thermal conductivity and the heat capacity of the cylinder presented by the parameters Rk and Rc seem to have little impact on heat transfer.
- Heat transfer is improved when the number of undulations N of the wavy wall is reduced and reaches its maximum when the hot wall is flat. This is due to the presence of a thermal boundary layer as well as the available space between the cylinder and the surrounding fluid when N is increased, hindering heat transfer.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary
| Latin letters | |
| A | the hot wall wave amplitude |
| C | the specific heat (kJ/kg.K) |
| Cr | the ratio of the heat capacity of the nanoliquid to the base liquid |
| f | the normalized fusion function |
| g | the gravity constant (m/s2) |
| H | the enclosure height (m) |
| k | thermal conductivity coefficient (W/m.K) |
| N | the number of oscillations |
| Nu | Nusselt number |
| p | the suspension pressure field (Pa) |
| P | non-dimensional suspension pressure field |
| Pr | Prandtl number |
| R | the cylinder radius |
| Ra | Rayleigh number |
| Rc | the heat capacity ratio of the cylinder to the base liquid |
| Rk | the thermal conductivity ratio of the cylinder to the base liquid |
| Ri | Richardson number |
| Ste | Stefan number |
| T | the temperature (°C) |
| Tm | the dimensionless fusion temperature |
| TMr | the melting temperature range (°C) |
| u | x axis velocity component (m/s) |
| U | X axis non-dimensional velocity component |
| v | y axis velocity component (m/s) |
| V | Y axis non-dimensional velocity component |
| x | x-Cartesian coordinate (m) |
| X | dimensionless X-Cartesian coordinate |
| y | y-Cartesian coordinate (m) |
| Y | dimensionless Y-Cartesian coordinate |
| Greek symbols | |
| α | the thermal diffusivity (m2/s) |
| β | the volumetric thermal expansion coefficient(1/K) |
| δT | the non-dimensional phase change band |
| ε | the non-dimensional ratio of the heat capacity |
| μ | the dynamic viscosity (kg s/m) |
| ζ | the core-shell weight ratio of the particles |
| ρ | density (kg/m3) |
| ϕ | the NEPCM volume fraction |
| Ψ | the stream function |
| ω | cylinder rotational speed |
| Subscript | |
| bl | the base liquid |
| c | the cold wall |
| c | the PCM core |
| cy | the cylinder |
| h | the hot wall |
| l | local |
| m | mean |
| na | the NEPCM nanoparticles |
| nl | the nanoliquid |
| r | the dimensionless ratios |
| s | the shell of NEPCM particle |
| * | normalized form of the parameters |
References
- Peterson, G.P.; Li, C.H. Heat and Mass Transfer in Fluids with Nanoparticle Suspensions. Adv. Heat Transf. 2006, 39, 257–376. [Google Scholar] [CrossRef]
- Jang, S.P.; Choi, S.U.S. Effects of Various Parameters on Nanofluid Thermal Conductivity. J. Heat Transf. 2007, 129, 617–623. [Google Scholar] [CrossRef]
- Wen, D.; Ding, Y. Natural Convective Heat Transfer of Suspensions of Titanium Dioxide Nanoparticles (Nanofluids). IEEE Trans. Nanotechnol. 2006, 5, 220–227. [Google Scholar]
- Sheikholeslami, M.; Mehryan, S.A.M.; Shafee, A.; Sheremet, M.A. Variable magnetic forces impact on magnetizable hybrid nanofluid heat transfer through a circular cavity. J. Mol. Liquids 2019, 277, 388–396. [Google Scholar] [CrossRef]
- Reza-E-Rabbi, S.; Ahmmed, S.F.; Arifuzzaman, S.; Sarkar, T.; Khan, M.S. Computational modelling of multiphase fluid flow behaviour over a stretching sheet in the presence of nanoparticles. Eng. Sci. Technol. Int. J. 2020, 23, 605–617. [Google Scholar] [CrossRef]
- Wakif, A.; Chamkha, A.; Thumma, T.; Animasaun, I.; Sehaqui, R. Thermal radiation and surface roughness effects on the thermo-magneto-hydrodynamic stability of alumina–copper oxide hybrid nanofluids utilizing the generalized Buongiorno’s nanofluid model. J. Therm. Anal. Calorim. 2020, 1–20. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Alsabery, A.I.; Hashim, I. Internal heat generation effect on transient natural convection in a nanofluid-saturated local thermal non-equilibrium porous inclined cavity. Phys. A Stat. Mech. Appl. 2018, 509, 275–293. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. Effect of Local Thermal Non-equilibrium on the Onset of Convection in a Porous Medium Layer Saturated by a Nanofluid. Transp. Porous Media 2009, 83, 425–436. [Google Scholar] [CrossRef]
- Bhadauria, B.S.; Agarwal, S. Convective Transport in a Nanofluid Saturated Porous Layer With Thermal Non Equilibrium Model. Transp. Porous Media 2011, 88, 107–131. [Google Scholar] [CrossRef]
- Sun, Q.; Pop, I. Free convection in a triangle cavity filled with a porous medium saturated with nanofluids with flush mounted heater on the wall. Int. J. Therm. Sci. 2011, 50, 2141–2153. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Ismael, M.A. Conjugate heat transfer in a porous cavity filled with nanofluids and heated by a triangular thick wall. Int. J. Therm. Sci. 2013, 67, 135–151. [Google Scholar] [CrossRef]
- Sheikholeslami, M. CuO-water nanofluid flow due to magnetic field inside a porous media considering Brownian motion. J. Mol. Liquids 2018, 249, 921–929. [Google Scholar] [CrossRef]
- Xuan, Y.; LI, Q. Investigation on convective heat transfer and flow features of nanofluids. J. Heat Transf. 2003, 125, 151–155. [Google Scholar] [CrossRef]
- Wen, D.; Ding, Y. Experimental investigation into convective heat transfer of nanofluids at the entrance region under laminar flow conditions. Int. J. Heat Mass Transf. 2004, 47, 5181–5188. [Google Scholar] [CrossRef]
- Hwang, K.S.; Jang, S.P.; Choi, S.U.S. Flow and convective heat transfer characteristics of water-based Al2O3 nanofluids in fully developed laminar flow regime. Int. J. Heat Mass Transf. 2009, 52, 193–199. [Google Scholar] [CrossRef]
- Sajid, M.U.; Ali, H.M. Recent advances in application of nanofluids in heat transfer devices: A critical review. Renew. Sustain. Energy Rev. 2019, 103, 556–592. [Google Scholar] [CrossRef]
- Kant, K.; Shukla, A.; Sharma, A. Advancement in phase change materials for thermal energy storage applications. Solar Energy Mater. Solar Cells 2017, 172, 82–92. [Google Scholar] [CrossRef]
- Khan, R.J.; Bhuiyan, M.Z.H.; Ahmed, D.H. Investigation of heat transfer of a building wall in the presence of phase change material (PCM). Energy Built Environ. 2020, 1, 199–206. [Google Scholar] [CrossRef]
- Hu, W.; Song, M.; Jiang, Y.; Yao, Y.; Gao, Y. A modeling study on the heat storage and release characteristics of a phase change material based double-spiral coiled heat exchanger in an air source heat pump for defrosting. Appl. Energy 2019, 236, 877–892. [Google Scholar] [CrossRef]
- Emam, M.; Ookawara, S.; Ahmed, M. Thermal management of electronic devices and concentrator photovoltaic systems using phase change material heat sinks: Experimental investigations. Renew. Energy 2019, 141, 322–339. [Google Scholar] [CrossRef]
- Isa, M.H.M.; Zhao, X.; Yoshino, H. Preliminary study of passive cooling strategy using a combination of PCM and copper foam to increase thermal heat storage in building facade. Sustainability 2010, 2, 2365–2381. [Google Scholar] [CrossRef]
- Baek, S.; Kim, S. Determination of optimum hot-water temperatures for PCM radiant floor-heating systems based on the wet construction method. Sustainability 2018, 10, 4004. [Google Scholar] [CrossRef]
- González-Peña, D.; Alonso-deMiguel, I.; Díez-Mediavilla, M.; Alonso-Tristán, C. Experimental analysis of a novel PV/T panel with PCM and heat pipes. Sustainability 2020, 12, 1710. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Kim, T.; Lu, T.J.; Hodson, H.P. Thermal Transport in High Porosity Cellular Metal Foams. J. Thermophys. Heat Transf. 2004, 18, 309–317. [Google Scholar] [CrossRef]
- Calmidi, V.V.; Mahajan, R.L. Forced convection in high porosity metal foams. J. Heat Transf. 2000, 122, 557–565. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Lu, T.J.; Hodson, H.P. Natural convection in metal foams with open cells. Int. J. Heat Mass Transf. 2005, 48, 2452–2463. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Lu, W.; Tian, Y. Heat transfer enhancement for thermal energy storage using metal foams embedded within phase change materials (PCMs). Solar Energy 2010, 84, 1402–1412. [Google Scholar] [CrossRef]
- Siahpush, A.; O’Brien, J.; Crepeau, J. Phase change heat transfer enhancement using copper porous foam. ASME Trans. J. Heat Transf. 2008, 130, 082301–082311. [Google Scholar] [CrossRef]
- Zhu, Y.; Qin, Y.; Wei, C.; Liang, S.; Luo, X.; Wang, J.; Zhang, L. Nanoencapsulated phase change materials with polymer-SiO2 hybrid shell materials: Compositions, morphologies, and properties. Energy Convers. Manag. 2018, 164, 83–92. [Google Scholar] [CrossRef]
- Alva, G.; Huang, X.; Liu, L.; Fang, G. Synthesis and characterization of microencapsulated myristic acid–palmitic acid eutectic mixture as phase change material for thermal energy storage. Appl. Energy 2017, 203, 677–685. [Google Scholar] [CrossRef]
- Cao, L.; Tang, F.; Fang, G. Preparation and characteristics of microencapsulated palmitic acid with TiO2 shell as shape-stabilized thermal energy storage materials. Solar Energy Mater. Solar Cells 2014, 123, 183–188. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, H.; Luo, J.; Liu, Y.; Song, G.; Tang, G. Fabrication and properties of microencapsulated n-octadecane with TiO2 shell as thermal energy storage materials. Solar Energy 2016, 127, 28–35. [Google Scholar] [CrossRef]
- Peng, J.; Cheng, Q. High-Performance Nanocomposites Inspired by Nature. Adv. Mater. 2017, 29. [Google Scholar] [CrossRef] [PubMed]
- Caruso, F.; Trau, D.; Möhwald, H.; Renneberg, R. Enzyme Encapsulation in Layer-by-Layer Engineered Polymer Multilayer Capsules. Langmuir 2000, 16, 1485–1488. [Google Scholar] [CrossRef]
- Shchukin, D.G.; Zheludkevich, M.; Yasakau, K.; Lamaka, S.; Ferreira, M.G.S.; Möhwald, H. Layer-by-Layer Assembled Nanocontainers for Self-Healing Corrosion Protection. Adv. Mater. 2006, 18, 1672–1678. [Google Scholar] [CrossRef]
- Soottitantawat, A.; Yoshii, H.; Furuta, T.; Ohkawara, M.; Linko, P. Microencapsulation by Spray Drying: Influence of Emulsion Size on the Retention of Volatile Compounds. J. Food Sci. 2003, 68, 2256–2262. [Google Scholar] [CrossRef]
- Su, J.-F.; Wang, L.-X.; Ren, L. Synthesis of polyurethane microPCMs containing n-octadecane by interfacial polycondensation: Influence of styrene-maleic anhydride as a surfactant. Colloids Surfaces A Physicochem. Eng. Asp. 2007, 299, 268–275. [Google Scholar] [CrossRef]
- Fang, G.; Li, H.; Yang, F.; Liu, X.; Wu, S. Preparation and characterization of nano-encapsulated n-tetradecane as phase change material for thermal energy storage. Chem. Eng. J. 2009, 153, 217–221. [Google Scholar] [CrossRef]
- Rodríguez-Cumplido, F.; Pabón-Gelves, E.; Chejne-Jana, F. Recent developments in the synthesis of microencapsulated and nanoencapsulated phase change materials. J. Energy Storage 2019, 24. [Google Scholar] [CrossRef]
- Huu-Quan, D.; Sheremet, M.; Kamel, M.S.; Izadi, M. Investigation of thermal-hydro dynamical behavior on nano-encapsulated PCM suspension: Effect of fin position, fractioning and aspect ratio. Chem. Eng. Process. Process. Intensif. 2020, 157, 108122. [Google Scholar] [CrossRef]
- Ouertatani, N.; Cheikh, N.B.; Beya, B.B.; Lili, T.; Campo, A. Mixed convection in a double lid-driven cubic cavity. Int. J. Therm. Sci. 2009, 48, 1265–1272. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Conjugate mixed convection of nanofluid in a cubic enclosure separated with a conductive plate and having an inner rotating cylinder. Int. J. Heat Mass Transf. 2019, 139, 1000–1017. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Selimefendigil, F. MHD mixed convection of nanofluid due to an inner rotating cylinder in a 3D enclosure with a phase change material. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3559–3583. [Google Scholar] [CrossRef]
- Alnajem, M.H.S.; Alsabery, A.I.; Hashim, I. Entropy generation and natural convection in a wavy-wall cavity filled with a nanofluid and containing an inner solid cylinder. IOP Conf. Series Mater. Sci. Eng. 2019, 518. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Mohebbi, R.; Chamkha, A.J.; Hashim, I. Effect of local thermal non-equilibrium model on natural convection in a nanofluid-filled wavy-walled porous cavity containing inner solid cylinder. Chem. Eng. Sci. 2019, 201, 247–263. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Sheremet, M.A.; Chamkha, A.J.; Hashim, I. Impact of nonhomogeneous nanofluid model on transient mixed convection in a double lid-driven wavy cavity involving solid circular cylinder. Int. J. Mech. Sci. 2019, 150, 637–655. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Revnic, C.; Pop, I. Free convection in a porous wavy cavity filled with a nanofluid using Buongiorno’s mathematical model with thermal dispersion effect. Appl. Math. Comput. 2017, 299, 1–15. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Tayebi, T.; Roslan, R.; Chamkha, A.J.; Hashim, I. Entropy Generation and Mixed Convection Flow Inside a Wavy-Walled Enclosure Containing a Rotating Solid Cylinder and a Heat Source. Entropy 2020, 22, 606. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Ismael, M.A.; Chamkha, A.J.; Hashim, I. Numerical investigation of mixed convection and entropy generation in a wavy-walled cavity filled with nanofluid and involving a rotating cylinder. Entropy 2018, 20, 664. [Google Scholar] [CrossRef]
- Khan, M.S.; Zou, R.; Yu, A. Computational simulation of air-side heat transfer and pressure drop performance in staggered mannered twisted oval tube bundle operating in crossflow. Int. J. Therm. Sci. 2020, 106748. [Google Scholar]
- Hashim, I.; Alsabery, A.; Sheremet, M.A.; Chamkha, A. Numerical investigation of natural convection of Al2O3-water nanofluid in a wavy cavity with conductive inner block using Buongiorno’s two-phase model. Adv. Powder Technol. 2019, 30, 399–414. [Google Scholar] [CrossRef]
- Kahveci, K. Buoyancy driven heat transfer of nanofluids in a tilted enclosure. J. Heat Transf. 2010, 132. [Google Scholar] [CrossRef]
- Corvaro, F.; Paroncini, M. An experimental study of natural convection in a differentially heated cavity through a 2D-PIV system. Int. J. Heat Mass Transf. 2009, 52, 355–365. [Google Scholar] [CrossRef]



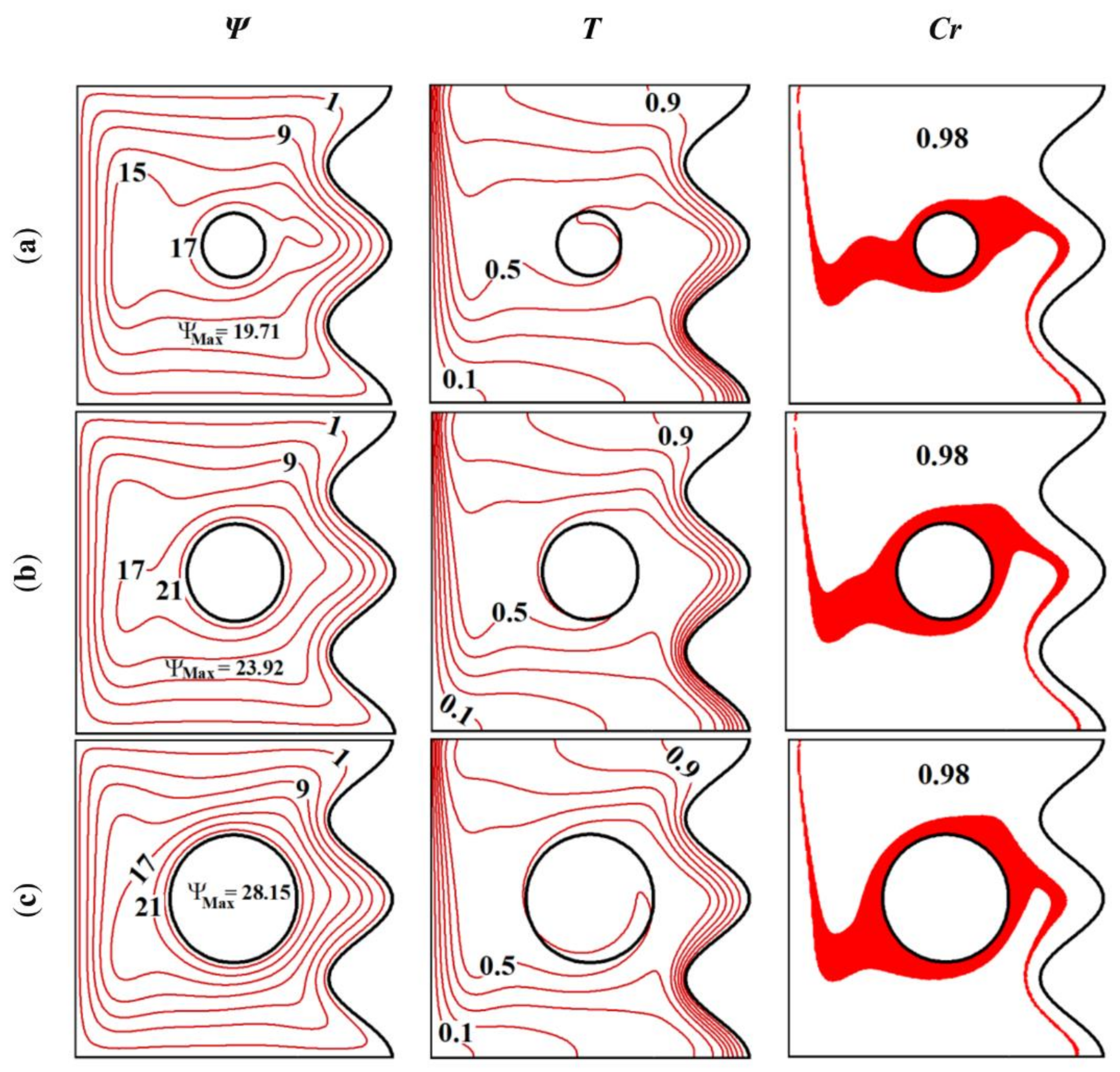

| Material | β (K−1) | C (kJ/kg K) | k (W/m K) | ρ (kg/m3) |
|---|---|---|---|---|
| Polyurethane: shell | 17.28 × 10−5 | 1.3177 | 786 | |
| Nonadecane: core | 2.037 | 721 | ||
| Water: base fluid | 21 × 10−5 | 4.179 | 0.613 | 997.1 |
| Volume Fraction of the Nano-Additives (%) | 0.0 | 1.68 | 3.36 |
|---|---|---|---|
| 1 | 1.1 | 1.2 | |
| 1 | 1.22 | 1.42 |
| Domain Elements | Case I (14,010) | Case II (23,388) | Case III (30,816) | Case IV (56,394) | Case V (68,781) | Case VI (80,496) |
|---|---|---|---|---|---|---|
| Num | 7.5744 | 7.5345 | 7.5341 | 7.5328 | 7.5355 | 7.5360 |
| Ψmax | 28.240 | 28.232 | 28.216 | 28.158 | 28.146 | 26.160 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehryan, S.A.M.; Raahemifar, K.; Gargari, L.S.; Hajjar, A.; El Kadri, M.; Younis, O.; Ghalambaz, M. Latent Heat Phase Change Heat Transfer of a Nanoliquid with Nano–Encapsulated Phase Change Materials in a Wavy-Wall Enclosure with an Active Rotating Cylinder. Sustainability 2021, 13, 2590. https://doi.org/10.3390/su13052590
Mehryan SAM, Raahemifar K, Gargari LS, Hajjar A, El Kadri M, Younis O, Ghalambaz M. Latent Heat Phase Change Heat Transfer of a Nanoliquid with Nano–Encapsulated Phase Change Materials in a Wavy-Wall Enclosure with an Active Rotating Cylinder. Sustainability. 2021; 13(5):2590. https://doi.org/10.3390/su13052590
Chicago/Turabian StyleMehryan, S. A. M., Kaamran Raahemifar, Leila Sasani Gargari, Ahmad Hajjar, Mohamad El Kadri, Obai Younis, and Mohammad Ghalambaz. 2021. "Latent Heat Phase Change Heat Transfer of a Nanoliquid with Nano–Encapsulated Phase Change Materials in a Wavy-Wall Enclosure with an Active Rotating Cylinder" Sustainability 13, no. 5: 2590. https://doi.org/10.3390/su13052590
APA StyleMehryan, S. A. M., Raahemifar, K., Gargari, L. S., Hajjar, A., El Kadri, M., Younis, O., & Ghalambaz, M. (2021). Latent Heat Phase Change Heat Transfer of a Nanoliquid with Nano–Encapsulated Phase Change Materials in a Wavy-Wall Enclosure with an Active Rotating Cylinder. Sustainability, 13(5), 2590. https://doi.org/10.3390/su13052590







