A Comprehensive Review of the Evolution of Networked Control System Technology and Its Future Potentials

Abstract

Networked control systems (NCSs) are attracting the attention of control system engineers. The NCS has created a paradigm shift in control system technology. An NCS consists of control loops joined through communication networks in which both the control signal and the feedback signal are exchanged between the system and the controller. However, its materialization faces several challenges as it requires the integration of advanced control and communication techniques. This paper presents an extensive review of NCSs from the perspective of control system design. The evolution of NCSs is broadly divided in three phases, namely NCSs prior to 2000, NCSs during 2001–2010, and NCSs from 2011 onwards. This division corresponds to the initial status, intermediate status, and the recent status of the developments in the design of NCSs. The advancement of different control techniques during these phases has been discussed comprehensively. This paper also describes the transition of control systems form continuous domain to networked domain, which makes it better than the traditional control systems. Some important practical applications, which have been implemented using NCSs, have also been discussed. The thrust areas for future research on NCS have also been identified.

1. Introduction

A networked control system (NCS) consists of control loops connected through communication networks, in which both the control signal and the feedback signal are exchanged between the system/plant and the controller. There are two types of approaches for design of NCSs, namely control of network approach and control over network approach. Only the control over network approach-based NCSs are considered in this review. A simple block diagram of this type of networked system is shown in Figure 1.

In an NCS, the plant output is measured using the sensors. These signals are converted into digital signals using the analog-digital (A/D) convertors, which are transmitted to the controller via a communication network. The controller determines the control signal based on the sensor output, which is transmitted back to the plant using same communication channel. The control signal before being fed to the actuator section of the plant, is converted from digital to analog signal using the digital-analog (D/A) convertor. In this manner, the plant dynamics can be controlled from a remote location.

1.1. Advantages and Disadvantages of NCS

There are several underlying advantages of an NCS, which is termed as the next generation control system. Key merits of networked control systems (NCSs) are as follows:

(i)

Effective reduction of system complexity: It is possible to minimize the complexity of control systems by interfacing them with the communication network. With the communication network, the data related to multiple plants can be easily stored at a single server which reduces the complexity of control systems.

(ii)

Efficient sharing of network data: Several parameters pertaining to the plant can be exchanged easily using the communication networks, which helps in the design of control algorithms.

(iii)

Simple to take intellectual decisions based on the information: The information can be used to make intelligent decisions easily.

(iv)

Eliminates unnecessary wiring: Today, it is possible to transmit data wirelessly at a very high speed. The wiring for interfacing controllers and plants can also be avoided. The wireless sensor networks are advanced enough to make the wireless control is a reality.

(v)

Simple to scale the networks by adding additional sensors, actuators, and controller: The wireless sensors and actuators can be replaced easily, which reduces the maintenance cost of the NCS. The controllers can also be replaced economically as compared to the traditional wired controllers. The expansion of sensors, actuators and controllers can also be achieved easily.

(vi)

Cyber-physical interface for tele-execution of control: The NCS provides a platform for cyber-physical interface and tele-execution of controls. The NCS permits the remote control of the plant.

(vii)

Wide range of applications: Applications in the area of distributed power systems, robots, unmanned aerial vehicles (UAVs), automobiles, space discovery, terrestrial discovery, industrial unit automation, remote problem-solving and troubleshooting, perilous environments, aircraft, production plant monitoring, and many more. More and more applications of NCS are coming into existence every day.

The NCS is also plagued by several problems. The disadvantages of NCS are:

(i.)

Loss of ability to determine the time of incoming data: The time at which the data arrives cannot be determined exactly, so uniform sampling cannot be used.

(ii.)

Loss of data integrity: Data may be lost during the transmission process, so it cannot give the complete information.

(iii.)

Communication Latency: In remotely located NCSs, due to the communication latency, the control action may not be implemented with immediate effect.

(iv.)

Complexity and Congestion: As the number of nodes increases, so does the complexity of the communication system, causing congestion and time delays. Therefore, the deployment in an industry with tens of thousands of sensors and actuators can be a challenging task.

1.2. Designing of Control System from Continuous Domain to Networked Control Domain

In the beginning, control signals were generated using analog computers. Frequency analysis and Laplace transform were the primary tools for analysis. The main drawbacks of this system are its limited accuracy, limited bandwidth, drift, noise, and limited capabilities to manage nonlinearities. Known delays could be handled at the time of control synthesis using the well-known Smith predictor.

Digital controllers replaced the analog technology with the advancement of processors. However, controlling an analog plant with a discrete electronic system inevitably introduces timing distortions. In particular, it will become necessary to sample and convert the sensor measurements to digital data and also convert them back to analog values. Sampling theory and z transform became the standard tools for the design and analysis of digital control systems analysis. For z transform, it is assumed that the sampling is uniform. Thus, for the design of digital controllers, periodic sampling became the standard. Note that, at the infancy of digital controls, as the computing power was poor and memory was expensive, it was vital to minimize the complexity of the controllers and the operating power. It is not obvious that the periodic sampling assumption is always the best choice. For example, adaptive sampling has been used in Reference [1], where the sampling frequency is changed based on the derivative of the error signal, and is far better than equidistant sampling in terms of computed samples (but possibly not in terms of disturbance rejection [2]). A summary of these efforts is provided in References [3,4]. However, with the decreasing computational costs, interest in adaptive sampling reduced, and the linearity preservation property of equidistant sampling has helped it to stay the undisputed standard.

From the computing side, real-time scheduling modeling and analysis were introduced in Reference [5]. This scheduling was based on restrictive assumptions, one of them being the periodicity of the tasks. Even if more assumptions were progressively introduced to cope with the practical problems, the periodicity presumption remains popular [6]. Moreover, the topology of the network can vary with time, allowing the mobility of the control devices. Hence, the whole control system can be highly adaptive in a dynamic environment. In particular, wireless communications allow for the rapid deployment of networks for connecting remotely located devices. However, networking also has problems, such as variable delays, message de-sequencing, and periodic data loss. These timing uncertainties and disturbances are in addition to the problems introduced by the digital controllers. 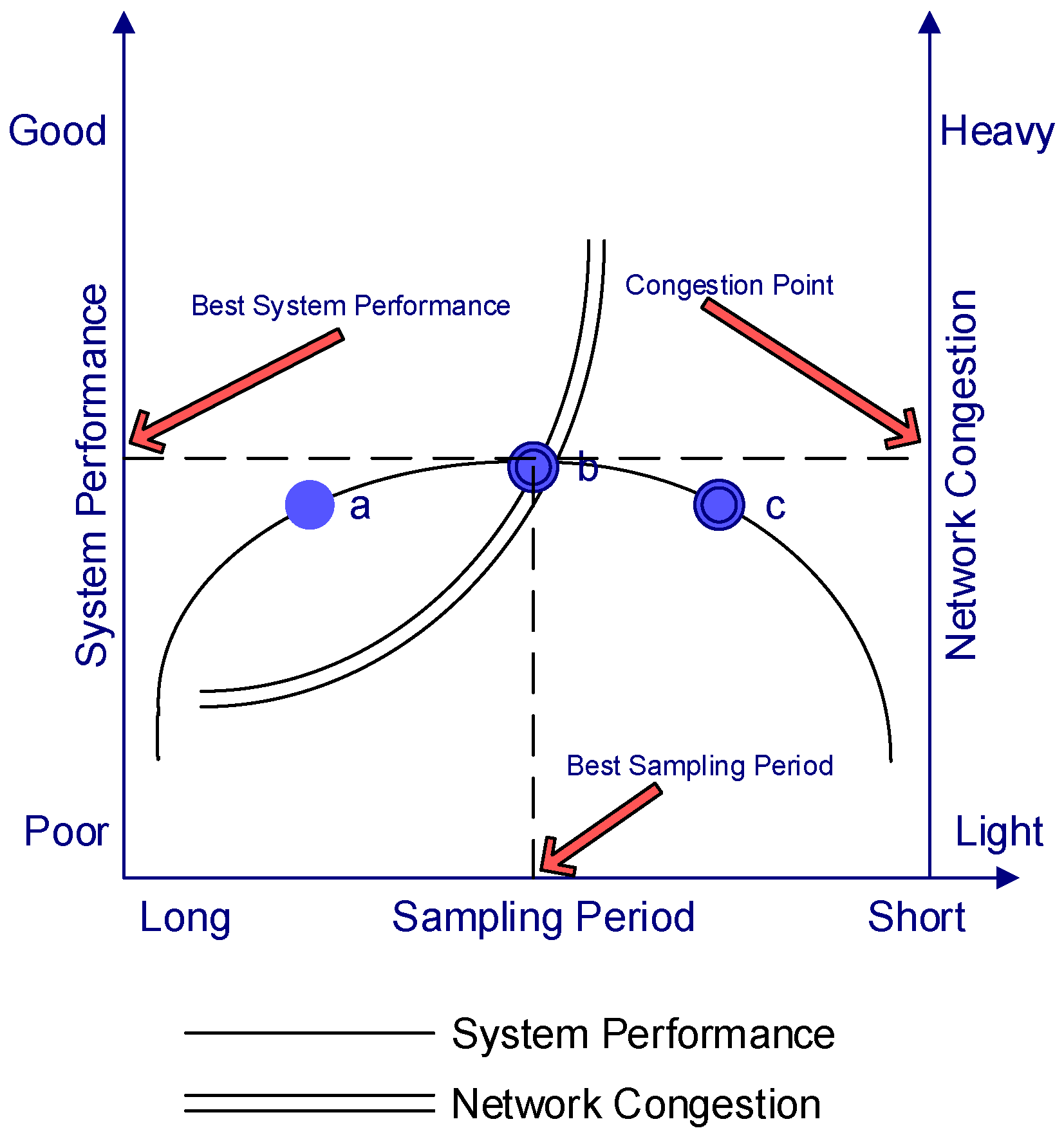Figure 2 shows the trade-off between control performance and the sampling rate.

Figure 2 shows that the control performance is only applicable for a range of sampling rate from P_B to P_C. Increasing the sampling rate above P_C increases the network-induced delays. This will result in the degradation of control performance.

Based on the above discussion, the difference between the conventional control systems and the NCS is been summarized in

Table 1. Differences between networked and conventional control systems.

Parameters	Networked System	Conventional System
Vital Function	Control of physical equipment	Data processing and transfer
Applications	Manufacturing, processing and utility distribution	Corporate and home environments
Hierarchical Process	Deep, functionally separated hierarchies	Shallow, integrated hierarchies
Failure Mode and its effect	High	Low
Reliability Requirement	High	Moderate
Deterministic	High	Low
Data Composition	Small packets of periodic and aperiodic traffic	Large, aperiodic packets
Reliability	Required	Not required
Operating Environment	Hostile conditions, often featuring high levels of dust, heat, and vibration	Clean environments, often specifically intended for sensitive equipment

as:

1.3. Co-Design Approach for the NCSs

The design of an NCS integrates the domains of control system, communication, and real-time computing. The increasing complexity of the computer systems, and their networks, requires advanced methods specifically suited for the NCS. The main issue to be addressed is the achievement of the control objective (i.e., a combination of security, performance, and reliability requirements), despite the disturbances. For instance, sharing of common computing resources and communication bandwidths by competing control loops, alongside the other functions, introduces random delays and data losses. Moreover, the use of heterogeneous computers and communication systems increases the complexity of the NCS.

Control plays a significant role in interconnected complex systems for their reliable performance [7]. The interconnection of elements and sub-systems, coming from different technologies, and which are subject to various constraints, calls for a design that can solve the conflicting constraints. Besides achieving the desired performance in normal situations, the reliability and safety-related problems are of concern for the system developers. A fundamental concept that is dependability, which is the device property that features various attributes, such as access, reliability, safety, confidentiality, integrity, and maintainability [8]. Being confronted with faults, errors, and failures, a system’s dependability could be achieved in numerous ways, i.e., fault prevention, fault threshold, and fault forecasting [9].

Except in the event of failures due to hardware or software components, most procedures run with nominal behavior, but, neither the process nor the execution resource parameters are completely known or modeled. One method is to allocate the system resources conservatively, which results in the wastage of resources. From the control viewpoint, specific inadequacies to be considered include poor timing, delays, and data loss. Control usually deals with modeling uncertainty, powerful adaptation, and disturbance attenuation. More correctly, as shown with recent results obtained on NCS [10], control loops tend to be robust and can tolerate networking and computing disturbances, up to a certain level. Therefore, the timing deviations, such as jitter or data loss, as long as they remain within the bounds, may be viewed as the nominal features of the system, but not as exceptions. Robustness allows for provisioning the execution resources according to needs that are average than for worst cases, and to take into account system reconfiguration only once the failures surpass the abilities of the controller tolerance that is running.

An NCS is composed of a collection of heterogeneous devices and information sub-systems. For designing the NCS, many conflicting constraints must be simultaneously fixed before reaching a satisfactory solution that is implementable. Issues related to networking control tracking performance, robustness, redundancy, reconfigurability, energy consumption, expense effectiveness, etc., are to be addressed. Traditional control usually deals with a procedure that requires a solitary computer, and the limitations of the communication links and computing resources usually do not notably affect its performance. Existing tools dealing with the modeling and identification, robust control, fault diagnosis and isolation, fault tolerant control, and flexible real-time scheduling need to be enhanced, adapted, and extended to handle the networked characteristics of the control system. Finally, the thought of a co-design system approach has emerged that allows the integration of control, as well as communication within the NCS design [10].

1.4. Main Contributions

The NCS is an emerging area of the control system. It is worth reviewing the state-of-the-art developments in NCS. Although many review papers have been published in this area, to the best of the authors’ knowledge, these focused only on a certain dimension of the NCS, and a comprehensive approach was lacking. In this paper, a comprehensive review on the evolution of NCSs in last the 30 years is discussed. The evolution of NCS is broadly divided in three phases as: (i) prior to 2000, (ii) 2001–2010, and (iii) 2011 onwards. The reason for this division is to understand the initial, the intermediate, and the latest developments related to NCS. The main focus of this discussion would be on the advancement of different control techniques during these phases. Based on the extensive review, the different types of NCSs and their related challenges are described. At the end, this review paper highlights the following innovations in the field of NCS: new novel methods for selecting the best sampling time in the NCS, new jitter compensation techniques, developing the theory and practice for control systems operating in a distributed and asynchronous packet-based environment, stability analysis of networked control systems in the presence of network-induced delays and packet dropouts (due to propagation delay and also due to the network congestion), and developing of advanced networked control methods that provide the desired performance in the presence of uncertainties and adversaries. This review paper also highlights some important practical applications that are implemented using the NCSs. Lastly, the important future research areas for NCSs are discussed.

The remaining sections are as follows: Section 2 reviews the development of NCS prior to 2000 AD; The development of NCS from 2001 AD to 2010 AD is discussed in Section 3; The advancement of NCS in recent phase after 2011 AD is discussed in Section 4; Section 5 describes about different topologies of NCSs; Section 6 presents different types of NCSs and their related challenges; Section 7 discusses some of the vital practical applications of the NCSs; Section 8 is the conclusion, along with the observations and potential future developments.

2. Initial Phase of NCS Prior to 2000

The NCS concept is not a recent phenomenon. It emerged in the early 1970s, with the progress of computation, as well as communication, technologies. However, the computation and communication technologies were still in the nascent stages and so the NCSs were designed as decentralized control systems, which remained prominent for the next three decades. One of the earliest works on decentralized NCS was proposed by Reference [11], where algebraic and geometric methods were discussed to obtain stable results. A dual-mode decentralized scheme for the networked control of a commodity’s flow has been presented in Reference [12]. First, local controllers located at network nodes, exchange simple messages with their neighbors to determine the confined optimum flows. Second, the local controllers adjust their flows to reach the optimal equilibrium state in finite time.

The stabilization of the decentralized linear time-invariant multivariable (LTI-MultiVar) system was proposed in Reference [13] by employing numerous local feedback control rules. A necessary and sufficient condition was obtained from the above rule for the stabilization of the given system. Later, in Reference [14], the properties of the closed loop were studied for both controllable and observable k-channel linear systems, by applying the consequences of decentralized feedback. In addition, the theory of a complete system was established. Complete systems can be made both controllable and observable for all channels by applying non-dynamic decentralized feedback.

Some development in the field of decentralized control was achieved in 1980s. In Reference [15], a new dynamic interaction measure was defined by using the perception of structured singular value (SSV) for multivariable systems under feedback. To predict the stability of the decentralized systems and to measure the loss of performance, dynamic interaction measure was used. Later, in Reference [16], F. Lin et al. presented several important studies on decentralized control systems. The decentralized regulation and synchronization for partially surveyed discrete-time-event systems was studied. In Reference [17], which was illustrated using a simple production system. This study was later extended in Reference [18], and it was concluded that decentralized supervision would be easier to design and use.

In the 1990s, several NCS-related ideas evolved based on the concepts developed in the recent years, such as smart networks for control, decentralized control of complex systems, supervisory control, control in multimedia wireless networks, quasi-decentralized control, scheduling, event-triggered control, stability analysis, and so on [19,20,21,22,23,24,25,26,27,28,29,30,31].

The decentralized control of systems, which is complex in nature, were described in Reference [19], wherein topics, such as stabilization, optimization, estimation and control, output control, decompositions, and reliable control, were discussed in detail. In Reference [20], the author discussed the role of distributed, as well as centralized, networks for control. The authors also differentiated the above two categories in different ways. It also discussed the benefits and drawbacks of data networks, as well as the control networks. In a discrete-time system [21], the events must be within the imposed time constraints. To achieve a given control objective, a controller can hinder, permit, or pressurize several events in the system. In Reference [22], the network-level management and control issues were discussed. The quasi-decentralized control for complex systems was analyzed in Reference [23] using the concept of power system stabilization to design a sample system.

Three types of data: periodic data, sporadic data, and messages, have been proposed in Reference [24] for the planning of the NCS. As a basic parameter, delay bound was used, which guarantees the stability of the given system using Lyapunov’s theorem. The above method can adjust the sampling period to be as minimum as possible, allocating all the network bandwidth. The basic properties of real time distributed systems were compared in Reference [25]. In addition, the characteristics of time triggered and event-triggered distributed systems in robotics were discussed in References [26,27] using the artificial intelligence, particularly focusing on the predictability, resource utilization, extensibility, etc. In Reference [28], the authors achieved the asymptotic stability and improved controller performance by scheduling the use of the network.

At the end of 20th century, a basic controller called an event-based proportional–integral–derivative (PID) controller was described in Reference [29], decreasing the resource consumption, only with the deprivation in the performance of trivial control. The proposed work was validated with simulations on a double-tank process. Next, two types of algorithms were suggested in Reference [30] for approximating the plant operation: one was an open-loop arrangement analyst, and the other was a closed-loop arrangement analyst/predictor. Again, the NCS’s stability was analyzed in Reference [31], showing the effects of sampling rate manipulation and network delay on the system stability.

The above historical developments are summarized in tabular form in

Table 2. Summarized discussion of development of NCS prior to 2000.

S.No.	Papers	Parameter/Area/Network
1	[11,12,13,14,15,16,17,18,19,23]	Decentralized, Robust Control Network
2	[20,21,22,24,25,26,27,28,29]	Smart, Wireless and Discreet Control Networks
3	[30,31]	Stable and Robust Networks

on the basis of area/network/parameter.

Table 2 shows the distribution of available papers in the different areas prior to year 2000: on decentralized-based networks, there are around 10 papers; on smart network-based systems, there are around 9 papers (during this period, the smart networks are in development stage); stable and robust networks can be found in all types of networks. The table here describes about the evolution of networked systems from decentralization of the available conventional networks. As there are many shortcomings in decentralized systems, the evolution of smart/wireless networks/discreet event-based networks came into existence. The distribution of the papers prior to 2000 is shown in Figure 3. The majority of the works are related to decentralized networks, followed by smart networks, and only a small percentage of works dealt with stable/robust networks.

3. Development of NCS between 2001 to 2010

During this period, the key concepts of NCS, which were proposed earlier, received more attention, and the volume of research increased tremendously. One of the main themes of this period was the controller design for NCS with stability analysis and time delay. An important work on scheduling method for NCS was proposed by Reference [32]. This method guaranteed the stability using Lyapunov method. Next, a work on the impact of modern networked architecture on control act of NCS was published by Reference [33]. In Reference [34], the procedures for selecting the message recognizers for vigorously scheduled networked systems were proposed and validated. In Reference [35], recital benefits were established by dispensing with queues and by vigorous traffic scheduling on the network.

An uncomplicated and easy model of a network system was proposed in Reference [36], in which local controllers connected by a network was addressed. In Reference [37], it was discussed that any complex self-motivated communications network typically has several layers and executive units and would be at risk of several disturbances. Therefore, the requirement for efficient and intelligent control of the systems must be used [38]. In Reference [39], an original networked control protocol, called try once-discard, has been proposed for multiple-input and multiple-output (MIMO) NCSs.

A style technique of memoryless-quantizers in sampled-data models was planned by Reference [40]. The objective was quadratic stability within the continuous time (CT) domain. In Reference [41] a general framework for the NCSs was given, where all elements were assumed to be connected through a communication network. They used the uncertainty threshold principle to point out that, with the bound conditions, even in an undisturbed NCS there would be data rates that degrade the performance of networked control due to the network induced delays and can lead the system to the instability [42].

In Reference [43], web-based multi-rate control systems were presented. It was suggested that the effect of web time delay on the control performance can be reduced by using the time delay compensation. A novel networked control strategy developed by Reference [44], analyzes the soundness of the networked systems with unsystematic delay in the communication. It consisted of a network control predictor and a traditional controller. The soundness criteria of a networked system were analytically derived for random communication delays. In Reference [45] a state observer for the networked systems with a delay in the time period was designed. Authors claimed that the state observer supported the satisfactory performance of the NCS, even with delay in the time period. Another review paper [46], which appeared within the same year, was centered on network-induced delays, sampling amount, jitter, information packet dropout, network programming, and stability of Ss.

In Reference [47], authors studied the result of a network within the feedback circuit of an NCS. A random packet-loss model for the network was considered. A classical work on the design of robust H-infinity (H∞) controllers for NCSs with uncertainties was given by Reference [48] that additionally considered the network-induced delay and information dropout. Next, the delays due to the sensor-to-controller and to-actuator were sculptured as two Markov/stochastic chains in Reference [49]. Input/output delay approach was considered by Reference [50] to style the strong sampled-data strong control. Enough LMI conditions were obtained by Lyapunov–Krasovskii functionals. In Reference [51], the straight line stability and straight line persistent disturbance attenuation problems were investigated for NCSs under the effects of random access delays and packet dropout. A robust controller was designed in Reference [52] for the NCSs with random time-delays, using the linear matrix inequality (LMI). The performance analysis of the event-triggered control for the detector sampling in a NCS was carried out by Reference [53]. The analytical formula for analyzing the mean and, therefore, the rate of event-driven traffic versus the sampling resolution was obtained. The simulation results in support of the obtained formula were additionally discussed.

A fault detection technique for NCSs supporting the parity relation and Principal Component Analysis (PCA) was projected in Reference [54]. The projected methodology noticed an honest decoupling from the unknown and random network-induced delay. In Reference [55] a fault bearing control methodology for the nonlinear NCSs with communication constraints was given. In Reference [56], the Tagaki-Sugeno (T-S) model was utilized to design a networked system with completely different delays induced by the network. When analyzed with the existing system modeling methods, this approach does not need the data of the actual delays induced by the network. The work in Reference [57] focused on the networked system with random time delays and, additionally, bestowed a brand new modeling methodology for the linear and nonlinear NCS with time delays that are random in nature and named those models as similar T-S fuzzy models.

A system supported bionic principles was introduced by Reference [58] to demonstrate the information obtained from an oversized range of numerous sensors. By means of that structure symbolization, the quantity of data to be processed was considerably reduced. In Reference [59] the event-triggered control was revisited, from an input-to-output perspective. Review of many modern results on evaluation, investigation, and controller synthesis for networked systems were administered in Reference [60]. Another paper, by Reference [10], surveyed appropriate work from the areas of systems and process control, detection, and estimation. Input delay approach, during which the sample-and-hold circuit can be implanted into an analog system with an input delay which is time-varying, was revised in Reference [61]. The loss of data-packets in the NCSs was mentioned in Reference [62]. In Reference [63], a mathematical model of a small rotorcraft was presented. The identification methodology and state estimation using Extended Kalman Filter were discussed. Control algorithms, based on PI, LQG and SDRE approaches, focused on rotorcraft were also proposed.

In Reference [64], the impact of a network within the electrical circuit of a system was discussed. They used an unsystematic loss of data-packet model for the network, and showed the results for discrete-time period systems with stochastic process jumping constraints. In Reference [65] the exponential stability of Nonlinear Time Varying (NLTV) impulsive systems was established with the help of Lyapunov functions separated at the impulse times. In Reference [66], it was observed that for NCSs with delays and output feedback stabilization, there was a deviation in the mean-square stability due to the random communication situations. In Reference [67], a state feedback controller was proposed for the stabilization of an uncertain linear networked control systems with random communication time delays, which differs from the Lyapunov–Razumikh methodology. In Reference [68], a sufficient condition was obtained for the exponential stability of the networked systems, and they also the mentioned relationship between the dropout rate of the data-packets. An occurrence-based discrete-time model (an exponential unsure system with delay) was proposed by Reference [69] that showed that the stability of the projected system can be achieved by finding an effect for a switched stochastic system with an additive norm delimited uncertainty.

In Reference [70], the state feedback controllers were considered for a closed-loop NCS that is represented as a delay in switched systems. A technical note involved with the stabilization drawback of NCS was revealed by Reference [71]. In Reference [72], compensation ways were studied, within the structure of NCS, while considering the protocol characteristics. A general framework was projected initially, wherever the zero-order hold had the logical capability of selecting the most recent control input packet. A category of period of time control systems during which every control task triggers its next unleash supported the worth of the last sampled state were examined by Reference [73]. In Reference [74], a memory less quantizer for steadying a single-input discrete-time Linear Time Invariant (LTI) system with random loss in data-packets, was proposed within the sense of unsystematic quadratic stability. Nesic et al. [75] generalized and unified a variety of recent developments in the literature pertaining to quantized control systems (QCS) and NCS. They provided a unified framework for the controller style with division and time planning via an emulation-like approach. Improved stability conditions were derived in Reference [76] for sampled-data feedback control systems with falteringly Linear Time Variant (LTV) sampling intervals. The cause of robust H∞ control was researched by Reference [77] for sampled-data systems with probabilistic sampling. By Linear Matrix Inequality (LMI) approach, enough situations were produced, that bonded the robust mean-square exponential stability of the system.

An event-driven state-feedback type of control technique in which a control input generator mimicked a continuous feedback between two successive event times was published by Reference [78]. In Reference [79], focus was given on different factors, such as networking technology, delay network induced delay, resource allocation of networks, scheduling, fault bearing capacity, etc. In Reference [80], an original totally time period dependent Lyapunov function was proposed in the construction of the input delay that improves the existing results. In Reference [81], the cause of the NCSs having exponential stability with the increase in delay time-periods, was studied. The cause of robust fault calculation for a class of tentative networked systems with arbitrary communication delays induced by the network was inspected by Reference [82], which also described the delays by Markov processes. In Reference [83], wireless sensor networks for networked manufacturing systems were proposed.

The above historical development is summarized in tabular form in

Table 3. Summarized discussion of development of NCS from 2001 to 2010.

S.No.	Papers	Parameter/Area/Network
1	[32,35,38,46,47,79]	Scheduled Networks
2	[34,36,39,40,41,46,47,49,50,51,57,62,71,76,81]	Stability Analysis/Approach
3	[37,42,46,47,75]	Complex/Interactive Networks
4	[10,43,46,63]	Internet/Communication Based Multi-rate Control Networks
5	[46,53,75,78]	Event Based Networks
6	[33,44,45,46,48,49,50,52,54,55,56,61,65,66,67,68,70,72,74,77,80,82]	Delay/Fault Detection/Packet Loss
7	[46,58,83]	Autonomous Networks

on the basis of area/network/parameter as follows.

The above, Table 3, gives a structured information about the distribution of papers in different areas published during the phase from 2001 to 2010. On scheduled networks, there are around 6 papers; on stability analysis-based systems, there are around 15 papers; on complex and interactive networks, there are around 5 papers; on communication and event-based networks there are around 4 papers, etc. Event-based approach was still in the developmental phase as it was a new technique. Delay-based systems were popular during this stage that were used to overcome the drawbacks of the research prior to year 2000. So, scheduled, autonomous, event-based, and communication-based approaches came into existence during this phase. The major drawbacks prior to year 2000 were: security issues, effect of delay on networked systems, effect of packet dropouts in communication networks, etc. So, to overcome these issues, scheduled approach-based network came into existence. The distribution of the papers during this phase are shown in Figure 4. The major focus was on delay-based approaches in networked system to improve the flow of information in networked system and make the system stable.

4. Development of NCS from 2011 Onwards

In the last decade, highly developed control methods were employed for improving the performance of NCS in terms of system stability, delays, event-triggering algorithms, network security, etc. In addition, the discrete time NCSs have received a considerable amount of attention.

Model-based predictive NCSs (MBPNCSs) were proposed by Reference [84] that compensated for the random delays and for the data losses in data transmission. The performance of the system was improved with the help of a predictive control scheme. In Reference [85], an approach for stabilization via discontinuous Lyapunov function was proposed, where sampling intervals that varied in terms of their nature, the dropouts, and network delays were taken into account. In Reference [86], a H2/H∞ control of random time delayed networked systems was proposed. In Reference [87], the stability investigation of a NCS was achieved, where the communication between the controller and the plant input is through a digital channel, with dropouts in data-packets and finite-level quantization. Again, in Reference [88], authors describe the stability of NCSs with respect to time-varying transmission intervals.

For discrete-time models, in Reference [89], the difficulty of the networking-based H∞ filtering method was described. A Markov jumping model based method was described to design H∞ filters, in which the filter gains depend on both the network delays and dropouts in data-packets. In Reference [90], a novel method was presented to calculate the stability of continuous linear systems with input containing the sampled data. In a technical note, Reference [91] presented a new method with control packet loss. In Reference [92], a networked control loop was considered in which the “slave” portion was a plant, and the “master” portion was the remote controller and observer. In networks, the fault detection of linear systems with restricted loss of data packets was proposed by Reference [93]. In Reference [94], a modern control system mapped on Networks-on-Chip was presented. The proposed architecture was supposed to play a pivotal role in real time applications like missile control system, robot trajectory, and satellite vehicle orbital trajectory control system. In Reference [95], a NCS framework for the coordinated control of distributed generation sources in smart power grids was proposed. The system measurements were transmitted to the controller through a real-time communication network and the effects of delays and packet dropouts due to the communication network were modeled.

An event-triggered transmission scheme was proposed by Reference [96] for a sampled-data control system. In Reference [97], an event-triggering method was designed to decrease the network communication load, which could also be used to decide the time moment of the sampled signals. In Reference [98], a methodology for the technological investigation of iterative learning control for sampled-data systems was proposed. In Reference [99], a new Lyapunov functional was constructed to drive some stability criteria. Then, a channel utilization-based switched controller was designed to asymptotically stabilize the networked system in the sense of mean-square. It was shown that the proposed approach enhances the robustness of the networked control system to data drift and external disturbances. In Reference [100], the cascade control was employed for stabilization of the singular NCSs. In Reference [101], a network-based output controlled T-S fuzzy system was investigated that is steadied using a delayed fuzzy static controller, and not by any non-delayed static controller. In Reference [102], a novel robust variable sampling period controller (RVSPC) was developed that takes into account random time delays and losses in data-packets. In Reference [103], a decentralized event-triggered dissipative control was studied for systems having diverse physical characteristics. In Reference [104], a distributed NCS scheme was proposed by considering the communication delays. The results were applied to reduce the inter-area swing oscillations in a power grid. A brief overview of NCSs was presented by Reference [105] regarding the system configurations, challenging issues, and the methodologies.

In Reference [106], a time-triggered zooming algorithm for the dynamic quantization at the sensor side was proposed that led to an exponentially stable closed-loop system. The algorithm included proper initialization of the zoom parameter. An exhaustive explanation of the various types of networked control techniques is given by Reference [107]. The H∞ output feedback control of NCSs with time delay and dropout in data-packets were considered in Reference [108], whereas Reference [109] discovered the nonlinear networked systems with tracking control problem. In Reference [110], the data that uses self-healing technology was reviewed as input and was justified as big data. In Reference [111] the method for time-delays in large-scale networked systems connecting sensors, controllers, and actuators was developed. A new sampling and control strategy was proposed by Reference [112] to search a sub-optimal sampling sequence and control input sequence to minimize the disordering of data-packets. Further, in Reference [113], an original state space model was set up, in which both the tracking error and the state variables were combined and optimized. The optimal estimation problem in lossy NCSs with randomly dropped control data-packets was elaborated in Reference [114]. In Reference [115], the problem of Sliding Mode Controller (SMC) for NCSs was considered with semi-stochastic switching, popularly known as Markov or stochastic switching and having unsystematic dimensions. In Reference [116], a phenomenon of self-triggered sampling was proposed for a networked system with considerations of data losses and delay in communication. In Reference [117], both the D-stability, as well as the properties of finite L2-gain, were studied for a class of uncertain discrete-time systems with time varying network-induced delays [118,119].

A summary of the distributed NCSs was presented by Reference [105]. In Reference [120], stochastic nonlinear time-delay systems were considered that take the help of observer-based fuzzy output-feedback control (OFOFC). In Reference [121], the stochastic linear systems with random data dropout designed by a Bernoulli random variable were described. In Reference [122], the state and fault estimation problem for Linear Time (LT) switched systems with immediate disturbances and faults, was considered. Also, the two types of observer-based approaches were considered.

A procedure to evaluate the wellbeing of Centralized Power Systems (CPSs) in the event of cyber-attacks was described by Reference [123]. The problem of switched type networked systems with external disturbance and faults was investigated in Reference [124]. In Reference [125], the main cause of H∞ control for uncertain discrete-time domain T-S fuzzy systems was considered.

The problem of state estimation for linear stochastic methods with event-triggered communication and packet loss was determined in Reference [126]. In Reference [127] event-triggered coordination for multi-agent structures/systems was elaborated. A survey on the distributed type of control and distributed type of filtering had been provided by Reference [128] for industrial CPSs, explained by different mathematical equations. In Reference [129], the problem of event-based network-induced time-varying delays with output tracking control for nonlinear NCSs approximated by type-2 fuzzy systems was investigated. In Reference [130], the authors addressed the concern for multi-layer, data-driven cyber-attacks, developed to boost ICS cyber security. In Reference [131], the control of automotive active suspension system using Proportional Integral Derivative (PID) and Linear Quadratic Regulator (LQR) methods was discussed. In Reference [132], a closed-loop controller model considering cyber-attacks and the mixed-triggering scheme, was proposed. In Reference [133], a robust fault detection scheme for networked control systems (NCSs) was developed with limited quality of services (QoS), such as network-induced time delay, data dropout, and error sequence. In Reference [134], a survey on time-delay approach to networked control systems (NCSs) was provided, which discusses the fundamental network-induced issues in NCSs and the main approaches to the modeling of NCSs. Again, an investigation on distributed type of control and distributed type of filtering for CPSs described by dynamic mathematical modeling equations was presented by Reference [135]. In Reference [136], a scheme called robust approximation-based model predictive control (RAMPC) was developed for the constrained networked control systems (NCSs) subject to external disturbances. This paper also provides a roadmap to evaluate the permissible sampling period and also evaluates the necessary conditions for the feasibility of the RAMPC.

In Reference [137], a sampled-data control problem was investigated for connected vehicles subject to switching topologies, communication delays, and external disturbances. It used an advanced tracking error-based sampled-data platoon control method. In Reference [138], authors were concerned with the modeling and controlling using the mixed event-triggered mechanism (ETM) for NCSs with varying time-delays and uncertainties. In Reference [139], authors investigated about the switching-like event-triggered control for networked control systems (NCSs) under the malicious denial of service (DoS) attacks. In Reference [140] authors proposed an iterative learning control (ILC) scheme to synchronize an array of non-identical neural network systems based on time-varying delay in a repetitive environment. In Reference [141], authors considered a resilient event-triggered control problem for a class of networked systems subject to randomly occurring deception attacks. In Reference [142], a novel method is proposed for line selection and fault location in a distribution network based on a cloud-edge-terminal hierarchical fault monitoring and control system. Reference [143] focuses on the event-triggered control problem for networked switched systems with actuator saturation. Here, an event-triggering strategy is developed based on discrete event-triggered samplings.

In Reference [144], authors investigated the stability problem for networked control systems. They have taken into consideration the input delays and multiple communication imperfections containing time-varying transmission intervals and transmission protocols. Reference [145] focused on addressing the sliding mode control problem of continuous-time nonlinear networked control systems. In Reference [146], the problem of fault-tolerant sampled-data H∞ control for a networked control system with random time delays and actuator faults is investigated. In Reference [147], the problem of event-triggered finite-time control for networked switched control systems with extended dissipative performance was investigated. In Reference [148], the authors proposed a scheduling approach which can minimize the impact of delays and conflicts on the network, to improve the system stability, which results in an economical allocation of network resources, minimizes the traffic congestion, and improves the overall performance of the NCS.

In Reference [149], the authors discussed about the effect of limited bandwidth on the system’s performance, particularly when the sampling period was small. In Reference [150], the authors discussed the amalgamation of control and communication in NCSs that offers remarkable achievement in the design and analysis of such controlled systems. In Reference [151], the authors discussed the LMI approach to effectively compensate for the random network-induced delays and provide the desired control performance. In Reference [152], a new ETM was proposed, under which data packets could be actively dropped within consecutive steps, thereby, saving more communication resources than the existing ETM. In Reference [153], the authors proposed the descriptive analysis about classification of cyber-attacks and threats related to security in industrial control systems. In Reference [154], the authors proposed a new quantization structure, and a mathematical treatment of this structure was given to illustrate the advantage for the quantization effects.

The above developments can be summarized in tabular form in

Table 4. Summarized discussion of development of NCS from 2011 onwards.

S.No.	Papers	Parameter/Area/Network
1	[86,89,90,91,99,100,101,102,103,107,112,113,119,122,128,131,136]	Model/Sampling Based Networks
2	[85,88,90,91,92,97,98,100,101,107,114,117,132,144]	Stability Analysis/Approach
3	[86,87,91,93,98,100,101,106,107,108,112,113,115,116,117,118,119,120,121,122,123,124,125,129,130,132,133,134,137,138,139,140,141,142,144,145,146,149,151]	Delay/Fault Detection/Packet Loss
4	[92,93,99,107,109,110,114,121,125,126,137,140,145]	Internet/Communication Based Multi-rate Control Networks
5	[95,104,105,107,111,118,128,135,142]	Distributed Networked Control Approach
6	[96,97,103,107,126,127,129,135,138,139,143,147,152,154]	Event Based Networks
7	[98,107]	Interactive Networks

on the basis of area/network/parameter as follows.

Table 4 gives the structured information on the distribution of papers in different areas published from the year 2011 onwards. The major focus of research during this phase was on the delay-based networks. The difference between the works published in the earlier phases is that the security approach, model-based approach, and the sampled-based approach involve the incorporation of delays. Secondly, the advanced model-based networked approaches, such as Model-Predictive Control (MPC), OFOFC networks, etc., were proposed, which make the networked system more stable and improve its performance. Figure 5 shows the distribution of papers during this phase. It can be clearly noticed that major focus is on the delay-based approach, which covers approximately 37% of the research contribution. The stability approach is also very important as the stability depends on delay. If the delay is maximum, the system has to be designed to make it stable. To achieve this purpose, many event-based techniques were developed.

5. Topologies in NCSs

Basically, there are three types of network topologies available in NCSs, namely centralized topology, decentralized topology, and distributed topology. A brief discussion on these topologies is given below.

5.1. Centralized Topology

The centralized topology is shown in Figure 6. Here, the sensed data is sent to a centralized controller for data fusion. Suitable data fusion methods are necessary to obtain the fused data which are utilized for computing processes and executions.

5.2. Decentralized Topology

This topology is shown in Figure 7. Each controller node depends only on the local information that the controller possesses for making its local decision. In this topology, the controller nodes do not share their information with the corresponding neighboring nodes. These types of topologies are helpful in reducing the time taken to analyze and synthesize the NCSs. Here, the controllers are decentralized controllers.

5.3. Distributed Topology

The pictorial representation of the distributed topology is shown in Figure 8. One example of distributed topology can be found in Reference [155], where the load frequency control of a networked multi-area power system was discussed. There are two important characteristics of this topology: the subsystem’s information is exchanged with the help of shared communication network, and the plant consists of a huge number of simple interacting units that are interconnected to achieve a desired objective. In this topology, each controller is allowed to share its local information with the corresponding neighboring controllers. Thus, the distributed controllers are capable to coordinate their behavior by transmitting/receiving information to/from other controllers within their corresponding neighboring area. Here, the controllers are distributed controllers. Advantages of this type of topology are: modularity, scalability, and robustness.

5.4. Distribution of Literature Based on the Topologies of NCSs

Table 5. Summarized discussion of different types of NCS topologies.

S.No.	NCS Topology	Reference No.
1	Centralized Topology	[20,48,83,96,97,128]
2	Decentralized Topology	[10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,43,46,53,63,75,78,96,97,103,104,107,126,127,129,135,138,139,143,147,152,154]
3	Distributed Topology	[20,25,26,27,46,58,83,95,104,105,107,111,118,126,127,128,129,134,135,142,155]

gives a summary of the literature based on the topology. It can clearly be seen that the majority of research works use decentralized topology as the controller works independently for the given number of plants, and it has many advantages over the centralized topology, such as network time reduction in sending the data, less network congestion, maximum number of paths available for transmission, etc. The distributed topology is in the developmental stage and has tremendous applications in the NCSs. Focus is now shifting towards the distributed topologies of NCSs. Figure 9 clearly shows that the major focus has been on decentralized (i.e., 59%) topology, followed by the distributed topology, that has share of 32%. Centralized topology has been the least preferred topology, with a share of 9%.

6. Types and Challenges of NCS

Based on the above review, we have identified types of NCSs and the related challenges, which are discussed in this section.

6.1. Types of NCS

The types of NCS developed in the literature are shown in Figure 10.

6.1.1. Sampled-Data Control

If all the control parts are placed in the similar venue, the resulting NCS is often considered to be a digital unit. Since the late 1950s, sampled data control theory has been very well developed for digital control systems. The strategy of delay in the input to this type of control, firstly planned in 1988 [79], has gained resurgent popularity, thanks to the advent of the LMI methodology and also to the advancement of network control technologies. The upper limit of two successive samples and the associated controller is often easily determined using the input delay technique.

6.1.2. Networked Control

Delays caused by the network and the packet losses are still difficult issues for NCSs. Reckoning on managing the network delays and the packet dropouts, different ways to measure stability, and managing styles for NCSs have been developed over the past decade. A brief review of a few of them is discussed below.

6.1.3. A Time-Delay System Approach

The delay in the input method for a sampled system motivates a time-delay system method [77]. Using this approach, the closed loop system is represented as a process with a time-varying lag. The delay in communicating the data from the sensors to the controller and from the controller to the actuators and the respective data-packet dropouts are indirectly incorporated within the input-delay. This approach obtains the maximum delay that the system can tolerate and still maintain its performance. On the other hand, it indicates the worst delay induced by the network and the corresponding packet dropouts that the networked system can tolerate. In the worst case scenario, the results obtained from this approach are definitely conservative [70].

6.1.4. A Markovian-Jumping System Approach

This approach is developed for the investigation and control of the networked systems. Network delays were considered, where the closed-loop NCSs were represented as stochastic-process systems and associated with Linear Quadratic Gaussian (LQG) optimum controllers [66]. The stabilization issue in networked systems is mentioned employing this system approach [39]. Its price remarking that the conception of packets-dropout of data dependent Lyapunov functions is established [71], resulting in some less traditional stability criteria. The Markovian approach is planned for NCSs with delays induced by the network [86]. The key plan is to model the sensor to the controller and the controller to the actuator delays as Markov chains, thus reproducing the closed-loop NCSs as a Markovian process with two modes portrayed by two Markov chains.

6.1.5. A Switched System Approach

This method with arbitrary switching is employed within the investigation and control of these systems. There are a variety of methods on how to build the networked system as a switched-system by means of arbitrary switching. Most of them support the discrete-time method, whereas few of them on the continuous-time method. Based on the idea that the control signal varies with time, a discrete-time switched model is developed [92], where the sampling amount is split into a variety of subintervals on which the controller operates better than the sampling frequency. With this model, the stability and the chronic disturbance attenuation were investigated for the NCSs. It is to be noted that the constraint on delays due to the network is not simple for some NCSs. So, to get rid of this constraint, efforts are created; see, e.g., References [49,68,88].

6.1.6. Event-Triggered Control

In this, the completion of control assignment is decided by the occurrence of an incident, instead of slip away of a fixed fundamental quantity as in the control of time-triggered systems. One of the main advantages of this type of control is the resource consumption with less control performance degradation. This control technique has received plenty of interest and has become a booming topic within the field of NCSs; see, e.g., References [29,72,89]. A key purpose of this control technique is to style an acceptable triggering circumstance that decides whether or not a control task is accomplished. Because of the above benefits, this control approach involves the fore. A variety of problems for these type of systems is tackled, such as Euclidean Norm, L₂, investigation and control style, tracking control, dynamic output feedback control, H∞ filtering, and accord of multi-agent systems.

6.2. Challenges of NCS

Apart from several advantages, there are many key challenges that have received a considerable attention of the research community. Many solutions have been proposed in the past, and many more are being proposed every day. Next, we will discuss some of the key challenges of NCS. Figure 11 presents a flow diagram of the challenges involved in the implementation of the NCS.

6.2.1. Sampling

Before being transmitted over a communication network, the continuous signals should be sampled for simplicity. For sampling the above continuous-time signals, there are basically two ways: one is time-triggered, and another is event-triggered. In time-triggered sampling also known as Riemann sampling, the sampling moment happens at fixed time intervals. Periodic sampling was usually employed in the early digital management systems, as the analysis and style of these sampled systems is simple. At the instance the value of the sampled signal approaches zero, the output obtained is equivalent to the continuous-time system. Another sampling is event-triggered, which is generally denoted as Lebesgue sampling. In this the sampling occurs when an event is triggered. This sampling significantly reduces the network traffic volumes. Over the last decade, there has been an increasing interest in the control of NCSs through event-triggering because of its advantage over time-triggering; see, e.g., References [59,73,78].

In NCSs, the limited bandwidth restricts the system performance [149]. This occurs when the sampling period is small, thereby generating a lot of data that overloads the network and causes congestion. It may result in increased packet losses and longer delays, which degrades the performance. The relationship between the sampling period, the network load, and the system performance in an NCS is illustrated in Figure 12 [150]. For instance, decreasing the sampling period through the values corresponding to points “a” and “b”, the device performance improves. In addition, the device performance deteriorates as a result of network congestion when the sampling period is reduced, as indicated by the values corresponding to points “b” to “c”. An optimal sampling period exists at which the system performance is the best (point “b” in Figure 12).

Table 6. Sampling rate considered in different studies.

Reference	Type of Sampling	Sampling Interval/Sampling Interval Range (in ms)
[1]	Aperiodic	16 to18
[4]	Periodic	40, 80
[40]	Periodic	22.1
[50]	Periodic	785
[65]	Periodic	132.77
[77]	Aperiodic	10 to 11
[80]	Aperiodic	104 to 169
[93]	Periodic	40
[96]	Aperiodic	30 to 1380
[103]	Aperiodic	0 to 299
[119]	Aperiodic	4 to 4.7
[137]	Periodic	100
[146]	Aperiodic	20 to 100
[149]	Periodic	1730

shows the quantitative data for the sampling rate considered in the different research works. There are mainly periodic and aperiodic sampling approaches. In periodic case, the lowest sampling rate considered was 22.1 ms [40], whereas the highest sampling rate considered was 1730 ms [149]. For the case of aperiodic sampling, the lowest range is between 4 ms to 4.7 ms in Reference [119], whereas the highest range was between 30 ms to 1380 ms in Reference [96].

6.2.2. Network-Induced Delay and Packet Dropout

In the literature, many delay induced network models have been proposed [48,49,60,70,84,86,98,99,100,118]. In Reference [84], four main delay models were discussed, namely: (a) constant delay model, (b) stochastic delay model, (c) Markov chain model, and (d) hidden Markov model. Reasons for these types of delays are: limited bandwidth, network traffic, and transmission protocols [99]. Two types of delays mainly occur: (i) sensor to-the controller delays and (ii) controller to-the actuator delays. Since network-induced delays depend on the networking circumstances [60], they are sometimes time-varying, unpredictable, and the upper bound is unknown. As a consequence, network-induced delays are ordinarily sculptured as interval time-varying delay [48,100] and a Markov chain with known transition chances [49,86], with partially transition chances [89] and with arbitrary shift [70]. As mentioned, in Reference [98], network-induced delays have been seen as a cause of degradation of performance of the system or possibly the cause for system instability. In Reference [118] authors proposed an algorithm based on the gradient push-sum method to solve the Electronic Data Processing (EDP) in a distributed manner over the communication networks with time-varying topologies and communication delays. This proposed algorithm is guaranteed to solve the EDP if the time-varying directed communication network is uniformly jointly strongly connected. There are some systems where the presence of communication delay may have a positive effect on the system performance as in Reference [119]. In Reference [151] authors proposed LMI approach to determine the two-mode-dependent static output feedback controller gains to compensate for the random network-induced delays efficiently and provide the desired control performance.

Table 7. Delay data considered in different studies.

Reference	Type of Delay	Delay/Delay Range (in ms)
[41]	Random Delay	160 to 132
[45]	Network-Induced Time Delay	15 to 35
[49]	Random Delay	0 to 2000
[50]	Time-Varying Delay	0 to 1000
[52]	Random Delay	0 to 1000
[56]	Random Delay	0 to 3000
[66]	Random Delay	2000 to 6000
[67]	Random Delay	0 to 123
[68]	Network Induced Delay	0 to 100
[70]	Network Induced Delay	500 to 1550
[80]	Variable Delay	104 to 169
[103]	Variable Delay	0 to 300
[137]	Constant Delay	250
[146]	Constant Delay	500
[149]	Constant Delay	1730

shows the quantitative data for the delay range considered in the different studies carried out in the literature. The highest delay considered was 6 s [66].

Data-packet dropout is a vital issue, which is due to the defective transmission pathway. Limited bandwidth and bulk data transfer over one line are responsible for this defective transmission. Many studies have considered packet losses in the NCSs [41,63,69,75,88,92,94,109,113,114]. These issues often occur because of exchanging the data amongst the various devices, which degrades the performance and can destabilize the system. Due to traffic congestion, the data-packet loss is also a major concern. Mostly, the dropout effect is also known as a Bernoulli or Markov process. In most communication networks, different data packets suffer different delays, which produces a situation where a data packet sent earlier may arrive at the destination later, or vice versa; see Figure 13 [46]. This phenomenon is referred to as data packet disorder.

Table 8. Packet loss rate considered in different studies.

Reference	Loss Rate/Loss Rate Range (in %)
[41]	10
[62]	0 to 80
[67]	26.39
[74]	25 to 31
[91]	25
[93]	10
[108]	30 to 70
[113]	20 to 40

shows the quantitative data of the packet loss rate considered in the different studies existing in the literature. The highest packet loss rate considered was 80% in Reference [63].

6.2.3. Network Security

Security of NCSs is one in the various foremost challenges that is receiving much attention these days [123,130,132]. Any network is prone to interception, particularly the wireless networks. Hence, network security is usually involved. Attacks to the NCS (as shown in Figure 14) will be described in brief as: A1 and A3 symbolize deception attacks, where a person sends forged data from either the sensors or the controllers. The forged data consists of: faulty activity, like the incorrect time of activity or the incorrect sender id. The person will instigate these types of attacks by getting the key or by cooperating with some attacks on sensors (A1) or controllers (A3). Attacks A2 and A4 signifies Denial of Service (DoS) attacks, where the person is barred by the controller from attaining device measurements. To launch DoS attacks, the person jams the associated communication channels, negotiates the devices to stop, and attacks the routing protocols. Attack A5 symbolizes an on-the-spot attack against the actuators. So, attempts should be made to prevent the negotiation of the actuators and the other direct attacks against the physical system, for example, by securing the attacked-physical system, observation cameras, etc. In Reference [152], a new ETM is proposed, under which data packets could be actively dropped within consecutive steps, saving more communication resource than the existing ETM. Here, mainly the effect of DoS attacks obeying Bernoulli distribution is considered and analyzed. Figure 15 shows that the numbers of security events have increased, which is reported by the industrial control systems (ICSs) cyber emergency response team.

In Figure 15, it can be seen that in the beginning, the security incidents were on the rise, but there is a drastic decrease in the security incidents from 2017 to 2020 because of the protective measures taken and the development of advanced networked security approaches in NCSs. Advanced NCSs security techniques are being developed so that the NCSs are safer to operate [153].

6.2.4. Quantization

In these systems, signals are typically quantified by a quantifier prior to sending over a communication network. A quantifier is the same as a nonlinear mapper that maps segments of real sets to completely diverse levels. The quantity of these levels is intimately joined for the flow of information between the physical plant and the filter. In step with the finite period of the word-quantization error, unit of measurement is ineluctable, that has negative effects on the NCS performance. For an NCS subject to quantization, associated random data-packet dropouts [74] were considered, where some relationship is disclosed between the magnitude of the quantization and data-packet dropout. For the NCS subject to finite-level quantization and dropouts in data packets, the results of the step-size quantifier and, additionally, the external variety of consecutive data-packet dropouts on the NCS attenuation level of disturbance are inspected [87]. An integrated generalized framework for the investigation and elegance of networked controlled systems is projected through an associated emulation-like approach that gives a distinct approach through the study of quantization effects on NCSs [75]. The uniform quantizer maps real-valued function to a finite number of quantization regions with arbitrary shape, as in Reference [106]. In Reference [154], the authors proposed a new quantization structure, and a mathematical treatment of this structure is given to illustrate the advantage for the quantization effects.

6.2.5. Jitter

Jitter is generally defined as the distortion of a signal or image caused by poor synchronization. It is defined by the Institute of Electrical and Electronics Engineers (IEEE) [46] as “time-related, abrupt, spurious variations in the duration of any specified related interval”, and it arises due to clock drift, branching in the code, scheduling, communication, and use of certain computer hardware structures, e.g., cache memory. Jitter can be classified into two types: delay jitter [156] and rate (sampling) jitter [157]. The goal of delay jitter is to minimize the difference between delay times of different packets. The goal of rate jitter is to minimize the difference between inter-arrive times [156].

7. Practical Applications of NCS

Apart from review of theoretical developments, many practical applications of NCS have been implemented to date. Some of the important areas of application of NCSs will be discussed briefly.

7.1. Autonomous Mobile Robots/Controlled Networks

For robots, the authority to perform and act dynamically is of vital importance. By itself, they comprise of mobile systems where the changes in environment activate changes in what purposes the system should convene the quality approach to structure the system, typically stated within the artificial intelligence literature because the behavior-based artificial intelligence framework [16,26,27]. Most plans are to spot completely different types of controllers and responses to sensory inputs, with desired mechanism performance. This practice of structuring the system into split behaviors, dedicated to playing bound responsibilities, has gained vital momentum in AI society. In Reference [158], implementation of a cloud service for remote control of a robotic manipulator is addressed, and an optimal control model restriction and control event-triggered communication are studied to be applied to a Robotic Manipulator as a Service. One more such example of the controlled network is the autonomous vehicular system designed by Toyota company called Prius, shown in Figure 16 [159]. This autonomous vehicular system consists of functions, such as automatic controlling the steering, acceleration, and brakes. This function is called Move-Box which is developed by Netherlands Organization for Applied Scientific Research. It functional system works as a line between the Peripheral Component Interface (PCI) extensions for Instrumentation (PXI) which is placed on the roof of vehicle. An eHorizon system designed by Continental company is proficient in controlling the vehicle by using Global Positioning System (GPS).

7.2. Power Systems and Smart Grids

Gradually proceeding to reliable information transmission to far-flung areas over communication networks, it is very difficult to reproduce the consequences of the communication system in the situation of stability in power grids. These types of communication system networks set up random variable time-delays and packet-dropouts in the data being transmitted. There are so many approaches to check such type of communication systems, commonly known as NCS [60]. Intensive analysis persists in control system theory to model the consequences of data-packet delays and dropouts because of the transmission of sensor, as well as actuator, signals via a constrained communication network on desired system stability [39]. Power grids are amongst the biggest styles of systems that are made-up by the human. For performance and transient stability analysis functions, the facility network has to be studied as a full because of the extremely interactive nature of its parts. Another issue is that the growth of an influence network beside time that moves it aloof from its properly designed initial structure and causes degradation of performance, stability and dependableness. Supported by these facts, it is expected that a networked management theme is ready to realize a superior performance compared to the historically decentralized controllers that use solely the regionally measured info [104].

In Reference [95], a modern coordinated NCS framework is designed for grids to control distributed generation sources. Measurements of the system are being transmitted to the networked-controller through the above mentioned period of time communication system network. The consequences of data transmission delays and data-dropouts are because of the communication system network is sculptured. Because this modern communication system network has become vital for grids, future power systems should be designed ready for instability.

In Reference [155], a distributed supervisory strategy for load/frequency control problems in networked multi-area power systems is discussed. Coordination between the control center and the areas is accomplished via data networks subject to communication latency, which is modeled by time-varying time-delay.

Figure 17 shows the block diagram of networked control of smart grid [160]. The block “Power System” shows the open-loop power system which is to be controlled. To this effect, real-power deviations in some of the lines are measured in real-time using current transformers (CTs) and potential transformers (PTs), and represented by y(t) in the block diagram. They are sampled and sent over the communication network as discrete data-packets, y(k). User datagram protocol is used for packet transmission, and packet-loss occurs during transmission. The final data which is received at the control unit after packet loss is given by y’(k). The control unit consists of a LQG controller, which is a combination of a Kalman filter and a linear quadratic regulator (LQR). Kalman filter uses the reduced-power system model and the output data-packets arriving at the controller, y’(k), to estimate the states, x’(k). The state estimates are then multiplied by the LQR gain to produce the control signals, u(k), which are then sent with the help of communication network to the actuators.

7.3. Manufacturing Systems

With the growth in economic processes that specialize in high price with low volume, the producing system design is growing from ancient centralized model to the distributed model and then proceeds to the modern networked system/model. In present situations, the producing systems are designed as in a networked model framework with the help of networking communication systems which consist of the diverse collections of manufacturing devices. Such a type of modern networked producing system monitors and controls by provision of maximizing the standard of service provided by the prevailing manufacturing resources [83].

A typical Industrial Manufacturing Control System is shown in Figure 18 [161]. It consists of large number of control loops, Human-Machine Interface (HMIs), remote diagnostics section, sensors, and actuators, built on layered network architectures, with the help of networked layer. A control loop consists of sensors, actuators, and controllers to deploy certain controlled processes. A sensor is a device that produces a measurement of some physical property and then sends this information as controlled variables to the controller. The controller interprets the signals and generates corresponding manipulated variables, based on a control algorithm and target set points, which it transmits to the actuators. Actuators are used to deploy the controlled processes based on the commands being received through the controller.

Although Radio-Frequency Identification (RFID) is widely used for the application of asset tracking, it requires a power supply for the operation. But, for some cases, where is no power supply available, such as monitoring the activities of the aircraft cabin’s maintenance workers, wireless sensor networks (WSN) is the best choice for workers as it requires no power supply [83].

7.4. Missiles

The system algorithms implementation in networks-on-chip is very helpful to address the varied problems with missile control systems, like power consumption, congestion management, and loss of data packets. Consideration of on-chip implementation of NCSs began to grow due to its potential in numerous applications; it conjointly provided several challenges for researchers to attain reliable and economical control. Moreover, the NCS has been analyzed for many years and has given rise to several necessary research topics in missile control systems [94]. With the progress in digital control systems, the data bus transmit scheme has secured more attention. However, communication networks inevitably introduce time delay. To compensate the time delay effects, an application of fuzzy controller to such a system was shown in Reference [162].

7.5. UAVs

Today, unmanned aerial vehicles (UAVs) have become more and more well-liked in a wide field of applications. Though principally for military functions within the earlier period, it is noticed that there are various areas which may prove helpful [163]. For example, in the agriculture domain, they are applied in field observations or for chemical distributions. They patrol as a fireguard for forests or are used for traffic observation within the cities. They may also be used for automatic landscape photographing. They are terribly attention-grabbing, like in educational analysis, e.g., as flying laboratories, a workplace for control algorithms, or as an education gear for college scholars [63].

Figure 19 shows the diagram of an autonomous UAV. The block diagram consists of various control modules, sensors, actuators (valves, motors), communication modules, etc., which acts as a bridge between the remote access system and the UAV system. The remote control system can access the information, as well as send the useful commands to the UAV. The power available in the vehicle is calculated by the computing power module.

7.6. Quasi-Decentralized Control System

In order to achieve robust stability for a wide range of power system operating conditions, there is a need to break the limit imposed by the decentralized controller structure by implementing a quasi-decentralized control structure. Figure 20 is a block diagram to represent such a scheme. Since time-synchronized phases of Alternating Current (AC) voltages and currents are essential for the coordinated control, synchronous sampling control units based on the Global Positioning System (GPS) are used for this purpose.

7.7. Cloud Computing

The cloud and networked control systems amalgamate the benefits of cloud computing technology, advanced theory of networked control system, and other recent developed wireless and communication-based approaches. Figure 21 represents the cloud computing-based NCS. This system consists of plants to be controlled, a gateway computer, the cloud, and the network. The cloud is equipped with a large quantity of computational and storage resources; however, the plants have restricted resources. The plants send the sensor data to the cloud through the available network, so that the desired control signals can be evaluated by the cloud. These control signals are then sent back to the plants as the input of the actuator.

In a large-scale networked control system, the bagged information consists of information captured by universal information-sensing mobile devices, sensory technologies related to aerials, such as remote sensing, cameras, microphones, RFIDs, and WSNs [164].

8. Concluding Remarks and Future Potentials

The progress of NCSs can be termed as the steady progress which was based on evolution of computation and communication technology. The research of NCSs started with decentralized control systems, which later converged to several theories related to the stability analysis of NCSs. Then, many research papers discussed issues, such as sampling, quantization, and time delays. In a recent phase of NCSs development, some new topics, such as controller design for NCSs with event-triggered sampling and cyber-attacks, have received a lot of attention. NCSs have also been implemented for many practical systems, like UAVs, power systems and smart grids, robots, missiles, and manufacturing systems. At present, the components are distributed over long distances, such as in a smart grid, teleoperation control system, etc. Conventional control cannot satisfy the latest challenges, so novel control structures are needed to resolve the newly-presented complex control systems. Even though a lot of advancement has been made in NCSs, their practical applications are very limited. Most of the research works dealt with simple-nodes and simple-system. Multi-sensors (or multi-nodes) and multi-system, in addition to coupling of numerous nodes or subsystems, should be considered in the future research. In accordance with the undeniable fact that the complex NCSs have characteristics of wide area, wide selection, and big data, we ought to combine the network control technology with the computer technology, the cloud storage technology, the data mining technology, and the wide-area measurement techniques in such a way that more effective control algorithms are developed. The research in NCSs has come a long way since its inception, but, in terms of real-time implementation, there is still a lot of scope. This is definitely going to be taken into account in further research problems.