A Model for Rapid Selection and COVID-19 Prediction with Dynamic and Imbalanced Data
Abstract
:1. Introduction
2. Sustainable Machine Learning
3. Methods
3.1. Metadata Collection for Finding Classification Algorithm Selection Rules
3.2. Dataset Characteristics Used in the Metadata
3.2.1. Number of Instances
3.2.2. Number of Numeric Variables
3.2.3. Number of Nominal Variables
3.2.4. Number of Missing Values
3.2.5. Herfindahl–Hirschman Index (HHI)
3.2.6. Number of Variables
3.2.7. Number of Classes
3.2.8. Entropy
3.2.9. Silhouette Score
3.2.10. Data Nonlinearity
3.2.11. Hub Score
3.2.12. Feature Overlap
3.2.13. Neighborhood
3.2.14. Dimensionality
3.3. Sampling Methods Used in the Metadata
3.4. Classification Algorithms Used in the Metadata
3.5. Classification Performance Measurement
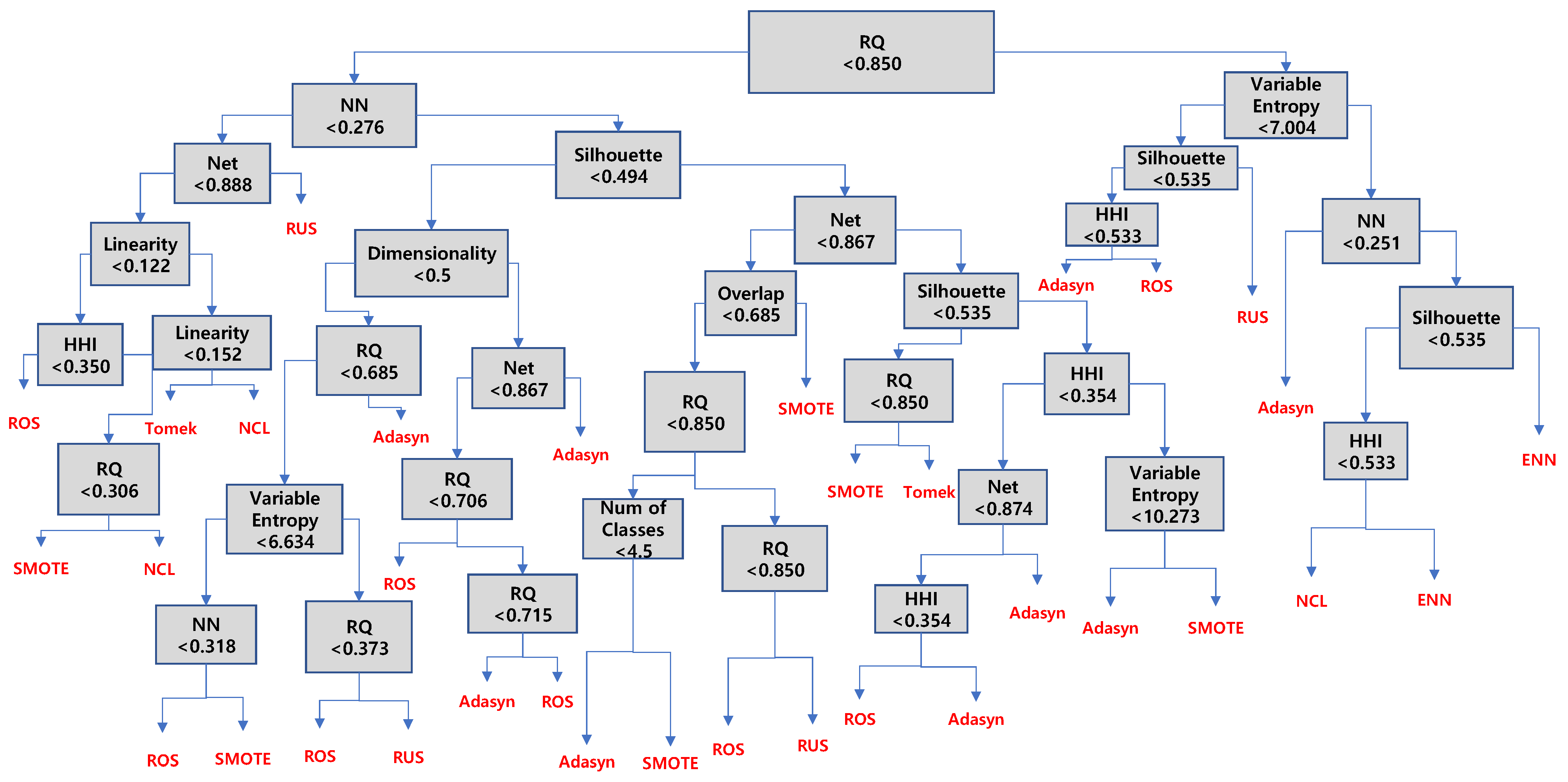
3.6. Extraction of Classification Algorithm Recommendation Rules According to Data Characteristics
4. Validation
4.1. COVID-19 Datasets
4.2. Performance Comparison
4.3. Recommendations
5. Discussion
5.1. Contributions
5.2. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhong, L.; Mu, L.; Li, J.; Wang, J.; Yin, Z.; Liu, D. Early prediction of the 2019 novel coronavirus outbreak in the mainland china based on simple mathematical model. IEEE Access 2020, 8, 51761–51769. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Ma, R.; Wang, L. Predicting turning point, duration and attack rate of COVID-19 outbreaks in major Western countries. Chaos Solitons Fractals 2020, 135, 109829. [Google Scholar] [CrossRef]
- Ghosal, S.; Sengupta, S.; Majumder, M.; Sinha, B. Prediction of the number of deaths in India due to SARS-CoV-2 at 5–6 weeks. Diabetes Metab. Syndr. Clin. Res. Rev. 2020, 14, 311–315. [Google Scholar] [CrossRef]
- Garcia, L.P.; Lorena, A.C.; de Souto, M.C.; Ho, T.K. Classifier recommendation using data complexity measures. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 874–879. [Google Scholar]
- Strubell, E.; Ganesh, A.; McCallum, A. Energy and policy considerations for deep learning in NLP. arXiv 2019, arXiv:1906.02243. [Google Scholar]
- Zhang, Z.; Schott, J.A.; Liu, M.; Chen, H.; Lu, X.; Sumpter, B.G.; Fu, J.; Dai, S. Prediction of carbon dioxide adsorption via deep learning. Angew. Chem. 2019, 131, 265–269. [Google Scholar] [CrossRef]
- Mardani, A.; Liao, H.; Nilashi, M.; Alrasheedi, M.; Cavallaro, F. A multi-stage method to predict carbon dioxide emissions using dimensionality reduction, clustering, and machine learning techniques. J. Clean. Prod. 2020, 275, 122942. [Google Scholar] [CrossRef]
- Siebert, M.; Krennrich, G.; Seibicke, M.; Siegle, A.F.; Trapp, O. Identifying high-performance catalytic conditions for carbon dioxide reduction to dimethoxymethane by multivariate modelling. Chem. Sci. 2019, 10, 10466–10474. [Google Scholar] [CrossRef] [Green Version]
- Schwartz, R.; Dodge, J.; Smith, N.A.; Etzioni, O. Green ai. arXiv 2019, arXiv:1907.10597. [Google Scholar]
- Sun, S.; Shi, H.; Wu, Y. A survey of multi-source domain adaptation. Inf. Fusion 2015, 24, 84–92. [Google Scholar] [CrossRef]
- Cano, J.R. Analysis of data complexity measures for classification. Expert Syst. Appl. 2013, 40, 4820–4831. [Google Scholar] [CrossRef]
- Barella, V.H.; Garcia, L.P.; de Souto, M.P.; Lorena, A.C.; de Carvalho, A. Data complexity measures for imbalanced classification tasks. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Zhu, B.; Baesens, B.; vanden Broucke, S.K. An empirical comparison of techniques for the class imbalance problem in churn prediction. Inf. Sci. 2017, 408, 84–99. [Google Scholar] [CrossRef] [Green Version]
- Brazdil, P.; Gama, J.; Henery, B. Characterizing the applicability of classification algorithms using meta-level learning. In Proceedings of the European Conference on Machine Learning, Catania, Italy, 6–8 April 1994; Springer: Berlin/Heidelberg, Germany, 1994; pp. 83–102. [Google Scholar]
- Dogan, N.; Tanrikulu, Z. A comparative analysis of classification algorithms in data mining for accuracy, speed and robustness. Inf. Technol. Manag. 2013, 14, 105–124. [Google Scholar] [CrossRef]
- Sim, J.; Lee, J.S.; Kwon, O. Missing values and optimal selection of an imputation method and classification algorithm to improve the accuracy of ubiquitous computing applications. Math. Probl. Eng. 2015, 2015, 538613. [Google Scholar] [CrossRef]
- Matsumoto, A.; Merlone, U.; Szidarovszky, F. Some notes on applying the Herfindahl–Hirschman Index. Appl. Econ. Lett. 2012, 19, 181–184. [Google Scholar] [CrossRef]
- Lu, C.; Qiao, J.; Chang, J. Herfindahl–Hirschman Index based performance analysis on the convergence development. Clust. Comput. 2017, 20, 121–129. [Google Scholar] [CrossRef]
- Wu, G.; Chang, E.Y. Aligning boundary in kernel space for learning imbalanced dataset. In Proceedings of the Fourth IEEE International Conference on Data Mining (ICDM’04), Brighton, UK, 1–4 November 2004; pp. 265–272. [Google Scholar]
- Andrić, K.; Kalpić, D.; Bohaček, Z. An insight into the effects of class imbalance and sampling on classification accuracy in credit risk assessment. Comput. Sci. Inf. Syst. 2019, 16, 155–178. [Google Scholar] [CrossRef]
- Nemhauser, G.; Wolsey, L. The scope of integer and combinatorial optimization. In Integer and Combinatorial Optimization; John Wiley & Sons: New York, NY, USA, 1999; pp. 1–26. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Morán-Fernández, L.; Bolón-Canedo, V.; Alonso-Betanzos, A. Can classification performance be predicted by complexity measures? A study using microarray data. Knowl. Inf. Syst. 2017, 51, 1067–1090. [Google Scholar] [CrossRef]
- Rok, B.; Lusa, L. Improved shrunken centroid classifiers for high-dimensional class-imbalanced data. BMC Bioinform. 2013, 14, 64. [Google Scholar]
- Prabakaran, S.; Sahu, R.; Verma, S. Classification of multi class dataset using wavelet power spectrum. Data Min. Knowl. Discov. 2007, 15, 297–319. [Google Scholar] [CrossRef]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef] [Green Version]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Brissaud, J.B. The meanings of entropy. Entropy 2005, 7, 68–96. [Google Scholar] [CrossRef] [Green Version]
- SáEz, J.A.; Luengo, J.; Herrera, F. Predicting noise filtering efficacy with data complexity measures for nearest neighbor classification. Pattern Recognit. 2013, 46, 355–364. [Google Scholar] [CrossRef]
- Garcia, L.P.; de Carvalho, A.C.; Lorena, A.C. Effect of label noise in the complexity of classification problems. Neurocomputing 2015, 160, 108–119. [Google Scholar] [CrossRef]
- Lorena, A.C.; Maciel, A.I.; de Miranda, P.B.; Costa, I.G.; Prudêncio, R.B. Data complexity meta-features for regression problems. Mach. Learn. 2018, 107, 209–246. [Google Scholar] [CrossRef] [Green Version]
- Leyva, E.; González, A.; Perez, R. A set of complexity measures designed for applying meta-learning to instance selection. IEEE Trans. Knowl. Data Eng. 2014, 27, 354–367. [Google Scholar] [CrossRef]
- Lorena, A.C.; Costa, I.G.; Spolaôr, N.; De Souto, M.C. Analysis of complexity indices for classification problems: Cancer gene expression data. Neurocomputing 2012, 75, 33–42. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- L’heureux, A.; Grolinger, K.; Elyamany, H.F.; Capretz, M.A. Machine learning with big data: Challenges and approaches. IEEE Access 2017, 5, 7776–7797. [Google Scholar] [CrossRef]
- He, H.; Garcia, E.A. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. IEEE world congress on computational intelligence. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks, Chemnitz, Germany, 1–8 June 2008; pp. 1322–1328. [Google Scholar]
- Hart, P. The condensed nearest neighbor rule (Corresp.). IEEE Trans. Inf. Theory 1968, 14, 515–516. [Google Scholar] [CrossRef]
- Wilson, D.L. Asymptotic properties of nearest neighbor rules using edited data. IEEE Trans. Syst. Man Cybern. 1972, 3, 408–421. [Google Scholar] [CrossRef] [Green Version]
- Tomek, I Two modifications of cnn. IEEE Trans. Syst. Man Cybern. 1976, 6, 769–772.
- Laurikkala, J. Improving identification of difficult small classes by balancing class distribution. In Proceedings of the Conference on Artificial Intelligence in Medicine in Europe, Hong Kong, China, 1–8 June 2008; Springer: Berlin/Heidelberg, Germany, 2001; pp. 63–66. [Google Scholar]
- Hussain, M.; Wajid, S.K.; Elzaart, A.; Berbar, M. A comparison of SVM kernel functions for breast cancer detection. Imaging and Visualization. In Proceedings of the 2011 Eighth International Conference Computer Graphics, Washington, DC, USA, 17–19 August 2011; pp. 145–150. [Google Scholar]
- Wu, X.; Kumar, V.; Ross, J.Q.; Ghosh, J.; Yang, Q.; Motoda, H.; Geoffrey, J.M.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef] [Green Version]


| Data | Number of Classes | Number of Features | Number of Instances | Imbalance Ratio | HHI |
|---|---|---|---|---|---|
| Wine | 3 | 13 | 178 | 0.676 | 0.342 |
| new_thyroid | 3 | 6 | 215 | 0.200 | 0.533 |
| hayes_roth | 3 | 5 | 132 | 0.588 | 0.350 |
| Cmc | 3 | 10 | 1473 | 0.529 | 0.354 |
| Dermatology | 6 | 35 | 366 | 0.179 | 0.201 |
| Glass | 6 | 10 | 214 | 0.118 | 0.263 |
| balance_scale | 3 | 5 | 625 | 0.170 | 0.431 |
| page_block | 5 | 11 | 5473 | 0.006 | 0.810 |
| Method | Description |
|---|---|
| Random Oversampling (ROS) | This is a method of iteratively recovering and extracting data by randomly selecting data until a few classes are equal to the data size of many classes. The random overextraction method has the advantage of being very convenient to use, with almost no loss of information. However, if the sampling rate is unreasonably increased, an overfitting problem may occur because data of a minority class are repeatedly reconstructed and extracted. |
| Synthetic Minority Oversampling Technique (SMOTE) | This is a method of selecting random data of a minority class and artificially generating new data between k-nearest neighbors [38]. Unlike ROS, which restores and extracts fractional class data, SMOTE has been proposed to avoid the overfitting problem by generating new data. |
| Adaptive Synthetic Sampling Approach for Imbalanced Learning (ADASYN) | This is a method of generating data with consideration of the density distribution of a minority class based on SMOTE [39]. The method is similar to the distribution of the original data because it considers the density distribution of the data. |
| Random Undersampling (RUS) | This is a sampling method in which the majority class is randomly deleted and its proportion adjusted. RUS has the advantage of being easy to use with large-scale data, which can reduce the cost by reducing the amount of data. However, there is a high possibility of losing important information because the data are arbitrarily reduced. |
| Condensed Nearest Neighbors (CNN) | CNN is a method of removing data until there are no data concentrated in a majority class, leaving only representative data in the data distribution. The CNN method leaves data with clear boundaries of different classes [40]. Data are stored one-by-one and a suitable dataset is constructed by removing duplicate data. |
| Edited Nearest Neighbors (ENN) | Unlike CNN, if the value included in set X is misclassified, it can be excluded from X [41]. |
| Tomek link | Based on the CNN sampling method, Tomek link is a method of removing internal data near the decision boundary. The method has the effect of removing ambiguous data overlapping with other classes [42]. Therefore, it is regarded as an efficient sampling method for removing abnormal data. |
| Neighborhood Cleaning Rule (NCL) | NCL is a method that combines condensed nearest neighbors (CNN) and edited nearest neighbors (ENN). It has the effect of clarifying class boundaries by removing data from multiple classes rather than the nearest data, avoiding fractional data [43]. |
| Mean Decrease Accuracy | Mean Decrease Gini | |
|---|---|---|
| Variable Entropy | 41.594 | 33.339 |
| Network | 39.014 | 33.990 |
| Coefficient of Determination | 38.380 | 27.771 |
| Mean Silhouette Score | 36.215 | 26.814 |
| Linearity | 34.618 | 25.051 |
| Overlap | 33.996 | 25.400 |
| Neighborhood | 33.315 | 25.976 |
| Number of Instances | 26.958 | 18.619 |
| Entropy of Classes | 20.992 | 15.608 |
| HHI | 19.424 | 13.738 |
| Dimensionality | 15.510 | 8.321 |
| Number of Missing Values | 13.542 | 3.068 |
| Number of Numeric Variables | 10.892 | 3.782 |
| Number of Features | 10.744 | 3.804 |
| Number of Classes | 6.075 | 0.964 |
| Number of Nominal Features | 0.000 | 0.000 |
| Mean Decrease Accuracy | Mean Decrease Gini | |
|---|---|---|
| Overlap | 41.423 | 34.153 |
| Coefficient of Determination | 39.421 | 29.778 |
| Network | 38.493 | 31.584 |
| Feature Entropy | 38.077 | 32.219 |
| Mean Silhouette Score | 37.022 | 31.640 |
| Neighborhood | 36.737 | 29.920 |
| Linearity | 33.677 | 24.640 |
| Number of Instances | 25.214 | 15.447 |
| Entropy of Classes | 23.919 | 14.360 |
| HHI | 23.122 | 13.595 |
| Number of Missing Values | 18.096 | 4.990 |
| Dimensionality | 15.644 | 6.733 |
| Number of Features | 8.798 | 1.925 |
| Number of Numeric Variables | 8.464 | 1.759 |
| Number of Classes | 6.160 | 0.532 |
| Number of Nominal Features | 0 | 0 |
| Data | Number of Classes | Number of Variables | Number of Instances | Imbalance Ratio | HHI |
|---|---|---|---|---|---|
| Africa | 3 | 5 | 583 | 0.379 | 0.402 |
| China | 3 | 18 | 341 | 0.190 | 0.513 |
| South Korea | 2 | 29 | 187 | 0.307 | 0.640 |
| United States | 3 | 10 | 561 | 0.275 | 0.423 |
| Number of Classes | Africa | China | Korea | United States |
|---|---|---|---|---|
| 3 | 3 | 2 | 3 | |
| HHI | 0.403 | 0.513 | 0.64 | 0.423 |
| Number of Instances | 524.7 | 306.9 | 168.3 | 504.9 |
| Number of Variables | 5 | 18 | 29 | 10 |
| Number of Nominal Variables | 4 | 17 | 28 | 9 |
| Number of Nominal Features | 0 | 0 | 0 | 0 |
| Number of Missing Values | 6 | 10 | 16 | 0 |
| Coefficient of Determination | 0.013 | 0.199 | 0.684 | 0.233 |
| Entropy of Classes | 1.444 | 1.22 | 0.787 | 1.394 |
| Entropy of Variables | 9.461 | 8.114 | 7.733 | 8.927 |
| Dimensionality | 0.25 | 0.353 | 0.107 | 0.444 |
| Linearity | 0.242 | 0.133 | 0.000 | 0.150 |
| Network | 0.882 | 0.71 | 0.749 | 0.899 |
| Overlap | 0.949 | 0.952 | 0.929 | 0.932 |
| Neighborhood | 0.478 | 0.489 | 0.47 | 0.472 |
| Mean Silhouette Score | 0.677 | 0.361 | 0.638 | 0.479 |
| Method | F-Score | F-Score (s.d.) | Elapsed Time (s) | Elapsed Time (s.d.) (s) |
|---|---|---|---|---|
| Random | 0.618 | 0.187 | 1.858 | 0.870 |
| Ensemble | 0.555 | 0.260 | 5.018 | 1.936 |
| Greedy | 0.763 | 0.263 | 9.288 | 4.348 |
| Proposed | 0.765 | 0.126 | 0.740 | 0.916 |
| Method | F-Score | F-Score (s.d.) | Elapsed Time (s) | Elapsed Time (s.d.) (s) |
|---|---|---|---|---|
| Ensemble | 0.679 | 0.172 | 5.627 | 2.704 |
| Random | 0.568 | 0.241 | 1.654 | 0.750 |
| Greedy | 0.693 | 0.418 | 13.236 | 5.998 |
| Proposed | 0.688 | 0.173 | 0.567 | 0.371 |
| Data | Performance | k-NN | Logistic Regression (LR) | Naïve Bayes (NB) | Random Forest (RF) | SVM | Ensemble | Recommended Algorithm |
|---|---|---|---|---|---|---|---|---|
| Africa | F-score | 0.49 | 0.17 | 0.67 | 0.56 | 0.34 | 0.27 | Random Forest |
| Elapsed | 0.01 | 0.11 | 0.00 | 0.08 | 0.03 | 0.21 | ||
| Elapsed Sum | 0.37 | 3.46 | 0.21 | 4.64 | 1.83 | 6.58 | ||
| Total Time | 4.30 | 5.99 | 0.78 | 5.10 | 2.36 | 9.23 | ||
| China | F-score | 0.39 | 0.53 | 0.71 | 0.53 | 0.55 | 0.45 | Naïve Bayes |
| Elapsed | 0.01 | 0.04 | 0.01 | 0.13 | 0.04 | 0.14 | ||
| Elapsed Sum | 0.46 | 1.16 | 0.37 | 7.18 | 2.35 | 4.71 | ||
| Total Time | 1.94 | 3.22 | 0.96 | 7.79 | 2.96 | 6.80 | ||
| South Korea | F-score | 0.72 | 0.81 | 0.94 | 0.95 | 0.88 | 0.88 | k-NN, Logistic Regression |
| Elapsed | 0.01 | 0.01 | 0.01 | 0.04 | 0.02 | 0.08 | ||
| Elapsed Sum | 0.38 | 0.45 | 0.59 | 2.11 | 0.87 | 2.40 | ||
| Total Time | 1.23 | 1.14 | 0.97 | 2.31 | 1.19 | 3.06 | ||
| United States | F-score | 0.54 | 0.56 | 0.73 | 0.67 | 0.62 | 0.62 | Naïve Bayes, Random Forest |
| Elapsed | 0.01 | 0.05 | 0.00 | 0.11 | 0.04 | 0.19 | ||
| Elapsed Sum | 0.38 | 1.80 | 0.27 | 6.11 | 2.16 | 6.38 | ||
| Total Time | 3.29 | 6.05 | 0.86 | 6.59 | 2.74 | 10.38 |
| Data | Performance | ADASYN | CNN | ENN | NCL | ROS | RUS | SMOTE | Tomek | Recommended Sampling Method | Suggested Method Elapsed |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Africa | F-score | 0.15 | 0.25 | 0.57 | 0.04 | 0.55 | 0.34 | 0.53 | 0.34 | ADASYN, SMOTE | 0.02 |
| Sampling Time | 0.05 | 0.11 | 0.02 | 0.09 | 0.04 | 0.10 | 0.04 | 0.21 | |||
| Sum of Sampling Time | 0.38 | 0.77 | 0.18 | 0.65 | 2.83 | 7.32 | 3.29 | 1.67 | |||
| Total Time | 0.61 | 8.62 | 0.31 | 1.25 | 3.14 | 7.42 | 4.18 | 2.23 | |||
| China | F-score | 0.28 | 0.45 | 0.49 | 0.06 | 0.62 | 0.51 | 0.62 | 0.41 | ROS | |
| Sampling Time | 0.08 | 0.09 | 0.03 | 0.06 | 0.06 | 0.06 | 0.06 | 0.07 | |||
| Sum of Sampling Time | 0.60 | 0.72 | 0.23 | 0.49 | 4.82 | 4.62 | 4.25 | 0.50 | |||
| Total Time | 0.79 | 5.15 | 0.35 | 1.10 | 5.16 | 4.90 | 5.41 | 0.81 | |||
| South Korea | F-score | 0.91 | 0.81 | 0.92 | 0.89 | 0.92 | 0.79 | 0.92 | 0.85 | SMOTE | |
| Sampling Time | 0.03 | 0.04 | 0.02 | 0.05 | 0.02 | 0.03 | 0.02 | 0.04 | |||
| Sum of Sampling Time | 0.22 | 0.25 | 0.17 | 0.36 | 1.54 | 2.30 | 1.64 | 0.32 | |||
| Total Time | 0.29 | 1.71 | 0.27 | 0.45 | 1.77 | 2.55 | 2.14 | 0.72 | |||
| United States | F-score | 0.68 | 0.54 | 0.67 | 0.60 | 0.68 | 0.58 | 0.66 | 0.56 | ADASYN, SMOTE, ROS | |
| Sampling Time | 0.06 | 0.15 | 0.03 | 0.09 | 0.05 | 0.08 | 0.05 | 0.10 | |||
| Sum of Sampling Time | 0.45 | 1.22 | 0.23 | 0.74 | 4.00 | 5.87 | 3.86 | 0.73 | |||
| Total Time | 0.69 | 10.80 | 0.39 | 1.71 | 4.22 | 5.98 | 4.89 | 1.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Kwon, O. A Model for Rapid Selection and COVID-19 Prediction with Dynamic and Imbalanced Data. Sustainability 2021, 13, 3099. https://doi.org/10.3390/su13063099
Kim J, Kwon O. A Model for Rapid Selection and COVID-19 Prediction with Dynamic and Imbalanced Data. Sustainability. 2021; 13(6):3099. https://doi.org/10.3390/su13063099
Chicago/Turabian StyleKim, Jeonghun, and Ohbyung Kwon. 2021. "A Model for Rapid Selection and COVID-19 Prediction with Dynamic and Imbalanced Data" Sustainability 13, no. 6: 3099. https://doi.org/10.3390/su13063099
APA StyleKim, J., & Kwon, O. (2021). A Model for Rapid Selection and COVID-19 Prediction with Dynamic and Imbalanced Data. Sustainability, 13(6), 3099. https://doi.org/10.3390/su13063099







