Thermo-Hydraulic Performance of U-Tube Borehole Heat Exchanger with Different Cross-Sections
Abstract
:1. Introduction
2. Physical Model
2.1. Stratigraphic Descriptions
2.2. Thermal Response Test (TRT)
3. Numerical Model
- The thermo-physical properties of the material are constant and do not change with the change in soil temperature;
- The effect of underground water flow on BHEs is neglected;
- The soil layer is homogeneous; and
- The fluid is incompressible.
3.1. Geometry and Meshing
3.2. Governing Equations
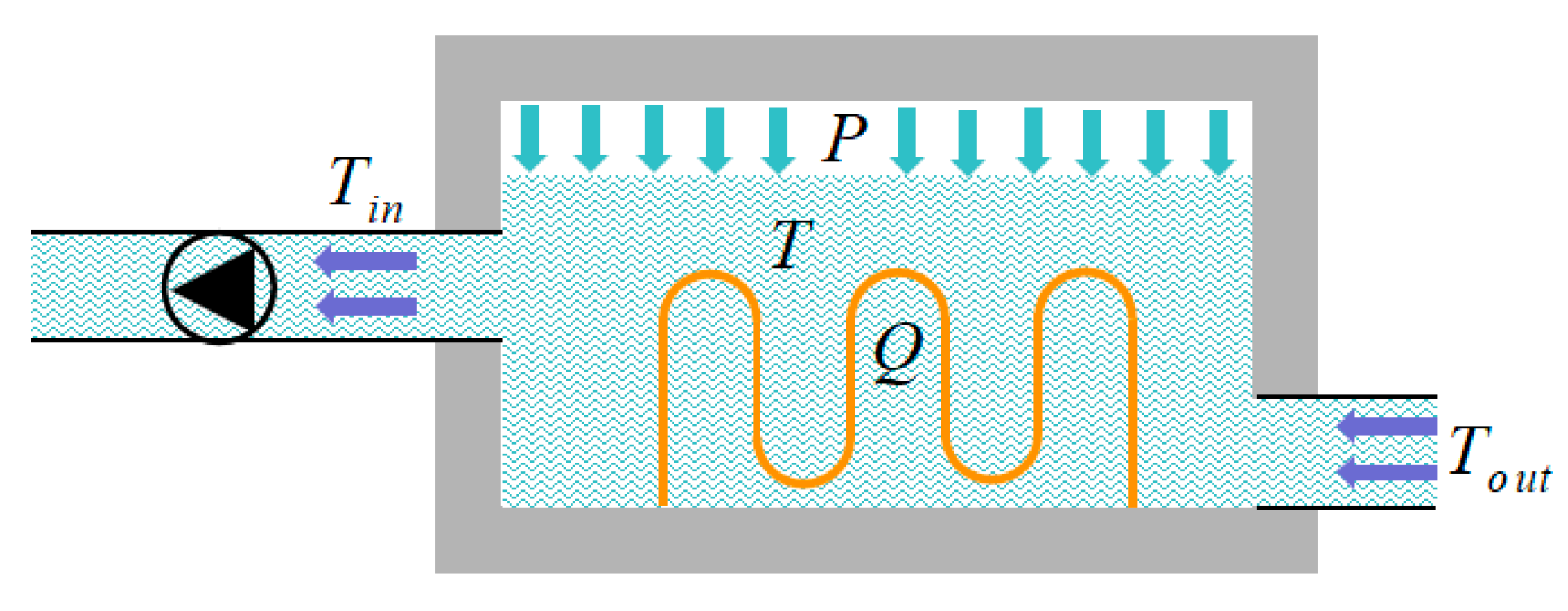
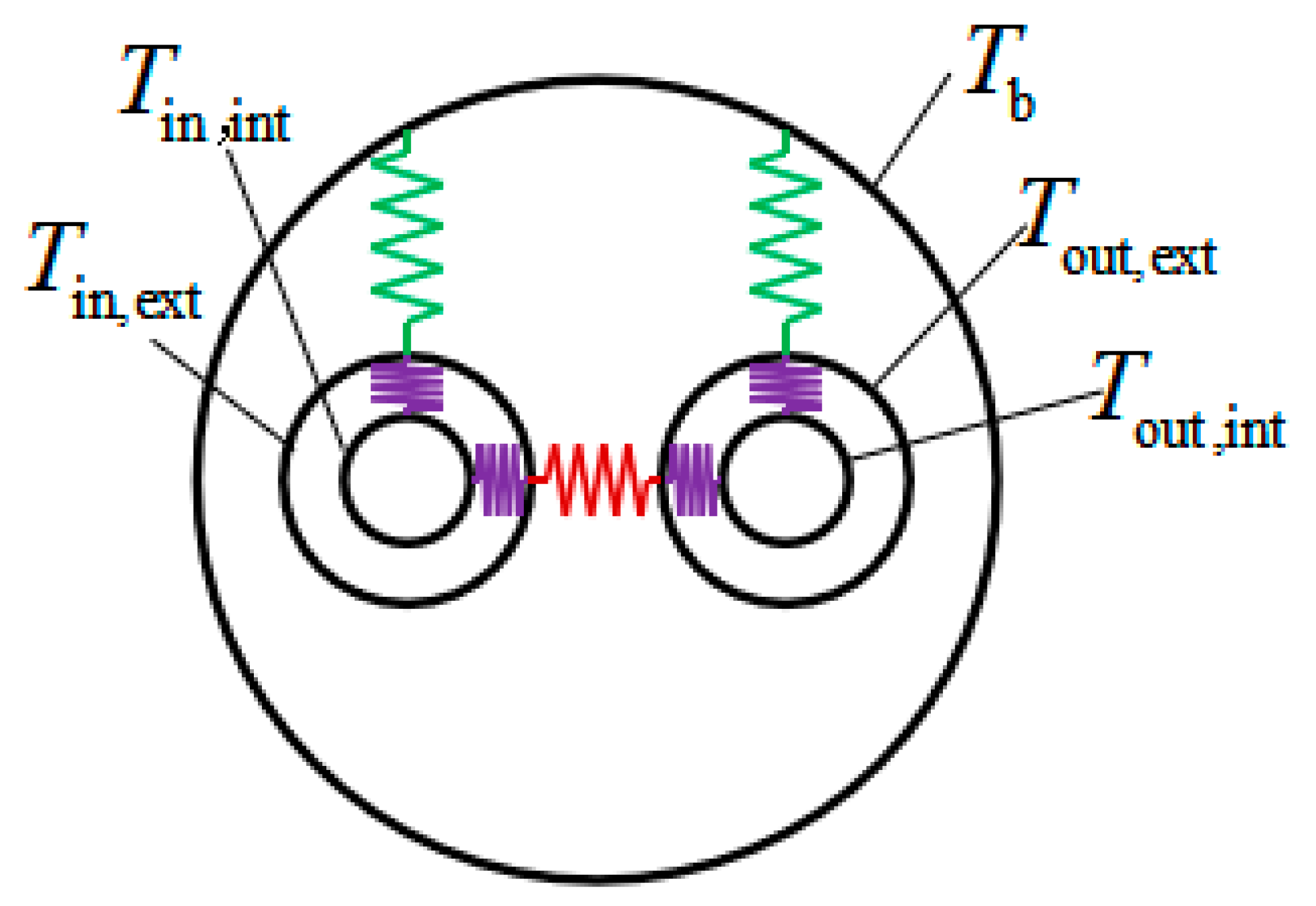
3.3. Initial Conditions and Boundary Conditions
3.4. Heating Model by Rated Power
4. Results and Discussion
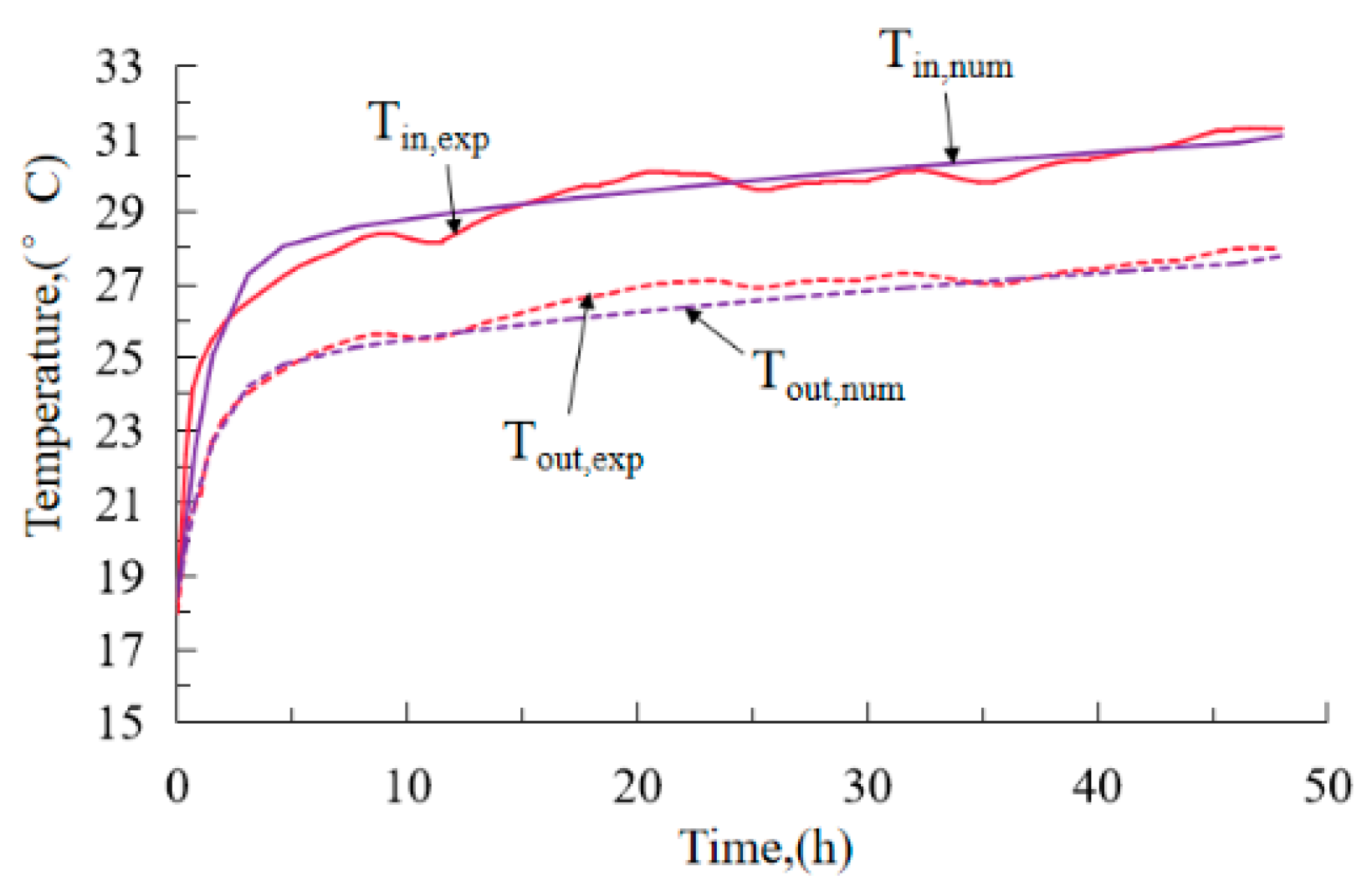
4.1. Model Validation
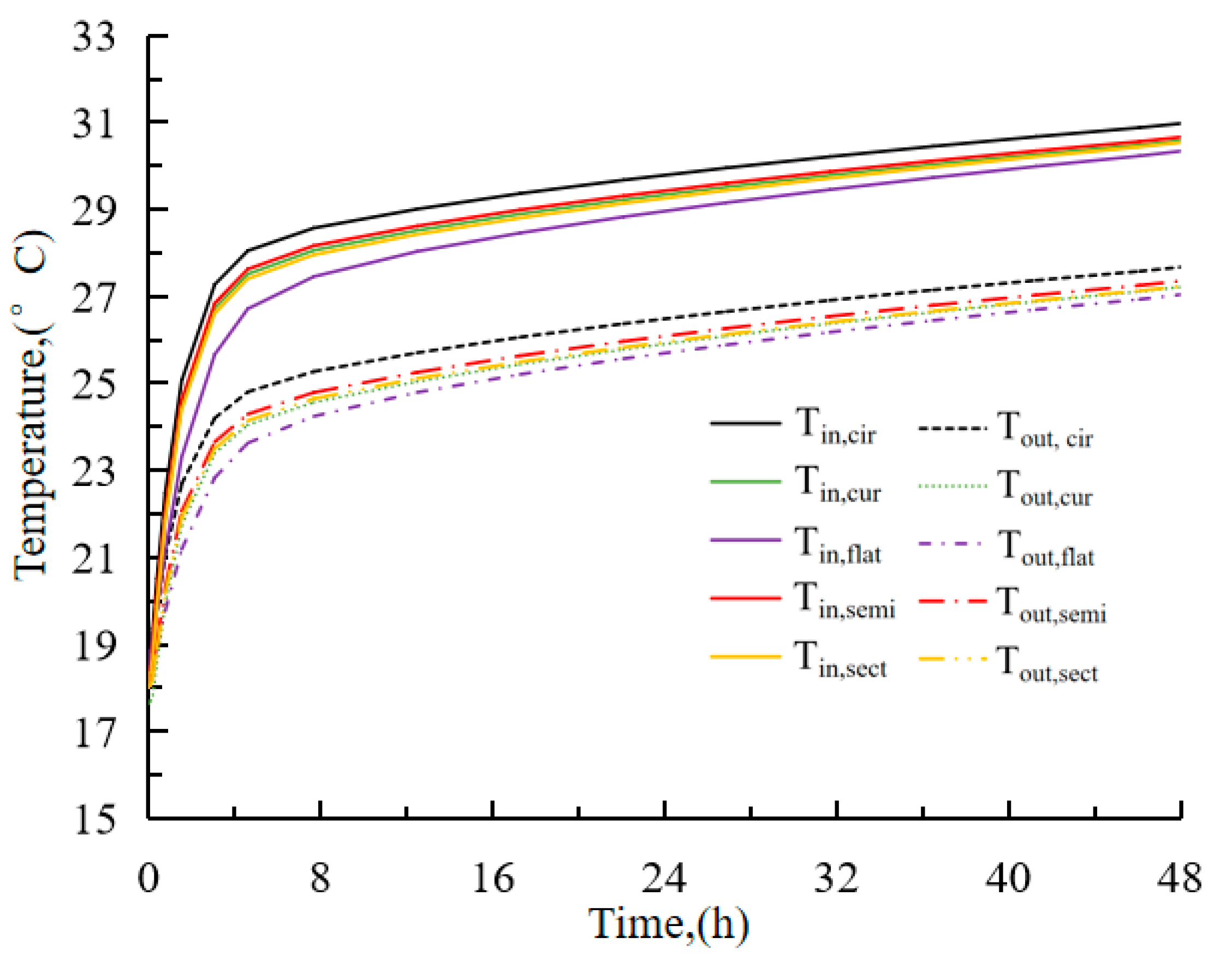
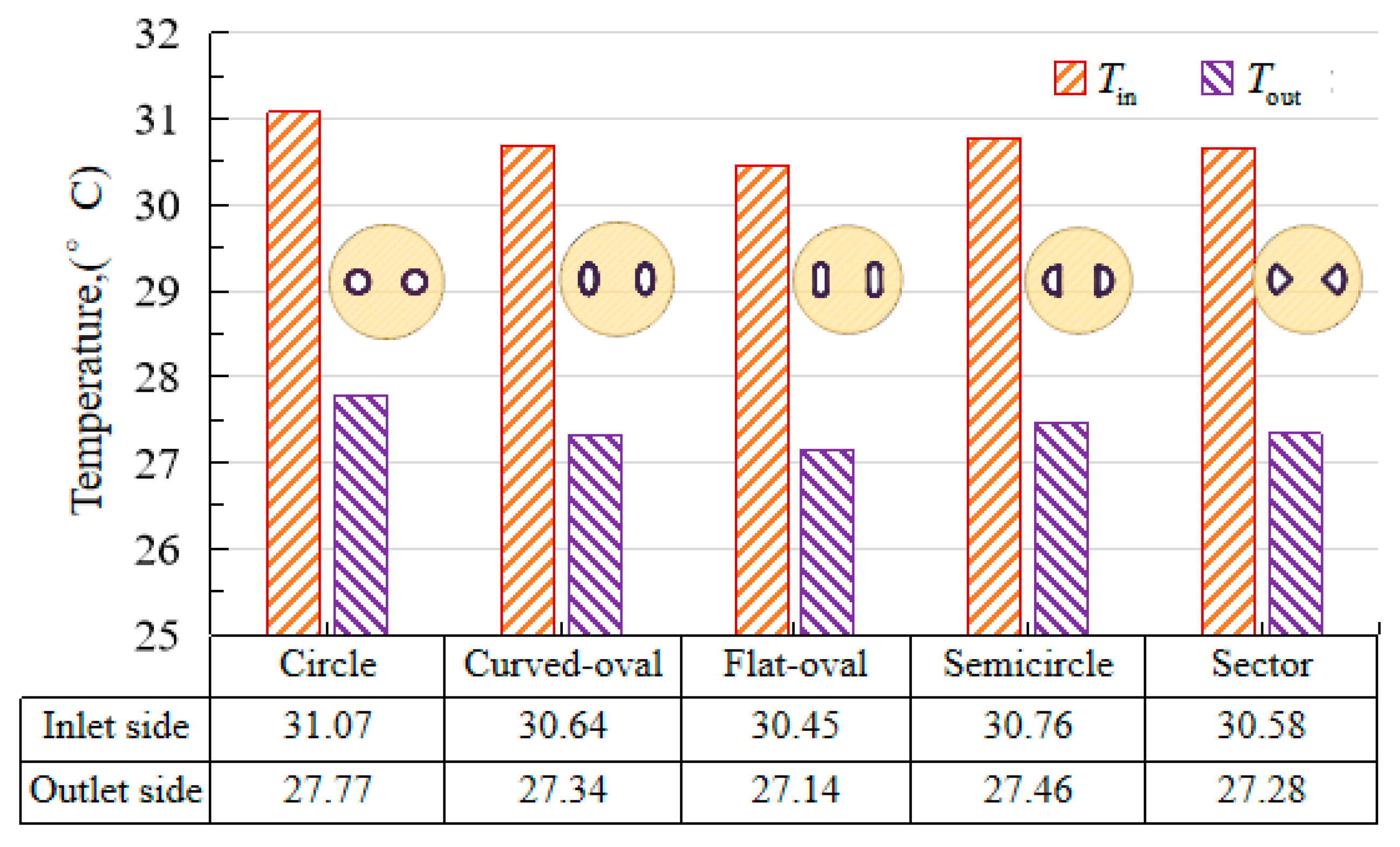
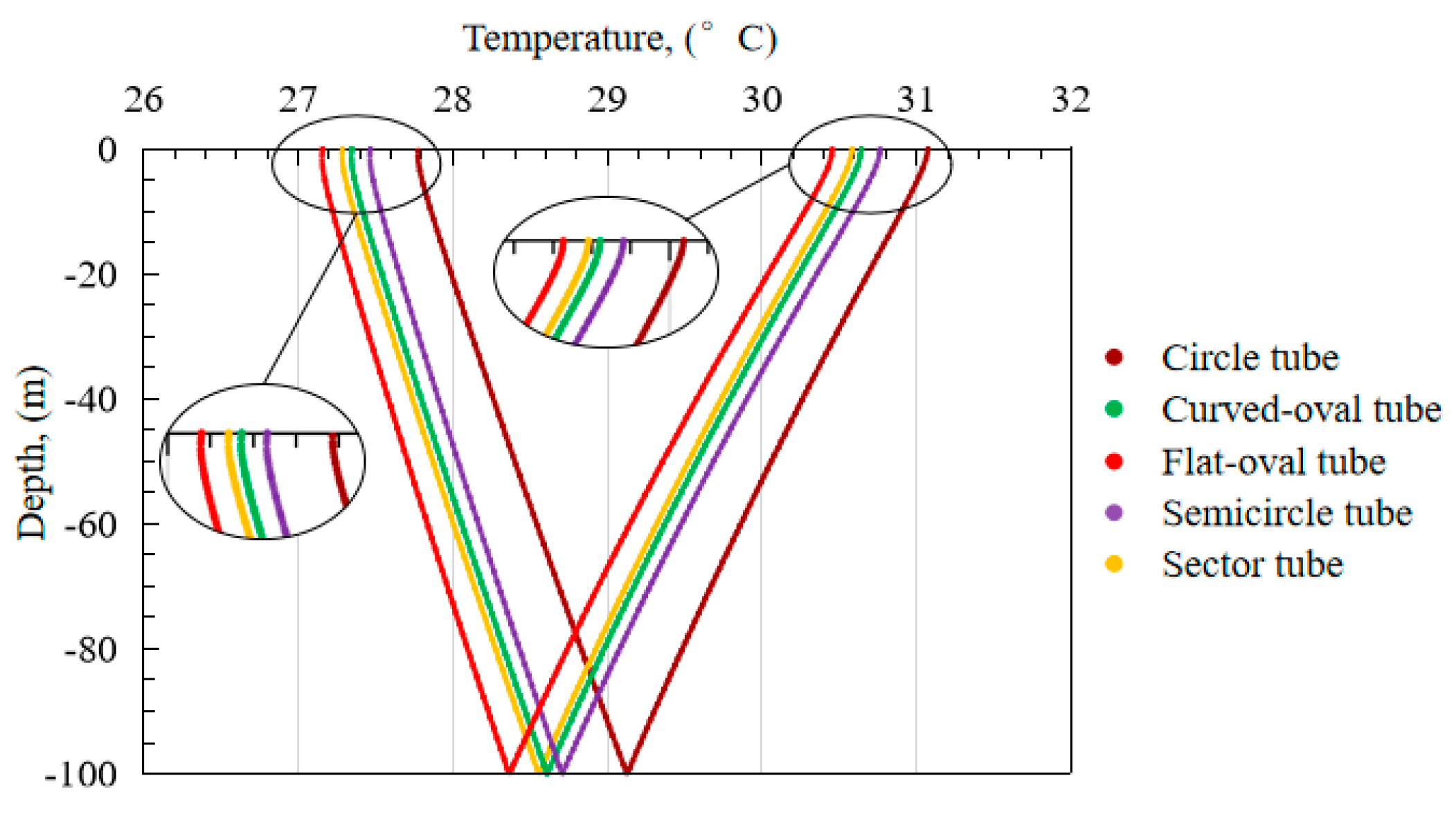
4.2. Temperature of Inlet and Outlet
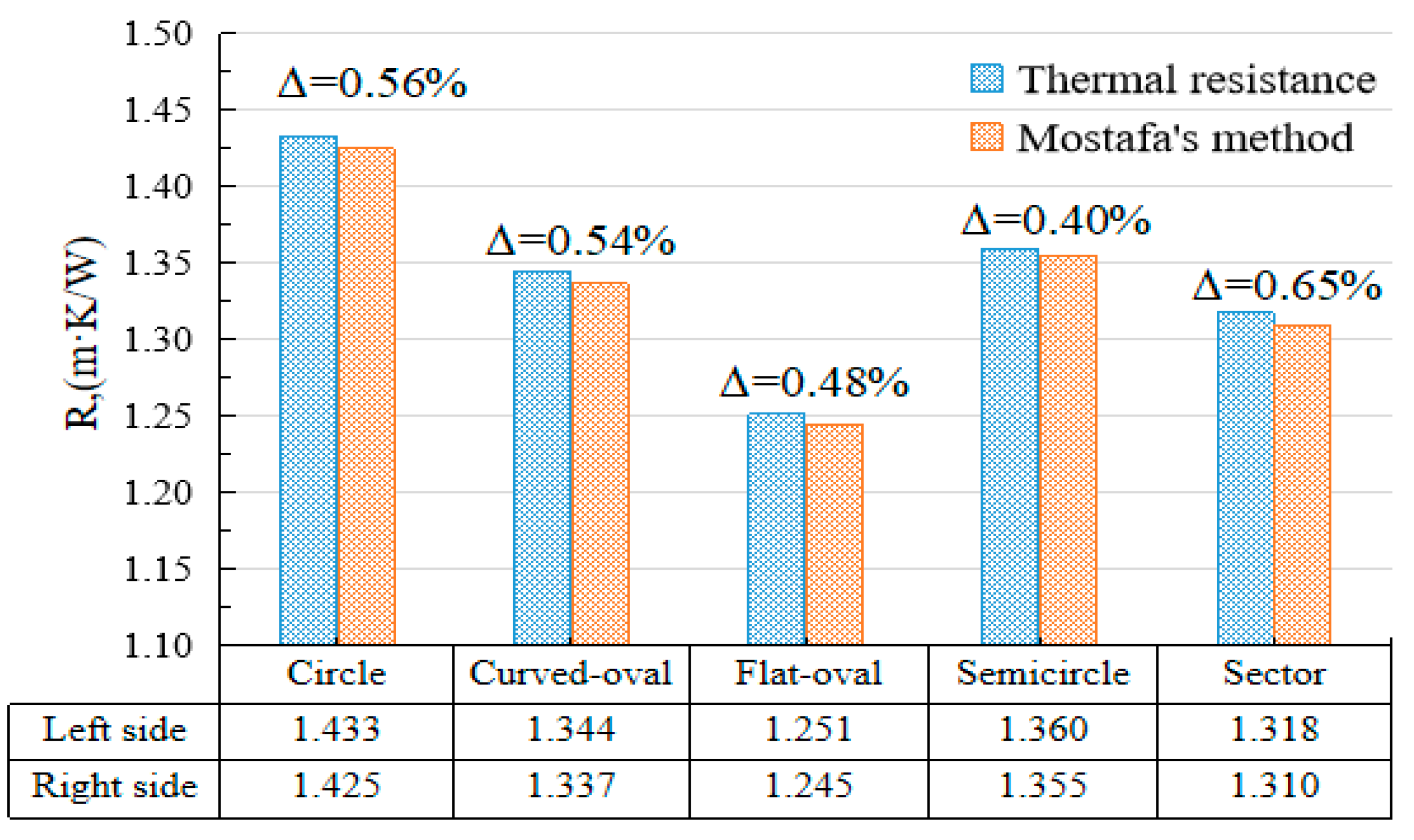
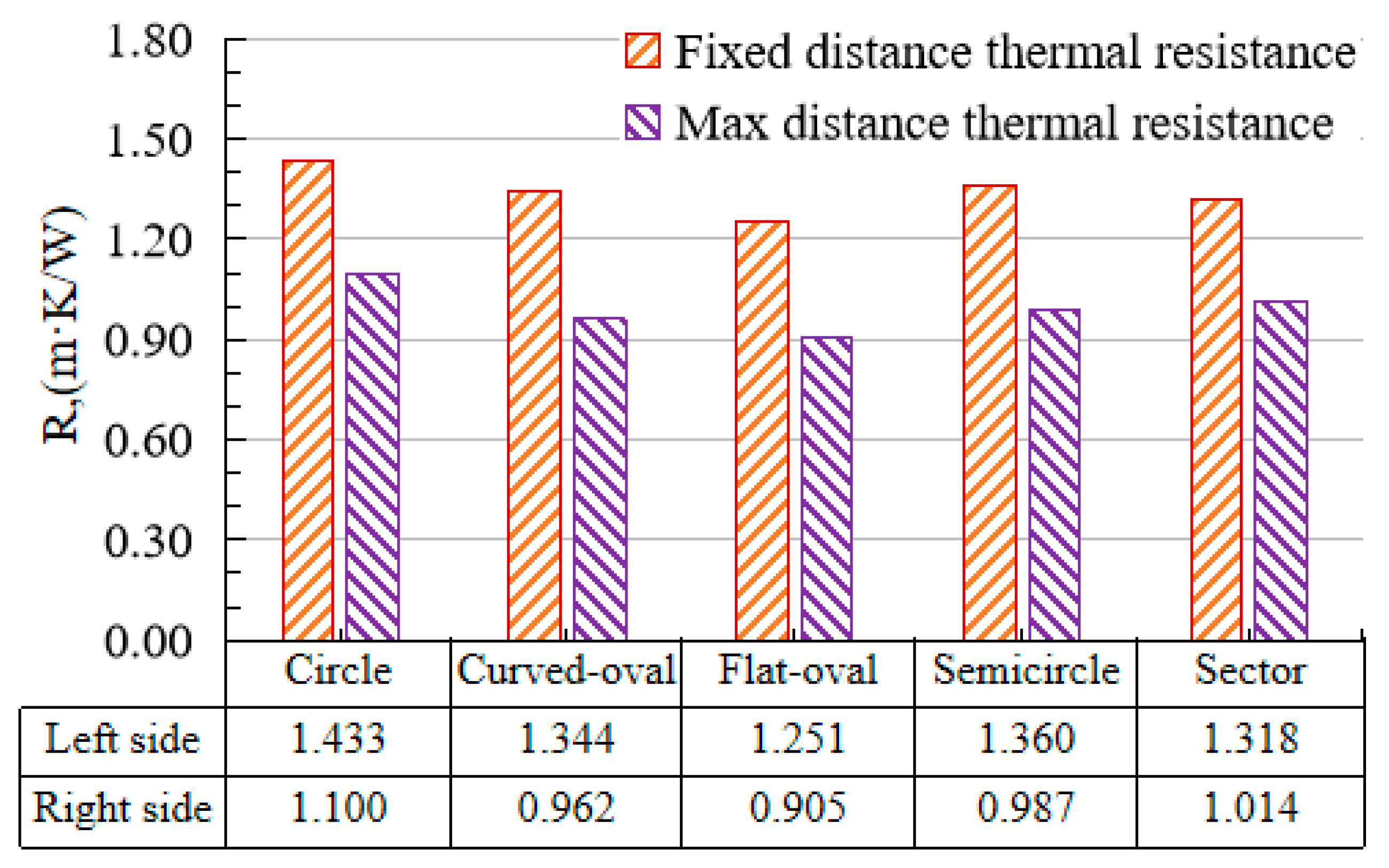
4.3. Thermal Resistance of BHEs
4.4. Temperature Distribution of U-Tube
4.5. Borehole Wall Temperature
5. Heat Resistance under Different Leg Distances
5.1. Control of Leg Distance
5.2. Heat Resistance with Different Leg Distances
6. Conclusions
- (1)
- Based on TRTs, we verified the reliability of using COMSOL Multi-physics with three-dimensional models to study the heat exchange characteristic of BHEs.
- (2)
- Compared with the inlet and outlet temperatures of the tube with a circle shape at 48 h, the results show that the heat exchange efficiency of the curved oval tube increases by 13.0%, the flat oval tube by 19.1%, the semicircle tube by 9.4%, and sector tube by 14.8%.
- (3)
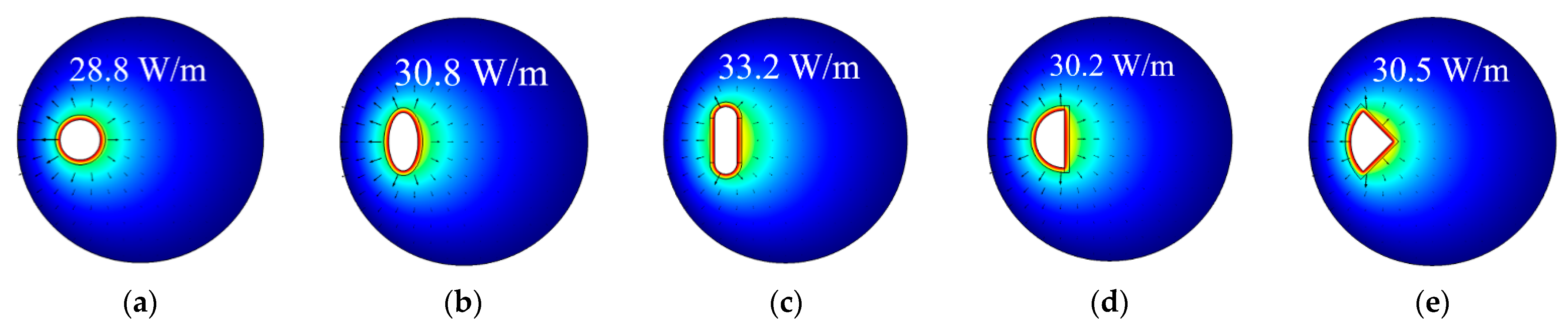
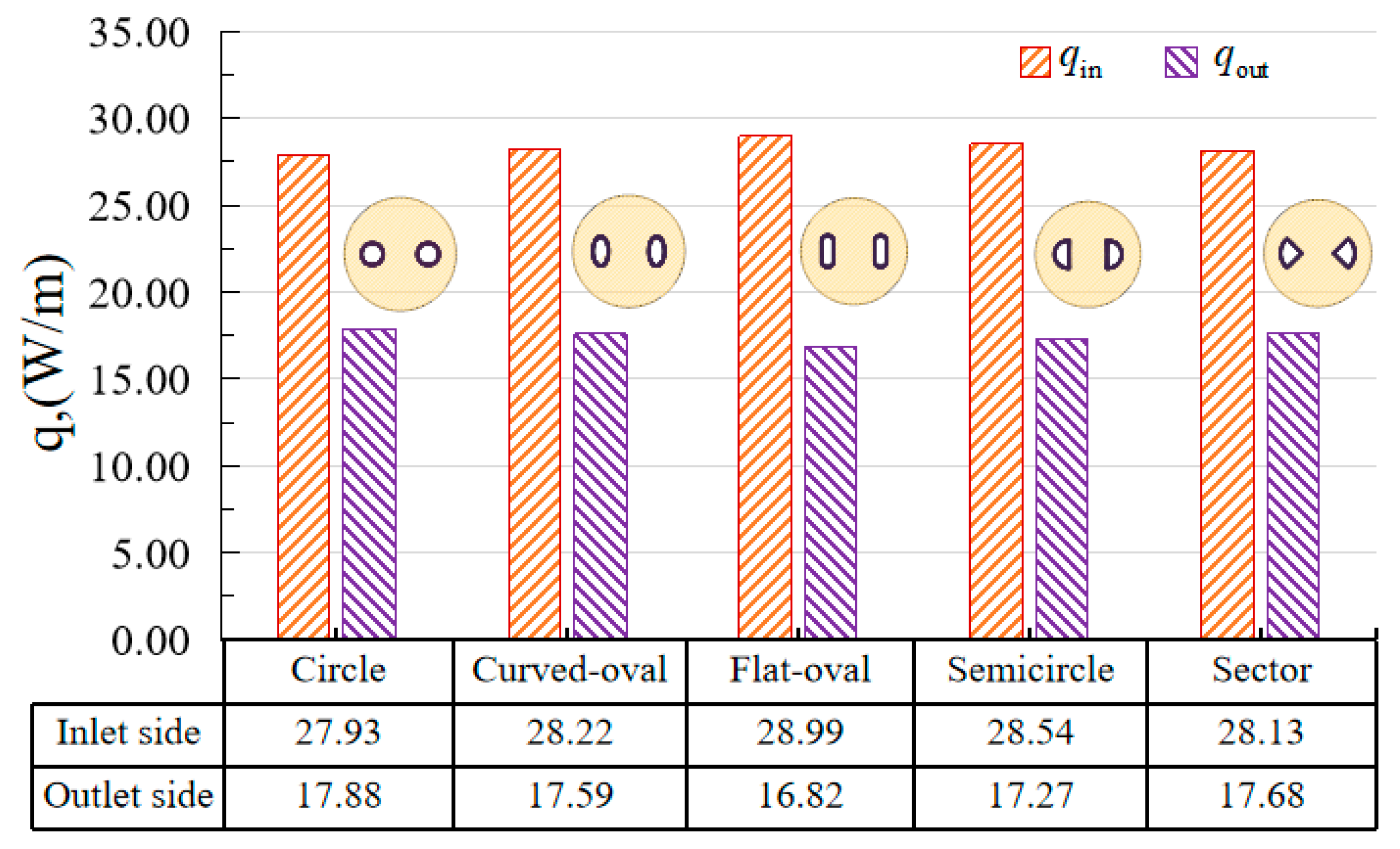
- The heat flux heterogeneity of the tube on the inlet and outlet sides in BHEs with different tube shapes in decreasing order is flat oval shape, semicircle shape, curved oval shape, sector shape, and circle shape.
- (4)
- The temperature heterogeneity of the borehole wall in BHEs with different tube shapes in decreasing order is circle shape, sector shape, curved oval shape, flat oval shape, and semicircle shape.
- (5)
- Compared with the heat resistance of the circle-shaped tube at 48 h, we found that the heat resistance of the curved oval tube decreased by 12.6%, the flat oval tube by 17.7%, the semicircle tube by 10.3%, and the sector tube by 7.8% at maximum leg distance.
- (6)
- The adjustment of the leg distance affects the heat resistance by about 25% and the adjustment of the tube shape affects the heat resistance by about 12%.
- (7)
- The adjustment of tube shape can improve the heat exchange efficiency of BHEs, and the flat-oval-shaped tube at maximum leg distance was found to be the best tube design for BHEs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, G.; Wang, H.J.; Wu, Q.G. Wind power development in the Belt and Road area of Xinjiang, China: Problems and solutions. Util. Policy 2020, 101024. [Google Scholar] [CrossRef]
- Domfeh, M.K.; Mark, S.G.; Robert, A.; Antwi, E.; Tabor, G. Free surface vortices at hydropower intakes: A state-of-the-art review. Sci. Afr. 2020, 21, e355. [Google Scholar] [CrossRef]
- Harcourt, F.; Angeloudis, A.; Piggott, M.D. Utilising the flexible generation potential of tidal range power plants to optimise economic value. Appl. Energy 2019, 237, 873–884. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.Q.; Liu, Y.X.; Dou, J.Y.; Li, M.Z.; Zeng, M. Geothermal energy in China: Status, challenges, and policy recommendations. Util. Policy 2020, 64, 101020. [Google Scholar] [CrossRef]
- Kumar, S.; Gupta, S.K.; Rawat, M. Resources and utilization of geothermal energy in India: An Eco—Friendly approach towards sustainabilit. Mater. Today Proc. 2020, 13. [Google Scholar] [CrossRef]
- Huang, X.W.; Zhou, A.Z.; Wang, W.; Jiang, P.M. Characterization of the dynamic properties of clay–gravel mixtures at low strain level. Sustainability 2020, 4, 1616. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Zhang, H.Z.; Chen, Z.Q. Study on heat transfer performance of geothermal pile-foundation heat exchanger with 3-U pipe configuration. Int. J. Heat Mass. Tran. 2020, 147, 119020. [Google Scholar] [CrossRef]
- Younas, U.; Khan, B.; Ali, S.M.; Arshad, C.M.; Vaccaro, A. Pakistan geothermal renewable energy potential for electric power generation: A survey. Renew. Sustain. Energy Rev. 2016, 63, 398–413. [Google Scholar] [CrossRef]
- Kerme, E.D.; Fung, A.S. Heat transfer simulation, analysis and performance study of single U-tube borehole heat exchanger. Renew. Energy 2020, 145, 1430–1448. [Google Scholar] [CrossRef]
- Zhang, W.K.; Yang, H.X.; Diao, N.R.; Lu, L.; Fang, Z.H. Exploration on the reverse calculation method of groundwater velocity by means of the moving line heat source. Int. J. Therm. Sci. 2016, 99, 52–63. [Google Scholar] [CrossRef]
- Li, H.; Xi, C.; Kong, X.F.; Lin, Z.; Wang, L. A comparative experimental investigation on radiant floor heating system and stratum ventilation. Sustain. Cities Soc. 2020, 52, 101823. [Google Scholar] [CrossRef]
- Jahanbin, A. Thermal performance of the vertical ground heat exchanger with a novel elliptical single U-tube. Geothermics 2020, 86, 101804. [Google Scholar] [CrossRef]
- Serageldin, A.; Sakata, Y.; Katsura, T.; Nagano, K. Thermo-hydraulic performance of the U-tube borehole heat exchanger with a novel oval cross-section: Numerical approach. Energy Convers. Manag. 2018, 177, 406–415. [Google Scholar] [CrossRef]
- Narei, H.; Fatehifar, M.; Ghasempour, R.; Noorollahi, Y. In pursuit of a replacement for conventional high-density polyethylene tubes in ground source heat pumps from their composites—A comparative study. Geothermics 2020, 87, 101819. [Google Scholar] [CrossRef]
- Zanchini, E.; Jahanbin, A. Effects of the temperature distribution on the thermal resistance of double u-tube borehole heat exchangers. Geothermics 2018, 71, 46–54. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, S.; Yang, Y.; Sun, Y. Transient heat transfer performance of a vertical double U-tube borehole heat exchanger under different operation conditions. Renew. Energy 2019, 131, 494–505. [Google Scholar] [CrossRef]
- Eicker, U.; Vorschulze, C. Potential of geothermal heat exchangers for office building climatisation. Renew. Energy 2009, 34, 1126–1133. [Google Scholar] [CrossRef]
- Lund, J.W.; Boyd, T.L. Direct utilization of geothermal energy 2015 worldwide review. Geothermics 2016, 60, 66–93. [Google Scholar] [CrossRef]
- Choab, N.; Allouhi, A.; Maakoul, A.E.; Kousksou, T.; Jamil, A. Review on greenhouse microclimate and application: Design parameters, thermal modeling and simulation, climate controlling technologies. Sol. Energy 2019, 191, 109–137. [Google Scholar] [CrossRef]
- Gajewski, A.; Gładyszewska, F.K.; Krawczyk, D.A. Carbon dioxide emissions during air, ground, or groundwater heat pump performance in białystok. Sustainability 2019, 18, 5087. [Google Scholar] [CrossRef] [Green Version]
- Marrasso, E.; Roselli, C.; Sasso, M.; Tariello, F. Global and local environmental and energy advantages of a geothermal heat pump interacting with a low temperature thermal micro grid. Energy Convers. Manag. 2018, 172, 540–553. [Google Scholar] [CrossRef]
- Wua, S.Y.; Daib, Y.C.; Lic, X.L.; Opponga, F.; Xu, C.S. Assessing the feasibility of using the heat demand-outdoor temperature function for a long-term district heat demand forecast. Energy Procedia 2018, 152, 413–418. [Google Scholar] [CrossRef]
- Ma, W.; Kim, M.K.; Hao, J. Numerical Simulation Modeling of a GSHP and WSHP System for an Office Building in the Hot Summer and Cold Winter Region of China: A Case Study in Suzhou. Sustainability 2019, 12, 3282. [Google Scholar] [CrossRef] [Green Version]
- Blomqvist, S.; La Fleur, L.; Amiri, S.; Rohdin, P.; Trygg, L.Ö.F. The impact on system performance when renovating a multifamily building stock in a district heated region. Sustainability 2019, 8, 2199. [Google Scholar] [CrossRef] [Green Version]
- Blum, P.; Campillo, G.; Kölbel, T. Techno-economic and spatial analysis of vertical ground source heat pump systems in Germany. Energy 2011, 5, 3001–3011. [Google Scholar] [CrossRef]
- Karytsas, S.; Choropanitis, I. Barriers against and actions towards renewable energy technologies diffusion: A Principal Component Analysis for residential ground source heat pump (GSHP) systems. Energy Rev. 2017, 78, 252–271. [Google Scholar] [CrossRef]
- Lu, Q.; Narsilio, G.A.; Aditya, G.R.; Johnston, I.W. Cost and performance data for residential buildings fitted with GSHP systems in Melbourne Australia. Data Brief. 2017, 12, 9–12. [Google Scholar] [CrossRef] [PubMed]
- Robert, F.; Gosselin, L. New methodology to design ground coupled heat pump systems based on total cost minimization. Appl. Therm. Eng. 2014, 2, 281–291. [Google Scholar] [CrossRef]
- Wu, S.Y.; Dai, Y.C.; Li, X.L.; Oppong, F.; Xu, C.S. A review of ground-source heat pump systems with heat pipes for energy efficiency in buildings. Energy Procedia 2018, 152, 413–418. [Google Scholar] [CrossRef]
- Karytsas, S.C.; Chaldezos, I.P. Review of the greek legislative framework for ground source heat pumps (gshps) and suggestions for its improvement. Procedia Environ. Sci. 2017, 38, 704–712. [Google Scholar] [CrossRef]
- Zhou, J.; Ding, M.; Bian, H.Z.; Zhang, Y.X.; Sun, Z.N. CFD simulation for the effect of the header match on the flow distribution in a central-type parallel heat exchanger. Chem. Eng. Res. Des. 2018, 136, 144–153. [Google Scholar] [CrossRef]
- Danielewicz, J.; Śniechowska, B.; Sayegh, M.A.; Fidorów, N.; Jouhara, H. Three-dimensional numerical model of heat losses from district heating network pre-insulated pipes buried in the ground. Energy 2016, 108, 172–184. [Google Scholar] [CrossRef] [Green Version]
- Gerlich, V.; Sulovská, K.; Zálešák, M. COMSOL Multiphysics validation as simulation software for heat transfer calculation in buildings: Building simulation software validation. Measurement 2013, 6, 2003–2012. [Google Scholar] [CrossRef] [Green Version]
- Bryś, K.; Bryś, T.; Sayegh, M.A.; Ojrzyńska, H. Characteristics of heat fluxes in subsurface shallow depth soil layer as a renewable thermal source for ground coupled heat pumps. Renew. Energy 2020, 146, 1846–1866. [Google Scholar] [CrossRef]
- Sayegh, M.A.; Jadwiszczak, P.; Axcell, B.P.; Niemierka, E.; Bryś, K.; Jouhara, H. Heat pump placement, connection and operational modes in European district heating. Energy Build. 2018, 166, 122–144. [Google Scholar] [CrossRef]
- Bryś, K.; Bryś, T.; Sayegh, M.A.; Ojrzyńska, H. Subsurface shallow depth soil layers thermal potential for ground heat pumps in Poland. Energy Build. 2018, 165, 64–75. [Google Scholar] [CrossRef]
- Zhang, C.X.; Xu, H.; Fan, J.H.; Sun, P.K.; Sun, S.C.; Kong, X.Q. The coupled two-step parameter estimation procedure for borehole thermal resistance in thermal response test. Renew. Energy 2020, 154, 672–683. [Google Scholar] [CrossRef]
- Marcotte, B.; Bernier, M. Experimental validation of a TRC model for a double U-tube borehole with two independent circuits. Appl. Therm. Eng. 2019, 162, 114–229. [Google Scholar] [CrossRef]
- Zhou, K.; Mao, J.F.; Li, Y.; Xiang, J.Y. Parameters optimization of borehole and internal thermal resistance for single U-tube ground heat exchangers using Taguchi method. Energy Convers. Manag. 2019, 201, 112177. [Google Scholar] [CrossRef]
- Javadi, H.; Ajarostaghi, S.S.M.; Rosen, M.A.; Pourfallah, M. Performance of ground heat exchangers: A comprehensive review of recent advances. Energy 2019, 178, 207–233. [Google Scholar] [CrossRef]
- Suzukia, M.; Yoneyam, K.; Amemiy, S.; Motoaki, O. Development of a spiral type heat exchanger for ground source heat pump system. Energy Procedia 2016, 503, 503–510. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.F.; Luo, X.W.; Huang, G.S.; Zhang, Q. Comparative analysis of U-pipe location on the sizing of borehole heat exchangers. Appl. Therm. Eng. 2019, 150, 666–673. [Google Scholar] [CrossRef]
- Marzena, N.O.; Ocłoń, P. Thermal and economic analysis of preinsulated and twin-pipe heat network operation. Energy 2020, 193, 116619. [Google Scholar] [CrossRef]
- Arif, W.; Shrestha, G.; Takeshi, I.; Kasumi, Y.; Youhei, U.; Mayumi, Y. Using a capillary mat as a shallow heat exchanger for a ground source heat pump system. Energy Build. 2020, 209, 109684. [Google Scholar] [CrossRef]
- Abuhamdeh, N.H.; Bantan, R.A.R.; Tlili, I. Analysis of the thermal and hydraulic performance of the sector-by-sector helically coiled tube heat exchangers as a new type of heat exchangers. Int. J. Therm. Sci. 2020, 150, 106229. [Google Scholar] [CrossRef]
- Technical Code for Ground-Source Heat Pump System. In GB 50366-2009; China Construction Industry Press: Beijing, China, 2009; Available online: http://www.doc88.com/p-9773941498889.html (accessed on 12 March 2021).
- Javed, S.; Spitler, J. Accuracy of borehole thermal resistance calculation methods for grouted single U-tube ground heat exchangers. Appl. Energy 2017, 187, 790–806. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Mokheimer, E.M.; Badr, H.M. Effective pipe-to-borehole thermal resistance for vertical ground heat exchangers. Geothermics 2009, 38, 271–277. [Google Scholar] [CrossRef]
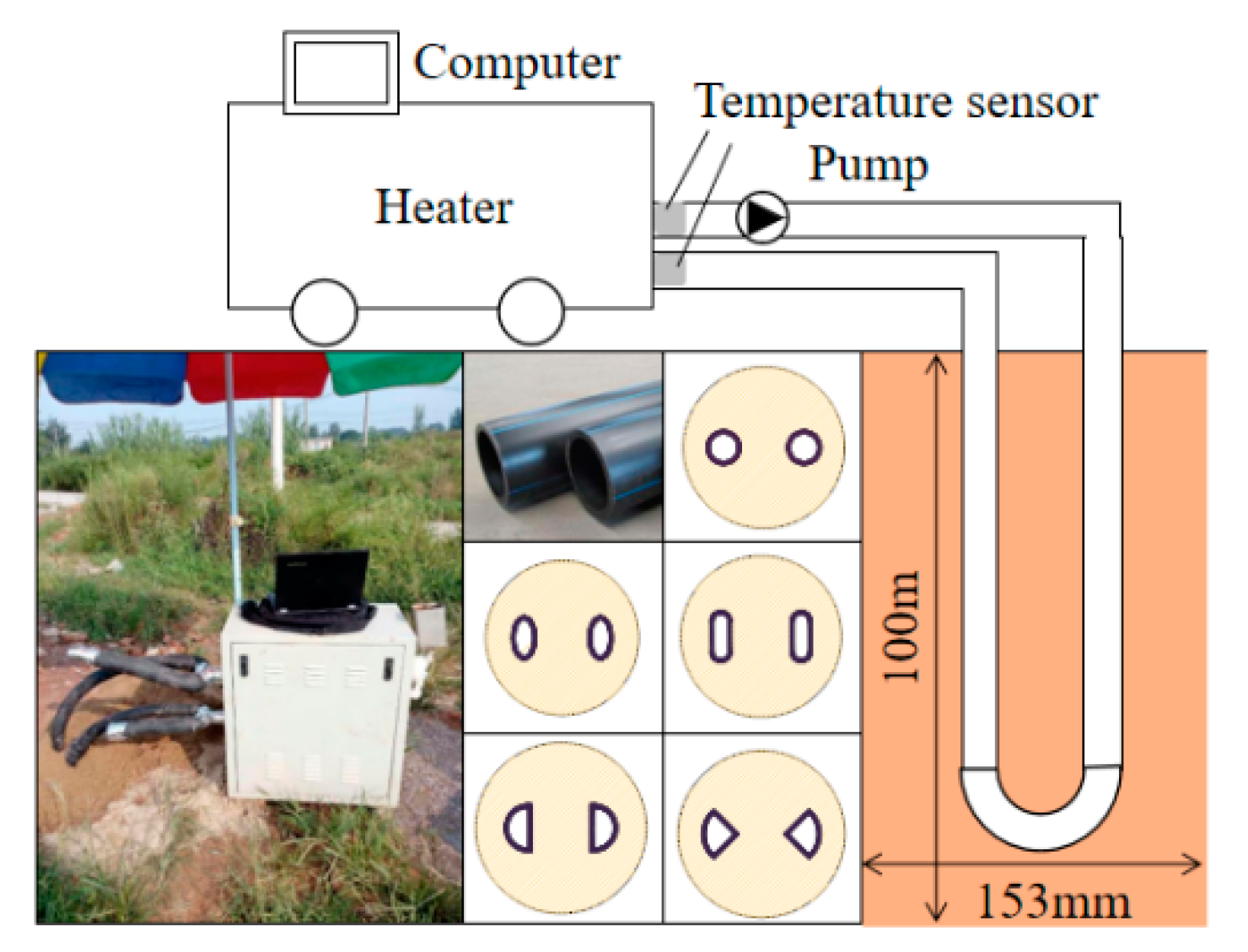
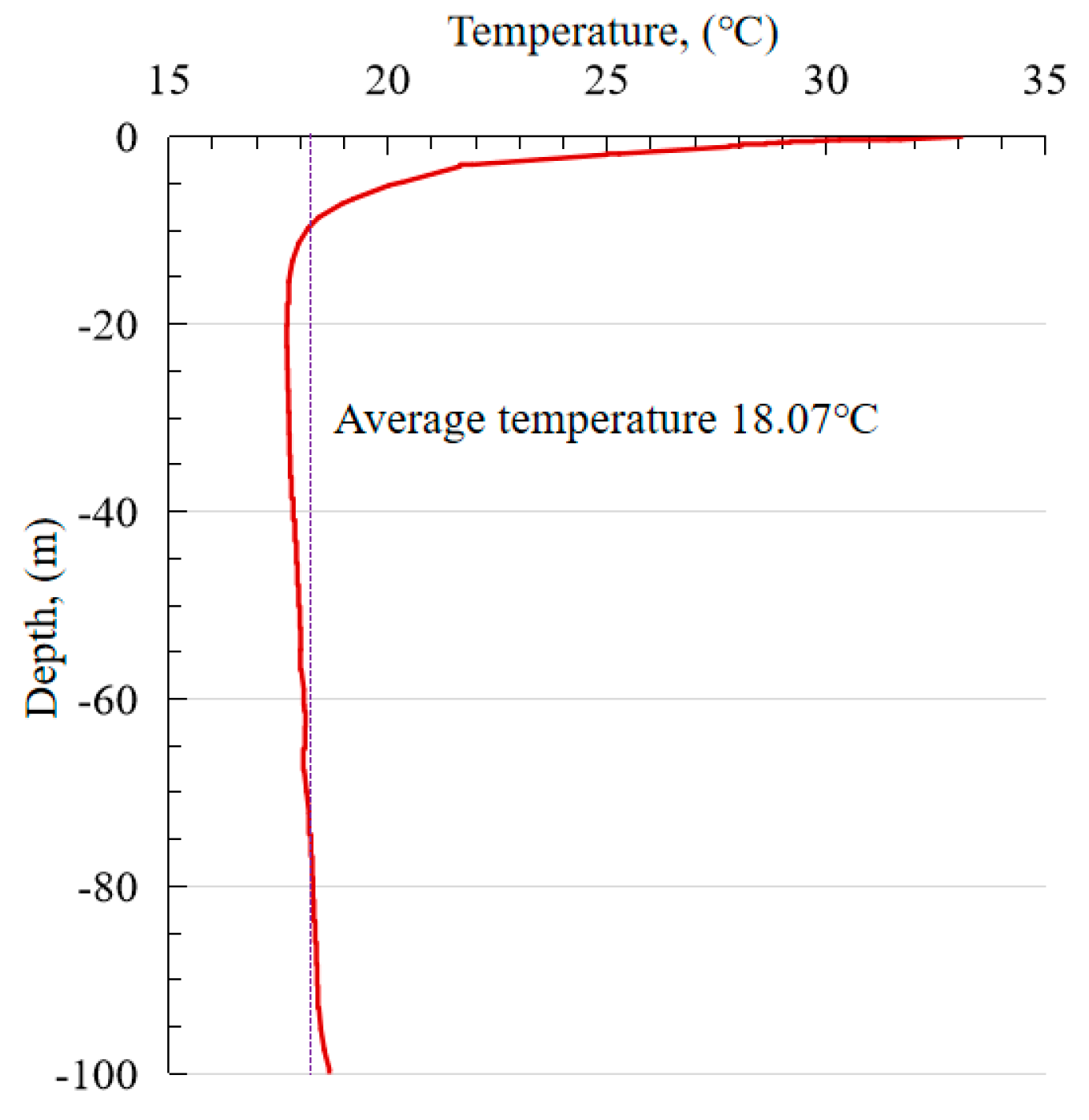

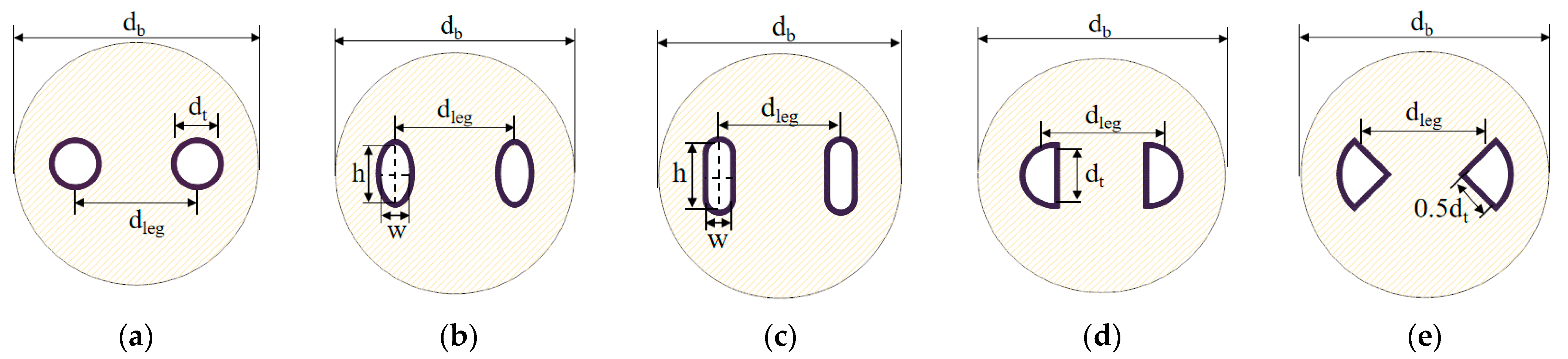




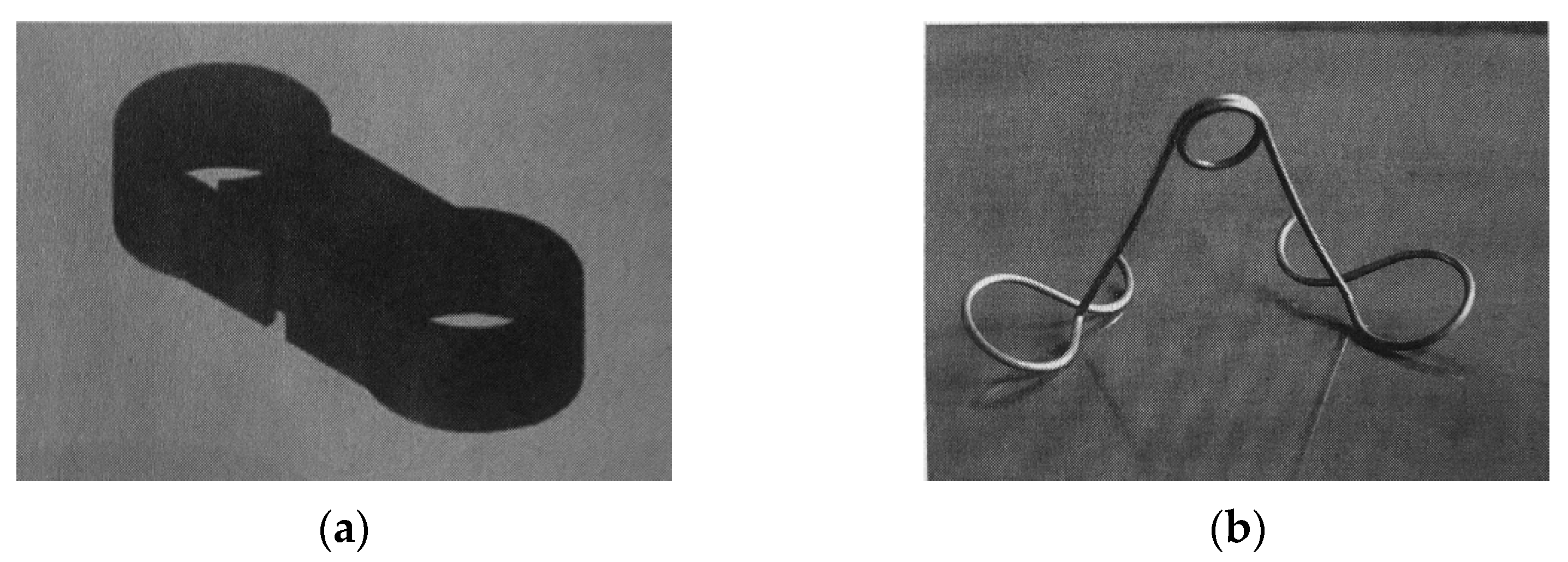

| No. | Depth (m) | Structure | No. | Depth (m) | Structure |
|---|---|---|---|---|---|
| 1 | 1 | Plain fill | 5 | 62 | Moderately weathered conglomerate |
| 2 | 18 | Silt clay | 6 | 84 | Moderately weathered mudstone |
| 3 | 21.5 | Strongly weathered mudstone | 7 | 92 | Fully glutenite |
| 4 | 40.5 | Moderately weathered argillaceous sandstone | 8 | 101 | Moderately weathered mudstone |
| Parameter | Unit | Soil | Backfill | Tube | Fluid |
|---|---|---|---|---|---|
| Density | kg/m3 | 1800 | 1800 | 1000 | 995.03 |
| Specific heat | J/(kg K) | 1353 | 1353 | 1824 | 4179.5 |
| Heat conductivity | W/(m K) | 2.39 | 2.39 | 0.4 | 0.6187 |
| Section Shape | Characteristic Size (mm) |
|---|---|
| Circle | Diameter dt: 26; angle: 360° |
| Curved-oval | Long axis h: 36.76; short axis w:18.38 |
| Flat-oval | Long axis h: 27.71; short axis x: 13.81 |
| Semicircle | Diameter dt: 36.76; angle:180° |
| Sector | Diameter dt: 52; angle: 90° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, A.; Huang, X.; Wang, W.; Jiang, P.; Li, X. Thermo-Hydraulic Performance of U-Tube Borehole Heat Exchanger with Different Cross-Sections. Sustainability 2021, 13, 3255. https://doi.org/10.3390/su13063255
Zhou A, Huang X, Wang W, Jiang P, Li X. Thermo-Hydraulic Performance of U-Tube Borehole Heat Exchanger with Different Cross-Sections. Sustainability. 2021; 13(6):3255. https://doi.org/10.3390/su13063255
Chicago/Turabian StyleZhou, Aizhao, Xianwen Huang, Wei Wang, Pengming Jiang, and Xinwei Li. 2021. "Thermo-Hydraulic Performance of U-Tube Borehole Heat Exchanger with Different Cross-Sections" Sustainability 13, no. 6: 3255. https://doi.org/10.3390/su13063255
APA StyleZhou, A., Huang, X., Wang, W., Jiang, P., & Li, X. (2021). Thermo-Hydraulic Performance of U-Tube Borehole Heat Exchanger with Different Cross-Sections. Sustainability, 13(6), 3255. https://doi.org/10.3390/su13063255









