Binary Linear Programming as a Tool of Cost Optimization for a Water Supply Operator
Abstract
1. Introduction
2. Materials and Methods
- binary—if equal to 1, the pump is operating during the timeslot ; if equal to 0, the pump is idle during the timeslot (; )
- —volume of water in the reservoir tank after the timeslot ends, expressed in m3
- —cost of electric power used by the pump operating during the timeslot , in PLN
- —capacity of the pump in m3/h ()
- —predicted demand for water in the timeslot in m3
- —minimal allowed volume of water in the reservoir tank (firefighting reserve) in m3
- —the capacity of the reservoir tank, i.e., the maximal volume of water that can be stored in the reservoir tank in m3
- —the initial volume of water in the reservoir tank at midnight in m3
- —maximal power of all the pumps operating during the timeslot , expressed in kW (optional parameters)
- binary—if equal to 1, the pump is operating during the timeslot (during the entire timeslot, i.e., one hour or shorter); if equal to 0, the pump is idle during the timeslot (;
- —a number from the interval [0, 1] denoting a fraction of one hour, i.e., the time during the timeslot when the pump operating; if equal to 0, the pump is idle during the timeslot (; The entire model now changes to the following
3. Results
- (1)
- Usage of pumps is not scheduled at all during peak timeslots (with medium and high energy prices).
- (2)
- Pump 7 is scheduled to be used during all the timeslots with non-zero usage of pumps. It results from the fact that it has the largest capacity-to-power ratio, i.e., its capacity in m3/h divided by power in kW is the largest (5.4545 m3/h per kW). Because the cost of the power supply is the same for all the pumps, pump 7 is the most cost-efficient.
- (3)
- The largest usage of pumps (the number of pumps used) is scheduled right after the morning peak (peak refers to the level of power prices), i.e., between 13:00 and 14:00 (timeslot 14), when four pumps are scheduled to work simultaneously. It is caused by the coincidence between peaks in water usage and electric power usage (the latter peak is reflected by the price level 2).
- (4)
- The total cost turned out to be slightly lower (0.27%) than in the case of the simple model. It cannot be larger for any valid input data because the simple model is the worst case of the extended model.
- (5)
- Two timeslots turned out to be partially used: timeslot 16 by pump 4 (0.071023 h, i.e., 4 min 15.7 s) and timeslot 24 by pump 7 (0.516333 h, i.e., 30 min 58.8 s).
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement.
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- —B5:J28 (initially they can be left empty)
- —M5: =SUMPRODUCT(D5:J5,D$2:J$2)+N1-B5
- —M6: =SUMPRODUCT(D6:J6,D$2:J$2)+M5-B6
- —obtained by copying M6 to M7:M28
- —not specified explicitly, calculated implicitly by formulas in L5:L28
- —D2:J2
- —B5:B28
- —N1
- —N2
- —N3
- —L2: =SUM(L5:L28) (because of the necessity of calculating parameters, the objective function is implemented not directly as a SUMPRODUCT-based but rather as SUM of SUMPRODUCT-based formulas)
- —L5: =SUMPRODUCT(D5:J5,D$3:J$3)*C5/1000
- —obtained by copying L5 to L6:L28
- —D30: =SUM(D5:D28)
- ; —obtained by copying D30 to E30:J30

Appendix B
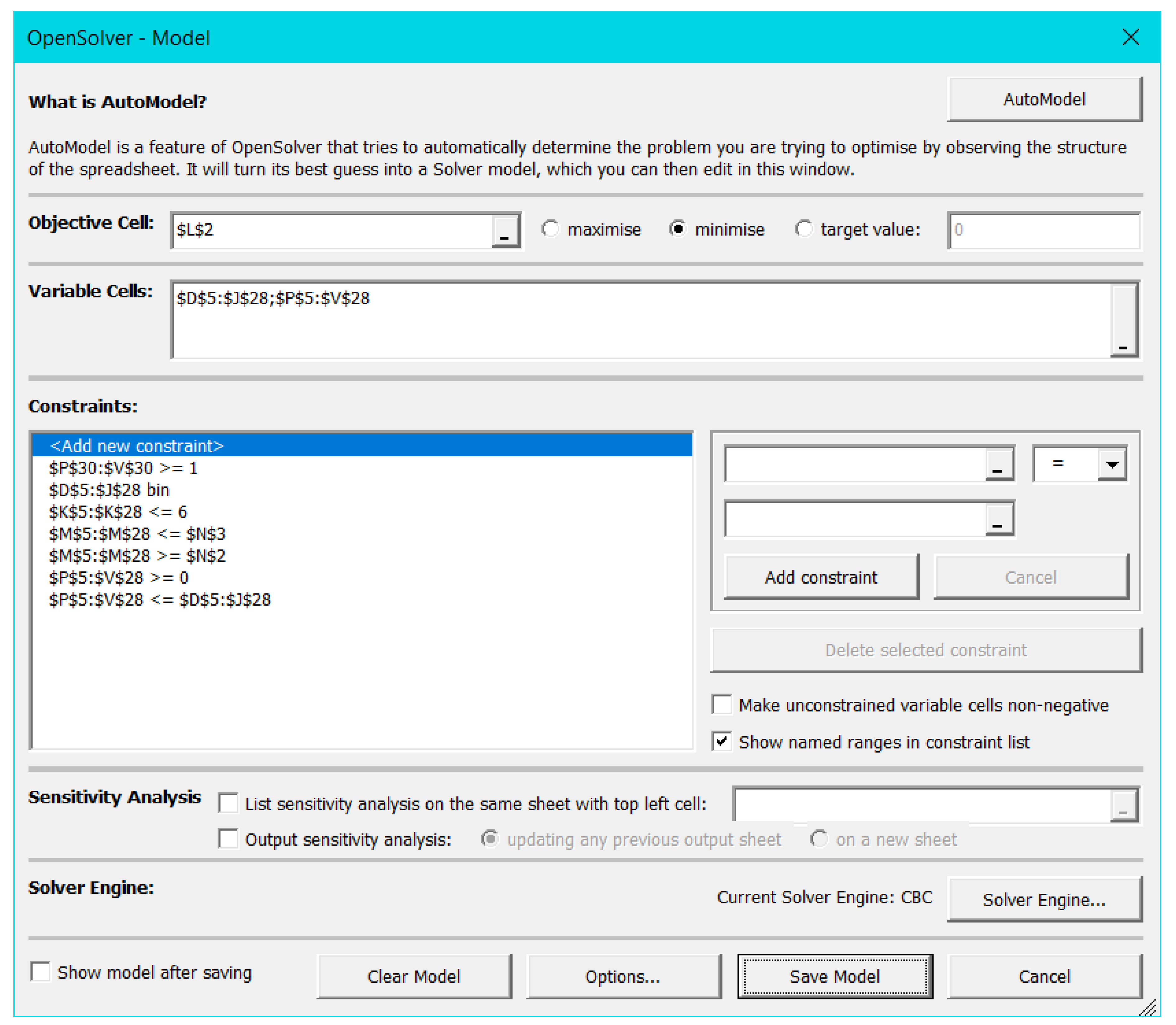
- —B5:J28 (initially they can be left empty)
- —P5:V28 (initially they can be left empty)
- —M5: =SUMPRODUCT(P5:V5,D$2:J$2)+N1-B5
- —M6: =SUMPRODUCT(P6:V6,D$2:J$2)+M5-B6
- —obtained by copying M6 to M7:M28
- —L5: =SUMPRODUCT(P5:V5,D$3:J$3)*C5/1000
- —obtained by copying L5 to L6:L28
- —P30: =SUM(P5:P28)
- ; —obtained by copying P30 to Q30:V30
References
- Abdallah, M.; Kapelan, Z. Fast Pump Scheduling Method for Optimum Energy Cost and Water Quality in Water Distribution Networks with Fixed and Variable Speed Pumps. J. Water Resour. Plan. Manag. 2019, 145, 13. [Google Scholar] [CrossRef]
- Bonvin, G.; Demassey, S.; Lodi, A. Pump scheduling in drinking water distribution networks with an LP/NLP-based branch and bound. Optim. Eng. 2021, 39. [Google Scholar] [CrossRef]
- Vrchota, J.; Pech, M.; Rolinek, L.; Bednar, J. Sustainability Outcomes of Green Processes in Relation to Industry 4.0 in Manufacturing: Systematic Review. Sustainability 2020, 12, 5968. [Google Scholar] [CrossRef]
- Lai, K.H.; Wong, C.W.V. Green logistics management and performance: Some empirical evidence from Chinese manufacturing exporters. Omega 2012, 40, 267–282. [Google Scholar] [CrossRef]
- Rajput, S.P.S.; Datta, S. Sustainable and green manufacturing? A narrative literature review. Mater. Today Proc. 2020, 26, 2515–2520. [Google Scholar] [CrossRef]
- Abdelmoez, W.; Ashour, E.; Naguib, S.M. A Review on Green Trend for Oil Extraction Using Subcritical Water Technology and Biodiesel Production. J. Oleo Sci. 2015, 64, 467–478. [Google Scholar] [CrossRef] [PubMed]
- Abkenar, S.M.S.; Stanley, S.D.; Miller, C.J.; Chase, D.V.; McElmurry, S.P. Evaluation of genetic algorithms using discrete and continuous method for pump optimization of water distribution system. Sustain. Comput. Inform. Syst. 2015, 8, 18–23. [Google Scholar]
- Bohórques, J.; Saldarriaga, J.; Vallejo, D. Pumping pattern optimization in order to reduce WDS operation costs. Procedia Eng. 2015, 119, 1069–1077. [Google Scholar] [CrossRef]
- Alrheeh, M.; Mahmoud, H. Using Genetics Algorithms in Pump Scheduling to Reduce the Pumping Cost. Damascous Univ. J. 2009, 25, 95–105. [Google Scholar]
- Kosicka, E.; Kozłowski, E.; Mazurkiewicz, D. The use of stationary tests for analysis of monitored residual processes. Maint. Reliab. 2015, 17, 604–609. [Google Scholar] [CrossRef]
- Rojek, I.; Studziński, J. Comparison of different types of neuronal nets for failures location within water-supply networks. Maint. Reliab. 2014, 16, 42–47. [Google Scholar]
- Romaniuk, M. On simulation of maintenance costs for water distribution system with fuzzy parameters. Maint. Reliab. 2016, 18, 514–527. [Google Scholar] [CrossRef]
- Mazurkiewicz, D.; Rudawska, A. (Eds.) Inspirations for Innovation the Causes and Effects of Progress in Production Engineering; Lublin University of Technology: Lublin, Poland, 2016. [Google Scholar]
- Jowitt, P.W.; Germanopolous, G. Optimal pump scheduling in water-supply networks. J. Water Resour. Plan. Manag. 1992, 118, 406–422. [Google Scholar] [CrossRef]
- Yu, G.; Powell, R.S.; Sterling, M.J.H. Optimized pump scheduling in water distribution system. J. Optim. Theory Appl. 1994, 83, 463–488. [Google Scholar] [CrossRef]
- Lansey, K.E.; Awumah, K. Optimal pump operations considering pump switches. J. Water Resour. Plan. Manag. 1994, 120, 17–35. [Google Scholar] [CrossRef]
- Ormsbee, L.E.; Reddy, S.L. Nonlinear heuristic for pump operations. J. Water Resour. Plan. Manag. 1995, 121, 302–309. [Google Scholar] [CrossRef]
- Wang, J.Y.; Chang, T.P.; Chen, J.S. An enhanced genetic algorithm for bi-objective pump scheduling in water supply. Expert Syst. Appl. 2009, 36, 10249–10258. [Google Scholar] [CrossRef]
- Baran, B.; Lücken, C.; Sotelo, A. Multi-objective pump scheduling optimisation using evolutionary strategies. Adv. Eng. Softw. 2005, 36, 39–47. [Google Scholar] [CrossRef]
- Puleo, V.; Morley, M.; Freni, G.; Savić, D. Multi-stage linear programming optimization for pump scheduling. Procedia Eng. 2014, 70, 1378–1385. [Google Scholar] [CrossRef]
- Turci, L.D.; Wang, J.C.; Brahmia, I. Adaptive and Improved Multi-population Based Nature-inspired Optimization Algorithms for Water Pump Station Scheduling. Water Resour. Manag. 2020, 34, 2869–2885. [Google Scholar] [CrossRef]
- Cimorelli, L.; D’Aniello, A.; Cozzolino, L. Boosting Genetic Algorithm Performance in Pump Scheduling Problems with a Novel Decision-Variable Representation. J. Water Resour. Plan. Manag. 2020, 146, 11. [Google Scholar] [CrossRef]
- Carpitella, S.; Brentan, B.; Montalvo, I.; Izquierdo, J.; Certa, A. Multi-criteria analysis applied to multi-objective optimal pump scheduling in water systems. Water Supply 2019, 19, 2338–2346. [Google Scholar] [CrossRef]
- Fooladivanda, D.; Taylor, J.A. Energy-Optimal Pump Scheduling and Water Flow. IEEE Trans. Control Netw. Syst. 2018, 5, 1016–1026. [Google Scholar] [CrossRef]
- Oh, H.; Eom, J.; Kim, T. Case study of pump scheduling using sensor-based real-time pump efficiency monitoring. Desalination Water Treat. 2020, 181, 141–150. [Google Scholar] [CrossRef]
- Muhammed, K.A.; Farmani, R. Energy Optimization Using a Pump Scheduling Tool in Water Distribution Systems. ARO Sci. J. Koya Univ. 2020, 8, 112–123. [Google Scholar] [CrossRef]
- Gutierrez-Bahamondes, J.H.; Salgueiro, Y.; Mora-Melia, D.; Alsina, M.A.; Silva-Rubio, S.A.; Iglesias-Rey, P.L. Multi-objective Evolutionary Algorithms Assessment for Pump Scheduling Problems. In Proceedings of the IEEE Chilean Conference on Electrical, Electronics Engineering, Information and Communication Technologies (Chilecon), Valparaiso, Chile, 13–27 November 2019; p. 6. [Google Scholar]
- Turci, L.D.; Sun, H.B.; Bai, M.S.; Wang, J.C.; Hu, P. Water pump station scheduling optimization using an improved genetic algorithm approach. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 944–951. [Google Scholar]
- Walters, G.A.; Savić, D.A. Recent applications of genetic algorithms to water system design. Trans. Ecol. Environ. 1996, 12. [Google Scholar] [CrossRef]
- Borkowski, D.; Wetula, A.; Bień, A. Design, optimization, and deployment of waterworks pumping station control system. ISA Trans. 2012, 51, 539–549. [Google Scholar] [CrossRef] [PubMed]
- Behandish, M.; Wu, Z.Y. Concurrent pump scheduling and storage level optimization using meta-models and evolutionary algorithms. Procedia Eng. 2014, 70, 103–112. [Google Scholar] [CrossRef]
- Niu, D.; Kuang, Z.G.; Chen, X.S.; Wei, S.; Yang, J.; Wang, X.Y. Optimizing Pump Scheduling for Water Supply through Improved Multiple Population Genetic Algorithm. In Proceedings of the 24th IEEE International Conference on Automation and Computing (ICAC ’18), Newcastle Upon Tyne, UK, 6–7 September 2018; pp. 632–637. [Google Scholar]
- Savić, D.A.; Walters, G.A.; Schwab, M. Multiobjective genetic algorithms for pump scheduling in water supply. Evol. Comput. Lect. Notes Comput. Sci. 1997, 1305, 227–235. [Google Scholar]
- Ormsbee, L.E.; Lansey, K.E. Optimal Control of Water Supply Pumping Systems. J. Water Resour. Plan. Manag. 1994, 120, 237–252. [Google Scholar] [CrossRef]
- Pasha, M.F.K.; Lansey, K. Optimal pump scheduling by linear programming. In Proceedings of the World Environmental and Water Resources Congress, Kansas City, MO, USA, 17–21 May 2009; pp. 395–404. [Google Scholar]
- Giacomello, C.; Kapelan, Z.; Nicolini, M. Fast Hybrid optimization method for effective pump scheduling. J. Water Resour. Plan. Manag. 2013, 139, 175–183. [Google Scholar] [CrossRef]
- Jasiulewicz-Kaczmarek, M. Practical aspects of the application of RCM to select optimal maintenance policy of the production line, in Safety and Reliability Methodology and Applications. In Proceedings of the European Safety and Reliability Conference, ESREL, Wroclaw, Poland, 14–18 September 2014; pp. 1187–1195. [Google Scholar]
- Kłos, S.; Patalas-Maliszewska, J.; Trebuna, P. Improving manufacturing processes using simulation methods. Appl. Comput. Sci. 2016, 12, 42–53. [Google Scholar]
- Loska, A. Methodology of variant assessment of exploitation policy using numerical taxonomy tools. Manag. Syst. Prod. Eng. 2015, 2, 98–104. [Google Scholar]
- Valis, D.; Pietrucha-Urbanik, K. Utilization of diffusion processes and fuzzy logic for vulnerability assessment. Maint. Reliab. 2014, 16, 48–55. [Google Scholar]
- Kozłowski, E.; Mazurkiewicz, D.; Kowalska, B.; Kowalski, D. Binary Linear Programming as a Decision-Making Aid for Water Intake Operators, Proceedings of the Intelligent Systems Production, Engineering and Maintenance (ISPEM 2017), Wroclaw, Poland, 28–29 September 2017; Burduk, A., Mazurkiewicz, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 199–208. [Google Scholar] [CrossRef]
- Walukiewicz, S. Integer Programming; PWN: Warsaw, Poland, 1991; pp. 60–61. [Google Scholar]
- Standard Excel Solver - Dealing with Problem Size Limits—Continued. Available online: https://www.solver.com/standard-excel-solver-dealing-problem-size-limits-continued (accessed on 3 December 2020).
- Mason, A.J. OpenSolver—An Open Source Add-in to Solve Linear and Integer Progammes in Excel. In Operations Research Proceedings 2011, Proceedings of the International Conference on Operations Research, Zurich, Switzerland, August 30–2 September 2011; Klatte, D., Lüthi, H.-J., Schmedders, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 401–406. [Google Scholar] [CrossRef]
- Luna, T.; Ribau, J.; Figueiredo, D.; Alves, R. Improving energy efficiency in water supply systems with pump scheduling optimization. J. Clean. Prod. 2019, 213, 342–356. [Google Scholar] [CrossRef]
- Hyung, J.; Seo, J.; Kim, K.; Kim, T.; Koo, J. Optimal water intake and supply pump scheduling considering water quality safety in multiple water intake system. Desalination Water Treat. 2020, 182, 49–60. [Google Scholar] [CrossRef]
| Number of Well () | Capacity (m3/h) | Power (kW) |
|---|---|---|
| 1 | 75 | 15 |
| 2 | 133 | 37 |
| 3 | 157 | 33 |
| 4 | 176 | 33 |
| 5 | 59 | 22 |
| 6 | 69 | 33 |
| 7 | 120 | 22 |
| Level 1 (Afternoon/Evening peak) 16:00–21:00 [PLN/MWh] | Level 2 (Morning Peak) 7:00–13:00 [PLN/MWh] | Level 3 (Off-Peak) 0:00–7:00, 13:00–16:00, 21:00–24:00 [PLN/MWh] |
|---|---|---|
| 336.00 | 283.00 | 169.00 |
| Number of Timeslot () | Demand per Timeslot (m3) | Power Price (PLN/MWh) |
|---|---|---|
| 1 | 44.62 | 169 |
| 2 | 31.27 | 169 |
| 3 | 26.22 | 169 |
| 4 | 27.51 | 169 |
| 5 | 31.50 | 169 |
| 6 | 46.18 | 169 |
| 7 | 69.47 | 169 |
| 8 | 100.36 | 283 |
| 9 | 131.85 | 283 |
| 10 | 148.51 | 283 |
| 11 | 149.89 | 283 |
| 12 | 142.21 | 283 |
| 13 | 132.09 | 283 |
| 14 | 129.29 | 169 |
| 15 | 124.06 | 169 |
| 16 | 114.68 | 169 |
| 17 | 109.33 | 336 |
| 18 | 115.76 | 336 |
| 19 | 126.95 | 336 |
| 20 | 131.48 | 336 |
| 21 | 138.86 | 336 |
| 22 | 131.91 | 169 |
| 23 | 111.53 | 169 |
| 24 | 70.43 | 169 |
| Timeslot Number | Pumps | ||||||
|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 15 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 16 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 22 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Timeslot Number | Pumps | ||||||
|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 4 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 16 | 1 | 0 | 0 | 0.071023 | 0 | 1 | 1 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 22 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0.516333 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kowalik, P.; Rzemieniak, M. Binary Linear Programming as a Tool of Cost Optimization for a Water Supply Operator. Sustainability 2021, 13, 3470. https://doi.org/10.3390/su13063470
Kowalik P, Rzemieniak M. Binary Linear Programming as a Tool of Cost Optimization for a Water Supply Operator. Sustainability. 2021; 13(6):3470. https://doi.org/10.3390/su13063470
Chicago/Turabian StyleKowalik, Przemysław, and Magdalena Rzemieniak. 2021. "Binary Linear Programming as a Tool of Cost Optimization for a Water Supply Operator" Sustainability 13, no. 6: 3470. https://doi.org/10.3390/su13063470
APA StyleKowalik, P., & Rzemieniak, M. (2021). Binary Linear Programming as a Tool of Cost Optimization for a Water Supply Operator. Sustainability, 13(6), 3470. https://doi.org/10.3390/su13063470






