More from Less? Environmental Rebound Effects of City Size
Abstract
1. Introduction
2. Urban Scaling
3. On the Relation between City Size and Environmental Impacts
3.1. City Size and Density
3.2. City Size and Income
3.3. City Size and Infrastructure
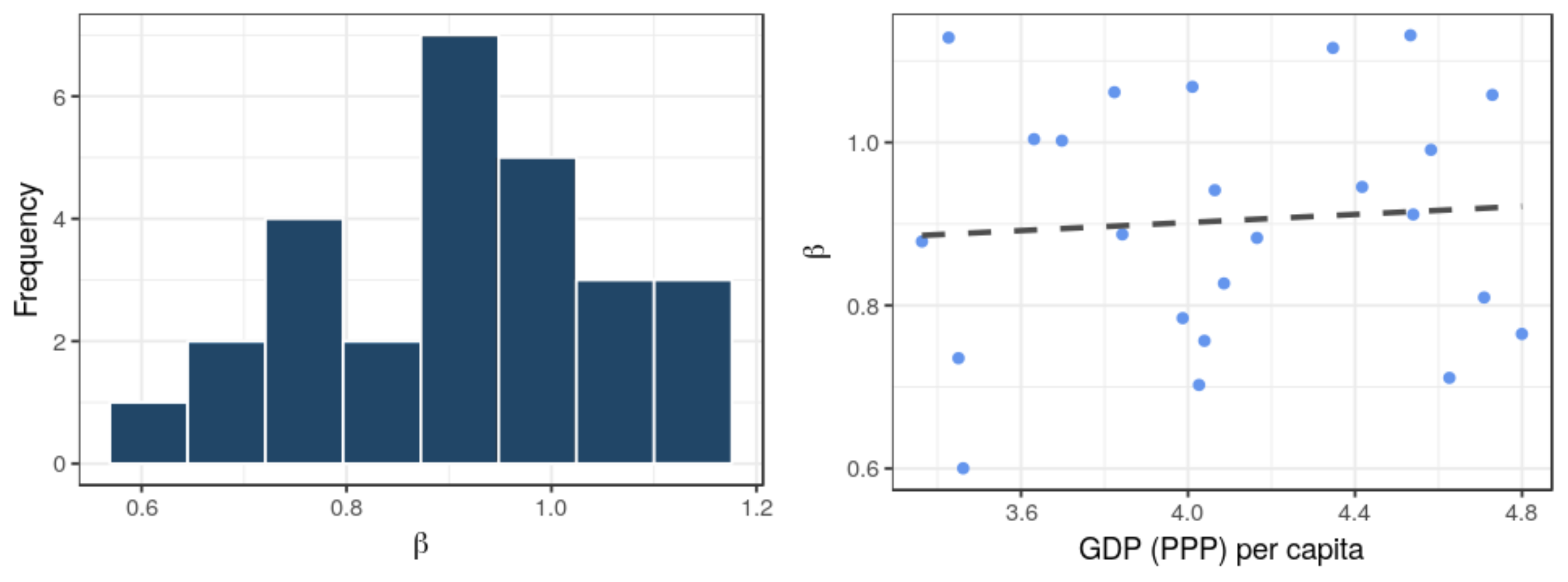
3.4. City Size and Emissions
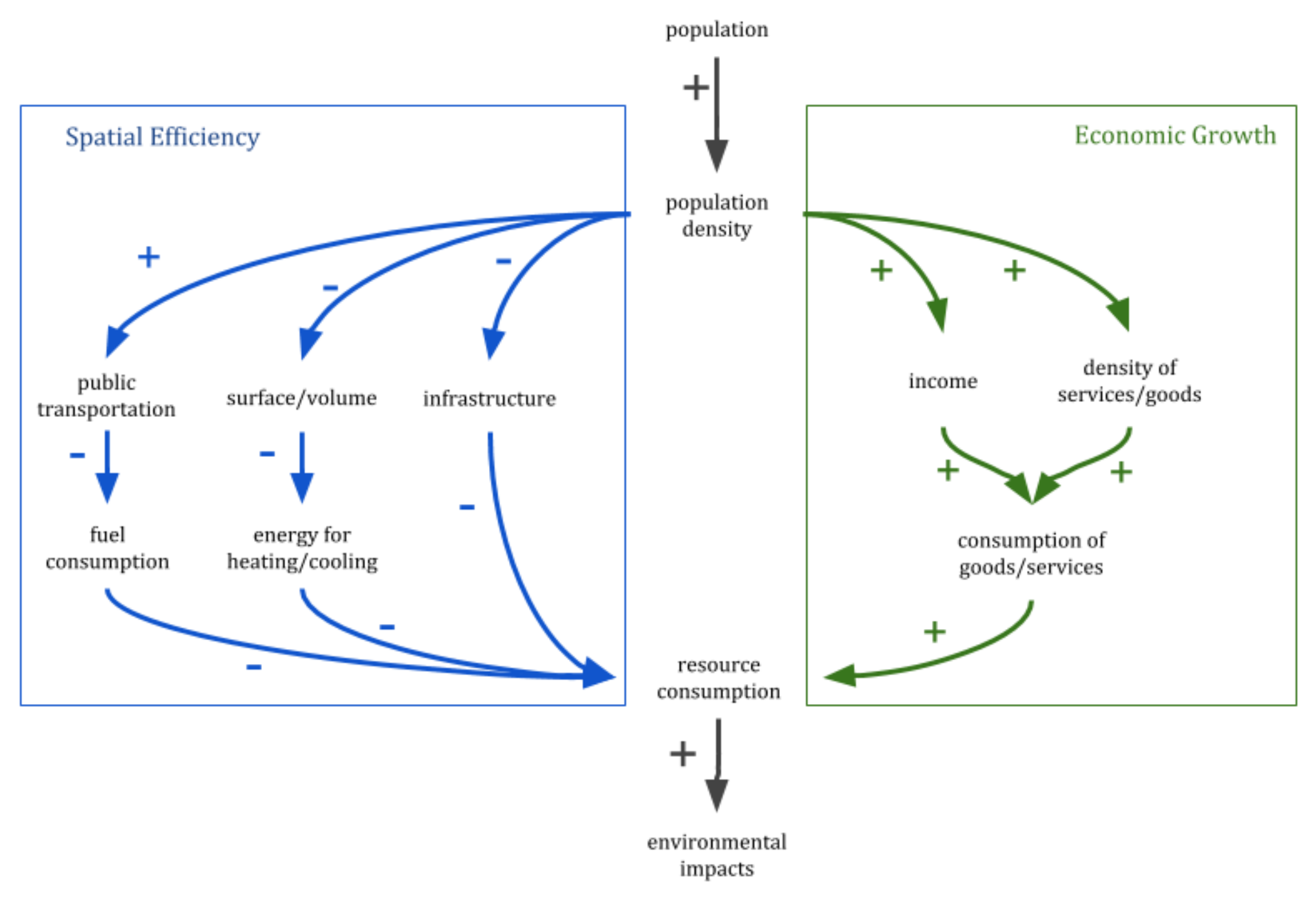
3.5. Causal Diagram
4. A Toy Model of Urban Carbon Footprint Based on Scaling Laws
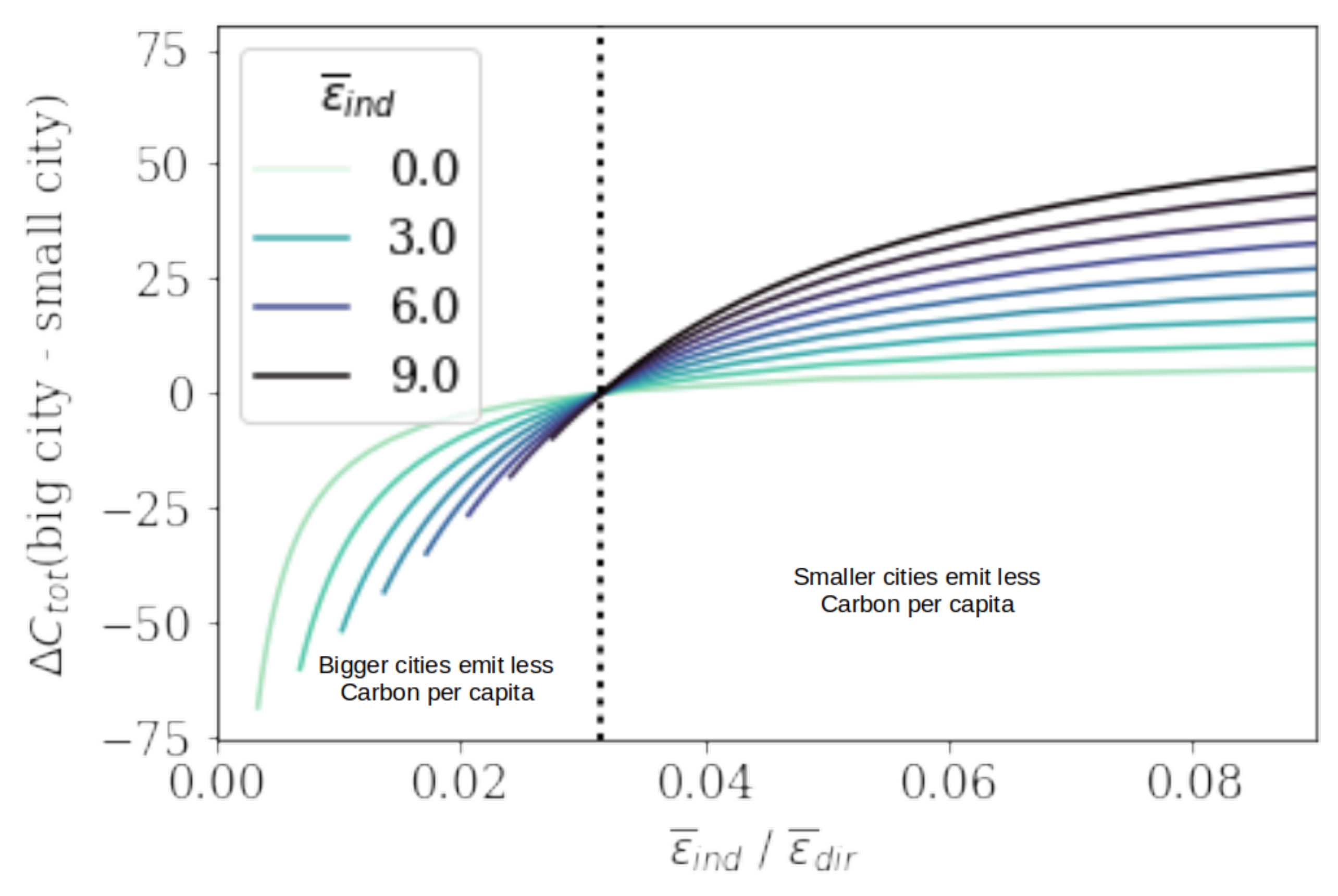
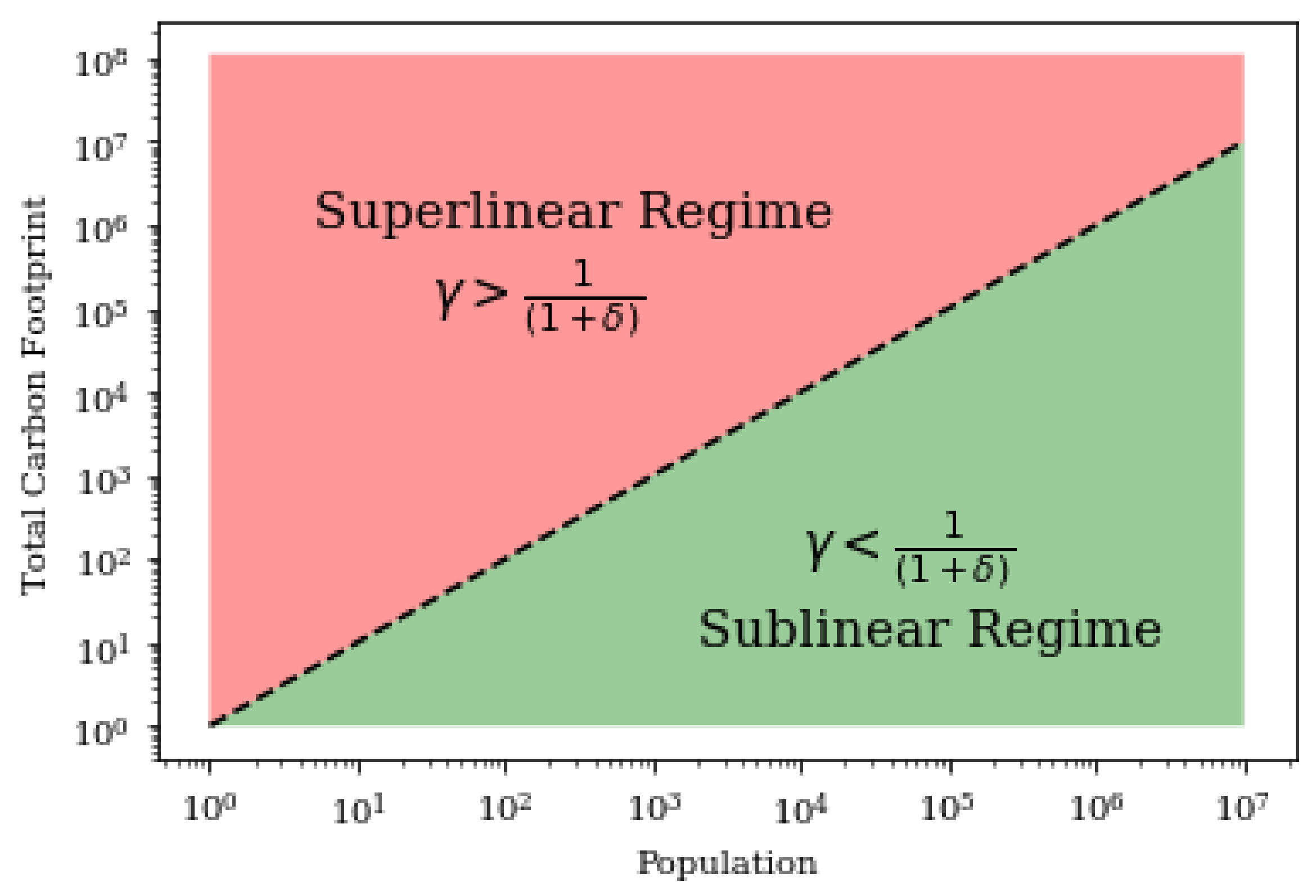
4.1. Environmental Rebound Effect of City Size
4.2. Decoupling Economic Growth from Environmental Impacts
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seto, K.C.; Solecki, W.D.; Griffith, C.A. The Routledge Handbook of Urbanization and Global Environmental Change; Routledge: London, UK, 2015. [Google Scholar]
- Glaeser, E.L.; Kahn, M.E. The greenness of cities: Carbon dioxide emissions and urban development. J. Urban Econ. 2010, 67, 404–418. [Google Scholar] [CrossRef]
- Rybski, D.; Reusser, D.E.; Winz, A.L.; Fichtner, C.; Sterzel, T.; Kropp, J.P. Cities as nuclei of sustainability? Environ. Plan. B Urban Anal. City Sci. 2017, 44, 425–440. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P.; et al. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Angel, S. Planet of Cities; Lincoln Institute of Land Policy: Cambridge, MA, USA, 2012. [Google Scholar]
- West, G.B. Scale: The Universal Laws of Growth, Innovation, Sustainability, and the Pace of Life in Organisms, Cities, Economies, and Companies; Penguin Press: New York, NY, USA, 2017. [Google Scholar]
- Barthelemy, M. The Structure and Dynamics of Cities; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Batty, M. The New Science of Cities; MIT Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Norman, J.; MacLean, H.L.; Kennedy, C.A. Comparing high and low residential density: Life-cycle analysis of energy use and greenhouse gas emissions. J. Urban Plan. Dev. 2006, 132, 10–21. [Google Scholar] [CrossRef]
- Newman, P.W.; Kenworthy, J.R. Gasoline consumption and cities: A comparison of us cities with a global survey. JAPA 1989, 55, 24–37. [Google Scholar] [CrossRef]
- Behsh, B. Building form as an option for enhancing the indoor thermal conditions. In Proceedings of the Building Physics 2002—6th Nordic Symposium, Trondheim, Norway, 17–19 June 2002. [Google Scholar]
- Bettencourt, L.M.; West, G.B. Bigger cities do more with less. Sci. Am. 2011, 305, 52–53. [Google Scholar] [CrossRef]
- Geddes, P. Civics: As Applied Sociology; Leicester University Press: Leicester, UK, 1979. [Google Scholar]
- Ahrend, R.; Farchy, E.; Kaplanis, I.; Lembcke, A.C. What Makes Cities More Productive? Evidence on the Role of Urban Governance from Five OECD Countries. OECD Reg. Dev. Work. Pap. 2014, 1–33. [Google Scholar] [CrossRef]
- Bettencourt, L.M.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar] [CrossRef]
- Bettencourt, L.M. The origins of scaling in cities. Science 2013, 340, 1438–1441. [Google Scholar] [CrossRef]
- Ribeiro, F.L.; Meirelles, J.; Ferreira, F.F.; Neto, C.R. A model of urban scaling laws based on distance-dependent interactions. R. Soc. Open Sci. 2017, 4, 160926. [Google Scholar] [CrossRef]
- Jacobs, J. The Death and Life of Great American Cities; Random House: New York, NY, USA, 1961. [Google Scholar]
- Soja, E. Writing the city spatially. City 2003, 7, 269–280. [Google Scholar] [CrossRef]
- Jacobs, J. The Economy of Cities; Random House: New York, NY, USA, 1969. [Google Scholar]
- Seto, K.C.; Dhakal, S.; Bigio, A.; Blanco, H.; Delgado, G.C.; Dewar, D.; Huang, L.; Inaba, A.; Kansal, A.; Lwasa, S.; et al. Human settlements, infrastructure and spatial planning. In Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- C40 Cities Climate Leadership Group. Consumption-Based GHG Emissions of C40 Cities. Available online: http://www.c40.org/researches/consumption-based-emissions (accessed on 2 July 2019).
- Steininger, K.; Lininger, C.; Droege, S.; Roser, D.; Tomlinson, L.; Meyer, L. Justice and cost effectiveness of consumption-based versus production-based approaches in the case of unilateral climate policies. Glob. Environ. Chang. 2014, 24, 75–87. [Google Scholar] [CrossRef]
- Chen, G.; Shan, Y.; Hu, Y.; Tong, K.; Wiedmann, T.; Ramaswami, A.; Guan, D.; Shi, L.; Wang, Y. A review on city-level carbon accounting. Environ. Sci. Technol. 2019, 53, 5545–5558. [Google Scholar] [CrossRef]
- Janet, R.; Laurent, C.; Simon, S.; Kjell, O.; Brian, D.; Matt, S.; Mike, B.; Pierre, B.; Environment, C.; Rob, F.; et al. The Greenhouse Gas Protocol: A Corporate Accounting and Reporting Standard; WBCSD/WRI 2004; World Resources Institute: Washington, DC, USA, 2004. [Google Scholar] [CrossRef]
- Fong, W.K.; Sotos, M.; Doust, M.M.; Schultz, S.; Marques, A.; Deng-Beck, C. Global Protocol for Community-Scale Greenhouse Gas Emission Inventories (gpc); World Resources Institute: New York, NY, USA, 2015. [Google Scholar]
- Mi, Z.; Zhang, Y.; Guan, D.; Shan, Y.; Liu, Z.; Cong, R.; Yuan, X.C.; Wei, Y.M. Consumption-based emission accounting for chinese cities. Ecol. Indic 2014, 47, 26–31. [Google Scholar] [CrossRef]
- Dhakal, S.; Hidefumi, I. Urban Energy Use and Greenhouse Gas Emissions in Asian Mega-Cities: Policies for a Sustainable Future; Urban Environmental Management Project; Institute for Global Environmental: Hayama, Japan, 2004. [Google Scholar]
- Minx, J.; Baiocchi, G.; Wiedmann, T.; Barrett, J.; Creutzig, F.; Feng, K.; Förster, M.; Pichler, P.P.; Weisz, H.; Hubacek, K. Carbon footprints of cities and other human settlements in the uk. Environ. Res. Lett. 2013, 8, 35039. [Google Scholar] [CrossRef]
- Gill, B.; Moeller, S. Ghg emissions and the rural-urban divide. a carbon footprint analysis based on the german official income and expenditure survey. Ecol. Econ. 2018, 145, 160–169. [Google Scholar] [CrossRef]
- Heinonen, J.; Kyrö, R.; Junnila, S. Dense downtown living more carbon intense due to higher consumption: A case study of helsinki. Environ. Res. Lett. 2011, 6, 034034. [Google Scholar] [CrossRef]
- Jones, C.; Kammen, D.M. Spatial distribution of us household carbon footprints reveals suburbanization undermines greenhouse gas benefits of urban population density. Environ. Sci. Technol. 2014, 48, 895–902. [Google Scholar] [CrossRef]
- Sudmant, A.; Gouldson, A.; Millward-Hopkins, J.; Scott, K.; Barrett, J. Producer cities and consumer cities: Using production-and consumption-based carbon accounts to guide climate action in china, the uk, and the us. J. Clean. Prod. 2018, 176, 654–662. [Google Scholar] [CrossRef]
- Netto, V.M.; Vargas, J.C.B.; Saboya, R.T. A revolução dos dados e a nova ciência das cidades (Editorial). RMU 2020, 8, e00173. [Google Scholar] [CrossRef]
- Ribeiro, F.L. Física das Cidades. RMU 2020, 8, e00159. [Google Scholar] [CrossRef]
- Bettencourt, L.; West, G. A unified theory of urban living. Nature 2010, 467, 912. [Google Scholar] [CrossRef]
- Netto, V.M.; Meirelles, J.; Ribeiro, F.L. Social Interaction and the City: The Effect of Space on the Reduction of Entropy. Complexity 2017, 2017. [Google Scholar] [CrossRef]
- Bettencourt, L.M.; Lobo, J. Urban scaling in europe. J. R. Soc. Interface 2016, 13, 20160005. [Google Scholar] [CrossRef]
- Ortman, S.G.; Cabaniss, A.H.; Sturm, J.O.; Bettencourt, L.M. The pre-history of urban scaling. PLoS ONE 2014, 9, e87902. [Google Scholar] [CrossRef]
- Gomez-Lievano, A.; Youn, H.; Bettencourt, L.M.A. The statistics of urban scaling and their connection to zipf’s law. PLoS ONE 2012, 7, e40393. [Google Scholar] [CrossRef]
- Gomez-Lievano, A.; Youn, H.; Bettencourt, L.M. Scaling in transportation networks. PLoS ONE 2014, 9, e102007. [Google Scholar]
- Adhikari, P.; de Beurs, K.M. Growth in urban extent and allometric analysis of west african cities. J. Land Use Sci. 2017, 12, 105–124. [Google Scholar] [CrossRef]
- Meirelles, J.; Neto, C.R.; Ferreira, F.F.; Ribeiro, F.L.; Binder, C.R. Evolution of urban scaling: Evidence from brazil. PLoS ONE 2018, 13, e0204574. [Google Scholar] [CrossRef] [PubMed]
- Krugman, P. Increasing returns and economic geography. J. Political Econ. 1991, 99, 483–499. [Google Scholar] [CrossRef]
- Schläpfer, M.; Bettencourt, L.M.A.; Grauwin, S.; Raschke, M.; Claxton, R.; Smoreda, Z.; West, G.B.; Ratti, C. The scaling of human interactions with city size. J. R. Soc. Interface 2014, 11, 20130789. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, F.L.; Meirelles, J.; Netto, V.M.; Neto, C.R.; Baronchelli, A. On the relation between Transversal and Longitudinal Scaling in Cities. PLoS ONE 2020, 15, e0233003. [Google Scholar]
- Youn, H.; Bettencourt, L.M.; Lobo, J.; Strumsky, D.; Samaniego, H.; West, G.B. Scaling and universality in urban economic diversification. Interface 2016, 13, 20150937. [Google Scholar] [CrossRef]
- Depersin, J.; Barthelemy, M. From global scaling to the dynamics of individual cities. Proc. Natl. Acad. Sci. USA 2017, 115, 1–6. [Google Scholar] [CrossRef]
- Molinero, C.; Thurner, S. How the geometry of cities explains urban scaling laws and determines their exponents. arXiv 2019, arXiv:1908.07470. [Google Scholar]
- Arcaute, E.; Hatna, E.; Ferguson, P.; Youn, H.; Johansson, A.; Batty, M. Constructing cities, deconstructing scaling laws. J. R. Soc. Interface 2015, 12, 20140745. [Google Scholar] [CrossRef]
- Louf, R.; Barthelemy, M. Scaling: Lost in the smog. Environ. Plan. B Plan. Des. 2014, 41, 767–769. [Google Scholar] [CrossRef]
- Leitao, J.C.; Miotto, J.M.; Gerlach, M.; Altmann, E.G. Is this scaling nonlinear? R. Soc. Open Sci. 2016, 3, 150649. [Google Scholar] [CrossRef]
- Strano, E.; Sood, V. Rich and poor cities in europe. an urban scaling approach to mapping the european economic transition. PLoS ONE 2016, 11, e0159465. [Google Scholar] [CrossRef]
- Muller, N.Z.; Jha, A. Does environmental policy affect scaling laws between population and pollution? evidence from american metropolitan areas. PLoS ONE 2017, 12, e0181407. [Google Scholar] [CrossRef]
- Batty, M.; Ferguson, P. Defining city size. Environ. Plan. B Plan. Des. 2011, 38, 753–756. [Google Scholar] [CrossRef]
- Cesaretti, R.; Lobo, J.; Bettencourt, L.M.; Ortman, S.G.; Smith, M.E. Population-area relationship for medieval european cities. PLoS ONE 2016, 11, e0162678. [Google Scholar] [CrossRef]
- Stewart, J.Q.; Warntz, W. Physics of population distribution. J. Reg. Sci. 1958, 1, 99–121. [Google Scholar] [CrossRef]
- Nordbeck, S. Urban allometric growth. Geogr. Ann. Ser. B 1971, 53, 54–67. [Google Scholar] [CrossRef]
- Paulsen, K. Yet even more evidence on the spatial size of cities: Urban spatial expansion in the us, 1980–2000. Reg. Sci. Urban Econ. 2012, 42, 561–568. [Google Scholar] [CrossRef]
- Cottineau, C.; Hatna, E.; Arcaute, E.; Batty, M. Diverse cities or the systematic paradox of urban scaling laws. Comput. Environ. Urban 2017, 63, 80–94. [Google Scholar] [CrossRef]
- Cleveland, T.; Dec, P.; Rainham, D. Shorter Roads go a Long Way: The relationship between density and road length per resident within and between cities. Can. Plan. Policy 2020, 2020, 71–89. [Google Scholar]
- Ribeiro, H.V.; Rybski, D.; Kropp, J.P. Effects of changing population or density on urban carbon dioxide emissions. Nat. Commun. 2019, 10, 3204. [Google Scholar] [CrossRef] [PubMed]
- Um, J.; Son, S.W.; Lee, S.I.; Jeong, H.; Kim, B.J. Scaling laws between population and facility densities. Proc. Natl. Acad. Sci. USA 2009, 106, 14236–14240. [Google Scholar] [CrossRef]
- Netto, V.M.; Ribeiro, F.L.; Silva de Carvalho, C.L.; Cabral, V.; Neto, C. As Cidades na Pandemia: O Papel do Tamanho e da Densidade Urbana. Available online: https://caosplanejado.com/as-cidades-na-pandemia-o-papel-do-tamanho-e-da-densidade-urbana/ (accessed on 2 July 2020).
- Fragkias, M. Urbanization, economic growth and sustainability. In The Routledge Handbook of Urbanization and Global Environmental Change; Routledge: London, UK, 2015; pp. 33–50. [Google Scholar]
- Quigley, J.M. Urban diversity and economic growth. JEP 1998, 12, 127–138. [Google Scholar] [CrossRef]
- Fujita, M. Urban Economic Theory: Land Use and City Size; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Van Raan, A.F.; Van Der Meulen, G.; Goedhart, W. Urban scaling of cities in the netherlands. PLoS ONE 2016, 11, e0146775. [Google Scholar] [CrossRef]
- Alves, L.G.; Ribeiro, H.V.; Lenzi, E.K.; Mendes, R.S. Distance to the scaling law: A useful approach for unveiling relationships between crime and urban metrics. PLoS ONE 2013, 8, e69580. [Google Scholar] [CrossRef]
- Ignazzi, C.A. Coevolution in the Brazilian System of Cities. Ph.D. Thesis, Université Paris 1, Panthéon-Sorbonne, Paris, France, 2015. [Google Scholar]
- Sobolevsky, S.; Sitko, I.; Tachet des Combes, R.; Hawelka, B.; Murillo Arias, J.; Ratti, C. Cities through the prism of people’s spending behavior. PLoS ONE 2016, 11, e0146291. [Google Scholar] [CrossRef]
- Kühnert, C.; Helbing, D.; West, G.B. Scaling laws in urban supply networks. Physica A 2006, 363, 96–103. [Google Scholar] [CrossRef]
- Schläpfer, M.; Lee, J.; Bettencourt, L. Urban skylines: Building heights and shapes as measures of city size. arXiv 2015, arXiv:1512.00946. [Google Scholar]
- McDonald, B.C.; Gentner, D.R.; Goldstein, A.H.; Harley, R.A. Does size matter? scaling of CO2 emissions and us urban areas. PLoS ONE 2013, 8, e64727. [Google Scholar]
- Oliveira, E.A.; Andrade, J.S.; Makse, H.A. Large cities are less green. Sci. Rep. 2014, 4, 4235. [Google Scholar] [CrossRef]
- Gudipudi, R.; Rybski, D.; Lüdeke, M.K.; Zhou, B.; Liu, Z.; Kropp, J.P. The efficient, the intensive, and the productive: Insights from urban kaya scaling. Appl. Energy 2019, 236, 155–162. [Google Scholar] [CrossRef]
- Gudipudi, R.; Rybski, D.; Lüdeke, M.K.; Kropp, J.P. Urban emission scaling—research insights and a way forward. Environ. Plan. B Urban Anal. City Sci. 2019, 46, 1678–1683. [Google Scholar] [CrossRef]
- Pang, M.; Meirelles, J.; Moreau, V.; Binder, C. Urban carbon footprints: A consumption-based approach for Swiss households. ERC 2019, 2, 011003. [Google Scholar] [CrossRef]
- Wiedenhofer, D.; Lenzen, M.; Steinberger, J.K. Energy requirements of consumption: Urban form, climatic and socio-economic factors, rebounds and their policy implications. Energy Policy 2013, 63, 696–707. [Google Scholar] [CrossRef]
- Heinonen, J.; Jalas, M.; Juntunen, J.K.; Ala-Mantila, S.; Junnila, S. Situated lifestyles: I. how lifestyles change along with the level of urbanization and what the greenhouse gas implications are—A study of finland. Environ. Res. Lett. 2013, 8, 025003. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. Urban Areas. In Climate Change 2014—Impacts, Adaptation and Vulnerability: Part A: Global and Sectoral Aspects: Working Group II Contribution to the IPCC Fifth Assessment Report; Cambridge University Press: Cambridge, UK, 2014; pp. 535–612. [Google Scholar] [CrossRef]
- Moran, D.; Kanemoto, K.; Jiborn, M.; Wood, R.; Többen, J.; Seto, K.C. Carbon footprints of 13,000 cities. Environ. Res. Lett. 2018, 13, 064041. [Google Scholar] [CrossRef]
- Binswanger, M. Technological progress and sustainable development: What about the rebound effect? Ecol. Econ. 2001, 36, 119–132. [Google Scholar] [CrossRef]
- Gillingham, K.; Rapson, D.; Wagner, G. The rebound effect and energy efficiency policy. Rev. Environ. Econ. Policy 2016, 10, 68–88. [Google Scholar] [CrossRef]
- Hubacek, K.; Baiocchi, G.; Feng, K.; Castillo, R.M.; Sun, L.; Xue, J. Global carbon inequality. Energy Ecol. Environ. 2017, 2, 361–369. [Google Scholar] [CrossRef]
- International Resource Panel; United Nations Environment Programme. Sustainable Consumption, and Production Branch. In Decoupling Natural Resource Use and Environmental Impacts from Economic Growth; UNEP/Earthprint: Nairobi, Kenya, 2011. [Google Scholar]
- Akizu-Gardoki, O.; Bueno, G.; Wiedmann, T.; Lopez-Guede, J.M.; Arto, I.; Hernandez, P.; Moran, D. Decoupling between human development and energy consumption within footprint accounts. J. Clean. Prod. 2018, 202, 1145–1157. [Google Scholar] [CrossRef]
- Ward, J.D.; Sutton, P.C.; Werner, A.D.; Costanza, R.; Mohr, S.H.; Simmons, C.T. Is decoupling gdp growth from environmental impact possible? PLoS ONE 2016, 11, e0164733. [Google Scholar] [CrossRef]
- de Coninck, H.C.; Chakravarty, S.; Chikkatur, A.; Pacala, S.; Socolow, R.; Tavoni, M. Sharing global CO2 emission reductions among one billion high emitters. Proc. Natl. Acad. Sci. USA 2009, 106, 11884–11888. [Google Scholar]
- Brown, J.H.; Burnside, W.R.; Davidson, A.D.; DeLong, J.P.; Dunn, W.C.; Hamilton, M.J.; Mercado-Silva, N.; Nekola, J.C.; Okie, J.G.; Woodruff, W.H.; et al. Energetic limits to economic growth. BioScience 2011, 61, 19–26. [Google Scholar] [CrossRef]
- Shikwambana, L.; Mhangara, P.; Kganyago, M. Assessing the Relationship between Economic Growth and Emissions Levels in South Africa between 1994 and 2019. SUSTDE 2021, 13, 2645. [Google Scholar] [CrossRef]
- Barrett, J.; Peters, G.; Wiedmann, T.; Scott, K.; Lenzen, M.; Roelich, K.; Le Quéré, C. Consumption-based GHG emission accounting: A UK case study. Clim. Policy 2013, 13, 451–470. [Google Scholar] [CrossRef]
- Ala-Mantila, S.; Heinonen, J.; Junnila, S. Relationship between urbanization, direct and indirect greenhouse gas emissions, and expenditures: A multivariate analysis. Ecol. Econ. 2014, 104, 129–139. [Google Scholar] [CrossRef]
- Afionis, S.; Sakai, M.; Scott, K.; Barrett, J.; Gouldson, A. Consumption-based carbon accounting: Does it have a future? WIREs Clim. Chang. 2017, 8, e438. [Google Scholar] [CrossRef]
- Ottelin, J.; Heinonen, J.; Nässén, J.; Junnila, S. Household carbon footprint patterns by the degree of urbanisation in Europe. Environ. Res. Lett. 2019, 14, 114016. [Google Scholar] [CrossRef]
- Binder, C.; Bader, H.P.; Scheidegger, R.; Baccini, P. Dynamic models for managing durables using a stratified approach: The case of Tunja, Colombia. Ecol. Econ. 2001, 38, 191–207. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meirelles, J.; Ribeiro, F.L.; Cury, G.; Binder, C.R.; Netto, V.M. More from Less? Environmental Rebound Effects of City Size. Sustainability 2021, 13, 4028. https://doi.org/10.3390/su13074028
Meirelles J, Ribeiro FL, Cury G, Binder CR, Netto VM. More from Less? Environmental Rebound Effects of City Size. Sustainability. 2021; 13(7):4028. https://doi.org/10.3390/su13074028
Chicago/Turabian StyleMeirelles, Joao, Fabiano L. Ribeiro, Gabriel Cury, Claudia R. Binder, and Vinicius M. Netto. 2021. "More from Less? Environmental Rebound Effects of City Size" Sustainability 13, no. 7: 4028. https://doi.org/10.3390/su13074028
APA StyleMeirelles, J., Ribeiro, F. L., Cury, G., Binder, C. R., & Netto, V. M. (2021). More from Less? Environmental Rebound Effects of City Size. Sustainability, 13(7), 4028. https://doi.org/10.3390/su13074028






