Abstract
Observing the growing energy demand of modern societies, many countries have recognized energy security as a looming problem and renewable energies as a solution to this issue. Renewable hydrogen production is an excellent method for the storage and transfer of energy generated by intermittent renewable sources such as wind and solar so that they can be used at a place and time of our choosing. In this study, the suitability of 15 cities in Fars province, Iran, for renewable hydrogen production was investigated and compared by the use of multiple multi-criteria decision-making methods including ARAS, SAW, CODAS, and TOPSIS. The obtained rankings were aggregated by rank averaging, Borda method, and Copeland method. Finally, the partially ordered set ranking technique was used to reach a general consensus about the ranking. The criteria that affect hydrogen production were found to be solar energy potential, wind energy potential, population, air temperature, natural disasters, altitude, relative humidity, land cost, skilled labor, infrastructure, topographic condition, and distance from main roads. These criteria were weighted using the best–worst method (BWM) based on the data collected by a questionnaire. Solar energy potential was estimated using the Angstrom model. Wind energy potential was estimated by using the Weibull distribution function for each month independently. The results of the multi-criteria decision-making methods showed Izadkhast to be the most suitable location for renewable hydrogen production in the studied area.
1. Introduction
Global warming caused by the emission of greenhouse gases and especially carbon dioxide from the burning of fossil fuels is certainly the world’s most pressing environmental issue. However, energy is essential for meeting many of our basic needs, and an essential input for many industrial, transportation, and agricultural activities that are the backbone of the world’s economic growth. Indeed, access to reliable sources of energy is a determinant of the economic development of a nation. Energy conservation and government policies designed to support energy security play an important role in a country’s sustainable economic development. With the emerging impacts of global warming and climate change, many nations have acknowledged that they cannot continue relying on their traditional energy sources and have therefore developed policies and strategies for transitioning to a mix of renewable and non-renewable energies []. As one of the world’s greatest producers of oil and gas, Iran relies heavily on fossil fuel resources to meet its energy needs []. Statistics show that more than 98% of this country’s energy demand is met by fossil energy sources; an overreliance that has created some major problems for Iranian people and decision-makers. One of these problems is air pollution, which has become a particularly great concern for people living in large cities. In 2017, for example, the number of days with clean air in Tehran, the capital of Iran, was less than 30 days [].
This shows the increasing urgency of replacing fossil fuels with reliable environment-friendly energy sources. Considering the unlimited nature of renewable energy sources available to humans, harvesting and use of these energies to address long-term energy problems while also protecting the environment is turning into a global trend and clean, renewable, and affordable energy sources are becoming important components of the world economy. One of the problems with renewable energy sources is that they are not available ubiquitously, meaning that they may not be accessed at any time or place where there is a need for energy. For example, solar energy cannot be generated at night, and wind energy can only be generated when and where there are strong winds blowing. Thus, these renewable energy systems require an energy storage component or procedure capable of not only intermittent energy storage, but also releasing the stored energy at any time and place. Energy is one of the essential inputs for economic development and industrialization. Fossil fuels play a major role for supplying global energy demand, but the reserves are limited [,,].
Hydrogen is a promising clean alternative to traditional energy carriers, with great potentials in terms of emission reduction and environmental protection []. Hydrogen production is one of the best chemical methods for the storage and transfer of the electrical energy produced by intermittent renewable energy sources. Solar–wind hybrid energy systems are known to be typically more efficient and economical and produce better environmental outcomes than independent solar and wind energy generation systems []. However, the location of a solar–wind hybrid power plant plays a key role in its output, efficiency and operating costs []. In cases where the use of sustainable energy sources, and particularly solar–wind hybrid energy, is believed to be the best solution, the first step is to determine the locations with the best conditions in terms of wind–solar energy availability and other requirements of these systems. Despite extensive research effort and significant financial resources spent on improving existing renewable energy technologies, there are still some unresolved technical problems with the use of these energies. For example, while wind energy can be harvested almost everywhere, the amount of energy produced by a wind turbine highly depends on the wind speed profile and can be affected by a sudden change in wind direction or speed. In the case of solar energy, maximum efficiency can be achieved in only a few hours of the day, which means the system will operate at lower efficiencies in other hours. These issues reduce the reliability of these sources, but can be avoided by combining renewable energy generation technologies with intermittent energy storage technologies such as hydrogen production. Hydrogen is the simplest and most abundant element in nature. Hydrogen can be converted to energy through a highly clean and efficient combustion process compared to other fuels. Hydrogen has the highest specific energy (energy capacity per unit weight) among conventional fuels. It also has a higher heat output by combustion per unit weight than any other fuel. Because of its chemical activity, pure hydrogen is not easily found in nature, but it can be obtained from its compounds with other elements [] such as water, which is a combination of hydrogen with oxygen (H2O), and hydrocarbon compounds like methane (CH4), coal, and oil, which are combinations of hydrogen with carbon.
Many see hydrogen as the most promising energy carrier that can help us transition into clean, reliable, and sustainable energy systems. Hydrogen gas can be produced from a variety of sources, including water, fossil fuels, and organic matter. Water electrolysis is an especially quick and easy method for hydrogen production. In recent years, many countries have considered using water electrolysis as a primary method of hydrogen production, as it can produce high-purity hydrogen and is also compatible with renewable energy sources. Water electrolysis can produce extremely pure hydrogen, which is partly why it is considered to be an excellent technology for small-scale hydrogen production. In fact, hydrogen production by electrolysis is believed to be the best option for combined use with renewable energy systems (especially solar energy) []. In addition to energy storage and transfer, hydrogen is also used in the production of various chemical compounds such as ammonia, which requires hydrogen along with nitrogen []. Figure 1 shows a conceptual illustration of the production–consumption cycle of a renewable energy system where hydrogen is used as an energy carrier. In this system, energy is converted from renewable sources into electricity by either wind turbines or solar panels. An electrolyzer then consumes the generated electricity to convert water into oxygen and hydrogen. The produced hydrogen is transferred to consumers through various methods such as high-pressure cylinders or gas transmission lines. In the end, hydrogen is either converted into electricity directly by fuel cells or used as fuel for heating or in internal combustion engines.
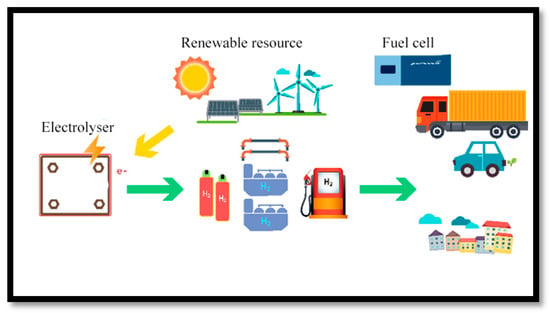
Figure 1.
Production–consumption cycle of hydrogen from renewable energies [].
2. Review of Literature
In this section, some of the previous studies in the field of renewable energy, multi-criteria decision-making (MCDM) methods, and renewable hydrogen are reviewed. Considering the use of MCDM methods in the study, some of the studies on the ranking of renewable energy sources are also reviewed in order to identify the criteria relevant to this discussion. The section also reviews some of the studies on renewable hydrogen production potential and those that have estimated solar–wind energy potentials in order to examine their methods and results.
With 300 sunny days in more than two-thirds of its area, an average irradiance of 4.5–5.5 kWh/m2 per day, and 2800 sunny hours per year, Iran could be an important solar power generation hub in West Asia and the world. It has been reported that, on average, Iran has approximately 700 sunshine hours in spring, 1050 h in summer, 830 h in autumn, and 500 h in winter [].
In a study by Zoghi et al. [], fuzzy logic, weighted linear composition, and the analytic hierarchy process (AHP) were used to determine the best location for building a solar energy system in Isfahan, Iran, based on the four criteria of geology, environment, location, and climate. The results of this study showed that some areas in Isfahan, like Barkhar, Nain, Shahinshahr, and Maymeh have a higher potential for solar energy harvesting with solar panels. They also found that using a combination of fuzzy logic and MCDM methods results in good accuracy in determining the optimal locations for solar energy sites.
Gigovi et al. [] proposed a model based on a combination of GIS (geographical information system) methods, MCDM methods, the analytic network process (ANP), and the multi-attributive border approximation area comparison (MABAC) method to identify the best location for a wind farm in Serbia. This study found that an area of about 321 km2 in Vojvodina (one of the provinces of Serbia) is suitable for the construction of a wind farm. The ranking performed with the MABAC method showed a place near the village of Laudonovac to be the best location for building a wind farm in Vojvodina.
In a study by Çolak and Kaya [], these researchers proposed an integrated MCDM method based on the fuzzy set theory for ranking renewable energies in Turkey. In this method, fuzzy AHP is used to determine the weight of decision criteria, and fuzzy TOPSIS (technique for order performance by similarity to ideal solution) is used to rank the alternatives. In this study, the proposed method was also applied to a real case with the help of experts in order to demonstrate its process and outputs. These researchers also performed a sensitivity analysis to determine the impact of criteria weights.
Mostafaeipour et al. [] investigate barriers related to solar energy development in Iran for Alborz Province. Fuzzy Best-Worst method was used for determining importance of the identified criteria and sub-criteria for developing of the solar energy sector in the province. It was concluded that the primary barriers to solar energy development were economic factors.
In a study by Ren and Toniolo [], they proposed a framework consisting of life cycle sustainability assessment (LCSA) and MCDM methods for ranking hydrogen production methods under uncertainty conditions. The four methods of hydrogen production considered in this study were coal gasification, biomass gasification, partial oxidation of methane, and wind-powered electrolysis. The results showed biomass gasification to be the most sustainable method, followed by partial oxidation of methane, wind-powered electrolysis, and coal gasification, respectively. A sensitivity analysis was also performed to determine the effect of criteria weights on the sustainability assessment. The proposed method was validated by TOPSIS, which also found biomass gasification as the best method for hydrogen production.
Acar and Beskese [] conducted a comprehensive study on the sustainability of several hydrogen production systems, including grid-powered electrolysis (electricity from fossil fuels), wind-powered electrolysis, solar-powered electrolysis, nuclear-powered electrolysis, thermochemical water splitting (from solar energy), and photoelectrochemical cells using fuzzy AHP method. Five criteria were considered in this model: economic performance (initial cost and operating cost), environmental performance (greenhouse gas emission, land use, wastewater quality, and solid waste), social performance (impact on public health, job opportunities, education, and public acceptance), technical performance (process control and initial input), and availability and reliability. The results showed that grid-powered electrolysis is the most sustainable method for hydrogen production and also reduces the costs associated with hydrogen production.
In a study by Yeh and Huang [], they examined the key factors of the site location of wind power stations. Six factors investigated in this study were safety and quality, economic value and revenue, social impact, environmental and ecological impact, and regulations and policy. These factors were correlated and measured by 28 evaluation criteria. DEMATEL (Decision-Making Trial and Evaluation Laboratory) and ANP were used to find the correlation between alternatives and the relative weights of the criteria, respectively. The results showed quality and environmental impact to be the two most important factors of site location.
Alemi Ardakani et al. [] investigated the effect of different criteria weighting methods in MCDM methods and used TOPSIS for ranking. In this study, first, several objective and subjective weighting methods including entropy, modified digital logic, and cross-correlation, were compared to determine the role of design criteria weights in MCDM methods. These researchers then introduced two new weighting methods called numeric logic (NL) and adjustable mean bars (AMB) to serve as effective and practical criteria weighting methods for decision-makers. It was claimed that AMB and NL offer a more interactive approach to criteria weighting for less experienced decision-makers.
Messaoudi et al. [] used a combination of MCDM and GIS methods for the site selection of solar power systems for hydrogen production in Algeria. The purpose of this study was to find suitable locations for building hydrogen production systems from solar energy sources based on a number of criteria. In GIS, two types of criteria were considered: restriction criteria and weighted criteria. Restriction criteria, which were used to limit the options by ruling out unsuitable areas, included land use, waterways, roads, railways, and power lines. The selected weighted criteria were the demand for hydrogen, solar-powered hydrogen production potential, digital elevation model (DEM), slope, and proximity to roads, railways, and power lines. Using MCDM methods, these criteria were weighted for the evaluation of potential sites for solar-powered hydrogen production systems. The weight analysis and calculation were performed using the AHP method. Ultimately, a time interval classification method was used to divide the studied areas into four groups of very low compatibility, low compatibility, medium compatibility, and high compatibility.
Lee and Chang [] conducted a comparative analysis on renewable energy sources that can be used for power generation in Taiwan by using four methods including WSM, VIKOR, TOPSIS, and ELECTRE. In this study, first, the Shannon entropy method was used for criteria weighting. Then the four MCDM methods were used in a quantitative evaluation with the purpose of ranking all available renewable energy options. In the criteria weighing process, it was found that the first priority should be efficiency, followed by job creation, and operating and maintenance costs. The ranking results showed that hydropower is the best option for Taiwan, followed by solar, wind, biomass, and geothermal power. A sensitivity analysis also showed that the obtained ranking was highly dependent on the weights assigned to the criteria. The results of the sensitivity analysis showed that when the economic or technical aspects were given higher priority, electricity generation from hydropower became the best option, as it is the most advanced and least expensive renewable technology in Taiwan. However, wind energy and solar energy were better options in terms of environmental impact and social impact, respectively. The findings of this study can give energy decision-makers useful insights into the relative advantages of renewable energy options and inform energy policies.
Mohsin et al. [] first examined the wind characteristics of four sites in Pakistan and then investigated the economic feasibility of using wind energy in these sites for renewable hydrogen production. Data were from the meteorological department of Pakistan. Wind data were measured at four different elevations of 30, 50, 60, and 80 m above the ground for different locations. In this study, wind speed and wind energy density were determined based on the Weibull distribution function. Then, the cost of setting up wind farms and the hydrogen production capacity at the considered sites were estimated. The results showed that renewable hydrogen production is economically viable in all four sites. It was also found that hydrogen output will depend on wind speed, air density, wind turbine size, and electrolysis system efficiency. It was estimated that using 660 kW turbines in the four studied sites, it is possible to achieve a hydrogen output of 545.10 kg/day with a total annual output of 51,917,390 kg/day at a cost of $4.304 per kilogram. Based on their findings, these researchers recommended a policy of reducing fossil fuel consumption and relying more on renewable hydrogen as fuel. This paper can serve as a model of a feasibility study on the production and use of renewable hydrogen.
In a study by Villacreses et al. [], a combination of GIS and MCDM methods was used to determine the best locations to build a wind farm in Ecuador. In this study, the Pearson correlation method was used to analyze the MCDM methods. The criteria and sub-criteria considered for site selection were meteorological parameters (wind speed, air density), slope, location (distance to posts, urban areas, and transmission lines), and environmental parameters (vegetation cover). The results showed that the best site for wind farms is the Andean region of Ecuador, which covers more than 617.5 km2. Ranking conducted with VIKOR, OCRA, TOPSIS, and OWA methods also produced similar results. This study also demonstrated the good capability of the combined GIS-MCDM method in finding suitable places for wind farms.
Dhunny et al. [] used fuzzy logic to evaluate a number of sites for the construction of wind, solar, and wind–solar hybrid stations on Mauritius island. They considered three main criteria, climatic conditions, topographic condition, and human factors, which were subdivided into several sub-criteria including wind potential, solar radiation potential, slope, habitable areas, and adjacency to grid lines. After validation, two areas named Moran and Malanga were identified as the best places to build a wind–solar station. The total annual wind–solar energy production potential in these two areas was estimated at 161.58 and 281.28, respectively. The results of this study showed that the fuzzy method offers better accuracy than linear models in this application.
Until 2015, Iran’s total photovoltaic (PV) power capacity was less than 5 MW. Following the government’s adoption of new support policies in 2016 to guarantee the purchase of solar energy, the installed capacity in 2018 increased to more than 45 MW. Of this capacity, 30 MW was realized in 2017, which indicates Iran’s positive view toward the construction of PV systems. However, since the installed capacity has not reached its ideal level, there are some plans to increase the electricity output of PV systems in the country. Given the vast size of Iran and its diverse environmental conditions, one of the most important challenges for investors in the field of solar energy is to locate the most suitable places for building power plants.
Fars province compared to other provinces has a suitable amount of solar radiation for exploitation due to its location in the solar belt of the earth, and also this province with ten percent has a large share of the country’s renewable energy production and has suitable capacities for expanding in the future. In addition, the challenges of water scarcity have also increased the need to use these capacities and attracted the attention of investors []. The province with high potential to absorb solar energy is one of the most suitable provinces for construction of solar power plants. Fars province with an average of 3400 h/year radiation has a significant advantage in the field of renewable energy [,].
In this study, the goal was to determine the best locations in Fars province for hydrogen production from the power produced by wind–solar hybrid stations based on 10 criteria including solar energy potential, wind energy potential, population, air temperature, natural disasters, altitude, relative humidity, cost items, topography, and distance from major roads. It should be noted that this is the first study of its kind for Fars province, which is one of the most suitable areas in Iran for harvesting renewable energies. The study also considered skilled labor and infrastructure as decision criteria; two factors that have not been considered in similar studies. The authors attempted to use new decision-making methods for criteria weighting as well as ranking. Because of the lack of solar radiation potential data for the study area, this potential was estimated by the use of a solar potential coefficient derived from the Angstrom equation instead of the sunshine hours criterion used in similar studies. Wind speed data were also converted to wind energy potential data using the Weibull distribution function. Since the use of GIS tools and layered maps can facilitate data analysis and representation, the study used ArcMap software for this purpose.
3. Study Area
Vast flat plains with excellent sunlight exposure and strong winds make Fars province in southern Iran an excellent choice for harvesting both wind and solar energy. This province is located in the south and southwest of Iran between 50°36′ and 55°35′ east longitudes and 27°03′ and 31°40′ north latitudes. Fars province has an area of about 122,000 km2, which is approximately 12.5% of the total land area of Iran and makes it the fourth largest Iranian province. The neighboring provinces of Fars are Isfahan to the north, Yazd to the northeast, Kerman to the east, Hormozgan to the south, and Bushehr to the west, all of which have hot and dry climates. Figure 2 shows the location of these provinces in Iran. The exact location (longitude and latitude) of cities in this area is given in Table 1.
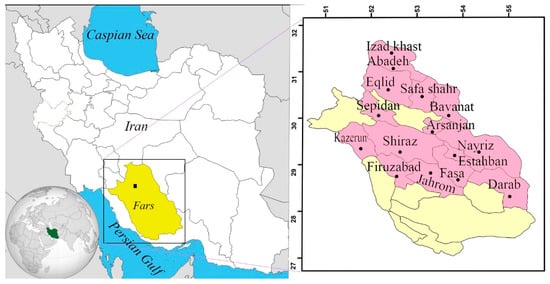
Figure 2.
Map of Iran and the study area.

Table 1.
Coordinates of cities in the study area.
4. Methodology
This study used two groups of methods. The first group comprised four MCDM methods, including ARAS, SAW, CODAS, and TOPSIS, which were used to rank the alternatives based on the criteria weighted with the best-worst method. The second group included the methods used to estimate solar energy, wind energy, and renewable hydrogen production potentials.
4.1. Multi-Criteria Decision-Making Methods
The purpose of multi-criteria decision making (MCDM) methods is to determine the best choice from among a set of options based on information available about those options based on a series of criteria []. In MCDM models, alternatives should be evaluated with respect to several criteria so that the relative superiority of alternatives over each other can be determined []. In general, multi-criteria decision making refers to the process of making a specific type of decisions (preferential type) such as evaluation, ranking, prioritization, or making a choice from existing options (which sometimes has to be done according to several conflicting criteria).
4.1.1. ARAS
The term ARAS stands for Additive Ratio Assessment. Proposed in 2010 by Zavadskas and Turskis, ARAS is one of the relatively new MCDM methods []. This method involves using a utility function to estimate the relative efficiency of the alternatives based on their relative effects and the weight assigned to the criteria and ranking them accordingly. The steps of this are described below [,]:
- Step 1:
- Forming the decision matrix (a matrix whose rows are decision alternatives and whose columns are evaluation criteria).
- Step 2:
- Determining the hypothetical ideal value (the highest value for positive criteria and the lowest value for negative criteria).
- Step 3:
- Normalizing the decision matrix using the linear method.
- Step 4:
- Weighting the decision matrix by multiplying the criteria weights of the decision matrix by the normalized criteria values using Equation (1).
- Step 5:
- Computing the total utility. In this step, the weighted normalized value should be summed in rows according to Equation (2). Here, the highest obtained value is the best, and the lowest value is the worst. The optimality function has a direct relationship with the values and criteria weights and their relative impact on the final result. Thus, the variable with the highest optimality function value is the most effective. The superiority of alternatives can therefore be determined according to their value. This is why this method is known to perform very well in the evaluation and ranking of decision options [].
- Step 6:
- Computing the relative utility. The degree of utility of each alternative is important not only for identifying the best option, but also for determining the relative quality (desirability) of lower-ranked options. In this step, Equation (3) is used to compute the degree of utility of each alternative through a comparison with an analyzed variable, which is determined by the ideal state, i.e., [].
The best alternative is determined based on the highest value of .
4.1.2. SAW
The term SAW stands for simple additive weighting. This method is one of the oldest and simplest methods used in MCDM. The steps of this method are as follows []:
- Step 1:
- Forming the decision matrix.
- Step 2:
- Obtaining the normalized decision matrix using the linear norm method.
- Step 3:
- Obtaining the weight matrix.
- Step 4:
- Determining the best alternative using Equation (4) []:
In other words, the SAW method identifies the alternative with the highest total sum of weighted normalized values as the best option.
4.1.3. CODAS
CODAS, which stands for combinative distance-based assessment, was first proposed in 2016 by Keshavarz et al. [] CODAS is a multi-attribute decision making (MADM) method for ranking a series of alternatives based on a number of criteria. CODAS determines the desirability of alternatives by two methods: 1—computing the Euclidean distance of each alternative from the negative ideal and 2—determining the Taxicab distance of each alternative from the negative ideal. In general, the steps of this method for m alternatives and n criteria are as follows [,]:
- Step 1:
- Forming the decision matrix
- Step 2:
- Normalizing the decision matrix using the linear method.
- Step 3:
- Forming the weighted normalized decision matrix by multiplying the criteria weight by the normalized matrix using Equation (5) []:
- Step 4:
- Computing the negative ideal point in terms of each criterion, which is denoted by , as shown in Equation (6):
- Step 5:
- Computing Euclidean and Taxicab distances from the negative ideal using Equations (7) and (8), respectively []
- Step 6:
- Forming the relative evaluation matrix using Equation (9) [].
In this equation, is a threshold function for determining the equality of the Euclidean distance of two alternatives, and is defined as Equation (10) []:
In this function, τ is a threshold parameter that is set by the decision-maker.
- Step 7:
- Ranking the alternatives by summing their values using Equation (11). The larger the value, the better the rank of the alternative [].
4.1.4. TOPSIS
TOPSIS, which stands for “technique for order performance by similarity to ideal solution”, is an MCDM method first introduced by Huang and Yun in 1981. This technique can be used to rank and compare different alternatives, identify the best alternative, determine the differences between alternatives, and group them. [] One of the advantages of this method is that the criteria used for comparison can be in different units and have a negative or positive nature. In other words, this technique allows for using a combination of negative and positive criteria. This technique is based on the concept that the desired alternative should have the shortest distance from the ideal positive solution (the best-case scenario) and the longest distance from the negative ideal solution (the worst-case scenario).
TOPSIS consists of the following steps [,]:
- Step 1:
- Forming the decision matrix.
- Step 2:
- Obtaining the normalized decision matrix using the vector norm method.
- Step 3:
- Creating the weight matrix based on one of the weighting methods.
- Step 4:
- Forming the weighted normalized matrix using Equation (12)
- Step 5:
- Determining the positive ideal solution , which is the largest value for positive criteria and the smallest value for negative criteria (i.e., the best value for each criterion), and also determining the negative ideal solution , which is the smallest value for positive criteria and the largest value for negative criteria (i.e., the worst value for each criterion).
- Step 6:
- Computing the Euclidean distance of each alternative from the positive and negative ideals using Equations (13) and (14) []:
- Step 7:
- Determining the relative closeness of each alternative to the ideal using Equation (15) []:
- Step 8:
- Ranking the alternatives in descending order of their values.
4.1.5. Aggregation Methods
Since using multiple MCDM methods may lead to inconsistent results, they need to be combined using a group of methods known as rank aggregation methods. The methods used in this study for this purpose are rank averaging, the Borda method, and the Copeland method [].
Rank Averaging
In this method, alternatives are ranked based on their average rank in the results of different methods. The final score of each alternative in this method is obtained by averaging its ranks [].
Borda Method
This method, which is based on the majority rule, involves comparing the ranks of each pair of alternatives in different methods. In this method, if the number of methods in which alternative K is superior to alternative L is greater than the number of methods in which the opposite is true, it counts as a win for K. If the number of times K is preferred over L is less than or equal to the number of times the opposite has occurred, it counts as a loss for K. The next step is to form a pairwise comparison matrix in which M represents a win and X represents a loss for the alternative of the corresponding row versus that of the corresponding column. Once this comparison is done for every pair of alternatives, the score of each alternative can be determined by counting its wins (the number of Ms in its row) [].
Copeland Method
This method is similar to the Borda method, except that it also considers the number of losses of each alternative. In this method, after forming the pairwise comparison matrix, the score of each alternative is determined by subtracting the number of losses (∑R) from the number of wins (∑W) [].
4.2. Decision Criteria
In the context of this study, criteria are the factors that decision-makers must consider in order to maximize the utility and satisfaction resulting from the decision. The criteria considered for each decision reflect the measures of success or goals of that decision. Criteria could be characteristics, qualities, or performance parameters that are relevant to the decision. Some criteria could be quantitative in nature and others may be qualitative. The spatial constraints considered in this study are listed in Table 2. These constraints were selected based on national, regional, urban, and environmental laws and regulations pertaining to the harvesting of renewable energies, and are expressed in terms of suitable distances from airports, urban and industrial areas, special zones, protected areas, high-voltage transmission lines, transportation networks, and road networks. In other words, these are the factors that affect the ranking of alternatives for the construction of a wind–solar hybrid power plant by ruling out the areas where plants cannot be built.

Table 2.
Location selection constraints.
This study considered a total of 10 criteria listed in Table 3, which included solar and wind energy potential, population, air temperature, natural disasters, altitude, relative humidity, cost items, topography, and distance from main roads. These decision criteria were derived from previous studies [] and were localized through consultation with experts. Solar energy potential was quantified using the Angstrom equation. The dimensionless coefficients of this equation were derived from previous studies. Using the Angstrom model to determine solar energy potential requires data on sunshine hours, latitude, sun declination angle, and Julian day number. These factors were calculated for all 15 alternatives, and the annual solar radiation potential diagram of the areas was plotted. The wind energy potential was quantified using the Weibull distribution function. Wind power was calculated using the Weibull distribution function based on wind speed, air pressure, and temperature. The wind energy potential of all 15 cities in the study area was calculated in the same way.

Table 3.
Decision criteria.
The criteria of a multi-criteria problem can be divided into positive and negative categories depending on their effect. Positive criteria are those with a positive impact on the decision process and need to be maximized. Negative criteria are the criteria that have an adverse effect and need to be minimized []. Figure 3a–j shows the information layers related to decision criteria on the geographic information maps. The required geographic information maps were obtained using the ArcGIS software.
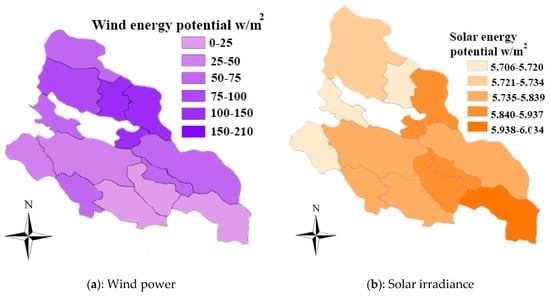
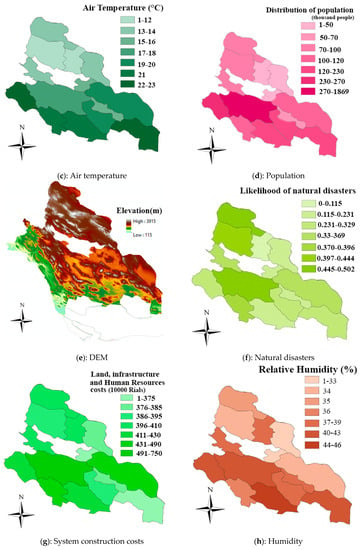
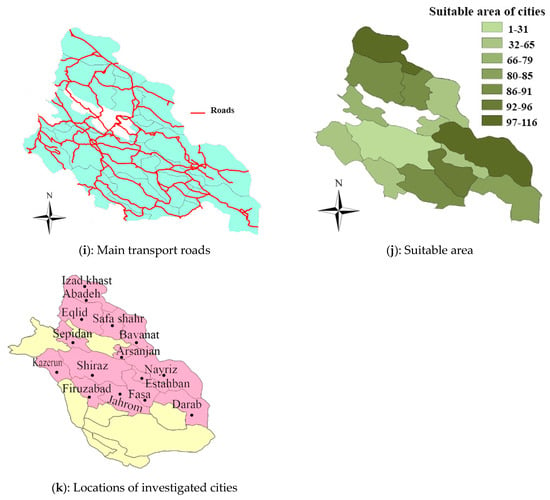
Figure 3.
Data layers of decision criteria for the study area.
4.2.1. Solar Energy Potential
In 1924, Angstrom proposed a formula for estimating solar energy radiation. This formula is a linear equation based on sunshine hours and the generated radiation. Using the Angstrom formula, one can easily calculate the amount of solar energy reaching the earth’s surface. This formula is in the form of Equation (16) []:
In the above equation, is the average radiation energy reaching a horizontal surface on normal days, is the average radiation energy reaching a horizontal surface in clear, cloudless sky conditions, A and B are Angstrom coefficients, n is the average number of sunshine hours per day, and N is the average number of possible sunshine hours per day. Coefficients A and B indicate the climatic conditions of the region. In the Angstrom model, , which represents the average radiation energy reaching a horizontal surface on clear and cloudless days (ideal conditions), is calculated from Equation (17) []:
In the above equation, d is the Julian day number or day in the year, (a number between 1 and 365), is the solar constant, which is equal to 1367, is the latitude, and δ is the solar declination angle, which is given by Equation (18) []:
The length of the day is calculated using Equation (19) []:
where the sunset hour angle is given by Equation (20) []:
4.2.2. Wind Energy Potential
Wind potential in the areas considered for turbine installation is one of the key criteria for determining the best location for a wind energy system. Wind speed is one of the most important parameters that express the wind potential of a region. Research has shown that the areas where the average wind speed is below a certain level (3 m/s) are not suitable for wind farms, as the wind is rarely strong enough to turn the turbine blades. It is also necessary to avoid areas with very high wind speeds, as they can damage the turbine. It should be noted that the thing that turns the turbine blade is wind energy, which depends not only on wind speed, but also air pressure and temperature []. In line with global meteorological standards, Iranian meteorological stations measure wind speed at a height of 10 m above ground. According to experts on the subject (Iran Renewable Energy Association and Electricity Efficiency Organization), the majority of turbine models commonly used in Iran have 40-m towers. Thus, calculations of this study were also conducted for this height. Therefore, it was necessary to convert the wind power-related data, i.e., wind speed, air temperature, and air pressure, from the height of 10 to 40 m. Since temperature and pressure variations over heights of less than 100 m are very small, they could be ignored without any significant impact on the results. However, the effect of height on wind speed had to be considered. The wind speed at the desired height can be determined using the wind profile power law, which is given in Equation (21) [].
In this equation, is the wind speed at the desired height, is the available wind speed (in this study, wind speed at a height of 10 m), is the desired height corresponding to , and is the height for which wind speed data are available (in this study, ). α is the coefficient of wind profile power law, which differs for hilly and highland areas. The wind speed data obtained for a height of 40 m are only valid within a 7.5 km radius of the meteorological station where the data are measured. Thus, all criteria also had to be considered within this radius, because otherwise the wind speed and consequently the wind power calculations could be incorrect, resulting in invalid conclusions. Since wind speed is a random variable, wind power in an area can be obtained using probability density functions. Wind speed can be described by several types of frequency distributions, including Rayleigh Weibull distribution, log-normal distribution, gamma distribution, and three-parameter beta distribution. However, it is more common to use Weibull distribution for this purpose. This distribution is given in Equation (22) []:
where is the probability density function, and V is the wind speed. This equation has two constants, scale parameter (c) and shape parameter (k), which must be calculated in advance. These two constants can be obtained from Equations (23) and (24) [].
In Equation (23), Γ is the gamma function, which is expressed by Equation (25):
Thus, to obtain c and k, the average annual wind speed in each year must be obtained from the available data and inserted in Equations (23) and (24). The average wind speed can be calculated by the simple formula , where n is the total number of wind speed data. Finally, wind energy can be obtained from Equation (26) []:
Here, ρ is the ambient air density, which is given by Equation (27):
In this equation, is the ambient air pressure in Pascals, is the average air temperature in Kelvin (), and is the gas constant for dry air (=287 J/kgK).
Once these calculations are complete, the last step is to determine the available wind power for area A, which is created by the rotation of the turbine blades. This parameter can be calculated from Equation (28) []:
The wind energy potential index was considered as a positive criterion for ranking.
4.2.3. Electrolyzer
An electrolyzer consumes the energy produced by the renewable energy systems to convert water into hydrogen. There are multiple types of water electrolysis methods with different efficiency levels. This study assumed that a proton exchange membrane electrolyzer will be used for this purpose. This method offers high efficiency, long life cycle, and high compatibility with renewable energy systems, where electricity output could be variable. Like wind and solar energy, hydrogen also needs to be stored. The hydrogen produced in the mentioned method will have a pressure of 1½ bar, which does not require further compression. Therefore, the output of electrolyzers can be directly connected to storage tanks. Proton exchange membrane electrolyzers have an average energy consumption of 53 kWh/kg. The mass of hydrogen produced from solar or wind energy can be obtained from Equation (29) [,].
where is the weight of hydrogen gas produced in kilograms, is the energy produced by renewable sources, is the low heating value of hydrogen in kWh/kg (here, it was considered to be 33.33 kWh/kg), is the energy consumed in Hydrogen production, is the efficiency of the electrolyzer system (here, it was considered to be 0.75), and is an additional efficiency factor to take the energy loss of the electrolyzer into account.
4.3. Criteria Weighting
Decision criteria can be weighted by a variety of methods, including Shannon entropy, LINMAP, best—worst, and eigenvector. In Shannon entropy and LINMAP methods, weighting is done by a decision matrix. However, the best—worst and eigenvector methods use a pairwise comparison matrix for this purpose. In this study, criteria weighting was done using the best-worst method, which is described below.
Best—Worst Method (BWM)
The best—worst method (BWM) is a new innovative MCDM method developed by Rezaei in 2015. The basic idea of this method is that instead of pairwise comparison of all criteria, the decision-maker can determine the best criterion (i.e., the most preferable or most important) and the worst criterion (i.e., the least preferable or least important) and conduct a pairwise comparison between these two criteria (best and worst) and other criteria [].
BWM can be used for weight calculation through the following steps []:
- Step 1:
- Specifying the set of criteria that will be used in the decision-making (c1, c2, …, cn).
- Step 2:
- Identifying the best (most preferable) and worst (least preferable) criteria (in this step, the decision-maker generally specifies the best and worst criteria without making any comparison).
- Step 3:
- Determining the preference of the best criterion over other criteria on a scale between 1 and 9, with 1 indicating equal preference and 9 indicating complete superiority. The result of this vector comparison should be in the form of Equation (30).
- Step 4:
- Determining the preference of all criteria over the worst criterion on a scale between 1 and 9, with 1 indicating equal preference and 9 indicating complete superiority. The result of this vector comparison will be in the form of Equation (31).
- Step 5:
- Finding the optimal weights. The importance weight of criteria should be obtained in the format of . This vector must be defined in such a way that for each criterion j, and . Thus, to meet the mentioned conditions, the terms and should be minimum. Additionally, since it is assumed that the importance weights are non-negative and sum up to 1, the problem can be expressed as the mathematical programming problem of Equation (32) []:
This problem (Equation (32)) can also be formulated as the following mathematical programming (Equation (33)):
Solving the above mathematical model gives the optimal value of . However, it should be noted that when there are more than three criteria, the solution to the above model may have multiple optimality. Therefore, models 33 and 34 are used to identify the upper and lower bounds of each of the weights () []:
After solving two Equations (34) and (35), the optimal weight of criteria can be obtained from Equation (36).
In BWM, if there are two or more decision-makers, the geometric mean of their opinions should be used. If there are k decision-makers (k = 1, 2, …, K), each with a weight λk defined such that , and their opinion about the preference of the j-th criterion relative to the best and worst criteria are and , respectively, then their opinions can be aggregated using Equations (37) and (38) [].
It should be noted that BWM is an extended version of AHP where pairwise comparisons are limited to the best and worst criteria in order to reach higher consistency in decision-makers’ judgments.
5. Analysis
In this study, first, the available data related to decision criteria were collected. The solar energy potential in the studied area was then calculated by the use of the Angstrom—Prescott equation based on sunshine hours, latitude, sun declination angle, and Julian day number. The wind energy potential was also calculated using the Weibull distribution function based on wind speed, air pressure, and temperature data. Population data were extracted from the 2016 statistics. For the natural disaster severity index, the Poisson probability function was used.
Figure 3a shows the wind energy potential information for the region. Three cities of Izad Khast, Bavanat, and Safa Shahr have the highest wind energy potential of 205, 132, and 130 W/m2, respectively. Jahrom has the lowest potential for wind energy with 15 W/m2. Figure 3b shows the information map of the solar radiant energy potential that per square meter of the solar panel in the region can obtain. Darab, Fasa, and Bavanat have the highest solar energy radiation of 6.03, 5.94, and 5.91, respectively. Figure 3c shows the average temperature in the studied cities of Fars province. Northern cities, which are mostly mountainous, have lower average temperatures than southern cities. Temperature is considered as a negative factor due to its negative role in hydrogen production and storage processes. Figure 3e is the digital elevation map (DEM) that shows the elevation of each point above sea level. North of Fars province is a mountainous region with an average altitude of 3000 m, and moving to the south, the elevation decreases. Figure 3d is the map for distribution of population in the study area. Shiraz, with a population of 1,869,000, is the most populous city in Fars province. The cities of Kazerun, and Jahrom with 266,217 and 228,532 people, respectively, are the most populous cities in the study area after Shiraz. Figure 3f shows the distribution of the probability of natural disasters of floods and earthquakes in the region. This factor has a negative effect on attracting investors due to the risk of damaging the equipment. Figure 3g shows the cost criteria in the form of a map. Costs include the cost of providing land, infrastructure, and the cost of providing human resources. Shiraz, Firozabad, and Neyriz rank first to third in this criterion. Locations with less investment cost attract more investors. Fars province, because it is close to the sea, is affected by the humidity of the Persian Gulf. Southern cities are most affected by this situation. Figure 3h shows the humidity of each city in the study area. Humidity is considered a negative factor in the ranking due to the negative impact on equipment. Figure 3i shows the distribution of the main communication roads in the area. Shiraz is the main connection point of these roads due to its central location. Among the cities, Izad Khast has the least access to the main roads. According to experts, this criterion is one of the effective factors in investors’ decisions. Due to the urban and environmental constraints mentioned in the Table 2, the number of suitable lands is limited. Figure 3j shows the number of these places for each city, for which Izad Khast and Neyriz have the highest value.
Table 4 presents the rankings obtained from TOPSIS, ARAS, SAW, and CODAS, and those obtained from the three rank aggregation techniques, i.e., Borda, Copeland, and averaging. As can be seen, in all rankings, the top two places belong to Izad Khast and Safa Shahr, and in most rankings, the third place belongs to Bavanat. However, for other places, there are some differences between the results of different methods. To achieve a more reliable solution, the results of these methods were aggregated.

Table 4.
Results of the rank averaging method.
In the rank integration stage, the partially ordered set ranking technique was used. In this technique, i can be placed higher than j in the final ranking only if it has been ranked higher than j by all methods; otherwise, no relationship can be defined for these two alternatives. As the results presented in Table 5 show, in the ranking obtained with this method, Izadkhast is placed on top, Safashahr is in second place, and Bavanat is in third place.

Table 5.
Results of the integration technique.
Hydrogen Production Potential
The energy generated by renewable energy systems must be sent to the electrolyzer. In this study, the electrolyzer was assumed to be of the proton exchange membrane type with an efficiency coefficient of 0.75. Table 6 shows the annual renewable hydrogen production potential of the alternatives per square meter of wind turbine and solar panel installed. To provide a more comprehensible illustration of the environmental impact of using renewable energy with a hydrogen carrier, the results are also presented in terms of CO2 emission reduction in kilograms []. This conversion is done by computing the greenhouse gas production equivalent of the amount of gasoline to be saved by using hydrogen as fuel. It should be noted that in the case of solar energy, a unit area (m2) refers to the horizontal surface on the ground, but in the case of wind energy, it refers to the area covered by turbine blades at a height of 40 m. Figure 4 shows the potential for renewable hydrogen production in the study area.

Table 6.
Hydrogen production from renewable sources.
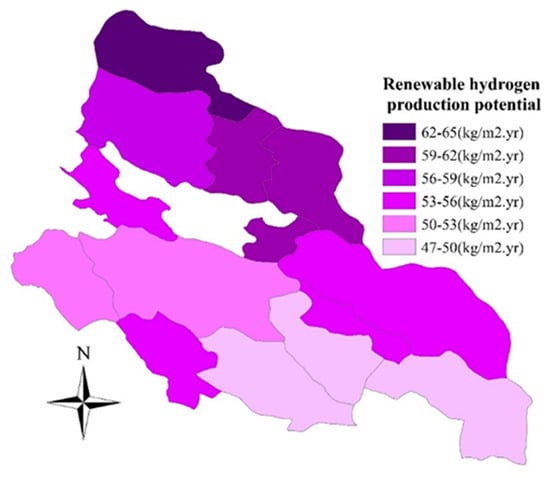
Figure 4.
Potential for hydrogen production from solar and wind energy sources in the study area.
Figure 4 shows renewable hydrogen production in the study area. Izad Khast, with the highest amount of hydrogen production, ranks first among the cities of Fars province. The city has the highest numbers of suitable locations for renewable power plants, which justifies the scattered production of energy. Additionally, the temperature of northern cities is lower than other cities, which adds to the popularity of these cities. Land prices and humidity are relatively low, which is another characteristic of this city. According to the information obtained from digital elevation maps, the lands of this city are mountainous and have the highest elevation, and the probability of natural disasters in this city is high, and on the other hand, it has the least access to the main roads. Despite these negative criteria, considering the weight that experts assigned to these criteria and using the prioritization methods, this city can be the most attractive destination for investors. For example, for every square meter of solar panel and one square meter of wind turbine in the city of Izad Khast, 571 kg of carbon dioxide can be prevented from being released into the atmosphere, and 64 kg renewable hydrogen that is equivalent to 179 L of gasoline can be produced, which can be used both directly in the transportation system or for other purposes. Shiraz, as the capital city of Fars province, has the highest population and the highest access to roads. With medium potential of wind and solar energy, altitude, humidity, and temperature compared to other cities, Shiraz has the highest cost of land and other costs and also has a relatively high probability of natural disasters. Due to these limitations, the number of suitable locations to build a power plant is the lowest for Shiraz. Under these conditions, the result obtained from the ranking methods for this city is 6. Izad Khast and Safashahr gained the first and second priority in all prioritization methods, respectively. The city of Bavanat ranked third except in the Aras method. The cities of Arsanjan and Bavanat ranked second and third in hydrogen production. Safa Shahr has the second rank in the prioritization and the fourth rank in the amount of hydrogen production. Because the cities obtained different ranks in different methods, the method of the average rank method, Borda, and Copeland were used to aggregate the results. Finally, using the ranking for the partially ordered set, the final ranking of cities was obtained.
After forming the decision matrix, the criteria were weighted using BWM, and then the alternatives were ranked using the ARAS, SAW, TOPSIS, and CODAS methods. Because the cities obtained different ranks in different methods, the obtained results were aggregated by rank averaging and Borda and Copeland methods. In the end, a final ranking was obtained by the use of the partially ordered set ranking technique.
6. Conclusions
Over the years, political and economic crises related to fossil fuel reliance and environmental concerns such as acid rains and climate change, in combination with the worldwide population boom and economic growth, have pushed many researchers to search for solutions for the world’s energy problems or at least avoid environmental crises resulting from these issues. For many developing countries, access to new types of energy could be essential for economic development. Recent studies have shown a direct relationship between the level of development of a country and its energy consumption regime. Given the limited reserves of fossil fuels and the rising level of energy demand across the world, it is no longer sustainable to rely solely on existing energy sources. Fortunately, many countries have realized the benefits of taking advantage of various energy sources, especially renewable sources, in meeting their current and future energy needs, and are heavily investing in the research and development of technologies and industries that are needed to tap into these essentially unlimited sources of energy. With the emerging impacts of global warming caused by excessive use of fossil fuels and excessive emission of greenhouse gases such as CO2, many countries have begun to think about securing clean, sustainable, and renewable energy sources. There are, however, some limitations to the use of renewable energy sources, such as low reliability. For example, solar energy is not available at all times, and wind does not blow at a reliably constant speed. One way to resolve this problem is to embed a hydrogen production unit into these renewable energy systems. This study investigated and compared the suitability of 15 cities in Fars province, Iran, for renewable hydrogen production. First, the evaluation criteria were determined through library research, review of previous studies, and consultation with experts. These criteria included solar energy potential, regional wind potential, population, air temperature, natural disasters, altitude, relative humidity, cost items, topography, and distance from main roads. After using a new method called BWM to weight the criteria, the cities were ranked using the ARAS method. SAW, CODAS, and TOPSIS methods were then used for validation. The results of these methods were aggregated by three methods, vis. rank averaging, Borda technique, and Copeland technique. Finally, the partially ordered set ranking technique was used to reach a final ranking based on the consensus approach. The cities of Izadkhast, Safashahr, and Bavanat were identified as the top three choices by the MCDM methods as well as the ranking aggregation methods. The final ranking also had the same cities in the top three places. It should be noted that the obtained ranking is dependent on the criteria weights obtained from BWM. In other words, the suitability of considered places for the construction of wind–solar hybrid power plants very much depend on solar and wind energy potential as well as population, air temperature, natural disasters, altitude, relative humidity, costs, topography, and distance from main roads. Overall, the results demonstrated that in any effort to build a wind–solar hybrid power plant in Fars province, higher priority should be given to the cities of Izadkhast, Safashahr, and Bavanat than other parts of this region. This study also considered the cost of land, labor, and infrastructure required for the construction of a hybrid power plant. In terms of this criterion, the cities of Shiraz and Izdakhast were found to be, respectively, the least and most suitable (most and least expensive) choices in the study area. Future studies are recommended to rank the regions of Fars province or other provinces in terms of suitability for the use of geothermal energy or bioethanol, use other new MCDM methods such as WASPAS, COPRAS, and MABAC for this purpose, and investigate the possibility of using the electricity generated by the incineration of municipal waste for renewable hydrogen production with the collaboration of individual experts in related fields including mechanical engineering, electrical engineering, and natural resource engineering or panels of these experts.
Author Contributions
Conceptualization: K.A., A.M. and Y.H.; methodology: K.A., S.C. and S.J.H.D.; software: Y.H., E.J. (Ehsan Jahanshahi); validation: E.J. (Ehsan Jahanshahi), S.S.H.D. and S.J.H.D.; formal analysis: E.J. (Ehsan Jahanshahi); investigation: A.M. and S.S.H.D.; resources: E.J. (Erfan Jooyandeh); data curation: M.J.; writing—original draft preparation: A.M.; writing—review and editing: S.C., K.A. and A.I.; visualization: A.I.; supervision: A.M. an S.S.H.D.; project administration: K.T.; funding acquisition: K.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by grant number-ENV6402012N from the Prince of Songkla University.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Normalized decision matrix | |
| The characteristic value of the i-th option relative to the j-th criterion | |
| Weight vector | |
| Criterion weight of j-th | |
| Normalized weighted matrix | |
| Normalized weighted matrix elements | |
| The Optimality Function value for the ith alternative in ARAS method | |
| The ideal mode in ARAS | |
| The degree of desirability of each option in ARAS | |
| The most suitable option in SAW | |
| Euclidean distance | |
| Taxicab distance | |
| Threshold parameter in CODAS | |
| Relative evaluation matrix | |
| Ranking | |
| The positive ideal solution | |
| The negative ideal solution | |
| Distance from the negative ideal solution | |
| Distance from the positive ideal solution | |
| The relative closeness of each alternative to the ideal solution | |
| Average energy radiation reaching a horizontal surface | |
| Average energy radiation reaching a horizontal surface in clear, cloudless conditions | |
| Angstrom coefficient | |
| Angstrom coefficient | |
| Average daily hours of sunshine | |
| The average number of possible hours of sunshine per day | |
| Julius number of the day of the year | |
| Solar constant | |
| Latitude of the place | |
| The sun declination angle | |
| The sunset hour angle | |
| Wind speed at the desired height | |
| Wind speed available | |
| The desired height | |
| Current height | |
| Power law index | |
| Probability density function | |
| V | Wind speed |
| Ambient air density | |
| Ambient air pressure in Pascal units | |
| Average air temperature in Kelvin | |
| Gas constant for dry air | |
| C | Scale parameter |
| k | Shape parameter |
| Weight of hydrogen gas produced in kilograms | |
| Energy produced by renewable energy sources | |
| The low calorific value of hydrogen in kilowatt hours per kilogram | |
| Electrolyzer system efficiency | |
| Extra efficiency factor to take into account the energy lost in the electrolyzer | |
| Indication of the performance of the best criterion B compared to the criterion j-th | |
| Indication of the performance of j relative to the worst criterion w | |
| Optimal value of BWM method |
References
- Sharvini, S.R.; Noor, Z.Z.; Chong, C.S.; Stringer, L.C.; Yusuf, R.O. Energy consumption trends and their linkages with renewable energy policies in East and Southeast Asian countries: Challenges and opportunities. Sustain. Environ. Res. 2018, 28, 257–266. [Google Scholar] [CrossRef]
- Yazdanpanah, M.; Komendantova, N.; Ardestani, R.S. Governance of energy transition in Iran: Investigating public acceptance and willingness to use renewable energy sources through socio-psychological model. Renew. Sustain. Energy Rev. 2015, 45, 565–573. [Google Scholar] [CrossRef]
- Tavana, A.; Javid, A.E.; Houshfar, E.; Andwari, A.M.; Ashjaee, M.; Shoaee, S.; Maghmoomi, A.; Marashi, F. Toward renewable and sustainable energies perspective in Iran. Renew. Energy 2019, 139, 1194–1216. [Google Scholar] [CrossRef]
- Mostafaeipour, A.; Abesi, S. Wind Turbine Productivity and Development in Iran. In Proceedings of the 2010 International Conference on Biosciences, Cancun, Mexico, 7–13 March 2010. [Google Scholar] [CrossRef]
- Mohammadi, K.; Mostafaeipour, A.; Dinpashoh, Y.; Poura, N. Electricity Generation and Energy Cost Estimation of Large-Scale Wind Turbines in Jarandagh, Iran. Hindawi Publishing Corporation. J. Energy 2014, 2014, 613681. [Google Scholar] [CrossRef]
- Zarezade, M.; Mostafaeipour, A. Identifying the effective factors on implementing the solar dryers for Yazd province, Iran. Renew. Sustain. Energy Rev. 2016, 57, 765–775. [Google Scholar] [CrossRef]
- Ren, J. Multi-criteria decision making for the prioritization of energy systems under uncertainties after life cycle sustainability assessment. Sustain. Prod. Consum. 2018, 16, 45–57. [Google Scholar] [CrossRef]
- Gigović, L.; Pamučar, D.; Božanić, D.; Ljubojević, S. Application of the GIS-DANP-MABAC multi-criteria model for selecting the location of wind farms: A case study of Vojvodina, Serbia. Renew. Energy 2017, 103, 501–521. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Yousefi, H.; Mohammadi, M. Multi-criteria decision support system for wind farm site selection using GIS. Sustain. Energy Technol. Assess. 2016, 13, 38–50. [Google Scholar] [CrossRef]
- Available online: http://www.satba.gov.ir (accessed on 15 March 2019).
- Menia, S.; Tebibel, H.; Lassouane, F.; Khellaf, A.; Nouicer, I. Hydrogen production by methanol aqueous electrolysis using photovoltaic energy: Algerian potential. Int. J. Hydrogen Energy 2017, 42, 8661–8669. [Google Scholar] [CrossRef]
- Kaur, M.; Pal, K. Review on hydrogen storage materials and methods from an electrochemical viewpoint. J. Energy Storage 2019, 23, 234–249. [Google Scholar] [CrossRef]
- Ju, H.; Badwal, S.; Giddey, S. A comprehensive review of carbon and hydrocarbon assisted water electrolysis for hydrogen production. Appl. Energy 2018, 231, 502–533. [Google Scholar] [CrossRef]
- Available online: http://www.jrenew.ir/ (accessed on 2 April 2021).
- Zoghi, M.; Houshang Ehsani, A.; Sadat, M.; Javad Amiri, M.; Karimi, S. Optimization solar site selection by fuzzy logic model and weighted linear combination method in arid and semi-arid region: A case study Isfahan-IRAN. Renew. Sustain. Energy Rev. 2017, 68, 986–996. [Google Scholar] [CrossRef]
- Çolak, M.; Kaya, İ. Prioritization of renewable energy alternatives by using an integrated fuzzy MCDM model: A real case application for Turkey. Renew. Sustain. Energy Rev. 2017, 80, 840–853. [Google Scholar] [CrossRef]
- Mostafaeipour, A.; Alvandimanesh, M.; Najafi, F.; Issakhov, A. Identifying challenges and barriers for development of solar energy by using fuzzy best-worst method: A case study. Energy 2021, 226, 120355. [Google Scholar] [CrossRef]
- Ren, J.; Toniolo, S. Life cycle sustainability decision-support framework for ranking of hydrogen production pathways under uncertainties: An interval multi-criteria decision making approach. J. Clean. Prod. 2018, 175, 222–236. [Google Scholar] [CrossRef]
- Acar, C.; Beskese, A.; Temur, G.T. Sustainability analysis of different hydrogen production options using hesitant fuzzy AHP. Int. J. Hydrogen Energy 2018, 43, 18059–18076. [Google Scholar] [CrossRef]
- Yeh, T.-M.; Huang, Y.-L. Factors in determining wind farm location: Integrating GQM, fuzzy DEMATEL, and ANP. Renew. Energy 2014, 66, 159–169. [Google Scholar] [CrossRef]
- Alemi-Ardakani, M.; Milani, A.S.; Yannacopoulos, S.; Shokouhi, G. On the effect of subjective, objective and combinative weighting in multiple criteria decision making: A case study on impact optimization of composites. Expert Syst. Appl. 2016, 46, 426–438. [Google Scholar] [CrossRef]
- Messaoudi, D.; Settou, N.; Negrou, B.; Settou, B. GIS based multi-criteria decision making for solar hydrogen production sites selection in Algeria. Int. J. Hydrogen Energy 2019, 44, 31808–31831. [Google Scholar] [CrossRef]
- Lee, H.-C.; Chang, C.-T. Comparative analysis of MCDM methods for ranking renewable energy sources in Taiwan. Renew. Sustain. Energy Rev. 2018, 92, 883–896. [Google Scholar] [CrossRef]
- Mohsin, M.; Rasheed, A.; Saidur, R. Economic viability and production capacity of wind generated renewable hydrogen. Int. J. Hydrogen Energy 2018, 43, 2621–2630. [Google Scholar] [CrossRef]
- Villacreses, G.; Gaona, G.; Martínez-Gómez, J.; Jijón, D.J. Wind farms suitability location using geographical information system (GIS), based on multi-criteria decision making (MCDM) methods: The case of continental Ecuador. Renew. Energy 2017, 109, 275–286. [Google Scholar] [CrossRef]
- Dhunny, A.Z.; Doorga, J.R.S.; Allam, Z.; Lollchund, M.R.; Boojhawon, R. Identification of optimal wind, solar and hybrid wind-solar farming sites using fuzzy logic modelling. Energy 2019, 188, 116056. [Google Scholar] [CrossRef]
- Available online: http://investinfars.ir (accessed on 2 April 2021).
- Available online: https://barghnews.com/fa/news/42970 (accessed on 2 April 2021).
- Zavadskas, E.K.; Turskis, Z. A new additive ratio assessment (ARAS) method in multicriteria decision-making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
- Kutut, V.; Zavadskas, E.K.; Lazauskas, M. Assessment of priority alternatives for preservation of historic buildings using model based on ARAS and AHP methods. Arch. Civ. Mech. Eng. 2014, 14, 287–294. [Google Scholar] [CrossRef]
- Paul, D.; Agarwal, P.; Chakraborty, S. Performance appraisal of Indian state police forces using ARAS method. Manag. Sci. Lett. 2016, 6, 361–372. [Google Scholar] [CrossRef]
- Wang, Y.-J. Interval-valued fuzzy multi-criteria decision-making based on simple additive weighting and relative preference relation. Inf. Sci. 2019, 503, 319–335. [Google Scholar] [CrossRef]
- Mostafaeipour, A.; Jooyandeh, E. Prioritizing the locations for hydrogen production using a hybrid wind-solar system: A case study. Adv. Energy Res. 2017, 5, 107. [Google Scholar]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. A New Combinative Distance-Based Assessment (Codas) Method for Multi-Criteria Decision-Making. Econ. Comput. Econ. Cybern. Stud. Res. Acad. Econ. Stud. 2016, 50, 25–44. [Google Scholar]
- Ijadi Maghsoodi, A.; Rasoulipanah, H.; Martínez López, L.; Liao, H.; Zavadskas, E.K. Integrating interval-valued multi-granular 2-tuple linguistic BWM-CODAS approach with target-based attributes: Site selection for a construction project. Comput. Ind. Eng. 2020, 139, 106147. [Google Scholar] [CrossRef]
- Ijadi Maghsoodi, A.; Ijadi Maghsoodi, A.; Poursoltan, P.; Antucheviciene, J.; Turskis, Z. Dam construction material selection by implementing the integrated SWARA—CODAS approach with target-based attributes. Arch. Civ. Mech. Eng. 2019, 19, 1194–1210. [Google Scholar] [CrossRef]
- Peng, C.; Du, H.; Liao, T.W. A research on the cutting database system based on machining features and TOPSIS. Robot. Comput. Integr. Manuf. 2017, 43, 96–104. [Google Scholar] [CrossRef]
- Phelipe, M.R.; Alexandre, P.B.; Glauco, B.S.; Helder, G.C. Analysis of the operational performance of brazilian airport terminals: A multicriteria approach with De Borda-AHP integration. J. Air Transp. Manag. 2016, 51, 19–26. [Google Scholar]
- Green, M.A.; Emery, K.; Hishikawa, Y.; Warta, W.; Dunlop, E.D. Solar cell efficiency tables (Version 45). Progress in photovoltaics. Res. Appl. 2015, 23, 1–9. [Google Scholar]
- Rezaei, M.; Mostafaeipour, A.; Qolipour, M.; Tavakkoli-Moghaddam, R. Investigation of the optimal location design of a hybrid wind-solar plant: A case study. Int. J. Hydrogen Energy 2018, 43, 100–114. [Google Scholar] [CrossRef]
- Esteves, N.B.; Sigal, A.; Leiva, E.P.M.; Rodríguez, C.R.; Cavalcante, F.S.A.; de Lima, L.C. Wind and solar hydrogen for the potential production of ammonia in the state of Ceará–Brazil. Int. J. Hydrogen Energy 2015, 40, 9917–9923. [Google Scholar] [CrossRef]
- Aryanpur, V.; Shafiei, E. Optimal deployment of renewable electricity technologies in Iran and implications for emissions reductions. Energy 2015, 91, 882–893. [Google Scholar] [CrossRef]
- Sigal, A.; Leiva, E.P.M.; Rodríguez, C.R. Assessment of the potential for hydrogen production from renewable resources in Argentina. Int. J. Hydrogen Energy 2014, 39, 8204–8214. [Google Scholar] [CrossRef]
- Komiyama, R.; Otsuki, T.; Fujii, Y. Energy modeling and analysis for optimal grid integration of large-scale variable renewables using hydrogen storage in Japan. Energy 2015, 81, 537–555. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Available online: https://ecoscore.be/en/info/ecoscore/co2 (accessed on 2 April 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).