Contribution to the Sustainability of Agricultural Production in Greenhouses Built on Slope Soils: A Numerical Study of the Microclimatic Behavior of a Typical Colombian Structure
Abstract
:1. Introduction
2. Materials and Methods
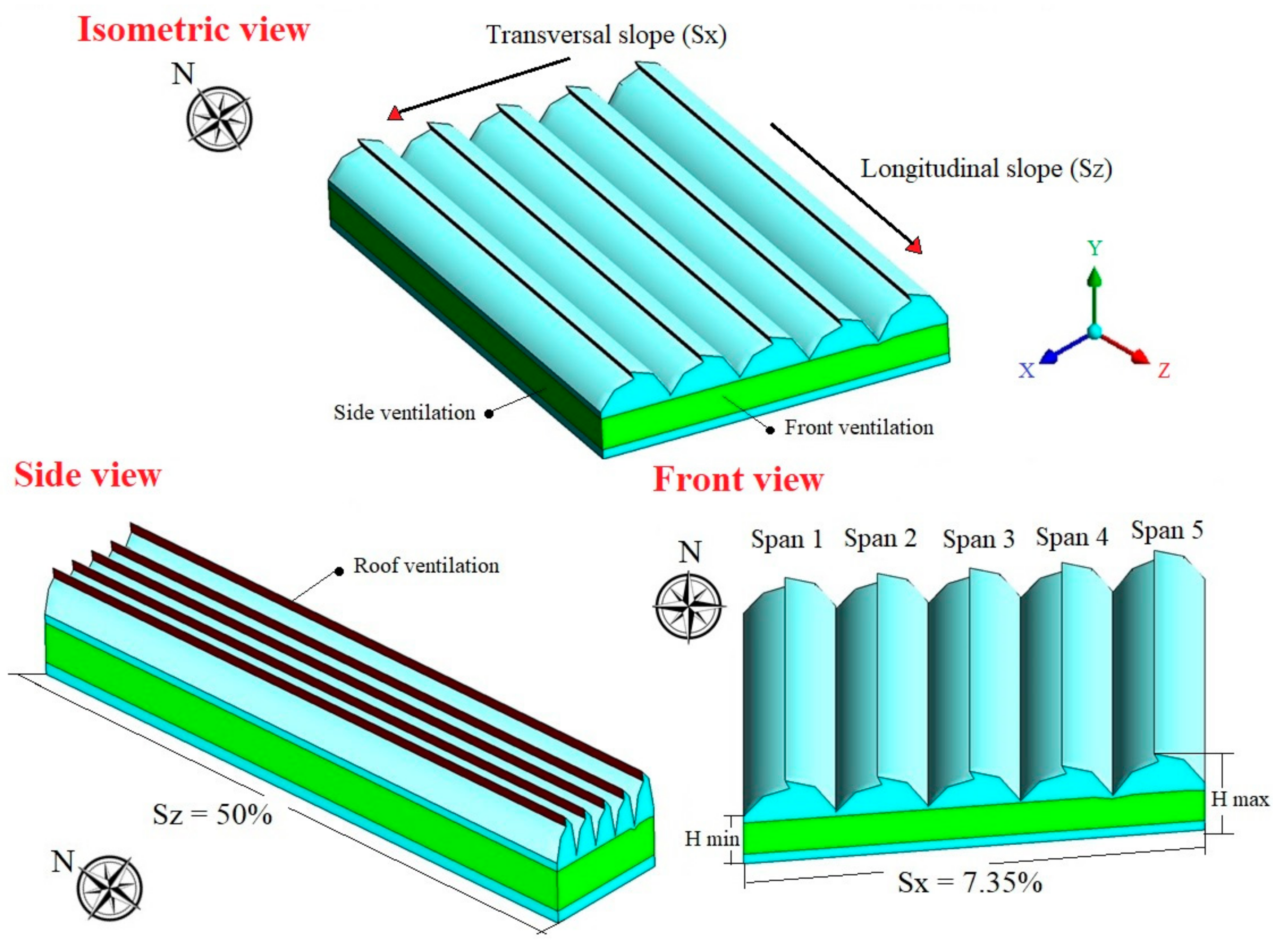
2.1. Description of the Greenhouse and Experimental Site
2.2. CFD Numerical Model
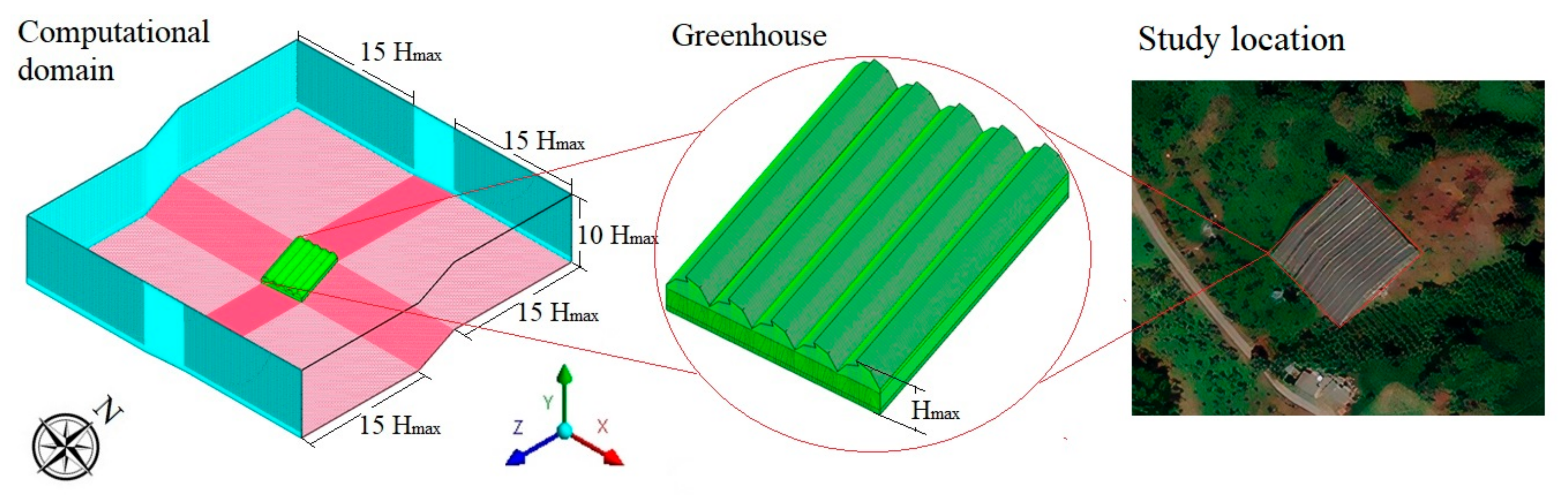
2.3. Discretisation of the Computational Domain
2.4. Boundary Conditions
2.5. CFD Model Validation and Simulated Scenarios
3. Results and Discussion
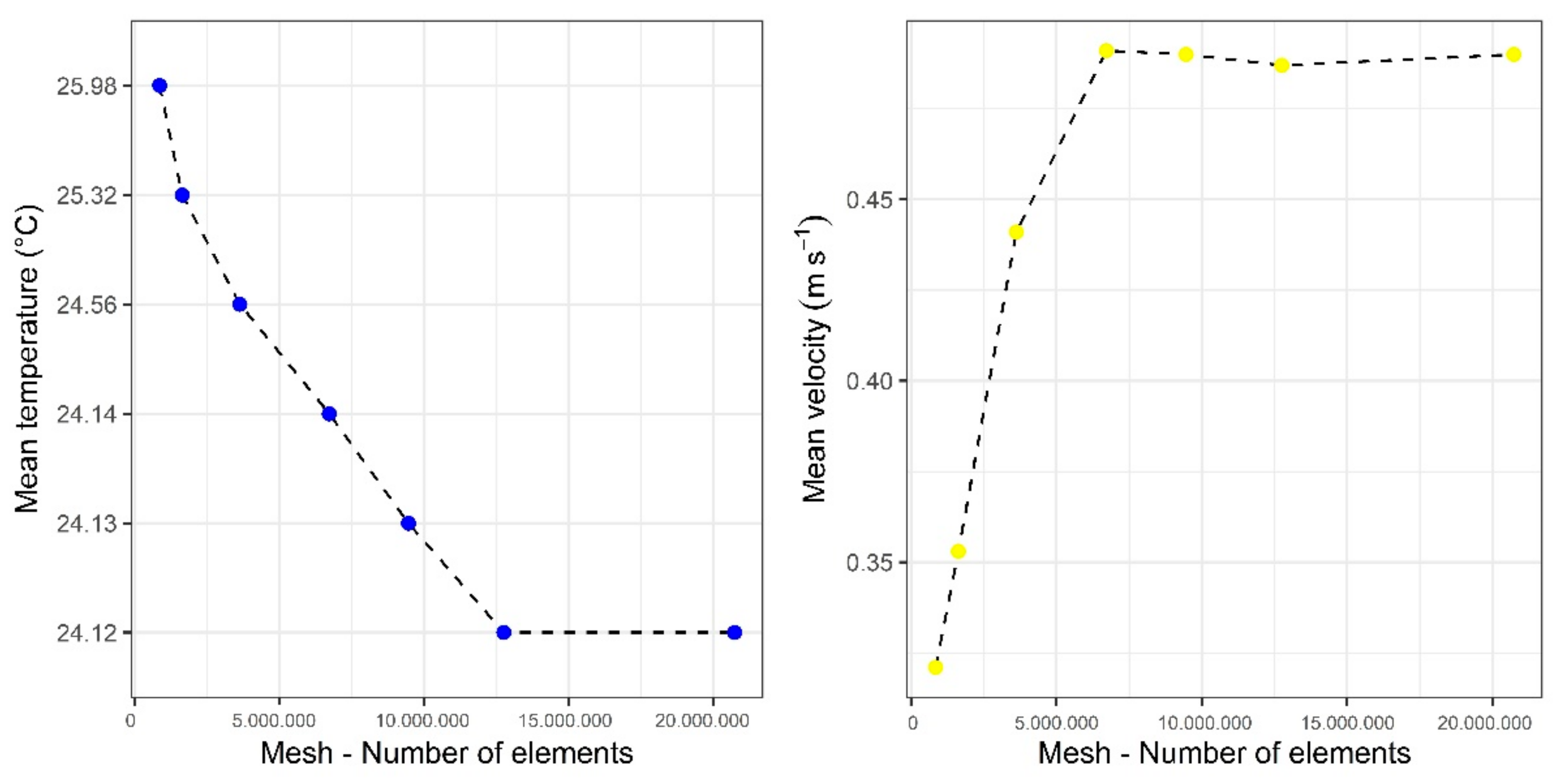
3.1. Grid Independence Test
3.2. Data and Validation of CFD Model
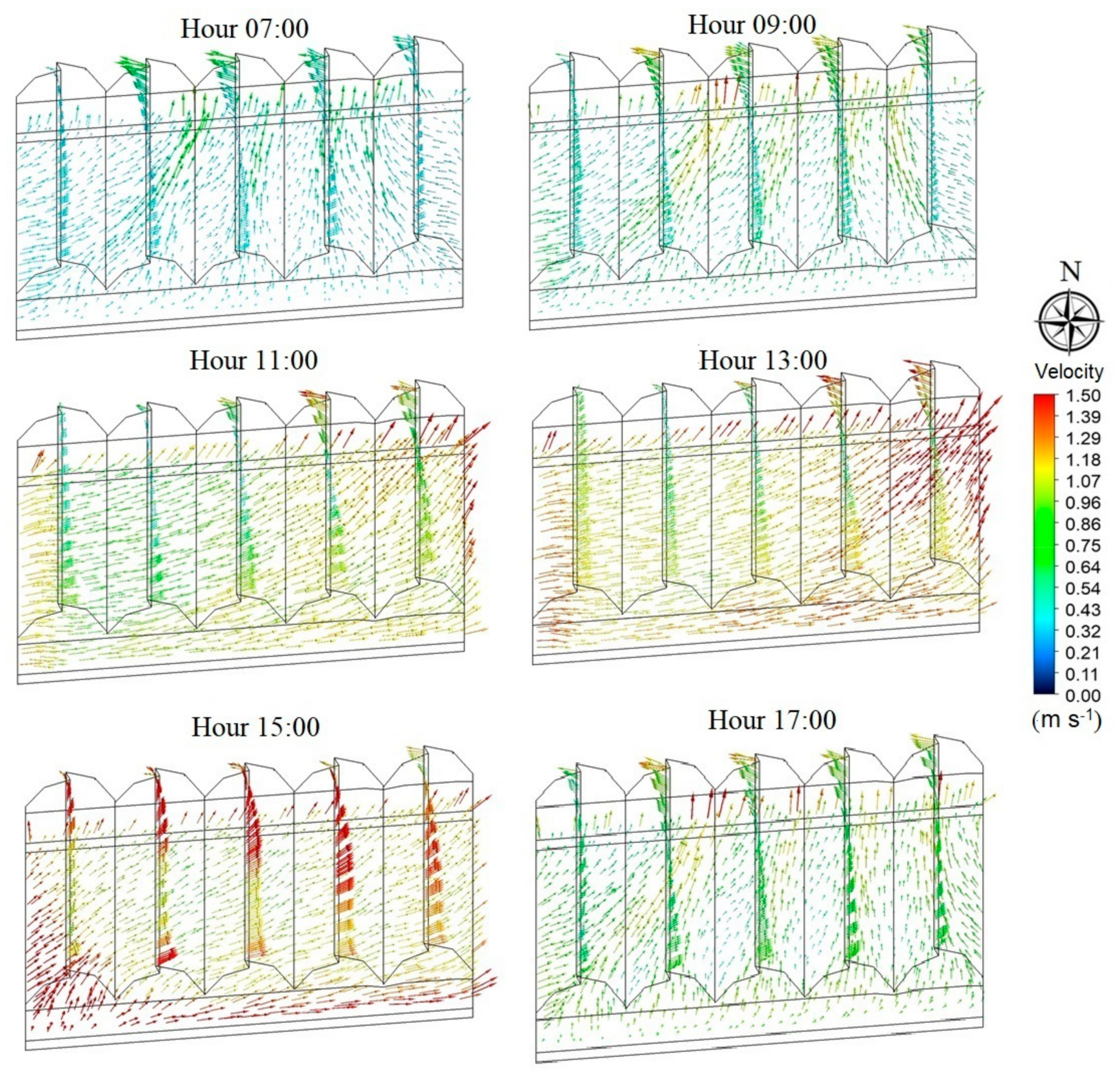
3.3. Qualitative and Quantitative Characteristics of Airflow Patterns
3.4. Air Velocity Inside the Greenhouse and Calculated Ventilation Rates
3.5. Qualitative and Quantitative Characteristics of the Spatial Distribution of Temperature
3.6. Temporal Behavior of the Temperature Inside the Greenhouse
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Villagran, E.; Ramirez, R.; Rodriguez, A.; Pacheco, R.L.; Jaramillo, J. Simulation of the thermal and aerodynamic behavior of an established screenhouse under warm tropical climate conditions: A numerical approach. Int. J. Sustain. Dev. Plan. 2020, 15, 487–499. [Google Scholar] [CrossRef]
- Villagran, E.; Leon, R.; Rodriguez, A.; Jaramillo, J. 3D numerical analysis of the natural ventilation behavior in a Colombian greenhouse established in warm climate conditions. Sustainability 2020, 12, 8101. [Google Scholar] [CrossRef]
- Hemming, S.; de Zwart, F.; Elings, A.; Petropoulou, A.; Righini, I. Cherry tomato production in intelligent greenhouses-sensors and ai for control of climate, irrigation, crop yield, and quality. Sensors 2020, 20, 6430. [Google Scholar] [CrossRef] [PubMed]
- McCartney, L.; Orsat, V.; Lefsrud, M.G. An experimental study of the cooling performance and airflow patterns in a model Natural Ventilation Augmented Cooling (NVAC) greenhouse. Biosyst. Eng. 2018, 174, 173–189. [Google Scholar] [CrossRef]
- Akrami, M.; Javadi, A.A.; Hassanein, M.J.; Farmani, R.; Dibaj, M.; Tabor, G.R.; Negm, A. Study of the effects of vent configuration on mono-span greenhouse ventilation using computational fluid dynamics. Sustainability 2020, 12, 986. [Google Scholar] [CrossRef] [Green Version]
- Reynafarje, X.; Villagrán, E.A.; Bojacá, C.R.; Gil, R.; Schrevens, E. Simulation and validation of the airflow inside a naturally ventilated greenhouse designed for tropical conditions. Acta Hortic. 2020, 1271, 55–62. [Google Scholar] [CrossRef]
- Villagrán, E.A.; Romero, E.J.B.; Bojacá, C.R. Transient CFD analysis of the natural ventilation of three types of greenhouses used for agricultural production in a tropical mountain climate. Biosyst. Eng. 2019, 188, 288–304. [Google Scholar] [CrossRef]
- Parra, J.P.; Baeza, E.; Montero, J.I.; Bailey, B.J. Natural ventilation of parral greenhouses. Biosyst. Eng. 2004, 355–366. [Google Scholar] [CrossRef]
- Teitel, M.; Montero, J.I.; Baeza, E.J. Greenhouse design: Concepts and trends. Acta Hortic. 2012, 952, 605–620. [Google Scholar] [CrossRef]
- Bartzanas, T.; Boulard, T.; Kittas, C. Numerical simulation of the airflow and temperature distribution in a tunnel greenhouse equipped with insect-proof screen in the openings. Comput. Electron. Agric. 2002, 34, 207–221. [Google Scholar] [CrossRef]
- Bournet, P.E.; Boulard, T. Effect of ventilator configuration on the distributed climate of greenhouses: A review of experimental and CFD studies. Comput. Electron. Agric. 2010, 74, 195–217. [Google Scholar] [CrossRef]
- Benni, S.; Tassinari, P.; Bonora, F.; Barbaresi, A.; Torreggiani, D. Efficacy of greenhouse natural ventilation: Environmental monitoring and CFD simulations of a study case. Energy Build. 2016, 125, 276–286. [Google Scholar] [CrossRef]
- Molina-Aiz, F.D.; Valera, D.L.; López, A. Airflow at the openings of a naturally ventilated Almería-type greenhouse with insect-proof screens. Acta Hortic. 2011, 893, 545–552. [Google Scholar] [CrossRef]
- Akrami, M.; Salah, A.H.; Javadi, A.A.; Fath, H.E.; Hassanein, M.J.; Farmani, R.; Negm, A. Towards a Sustainable Greenhouse: Review of Trends and Emerging Practices in Analysing Greenhouse Ventilation Requirements to Sustain Maximum Agricultural Yield. Sustainability 2020, 12, 2794. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.W.; Lee, I.B.; Hwang, H.S.; Seo, I.H.; Bitog, J.P.; Yoo, J.I. Numerical simulation of ventilation efficiencies of naturally ventilated multi-span greenhouse in Korea. Trans. ASABE 2008, 51, 1417–1432. [Google Scholar] [CrossRef]
- Baxevanou, C.; Bartzanas, T.; Fidaros, D.; Kittas, C. Solar radiation distribution in a tunnel greenhouse. Acta Hortic. 2008, 801, 855–862. [Google Scholar] [CrossRef]
- Liu, X.; Li, H.; Li, Y.; Yue, X.; Tian, S.; Li, T. Effect of internal surface structure of the north wall on Chinese solar greenhouse thermal microclimate based on computational fluid dynamics. PLoS ONE 2020, 15, e0231316. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.H. Optimization of indoor climate conditioning with passive and active methods using GA and CFD. Build. Environ. 2007, 9, 3333–3340. [Google Scholar] [CrossRef]
- Jia, Y.; Wang, C.; Zhang, C.; Li, W. Numerical Modelling of Radiation-Convection Coupling of Greenhouse Using Underfloor Heating. Open J. Fluid Dyn. 2017, 3, 448–461. [Google Scholar] [CrossRef] [Green Version]
- Ghernaout, B.; Attia, M.E.; Bouabdallah, S.; Driss, Z.; Benali, M.L. Heat and Fluid Flow in an Agricultural Greenhouse. Int. J. Heat Technol. 2020, 3, 92–98. [Google Scholar] [CrossRef]
- Villagrán, E.A.; Jaramillo, J.E.; León-Pacheco, R.I. Natural ventilation in greenhouse with anti-insect screens evaluated with a computational fluid model. Agron. Mesoam. 2020, 31, 698–717. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Zou, Z.; Wang, S. CFD and weighted entropy based simulation and optimisation of Chinese Solar Greenhouse temperature distribution. Biosyst. Eng. 2016, 142, 12–26. [Google Scholar] [CrossRef]
- Bournet, P.E. Assessing greenhouse climate using CFD: A focus on air humidity issues. Acta Hortic. 2014, 1037, 971–986. [Google Scholar] [CrossRef]
- Dhiman, M.; Sethi, V.P.; Singh, B.; Sharma, A. CFD analysis of greenhouse heating using flue gas and hot water heat sink pipe networks. Comput. Electron. Agric. 2019, 163, 104853. [Google Scholar] [CrossRef]
- Flores-Velazquez, J.; Villarreal-Guerrero, F.; Rojano-Aguilar, A.; Schdmith, U. CFD to analyze energy exchange by convection in a closed greenhouse with a pipe heating system. Acta Univ. 2019, 29. [Google Scholar] [CrossRef]
- Aguilar-Rodriguez, C.; Flores-Velazquez, J.; Ojeda-Bustamante, W.; Rojano, F.; Iñiguez-Covarrubias, M. Valuation of the energy performance of a greenhouse with an electric heater using numerical simulations. Processes 2020, 8, 600. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Y.; Lü, E. Numerical simulation of temperature decrease in greenhouses with summer water-sprinkling roof. Energies 2019, 12, 2435. [Google Scholar] [CrossRef] [Green Version]
- Sapounas, A.; Bartzanas, T.; Nikita-Martzopoulou, C.; Kittas, C. Aspects of CFD modelling of a fan and pad evaporative cooling system in greenhouses. Int. J. Vent. 2008, 797, 131–137. [Google Scholar] [CrossRef]
- Tamimi, E.; Kacira, M.; Choi, C.Y.; An, L. Analysis of microclimate uniformity in a naturally vented greenhouse with a high-pressure fogging system. Trans. ASABE 2013, 1241–1254. [Google Scholar] [CrossRef]
- Akrami, M.; Mutlum, C.D.; Javadi, A.A.; Salah, A.H.; Fath, H.; Dibaj, M.; Farmani, R.; Mohammed, R.H.; Negm, A. Analysis of inlet configurations on the microclimate conditions of a novel standalone agricultural greenhouse for Egypt using computational fluid dynamics. Sustainability 2021, 13, 1446. [Google Scholar] [CrossRef]
- Jiao, W.; Liu, Q.; Gao, L.; Liu, K.; Shi, R.; Ta, N. Computational Fluid Dynamics-Based Simulation of Crop Canopy Temperature and Humidity in Double-Film Solar Greenhouse. J. Sens. 2020. [Google Scholar] [CrossRef]
- Villagran, V. Implementation of ventilation towers in a greenhouse established in low altitude tropical climate conditions: Numerical approach to the behavior of the natural ventilation. Rev. Ceres 2021, 68, 10–22. [Google Scholar] [CrossRef]
- Villagrán, E.A.; Bojaca, C.R. Determination of the thermal behavior of a Colombian hanging greenhouse applying CFD simulation. Rev. Cienc. Téc. Agropecu. 2019, 3, 28–38. [Google Scholar]
- Villagrán, E.A.; Bojacá, C.R. Study of natural ventilation in a Gothic multi-tunnel greenhouse designed to produce rose (Rosa spp.) in the high-Andean tropic. Ornam. Hortic. 2019, 25, 133–143. [Google Scholar] [CrossRef] [Green Version]
- Villagrán, E.A.; Bojacá, C.R. CFD simulation of the increase of the roof ventilation area in a traditional Colombian greenhouse: Effect on air flow patterns and thermal behavior. Int. J. Heat Technol. 2019, 37, 881–892. [Google Scholar] [CrossRef]
- Rodríguez-Leyton, M. Desafíos para el consumo de frutas y verduras. Rev. Fac. Med. Hum. 2019, 19, 105–112. [Google Scholar] [CrossRef]
- Kumar, K.S.; Jha, M.K.; Tiwari, K.N.; Singh, A. Modeling, and evaluation of greenhouse for floriculture in subtropics. Energy Build. 2010, 7, 1075–1083. [Google Scholar] [CrossRef]
- Rojas Rishor, A. Análisis del Comportamiento Térmico de un Invernadero Construido en Ladera, Aplicando Dinámica de Fluidos Computacional. Bachelor’s Thesis, Costa Rica University, San Jose, Costa Rica, 2015. Available online: https://www.ingbiosistemas.ucr.ac.cr/wp-content/uploads/2016/02/tesis-adriana-rojas.pdf (accessed on 16 January 2021).
- Flores-Velazquez, J.; Rishor, A.R.; Aguilar, A.; Bustamante, W. CFD modeling to assessing environment of a greenhouse typical in Costa Rica, in: ASABE Annual International Meeting. Int. Meet. ASABE 2016. [Google Scholar] [CrossRef]
- Kuroyanagi, T.; Nagasaki, Y.; Nakamoto, Y.; Tanaka, H.; Ibuki, T. Simulation of microclimate in a sloping greenhouse using CFD. Acta Hortic. 2008, 801, 909–916. [Google Scholar] [CrossRef]
- Aich, W.; Kolsi, L.; Borjini, M.N.; Al-Rashed, A.A.; Aissia, H.B.; Oztop, H.F.; Abu-Hamdeh, N. Three-dimensional computational fluid dynamics analysis of buoyancy-driven natural ventilation and entropy generation in a prismatic greenhouse. Therm. Sci. 2018, 22, 73–85. [Google Scholar] [CrossRef]
- Baxevanou, C.; Fidaros, D.; Bartzanas, T.; Kittas, C. Yearly numerical evaluation of greenhouse cover materials. Comput. Electron. Agric. 2017, 149, 54–70. [Google Scholar] [CrossRef]
- Franke, J.; Hellsten, A.; Schlunzen, H.A.; Carissimo, B. The Best Practice Guideline for the CFD simulation of flows in the urban environment: An outcome of COST 732. In Proceedings of the Fifth International Symposium on Computational Wind Engineering, Chapel Hill, NC, USA, 23–27 May 2010. [Google Scholar]
- Kim, R.W.; Lee, I.B.; Kwon, K.S. Evaluation of wind pressure acting on multi-span greenhouses using CFD technique, Part 1: Development of the CFD model. Biosyst. Eng. 2017, 164, 235–256. [Google Scholar] [CrossRef]
- Toghraie, D.; Abdollah, M.M.D.; Pourfattah, F.; Akbari, O.A.; Ruhani, B. Numerical investigation of flow and heat transfer characteristics in smooth, sinusoidal, and zigzag-shaped microchannel with and without nanofluid. J. Therm. Anal. Calorim. 2018, 131, 1757–1766. [Google Scholar] [CrossRef]
- Zhang, Y.; Kacira, M.; An, L. A CFD study on improving air flow uniformity in indoor plant factory system. Biosyst. Eng 2016, 147, 193–205. [Google Scholar] [CrossRef]
- Senhaji, A.; Mouqallid, M.; Majdoubi, H. CFD Assisted Study of Multi-Chapels Greenhouse Vents Openings Effect on Inside Airflow Circulation and Microclimate Patterns. Open J. Fluid Dyn. 2019, 9, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Bañuelos-Ruedas, F.; Angeles-Camacho, C.; Rios-Marcuello, S. Analysis and validation of the methodology used in the extrapolation of wind speed data at different heights. Renew. Sustain. Energy Rev. 2010. [Google Scholar] [CrossRef]
- Lee, I.; Lee, S.; Kim, G.; Sung, J.; Sung, S.; Yoon, Y. PIV verification of greenhouse ventilation air flows to evaluate CFD accuracy. Trans. ASAE 2005, 48, 2277–2288. [Google Scholar] [CrossRef]
- Villagrán, E.; Bojacá, C. Study using a CFD approach of the efficiency of a roof ventilation closure system in a multi-tunnel greenhouse for nighttime microclimate optimization. Rev. Ceres 2020, 67, 345–356. [Google Scholar] [CrossRef]
- He, X.; Wang, J.; Guo, S.; Zhang, J.; Wei, B.; Sun, J.; Shu, S. Ventilation optimization of solar greenhouse with removable back walls based on CFD. Comput. Electron. Agric. 2017, 149, 16–25. [Google Scholar] [CrossRef]
- Espejel Trujano, D.; López Cruz, I.L. Determinación de las tasas de ventilación natural en un invernadero mediante modelos teóricos y gases trazadores. Rev. Mex. Cienc. Agrícolas 2013, 4, 185–198. [Google Scholar] [CrossRef] [Green Version]
- Baille, A. Trends in greenhouse technology for improved climate control in mild winter climates. Acta Hortic. 2001, 559, 161–168. [Google Scholar] [CrossRef]
- Bournet, P.E.; Khaoua, S.O.; Boulard, T.; Migeon, C.; Chassériaux, G. Effect of Roof and Side Opening Combinations on the Ventilation of a Greenhouse Using Computer Simulation. Trans. ASABE 2007, 50, 201–212. [Google Scholar] [CrossRef]
- Taloub, D.; Bouras, A.; Driss, Z. Effect of the soil inclination on natural convection in half-elliptical greenhouses. Int. J. Eng. Res. Afr. 2020, 50, 70–78. [Google Scholar] [CrossRef]
- Teitel, M.; Ziskind, G.; Liran, O.; Dubovsky, V.; Letan, R. Effect of wind direction on greenhouse ventilation rate, airflow patterns and temperature distributions. Biosyst. Eng. 2008, 101, 351–369. [Google Scholar] [CrossRef]
- Pakari, A.; Ghani, S. Airflow assessment in a naturally ventilated greenhouse equipped with wind towers: Numerical simulation and wind tunnel experiments. Energy Build. 2019, 199, 1–11. [Google Scholar] [CrossRef]
- McCartney, L.; Lefsrud, M.G. Field trials of the Natural Ventilation Augmented Cooling (NVAC) greenhouse. Biosyst. Eng. 2018, 174, 159–172. [Google Scholar] [CrossRef]
- Romero, P.; Giacomelli, G.A.; Choi, C.Y.; Lopez-Cruz, I. Ventilation rates for a naturally ventilated greenhouse in Central Mexico. Acta Hortic. 2006, 719, 65–72. [Google Scholar] [CrossRef]
- Mesmoudi, K.; Bougoul, S.; Bournet, P.E. Thermal performance of an unheated greenhouse under semi-arid conditions during the night. Acta Hortic. 2012, 952, 417–424. [Google Scholar] [CrossRef]
- Espinal-Montes, V.; Lorenzo López-Cruz, I.L.; Rojano-Aguilar, A.; Romantchik-Kriuchova, E.; Ramírez-Arias, A. Determination of night-time thermal gradients in a greenhouse using computational thermal dynamics. Agrociencia 2015, 49, 233–247. [Google Scholar]
- Villagrán, E.; Bojacá, C.R. Numerical evaluation of passive strategies for nocturnal climate optimization in a greenhouse designed for rose production (Rosa spp.). Ornam. Hortic. 2019, 25, 351–364. [Google Scholar] [CrossRef] [Green Version]
- Valera, D.L.; Molina-Aiz, F.D.; Moreno, M.A.; López, A.; Marın, P. Ventilation surface area: Key to modify morphology, quality, and photosynthetic activity of tomato crops in Mediterranean greenhouses. Acta Hortic. 2020, 1296, 185–192. [Google Scholar] [CrossRef]
- Baeza, E.; Montero, J.I.; Pérez-Parra, J.; Bailey, B.J.; López, J.C.; Vázquez, J.C. Avances en el Estudio de la Ventilación Natural. 2012. Available online: http://www.publicacionescajamar.es/pdf/series-tematicas/centros-experimentales-las-palmerillas/avances-en-el-estudio-de-la-ventilacion.pdf (accessed on 7 January 2021).
- Villagran, E.; Bojacá, C. Analysis of the microclimatic behavior of a greenhouse used to produce carnation (Dianthus caryophyllus L.). Ornam. Hortic. 2020, 26, 109–204. [Google Scholar] [CrossRef]
- Villagran, E.A.; Noreña, J.E. Microclimatic behavior of a screen house proposed for horticultural production in low-altitude tropical climate conditions. Comun. Sci. 2020, 11, e3350. [Google Scholar] [CrossRef]
- Fernández, M.D.; Bonachela, S.; Orgaz, F.; Thompson, R.; López, J.C.; Granados, M.R.; Fereres, E. Measurement and estimation of plastic greenhouse reference evapotranspiration in a Mediterranean climate. Irrig. Sci. 2010, 28, 497–509. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.; Carpenter, N.; Maki, H.; Rehman, T.U.; Tuinstra, M.R.; Jin, J. Greenhouse environment modeling and simulation for microclimate control. Comput. Electron. Agric. 2019, 162, 134–142. [Google Scholar] [CrossRef]
- Saberian, A.; Sajadiye, S.M. The effect of dynamic solar heat load on the greenhouse microclimate using CFD simulation. Renew. Energy 2019, 138, 722–737. [Google Scholar] [CrossRef]
- Villagran, E.; Bojacá, C. Experimental evaluation of the thermal and hygrometric behavior of a Colombian greenhouse used for the production of roses (Rosa spp.). Ornam. Hortic. 2020, 26, 205–219. [Google Scholar] [CrossRef]
- Bojacá, C.R.; Gil, R.; Gómez, S.; Cooman, A.; Schrevens, E. Analysis of greenhouse air temperature distribution using geostatistical methods. Trans. ASABE 2009, 52, 957–968. [Google Scholar] [CrossRef]
- Ahemd, H.A.; Al-Faraj, A.A.; Abdel-Ghany, A.M. Shading greenhouses to improve the microclimate, energy and water saving in hot regions: A review. Sci. Hortic. 2016, 201, 36–45. [Google Scholar] [CrossRef]
- Ben Amara, H.; Bouadila, S.; Fatnassi, H.; Arici, M.; Allah Guizani, A. Climate assessment of greenhouse equipped with south-oriented PV roofs: An experimental and computational fluid dynamics study. Sustain. Energy Technol. Assess. 2021. [Google Scholar] [CrossRef]
- López-Díaz, G.; Carreño-Ortega, A.; Fatnassi, H.; Poncet, C.; Díaz-Pérez, M. The effect of different levels of shading in a photovoltaic greenhouse with a north-south orientation. Appl. Sci. 2020, 10, 882. [Google Scholar] [CrossRef] [Green Version]
- Gourdo, L.; Fatnassi, H.; Tiskatine, R.; Wifaya, A.; Demrati, H.; Aharoune, A.; Bouirden, L. Solar energy storing rock-bed to heat an agricultural greenhouse. Energy 2019, 169, 206–212. [Google Scholar] [CrossRef]
- Bazgaou, A.; Fatnassi, H.; Bouharroud, R.; Elame, F.; Ezzaeri, K.; Gourdo, L.; Wifaya, A.; Demrati, H.; Tiskatine, R.; Bekkaoui, A.; et al. Performance assessment of combining rock-bed thermal energy storage and water filled passive solar sleeves for heating Canarian greenhouse. Sol. Energy 2020, 198, 8–24. [Google Scholar] [CrossRef]
- Baeza, E.J.; Pérez-Parra, J.J.; Montero, J.I.; Bailey, B.J.; López, J.C.; Gázquez, J.C. Analysis of the role of sidewall vents on buoyancy-driven natural ventilation in parral-type greenhouses with and without insect screens using computational fluid dynamics. Biosyst. Eng. 2009, 104, 86–96. [Google Scholar] [CrossRef]
- Villagrán, E.A.; Gil, R.; Acuña, J.F.; Bojacá, C.R. Optimization of ventilation and its effect on the microclimate of a colombian multispan greenhouse. Agron. Colomb. 2012, 30, 282–288. [Google Scholar]



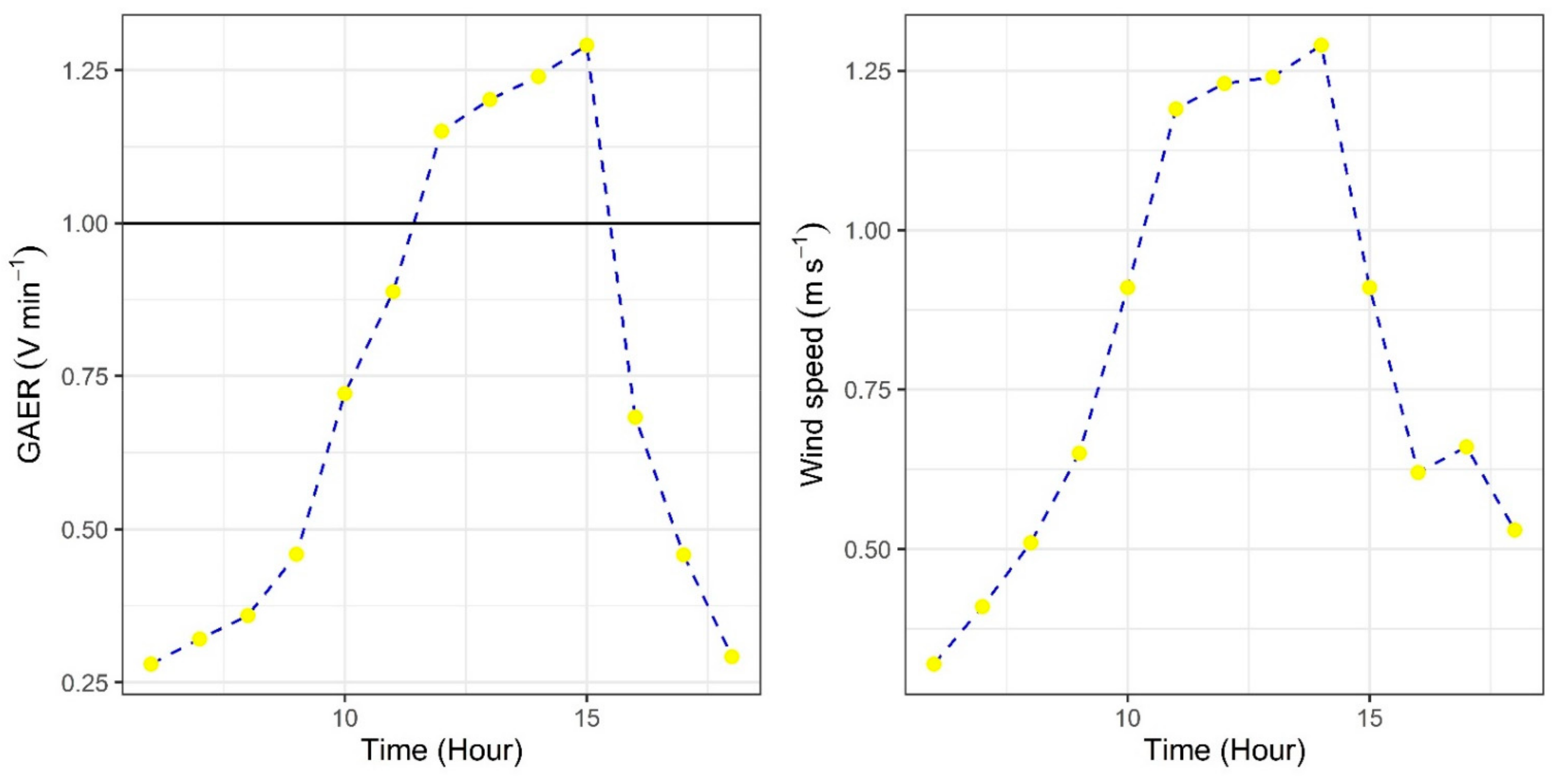
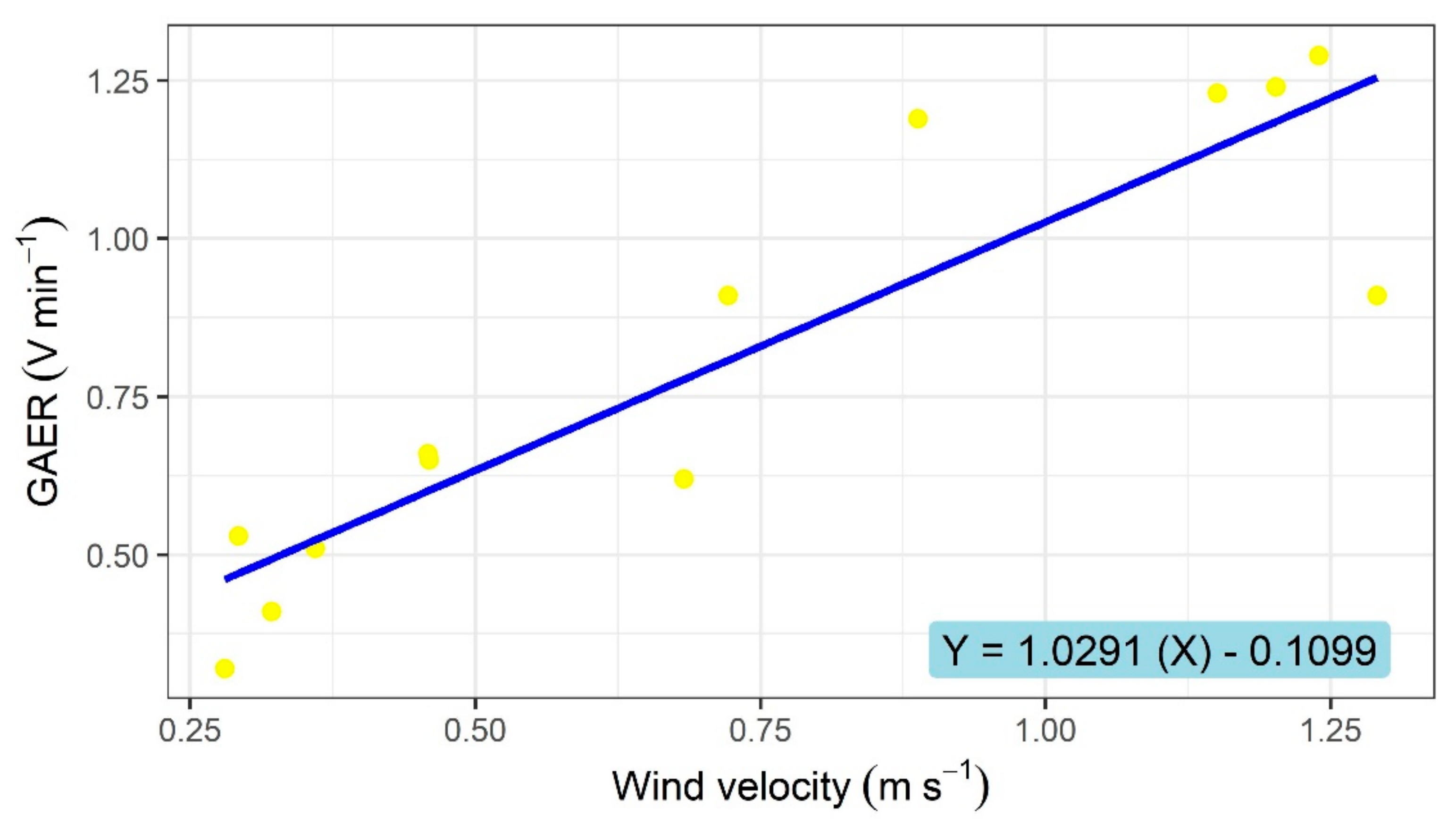

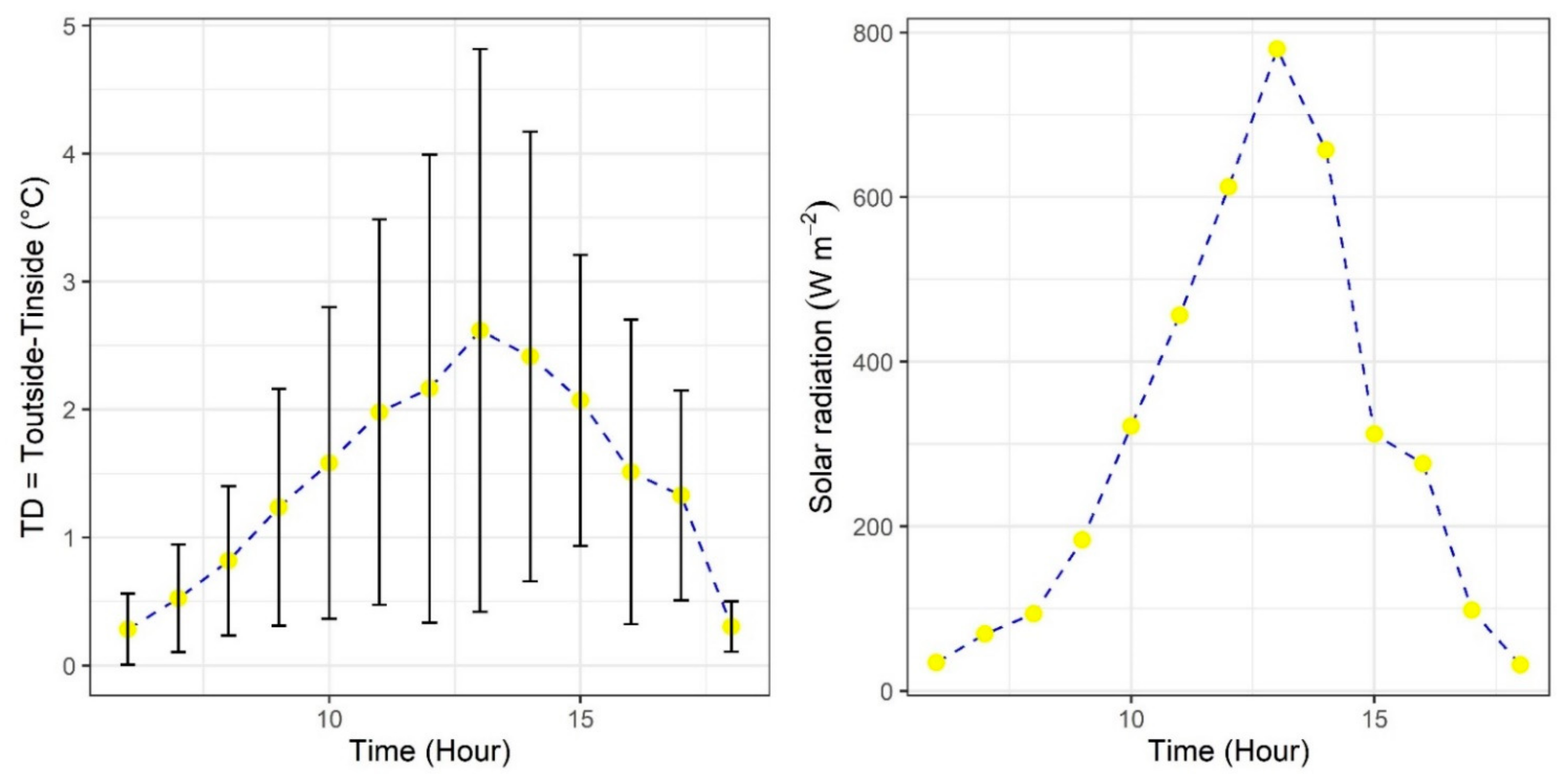
| Property | Soil | Air | Cover Greenhouse | Perimeter Walls |
|---|---|---|---|---|
| Density (ρ, kg m−3) | 1.300 | 1.023 | 923 | 923 |
| Thermal conductivity (k, W m−1 K−1) | 1.3 | 0.0242 | 0.4 | 0.4 |
| Specific heat (Cp, J K−1 kg−1) | 800 | 1006.43 | 2300 | 2300 |
| Absorptivity | 0.90 | 0.19 | 0.06 | 0.93 |
| Scattering coefficient | −15 | 0 | 0 | 0 |
| Refractive index | 1.92 | 1 | 1.53 | 1.53 |
| Emissivity | 0.95 | 0.9 | 0.7 | 0.7 |
| Hour | Solar Radiation (Wm−2) | Temperature (°C) | Wind Velocity (ms−1) | Wind Direction |
|---|---|---|---|---|
| 6:00 | 34.3 | 16.7 | 0.32 | S |
| 7:00 | 69.2 | 17.6 | 0.41 | S |
| 8:00 | 93.7 | 19.1 | 0.51 | SS |
| 9:00 | 183.5 | 20.9 | 0.65 | S |
| 10:00 | 321.9 | 22.3 | 0.91 | WSW |
| 11:00 | 456.6 | 22.9 | 1.19 | W |
| 12:00 | 612.4 | 24.5 | 1.23 | W |
| 13:00 | 780.1 | 25.3 | 1.24 | W |
| 14:00 | 657.2 | 25.5 | 1.29 | SSW |
| 15:00 | 312.1 | 23.4 | 0.91 | SSW |
| 16:00 | 276.1 | 21.9 | 0.62 | S |
| 17:00 | 98.1 | 20.3 | 0.66 | S |
| 18:00 | 31.5 | 19.4 | 0.53 | S |
| Hour | Sensor | MAV * (ms−1) | SAV * (ms−1) | Hour | Sensor | MAV * (ms−1) | SAV * (ms−1) | Hour | Sensor | MAV * (ms−1) | SAV * (ms−1) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 6:00 | 1 | 0.34 | 0.39 | 11:00 | 1 | 0.83 | 0.79 | 16:00 | 1 | 0.97 | 1.03 |
| 6:00 | 2 | 0.42 | 0.43 | 11:00 | 2 | 0.85 | 0.83 | 16:00 | 2 | 0.95 | 1.00 |
| 6:00 | 3 | 0.37 | 0.36 | 11:00 | 3 | 0.90 | 1.00 | 16:00 | 3 | 1.04 | 1.13 |
| 7:00 | 1 | 0.50 | 0.47 | 12:00 | 1 | 1.12 | 0.98 | 17:00 | 1 | 0.89 | 0.90 |
| 7:00 | 2 | 0.48 | 0.47 | 12:00 | 2 | 1.10 | 0.93 | 17:00 | 2 | 0.78 | 0.82 |
| 7:00 | 3 | 0.44 | 0.43 | 12:00 | 3 | 1.12 | 1.13 | 17:00 | 3 | 0.7 | 0.72 |
| 8:00 | 1 | 0.49 | 0.53 | 13:00 | 1 | 1.05 | 1.02 | 18:00 | 1 | 0.61 | 0.51 |
| 8:00 | 2 | 0.61 | 0.59 | 13:00 | 2 | 1.02 | 0.99 | 18:00 | 2 | 0.60 | 0.52 |
| 8:00 | 3 | 0.62 | 0.64 | 13:00 | 3 | 1.14 | 1.25 | 18:00 | 3 | 0.54 | 0.41 |
| 9:00 | 1 | 0.71 | 0.67 | 14:00 | 1 | 1.15 | 1.11 | ||||
| 9:00 | 2 | 0.81 | 0.76 | 14:00 | 2 | 1.16 | 1.10 | ||||
| 9:00 | 3 | 0.87 | 0.87 | 14:00 | 3 | 1.19 | 1.18 | ||||
| 10:00 | 1 | 0.70 | 0.70 | 15:00 | 1 | 1.02 | 1.07 | ||||
| 10:00 | 2 | 0.75 | 0.77 | 15:00 | 2 | 0.89 | 0.98 | ||||
| 10:00 | 3 | 0.73 | 0.74 | 15:00 | 3 | 1.23 | 1.28 |
| Hour | Sensor | MT * (°C) | ST * (°C) | Hour | Sensor | MT * (°C) | ST * (°C) | Hour | Sensor | MT * (°C) | ST * (°C) | Hour | Sensor | MT * (°C) | ST * (°C) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6:00 | 1 | 16.8 | 16.7 | 10:00 | 1 | 23.0 | 22.5 | 14:00 | 1 | 26.2 | 26.0 | 18:00 | 1 | 20.1 | 19.5 |
| 6:00 | 2 | 16.9 | 17.1 | 10:00 | 2 | 23.2 | 22.9 | 14:00 | 2 | 26.7 | 26.9 | 18:00 | 2 | 19.9 | 19.8 |
| 6:00 | 3 | 16.9 | 17.0 | 10:00 | 3 | 24.1 | 23.8 | 14:00 | 3 | 27.8 | 27.8 | 18:00 | 3 | 19.8 | 19.7 |
| 6:00 | 4 | 17.0 | 17.2 | 10:00 | 4 | 24.6 | 24.7 | 14:00 | 4 | 29.2 | 28.8 | 18:00 | 4 | 19.9 | 19.7 |
| 6:00 | 5 | 17.1 | 17.2 | 10:00 | 5 | 24.6 | 24.3 | 14:00 | 5 | 29.2 | 28.8 | 18:00 | 5 | 20.0 | 19.8 |
| 6:00 | 6 | 17.1 | 17.1 | 10:00 | 6 | 24.5 | 24.2 | 14:00 | 6 | 29.0 | 28.4 | 18:00 | 6 | 19.8 | 19.7 |
| 6:00 | 7 | 16.9 | 16.7 | 10:00 | 7 | 25.1 | 25.0 | 14:00 | 7 | 29.0 | 29.0 | 18:00 | 7 | 19.8 | 19.6 |
| 7:00 | 1 | 17.8 | 17.7 | 11:00 | 1 | 23.3 | 23.1 | 15:00 | 1 | 24.2 | 24.2 | ||||
| 7:00 | 2 | 18.2 | 18.2 | 11:00 | 2 | 23.7 | 23.6 | 15:00 | 2 | 24.8 | 25.0 | ||||
| 7:00 | 3 | 18.3 | 18.2 | 11:00 | 3 | 24.4 | 24.5 | 15:00 | 3 | 25.9 | 25.6 | ||||
| 7:00 | 4 | 18.6 | 18.4 | 11:00 | 4 | 25.3 | 25.6 | 15:00 | 4 | 26.2 | 26.0 | ||||
| 7:00 | 5 | 18.7 | 18.5 | 11:00 | 5 | 26.6 | 26.5 | 15:00 | 5 | 26.1 | 25.9 | ||||
| 7:00 | 6 | 18.4 | 18.2 | 11:00 | 6 | 25.7 | 25.6 | 15:00 | 6 | 26.1 | 25.7 | ||||
| 7:00 | 7 | 18.1 | 17.7 | 11:00 | 7 | 26.0 | 26.2 | 15:00 | 7 | 26.0 | 26.4 | ||||
| 8:00 | 1 | 19.5 | 19.4 | 12:00 | 1 | 24.9 | 24.7 | 16:00 | 1 | 22.5 | 22.3 | ||||
| 8:00 | 2 | 20.2 | 19.9 | 12:00 | 2 | 25.1 | 24.9 | 16:00 | 2 | 23.8 | 24.0 | ||||
| 8:00 | 3 | 20.4 | 20.0 | 12:00 | 3 | 26.2 | 25.8 | 16:00 | 3 | 23.7 | 23.6 | ||||
| 8:00 | 4 | 20.4 | 20.3 | 12:00 | 4 | 27.4 | 27.2 | 16:00 | 4 | 24.1 | 24.2 | ||||
| 8:00 | 5 | 20.8 | 20.4 | 12:00 | 5 | 28.7 | 28.3 | 16:00 | 5 | 24.1 | 24.0 | ||||
| 8:00 | 6 | 20.8 | 20.5 | 12:00 | 6 | 28.3 | 28.2 | 16:00 | 6 | 24.3 | 24.5 | ||||
| 8:00 | 7 | 19.9 | 19.4 | 12:00 | 7 | 28.9 | 28.4 | 16:00 | 7 | 23.2 | 22.4 | ||||
| 9:00 | 1 | 21.2 | 21.3 | 13:00 | 1 | 25.4 | 25.5 | 17:00 | 1 | 21.0 | 20.9 | ||||
| 9:00 | 2 | 22.3 | 22.1 | 13:00 | 2 | 26.1 | 25.8 | 17:00 | 2 | 21.9 | 22.0 | ||||
| 9:00 | 3 | 22.5 | 22.3 | 13:00 | 3 | 26.5 | 26.9 | 17:00 | 3 | 21.8 | 21.5 | ||||
| 9:00 | 4 | 22.9 | 22.7 | 13:00 | 4 | 27.9 | 28.6 | 17:00 | 4 | 22.0 | 21.9 | ||||
| 9:00 | 5 | 23.0 | 23.0 | 13:00 | 5 | 29.4 | 29.9 | 17:00 | 5 | 21.9 | 21.9 | ||||
| 9:00 | 6 | 23.4 | 23.1 | 13:00 | 6 | 29.4 | 29.6 | 17:00 | 6 | 21.8 | 21.7 | ||||
| 9:00 | 7 | 22.3 | 21.3 | 13:00 | 7 | 29.8 | 30.0 | 17:00 | 7 | 21.5 | 20.9 |
| F Test to Compare Two Variances | H0: σ(Dm)2 = σ(Ds)2 o H1: σ(Dm)2 ≠ σ(Ds)2 | |
|---|---|---|
| Temperature | Air Velocity | |
| F | 0.9787 | 0.926 |
| p-value | 0.919 | 0.815 |
| 95% confidence interval. | [0.646, 1.483] | [0.486, 1.767] |
| Two sample t-test | H0: µDm = µDs o H1: µDm ≠ µDs | |
| Temperature | Air velocity | |
| t | 0.238 | 0.053 |
| p-value | 0.811 | 0.957 |
| 95% confidence interval. | [−0.928, 1.184] | [0.114, 0.121] |
| Hour | Temperature | Air Velocity | ||
|---|---|---|---|---|
| MAE (°C) | RMSE (°C) | MAE (ms−1) | RMSE (ms−1) | |
| 6:00 | 0.124 | 0.140 | 0.025 | 0.032 |
| 7:00 | 0.165 | 0.195 | 0.014 | 0.016 |
| 8:00 | 0.309 | 0.336 | 0.024 | 0.026 |
| 9:00 | 0.289 | 0.429 | 0.030 | 0.037 |
| 10:00 | 0.267 | 0.295 | 0.010 | 0.012 |
| 11:00 | 0.153 | 0.169 | 0.052 | 0.062 |
| 12:00 | 0.274 | 0.300 | 0.107 | 0.128 |
| 13:00 | 0.345 | 0.397 | 0.054 | 0.065 |
| 14:00 | 0.269 | 0.336 | 0.035 | 0.040 |
| 15:00 | 0.242 | 0.267 | 0.065 | 0.068 |
| 16:00 | 0.266 | 0.354 | 0.070 | 0.072 |
| 17:00 | 0.186 | 0.262 | 0.029 | 0.030 |
| 18:00 | 0.218 | 0.267 | 0.096 | 0.097 |
| Hour | Average Air Velocity (ms−1) | Normalized Air Velocity (%) |
|---|---|---|
| 6:00 | 0.312 ± 0.08 | 97.1 |
| 7:00 | 0.404 ± 0.10 | 98.5 |
| 8:00 | 0.505 ± 0.12 | 99.1 |
| 9:00 | 0.641 ± 0.15 | 98.6 |
| 10:00 | 0.871 ± 0.14 | 95.7 |
| 11:00 | 0.989 ± 0.15 | 83.1 |
| 12:00 | 1.129 ± 0.16 | 91.8 |
| 13:00 | 1.191 ± 0.18 | 96.7 |
| 14:00 | 1.269 ± 0.20 | 98.3 |
| 15:00 | 1.336 ± 0.29 | 146.8 |
| 16:00 | 0.819 ± 0.17 | 132.1 |
| 17:00 | 0.812 ± 0.14 | 123.1 |
| 18:00 | 0.565 ± 0.10 | 106.7 |
| Hour | Tinside | ΔTinside = Tmax − Tmin |
|---|---|---|
| 6:00 | 16.98 ± 0.28 | 1.55 |
| 7:00 | 18.12 ± 0.42 | 2.15 |
| 8:00 | 19.91 ± 0.55 | 3.05 |
| 9:00 | 22.13 ± 0.92 | 4.84 |
| 10:00 | 23.88 ± 1.21 | 8.50 |
| 11:00 | 24.87 ± 1.50 | 11.18 |
| 12:00 | 26.66 ± 1.82 | 13.15 |
| 13:00 | 27.91 ± 2.19 | 16.93 |
| 14:00 | 27.92 ± 1.75 | 11.22 |
| 15:00 | 25.47 ± 1.13 | 7.90 |
| 16:00 | 23.41 ± 1.19 | 8.45 |
| 17:00 | 21.62 ± 0.82 | 5.09 |
| 18:00 | 19.70 ± 0.19 | 1.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villagran, E.; Bojacá, C.; Akrami, M. Contribution to the Sustainability of Agricultural Production in Greenhouses Built on Slope Soils: A Numerical Study of the Microclimatic Behavior of a Typical Colombian Structure. Sustainability 2021, 13, 4748. https://doi.org/10.3390/su13094748
Villagran E, Bojacá C, Akrami M. Contribution to the Sustainability of Agricultural Production in Greenhouses Built on Slope Soils: A Numerical Study of the Microclimatic Behavior of a Typical Colombian Structure. Sustainability. 2021; 13(9):4748. https://doi.org/10.3390/su13094748
Chicago/Turabian StyleVillagran, Edwin, Carlos Bojacá, and Mohammad Akrami. 2021. "Contribution to the Sustainability of Agricultural Production in Greenhouses Built on Slope Soils: A Numerical Study of the Microclimatic Behavior of a Typical Colombian Structure" Sustainability 13, no. 9: 4748. https://doi.org/10.3390/su13094748






