Jet Impingement Heat Transfer of Confined Single and Double Jets with Non-Newtonian Power Law Nanofluid under the Inclined Magnetic Field Effects for a Partly Curved Heated Wall
Abstract
1. Introduction
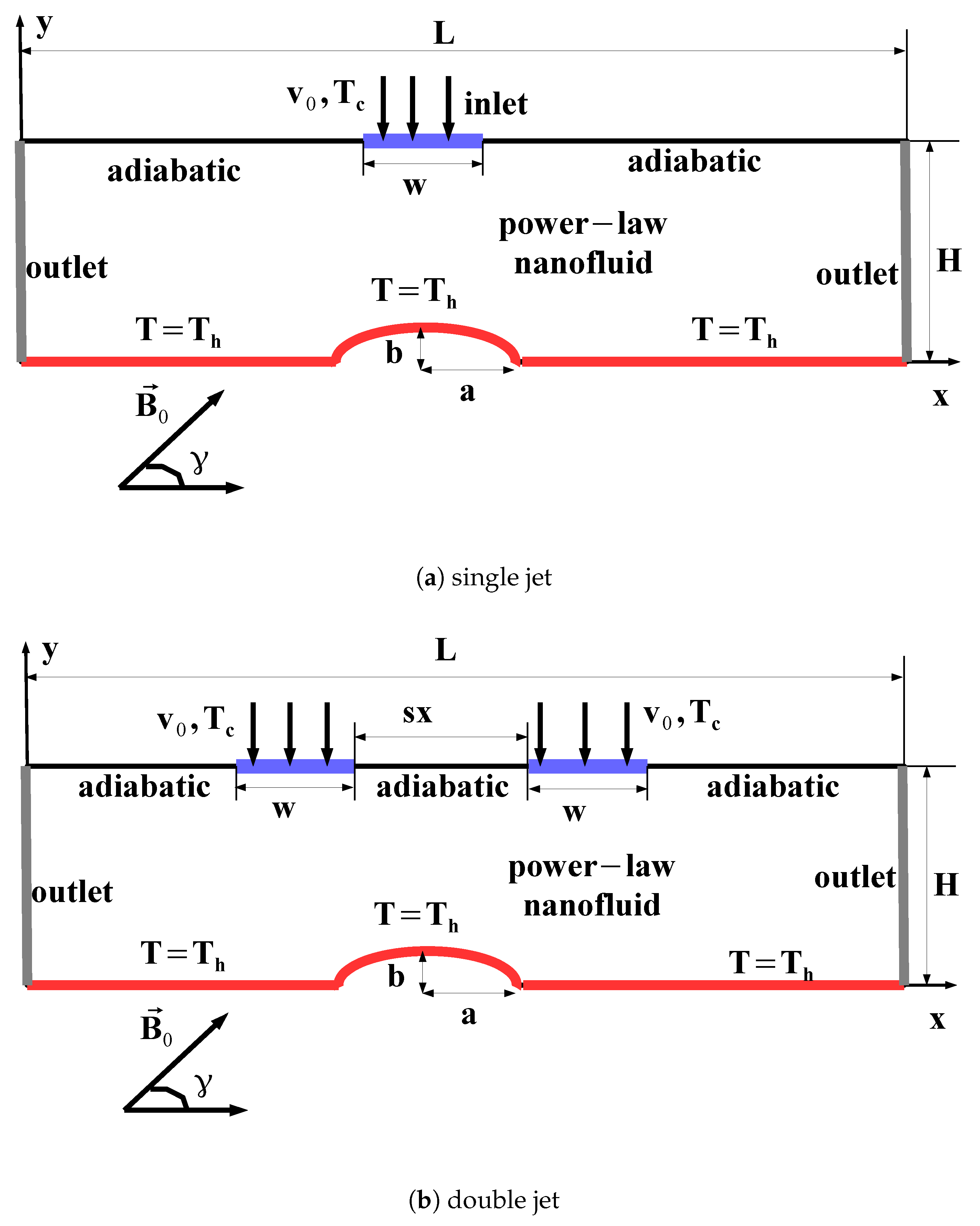
2. Mathematical Formulation
- At the jet inlet, temperature and velocity are uniform, .
- For the bottom plate, temperature is constant and no-slip BC is used, .
- The top plate is adiabatic and no-slip BC is considered,
- At the side surfaces, x-direction gradients are set to zero,
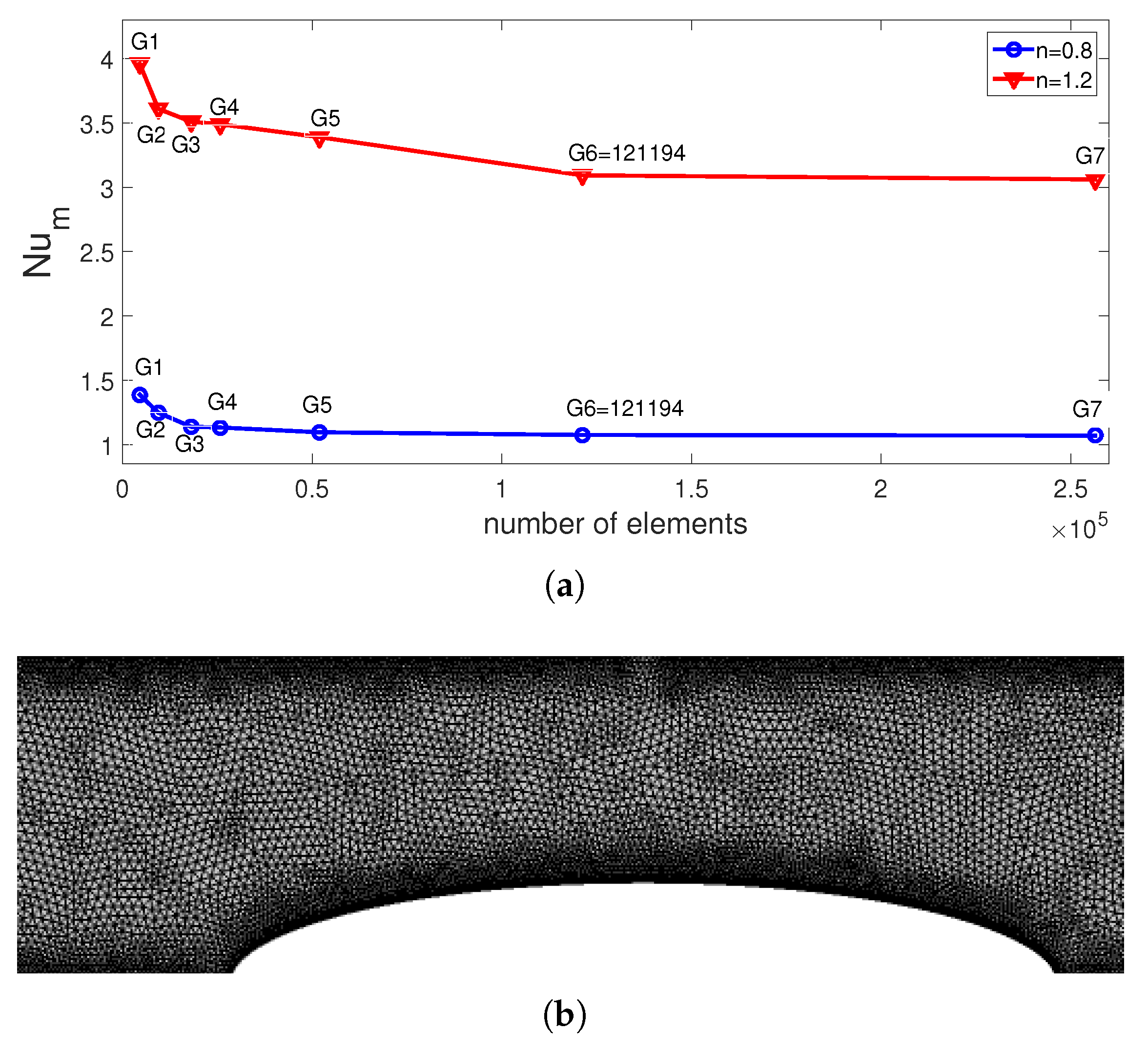
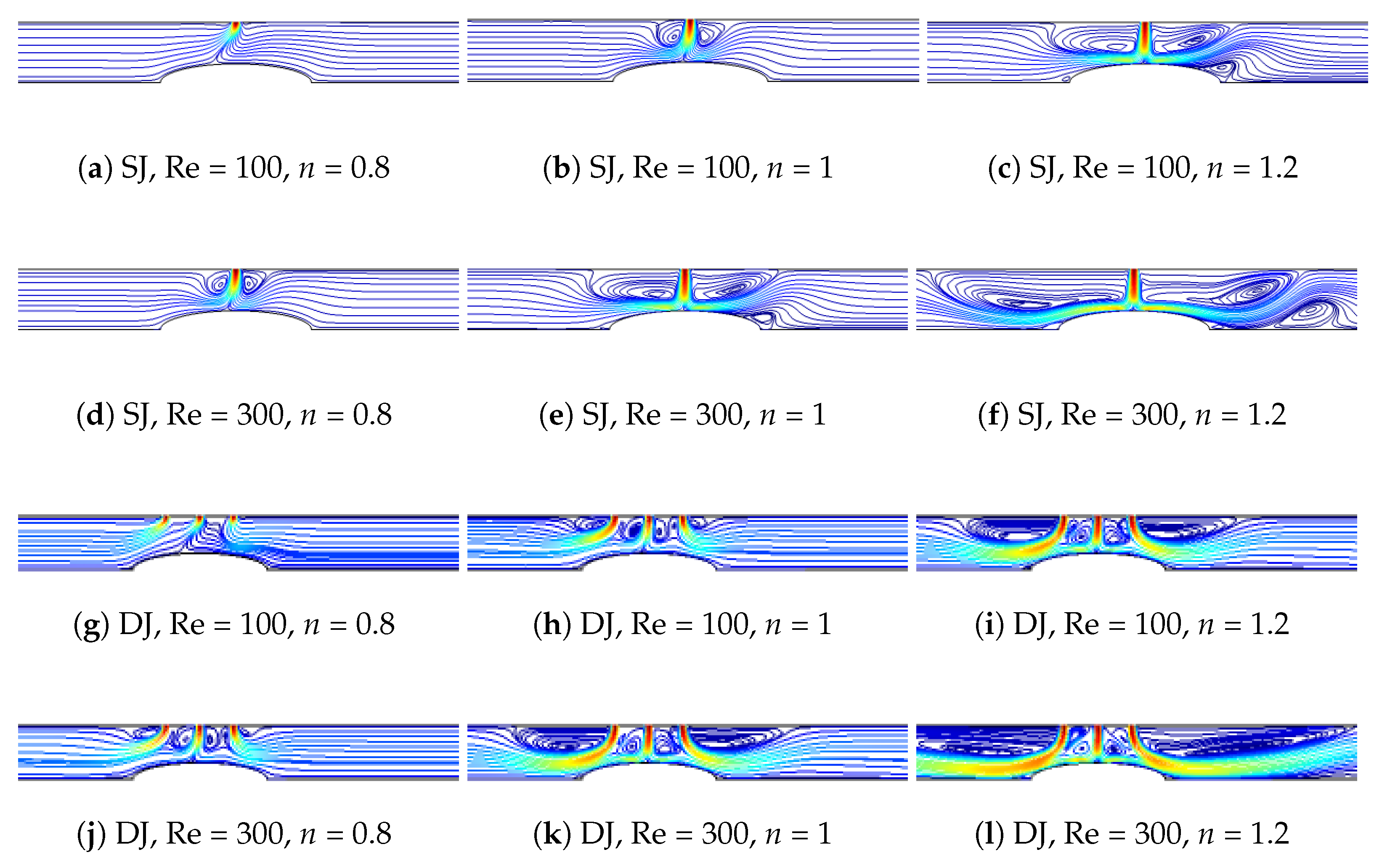
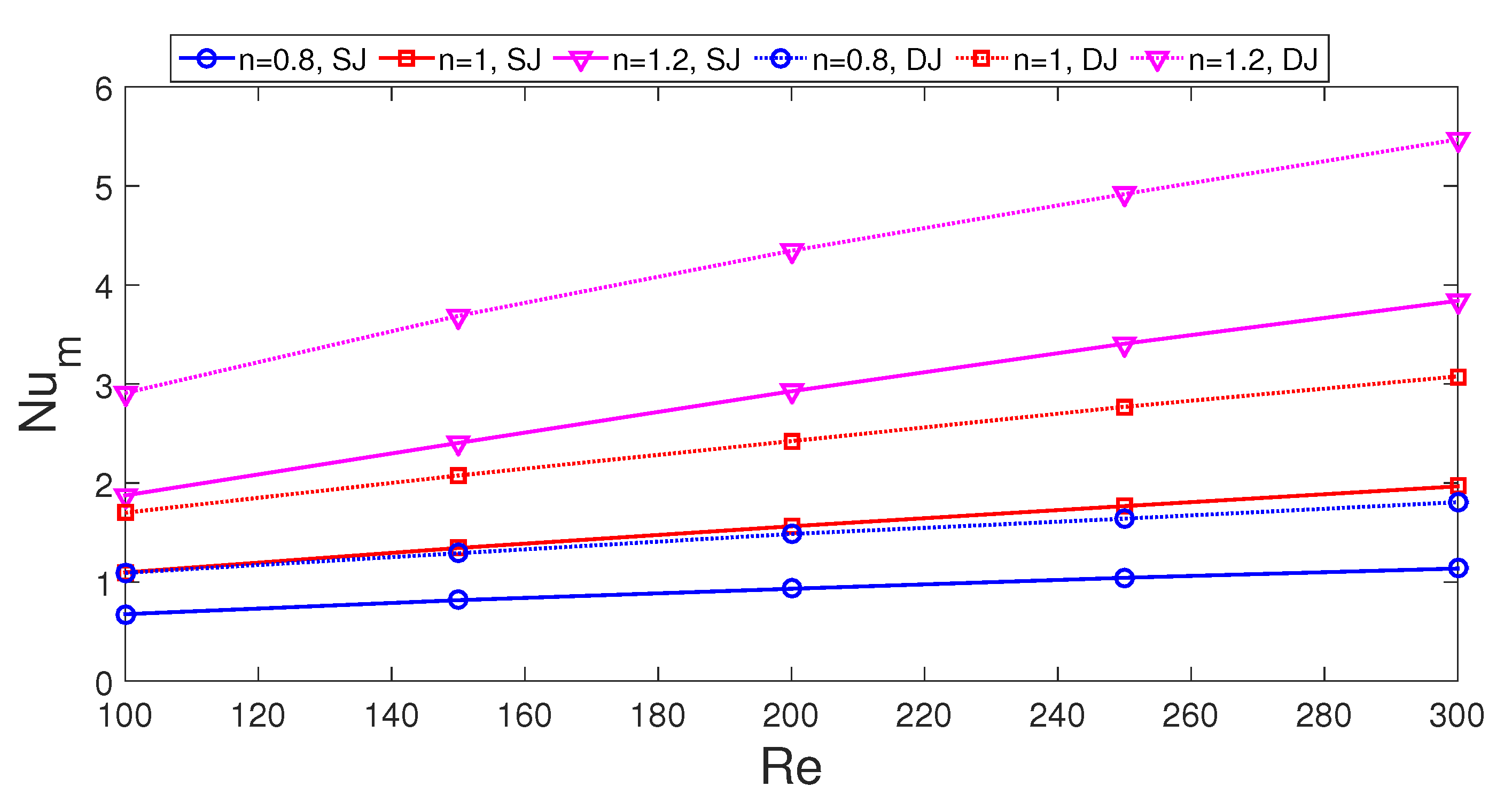
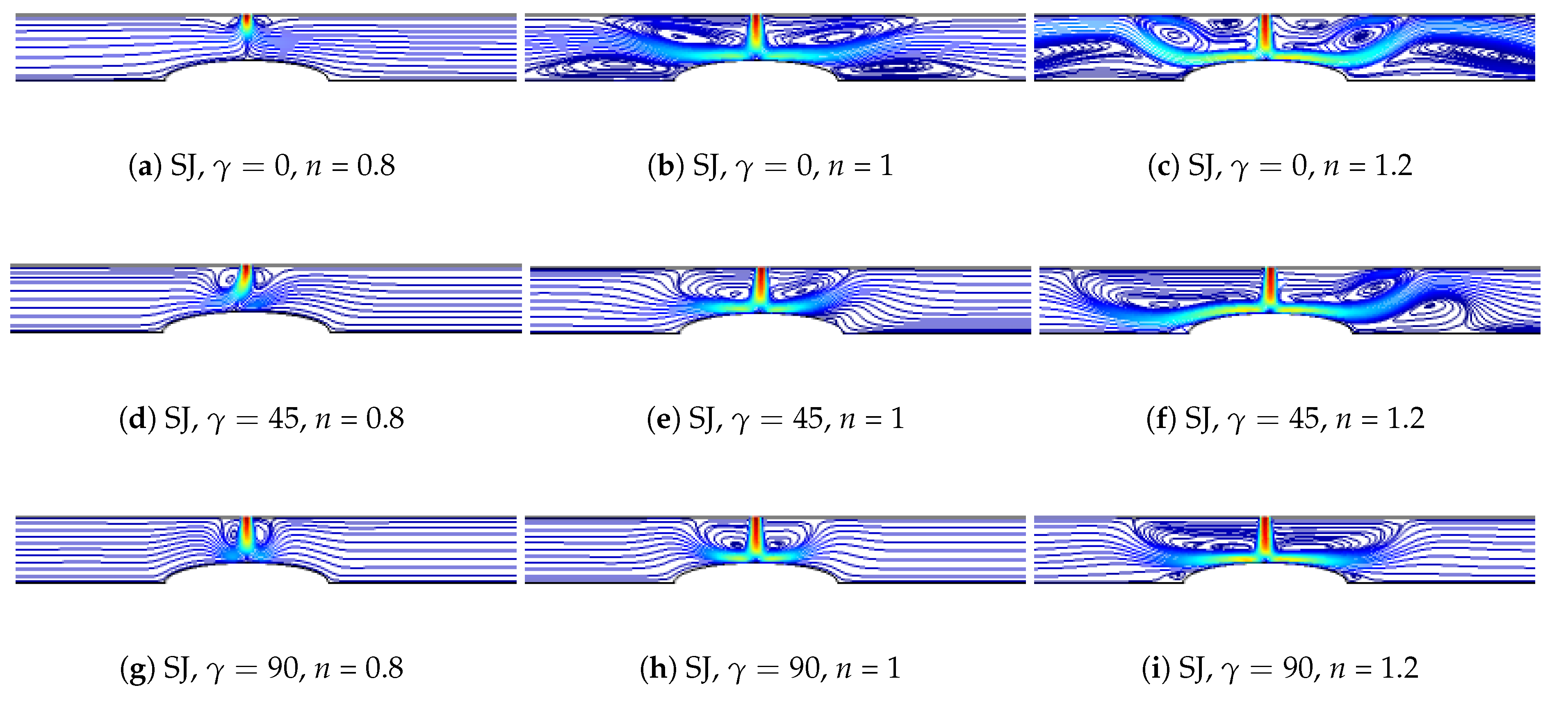
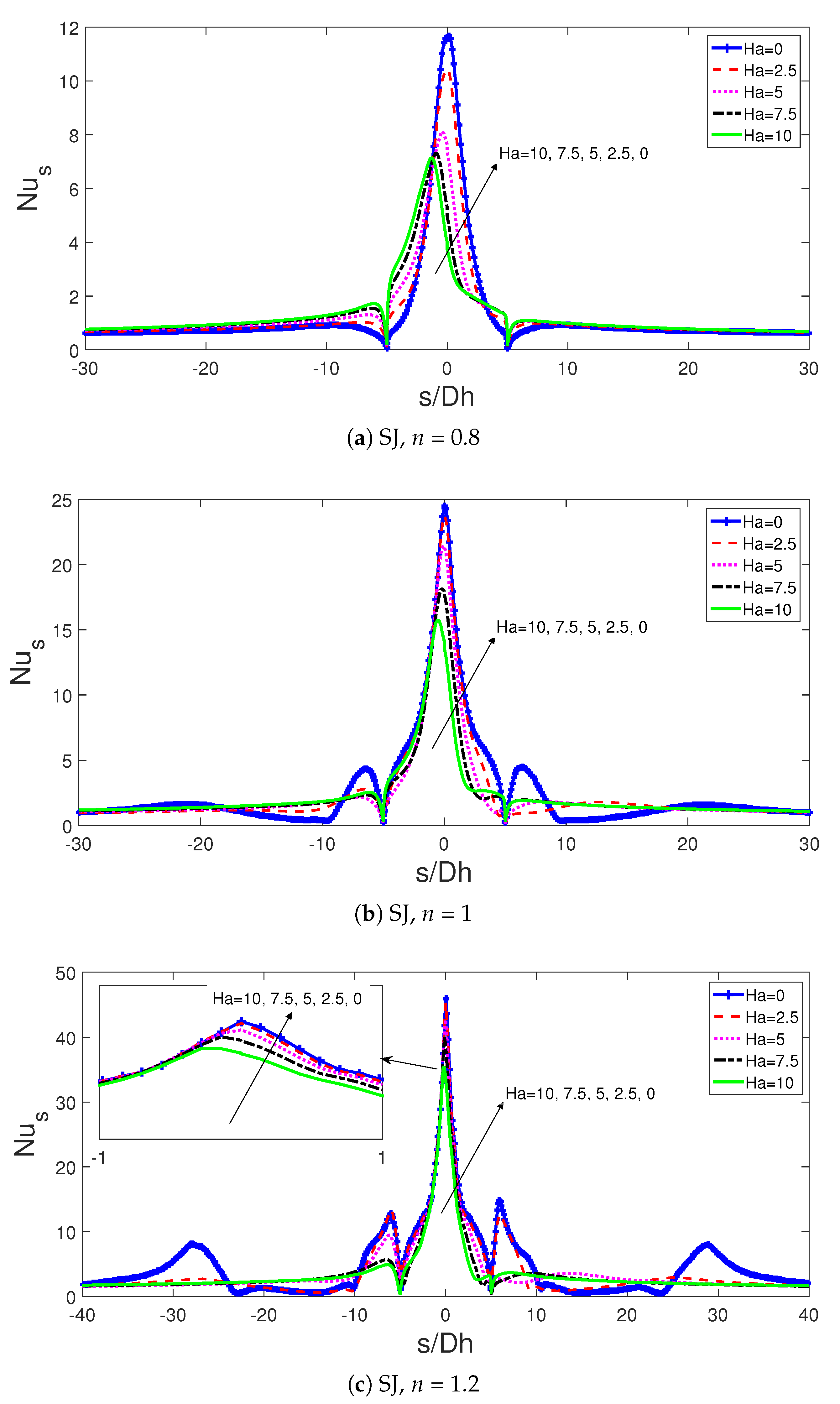
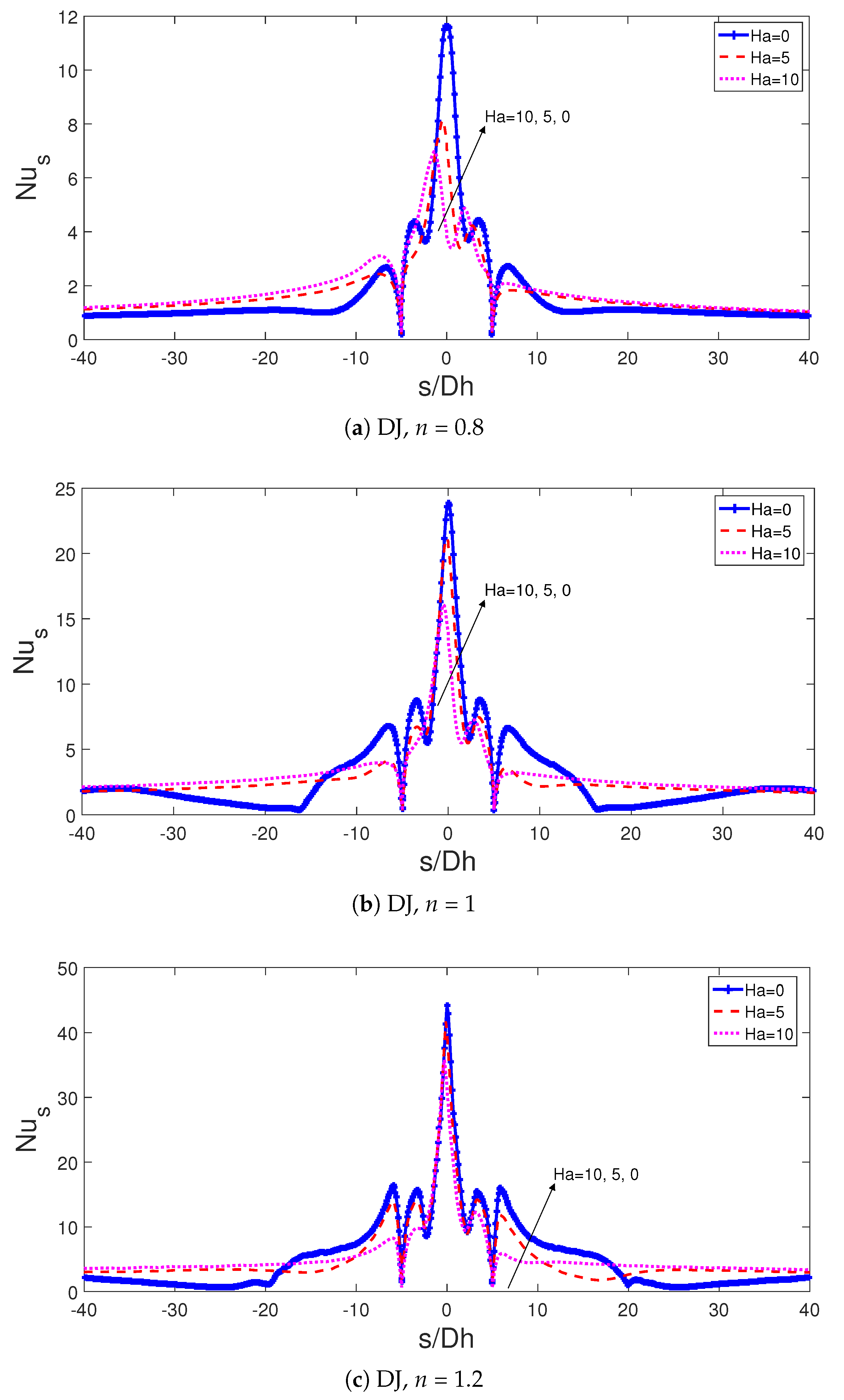
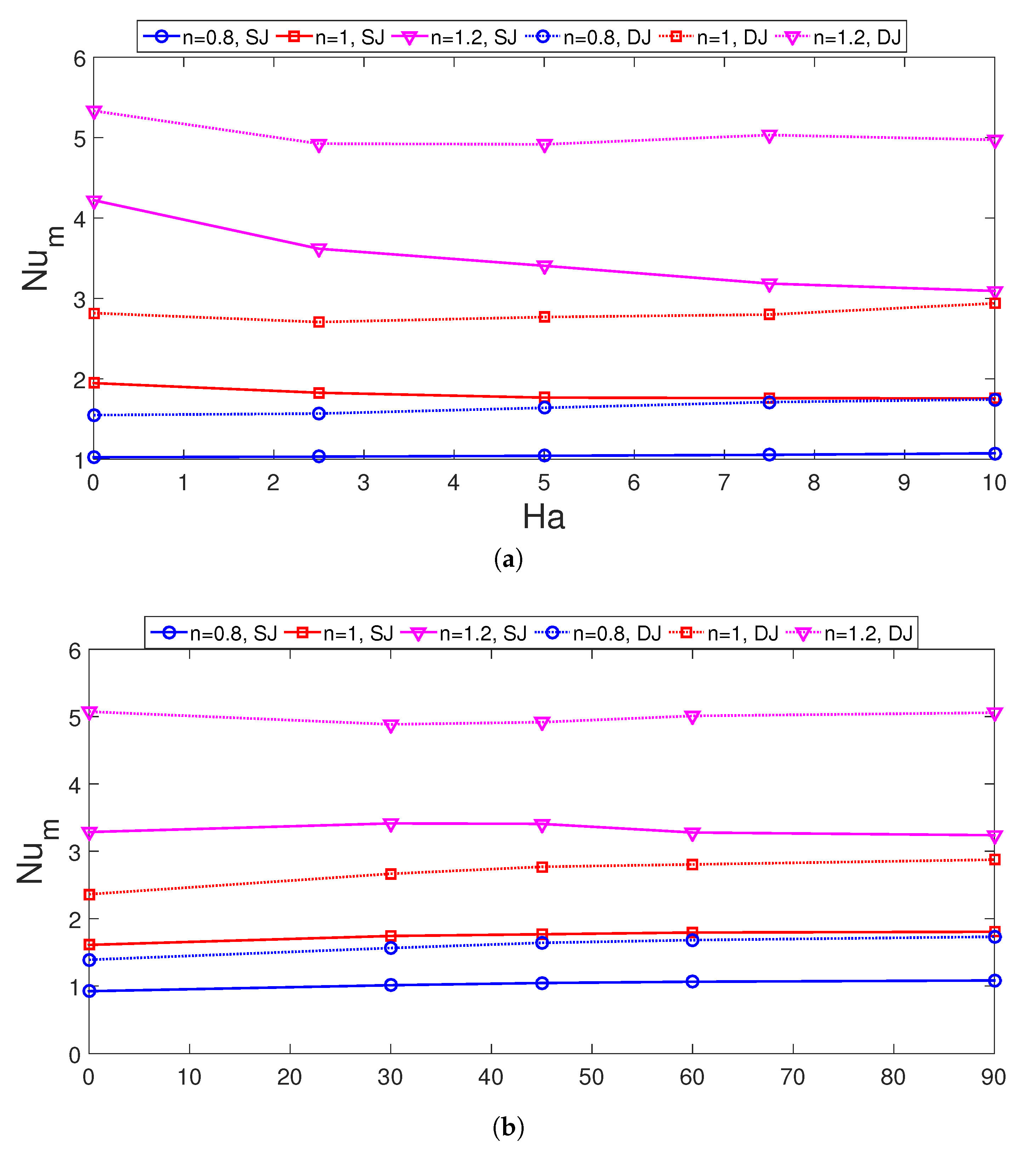
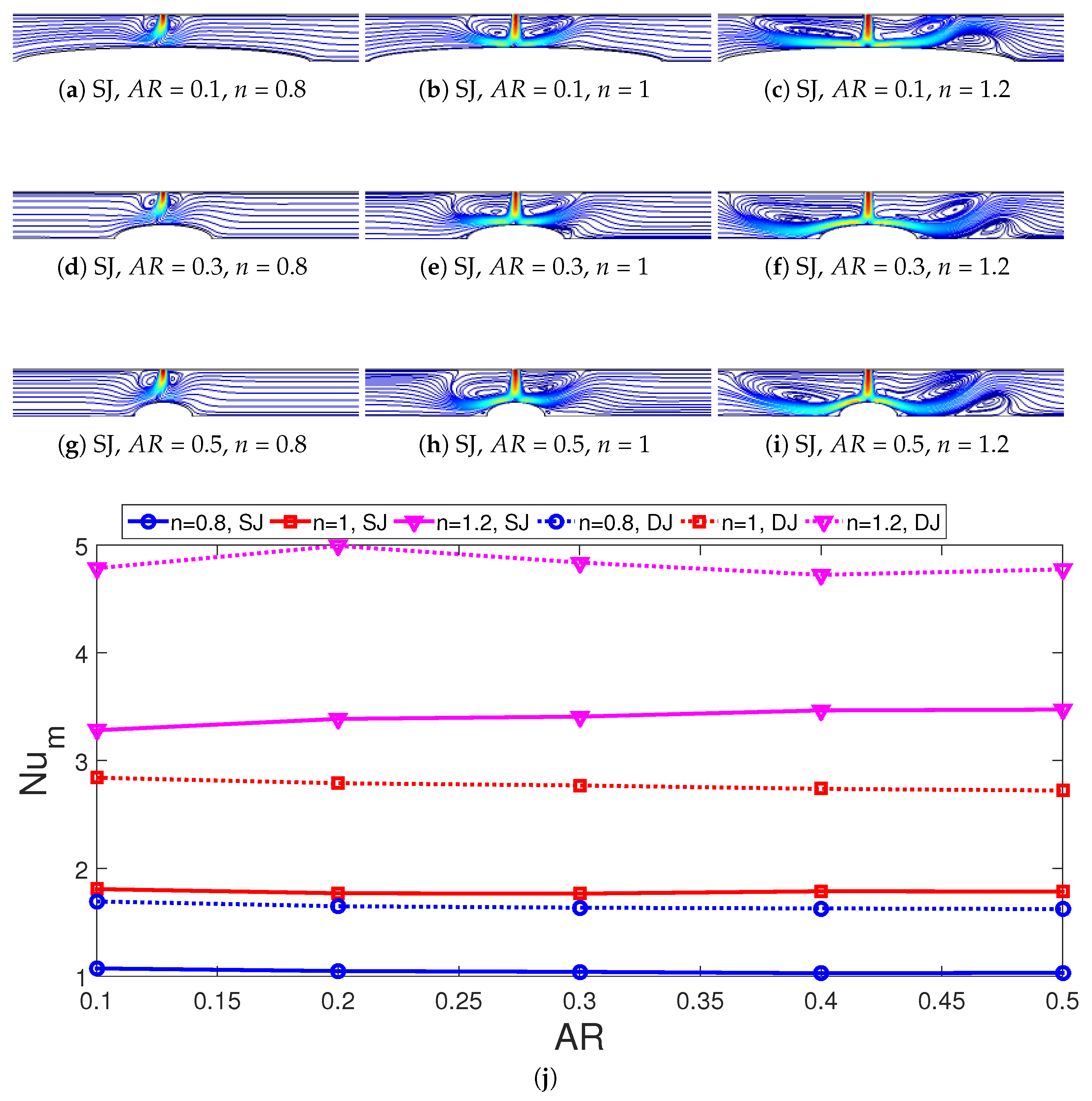
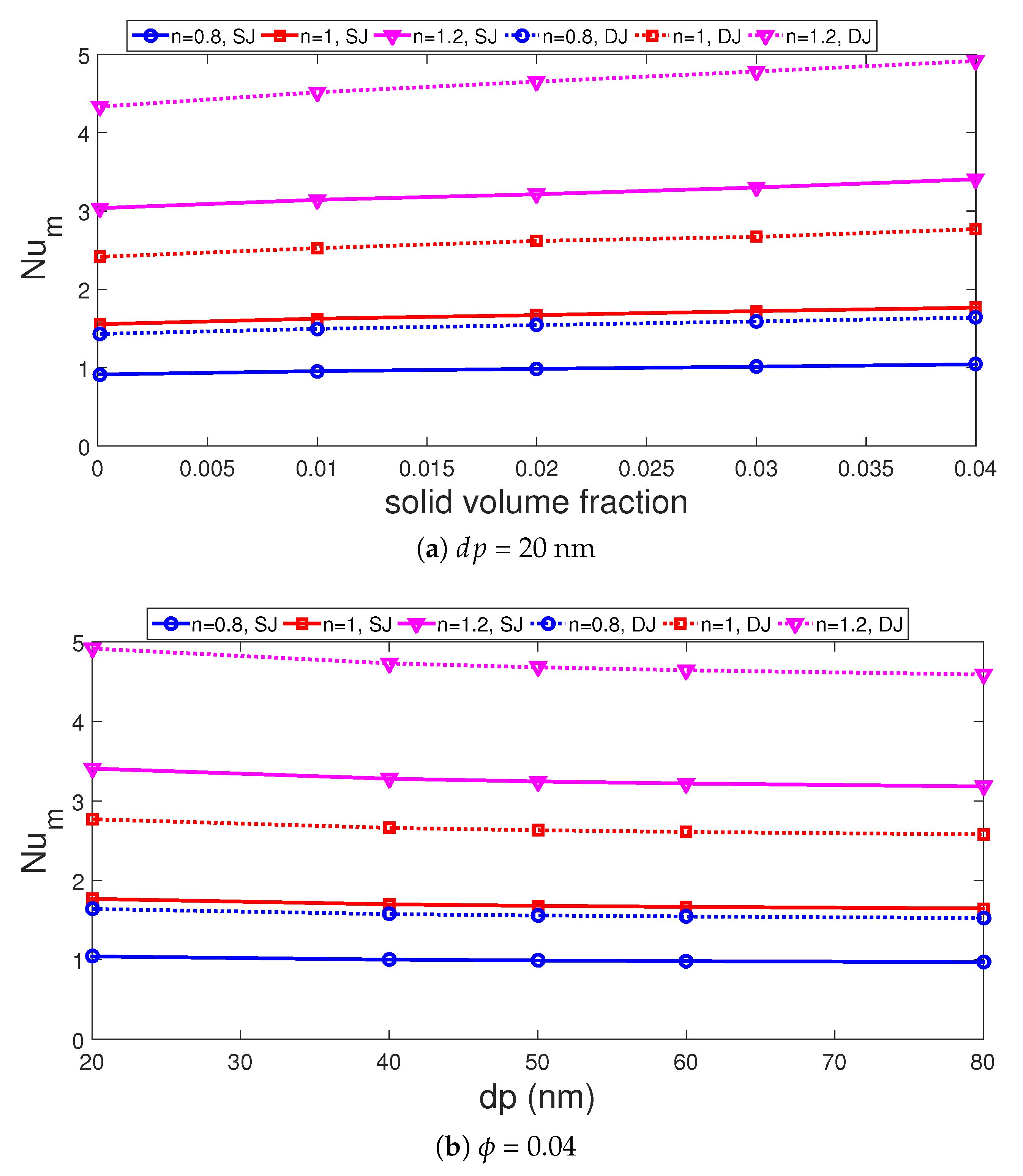
3. Results and Discussion
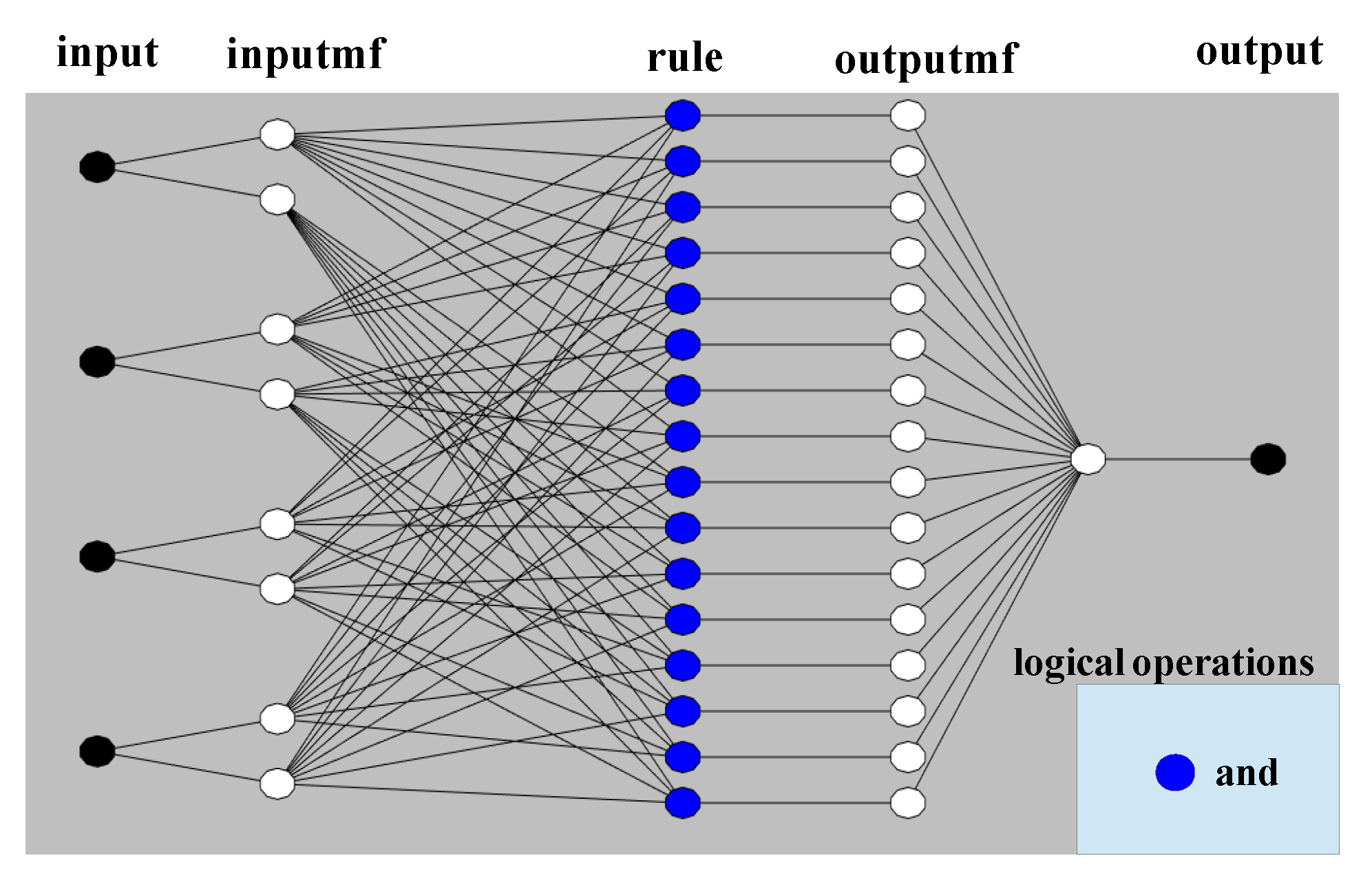
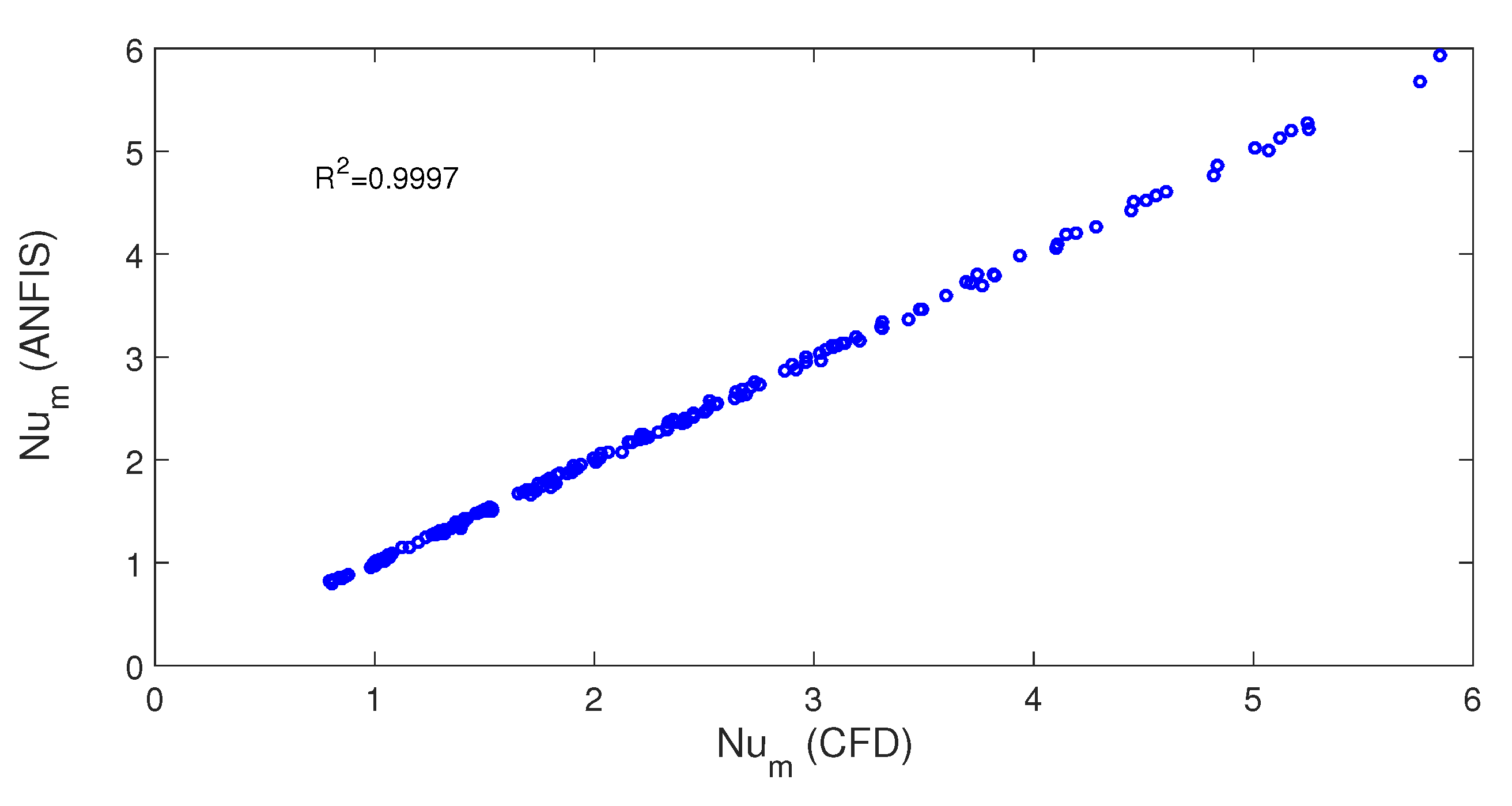
ANFIS (Adaptive Neuro-Fuzzy Interface System) Based Modeling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| a, b | radii of the elliptic curvature |
| AR | aspect ratio |
| dp | particle diameter |
| h | local heat transfer coefficient |
| k | thermal conductivity |
| H | distance between the plates |
| Ha | Hartmann number |
| n | power law index |
| Nu | local Nusselt number |
| Nu | average Nusselt number |
| p | pressure |
| Pr | Prandtl number |
| Re | Reynolds number |
| T | temperature |
| u, v | x-y velocity components |
| x, y | Cartesian coordinates |
| Greek Characters | |
| thermal diffusivity | |
| solid volume fraction | |
| kinematic viscosity | |
| non-dimensional temperature | |
| density of the fluid | |
| inclination angle | |
| shear stress | |
| Subscripts | |
| c | cold |
| h | hot |
| m | average |
| nf | nanofluid |
| p | solid particle |
References
- Maghrabie, H.M. Heat transfer intensification of jet impingement using exciting jets-A comprehensive review. Renew. Sustain. Energy Rev. 2021, 139, 110684. [Google Scholar] [CrossRef]
- Garimella, S.V. Heat transfer and flow fields in confined jet impingement. Annu. Rev. Heat Transf. 2000, 11, 413–494. [Google Scholar] [CrossRef]
- Bahaidarah, H.M. Experimental performance evaluation and modeling of jet impingement cooling for thermal management of photovoltaics. Sol. Energy 2016, 135, 605–617. [Google Scholar] [CrossRef]
- Javidan, M.; Moghadam, A.J. Experimental investigation on thermal management of a photovoltaic module using water-jet impingement cooling. Energy Convers. Manag. 2021, 228, 113686. [Google Scholar] [CrossRef]
- Hasan, H.A.; Sopian, K.; Jaaz, A.H.; Al-Shamani, A.N. Experimental investigation of jet array nanofluids impingement in photovoltaic/thermal collector. Sol. Energy 2017, 144, 321–334. [Google Scholar] [CrossRef]
- Nadda, R.; Kumar, A.; Maithani, R. Efficiency improvement of solar photovoltaic/solar air collectors by using impingement jets: A review. Renew. Sustain. Energy Rev. 2018, 93, 331–353. [Google Scholar] [CrossRef]
- Zhong, X.; Zhang, Y.; Hou, Y.; Feng, H.; Sun, L. Unique dynamics of water-ethanol binary droplets impacting onto a superheated surface with nanotubes. Int. J. Heat Mass Transf. 2021, 164, 120571. [Google Scholar] [CrossRef]
- Izadi, S.; Armaghani, T.; Ghasemiasl, R.; Chamkha, A.J.; Molana, M. A comprehensive review on mixed convection of nanofluids in various shapes of enclosures. Powder Technol. 2019, 343, 880–907. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Arshad, W.; Ali, H.M. Graphene nanoplatelets nanofluids thermal and hydrodynamic performance on integral fin heat sink. Int. J. Heat Mass Transf. 2017, 107, 995–1001. [Google Scholar] [CrossRef]
- Yang, L.; Jiang, W.; Ji, W.; Mahian, O.; Bazri, S.; Sadri, R.; Badruddin, I.A.; Wongwises, S. A review of heating/cooling processes using nanomaterials suspended in refrigerants and lubricants. Int. J. Heat Mass Transf. 2020, 153, 119611. [Google Scholar] [CrossRef]
- Abbas, F.; Ali, H.M.; Shah, T.R.; Babar, H.; Janjua, M.M.; Sajjad, U.; Amer, M. Nanofluid: Potential evaluation in automotive radiator. J. Mol. Liq. 2020, 297, 112014. [Google Scholar] [CrossRef]
- Singh, T.; Atieh, M.A.; Al-Ansari, T.; Mohammad, A.W.; McKay, G. The role of nanofluids and renewable energy in the development of sustainable desalination systems: A review. Water 2020, 12, 2002. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Performance assessment of a thermoelectric module by using rotating circular cylinders and nanofluids in the channel flow for renewable energy applications. J. Clean. Prod. 2021, 279, 123426. [Google Scholar] [CrossRef]
- Shamshirgaran, S.R.; Al-Kayiem, H.H.; Sharma, K.V.; Ghasemi, M. State of the Art of Techno-Economics of Nanofluid-Laden Flat-Plate Solar Collectors for Sustainable Accomplishment. Sustainability 2020, 12, 9119. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; et al. Recent advances in modeling and simulation of nanofluid flows-Part I: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Molana, M.; Rahnama, A.; Ghadami, F. On the nanofluids applications in microchannels: A comprehensive review. Powder Technol. 2018, 332, 287–322. [Google Scholar] [CrossRef]
- Shahsavar, A. Experimental evaluation of energy and exergy performance of a nanofluid-based photovoltaic/thermal system equipped with a sheet-and-sinusoidal serpentine tube collector. J. Clean. Prod. 2020, 287, 125064. [Google Scholar] [CrossRef]
- Bozorg, M.V.; Siavashi, M. Two-phase mixed convection heat transfer and entropy generation analysis of a non-Newtonian nanofluid inside a cavity with internal rotating heater and cooler. Int. J. Mech. Sci. 2019, 151, 842–857. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Identification of pulsating flow effects with CNT nanoparticles on the performance enhancements of thermoelectric generator (TEG) module in renewable energy applications. Renew. Energy 2020, 162, 1076–1086. [Google Scholar] [CrossRef]
- Manca, O.; Mesolella, P.; Nardini, S.; Ricci, D. Numerical study of a confined slot impinging jet with nanofluids. Nanoscale Res. Lett. 2011, 6, 188. [Google Scholar] [CrossRef] [PubMed]
- Zahmatkesh, I.; Ali Naghedifar, S. Oscillatory mixed convection in the jet impingement cooling of a horizontal surface immersed in a nanofluid-saturated porous medium. Numer. Heat Transf. Part A Appl. 2017, 72, 401–416. [Google Scholar] [CrossRef]
- Mahdavi, M.; Sharifpur, M.; Meyer, J.P. Fluid flow and heat transfer analysis of nanofluid jet cooling on a hot surface with various roughness. Int. Commun. Heat Mass Transf. 2020, 118, 104842. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Analysis and predictive modeling of nanofluid-jet impingement cooling of an isothermal surface under the influence of a rotating cylinder. Int. J. Heat Mass Transf. 2018, 121, 233–245. [Google Scholar] [CrossRef]
- Li, Q.; Xuan, Y.; Yu, F. Experimental investigation of submerged single jet impingement using Cu–water nanofluid. Appl. Therm. Eng. 2012, 36, 426–433. [Google Scholar] [CrossRef]
- Lv, J.; Hu, C.; Bai, M.; Zeng, K.; Chang, S.; Gao, D. Experimental investigation of free single jet impingement using SiO2-water nanofluid. Exp. Therm. Fluid Sci. 2017, 84, 39–46. [Google Scholar] [CrossRef]
- Mohammadpour, J.; Lee, A. Investigation of nanoparticle effects on jet impingement heat transfer: A review. J. Mol. Liq. 2020, 316, 113819. [Google Scholar] [CrossRef]
- Ellahi, R.; Aziz, S.; Zeeshan, A. Non-Newtonian nanofluid flow through a porous medium between two coaxial cylinders with heat transfer and variable viscosity. J. Porous Media 2013, 16, 205–216. [Google Scholar] [CrossRef]
- Domairry, D.; Sheikholeslami, M.; Ashorynejad, H.R.; Gorla, R.S.R.; Khani, M. Natural convection flow of a non-Newtonian nanofluid between two vertical flat plates. Proc. Inst. Mech. Eng. Part N J. Nanoeng. Nanosyst. 2011, 225, 115–122. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, Z.; Ghafoor, A. A review of performance enhancement of PCM based latent heat storage system within the context of materials, thermal stability and compatibility. Energy Convers. Manag. 2016, 115, 132–158. [Google Scholar] [CrossRef]
- Kefayati, G. Simulation of double diffusive MHD (magnetohydrodynamic) natural convection and entropy generation in an open cavity filled with power-law fluids in the presence of Soret and Dufour effects (part II: Entropy generation). Energy 2016, 107, 917–959. [Google Scholar] [CrossRef]
- Alsabery, A.; Chamkha, A.; Saleh, H.; Hashim, I. Transient natural convective heat transfer in a trapezoidal cavity filled with non-Newtonian nanofluid with sinusoidal boundary conditions on both sidewalls. Powder Technol. 2017, 308, 214–234. [Google Scholar] [CrossRef]
- Kefayati, G.R. Simulation of heat transfer and entropy generation of MHD natural convection of non-Newtonian nanofluid in an enclosure. Int. J. Heat Mass Transf. 2016, 92, 1066–1089. [Google Scholar] [CrossRef]
- Gharraei, R.; Vejdani, A.; Baheri, S.; Davani, A.A. Numerical investigation on the fluid flow and heat transfer of non-Newtonian multiple impinging jets. Int. J. Therm. Sci. 2016, 104, 257–265. [Google Scholar] [CrossRef]
- Gorla, R.S.R. Laminar swirling power law non-newtonian fluid jet impinging on a normal plane. J. Non-Newton. Fluid Mech. 1977, 2, 299–306. [Google Scholar] [CrossRef]
- Chatterjee, A.; Dhingra, S.; Kapur, S.S. Laminar impinging jet heat transfer with a purely viscous inelastic fluid. Numer. Heat Transf. Part A Appl. 2002, 42, 193–213. [Google Scholar] [CrossRef]
- Lamraoui, H.; Mansouri, K.; Saci, R. Numerical investigation on fluid dynamic and thermal behavior of a non-Newtonian Al2O3-water nanofluid flow in a confined impinging slot jet. J. Non-Newton. Fluid Mech. 2019, 265, 11–27. [Google Scholar] [CrossRef]
- Nakharintr, L.; Naphon, P. Magnetic field effect on the enhancement of nanofluids heat transfer of a confined jet impingement in mini-channel heat sink. Int. J. Heat Mass Transf. 2017, 110, 753–759. [Google Scholar] [CrossRef]
- Lee, H.; Ha, M.; Yoon, H. A numerical study on the fluid flow and heat transfer in the confined jet flow in the presence of magnetic field. Int. J. Heat Mass Transf. 2005, 48, 5297–5309. [Google Scholar] [CrossRef]
- Ha, M.Y.; Lee, H.G.; Seong, S.H. Numerical simulation of three-dimensional flow, heat transfer, and solidification of steel in continuous casting mold with electromagnetic brake. J. Mater. Process. Technol. 2003, 133, 322–339. [Google Scholar] [CrossRef]
- Izadi, A.; Siavashi, M.; Rasam, H.; Xiong, Q. MHD enhanced nanofluid mediated heat transfer in porous metal for CPU cooling. Appl. Therm. Eng. 2020, 168, 114843. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Al2O3-water nanofluid jet impingement cooling with magnetic field. Heat Transf. Eng. 2020, 41, 50–64. [Google Scholar] [CrossRef]
- Nimmagadda, R.; Haustein, H.D.; Asirvatham, L.G.; Wongwises, S. Effect of uniform/non-uniform magnetic field and jet impingement on the hydrodynamic and heat transfer performance of nanofluids. J. Magn. Magn. Mater. 2019, 479, 268–281. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. MHD Pulsating forced convection of nanofluid over parallel plates with blocks in a channel. Int. J. Mech. Sci. 2019, 157, 726–740. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Cooling of a partially elastic isothermal surface by nanofluids jet impingement. J. Heat Transf. 2018, 140, 042205. [Google Scholar] [CrossRef]
- Cornaro, C.; Fleischer, A.S.; Rounds, M.; Goldstein, R.J. Jet impingement cooling of a convex semi-cylindrical surface. Int. J. Therm. Sci. 2001, 40, 890–898. [Google Scholar] [CrossRef]
- Gau, C.; Chung, C. Surface curvature effect on slot-air-jet impingement cooling flow and heat transfer process. J. Heat Transf. 1991, 113, 858–864. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Jet impingement cooling and optimization study for a partly curved isothermal surface with CuO-water nanofluid. Int. Commun. Heat Mass Transf. 2017, 89, 211–218. [Google Scholar] [CrossRef]
- Sharif, M.; Mothe, K. Evaluation of turbulence models in the prediction of heat transfer due to slot jet impingement on plane and concave surfaces. Numer. Heat Transf. Part B Fundam. 2009, 55, 273–294. [Google Scholar] [CrossRef]
- Chai, Z.; Shi, B.; Guo, Z.; Rong, F. Multiple-relaxation-time lattice Boltzmann model for generalized Newtonian fluid flows. J. Non-Newton. Fluid Mech. 2011, 166, 332–342. [Google Scholar] [CrossRef]
- Pravesh, R.; Dhiman, A.; Bharti, R. Non-Newtonian power-law fluids thermal characteristics across periodic array of circular cylinders. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 88. [Google Scholar] [CrossRef]
- Corcione, M. Empirical correlating equations for predicting the effective thermal conductivity and dynamic viscosity of nanofluids. Energy Convers. Manag. 2011, 52, 789–793. [Google Scholar] [CrossRef]
- Sharif, M.A. Heat transfer from an isothermally heated flat surface due to confined laminar twin oblique slot-jet impingement. J. Therm. Sci. Eng. Appl. 2015, 7, 031001. [Google Scholar] [CrossRef]
- Manca, O.; Ricci, D.; Nardini, S.; Di Lorenzo, G. Thermal and fluid dynamic behaviors of confined laminar impinging slot jets with nanofluids. Int. Commun. Heat Mass Transf. 2016, 70, 15–26. [Google Scholar] [CrossRef]
- Chou, Y.; Hung, Y. Impingement cooling of an isothermally heated surface with a confined slot jet. ASME Trans. J. Heat Transf. 1994, 116, 479–482. [Google Scholar] [CrossRef]
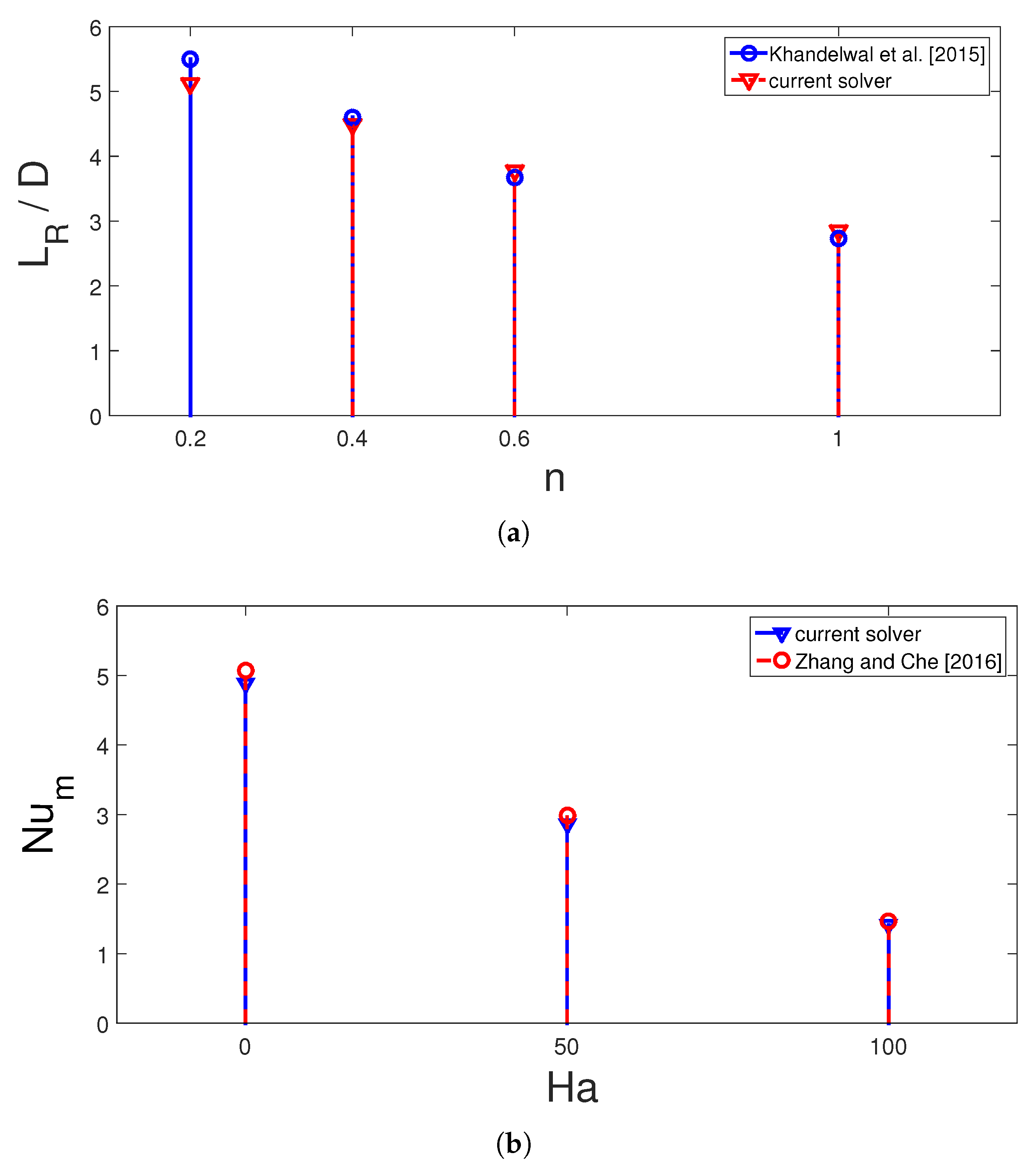
- Khandelwal, V.; Dhiman, A.; Baranyi, L. Laminar flow of non-Newtonian shear-thinning fluids in a T-channel. Comput. Fluids 2015, 108, 79–91. [Google Scholar] [CrossRef]
- Zhang, T.; Che, D. Double MRT thermal lattice Boltzmann simulation for MHD natural convection of nanofluids in an inclined cavity with four square heat sources. Int. J. Heat Mass Transf. 2016, 94, 87–100. [Google Scholar] [CrossRef]
- Mellit, A.; Kalogirou, S.A. ANFIS-based modelling for photovoltaic power supply system: A case study. Renew. Energy 2011, 36, 250–258. [Google Scholar] [CrossRef]
- Ryoo, J.; Dragojlovic, Z.; Kaminski, D. Control of convergence in a computational fluid dynamics simulation using ANFIS. IEEE Trans. Fuzzy Syst. 2005, 13, 42–47. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 116–132. [Google Scholar] [CrossRef]
- Varol, Y.; Avci, E.; Koca, A.; Oztop, H.F. Prediction of flow fields and temperature distributions due to natural convection in a triangular enclosure using Adaptive-Network-Based Fuzzy Inference System (ANFIS) and Artificial Neural Network (ANN). Int. Commun. Heat Mass Transf. 2007, 34, 887–896. [Google Scholar] [CrossRef]




| Property | Symbol | Water | AlO |
|---|---|---|---|
| Density (kg/m) | 997 | 3970 | |
| Specific heat (J/kg K) | c | 4179 | 765 |
| Viscosity (mPa.s) | 0.895 | - | |
| Thermal conductivity (W/mK) | k | 0.613 | 40 |
| Location (X) | Nu-Present Code | Nu-Ref. [53] |
|---|---|---|
| 1.31 | 0.50 | 0.49 |
| 2.28 | 1.91 | 1.98 |
| 3.87 | 2.89 | 2.79 |
| 7.55 | 1.02 | 1.01 |
| 21.4 | 0.35 | 0.33 |
| Source | Re = 100 | Re = 300 |
|---|---|---|
| Ref. [54] | 5.66 | 9.66 |
| Ref. [55] | 5.79 | 9.85 |
| Present study | 5.60 | 9.81 |
| Property | Value-Name |
|---|---|
| # of layers | 5 |
| # of inputs | 4 |
| # of outputs | 1 |
| # input membership functions | 2 2 2 2 |
| Membership function type | Bell shaped |
| Learning rule | Hybrid (Back-propagation + least squares errors) |
| Epochs | 100 |
| Training (438) | Testing (187) | |
|---|---|---|
| MSE | 5.11 × | 7.35 × |
| MAE | 0.0169 | 0.0210 |
| R | 0.9998 | 0.9997 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selimefendigil, F.; Oztop, H.F.; Chamkha, A.J. Jet Impingement Heat Transfer of Confined Single and Double Jets with Non-Newtonian Power Law Nanofluid under the Inclined Magnetic Field Effects for a Partly Curved Heated Wall. Sustainability 2021, 13, 5086. https://doi.org/10.3390/su13095086
Selimefendigil F, Oztop HF, Chamkha AJ. Jet Impingement Heat Transfer of Confined Single and Double Jets with Non-Newtonian Power Law Nanofluid under the Inclined Magnetic Field Effects for a Partly Curved Heated Wall. Sustainability. 2021; 13(9):5086. https://doi.org/10.3390/su13095086
Chicago/Turabian StyleSelimefendigil, Fatih, Hakan F. Oztop, and Ali J. Chamkha. 2021. "Jet Impingement Heat Transfer of Confined Single and Double Jets with Non-Newtonian Power Law Nanofluid under the Inclined Magnetic Field Effects for a Partly Curved Heated Wall" Sustainability 13, no. 9: 5086. https://doi.org/10.3390/su13095086
APA StyleSelimefendigil, F., Oztop, H. F., & Chamkha, A. J. (2021). Jet Impingement Heat Transfer of Confined Single and Double Jets with Non-Newtonian Power Law Nanofluid under the Inclined Magnetic Field Effects for a Partly Curved Heated Wall. Sustainability, 13(9), 5086. https://doi.org/10.3390/su13095086







