Analysis of Bus Fare Structure to Observe Modal Shift, Operator Profit, and Land-Use Choices through Combined Unified Transport Model
Abstract
:1. Introduction
2. Model Assumptions and Behavioral Formulation
2.1. Modeling Assumptions and Hypothesis
- A1: Each user first chooses a workplace, then residence place and then route or mode choice is made. Before starting a journey, each user chooses a travel strategy (i.e., private car or public bus), depending upon minimum travel costs. Figure 1 shows the workers’ choice structure.
- A2: Only commuting trips are considered in this modeling process in the peak time period for simplicity purposes. The overall traffic demand is given between any Zones i and j.
- A3: In this modeling process, firms, households, and landlords are considered homogenous. Each of the decision maker is considered homogenous for the sake of simplicity and their behavior is modeled as multinomial (or nested) logit structure. From each household, a single worker makes a commuting round trip daily.
- A4: A firm chooses its location based on random profit, , where is the production of the firm in Zone i, is the number of workers in each firm, is wage in Zone i, is the area of land used by each firm, is the rent for commercial lot in Zone i, and is an error term.
- A5: The profit of public bus operator is measured as a function of number of passengers, route length, fare rate (currency/km), operation cost, and number of vehicles.
- A6: The transport service revenue is proportionate to passenger-km (bus passenger flow) traveled but operations costs depend upon vehicle-km traveled.
2.2. Behavioral Formulation
2.2.1. Work Choice Behavior of Employees
2.2.2. Residence Choice Behavior of Employees
2.2.3. Route and Mode Choice Behavior of Employees
2.2.4. Firms’ Behavior
2.2.5. Landowners’ Behavior
2.2.6. Total Quantity Conditions
2.2.7. The Unified Equilibrium Model Formulation of Three Players
2.2.8. Bus Operator Behavior
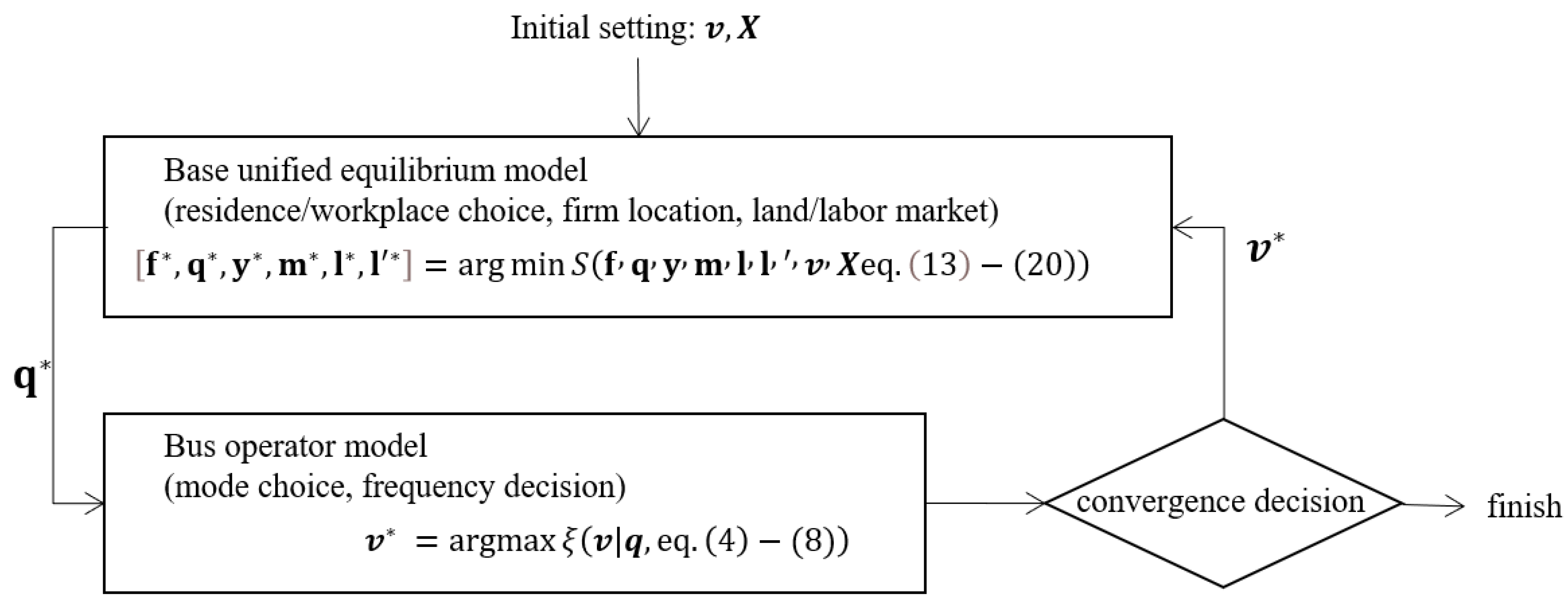
2.3. Algorithm
2.4. Sample Transit Network
2.5. Parameter Setting
3. Results and Discussions
3.1. Simulations with Fixed Fare ( = 30)
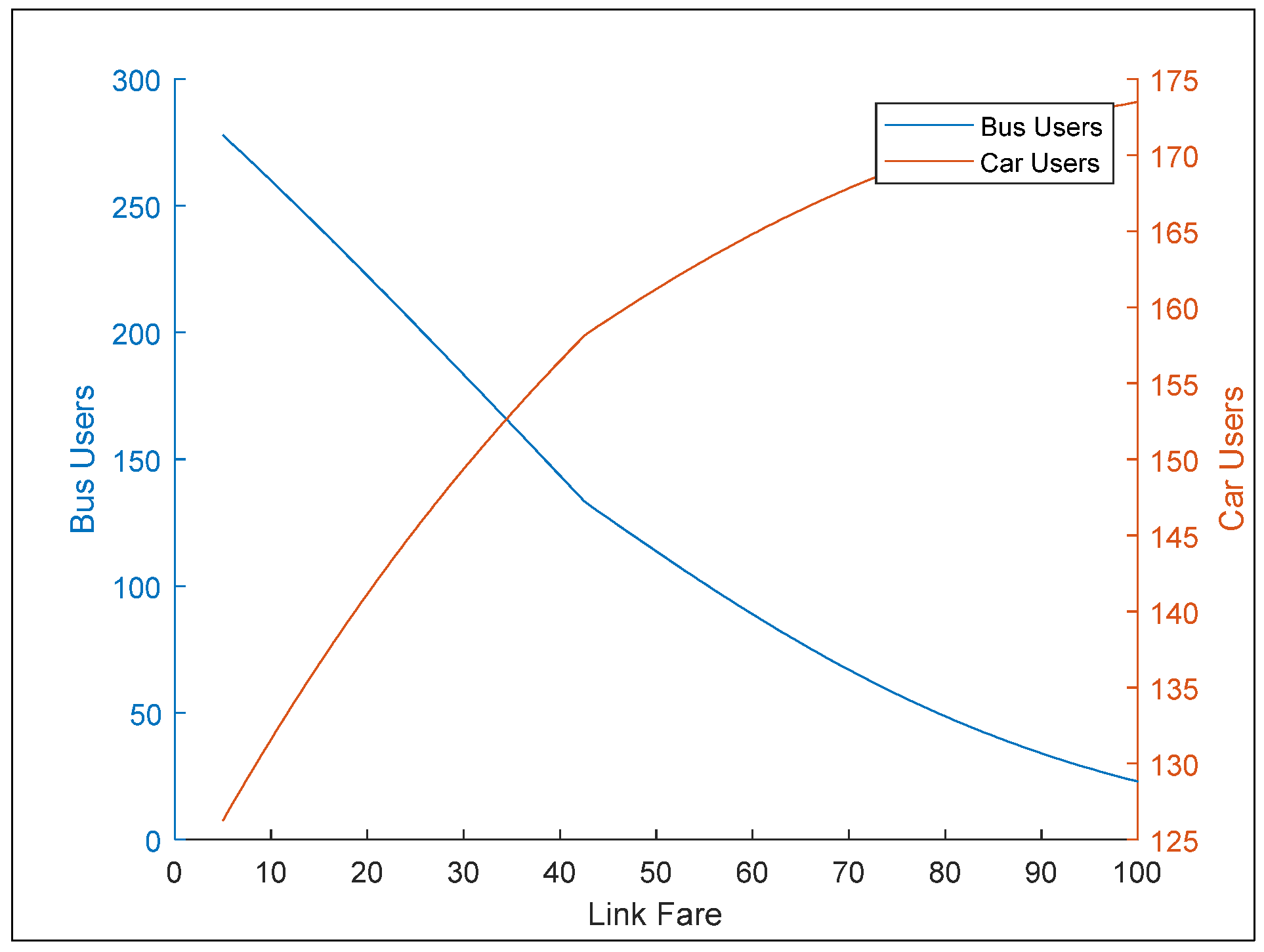
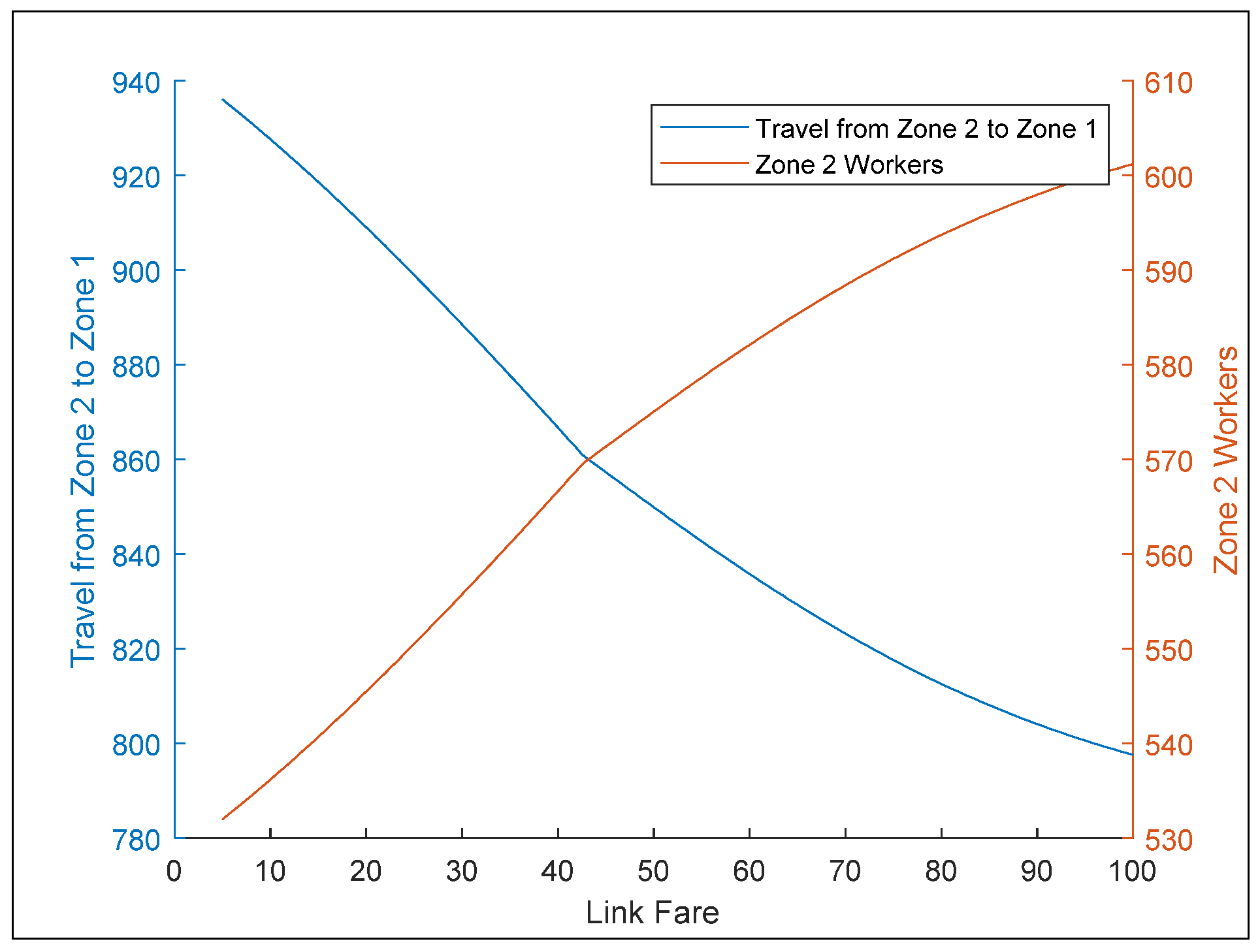
3.2. Simulations with Fare Range
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiao, L.-L.; Liu, T.-L.; Huang, H.-J. On the morning commute problem with carpooling behavior under parking space constraint. Transp. Res. Part B Methodol. 2016, 91, 383–407. [Google Scholar] [CrossRef]
- Guarda, P.; Galilea, P.; Paget-Seekins, L.; Ortúzar, J.D.D. What is behind fare evasion in urban bus systems? An econometric approach. Transp. Res. Part A Policy Pract. 2016, 84, 55–71. [Google Scholar] [CrossRef]
- Macioszek, E.; Kurek, A. The Use of a Park and Ride System—A Case Study Based on the City of Cracow (Poland). Energies 2020, 13, 3473. [Google Scholar] [CrossRef]
- Kitthamkesorn, S.; Chen, A.; Opasanon, S.; Jaita, S. A P-Hub Location Problem for Determining Park-and-Ride Facility Locations with the Weibit-Based Choice Model. Sustainability 2021, 13, 7928. [Google Scholar] [CrossRef]
- Macioszek, E.; Kurek, A. The Analysis of the Factors Determining the Choice of Park and Ride Facility Using a Multinomial Logit Model. Energies 2021, 14, 203. [Google Scholar] [CrossRef]
- LeBlanc, L.J. Transit system network design. Transp. Res. Part B Methodol. 1988, 22, 383–390. [Google Scholar] [CrossRef]
- Tirachini, A. Estimation of travel time and the benefits of upgrading the fare payment technology in urban bus services. Transp. Res. Part C Emerg. Technol. 2013, 30, 239–256. [Google Scholar] [CrossRef]
- Yang, Y.; Deng, L.; Wang, Q.; Zhou, W. Zone Fare System Design in a Rail Transit Line. J. Adv. Transp. 2020, 2020, 2470579. [Google Scholar] [CrossRef]
- Tom, V.M.; Mohan, S. Transit Route Network Design Using Frequency Coded Genetic Algorithm. J. Transp. Eng. 2003, 129, 186–195. [Google Scholar] [CrossRef]
- Canca, D.; De-Los-Santos, A.; Laporte, G.; Mesa, J.A. Integrated Railway Rapid Transit Network Design and Line Planning problem with maximum profit. Transp. Res. Part E Logist. Transp. Rev. 2019, 127, 1–30. [Google Scholar] [CrossRef]
- Uchida, K.; Sumalee, A.; Watling, D.; Connors, R. Study on optimal frequency design problem for multimodal network using probit-based user equilibrium assignment. Transp. Res. Rec. 2002, 236–245. [Google Scholar] [CrossRef]
- Constantin, I.; Florian, M. Optimizing frequencies in a transit network: A nonlinear bi-level programming approach. Int. Trans. Oper. Res. 1995, 2, 149–164. [Google Scholar] [CrossRef]
- Zhu, W.; Chen, M.; Wang, D.; Ma, D. Policy-Combination Oriented Optimization for Public Transportation Based on the Game Theory. Math. Probl. Eng. 2018, 2018, 7510279. [Google Scholar] [CrossRef]
- Yu, B.; Yang, Z.; Yao, J. Genetic Algorithm for Bus Frequency Optimization. J. Transp. Eng. 2010, 136, 576–583. [Google Scholar] [CrossRef]
- Zhou, J.; Lam, W.H.; Heydecker, B.G. The generalized Nash equilibrium model for oligopolistic transit market with elastic demand. Transp. Res. Part B Methodol. 2005, 39, 519–544. [Google Scholar] [CrossRef]
- Harris, A.E.; Thomas, R.; Boyle, D. Metropolitan Atlanta Rapid Transit Authority Fare Elasticity Model. Transp. Res. Rec. J. Transp. Res. Board 1999, 1669, 123–128. [Google Scholar] [CrossRef]
- Cummings, C.P.; Fairhurst, M.; Labelle, S.; Stuart, D. Market Segmentation of Transit Fare Elasticities. Transp. Q. 1989, 43, 407–420. [Google Scholar]
- Wang, Q.; Schonfeld, P.; Deng, L. Profit Maximization Model with Fare Structures and Subsidy Constraints for Urban Rail Transit. J. Adv. Transp. 2021, 2021, 6659384. [Google Scholar] [CrossRef]
- Jin, Z.; Schmöcker, J.-D.; Maadi, S. On the interaction between public transport demand, service quality and fare for social welfare optimisation. Res. Transp. Econ. 2019, 76, 100732. [Google Scholar] [CrossRef]
- Lam, W.H.K.; Zhou, J. Optimal Fare Structure for Transit Networks with Elastic Demand. Transp. Res. Rec. J. Transp. Res. Board 2000, 1733, 8–14. [Google Scholar] [CrossRef]
- Spasovic, L.N.; Schonfeld, P.M. Method for optimizing transit service coverage. Transp. Res. Rec. 1993, 1402, 28–39. [Google Scholar]
- Wirasinghe, S. Nearly optimal parameters for a rail/feeder-bus system on a rectangular grid. Transp. Res. Part A Gen. 1980, 14, 33–40. [Google Scholar] [CrossRef]
- Chang, S.K.; Schonfeld, P.M. Optimal Dimensions of Bus Service Zones. J. Transp. Eng. 1993, 119, 567–585. [Google Scholar] [CrossRef]
- Byrne, B.F. Cost minimizing positions, lengths and headways for parallel public transit lines having different speeds. Transp. Res. 1976, 10, 209–214. [Google Scholar] [CrossRef]
- Holroyd, E.M. The Optimum Bus Service: A Theoretical Model for a Large Uniform Urban Area. 1967. Available online: https://trid.trb.org/view/693339 (accessed on 30 October 2021).
- Byrne, B.F. Public transportation line positions and headways for minimum user and system cost in a radial case. Transp. Res. 1975, 9, 97–102. [Google Scholar] [CrossRef]
- Hurdle, V.F. Minimum Cost Locations for Parallel Public Transit Lines. Transp. Sci. 1973, 7, 340–350. [Google Scholar] [CrossRef]
- Kocur, G.; Hendrickson, C. Design of Local Bus Service with Demand Equilibration. Transp. Sci. 1982, 16, 149–170. [Google Scholar] [CrossRef]
- Kuah, G.K.; Perl, J. Optimization of Feeder Bus Routes and Bus-Stop Spacing. J. Transp. Eng. 1988, 114, 341–354. [Google Scholar] [CrossRef]
- Chang, S.K.; Schonfeld, P.M. Multiple period optimization of bus transit systems. Transp. Res. Part B Methodol. 1991, 25, 453–478. [Google Scholar] [CrossRef]
- Spasovic, L.; Boile, M.; Bladikas, A. Bus transit service coverage for maximum profit and social welfare. Transp. Res. Board. 1994, 1451, 12–22. [Google Scholar]
- Li, Z.-C.; Lam, W.H.K.; Wong, S.C. The Optimal Transit Fare Structure under Different Market Regimes with Uncertainty in the Network. Networks Spat. Econ. 2009, 9, 191–216. [Google Scholar] [CrossRef]
- Chien, S.I.-J.Y.; Tsai, C.F.M. Optimization of Fare Structure and Service Frequency for Maximum Profitability of Transit Systems. Transp. Plan. Technol. 2007, 30, 477–500. [Google Scholar] [CrossRef]
- Van Nes, R. Multilevel Network Optimization for Public Transport Networks. Transp. Res. Board. 2002, 2, 50–57. [Google Scholar] [CrossRef]




| Authors | Objective Function | Transit Mode | Decision Variables | Passenger Demand |
|---|---|---|---|---|
| Spasovic and Schonfled (1993) [21] | Min. of operator and user cost | Bus | Route length, headway, spacing, stop spacing | Uniform and linear |
| Wirasinghe and Seneviratne (1986) [22] | Min. of operator and user cost | Rail | Route length | General, inelastic |
| Chang and Schonfeld (1993) [23] | Min. of operator and user cost | Bus | Route spacing, zone length, headway | Uniform, inelastic |
| Byrne (1976) [24] | Min. of operator and user cost | Bus and rail | Route spacing, headway, and lengths | Uniform, inelastic |
| Holroyd (1976) [25] | Min. of operator and user cost | Bus | Route spacing | Uniform, inelastic |
| Byrne and Vuchic (1972) [26] | Min. of operator and user cost | Bus | Route spacing and headway | Uniform, inelastic |
| Hurdle (1973) [27] | Min. of operator and user cost | Bus | Route density and frequency | General linear, inelastic |
| Kocur and Hendrickson (1982) [28] | Max. operator profit, Max. user profit, etc. | Bus | Route spacing, fare and headway | Uniform elastic |
| Kuah and Perl (1988) [29] | Min. of operator and user cost | Feeder bus to rail | Route spacing, stop spacing, and headway | General inelastic |
| Chang and Schonfeld (1989) [30] | Max. operator profit, Min. user profit, etc. | Bus | Route spacing, fare and headway | Irregular elastic |
| Spasovic et al. (1994) [31] | Max. operator profit, Max. social welfare | Bus | Route length, route spacing, fare and headway | Uniform elastic |
| Li et al., (2009) [32] | Max. operator profit, Min. user profit, etc. | Bus and rail | Route length, fare | Uniform elastic |
| Chien and Tsai (2007) [33] | Max. operator profit, Min. user profit, etc. | Rail | Route length, fare, and headway | Uniform elastic |
| Rob Van Nes (2002) [34] | Max. operator profit, Max. social welfare | Bus and car | Route length, route spacing, | Uniform and linear |
| Wang et al. (2021) [18] | Max. operator profit, Max. social welfare | Bus | Route length, headway, and fare | Uniform elastic |
| (a) General parameters | ||||
| Parameter | Value | |||
| Total Population_N | 1000 | |||
| 0.04 | ||||
| 0.03 | ||||
| 0.02 | ||||
| 0.05 | ||||
| 0.2 | ||||
| 20 | ||||
| 10 | ||||
| (b) Zone parameters | ||||
| Zone Code | Zone Size | Zone Production | ||
| 1 | 1000 | 2000 | ||
| 2 | 2000 | 0 | ||
| Path No | Residence | Firm | Car Link | Bus Link |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 2 | 1 | 1 | 0 |
| 3 | 2 | 1 | 0 | 1 |
| 4 | 2 | 2 | 0 | 0 |
| (d) Link parameters | ||||
| Link Code | Link Free Flow Time | Capacity | BPR Alpha | BPR Beta |
| 1 | 20 | 100 | 0.5 | 3 |
| 2 | 20 | 50 | 0 | 0 |
| Passenger Flow | Residence Choice Behavior | ||
|---|---|---|---|
| Zone 1 flow, f11 | 111.489 | 0 | |
| Zone 2 to 1 car flow, f21c | 149.352 | 10.378 | |
| Zone 2 to 1 bus flow, f21p | 183.414 | −79.736 | |
| Zone 2 flow, f22 | 555.745 | −78.617 | |
| Land Use Choice Behavior | Zone 1 households | 5020 | |
| 111 | Zone 2 households | 14,980 | |
| 889 | Workplace Choice Behavior | ||
| 888 | 22.458 | ||
| 1112 | 0 | ||
| Mode Choice Behavior | 8880 | ||
| 63.314 | 11,120 | ||
| 58.178 | Firm Choice Behavior | ||
| 0.449 | 444 | ||
| 0.551 | 556 | ||
| Bus Operator Model | |||
| 3.668 | 4035.1 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, N.; Nakayama, S.; Yamaguchi, H. Analysis of Bus Fare Structure to Observe Modal Shift, Operator Profit, and Land-Use Choices through Combined Unified Transport Model. Sustainability 2022, 14, 139. https://doi.org/10.3390/su14010139
Ali N, Nakayama S, Yamaguchi H. Analysis of Bus Fare Structure to Observe Modal Shift, Operator Profit, and Land-Use Choices through Combined Unified Transport Model. Sustainability. 2022; 14(1):139. https://doi.org/10.3390/su14010139
Chicago/Turabian StyleAli, Nazam, Shoichiro Nakayama, and Hiromichi Yamaguchi. 2022. "Analysis of Bus Fare Structure to Observe Modal Shift, Operator Profit, and Land-Use Choices through Combined Unified Transport Model" Sustainability 14, no. 1: 139. https://doi.org/10.3390/su14010139
APA StyleAli, N., Nakayama, S., & Yamaguchi, H. (2022). Analysis of Bus Fare Structure to Observe Modal Shift, Operator Profit, and Land-Use Choices through Combined Unified Transport Model. Sustainability, 14(1), 139. https://doi.org/10.3390/su14010139






