An Integrated Analysis of GWR Models and Spatial Econometric Global Models to Decompose the Driving Forces of the Township Consumption Development in Gansu, China
Abstract
1. Introduction
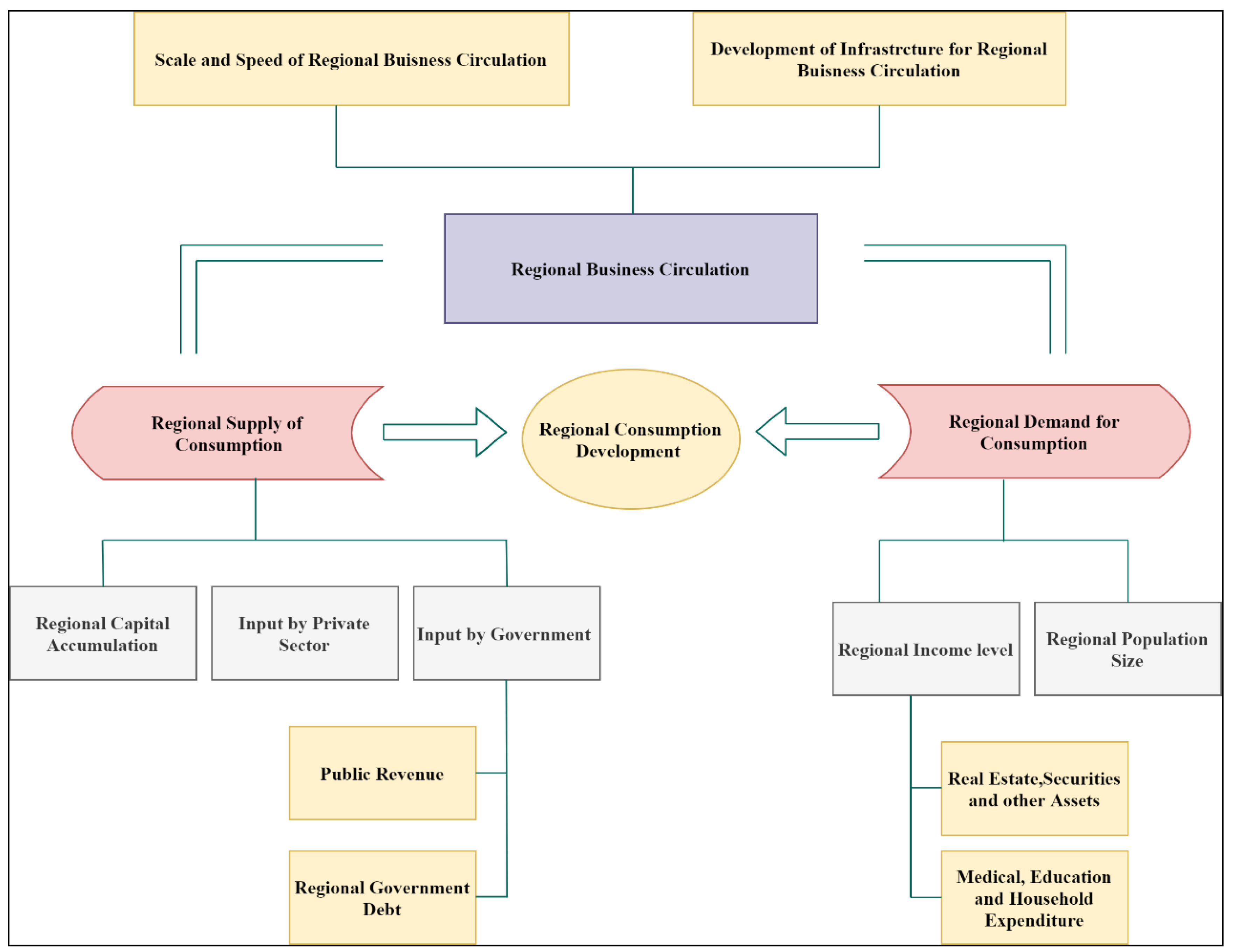
2. Methodological Framework for Driving Force Decomposition of Township Consumption Development
2.1. GWR Models: A Spatial Econometric Local Analysis
2.2. General Nesting Spatial Model and Its Degradation Models: A Spatial Econometric Global Analysis
2.3. Integration of Spatial Econometric Local and Global Analysis: Through the Consistent Settings of Elements of the Spatial Weight Matrices
3. Data Sources and Variables Descriptions
4. Models’ Estimation and Calibration
4.1. The Estimated Results for the Benchmark Model and Their Robustness
4.2. The Estimated Results for the Local Models and Their Calibration
4.3. The Estimated Results of the Global Models and Their Calibration
5. Conclusions
6. Policy Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Long, H.; Li, Y.; Liu, Y.; Woods, M.; Zou, J. Accelerated restructuring in rural China fueled by ‘increasing vs. decreasing balance’ land-use policy for dealing with hollowed villages. Land Use Policy 2012, 29, 11–22. [Google Scholar] [CrossRef]
- Zhang, Y.; Westlund, H.; Klaesson, J. Report from a Chinese Village 2019: Rural Homestead Transfer and Rural Vitalization. Sustainability 2020, 12, 8635. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y. Revitalize the world’s countryside. Nat. News 2017, 548, 275. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Yan, M. Spatial and temporal change in urban-rural land use transformation at village scale—A case study of Xuanhua district, North China. J. Rural Stud. 2016, 47, 425–434. [Google Scholar] [CrossRef]
- Hu, C.T.; Myrdal, J.; Kessle, G.; Michael, M. Report from a Chinese Village. Political Sci. Q. 1966, 81, 164. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y. Rural land engineering and poverty alleviation: Lessons from typical regions in China. J. Geogr. Sci. 2019, 29, 643–657. [Google Scholar] [CrossRef]
- Liu, Y.; Zang, Y.; Yang, Y. China’s rural revitalization and development: Theory, technology and management. J. Geogr. Sci. 2020, 30, 1923–1942. [Google Scholar] [CrossRef]
- Unger, J.; Chan, A. Inheritors of the boom: Private enterprise and the role of local government in a rural South China township. China J. 1999, 42, 45–74. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, F.; Wang, Z.; Li, X.; Zhang, T. An Extended Input Output Table Compiled for Analyzing Water Demand and Consumption at County Level in China. Sustainability 2014, 6, 3301–3320. [Google Scholar] [CrossRef]
- Qi, J.; Li, W.; Wang, Z.; Fang, H. Measurement and Path Selection of Rural Development Level in Enclave Areas: A Case Study of Jingyuan County, Gansu Province. Sustainability 2021, 13, 9904. [Google Scholar] [CrossRef]
- Liao, F.H.; Wei, Y.D. Dynamics, space, and regional inequality in provincial China: A case study of Guangdong province. Appl. Geogr. 2012, 35, 71–83. [Google Scholar] [CrossRef]
- Martin, S. Advanced Industrial Economics 2E [M]. 2003. Available online: https://www.krannert.purdue.edu/faculty/smartin/aie2/aie2ans.pdf (accessed on 3 November 2021).
- Nicholson, W.; Snyder, C.M. Microeconomic Theory: Basic Principles and Extensions; Cengage Learning: Mason, OH, USA, 2012. [Google Scholar]
- An, H.; Xu, J.; Ma, X. Does technological progress and industrial structure reduce electricity consumption? Evidence from spatial and heterogeneity analysis. Struct. Chang. Econ. Dyn. 2020, 52, 206–220. [Google Scholar] [CrossRef]
- Vries, J. The Industrious Revolution: Consumer Behavior and the Household Economy, 1650 to the Present; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Sun, T.; Wu, G. Consumption patterns of Chinese urban and rural consumers. J. Consum. Mark. 2004, 21, 245–253. [Google Scholar] [CrossRef]
- Abed, O.; Bellemans, T.; Janssens, G.; Patil, B.; Yasar, A.; Janssens, D.; Wets, G. A Micro Simulated and Demand Driven Supply Chain Model to Calculate Regional Production and Consumption Matrices. Procedia Comput. Sci. 2013, 19, 404–411. [Google Scholar] [CrossRef][Green Version]
- Solér, C.; Koroschetz, B.; Salminen, E. An infrastructural perspective on sustainable consumption—Activating and obligating sustainable consumption through infrastructures. J. Clean. Prod. 2020, 243, 118601. [Google Scholar] [CrossRef]
- Daitoh, I. Control. Productive consumption and population dynamics in an endogenous growth model: Demographic trends and human development aid in developing economies. J. Econ. Dyn. Control 2010, 34, 696–709. [Google Scholar] [CrossRef]
- Bayer, C.; Rendall, A.D.; Wälde, K. The invariant distribution of wealth and employment status in a small open economy with precautionary savings. J. Math. Econ. 2019, 85, 17–37. [Google Scholar] [CrossRef]
- Gradín, C.; Wu, B. Income and consumption inequality in China: A comparative approach with India. China Econ. Rev. 2020, 62, 101463. [Google Scholar] [CrossRef]
- Marrinan, J. Finance. Government consumption and private consumption correlations. J. Int. Money Financ. 1998, 17, 615–636. [Google Scholar] [CrossRef]
- Crewe, L.; Beaverstock, J. Fashioning the city: Cultures of consumption in contemporary urban spaces. Geoforum 1998, 29, 287–308. [Google Scholar] [CrossRef]
- Boehm, C.E. Government consumption and investment: Does the composition of purchases affect the multiplier? J. Monet. Econ. 2020, 115, 80–93. [Google Scholar] [CrossRef]
- Brueckner, J.K. Infrastructure financing and urban development: The economics of impact fees. J. Public Econ. 1997, 66, 383–407. [Google Scholar] [CrossRef]
- Foster, S.A.; Gorr, W.L. An Adaptive Filter for Estimating Spatially-Varying Parameters: Application to Modeling Police Hours Spent in Response to Calls for Service. Manag. Sci. 1986, 32, 878–889. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically weighted regression. J. R. Stat. Soc. Ser. D 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Mennis, J. Mapping the Results of Geographically Weighted Regression. Cartogr. J. 2006, 43, 171–179. [Google Scholar] [CrossRef]
- Ruppert, D. Empirical-bias bandwidths for local polynomial nonparametric regression and density estimation. J. Am. Stat. Assoc. 1997, 92, 1049–1062. [Google Scholar] [CrossRef]
- Varga, A. University Research and Regional Innovation: A Spatial Econometric Analysis of Academic Technology Transfers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998; Volume 13. [Google Scholar]
- Elhorst, J.P. Spatial Econometrics from Cross-Sectional Data to Spatial Panels; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Huang, H.; Wang, F.; Song, M.; Balezentis, T.; Streimikiene, D. Green innovations for sustainable development of China: Analysis based on the nested spatial panel models. Technol. Soc. 2021, 65, 101593. [Google Scholar] [CrossRef]
- Lesage, J.; Pace, R.K. Introduction to Spatial Econometrics; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- LeSage, J.P.; Pace, R.K. Spatial econometric models. In Handbook of Applied Spatial Analysis; Springer: Berlin/Heidelberg, Germany, 2010; pp. 355–376. [Google Scholar]
- Pace, R.K.; LeSage, J.P.; Zhu, S. Spatial Dependence in Regressors and its Effect on Performance of Likelihood-Based and Instrumental Variable Estimators; Emerald: Bingley, UK, 2012; pp. 257–295. [Google Scholar] [CrossRef]
- Getis, A.; Aldstadt, J. Constructing the spatial weights matrix using a local statistic. Geogr. Anal. 2004, 36, 90–104. [Google Scholar] [CrossRef]
- Qu, X.; Lee, L.-F. Estimating a spatial autoregressive model with an endogenous spatial weight matrix. J. Econ. 2015, 184, 209–232. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Jensen-Butler, C. Estimation of the spatial weights matrix under structural constraints. Reg. Sci. Urban Econ. 2013, 43, 617–634. [Google Scholar] [CrossRef]
- Kelejian, H.H.; Piras, G. Estimation of spatial models with endogenous weighting matrices, and an application to a demand model for cigarettes. Reg. Sci. Urban Econ. 2014, 46, 140–149. [Google Scholar] [CrossRef]
- Minard, P. Institutions and China’s comparative development. arXiv 2020, arXiv:2001.02804. [Google Scholar]
- Li, H.; Xu, X.; Li, S. Does Entrepreneurship Contribute to Innovation Performance When Considering Spatial Spillover Effects? Evidence from the Automobile Industrial Cluster in China. SAGE Open 2020, 10. [Google Scholar] [CrossRef]
- Yang, W.; Fan, B.; Desouza, K. Spatial-temporal effect of household solid waste on illegal dumping. J. Clean. Prod. 2019, 227, 313–324. [Google Scholar] [CrossRef]
- Romdhonah, Y.; Fujiuchi, N.; Takahashi, N.; Nishina, H.; Takayama, K. Empirical Model for the Estimation of Whole-plant Photosynthetic Rate of Cherry Tomato Grown in a Commercial Greenhouse. Environ. Control Biol. 2021, 59, 117–124. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, X.; Zhou, M.; He, S.; Gan, M.; Yang, L.; Wang, K. Impacts of urbanization and landscape pattern on habitat quality using OLS and GWR models in Hangzhou, China. Ecol. Indic. 2020, 117, 106654. [Google Scholar] [CrossRef]
- Tang, J.; Gao, F.; Liu, F.; Zhang, W.; Qi, Y. Understanding Spatio-Temporal Characteristics of Urban Travel Demand Based on the Combination of GWR and GLM. Sustainability 2019, 11, 5525. [Google Scholar] [CrossRef]
- Li, C.; Li, F.; Wu, Z.; Cheng, J. Exploring spatially varying and scale-dependent relationships between soil contamination and landscape patterns using geographically weighted regression. Appl. Geogr. 2017, 82, 101–114. [Google Scholar] [CrossRef]
- Lesage, J.P.; Fischer, M.M. Spatial Growth Regressions: Model Specification, Estimation and Interpretation. Spat. Econ. Anal. 2008, 3, 275–304. [Google Scholar] [CrossRef]
- Elhorst, P.; Vega, S.H. On Spatial Econometric Models, Spillover Effects, and W. 2013. Available online: http://hdl.handle.net/10419/123888 (accessed on 3 November 2021).
- Liu, Y.; Yamauchi, F. Population density, migration, and the returns to human capital and land: Insights from Indonesia. Food Policy 2014, 48, 182–193. [Google Scholar] [CrossRef]
- Paddison, A.; Calderwood, E. Rural retailing: A sector in decline? Int. J. Retail Distrib. Manag. 2007, 35, 136–155. [Google Scholar] [CrossRef]



| Name of Indicators | Corresponding Census Codes | |||
|---|---|---|---|---|
| Explanatory Variables | Economic Characteristics | Permanent Resident Population | X1 | Z18 |
| Government Revenue | X2 | Z20 | ||
| Public Expenditure | X3 | Z21 | ||
| Township Total Assets | X4 | Z22 | ||
| Trading Volume of Commodity Market | X5 | Z37 | ||
| The Ratio of Residents Covered by Basic Endowment Insurance | X6 | Z60 | ||
| The Ratio of Residents Covered by Basic Medical Insurance | X7 | Z61 | ||
| Number of Outlets of Financial Institutions | X8 | Z65 | ||
| Policy Characteristics | Township Types | X9 | Z01 | |
| Township Attributes | X10 | Z02 | ||
| Old Revolutionary Areas, | X11 | Z04 | ||
| Border Areas, | Z05 | |||
| and Ethnic Minority Areas | Z06 | |||
| Dependent Variable | Total Retail Sales of Consumer Goods | Y | Z35 | |
| The Benchmark Model | Extension Model 1 (X6) | Extension Model 2 (X4) | Extension Model 3 (X2) | Extension Model 4 (X5) | Extension Model 5 (X3) | Extension Model 6 (X11) | |
|---|---|---|---|---|---|---|---|
| Constant | 15,667.28 | 15,652.78 | 15,714.43 | 15,830.74 | 15,819.76 | 15,653.15 | 15,867.98 |
| (3.90 ***) | (3.89 ***) | (3.91 ***) | (3.93 ***) | (3.93 ***) | (3.89 ***) | (3.95 ***) | |
| X1 | 0.36 | 0.36 | 0.36 | 0.36 | 0.36 | 0.36 | 0.36 |
| (8.94 ***) | (8.83 ***) | (8.98 ***) | (8.95 ***) | (8.94 ***) | (8.94 ***) | (9.02 ***) | |
| X8 | 1953.48 | 1954.81 | 1950.98 | 1954.41 | 1954 | 1955.42 | 1938.62 |
| (15.46 ***) | (15.45 ***) | (15.44 ***) | (15.46 ***) | (15.46 ***) | (15.44 ***) | (15.33 ***) | |
| X7 | −23,107.11 | −22,561.13 | −23,144.20 | −23,179.91 | −23,253.52 | −23,079.35 | −23,661.41 |
| (−5.71 ***) | (−4.76 ***) | (−5.72 ***) | (−5.73 ***) | (−5.73 ***) | (−5.70 ***) | (−5.84 ***) | |
| X9 | 4300.36 | 4304.82 | 4481.74 | 4441.88 | 4283.39 | 4299.4 | 4334.52 |
| (2.69 ***) | (2.70 ***) | (2.79 ***) | (2.74 ***) | (2.68 ***) | (2.69 ***) | (2.72 ***) | |
| X10 | 5723.38 | 5711.66 | 5635.39 | 5764.75 | 5695.63 | 5757.29 | 5676.87 |
| (3.21 ***) | (3.20 ***) | (3.15 ***) | (3.22 ***) | (3.19 ***) | (3.21 ***) | (3.18 ***) | |
| Added Variable | −818.01 | −0.04 | −0.15 | −10.75 | −0.02 | 2771.16 | |
| (−0.22) | (−1.02) | (−0.52) | (−0.49) | (−0.25) | (1.92 *) | ||
| R2 | 0.5031 | 0.5028 | 0.5032 | 0.5028 | 0.5028 | 0.5028 | 0.5042 |
| AIC | 22.14 | 22.14 | 22.14 | 22.14 | 22.14 | 22.14 | 22.14 |
| F | 250.56 | 208.65 | 208.98 | 208.72 | 208.71 | 208.65 | 209.88 |
| D-W | 1.7394 | 1.7384 | 1.7324 | 1.7401 | 1.7393 | 1.7394 | 1.7393 |
| Constant | X1 | X8 | X7 | X9 | X10 | R2 | AICc | Bandwidth | GWR F | |
|---|---|---|---|---|---|---|---|---|---|---|
| GWR 2_9 | [−1908.9] 【6543.2】 | 0.5 (10.47 ***) | 1829.1 (14.72 ***) | [−6280.0] 【6680.3】 | 2833.8 (1.90 *) | [9348.4] 【20,779.4】 | 0.6214 | 27,273.8 | 52 | 2.9108 |
| GWR 3_1 | [−1808.2] 【8044.6】 | [0.5] 【0.5】 | [1453.9] 【1648.0】 | [−4710.5] 【4669.2】 | 4535.9 (3.58) | 5049.2 (3.48) | 0.7399 | 26,862.4 | 52 | 5.2670 |
| GWR 3_4 | [−2181.9] 【8483.7】 | [0.5] 【0.5】 | 1334.1 (11.22 ***) | [−4835.6] 【5822.4】 | [7910.7] 【11,697.3】 | 6579.3 (4.38 ***) | 0.7079 | 26,998.9 | 55 | 4.3746 |
| GWR 3_5 | [−2057.1] 【8160.8】 | [0.5] 【0.6】 | 1324.6 (11.14 ***) | [−4659.2] 【5171.2】 | 3537.9 (2.69 ***) | [12,285.1] 【16,145.4】 | 0.7175 | 26,967.8 | 52 | 4.5717 |
| GWR 3_7 | [−2015.6] 【5779.2】 | 0.5 (10.24 ***) | [1399.3] 【1686.1】 | [−4435.8] 【5132.9】 | [8413.3] 【12,058.4】 | 5785.7 (4.10 ***) | 0.7543 | 26,802.3 | 52 | 5.7534 |
| GWR 3_8 | [−32690.8] 【5167.8】 | 0.4 (9.60 ***) | [−2094.6] 【1755.8】 | [−107,413.4] 【4541.8】 | 4031.2 (3.22 ***) | [−81,186.6] 【15,945.4】 | 0.7509 | 26,812.4 | 52 | 5.7834 |
| GWR 5_1 | [−2088.8] 【7060.3】 | [0.4] 【0.4】 | [1588.2] 【1624.2】 | [−3119.7] 【4573.9】 | [7089.9] 【8827.5】 | [8086.3] 【12,838.1】 | 0.7884 | 26,730.5 | 54 | 5.7743 |
| SAR | SEM | SXL | SAC | SDM | SDEM | GNSM | |
|---|---|---|---|---|---|---|---|
| Constant | 15,094.36 | 16,020.26 | −10,331.51 | 17,611.64 | −8923.12 | −8876.13 | −7357.07 |
| (3.76 ***) | (3.96 ***) | (−0.53) | (4.18 ***) | (−0.46) | (−0.44) | (−0.48) | |
| X1 | 0.36 | 0.38 | 0.40 | 0.39 | 0.40 | 0.40 | 0.42 |
| (8.92 ***) | (9.24 ***) | (9.47 ***) | (9.38 ***) | (9.54 ***) | (9.51 ***) | (9.72 ***) | |
| X8 | 1937.11 | 1909.72 | 1882.46 | 1883.06 | 1878.36 | 1884.23 | 1850.25 |
| (15.39 ***) | (15.12 ***) | (14.82 ***) | (14.88 ***) | (14.85 ***) | (14.91 ***) | (14.59 ***) | |
| X7 | −23,822.5 | −23,514.70 | −23,107.34 | −23,222.47 | −23,171.09 | −23,092.31 | −23,425.30 |
| (−5.89 ***) | (−5.82 ***) | (−5.66 ***) | (−5.75 ***) | (−5.70 ***) | (−5.68 ***) | (−5.74 ***) | |
| X9 | 4194.44 | 3743.16 | 3531.78 | 3543.10 | 3472.07 | 3538.01 | 3406.12 |
| (2.64 ***) | (2.35 **) | (2.20 **) | (2.23 **) | (2.18 **) | (2.22 **) | (2.14 **) | |
| X10 | 5773.24 | 5680.96 | 5538.49 | 5547.90 | 5548.88 | 5556.86 | 5242.71 |
| (3.25 ***) | (3.21 ***) | (3.11 ***) | (3.15 ***) | (3.13 ***) | (3.13 ***) | (2.97 ***) | |
| WX1 | −0.41 | −0.41 | −0.38 | −0.49 | |||
| (−3.06 ***) | (−3.05 ***) | (−2.75 ***) | (−4.72 ***) | ||||
| WX2 | 1040.02 | 541.45 | 918.49 | −560.54 | |||
| (1.55) | (0.72) | (1.33) | (−0.80) | ||||
| WX7 | 29,675.53 | 28,912.72 | 27,985.82 | 30,039.73 | |||
| (1.46) | (1.43) | (1.34) | (1.79 *) | ||||
| WX9 | 19,117.61 | 18,733.33 | 20,170.29 | 11,921.64 | |||
| (1.85 *) | (1.80 *) | (1.92 *) | (1.32) | ||||
| WX10 | 3015.96 | 639.77 | 1865.26 | −2150.66 | |||
| (0.24) | (0.05) | (0.15) | (−0.19) | ||||
| rho | 0.18 | −0.23 | 0.15 | 0.60 | |||
| (1.83 *) | (−1.39) | (1.16) | (4.28 ***) | ||||
| lamda | 0.31 | 0.50 | 0.09 | −0.66 | |||
| (2.54 **) | (3.53 ***) | (0.69) | (−2.58 **) | ||||
| R2 | 0.5048 | 0.5065 | 0.5080 | 0.5087 | 0.5087 | 0.5082 | 0.5160 |
| Log(L) | −13,644.92 | −13,643.5 | −13,638.2 | −13,642.9 | −13,637.5 | −13,637.9 | −13,635.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Fan, Q.; Zhou, P. An Integrated Analysis of GWR Models and Spatial Econometric Global Models to Decompose the Driving Forces of the Township Consumption Development in Gansu, China. Sustainability 2022, 14, 281. https://doi.org/10.3390/su14010281
Zhao Q, Fan Q, Zhou P. An Integrated Analysis of GWR Models and Spatial Econometric Global Models to Decompose the Driving Forces of the Township Consumption Development in Gansu, China. Sustainability. 2022; 14(1):281. https://doi.org/10.3390/su14010281
Chicago/Turabian StyleZhao, Qianqian, Qiao Fan, and Pengfei Zhou. 2022. "An Integrated Analysis of GWR Models and Spatial Econometric Global Models to Decompose the Driving Forces of the Township Consumption Development in Gansu, China" Sustainability 14, no. 1: 281. https://doi.org/10.3390/su14010281
APA StyleZhao, Q., Fan, Q., & Zhou, P. (2022). An Integrated Analysis of GWR Models and Spatial Econometric Global Models to Decompose the Driving Forces of the Township Consumption Development in Gansu, China. Sustainability, 14(1), 281. https://doi.org/10.3390/su14010281






