Risk-Averse Co-Decision for Lower-Carbon Product Family Configuration and Resilient Supplier Selection
Abstract
:1. Introduction
2. Related Work
2.1. Product Family Configuration and Supplier Selection
2.2. Supply Risks and Resiliency
2.3. Risk Preference and Measurement
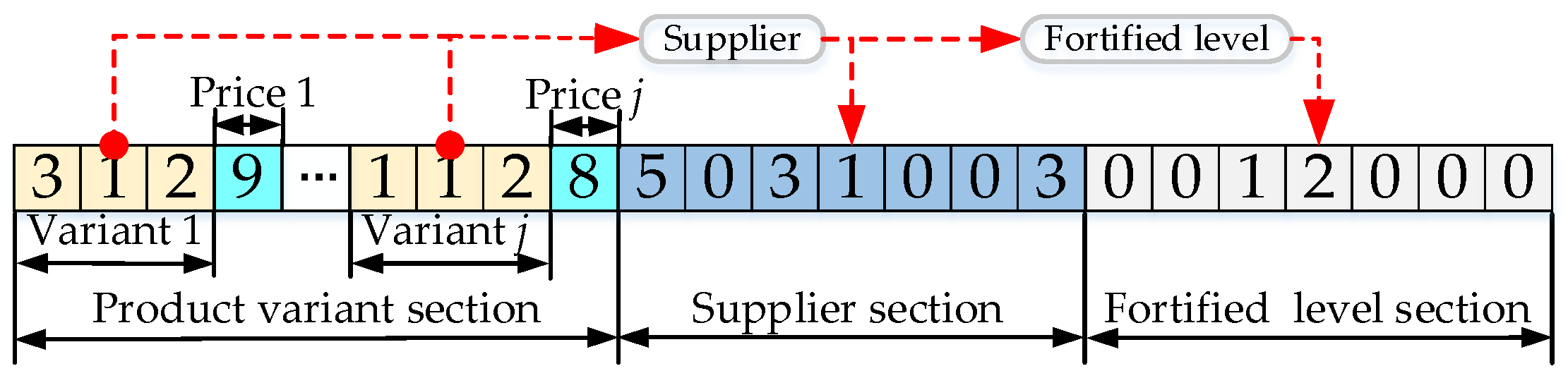
3. Problem Descriptions and Model Development
3.1. Problem Descriptions
3.2. Symbols
- 1.
- Indices
- : Index of market segment,
- : Index of variant,
- : Index of module,
- : Index of module instance,
- : Index of supplier,
- : Index of scenario,
- : Index of fortified level, t
- 2.
- Abbreviations
- : Module instance l of module k
- : Module instance l of module k supplied by the supplier v
- 3.
- Parameters
- : Part-worth utility of module instance in market segment i
- : Constant related to the derivation of the utility from part utilities of variant j
- : Demand for products in market segment i
- : Selling price of variant j
- : Number of products from competitive companies and number of products that have been launched in the market by this company, respectively
- : Utility surplus of the new, existing and competitive variant j in segment i
- : Fixed cost part of the intra-manufacturer for a product family which has J product variants
- : Variable unit cost of intra-manufacturer for module instance
- : Outsourcing-related fixed cost paid to the supplier v for module instance
- : Unit purchase cost (including transported cost) for module instance
- : Unit shortage cost of product variant j due to disruption
- : Percentage of unit fortified cost for module instance fortified to level t to its unit purchase cost
- : Percentage of the supply quantity of module instance corresponding to fortified level t to its order quantity while supplier v fails
- : Fixed GHG emission of intra-manufacturer for a product family which has J product variants
- : Variable unit GHG emission of intra-manufacturer for module instance
- : Binary variable to indicate whether the supplier v to disruption occurs in scenario s
- : The targeted profit based on the -percentile of total profit, i.e., in of scenarios, the outcome does not exceed (Value-at-risk of profit)
- 4.
- Decision variables
- : Binary decision variable to indicate whether module instance has been selected in variant j
- : Binary decision variable to indicate whether supplier v is preferred supplier for module instance
- : Binary decision variable to indicate whether the module instance is fortified to level t
3.3. Customer Preference and Demand Analysis
3.4. Disruption and Delivery
3.5. Risk-Neutral Model
3.5.1. Modeling Product Family Cost
3.5.2. GHG Emission Model of Product Family
3.5.3. Optimization Model
3.6. Risk-Averse Model
4. Algorithm Design
5. Case Study
5.1. Case Description
5.2. Results and Analysis
5.2.1. The Convergence of NSGA-II
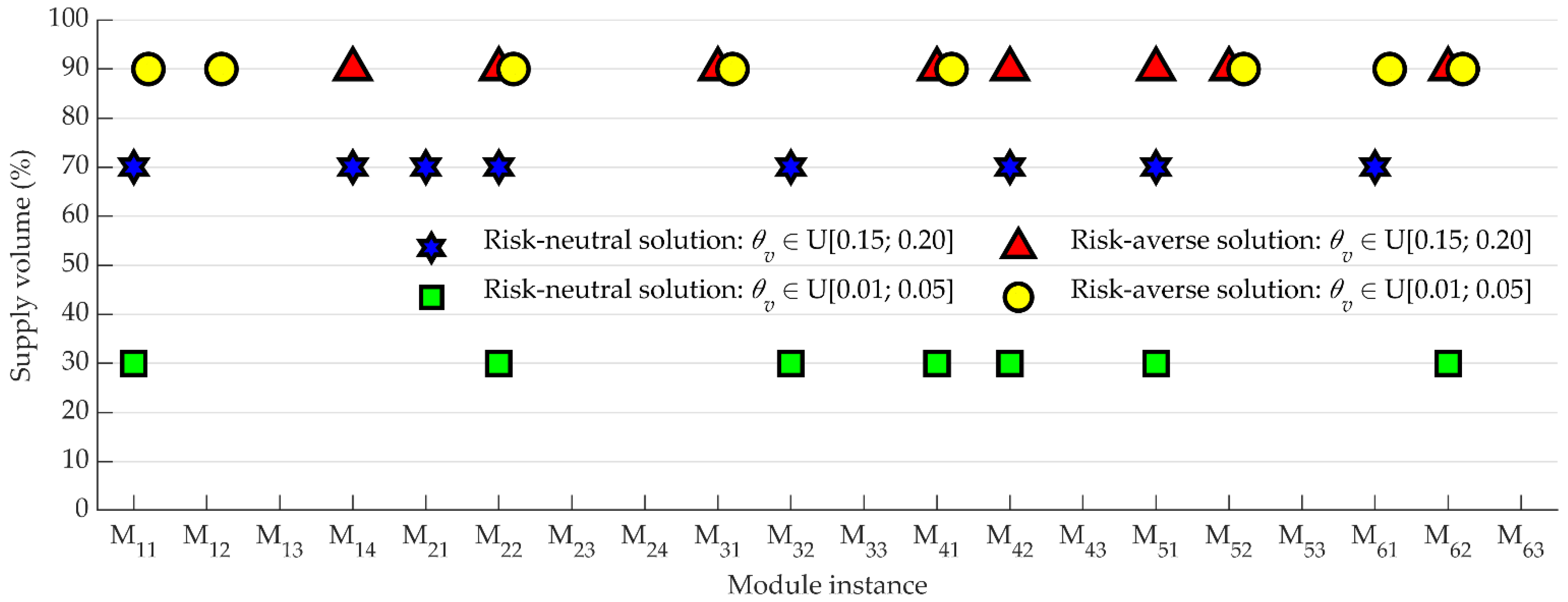
5.2.2. Influence of Disruption Probability on Results
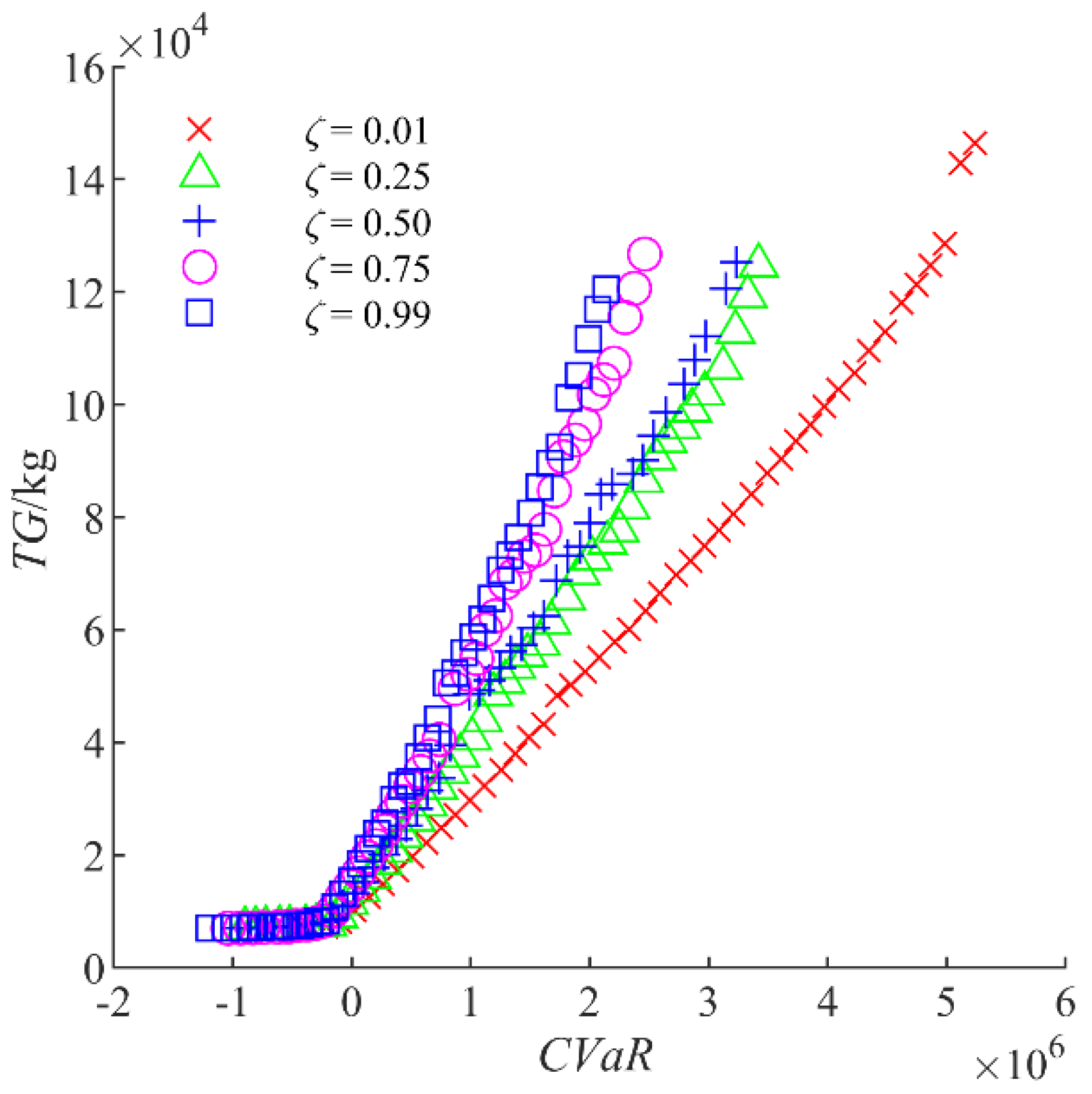
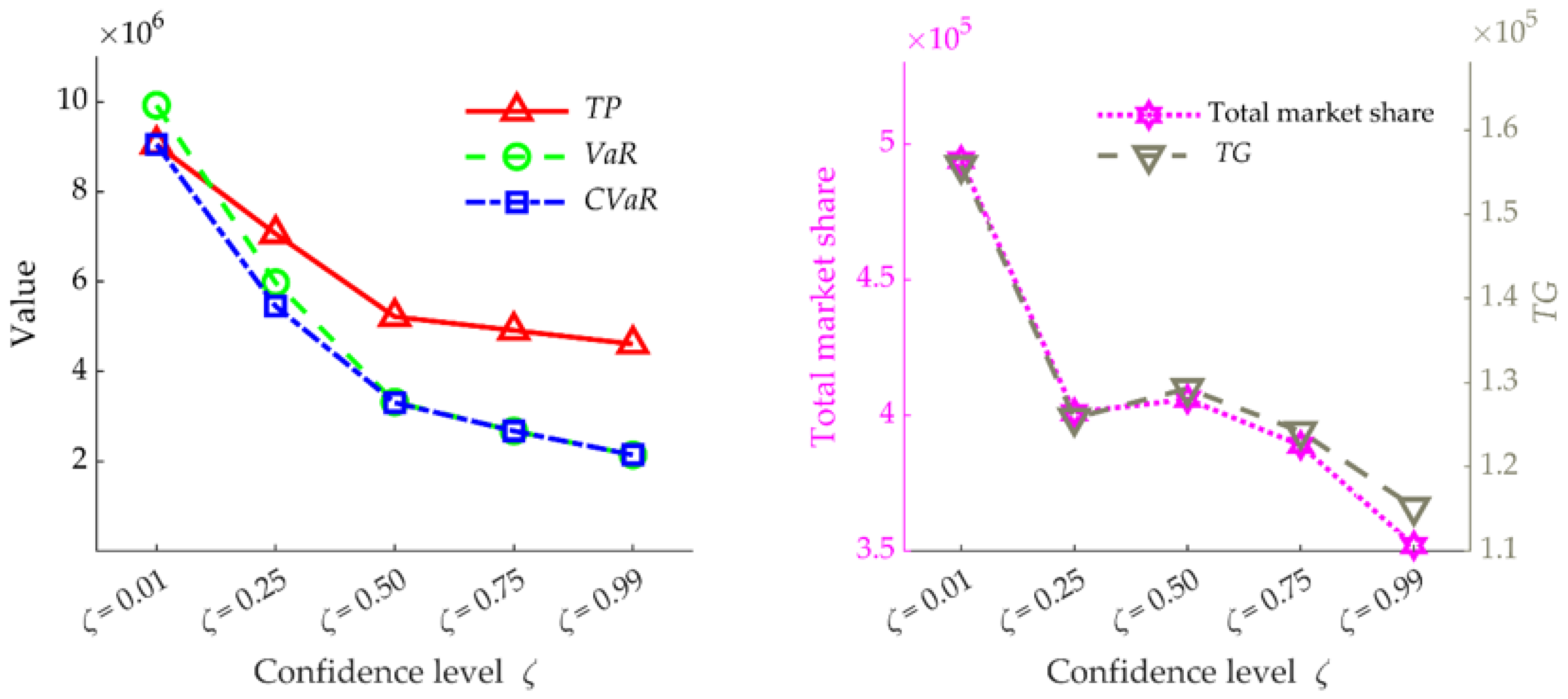
5.2.3. Influence of Confidence Level on the Risk-Averse Solutions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, C.; Tomlin, B. The Power of Flexibility for Mitigating Supply Chain Risks. Int. J. Prod. Econ. 2008, 116, 12–27. [Google Scholar] [CrossRef] [Green Version]
- Pakseresht, M.; Mahdavi, I.; Shirazi, B.; Mahdavi-Amiri, N. Co-reconfiguration of product family and supply chain using leader–follower Stackelberg game theory: Bi-level multi-objective optimization. Appl. Soft Comput. 2020, 91, 106203. [Google Scholar] [CrossRef]
- Rajak, S.; Mathiyazhagan, K.; Agarwal, V.; Sivakumar, K.; Kumar, V.; Appolloni, A. Issues and analysis of critical success factors for the sustainable initiatives in the supply chain during COVID-19 pandemic outbreak in India: A case study. Res. Transp. Econ. 2021, 101114. [Google Scholar] [CrossRef]
- Luo, X.; Li, W.; Kwong, C.; Cao, Y. Optimisation of product family design with consideration of supply risk and discount. Res. Eng. Des. 2016, 27, 37–54. [Google Scholar] [CrossRef]
- Rezapour, S.; Farahani, R.Z.; Pourakbar, M. Resilient supply chain network design under competition: A case study. Eur. J. Oper. Res. 2017, 259, 1017–1035. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.-H. A fuzzy multi-objective programming approach for determination of resilient supply portfolio under supply failure risks. J. Purch. Supply Manag. 2017, 23, 211–220. [Google Scholar] [CrossRef]
- Shahzad, M.; Qu, Y.; Zafar, A.U.; Appolloni, A. Does the interaction between the knowledge management process and sustainable development practices boost corporate green innovation? Bus. Strategy Environ. 2021, 30, 4206–4222. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, D.; Yin, L.; Ullah, I.; Salido, M.A.; Giret, A. An Optimization Method for Coordinating Supplier Selection and Low-Carbon Design of Product Family. Int. J. Precis. Eng. Manuf. 2018, 19, 1715–1726. [Google Scholar] [CrossRef]
- Huang, F.Y.; He, J.; Lei, Q. Coordination in a retailer-dominated supply chain with a risk-averse manufacturer under mar-keting dependency. Int. Trans. Oper. Res. 2020, 27, 3056–3078. [Google Scholar] [CrossRef]
- An, J.; Mikhaylov, A.; Jung, S.-U. A Linear Programming approach for robust network revenue management in the airline industry. J. Air Transp. Manag. 2020, 91, 101979. [Google Scholar] [CrossRef]
- Talaei, M.; Moghaddam, B.F.; Pishvaee, M.S.; Bozorgi-Amiri, A.; Gholamnejad, S. A robust fuzzy optimization model for carbon-efficient closed-loop supply chain network design problem: A numerical illustration in electronics industry. J. Clean. Prod. 2016, 113, 662–673. [Google Scholar] [CrossRef]
- Farrokh, M.; Azar, A.; Jandaghi, G.; Ahmadi, E. A novel robust fuzzy stochastic programming for closed loop supply chain network design under hybrid uncertainty. Fuzzy Sets Syst. 2018, 341, 69–91. [Google Scholar] [CrossRef]
- Ramezani, M.; Bashiri, M.; Tavakkoli-Moghaddam, R. A robust design for a closed-loop supply chain network under an uncertain environment. Int. J. Adv. Manuf. Technol. 2012, 66, 825–843. [Google Scholar] [CrossRef]
- Berger, P.D.; Gerstenfeld, A.; Zeng, A.Z. How many suppliers are best? A decision-analysis approach. Omega-Int. J. Manag. Sci. 2004, 32, 9–15. [Google Scholar] [CrossRef]
- Ruiz-Torres, A.J.; Mahmoodi, F. The optimal number of suppliers considering the costs of individual supplier failures. Omega-Int. J. Manag. Sci. 2007, 35, 104–115. [Google Scholar] [CrossRef]
- Madadi, A.; Kurz, M.E.; Taaffe, K.M.; Sharp, J.L.; Mason, S.J. Supply network design: Risk-averse or risk-neutral? Comput. Ind. Eng. 2014, 78, 55–65. [Google Scholar] [CrossRef]
- Luo, X.; Kwong, C.; Tang, J.; Deng, S.; Gong, J. Integrating supplier selection in optimal product family design. Int. J. Prod. Res. 2011, 49, 4195–4222. [Google Scholar] [CrossRef]
- Cao, Y.; Luo, X.G.; Kwong, C.K.; Tang, J.F.; Zhou, W. Joint optimization of product family design and supplier selection under multinomial logit consumer choice rule. Concurr. Eng. 2012, 20, 335–347. [Google Scholar] [CrossRef]
- Liu, X.; Du, G.; Jiao, R.J.; Xia, Y. Co-evolution of product family configuration and supplier selection: A game-theoretic bilevel optimisation approach. J. Eng. Des. 2018, 29, 201–234. [Google Scholar] [CrossRef]
- Olivares-Aguila, J.; ElMaraghy, H. Co-development of product and supplier platform. J. Manuf. Syst. 2020, 54, 372–385. [Google Scholar] [CrossRef]
- Liu, D.Z.; Li, Z.K. Joint decision-making of product family configuration and order allocation by coordinating suppliers under disruption risks. J. Eng. Des. 2021, 32, 213–246. [Google Scholar] [CrossRef]
- Tang, C.S. Perspectives in supply chain risk management. Int. J. Prod. Econ. 2006, 103, 451–488. [Google Scholar] [CrossRef]
- Yu, H.; Zeng, A.Z.; Zhao, L. Single or dual sourcing: Decision-making in the presence of supply chain disruption risks. Omega-Int. J. Manag. Sci. 2009, 37, 788–800. [Google Scholar] [CrossRef]
- Hou, J.; Zeng, A.Z.; Zhao, L. Coordination with a backup supplier through buy-back contract under supply disruption. Transp. Res. Part E Logist. Transp. Rev. 2010, 46, 881–895. [Google Scholar] [CrossRef]
- Sawik, T. Selection of resilient supply portfolio under disruption risks. Omega 2013, 41, 259–269. [Google Scholar] [CrossRef]
- Torabi, S.A.; Baghersad, M.; Mansouri, A. Resilient supplier selection and order allocation under operational and disruption risks. Transp. Res. Part E Logist. Transp. Rev. 2015, 79, 22–48. [Google Scholar] [CrossRef]
- Esmaeili-Najafabadi, E.; Nezhad, M.S.F.; Pourmohammadi, H.; Honarvar, M.; VahdatZad, M.A. A joint supplier selection and order allocation model with disruption risks in centralized supply chain. Comput. Ind. Eng. 2019, 127, 734–748. [Google Scholar] [CrossRef]
- Kim, Y.S.; Jiang, D.; Stoyanov, S. Long and Short Memory in the Risk-Neutral Pricing Process. J. Deriv. 2019, 26, 71–88. [Google Scholar] [CrossRef]
- Parada-Contzen, M.V. The Value of a Statistical Life for Risk-Averse and Risk-Seeking Individuals. Risk Anal. 2019, 39, 2369–2390. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Yin, Z. Using backup supply with responsive pricing to mitigate disruption risk for a risk-averse firm. Int. J. Prod. Res. 2017, 56, 5660–5676. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.; Yang, P. Robust equilibrium control-measure policy for a DC pension plan with state-dependent risk aversion under mean-variance criterion. J. Ind. Manag. Optim. 2021, 17, 1203–1233. [Google Scholar] [CrossRef] [Green Version]
- Devjak, S.; Bogataj, L. Portfolio Optimisation Using Mean Absolute Deviation as a Risk Measure in Risk Management Process; Department of Mathematics, University of Osijek: Osijek, Croatia, 2005; pp. 223–231. [Google Scholar]
- Tan, Z.; Wang, G.; Ju, L.; Tan, Q.; Yang, W. Application of CVaR risk aversion approach in the dynamical scheduling optimization model for virtual power plant connected with wind-photovoltaic-energy storage system with uncertainties and demand response. Energy 2017, 124, 198–213. [Google Scholar] [CrossRef] [Green Version]
- Khishtandar, S. Simulation based evolutionary algorithms for fuzzy chance-constrained biogas supply chain design. Appl. Energy 2019, 236, 183–195. [Google Scholar] [CrossRef]
- Tulli, V.; Gallegati, M.; Weinrich, G. Financial conditions and supply decisions when firms are risk averse. J. Econ. 2019, 128, 259–289. [Google Scholar] [CrossRef]
- Rahimi, M.; Ghezavati, V.; Asadi, F. A stochastic risk-averse sustainable supply chain network design problem with quantity discount considering multiple sources of uncertainty. Comput. Ind. Eng. 2019, 130, 430–449. [Google Scholar] [CrossRef]
- Sawik, T. On the risk-averse optimization of service level in a supply chain under disruption risks. Int. J. Prod. Res. 2015, 54, 98–113. [Google Scholar] [CrossRef]
- Fan, Y.; Feng, Y.; Shou, Y. A risk-averse and buyer-led supply chain under option contract: CVaR minimization and channel coordination. Int. J. Prod. Econ. 2020, 219, 66–81. [Google Scholar] [CrossRef]
- Tao, L.; Liu, S.; Xie, N.; Javed, S.A. Optimal position of supply chain delivery window with risk-averse suppliers: A CVaR optimization approach. Int. J. Prod. Econ. 2021, 232, 107989. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, H.; Liu, W.; Song, S.; Liao, Y. Supply Chain Coordination with a Risk-Averse Retailer and the Call Option Contract in the Presence of a Service Requirement. Mathematics 2021, 9, 787. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; Lerman, S. Discrete Choice Analysis: Theory and Application to Travel Demand; The MIT Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Train, K. Discrete Choice Methods with Simulation; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Dupont, L.; Bernard, C.; Hamdi, F.; Masmoudi, F. Supplier selection under risk of delivery failure: A decision-support model considering managers’ risk sensitivity. Int. J. Prod. Res. 2017, 56, 1054–1069. [Google Scholar] [CrossRef]
- Fruchter, G.E.; Fligler, A.; Winer, R.S. Optimal Product Line Design: Genetic Algorithm Approach to Mitigate Cannibalization. J. Optim. Theory Appl. 2006, 131, 227–244. [Google Scholar] [CrossRef]
- Green, P.E.; Krieger, A.M. An Application of a Product Positioning Model to Pharmaceutical Products. Mark. Sci. 1992, 11, 117–132. [Google Scholar] [CrossRef]
- Magazzino, C.; Mele, M.; Schneider, N. The relationship between municipal solid waste and greenhouse gas emissions: Evidence from Switzerland. Waste Manag. 2020, 113, 508–520. [Google Scholar] [CrossRef] [PubMed]
- Ruszczynski, A.; Shapiro, A. Optimization of convex risk functions. Math. Oper. Res. 2006, 31, 433–452. [Google Scholar] [CrossRef] [Green Version]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2000, 2, 21–41. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| From literature [8] | |||
| From literature [8] | 1500 | ||
| 400,000 | |||
| Supplier | The Fortified Cost Percentage [The Supply Volume Percentage | Disruption Probability | ||||
|---|---|---|---|---|---|---|
| Level 0 | Level 1 | Level 2 | Level 3 | Level 4 | ||
| 1 | 40 [0] | 50 [12] | 60 [24] | 70 [36] | / | 0.17 |
| 2 | 50 [0] | 60 [16] | 70 [32] | / | / | 0.20 |
| 3 | 50 [0] | 70 [28] | / | / | / | 0.16 |
| 4 | 30 [0] | 40 [7.2] | 50 [14.4] | 60 [21.6] | 70 [28.8] | 0.17 |
| 5 | 40 [0] | 50 [10.4] | 60 [20.8] | 70 [31.2] | 80 [41.6] | 0.16 |
| 6 | 50 [0] | 60 [15.2] | 70 [30.4] | 80 [45.6] | / | 0.19 |
| 7 | 40 [0] | 60 [16] | 80 [32] | / | / | 0.18 |
| 8 | 30 [0] | 50 [14.4] | 70 [28.8] | 90 [43.2] | / | 0.18 |
| 9 | 50 [0] | 70 [21.6] | 90 [43.2] | / | / | 0.20 |
| 10 | 40 [0] | 50 [13.6] | 60 [27.2] | 80 [40.8] | / | 0.15 |
| 11 | 30 [0] | 60 [20] | 90 [40] | / | / | 0.16 |
| 12 | 30 [0] | 45 [11.2] | 60 [22.4] | 75 [33.6] | 90 [44.8] | 0.20 |
| Item | Module | Price ($) | Demand (×102) | TP (×103) | TG (×102) | 0.99-VaR (×103) | 0.99-CVaR (×103) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | |||||||||||
| θv ∈ U[0.15; 0.20] | ||||||||||||||||
| Product configuration | Variant 1 | M11 | M21 | M32 | M42 | M51 | M61 | 74 | 366 | 5351 | 1496 | −1438 | −1438 | |||
| Variant 2 | M14 | M22 | M32 | M42 | M51 | M61 | 77 | 107 | ||||||||
| Supplier | 8 | 8 | 2 | 2 | 8 | 2 | 8 | 2 | ||||||||
| (Fortified level) | (2) | (2) | (2) | (2) | (2) | (2) | (2) | (2) | ||||||||
| θv ∈ U[0.01; 0.05] | ||||||||||||||||
| Product configuration | Variant 1 | M11 | M22 | M32 | M42 | M51 | M62 | 74 | 263 | 9071 | 1566 | −16182 | −16182 | |||
| Variant 2 | M11 | M22 | M32 | M41 | M51 | M62 | 74 | 234 | ||||||||
| Supplier | 8 | 11 | 8 | 11 | 11 | 8 | 8 | |||||||||
| (Fortified level) | (0) | (0) | (0) | (0) | (0) | (0) | (0) | |||||||||
| Item | Module | Price ($) | Demand (×102) | TP (×103) | TG (×102) | 0.99-VaR (×103) | 0.99-CVaR (×103) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | M5 | M6 | ||||||||||||
| θv ∈ U[0.15; 0.20] | |||||||||||||||||
| Product configuration | Variant 1 | M14 | M22 | M31 | M42 | M51 | M62 | 77 | 192 | 4438 | 1338 | 2191 | 2191 | ||||
| Variant 2 | M14 | M22 | M31 | M41 | M52 | M62 | 77 | 226 | |||||||||
| Supplier | 8 | 11 | 8 | 11 | 9 | 8 | 9 | 8 | |||||||||
| (Fortified level) | (3) | (2) | (3) | (2) | (2) | (3) | (2) | (3) | |||||||||
| θv ∈ U[0.01; 0.05] | |||||||||||||||||
| Product configuration | Variant 1 | M12 | M22 | M31 | M41 | M52 | M61 | 77 | 190 | 4608 | 1152 | 2140 | 2140 | ||||
| Variant 2 | M11 | M22 | M31 | M41 | M52 | M62 | 77 | 162 | |||||||||
| Supplier | 8 | 8 | 12 | 8 | 9 | 9 | 12 | 8 | |||||||||
| (Fortified level) | (3) | (3) | (4) | (3) | (2) | (2) | (4) | (3) | |||||||||
| Item | Confidence Level ζ | ||||
|---|---|---|---|---|---|
| 0.01 | 0.25 | 0.50 | 0.75 | 0.99 | |
| θv ∈ U[0.15; 0.20] | |||||
| Price [P1; P2] | [74; 77] | [77; 77] | [77; 77] | [77; 77] | [77; 77] |
| Market share [d1; d2] (×103) | [366; 107] | [185; 220] | [159; 247] | [196; 226] | 192; 226 |
| TP (×103) | 5351 | 4329 | 4406 | 4438 | 4438 |
| TG (×102) | 1496 | 1268 | 1286 | 1338 | 1338 |
| VaR (×103) | 8579 | 3645 | 3368 | 2577 | 2191 |
| CVaR (×103) | 5351 | 3463 | 3257 | 2537 | 2191 |
| θv ∈ U[0.01; 0.15] | |||||
| Price [P1; P2] | [74; 74] | [77; 77] | [77; 77] | [77; 77] | [77; 77] |
| Market share [d1; d2] (×103) | [175; 319] | [176; 225] | [258; 147] | [127; 262] | [190; 162] |
| TP (×103) | 9051 | 7062 | 5216 | 4912 | 4608 |
| TG (×102) | 1558 | 1258 | 1293 | 1242 | 1152 |
| VaR (×103) | 9923 | 5975 | 3317 | 2673 | 2140 |
| CVaR (×103) | 9051 | 5450 | 3303 | 2673 | 2140 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Li, Z.; He, C.; Wang, S. Risk-Averse Co-Decision for Lower-Carbon Product Family Configuration and Resilient Supplier Selection. Sustainability 2022, 14, 384. https://doi.org/10.3390/su14010384
Liu D, Li Z, He C, Wang S. Risk-Averse Co-Decision for Lower-Carbon Product Family Configuration and Resilient Supplier Selection. Sustainability. 2022; 14(1):384. https://doi.org/10.3390/su14010384
Chicago/Turabian StyleLiu, Dengzhuo, Zhongkai Li, Chao He, and Shuai Wang. 2022. "Risk-Averse Co-Decision for Lower-Carbon Product Family Configuration and Resilient Supplier Selection" Sustainability 14, no. 1: 384. https://doi.org/10.3390/su14010384






