Assessment of Variations in Runoff Due to Landcover Changes Using the SWAT Model in an Urban River in Dublin, Ireland
Abstract
:1. Introduction
2. Methodology
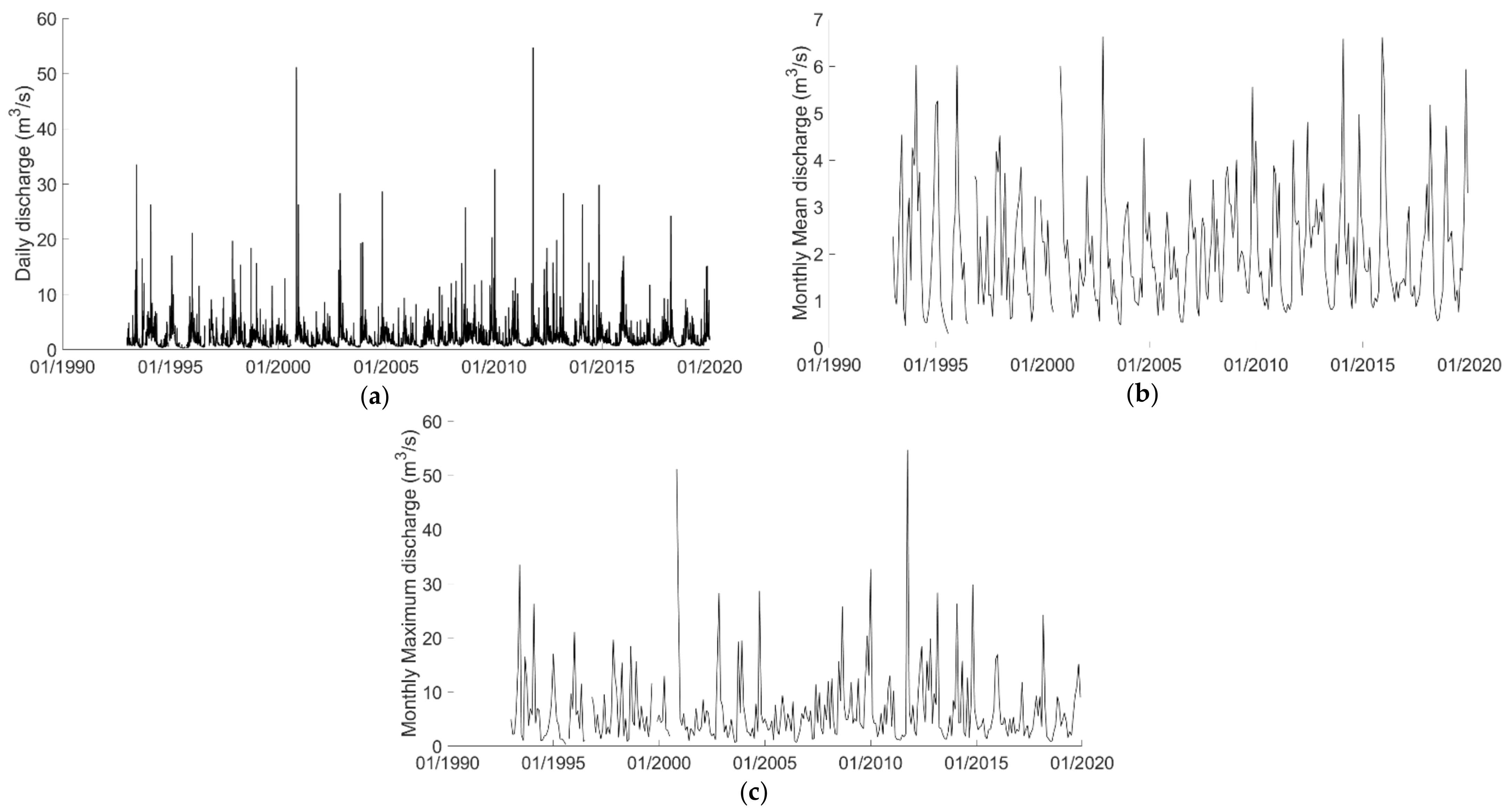
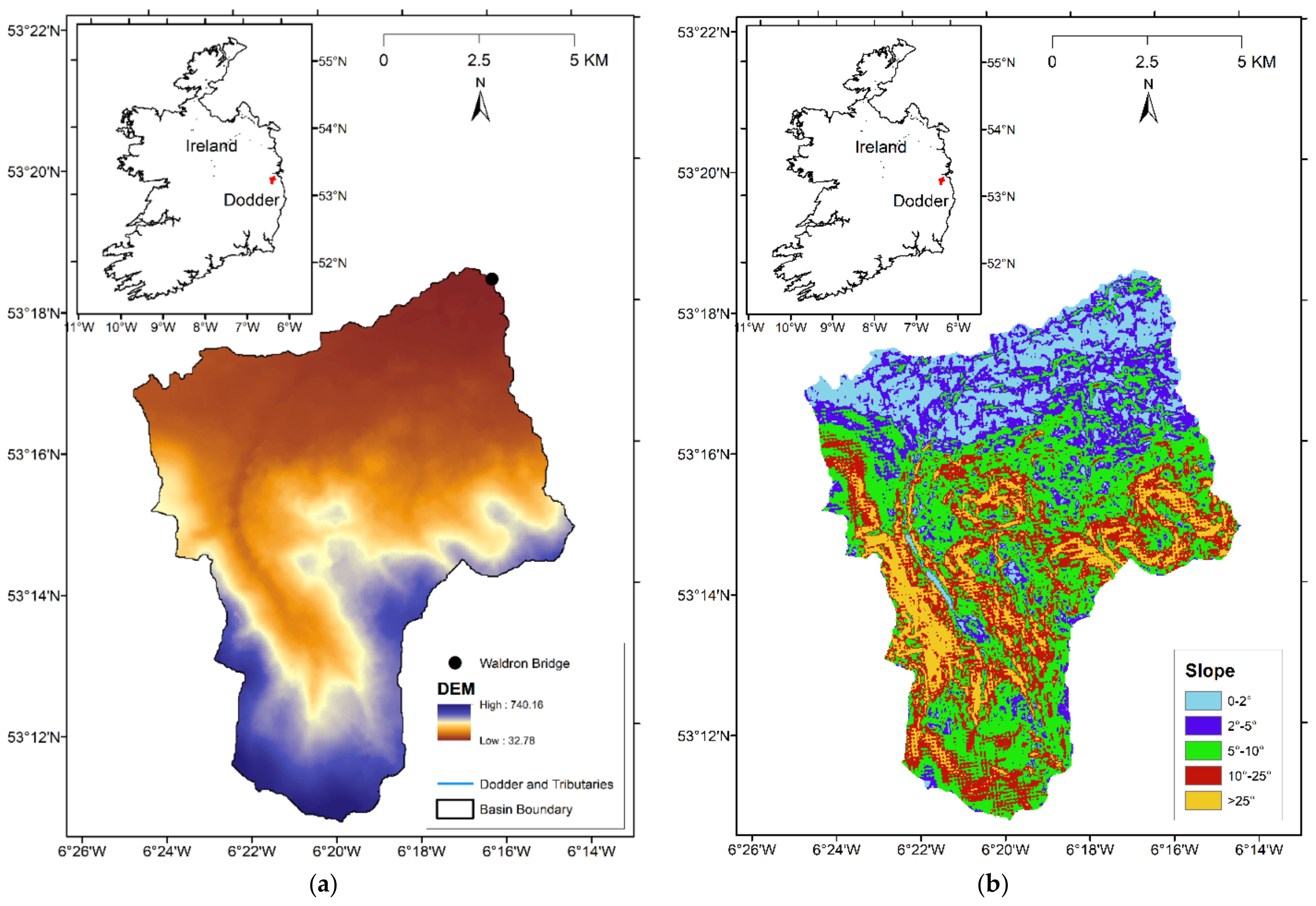
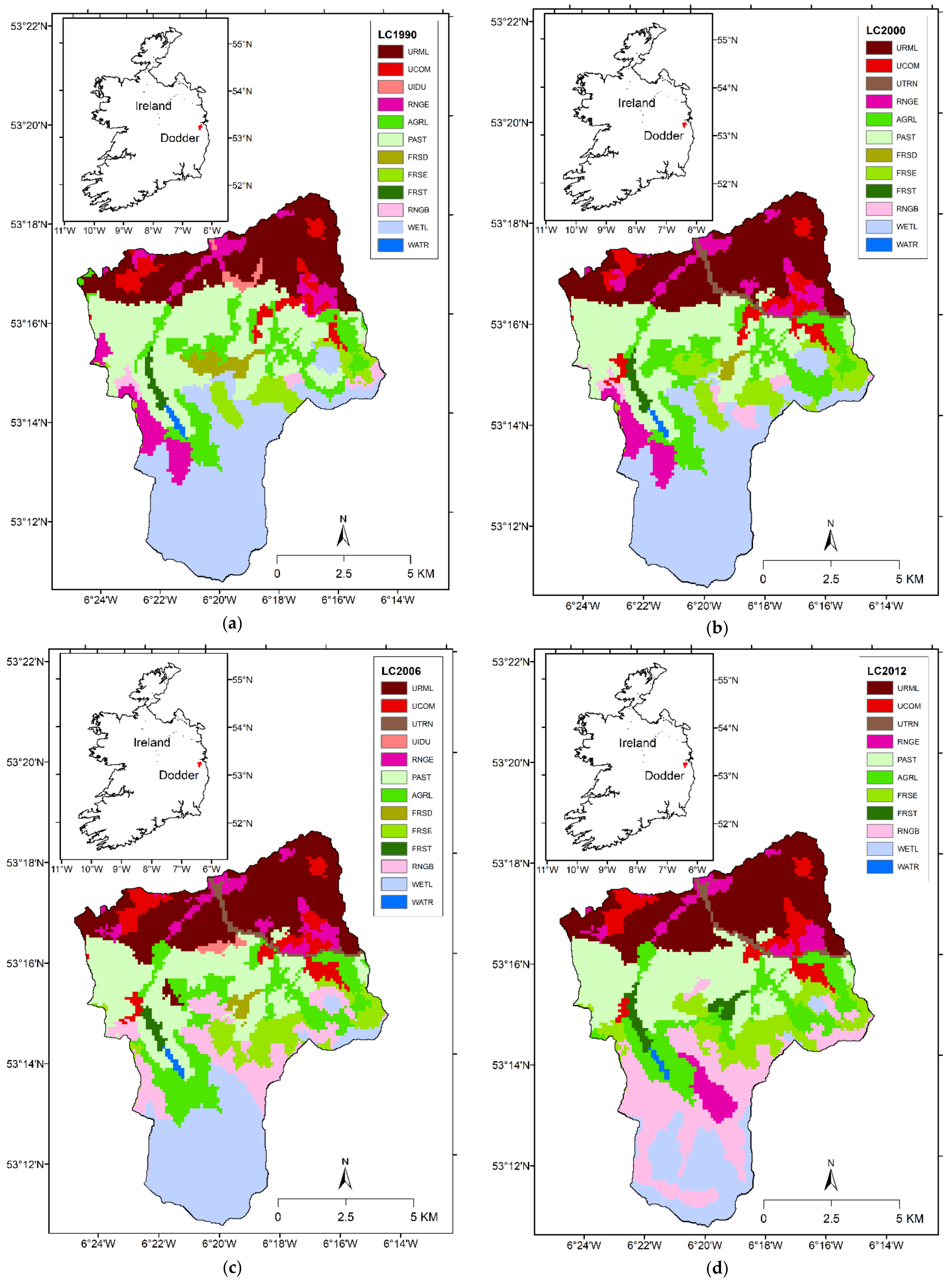
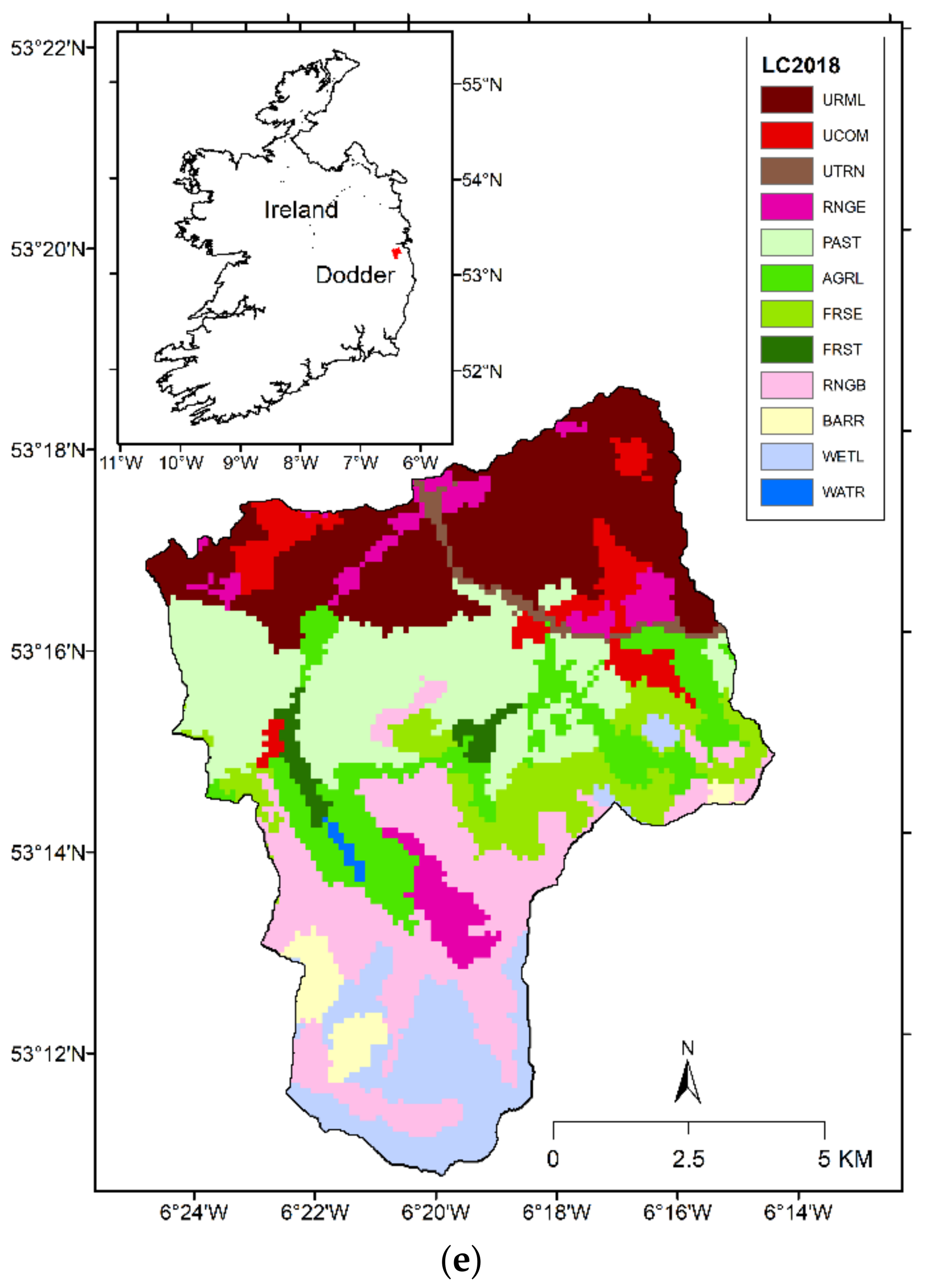
2.1. River Basin and Data Description
2.2. Soil Water Assessment Tool (SWAT) Model and Performance Evaluation
2.3. Kappa and Generalized Extreme Value Distribution
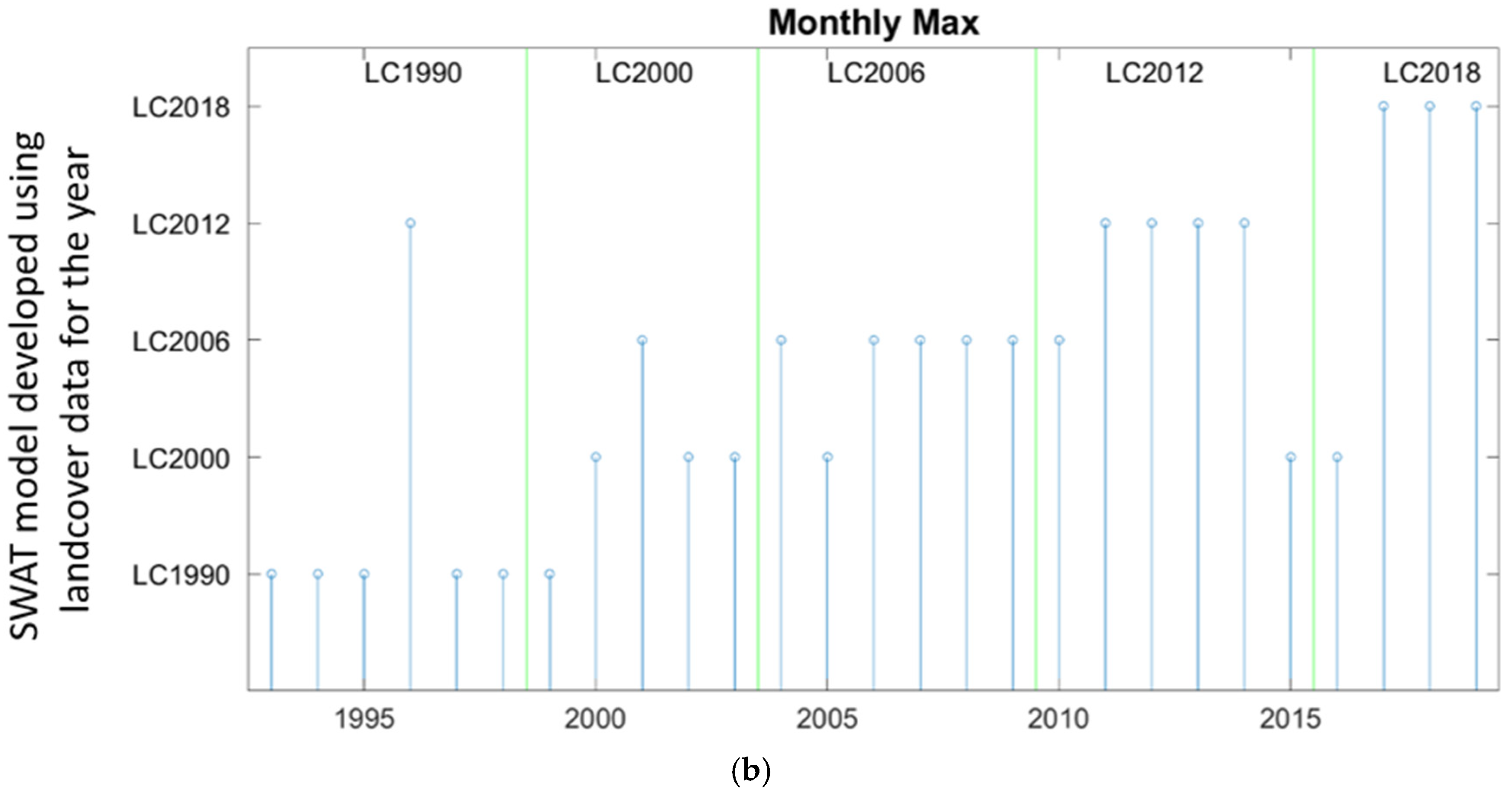
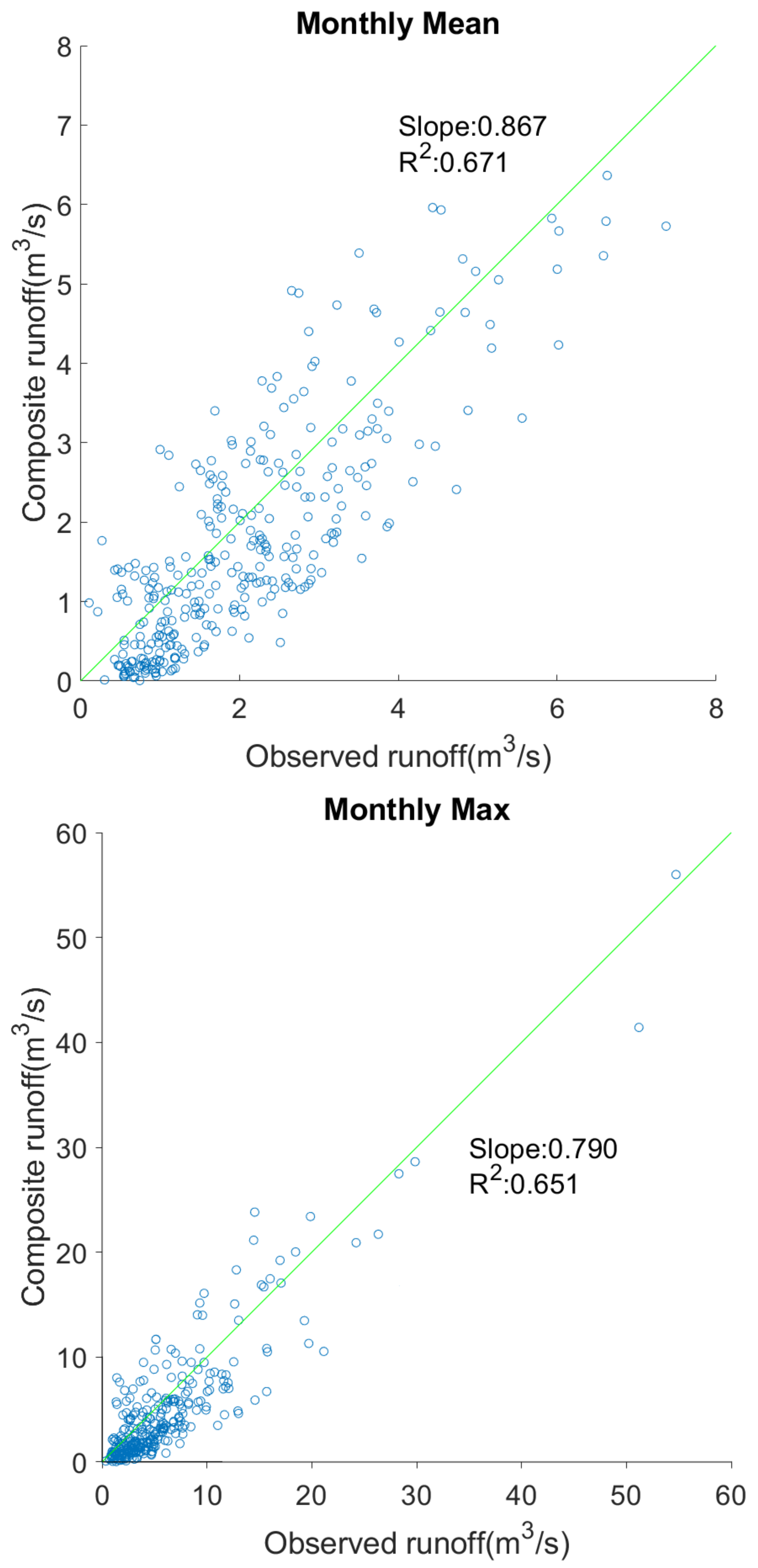
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ye, X.; Zhang, Q.; Liu, J.; Li, X.; Xu, C.Y. Distinguishing the relative impacts of climate change and human activities on variation of streamflow in the Poyang Lake catchment, China. J. Hydrol. 2013, 494, 83–95. [Google Scholar] [CrossRef]
- Viero, D.P.; Roder, G.; Matticchio, B.; Defina, A.; Tarolli, P. Floods, landscape modifications and population dynamics in anthropogenic coastal lowlands: The Polesine (northern Italy) case study. Sci. Total Environ. 2019, 651, 1435–1450. [Google Scholar] [CrossRef]
- Mahmoud, S.H.; Gan, T.Y. Urbanization and climate change implications in flood risk management: Developing an efficient decision support system for flood susceptibility mapping. Sci. Total Environ. 2018, 636, 152–167. [Google Scholar] [CrossRef]
- Miller, J.D.; Hutchins, M. The impacts of urbanisation and climate change on urban flooding and urban water quality: A review of the evidence concerning the United Kingdom. J. Hydrol. Reg. Stud. 2017, 12, 345–362. [Google Scholar] [CrossRef] [Green Version]
- Erena, S.H.; Worku, H. Dynamics of land use land cover and resulting surface runoff management for environmental flood hazard mitigation: The case of Dire Daw city, Ethiopia. J. Hydrol. Reg. Stud. 2019, 22, 100598. [Google Scholar] [CrossRef]
- Shuster, W.D.; Bonta, J.; Thurston, H.; Warnemuende, E.; Smith, D.R. Impacts of impervious surface on watershed hydrology: A review. Urban Water J. 2005, 2, 263–275. [Google Scholar] [CrossRef]
- Locatelli, L.; Mark, O.; Mikkelsen, P.S.; Arnbjerg-Nielsen, K.; Deletic, A.; Roldin, M.; Binning, P.J. Hydrologic impact of urbanization with extensive stormwater infiltration. J. Hydrol. 2017, 544, 524–537. [Google Scholar] [CrossRef] [Green Version]
- Borrelli, P.; Robinson, D.A.; Fleischer, L.R.; Lugato, E.; Ballabio, C.; Alewell, C.; Meusburger, K.; Modugno, S.; Schütt, B.; Ferro, V.; et al. An assessment of the global impact of 21st century land use change on soil erosion. Nat. Commun. 2017, 8, 2013. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Kanae, S.; Oki, T.; Koike, T.; Musiake, K. Global potential soil erosion with reference to land use and climate changes. Hydrol. Process. 2003, 17, 2913–2928. [Google Scholar] [CrossRef]
- Tibebe, D.; Bewket, W. Surface runoff and soil erosion estimation using the SWAT model in the Keleta watershed, Ethiopia. Land Degrad. Dev. 2011, 22, 551–564. [Google Scholar] [CrossRef]
- Rodriguez, F.; Andrieu, H.; Creutin, J.D. Surface runoff in urban catchments: Morphological identification of unit hydrographs from urban databanks. J. Hydrol. 2003, 283, 146–168. [Google Scholar] [CrossRef]
- Cheng, S.J.; Wang, R.Y. An approach for evaluating the hydrological effects of urbanization and its application. Hydrol. Process. 2002, 16, 1403–1418. [Google Scholar] [CrossRef]
- Beven, K.J.; Wood, E.F.; Sivapalan, M. On hydrological heterogeneity—catchment morphology and catchment response. J. Hydrol. 1988, 100, 353–375. [Google Scholar] [CrossRef]
- Karamage, F.; Zhang, C.; Fang, X.; Liu, T.; Ndayisaba, F.; Nahayo, L.; Kayiranga, A.; Nsengiyumva, J.B. Modeling rainfall-runoff response to land use and land cover change in Rwanda (1990–2016). Water 2017, 9, 147. [Google Scholar] [CrossRef] [Green Version]
- Gwate, O.; Woyessa, Y.E.; Wiberg, D. Dynamics of land cover and impact on stream flow in the Modder River Basin of South Africa: Case study of a Quaternary Catchment. Int. J. Environ. Prot. Policy 2015, 3, 31–38. [Google Scholar] [CrossRef]
- Niemi, T.J.; Kokkonen, T.; Sillanpää, N.; Setälä, H.; Koivusalo, H. Automated Urban Rainfall–Runoff Model Generation with Detailed Land Cover and Flow Routing. J. Hydrol. Eng. 2019, 24, 04019011. [Google Scholar] [CrossRef] [Green Version]
- White, M.D.; Greer, K.A. The effects of watershed urbanization on the stream hydrology and riparian vegetation of Los Penasquitos Creek, California. Landsc. Urban Plan. 2006, 74, 125–138. [Google Scholar] [CrossRef]
- Costa, M.H.; Botta, A.; Cardille, J.A. Effects of large-scale changes in land cover on the discharge of the Tocantins River, Southeastern Amazonia. J. Hydrol. 2003, 283, 206–217. [Google Scholar] [CrossRef]
- De Oliveira, T.E.; de Freitas, D.S.; Gianezini, M.; Ruviaro, C.F.; Zago, D.; Mércio, T.Z.; Dias, E.A.; do Nascimento Lampert, V.; Barcellos, J.O.J. Agricultural land use change in the Brazilian Pampa Biome: The reduction of natural grasslands. Land Use Policy 2017, 63, 394–400. [Google Scholar] [CrossRef]
- Wachiye, S.A.; Kuria, D.N.; Musiega, D. GIS based forest cover change and vulnerability analysis: A case study of the Nandi North forest zone. J. Geogr. Reg. Plan. 2013, 6, 159–171. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Feng, Q.; Yin, Z.; Wen, X.; Si, J.; Li, C.; Deo, R.C. Identifying separate impacts of climate and land use/cover change on hydrological processes in upper stream of Heihe River, Northwest China. Hydrol. Process. 2017, 31, 1100–1112. [Google Scholar] [CrossRef]
- Yang, L.; Feng, Q.; Yin, Z.; Deo, R.C.; Wen, X.; Si, J.; Li, C. Separation of the climatic and land cover impacts on the flow regime changes in two watersheds of Northeastern Tibetan Plateau. Adv. Meteorol. 2017, 2017, 6310401. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.M.; Roostaei, S.; Rostamzadeh, H. Estimation of flood land use/land cover mapping by regional modelling of flood hazard at sub-basin level case study: Marand basin. Geomat. Nat. Hazards Risk 2019, 10, 1155–1175. [Google Scholar] [CrossRef] [Green Version]
- Kaźmierczak, A.; Cavan, G. Surface water flooding risk to urban communities: Analysis of vulnerability, hazard and exposure. Landsc. Urban Plan. 2011, 103, 185–197. [Google Scholar] [CrossRef]
- Diaz-Pacheco, J.; Gutiérrez, J. Exploring the limitations of CORINE Land Cover for monitoring urban land-use dynamics in metropolitan areas. J. Land Use Sci. 2014, 9, 243–259. [Google Scholar] [CrossRef]
- Bajocco, S.; De Angelis, A.; Perini, L.; Ferrara, A.; Salvati, L. The impact of land use/land cover changes on land degradation dynamics: A Mediterranean case study. Environ. Manag. 2012, 49, 980–989. [Google Scholar] [CrossRef]
- Kleeschulte, S.; Büttner, G. European land cover mapping–the CORINE experience. In Proceedings of the North America Land Cover Summit, Washington, DC, USA, 20–22 September 2006; pp. 31–44. [Google Scholar]
- Cieślak, I.; Biłozor, A.; Szuniewicz, K. The use of the CORINE land cover (CLC) database for analyzing urban sprawl. Remote Sens. 2020, 12, 282. [Google Scholar] [CrossRef] [Green Version]
- Kucsicsa, G.; Dumitrică, C. Spatial modelling of deforestation in Romanian Carpathian Mountains using GIS and Logistic Regression. J. Mt. Sci. 2019, 16, 1005–1022. [Google Scholar] [CrossRef]
- O’farrell, P.N.; Crouchley, R. An industrial and spatial analysis of new firm formation in Ireland. Reg. Stud. 1984, 18, 221–236. [Google Scholar] [CrossRef]
- Ahrens, A.; Lyons, S. Changes in land cover and urban sprawl in Ireland from a comparative perspective over 1990–2012. Land 2019, 8, 16. [Google Scholar] [CrossRef] [Green Version]
- Arribas-Bel, D.; Nijkamp, P.; Scholten, H. Multidimensional urban sprawl in Europe: A self-organizing map approach. Comput. Environ. Urban Syst. 2011, 35, 263–275. [Google Scholar] [CrossRef] [Green Version]
- Aurambout, J.P.; Barranco, R.; Lavalle, C. Towards a simpler characterization of urban sprawl across urban areas in Europe. Land 2018, 7, 33. [Google Scholar] [CrossRef] [Green Version]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Gras, D. EU-DEM Statistical Validation Report; European Environment Agency: Copenhagen, Denmark, 2014. [Google Scholar]
- Basu, B. Development of soil and land cover databases for use in the Soil Water Assessment Tool from Irish National Soil Maps and CORINE Land Cover Maps for Ireland. Earth Syst. Sci. Data Discuss. 2021; preprint, under review. [Google Scholar] [CrossRef]
- Basu, B. Soil, Landcover and DEM database for Ireland to be used with SWAT model. Zenodo 2021. [Google Scholar] [CrossRef]
- Nolan, P.; O’Sullivan, J.; McGrath, R. Impacts of climate change on mid-twenty-first-century rainfall in Ireland: A high-resolution regional climate model ensemble approach. Int. J. Climatol. 2017, 37, 4347–4363. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Bernhardt, G. A comprehensive surface-groundwater flow model. J. Hydrol. 1993, 142, 47–69. [Google Scholar] [CrossRef]
- Arnold, J.G.; Muttiah, R.S.; Srinivasan, R.; Allen, P.M. Regional estimation of base flow and groundwater recharge in the Upper Mississippi river basin. J. Hydrol. 2000, 227, 21–40. [Google Scholar] [CrossRef]
- Williams, J.R. Flood routing with variable travel time or variable storage coefficients. Trans. ASAE 1969, 12, 100–103. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Arnold, J.G.; Allen, P.M. Estimating hydrologic budgets for three Illinois watersheds. J. Hydrol. 1996, 176, 57–77. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; Volume 208, p. 208. [Google Scholar]
- Blum, A.G.; Archfield, S.A.; Vogel, R.M. On the probability distribution of daily streamflow in the United States. Hydrol. Earth Syst. Sci. 2017, 21, 3093–3103. [Google Scholar] [CrossRef] [Green Version]
- Svensson, C.; Hannaford, J.; Prosdocimi, I. Statistical distributions for monthly aggregations of precipitation and streamflow in drought indicator applications. Water Resour. Res. 2017, 53, 999–1018. [Google Scholar] [CrossRef] [Green Version]
- Langat, P.K.; Kumar, L.; Koech, R. Identification of the most suitable probability distribution models for maximum, minimum, and mean streamflow. Water 2019, 11, 734. [Google Scholar] [CrossRef] [Green Version]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Te Chow, V. Applied Hydrology; Tata McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]





| Sl. | Land Cover CODE | Land Cover Description | SWAT Class | Sl. | Land Cover CODE | Land Cover Description | SWAT Class |
|---|---|---|---|---|---|---|---|
| 1 | 111 | Continuous urban fabric | URBN | 23 | 311 | Broad-leaved forest | FRSD |
| 2 | 112 | Discontinuous urban fabric | URML | 24 | 312 | Coniferous forest | FRSE |
| 3 | 121 | Industrial or commercial units | UCOM | 25 | 313 | Mixed forest | FRST |
| 4 | 122 | Road and rail networks and associated land | UTRN | 26 | 321 | Natural grasslands | RNGE |
| 5 | 123 | Port areas | UTRN | 27 | 322 | Moors and heathland | RNGB |
| 6 | 124 | Airports | UTRN | 28 | 323 | Sclerophyllous vegetation | RNGB |
| 7 | 131 | Mineral extraction sites | SWRN | 29 | 324 | Transitional woodland-shrub | RNGB |
| 8 | 132 | Dump sites | UIDU | 30 | 331 | Beaches, dunes, sands | WETN |
| 9 | 133 | Construction sites | UIDU | 31 | 332 | Bare rocks | BARR |
| 10 | 141 | Green urban areas | RNGE | 32 | 333 | Sparsely vegetated areas | BARR |
| 11 | 142 | Sport and leisure facilities | UCOM | 33 | 334 | Burnt areas | BARR |
| 12 | 211 | Non-irrigated arable land | AGRL | 34 | 335 | Glaciers and perpetual snow | WATR |
| 13 | 212 | Permanently irrigated land | AGRL | 35 | 411 | Inland marshes | WETN |
| 14 | 213 | Rice fields | RICE | 36 | 412 | Peat bogs | WETL |
| 15 | 221 | Vineyards | GRAP | 37 | 421 | Salt marshes | WETL |
| 16 | 222 | Fruit trees and berry plantations | AGRL | 38 | 422 | Salines | WETL |
| 17 | 223 | Olive groves | OLIV | 39 | 423 | Intertidal flats | WETL |
| 18 | 231 | Pastures | PAST | 40 | 511 | Water courses | WATR |
| 19 | 241 | Annual crops associated with permanent crops | AGRL | 41 | 512 | Water bodies | WATR |
| 20 | 242 | Complex cultivation patterns | AGRL | 42 | 521 | Coastal lagoons | WATR |
| 21 | 243 | Land principally occupied by agriculture, with significant areas of natural vegetation | AGRL | 43 | 522 | Estuaries | WATR |
| 22 | 244 | Agro-forestry areas | FRST | 44 | 523 | Sea and ocean | WATR |
| Gauge Number | Location Details | Data Range | Available Variables | |
|---|---|---|---|---|
| Lat | Lon | |||
| S175 | 53.364 | −6.350 | 16/08/2003–31/12/2020 | R, T, RH, WS, SR |
| S1823 | 53.370 | −6.270 | 01/01/1984–31/10/2020 | R, T |
| S1923 | 53.239 | −6.367 | 01/01/1984–30/09/2014 | R |
| S3723 | 53.306 | −6.439 | 01/01/1964–31/10/2020 | R, T, RH, WS, SR |
| S3923 | 53.341 | −6.253 | 01/01/1948–31/10/2020 | R, T |
| S5623 | 53.239 | −6.364 | 01/10/1959–31/10/2020 | R |
| S6623 | 53.276 | −6.304 | 01/02/1967–31/10/2020 | R |
| S7523 | 53.325 | −6.225 | 01/08/1972–28/02/2015 | R |
| Year | (a) Monthly Mean Runoff | (b) Monthly Maximum Runoff | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LC1990 | LC2000 | LC2006 | LC2012 | LC2018 | LC1990 | LC2000 | LC2006 | LC2012 | LC2018 | |
| 1993 | 0.55 | 0.51 | 0.47 | 0.45 | 0.41 | 0.56 | 0.53 | 0.47 | 0.41 | 0.44 |
| 1994 | 0.85 | 0.77 | 0.80 | 0.82 | 0.74 | 0.58 | 0.46 | 0.49 | 0.55 | 0.52 |
| 1995 | 0.65 | 0.60 | 0.55 | 0.57 | 0.62 | 0.56 | 0.47 | 0.50 | 0.40 | 0.43 |
| 1996 | 0.52 | 0.43 | 0.49 | 0.54 | 0.46 | 0.52 | 0.43 | 0.47 | 0.55 | 0.49 |
| 1997 | 0.59 | 0.52 | 0.50 | 0.55 | 0.46 | 0.57 | 0.51 | 0.55 | 0.48 | 0.45 |
| 1998 | 0.54 | 0.47 | 0.44 | 0.51 | 0.41 | 0.52 | 0.48 | 0.42 | 0.45 | 0.38 |
| 1999 | 0.50 | 0.57 | 0.45 | 0.53 | 0.42 | 0.57 | 0.46 | 0.51 | 0.48 | 0.39 |
| 2000 | 0.80 | 0.83 | 0.77 | 0.71 | 0.75 | 0.82 | 0.91 | 0.85 | 0.79 | 0.88 |
| 2001 | 0.45 | 0.53 | 0.34 | 0.48 | 0.39 | 0.26 | 0.44 | 0.51 | 0.23 | 0.35 |
| 2002 | 0.77 | 0.74 | 0.71 | 0.79 | 0.82 | 0.43 | 0.55 | 0.50 | 0.39 | 0.47 |
| 2003 | 0.46 | 0.60 | 0.43 | 0.55 | 0.51 | 0.54 | 0.57 | 0.48 | 0.51 | 0.45 |
| 2004 | 0.54 | 0.46 | 0.58 | 0.51 | 0.43 | 0.57 | 0.53 | 0.66 | 0.60 | 0.63 |
| 2005 | 0.51 | 0.46 | 0.59 | 0.54 | 0.43 | 0.48 | 0.51 | 0.43 | 0.36 | 0.40 |
| 2006 | 0.47 | 0.39 | 0.52 | 0.44 | 0.36 | 0.53 | 0.40 | 0.56 | 0.51 | 0.45 |
| 2007 | 0.36 | 0.41 | 0.50 | 0.46 | 0.29 | 0.45 | 0.49 | 0.57 | 0.53 | 0.40 |
| 2008 | 0.58 | 0.43 | 0.52 | 0.47 | 0.39 | 0.48 | 0.43 | 0.51 | 0.45 | 0.39 |
| 2009 | 0.41 | 0.44 | 0.52 | 0.47 | 0.37 | 0.47 | 0.37 | 0.52 | 0.34 | 0.31 |
| 2010 | 0.48 | 0.44 | 0.41 | 0.50 | 0.38 | 0.44 | 0.49 | 0.55 | 0.52 | 0.46 |
| 2011 | 0.51 | 0.54 | 0.57 | 0.45 | 0.48 | 0.78 | 0.83 | 0.86 | 0.89 | 0.81 |
| 2012 | 0.47 | 0.44 | 0.41 | 0.54 | 0.35 | 0.51 | 0.47 | 0.44 | 0.54 | 0.41 |
| 2013 | 0.47 | 0.41 | 0.38 | 0.51 | 0.45 | 0.44 | 0.41 | 0.47 | 0.52 | 0.49 |
| 2014 | 0.69 | 0.66 | 0.63 | 0.71 | 0.60 | 0.51 | 0.42 | 0.45 | 0.54 | 0.48 |
| 2015 | 0.73 | 0.70 | 0.67 | 0.77 | 0.64 | 0.51 | 0.54 | 0.46 | 0.40 | 0.43 |
| 2016 | 0.87 | 0.82 | 0.85 | 0.67 | 0.90 | 0.48 | 0.52 | 0.42 | 0.34 | 0.40 |
| 2017 | 0.86 | 0.81 | 0.80 | 0.84 | 0.91 | 0.47 | 0.38 | 0.42 | 0.35 | 0.52 |
| 2018 | 0.61 | 0.58 | 0.63 | 0.55 | 0.66 | 0.88 | 0.79 | 0.82 | 0.85 | 0.90 |
| 2019 | 0.71 | 0.66 | 0.68 | 0.63 | 0.74 | 0.49 | 0.52 | 0.55 | 0.46 | 0.58 |
| Data Type | Location ( ) | Scale ( ) | Shape | |
| Composite | 0.345 | 1.668 | 0.126 | 0.781 |
| LC1990 | −0.137 | 2.063 | 0.187 | 1.072 |
| LC2000 | −0.097 | 2.024 | 0.178 | 1.052 |
| LC2006 | −0.064 | 1.983 | 0.171 | 1.036 |
| LC2012 | −0.116 | 2.030 | 0.179 | 1.066 |
| LC2018 | 0.261 | 1.727 | 0.138 | 0.830 |
| (a) Kappa distribution parameters | ||||
| Data Type | Location () | Scale () | Shape () | |
| Composite | 2.313 | 2.487 | −0.395 | |
| LC1990 | 2.344 | 2.470 | −0.396 | |
| LC2000 | 2.369 | 2.511 | −0.392 | |
| LC2006 | 2.387 | 2.503 | −0.393 | |
| LC2012 | 2.330 | 2.442 | −0.396 | |
| LC2018 | 2.410 | 2.488 | −0.390 | |
| (b) Generalized extreme value distribution parameters | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basu, A.S.; Gill, L.W.; Pilla, F.; Basu, B. Assessment of Variations in Runoff Due to Landcover Changes Using the SWAT Model in an Urban River in Dublin, Ireland. Sustainability 2022, 14, 534. https://doi.org/10.3390/su14010534
Basu AS, Gill LW, Pilla F, Basu B. Assessment of Variations in Runoff Due to Landcover Changes Using the SWAT Model in an Urban River in Dublin, Ireland. Sustainability. 2022; 14(1):534. https://doi.org/10.3390/su14010534
Chicago/Turabian StyleBasu, Arunima Sarkar, Laurence William Gill, Francesco Pilla, and Bidroha Basu. 2022. "Assessment of Variations in Runoff Due to Landcover Changes Using the SWAT Model in an Urban River in Dublin, Ireland" Sustainability 14, no. 1: 534. https://doi.org/10.3390/su14010534






