Multi-Indicator and Geospatial Based Approaches for Assessing Variation of Land Quality in Arid Agroecosystems
Abstract
:1. Introduction
2. Materials and Methods
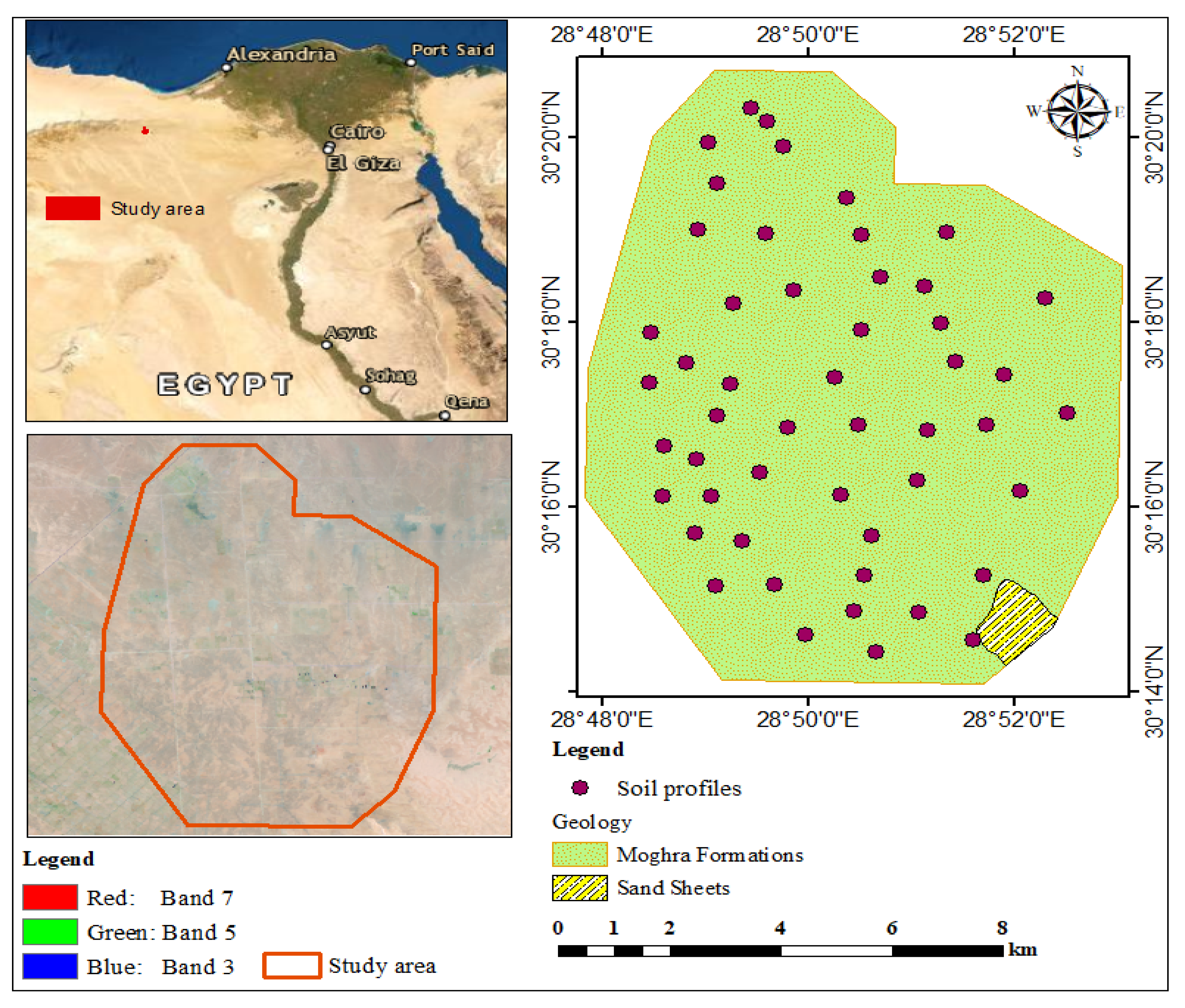
2.1. Study Area
2.2. Remote Sensing Data
2.3. Field Work and Laboratory Analyses
2.4. Modeling Land Quality
2.4.1. Characterization of Indicators
2.4.2. Generating Thematic Layers
2.4.3. Standardization of Thematic Layers
2.4.4. Weighting Procedure
2.4.5. Land Quality Index and Classes
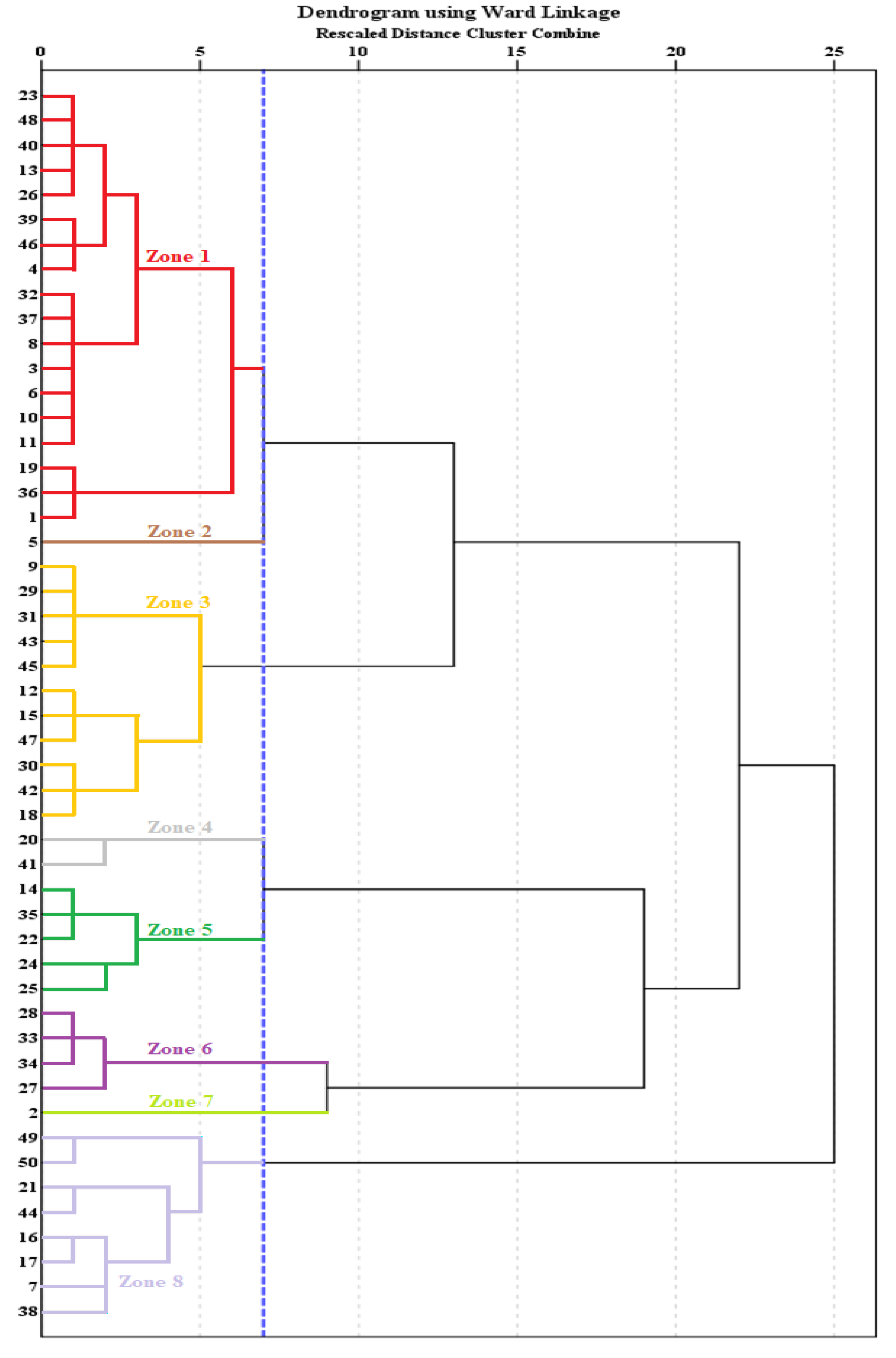
2.5. Developing SLQZs
2.6. Performance Evaluation
3. Results
3.1. Spatial Variability of Soil Attributes
3.2. Multivariate Statistical Analysis
3.2.1. Correlation Analysis
3.2.2. Principal Component Analysis
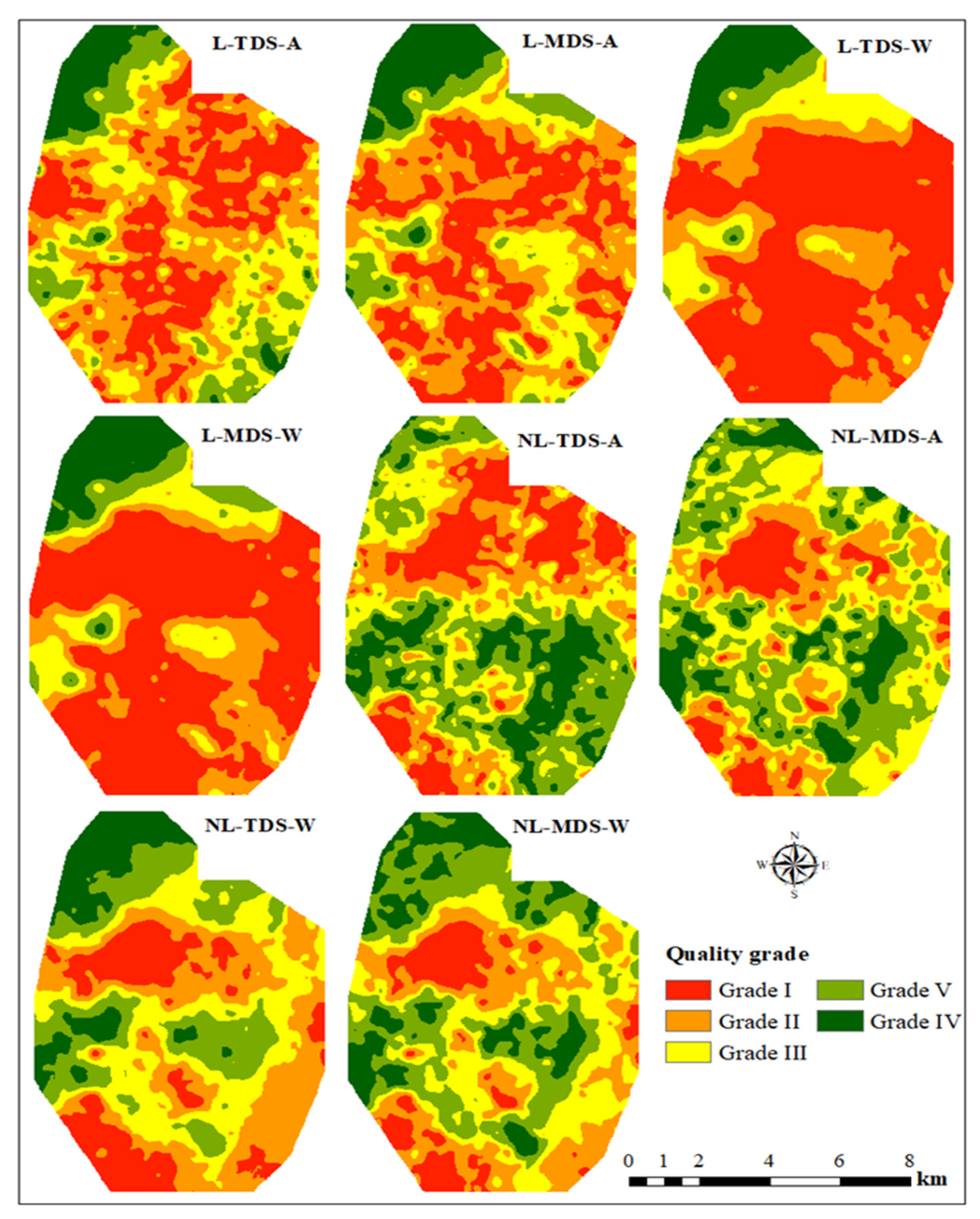
3.3. Land Quality Assessment
3.3.1. According to TDS
3.3.2. According to MDS
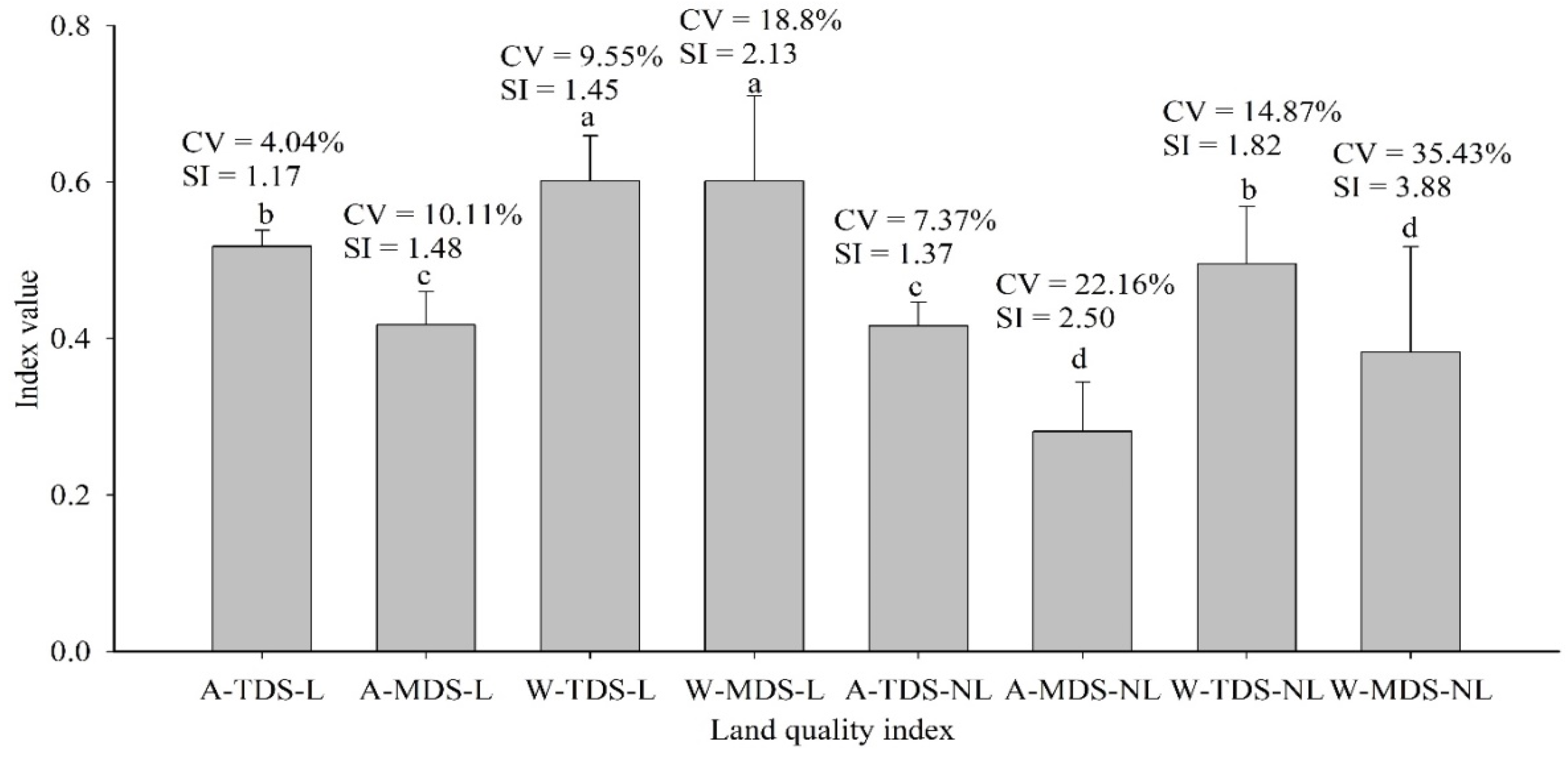
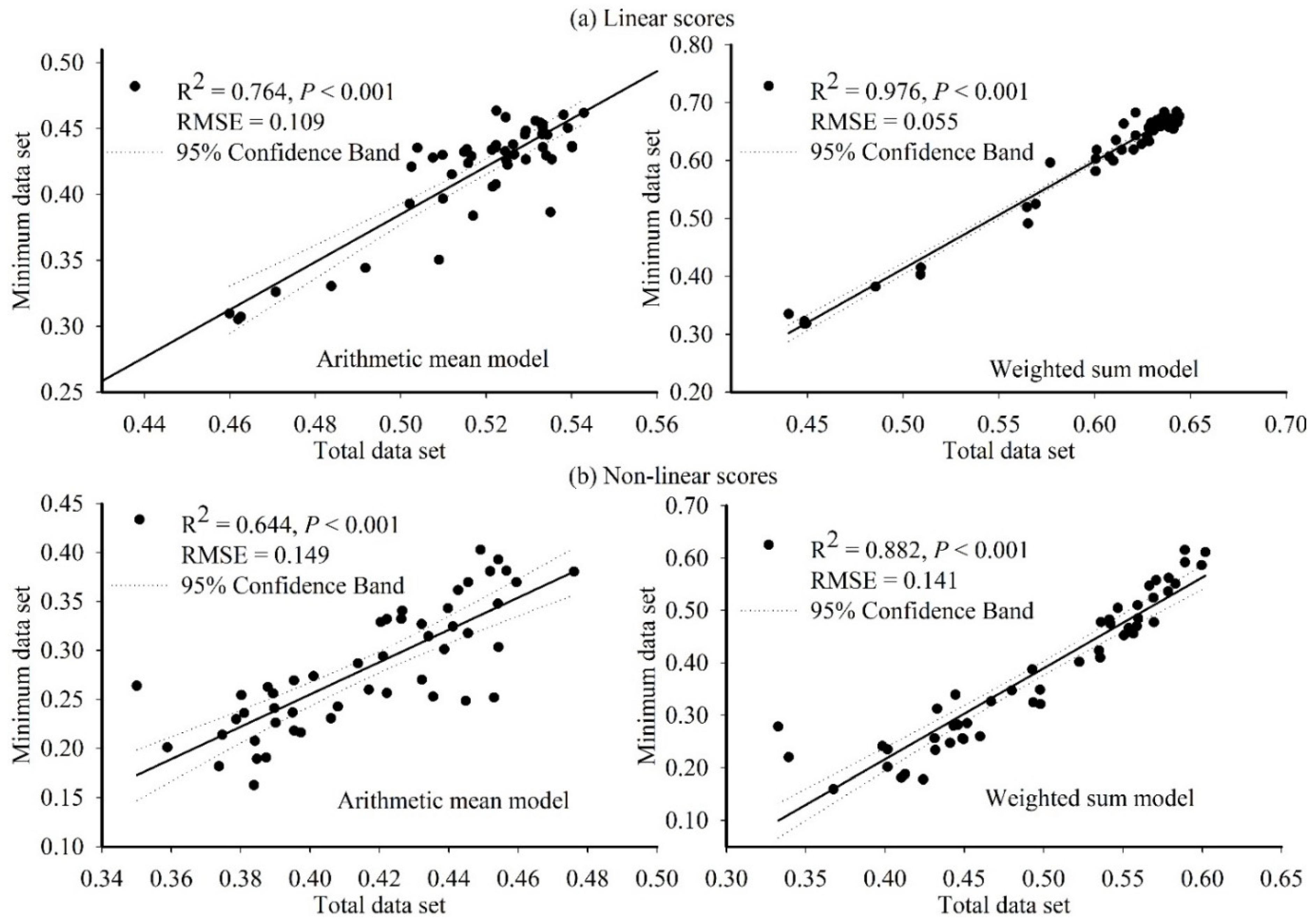
3.4. Comparison of Indices
4. Discussion
4.1. Spatial Variability of Soil Attributes
4.2. Relationships among Land Quality Attributes
4.2.1. Correlation Analysis
4.2.2. Principal Component Analysis
4.2.3. Cluster Analysis
4.3. Land Quality Assessment
4.3.1. According to TDS
4.3.2. According to MDS
4.3.3. Land Quality Grades
4.4. Comparison of Indices
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prăvălie, R.; Bandoc, G.; Patriche, C.; Sternberg, T. Recent changes in global drylands: Evidences from two major aridity databases. CATENA 2019, 178, 209–231. [Google Scholar] [CrossRef]
- Fadl, M.E.; Abuzaid, A.S.; AbdelRahman, M.A.E.; Biswas, A. Evaluation of desertification severity in El-Farafra Oasis, Western Desert of Egypt: Application of modified MEDALUS approach using wind erosion index and factor analysis. Land 2022, 11, 54. [Google Scholar] [CrossRef]
- Abuzaid, A.S.; AbdelRahman, M.A.E.; Fadl, M.E.; Scopa, A. Land degradation vulnerability mapping in a newly-reclaimed desert oasis in a hyper-arid agro-ecosystem using AHP and geospatial techniques. Agronomy 2021, 11, 1426. [Google Scholar] [CrossRef]
- El Behairy, R.A.; El Baroudy, A.A.; Ibrahim, M.M.; Kheir, A.M.S.; Shokr, M.S. Modelling and Assessment of Irrigation Water Quality Index Using GIS in Semi-arid Region for Sustainable Agriculture. Water Air Soil Pollut. 2021, 232, 352. [Google Scholar] [CrossRef]
- Özkan, B.; Dengiz, O.; Turan, İ.D. Site suitability analysis for potential agricultural land with spatial fuzzy multi-criteria decision analysis in regional scale under semi-arid terrestrial ecosystem. Sci. Rep. 2020, 10, 22074. [Google Scholar] [CrossRef]
- Shokr, M.S.; El Baroudy, A.A.; Fullen, M.A.; El-Beshbeshy, T.R.; Ali, R.R.; Elhalim, A.; Guerra, A.J.T.; Jorge, M.C.O. Mapping of heavy metal contamination in alluvial soils of the Middle Nile Delta of Egypt. J. Environ. Eng. Landsc. Manag. 2016, 24, 218–231. [Google Scholar] [CrossRef]
- Karaca, S.; Dengiz, O.; Turan, I.D.; Özkan, B.; Dedeoğlu, M.; Gülser, F.; Sargin, B.; Demirkaya, S.; Ay, A. An assessment of pasture soils quality based on multi-indicator weighting approaches in semi-arid ecosystem. Ecol. Indic. 2021, 121, 107001. [Google Scholar] [CrossRef]
- Raiesi, F. A minimum data set and soil quality index to quantify the effect of land use conversion on soil quality and degradation in native rangelands of upland arid and semiarid regions. Ecol. Indic. 2017, 75, 307–320. [Google Scholar] [CrossRef]
- Vasu, D.; Singh, S.K.; Ray, S.K.; Duraisami, V.P.; Tiwary, P.; Chandran, P.; Nimkar, A.M.; Anantwar, S.G. Soil quality index (SQI) as a tool to evaluate crop productivity in semi-arid Deccan plateau, India. Geoderma 2016, 282, 70–79. [Google Scholar] [CrossRef]
- Jahin, H.S.; Abuzaid, A.S.; Abdellatif, D.A. Using multivariate analysis to develop irrigation water quality index for surface water in Kafr El-Sheikh Governorate, Egypt. Environ. Technol. Innov. 2020, 17, 100532. [Google Scholar] [CrossRef]
- Andrews, S.S.; Karlen, D.L.; Mitchell, J.P. A comparison of soil quality indexing methods for vegetable production systems in Northern California. Agric. Ecosyst. Environ. 2002, 90, 25–45. [Google Scholar] [CrossRef]
- Aljandali, A. Factor Analysis, in Multivariate Methods and Forecasting with IBM® SPSS® Statistics; Aljandali, A., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 97–106. [Google Scholar]
- Abdellatif, A.D.; Abuzaid, A.S. Integration of multivariate analysis and spatial modeling to assess agricultural potentiality in Farafra Oasis, Western Desert of Egypt. Egypt. J. Soil Sci. 2021, 61, 201–218. [Google Scholar]
- Budak, M.; Gunal, H.; Celik, I.; Yildiz, H.; Acir, N.; Acar, M. Soil quality Assessment of Upper Tigris Basin. Carpathian J. Earth Environ. Sci. 2018, 13, 301–316. [Google Scholar] [CrossRef]
- Mamehpour, N.; Rezapour, S.; Ghaemian, N. Quantitative assessment of soil quality indices for urban croplands in a calcareous semi-arid ecosystem. Geoderma 2021, 382, 114781. [Google Scholar] [CrossRef]
- Sutadian, A.D.; Muttil, N.; Yilmaz, A.G.; Perera, B.J.C. Using the Analytic Hierarchy Process to identify parameter weights for developing a water quality index. Ecol. Indic. 2017, 75, 220–233. [Google Scholar] [CrossRef]
- Abuzaid, A.S.; Abdelatif, A.D. Assessment of desertification using modified MEDALUS model in the north Nile Delta, Egypt. Geoderma 2022, 405, 115400. [Google Scholar] [CrossRef]
- Abuzaid, A.S.; Jahin, H.S. Combinations of multivariate statistical analysis and analytical hierarchical process for indexing surface water quality under arid conditions. J. Contam. Hydrol. 2022, 248, 104005. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Abdellatif, M.A.; El Baroudy, A.A.; Arshad, M.; Mahmoud, E.K.; Saleh, A.M.; Moghanm, F.S.; Shaltout, K.H.; Eid, E.M.; Shokr, M.S. A GIS-based approach for the quantitative assessment of soil quality and sustainable agriculture. Sustainability 2021, 13, 13438. [Google Scholar] [CrossRef]
- Abdel-Fattah, M.K.; Mohamed, E.S.; Wagdi, E.M.; Shahin, S.A.; Aldosari, A.A.; Lasaponara, R.; Alnaimy, M.A. Quantitative evaluation of soil quality using principal component analysis: The case study of El-Fayoum Depression Egypt. Sustainability 2021, 13, 1824. [Google Scholar] [CrossRef]
- Deutsch, C.V. Geostatistics, in Encyclopedia of Physical Science and Technology, 3rd ed.; Meyers, R.A., Ed.; Academic Press: New York, NY, USA, 2003; pp. 697–707. [Google Scholar]
- Pilevar, A.R.; Matinfar, H.R.; Sohrabi, A.; Sarmadian, F. Integrated fuzzy, AHP and GIS techniques for land suitability assessment in semi-arid regions for wheat and maize farming. Ecol. Indic. 2020, 110, 105887. [Google Scholar] [CrossRef]
- Goenster-Jordan, S.; Jannoura, R.; Jordan, G.; Buerkert, A.; Joergensen, R.G. Spatial variability of soil properties in the floodplain of a river oasis in the Mongolian Altay Mountains. Geoderma 2018, 330, 99–106. [Google Scholar] [CrossRef]
- Gavioli, A.; de Souza, E.G.; Bazzi, C.L.; Schenatto, K.; Betzek, N.M. Identification of management zones in precision agriculture: An evaluation of alternative cluster analysis methods. Biosyst. Eng. 2019, 181, 86–102. [Google Scholar] [CrossRef]
- Lajili, A.; Cambouris, A.; Chokmani, K.; Duchemin, M.; Perron, I.; Zebarth, B.; Biswas, A.; Adamchuk, V. Analysis of four delineation methods to identify potential management zones in a commercial potato field in eastern Canada. Agronomy 2021, 11, 432. [Google Scholar] [CrossRef]
- Aref, M.A.M.; El-Khoriby, E.; Hamdan, M.A. The role of salt weathering in the origin of the Qattara Depression, Western Desert, Egypt. Geomorphology 2002, 45, 181–195. [Google Scholar] [CrossRef]
- CONCO-Coral/EGPC, Geologic Map of Egypt, Scale 1:500,000; Conoco-Coral and Egyptian General Petroleum Company (EGPC): Cairo, Egypt, 1987.
- Torabi Haghighi, A.; Darabi, H.; Karimidastenaei, Z.; Davudirad, A.A.; Rouzbeh, S.; Rahmati, O.; Sajedi-Hosseini, F.; Klöve, B. Land degradation risk mapping using topographic, human-induced, and geo-environmental variables and machine learning algorithms, for the Pole-Doab watershed, Iran. Environ. Earth Sci. 2021, 80, 1. [Google Scholar] [CrossRef]
- Ettazarini, S. GIS-based land suitability assessment for check dam site location, using topography and drainage information: A case study from Morocco. Environ. Earth Sci. 2021, 80, 1–17. [Google Scholar] [CrossRef]
- Ostovari, Y.; Ghorbani-Dashtaki, S.; Bahrami, H.-A.; Naderi, M.; Dematte, J.A.M. Soil loss estimation using RUSLE model, GIS and remote sensing techniques: A case study from the Dembecha Watershed, Northwestern Ethiopia. Geoderma Reg. 2017, 11, 28–36. [Google Scholar] [CrossRef]
- FAO. Guidelines for Soil Description, 4th ed.; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2006. [Google Scholar]
- Soil Survey Staff. Soil Survey Field and Laboratory Methods Manual; Burt, R., Soil Survey Staff, Eds.; Soil Survey Investigations Report No. 51, Version 2.0; U.S. Department of Agriculture, Natural Resources Conservation Service: Washington, DC, USA, 2014.
- Johnston, K.; Ver Hoef, J.M.; Krivoruchko, K.; Lucas, N. Using ArcGIS Geostatistical Analyst; Esri Redlands: Redlands, CA, USA, 2001; Volume 380, p. 307. [Google Scholar]
- Wackernagel, H. Ordinary Kriging, in Multivariate Geostatistics: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 1995; pp. 74–81. [Google Scholar]
- Olea, R.A. The Semivariogram, in Geostatistics for Engineers and Earth Scientists; Springer: Boston, MA, USA, 1999; pp. 67–90. [Google Scholar]
- Chamchali, M.M.; Ghazifard, A. The use of fuzzy logic spatial modeling via GIS for landfill site selection (case study: Rudbar-Iran). Environ. Earth Sci. 2019, 78, 305. [Google Scholar] [CrossRef]
- Masto, R.E.; Chhonkar, P.K.; Singh, D.; Patra, A.K. Alternative soil quality indices for evaluating the effect of intensive cropping, fertilisation and manuring for 31 years in the semi-arid soils of India. Environ. Monit. Assess. 2008, 136, 419–435. [Google Scholar] [CrossRef]
- Cambardella, C.A.; Moorman, T.B.; Novak, J.M.; Parkin, T.B.; Karlen, D.L.; Turco, R.F.; Konopka, A.E. Field-scale variability of soil properties in central Iowa soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
- Navarro-Pedreño, J.; Jordan, M.M.; Meléndez-Pastor, I.; Gómez, I.; Juan, P.; Mateu, J. Estimation of soil salinity in semi-arid land using a geostatistical model. Land Degrad. Dev. 2007, 18, 339–353. [Google Scholar] [CrossRef]
- Zawadzki, J.; Fabijańczyk, P. Geostatistical evaluation of lead and zinc concentration in soils of an old mining area with complex land management. Int. J. Environ. Sci. Technol. 2013, 10, 729–742. [Google Scholar] [CrossRef] [Green Version]
- Osman, K.T. Saline and Sodic Soils, in Management of Soil Problems; Osman, K.T., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 255–298. [Google Scholar]
- Wassif, M.M.; Wassif, O.M. Types and Distribution of Calcareous Soil in Egypt, in Management and Development of Agricultural and Natural Resources in Egypt’s Desert; Elkhouly, A.A., Negm, A., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 51–88. [Google Scholar]
- Hazelton, P.; Murphy, B. Interpreting Soil Test Results: What Do All the Numbers Mean? 2nd ed.; CSIRO Publishing: Collingwood, VIC, Australia, 2016. [Google Scholar]
- Bassouny, M.A.; Abuzaid, A.S. Impact of biogas slurry on some physical properties in sandy and calcareous soils, Egypt. Int. J. Plant Soil Sci. 2017, 16, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Abuzaid, A.S.; Jahin, H.S. Profile distribution and source identification of potentially toxic elements in north Nile Delta, Egypt. Soil Sediment Contam. Int. J. 2019, 28, 582–600. [Google Scholar] [CrossRef]
- Saleh, A.M.; Elsharkawy, M.M.; AbdelRahman, M.A.E.; Arafat, S.M. Evaluation of soil quality in arid western fringes of the Nile Delta for sustainable agriculture. Appl. Environ. Soil Sci. 2021, 2021, 1434692. [Google Scholar] [CrossRef]
- Amiri, M.; Pourghasemi, H.R.; Ghanbarian, G.A.; Afzali, S.F. Assessment of the importance of gully erosion effective factors using Boruta algorithm and its spatial modeling and mapping using three machine learning algorithms. Geoderma 2019, 340, 55–69. [Google Scholar] [CrossRef]
- John, K.; Afu, S.M.; Isong, I.A.; Aki, E.E.; Kebonye, N.M.; Ayito, E.O.; Chapman, P.A.; Eyong, M.O.; Penížek, V. Mapping soil properties with soil-environmental covariates using geostatistics and multivariate statistics. Int. J. Environ. Sci. Technol. 2021, 18, 3327–3342. [Google Scholar] [CrossRef]
- Nabiollahi, K.; Golmohamadi, F.; Taghizadeh-Mehrjardi, R.; Kerry, R.; Davari, M. Assessing the effects of slope gradient and land use change on soil quality degradation through digital mapping of soil quality indices and soil loss rate. Geoderma 2018, 318, 16–28. [Google Scholar] [CrossRef]
- Fadl, M.E.; Abuzaid, A.S. Assessment of land suitability and water requirements for different crops in Dakhla Oasis, Western Desert, Egypt. Int. J. Plant Soil Sci. 2017, 16, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Ma, H.; Xie, Y.; Jia, X.; Su, T.; Li, J.; Shen, Y. Assessment of soil quality indexes for different land use types in typical steppe in the loess hilly area, China. Ecol. Indic. 2020, 118, 106743. [Google Scholar] [CrossRef]
- Abuzaid, A.S.; Bassouny, M.A. Multivariate and spatial analysis of soil quality in Kafr El-Sheikh Governorate, Egypt. J. Soil Sci. Agric. Eng. Mansoura Univ. 2018, 9, 333–339. [Google Scholar] [CrossRef]
- Soil Science Division Staff. Soil survey manual. In USDA Handbook 18; Government Printing Office: Washington, DC, USA, 2017. [Google Scholar]
- Gupta, R.K.; Abrol, I.P. Salt-affected soils: Their reclamation and management for crop production. In Advances in Soil Science: Soil Degradation Volume 11; Lal, R., Stewart, B.A., Eds.; Springer: New York, NY, USA, 1990; pp. 223–288. [Google Scholar]
| Indicator | Slope | Aspect | TWI | SRI | LS | pH | EC | ESP | OM | CaCO3 | Depth | Sand | Silt | Clay | WHC | BD | HC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Slope | 1.00 | ||||||||||||||||
| Aspect | 0.34 * | 1.00 | |||||||||||||||
| TWI | −0.48 ** | −0.23 | 1.00 | ||||||||||||||
| SRI | 0.02 | −0.11 | −0.48 ** | 1.00 | |||||||||||||
| LS | 0.59 ** | 0.20 | 0.14 | −0.47 ** | 1.00 | ||||||||||||
| pH | 0.12 | 0.15 | −0.18 | 0.14 | 0.12 | 1.00 | |||||||||||
| EC | −0.16 | −0.02 | 0.12 | 0.01 | −0.10 | −0.27 | 1.00 | ||||||||||
| ESP | −0.25 | −0.03 | 0.23 | −0.15 | −0.07 | −0.13 | 0.82 ** | 1.00 | |||||||||
| OM | 0.14 | −0.05 | −0.23 | 0.06 | −0.08 | −0.06 | −0.25 | −0.15 | 1.00 | ||||||||
| CaCO3 | −0.41 ** | −0.20 | 0.23 | −0.01 | −0.23 | −0.15 | 0.33 * | 0.26 | −0.14 | 1.00 | |||||||
| Depth | 0.16 | 0.06 | −0.33 * | 0.04 | 0.05 | 0.13 | 0.03 | 0.04 | −0.13 | −0.38 ** | 1.00 | ||||||
| Sand | 0.27 | 0.00 | −0.03 | −0.11 | 0.22 | 0.20 | 0.02 | 0.07 | 0.05 | −0.33 * | 0.29 * | 1.00 | |||||
| Silt | −0.26 | −0.12 | 0.00 | 0.11 | −0.25 | −0.27 | −0.01 | −0.14 | 0.08 | 0.35 * | −0.19 | −0.88 ** | 1.00 | ||||
| Clay | −0.23 | 0.10 | 0.06 | 0.08 | −0.15 | −0.02 | −0.02 | 0.00 | −0.16 | 0.26 | −0.33 * | −0.91 ** | 0.62 ** | 1.00 | |||
| WHC | −0.27 | 0.04 | 0.05 | 0.10 | −0.19 | −0.10 | 0.00 | 0.00 | −0.11 | 0.33 * | −0.33 * | −0.96 ** | 0.74 ** | 0.98 ** | 1.00 | ||
| BD | 0.23 | −0.06 | 0.06 | 0.04 | 0.21 | 0.11 | 0.01 | 0.03 | −0.07 | −0.13 | 0.12 | 0.413 ** | −0.48 ** | −0.27 | −0.35 * | 1.00 | |
| HC | 0.25 | 0.00 | −0.04 | −0.10 | 0.17 | 0.02 | −0.13 | −0.16 | 0.10 | −0.52 ** | 0.28 | 0.80 ** | −0.59 ** | −0.84 ** | −0.88 ** | 0.32 * | 1.00 |
| NDVI | 0.12 | 0.02 | −0.03 | −0.11 | −0.03 | 0.03 | −0.15 | −0.06 | 0.29 * | 0.11 | −0.47 ** | 0.02 | −0.04 | −0.01 | −0.02 | 0.08 | −0.04 |
| Property | Model | Nugget | Sill | Nugget/Sill | SPD | ME | RMSE | MSE | RMSSE | ASE |
|---|---|---|---|---|---|---|---|---|---|---|
| pH | Spherical | 0.08 | 0.09 | 0.88 | Weak | −0.01 | 0.30 | −0.03 | 0.98 | 0.31 |
| EC | Exponential | 0.00 | 0.74 | 0.00 | Strong | −0.05 | 6.30 | −0.06 | 0.77 | 8.80 |
| ESP | Exponential | 0.00 | 0.10 | 0.00 | Strong | 0.00 | 2.88 | −0.02 | 1.04 | 2.72 |
| CaCO3 | Circular | 0.00 | 0.43 | 0.00 | Strong | 0.00 | 14.89 | −0.16 | 1.18 | 21.25 |
| OM | Circular | 0.24 | 0.25 | 0.95 | Weak | 0.01 | 0.51 | 0.02 | 1.01 | 0.50 |
| Sand | Exponential | 0.03 | 0.03 | 0.79 | Weak | 0.08 | 12.82 | 0.00 | 0.89 | 14.24 |
| Silt | Circular | 0.44 | 0.71 | 0.62 | Moderate | −0.07 | 8.02 | −0.01 | 1.07 | 7.43 |
| Clay | Spherical | 0.50 | 0.54 | 0.93 | Weak | −0.04 | 7.39 | −0.01 | 1.01 | 7.32 |
| Depth | Gaussian | 0.01 | 0.02 | 0.47 | Moderate | −0.01 | 13.65 | −0.01 | 0.88 | 15.16 |
| WHC | Spherical | 0.07 | 0.10 | 0.70 | Moderate | −0.06 | 4.81 | −0.03 | 1.20 | 4.23 |
| BD | Gaussian | 0.0526 | 0.06 | 0.82 | Weak | −0.01 | 0.25 | −0.03 | 0.98 | 0.26 |
| HC | Spherical | 0.16 | 0.30 | 0.53 | Moderate | −0.07 | 46.24 | 0.00 | 1.01 | 45.65 |
| Parameter | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 |
|---|---|---|---|---|---|---|
| Eigenvalue | 4.751 | 2.170 | 2.109 | 1.900 | 1.593 | 1.385 |
| Variance, % | 26.392 | 12.057 | 11.717 | 10.557 | 8.849 | 7.696 |
| Cumulative, % | 26.392 | 38.449 | 50.166 | 60.723 | 69.573 | 77.269 |
| Indicator | Eigenvector | |||||
| Slope | 0.234 | 0.825 | −0.149 | 0.096 | 0.068 | −0.018 |
| Aspect | −0.115 | 0.697 | 0.049 | 0.006 | −0.063 | 0.103 |
| TWI | −0.027 | −0.454 | 0.111 | −0.784 | 0.065 | 0.158 |
| SRI | −0.092 | −0.169 | −0.035 | 0.826 | −0.076 | 0.190 |
| LS | 0.169 | 0.631 | −0.086 | −0.566 | 0.008 | 0.134 |
| pH | 0.100 | 0.170 | −0.234 | 0.260 | 0.027 | 0.703 |
| EC | −0.004 | −0.052 | 0.951 | 0.004 | −0.092 | −0.049 |
| ESP | 0.035 | −0.060 | 0.921 | −0.090 | −0.011 | 0.012 |
| OM | 0.154 | 0.148 | −0.224 | 0.366 | 0.263 | −0.613 |
| CaCO3 | −0.353 | −0.450 | 0.383 | −0.047 | 0.351 | 0.022 |
| Depth | 0.308 | 0.207 | 0.021 | 0.227 | −0.714 | 0.111 |
| Sand | 0.969 | 0.079 | 0.049 | −0.016 | −0.021 | 0.138 |
| Silt | −0.786 | −0.178 | −0.092 | 0.034 | −0.041 | −0.428 |
| Clay | −0.945 | 0.022 | −0.003 | −0.003 | 0.071 | 0.141 |
| WHC | −0.981 | −0.035 | 0.010 | 0.010 | 0.057 | 0.023 |
| SBD | 0.448 | 0.137 | 0.065 | −0.049 | 0.150 | 0.408 |
| HC | 0.878 | 0.045 | −0.195 | −0.063 | −0.156 | −0.091 |
| NDVI | 0.069 | 0.093 | −0.078 | 0.052 | 0.898 | −0.112 |
| Kaiser–Meyer–Olkin (KMO) and Bartlett’s statistics | ||||||
| KMO Measure of Sampling Adequacy | 0.664 | |||||
| Bartlett’s Test of Sphericity | Approx. chi-square | 1246.58 | ||||
| Degree of freedom | 153 | |||||
| Significance | 0.000 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abuzaid, A.S.; Mazrou, Y.S.A.; El Baroudy, A.A.; Ding, Z.; Shokr, M.S. Multi-Indicator and Geospatial Based Approaches for Assessing Variation of Land Quality in Arid Agroecosystems. Sustainability 2022, 14, 5840. https://doi.org/10.3390/su14105840
Abuzaid AS, Mazrou YSA, El Baroudy AA, Ding Z, Shokr MS. Multi-Indicator and Geospatial Based Approaches for Assessing Variation of Land Quality in Arid Agroecosystems. Sustainability. 2022; 14(10):5840. https://doi.org/10.3390/su14105840
Chicago/Turabian StyleAbuzaid, Ahmed S, Yasser S. A. Mazrou, Ahmed A El Baroudy, Zheli Ding, and Mohamed S. Shokr. 2022. "Multi-Indicator and Geospatial Based Approaches for Assessing Variation of Land Quality in Arid Agroecosystems" Sustainability 14, no. 10: 5840. https://doi.org/10.3390/su14105840
APA StyleAbuzaid, A. S., Mazrou, Y. S. A., El Baroudy, A. A., Ding, Z., & Shokr, M. S. (2022). Multi-Indicator and Geospatial Based Approaches for Assessing Variation of Land Quality in Arid Agroecosystems. Sustainability, 14(10), 5840. https://doi.org/10.3390/su14105840








