Analysis of the Dynamic Characteristics of the Top Flange Pile Driving Process of a Novel Monopile Foundation without a Transition Section

Abstract

As the most widely used foundation type, the pile-driving capacity of large-diameter monopile foundations and the hammer force of pile top flanges is increasing, as are the stress and strain of traditional flange structures under the resistance to the cyclic impact load of pile hammers. This paper conducts an empirical study on the Rudong 150 MW offshore wind farm project in Longyuan, Jiangsu Province. The numerical simulation and calculation method of large-diameter pile fatigue damage is mastered and proposed, and a simulation analysis and comparison is conducted, as is an analysis of the sensitivity and feedback of the key software parameters. Based on the results of the above analysis, a pile simulation analysis of the offshore wind power projects under construction and those that are about to be started is performed. The pile hammer stroke energy and pile top hammer stroke process curve are extracted. According to the time range curve of limit and hammer stroke forces, the flange limit stress and distribution of the pile roof are simulated. Combined with the process characteristics of large-diameter pile sinking and analysis in the case of high hammer energy and high acceleration, the effect of the impact on the sensor is discussed. The results show that the instantaneous loading analysis could load at the flange of the pile, the maximum instantaneous stress was above 500 MPa, and the final maximum stress was approximately 307 MPa. Different loading methods vary greatly in the calculation results of the structure, so choosing the appropriate loading simulation method is key to pile sinking analysis.

1. Introduction

With the excessive consumption of traditional fossil energy, clean renewable offshore wind energy has attracted increasing attention worldwide [1]. To further exploit offshore wind energy from various depths of water, various floating offshore wind foundation and gravity foundation concepts have been proposed. Floating offshore wind foundations mainly include spar [2], semisubmersible foundations [3,4], tension leg platforms (TLPs) [5], and so on. Gravity foundations mainly include monopile foundations [6], jacket foundations, and so on. Currently, large-diameter monopile foundations are the most widely used foundation type in offshore wind power and are especially suitable for shallow and medium-depth water. The advantages of a monopile foundation are the simple and quick construction, low foundation cost, and strong adaptability. According to statistics, in more than two-thirds of cases, offshore wind farms built abroad adopt a monopile, whereas few offshore wind farms adopt a gravity type, suction type, or jacket pile foundation [7,8].

Many scholars at home and abroad use numerical methods to study piling problems. So far, the analysis methods mainly include the hole expansion method, finite element method, and wave equation method. Randolph et al. [9] first applied the cylindrical hole expansion theory to simulate the pile-driving process and obtained a series of results about the impact of pile driving on the surrounding soil. Scholars such as Zhu and Yin [10] used the hole expansion theory to study the pile-driving problem and developed the hole expansion theory to a certain extent. Using the finite element method to simulate the pile penetration process can solve the nonlinear problem in the process of driving a pile, and the complex soil constitutive model can be considered. Carter et al. [11] proposed a finite element analysis method for a pile-driving simulation. Mabsout [12] studied the effect of pile driving on the soil at different depths. In 1931, Isaacs [13] proposed that the one-dimensional wave equation can be used to describe the propagation process of stress waves. In 1960, Smith [14] applied the wave equation theory to an actual pile-driving analysis for the first time. Yuan et al. [15] presented an optimization method for soil parameter adjustment. With the wider application of wave equation analysis at home and abroad, many wave equation analysis programs have begun to appear one after another, such as the TTI program designed by the Texas Transportation Research Institute, the WEAP program completed by Goble et al., and the improved WEAP86, WEAP87, GRLWEAP, and so on. The latest GRLWEAP program has more complete functions and is very convenient to use.

With a traditional monopile foundation, the subject of the pile body and the upper transition section through the grouting connection are based on a steel structure, and the connection material for high-strength grouting material, the material properties between steel and concrete grouting materials, and the strength index difference are bigger, so the weakest link of a monopile foundation wind turbine is the traditional high-strength grouting site. Ozgurluk et al. [16,17] investigated the properties of thermal barrier coatings (TBCs) and found that the use of the cold gas dynamic spray (CGDS) method, which is a new generation thermal spray-coating method, could prolong the lifetime of hot section components in gas turbines. Since 2009, failure of grout connections has also occurred in offshore wind farms built in Europe [18,19,20,21,22].

In 2011, a new type of monopile foundation without a transition section in the Jiangsu Longyuan Rudong intertidal zone 150 MW project was developed. The foundation structure is a welded flange at the top of the pile body, and the flange at the bottom of the foundation is connected by bolts, eliminating the transition section and the high-strength grouting material used for the connection. The advantages of this infrastructure are that the transition section and grouting materials are eliminated, which saves engineering investment and avoids the risk of possible failure of the grouting materials, which is conducive to the long-term operation of wind turbine foundations [23,24,25].

However, the adoption of the new wind turbine foundation also brings some new technical problems to be urgently solved:

(1) The requirement of the vertical sinking of a monopile foundation without a transition section is higher, so it is difficult to sink the pile smoothly in the offshore sea and achieve the required perpendicularity;

(2) Whether the flange at the top of the foundation will cause large fatigue damage due to hammering or even cause flange fracture due to excessive hammering force.

In the Jiangsu Longyuan Rudong 150 MW intertidal wind farm project, the selection of a large pile hammer was carried out to obtain the related technical parameters of the pile hammer, and in the engineering design and implementation, the process curve of the pile tip hammer force was extracted to carry out a preliminary analysis of the pile tip flange, mainly according to the static treatment. However, the pile diameter of the early project is 5.0 m, and the number of hammer drives is limited to approximately 3000~4000.

2. Theory of Computation

2.1. Hiley Equation

For double-acting or differential steam hammers, Hiley’s equation is used in the following form [26].

$$P_u=\frac{e_h{E}_h}{s+0.5(k1+k2+k3)}\cdot \frac{W_r+n^2{W}_p}{W+W_p}$$

(1)

where ultimate load is $P_u$, pile tip displacement is $s$, pile tip instantaneous displacement is $s+k1+k2+k3$, rated energy is $E_h$, equivalent hammer weight is $W$, impact hammer weight is $W_r$, impact pile weight is $W_p$, and box weight is $W_b$. Considering strain energy, multiply all $k$ by a coefficient of 0.5 to obtain Equation (1). According to Chellis, the manufacturer’s rated energy is based on the formula above for equivalent hammer weight $W$ and hammer drop height $H$, as follows:

$$E_h=Wh=(W_r+W_b)\mathrm{h}$$

(2)

Checking the derivation of Hiley’s equation, the result shows that the energy loss should be modified for $W$, as follows:

Energy input = power + impact loss + pile cap loss + pile loss + soil loss

$$e_h{W}_{r}h=P_{u}s+e_{h}Wh\frac{W_p(1-n^2)}{W_p+w_r}+P_u(k1+k2+k3)$$

(3)

When several loss coefficients are evaluated in detail, the best result can be obtained from the dynamic formula, which is used as a tool for predicting pile-bearing capacity.

2.2. Wave Equation

In 1931, Isaacs applied the stress wave theory to describe piling [13] and introduced the parameter [18,27,28] R, reflecting soil resistance into the classical one-dimensional wave equation:

$$\frac{{\partial }^{2}u}{\partial x^2}=\frac{1}{c^2}\frac{{\partial }^{2}u}{\partial t^2}+R$$

(4)

where $x$ is the position of the pile cross section, $u$ is the displacement at cross section $x$, $t$ is time, $c$ is the propagation velocity of the stress wave in the pile, $c=\sqrt{E/\rho }$, and $R$ is the parameter reflecting the soil resistance.

It is very difficult to directly solve the above formula because of the complicated and changeable piling conditions in practical engineering. It was not until 1960 that Smith proposed the differential method to solve the problem. Smith’s differential method divides the pile-sinking process into several steps to calculate the number of hammer strokes [14]. In the actual pile-driving process, the number of hammer strikes is as high as the thousands, and the calculation amount for this method is large. Therefore, pile-driving analysis can only be completed by a computer [26,29,30].

3. Numerical Model

3.1. Introduction to GRLWEAP Software

In this paper, GRLWEAP is used for numerical simulation. GRLWEAP is a wave equation analysis software developed by the American Pile Foundation Dynamics Corporation for pile-driving analysis. Its basic principle is based on the one-dimensional wave equation theory. After approximately 40 years of development, GRLWEAP theory and practice have developed to a higher level, have been widely used around the world, are currently recognized in worldwide professional piling process simulation software, and have become the world’s leading and preferred software in the field of pile driving analysis. At present, GRLWEAP has been developed to the 2010 version. Compared with the previous version, this version has a more user-friendly interface, more accurate test results, faster calculation, and other features, but also expands the pile hammer database and pile-driving system database.

The analysis types of GRLWEAP include the following: (1) Bearing Graph: A Bearing Graph is the relationship between pile-bearing capacity and hammering number. (2) Inspector’s Chart: For a certain bearing capacity, the Inspector’s Chart can calculate the minimum number of blows and the stress level in the pile required for the hammer to achieve this bearing capacity at different drop heights or different energy levels. (3) Drivability: When all the parameters of the hammer–pile–soil system are known, the ability to drive the pile can be predicted, and the relationship between the penetration and the number of hammer blows during piling can be estimated. The drivability analysis can obtain the maximum stress of the pile body during the piling process. It is very important to carry out drivability analysis before pile driving, and drivability analysis has become a necessary link in the design of pile foundations for offshore platforms.

3.2. Numerical Model Description

To accurately simulate the transmission mode of the pile-driving force, the substitute driving force used in pile driving was also simulated, and the pile-driving hammer force was directly applied to the substitute driving top in the mode of static loading. Since the pile-driving stress calculated by the pile was not large, the maximum stress of the pile was 146 MPa, so only the flange part was simulated here. For simplicity, 1 m below the flange was brought into the simulation with a fixed constraint at the bottom.

The main parameters of the numerical models are shown in

Table 1. Parameters of numerical models.

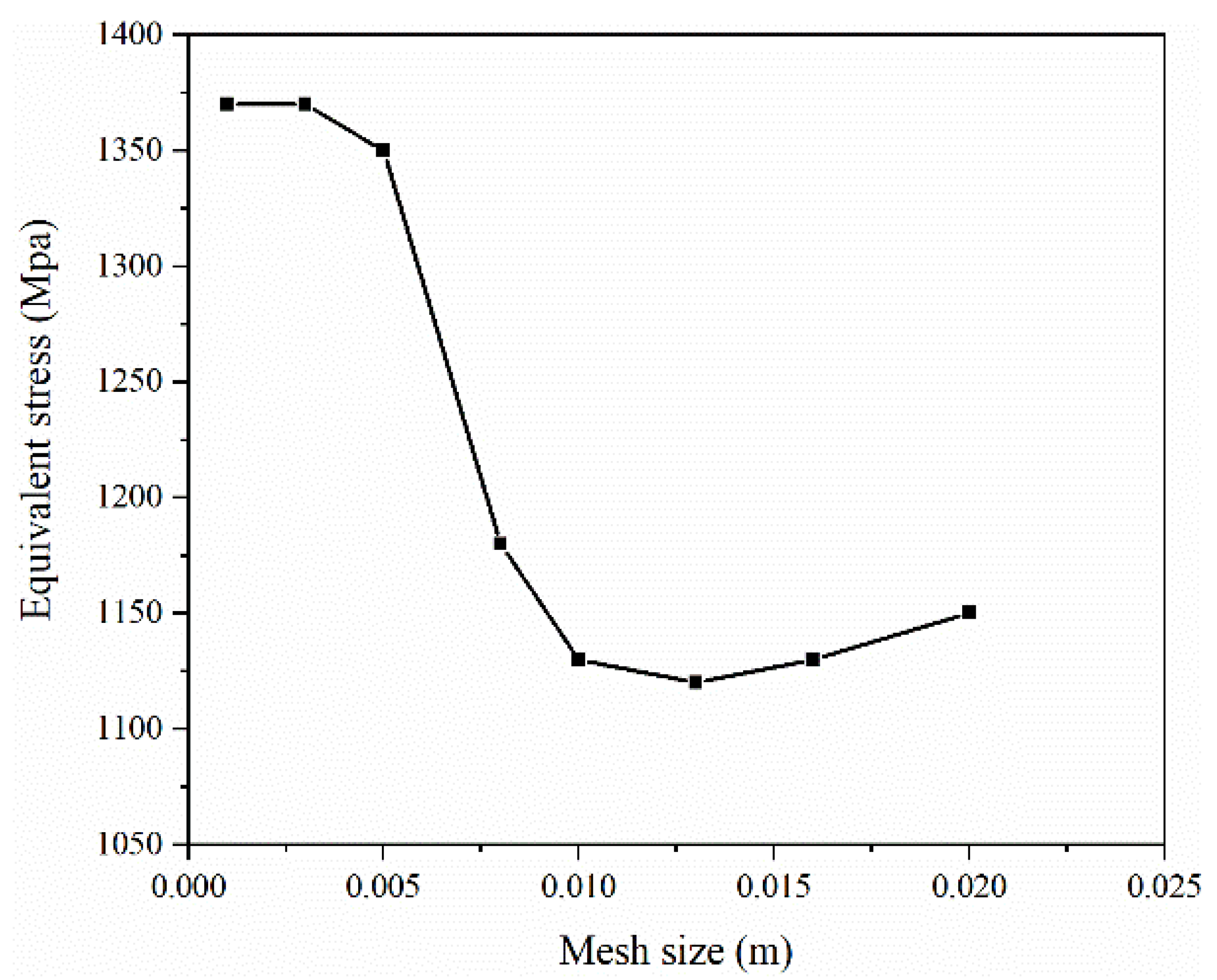
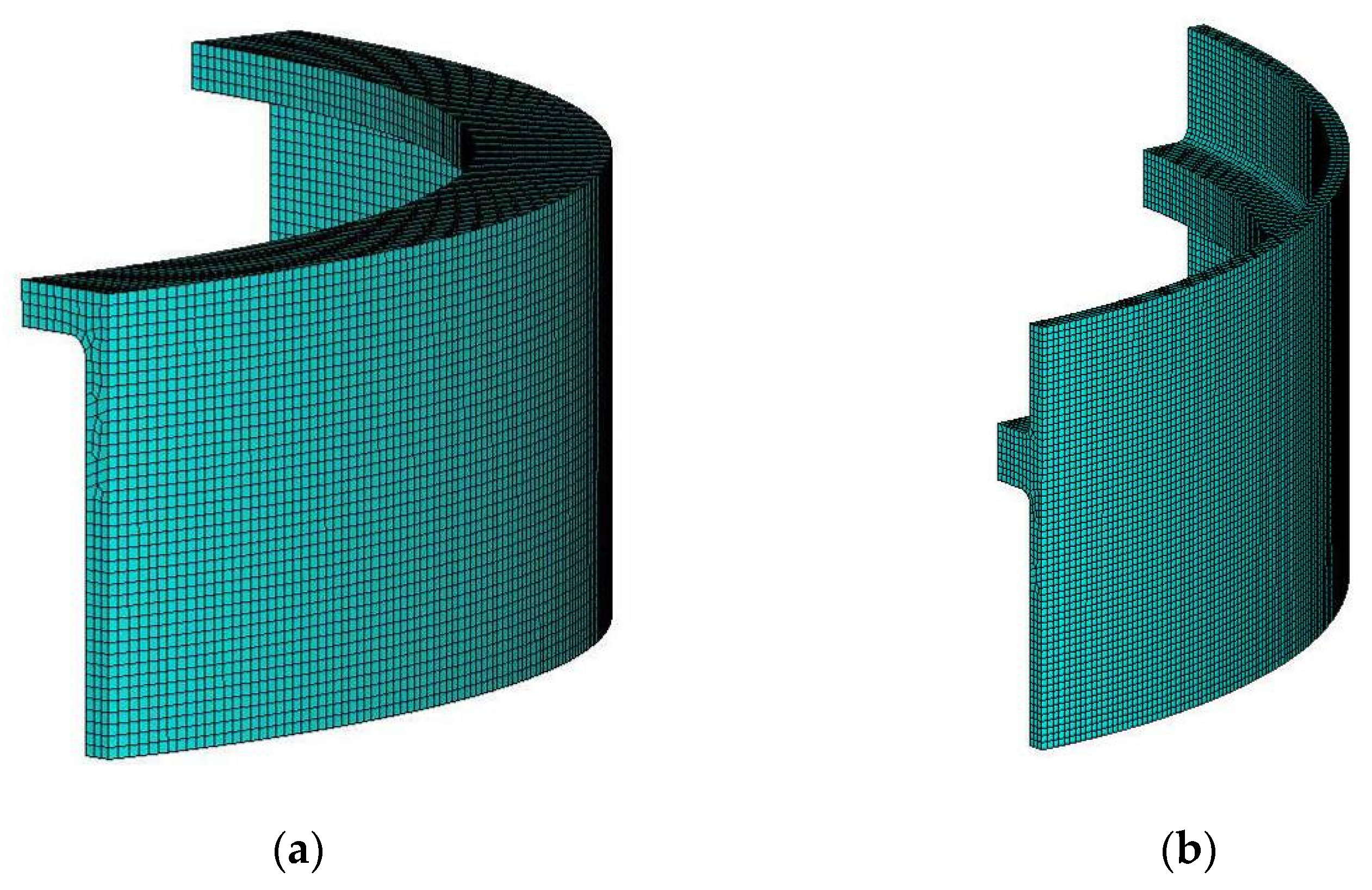
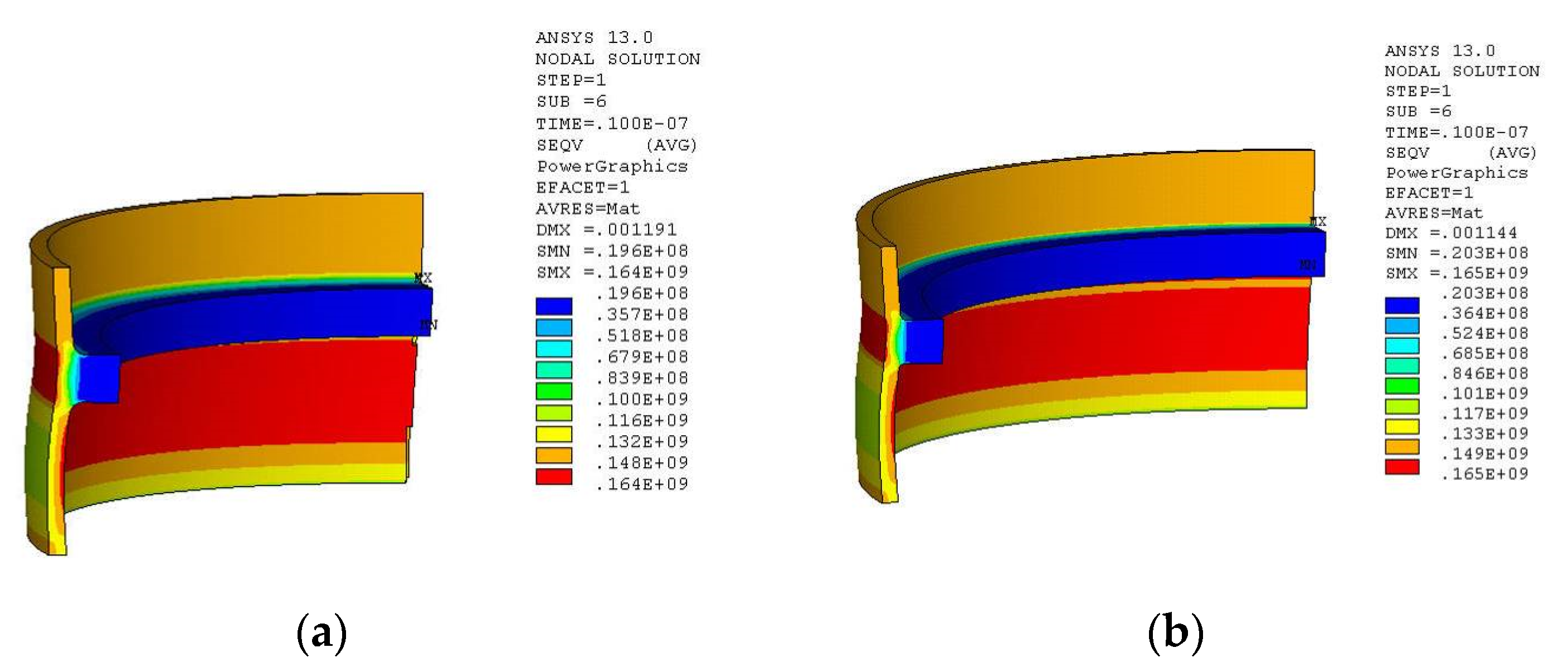
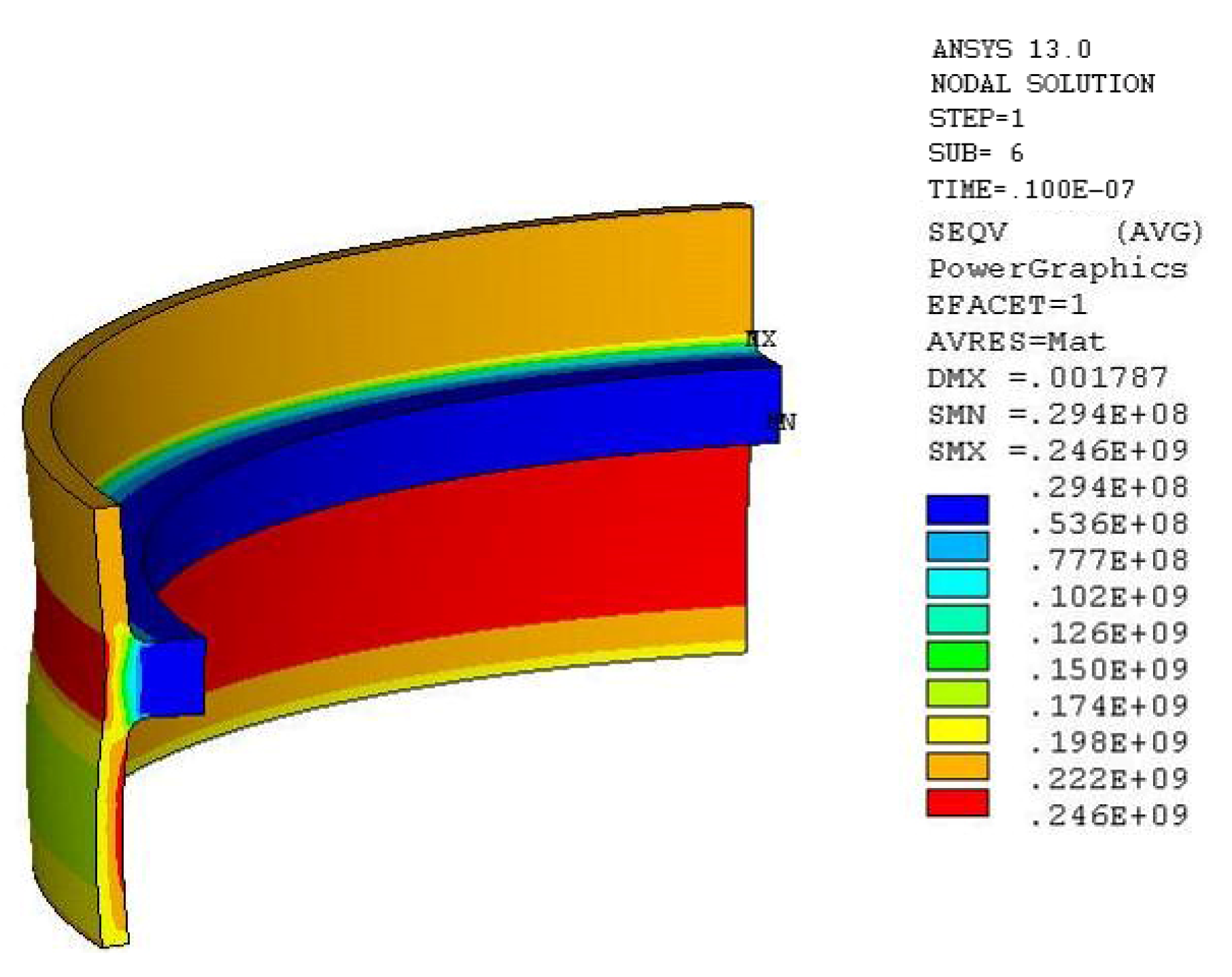
Parameters	Values
Piling hammer type	IHC-S1800
Surface load applied to the piling hammer (kN)	1.35 × 105
Turning radius of flange corners (mm)	20
Wall thickness (mm)	60
Grid size (m)	0.01 × 0.01

. The flange corner radius is 20 mm, and the wall thickness is 60 mm. A load of 1.35 × 10⁵ kN was uniformly applied to the replacement machine according to the surface load. The mesh size of the model was 0.01 m × 0.01 m, and the sectional view of the numerical calculation model is shown in Figure 1. The mesh convergence analysis is shown in Figure 2. It can be seen that when the mesh size was less than 0.005 m, the equivalent stress basically tended to be gentle; when the mesh size was 0.005–0.01 m, the equivalent stress decreased rapidly; and when the mesh size was greater than 0.01 m, the equivalent stress gradually increased, so the final mesh size was selected as 0.01 m.

4. Stress Analysis of Pile Head Flange

4.1. Statical Analysis

The maximum stress of the section stress and overall stress at the flange was calculated to be 229 MPa < 250 MPa, which occurred at the flange angle and the part where the replacement drive contacts the pile top (Figure 3). According to the GRLWEAP pile-driving software, the acceleration of each section of the pile was analyzed over time. The acceleration of the pile top was the largest, with a maximum upwards acceleration of approximately 200 g and a downwards acceleration of approximately 100 g in the process of pile driving. According to the pile-driving analysis results, when the IHC S-1800 pile-driving hammer was used, the pile-driving energy reached the maximum, with a maximum impact force on the pile top of a monopile foundation of 171.46 MN. Therefore, in the following analysis of pile top flange stress, 171.46 MN load was considered.

To accurately simulate the stress characteristics of the flange, the pile top flange was modeled with Solid45 units. The pile top flange model is shown below (Figure 4a). The flange and steel pipe pile are welded together. The elastic model of the steel structure is large. The analysis of flange pile driving in this paper was calculated according to the theory of linear elasticity.

If the pile hammer directly acts on the top of the flange, the flange is in a “『” shape, and the connecting part of the flange and steel pipe pile produce a large stress concentration. The maximum stress calculated appeared at the turning point of the foundation flange, and the maximum stress reached 1040 MPa (Figure 5), which is far beyond the stress requirement of steel. Therefore, this paper proposes adding a process flange, that is, considering the principle of pile driving and force transmission, and setting a temporary construction process flange at the top of the monopile foundation without a transition section during construction. The pile hammer load is reasonably transferred to the top of the foundation after the process flange to reduce the damage caused by the hammer blow on the top of the foundation as much as possible.

The section of the proposed process flange is shown in Figure 4b. The load is applied to the top surface of the process flange “』”, and the outer diameter and inner diameter of the contact fracture face with the pile hammer are 5.5 m and 5.36 m, respectively. If the connection between the flange and steel pipe transitions at right angles, there will be a large stress concentration at the sharp corners. The calculation of turning radii of 0.05 m and 0.03 m is shown in Figure 6.

According to the calculation and setting of the process flange, the maximum stress of the flange corresponding to turning radii of 0.05 and 0.03 m was 164 MPa and 165 MPa, respectively. It can be seen from the flange stress diagram that the stress of the flange was significantly reduced after the process flange was set up under pile-driving load compared with the stress of the process flange not set up before. There was little difference between the local maximum stress of the flange at turning radii of 0.05 m and 0.03 m. The cumulative fatigue damage was approximately 0.02 considering 5000 hammer blows of pile driving.

The pile driving impact load is the dynamic load, which needs to consider a load coefficient of 1.5. The flange stress under a load of 1.5 × 171.46 MN is given below (Figure 7).

According to the above calculation results, the maximum stress of the flange was 246 MPa after considering the load component coefficient of 1.5, which is less than the design value of allowable steel stress. It can be seen that the setting process flange meets the design requirements.

4.2. Dynamic Analysis

4.2.1. Calculation of Static Force

In the process of pile test monitoring, initial driving with high strain variation was adopted, and the cross-sectional area was approximately 0.3 m². The maximum stress during pile-driving software analysis was approximately 180–190 MPa (

Table 2. Stress analysis of piling software.

Pile End Bearing Capacity Reduction Factor	Total Hammers	Penetration of Final Hammer (mm)	Ultimate Bearing Capacity of Pile (kN)	Maximum Compressive Stress of Pile Body (Mpa)	Maximum Tensile Stress of Pile Body (Mpa)
0.3	6015	3.51	58864.9	182.2	74.98
0.4	8067	2.28	65268.8	182.2	52.80
0.5	11072	1.38	71672.6	190.4	53.10

). The calculated results are close to the maximum stress of the pile tip under static loading. The comparison here is based on static calculation. The model was established. The upper part was set with a process flange, and the lower part was fixed at the 7 m position. Only a local model was established.

When a load of 1.716 × 10⁸ N was distributed on the top surface of the process flange, the maximum stress of the flange was calculated to be 169 MPa (Figure 8).

4.2.2. Study on Different Sudden Loading Methods

Three different sudden loading modes were defined (i.e., the top surface of the flange was loaded with a 1.716 × 10⁸ N load at an instant, and no unloading was performed), as shown in

Table 3. Different sudden loading methods.

Different Sudden Loading Methods	Load Step (s)	Load Time (s)	Maximum Stress (Mpa)	Maximum Stress Moment (s)
Sudden load 1	1.0 × 10−4	0.01	528	0.0050
Sudden load 2	1.0 × 10−8	0.01	554	0.0048
Sudden load 3	1.0 × 10−8	0.05	595	0.0030

, to study the dynamic response of the pile top flange stress under different sudden loading modes. At this point, the stress of the pile top flange is shown in Figure 9.

As shown in Figure 9, the maximum stress of sudden loading occurred at 0.005 s, and the maximum stress reached 528 MPa, which exceeds the allowable stress level of the structure. In the actual loading process, the maximum stress was 546 MPa, and the location of the maximum stress at each moment was different. When the second time step of sudden loading was further intensified, the stress of the structure was further increased, and the maximum stress was 560 MPa, which is approximately 2–3% higher than that of 10 × 10⁻⁴ s. When the time step was unchanged, the action time was further shortened, the stress of the structure under sudden loading was further increased, and the maximum stress was 595 MPa. Under the above three sudden loading modes, the stress increased greatly after sudden loading compared to that under static loading.

It can be seen that there were great differences in the stress of flanges under different sudden loading modes. The maximum stress under the three sudden loading modes (546 mPa, 560 mPa, and 595 MPa) was greater than the maximum stress under static loading, and the maximum stress under sudden loading (595 MPa) was about 3.52 times of the maximum stress under static loading. When the sudden loading time was unchanged and the loading time step was encrypted, the maximum stress of sudden loading 2 increased by about 2.6% compared with that of sudden loading 1. The maximum stress time was basically the same, and the results of changing the loading time step showed little difference. When the time step was unchanged, when the sudden loading time increased, the maximum stress increased by about 7.4%, and the time when the maximum stress appeared was about 0.002 s earlier. Changing the loading time had a significant effect on the results.

4.2.3. Time-Procedure Analysis

According to the following simulation pile hammer analysis results, the loading duration was 1.0 × 10⁻⁴ s (Figure 10a) and 1.0 × 10⁻⁵ s (Figure 10b), and the loading time was 0.05 s. The maximum stress of the pile top flange is shown in Figure 10.

According to the above calculation results, in the range of 0.05 s, when the load was suddenly applied and rapidly unloaded, the stress of the pile top flange was smaller than that of sudden loading, and the maximum stress in the loading process was only 65 MPa.

Then, according to the extended total acting time, that is, to check the action of the four hammers in total within 6 s, the four hammers were continuously hit according to the pile hammer load. The loading step length of the load duration was 1.0 × 10⁻⁴ s, and the time interval of each hammer was 1.5 s. The pile top flange stress is shown in Figure 11 below.

Paying attention to the stress of the pile top flange after the pile top hammer load in 6 s, calculated by one hammer action in 1.5 s time, it may be observed that the stress of the pile head was too small because the sudden loading time of extraction was too short.

It can be seen that according to sinusoidal assumption (load is suddenly applied and unloaded rapidly), the loading time was the same, the loading step was different, and the maximum stress occurred at the same time (0.01 s). The maximum stress was 65 Mpa, and the maximum stress of sudden loading method 1 was about 8.4 times more. The sinusoidal loading method was changed, and four hammers were continuously hit at an interval of 1.5 s within 6s, but the sudden loading time of extraction was too short and the pile head stress was too small.

5. Conclusions

Combined with GRLWEAP pile-driving software, this paper carried out numerical simulation analysis on pile driving of large-diameter monopile foundations. Based on static and dynamic analyses in the pile-driving process, the following conclusions are drawn:

(1) The setting of the process flange can improve the stress of the foundation top flange, and the setting of the process flange can greatly reduce the stress of the pile top flange in the process of pile driving.

(2) Instantaneous loading analysis was adopted to load according to the maximum load. In the process of piling, the stress at the corner of the pile top flange was too large, the maximum instantaneous stress was more than 500 MPa, and the final stress was approximately 307 MPa. (It was larger than the calculation result of static load, with a difference of approximately 1.8 times).

(3) The action time of the pile top load curve extracted from pile-driving analysis was too short, and the impulse acting on the pile top was reduced, so the pile top stress calculated was insufficient. This was much smaller than the calculation result of the static load (with a difference of more than 10 times).

(4) Different loading methods had a great difference on the calculation results of the structure. Therefore, the selection of an appropriate loading simulation method is the key to pile-driving analysis.

(5) In the actual pile-driving process, the load that the hammer forces to feed back to the pile top is a load that increases suddenly and disappears quickly. However, in the actual loading process, since the energy is further uploaded from the bottom of the pile to the pile top, there is a phenomenon of superposition, so it is necessary to conduct solid modeling in the modeling process for further verification.