Quantifying Effect of Post-Tensioned Bars for Precast Concrete Shear Walls
Abstract
:1. Introduction
2. Constitutive Modeling of Concrete
2.1. The KCC Model with Mat-Concrete Damage (MAT072R3)
2.2. The CDP Model with Mat-CDP Damage (MAT273)
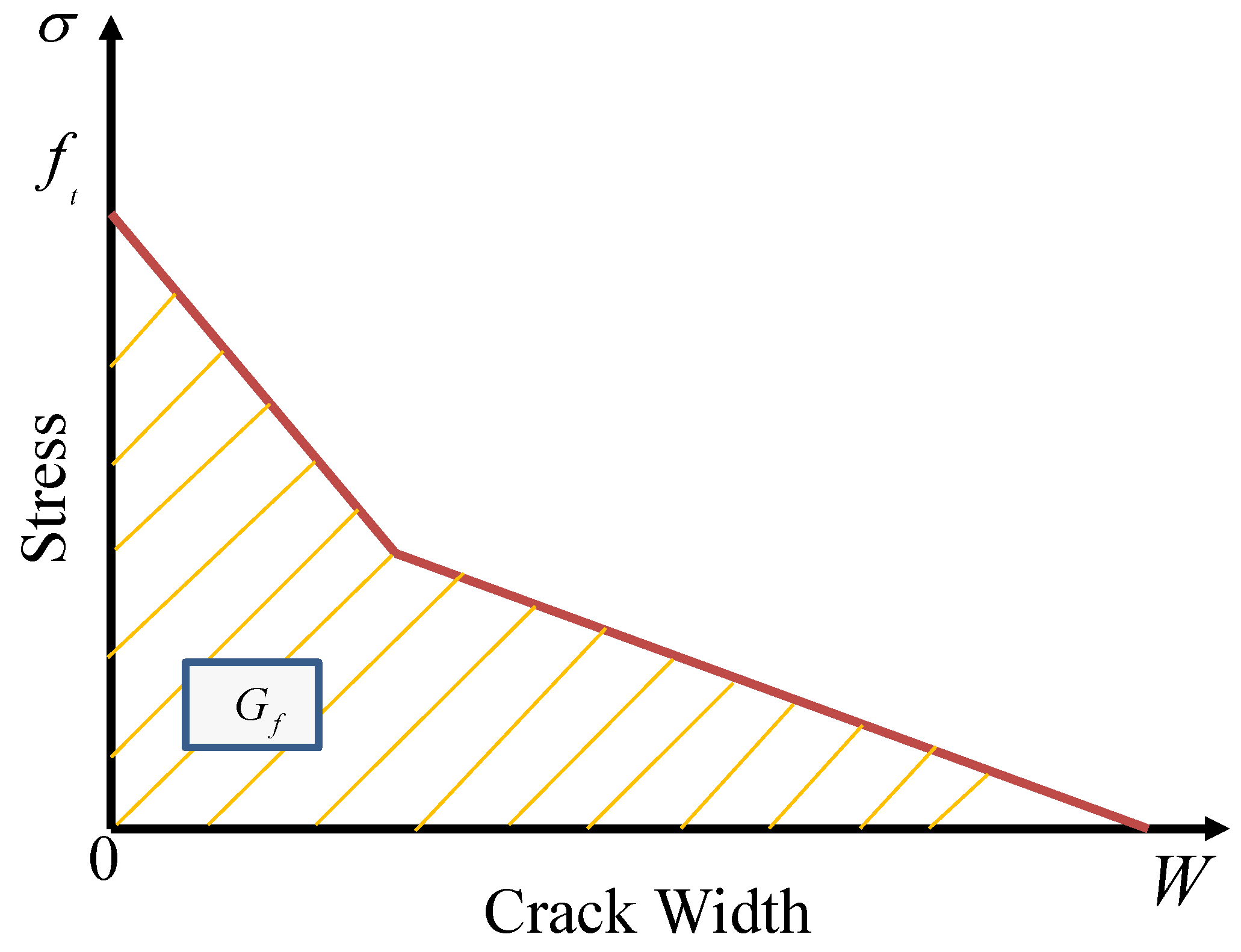
2.3. The Winfrith Model with Mat-Winfrith Damage (Mat085)
3. Analytical Methodology Validation
3.1. Experimental Investigation
3.2. Constitutive Material Models
3.3. Contact and Boundary Conditions
4. Numerical Analysis and Comparison with Experimental Results
4.1. Analysis of PT 2D Wall under Pushover Analysis
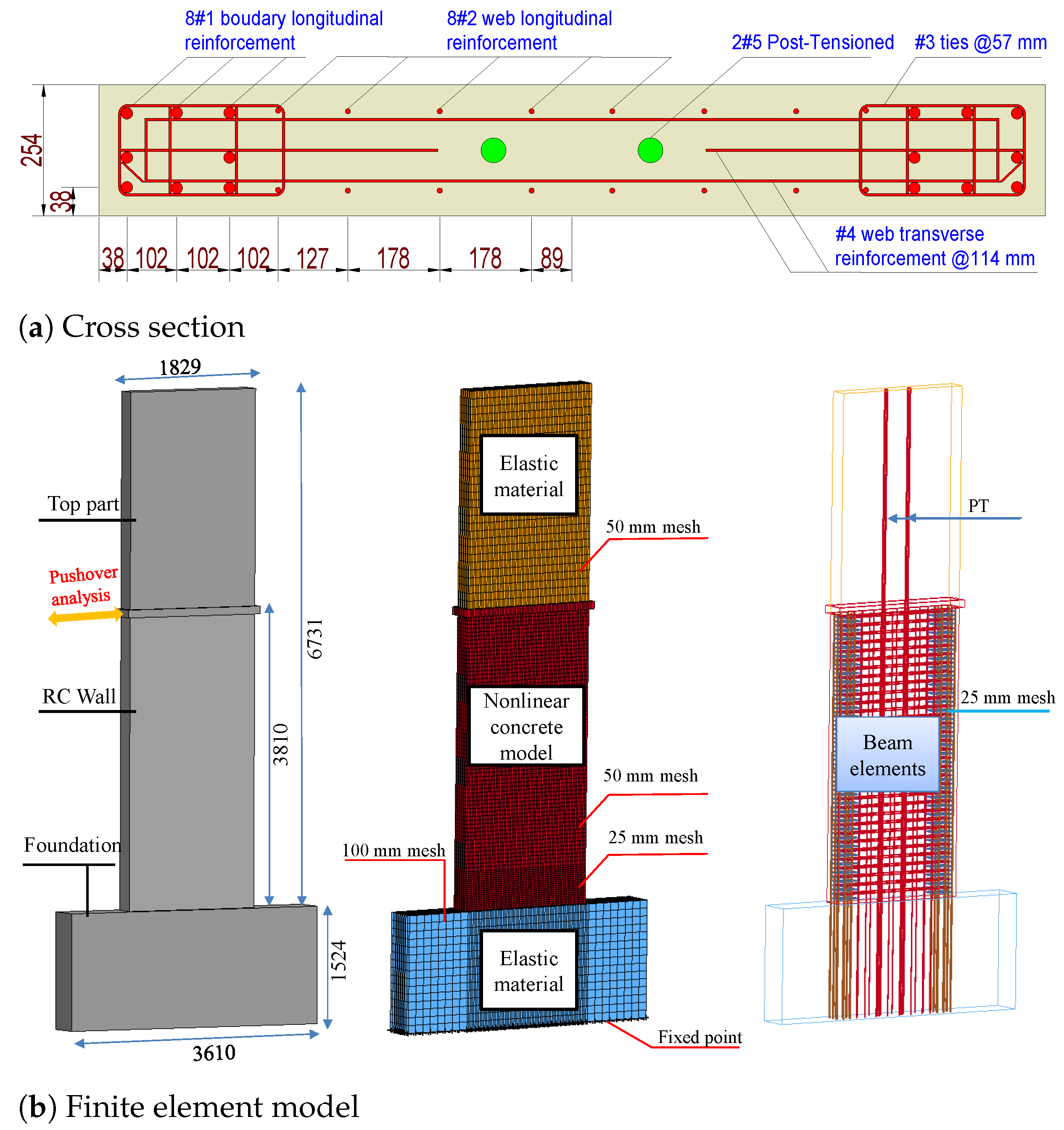
4.1.1. Geometric and Finite Element (FE) Model
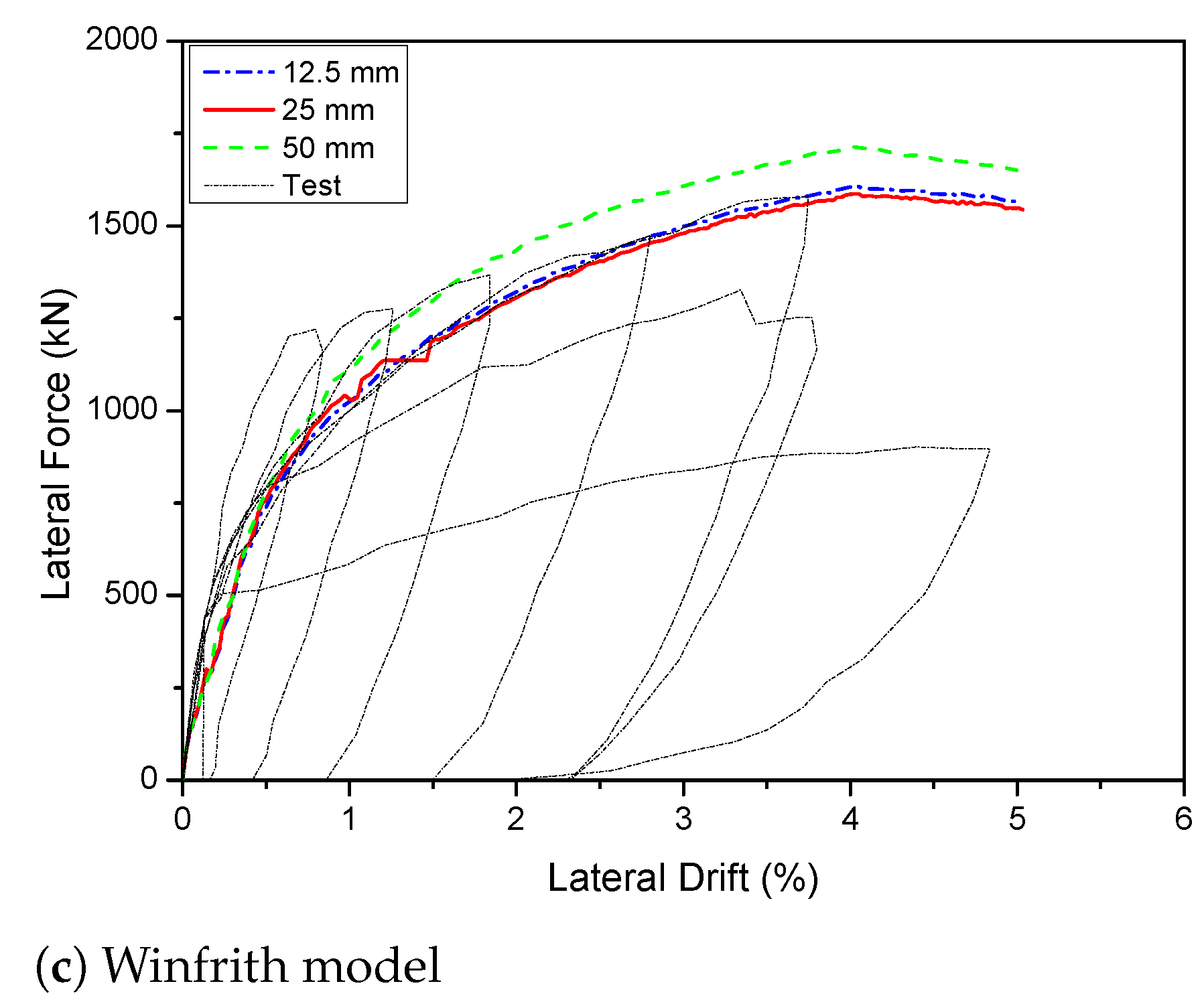
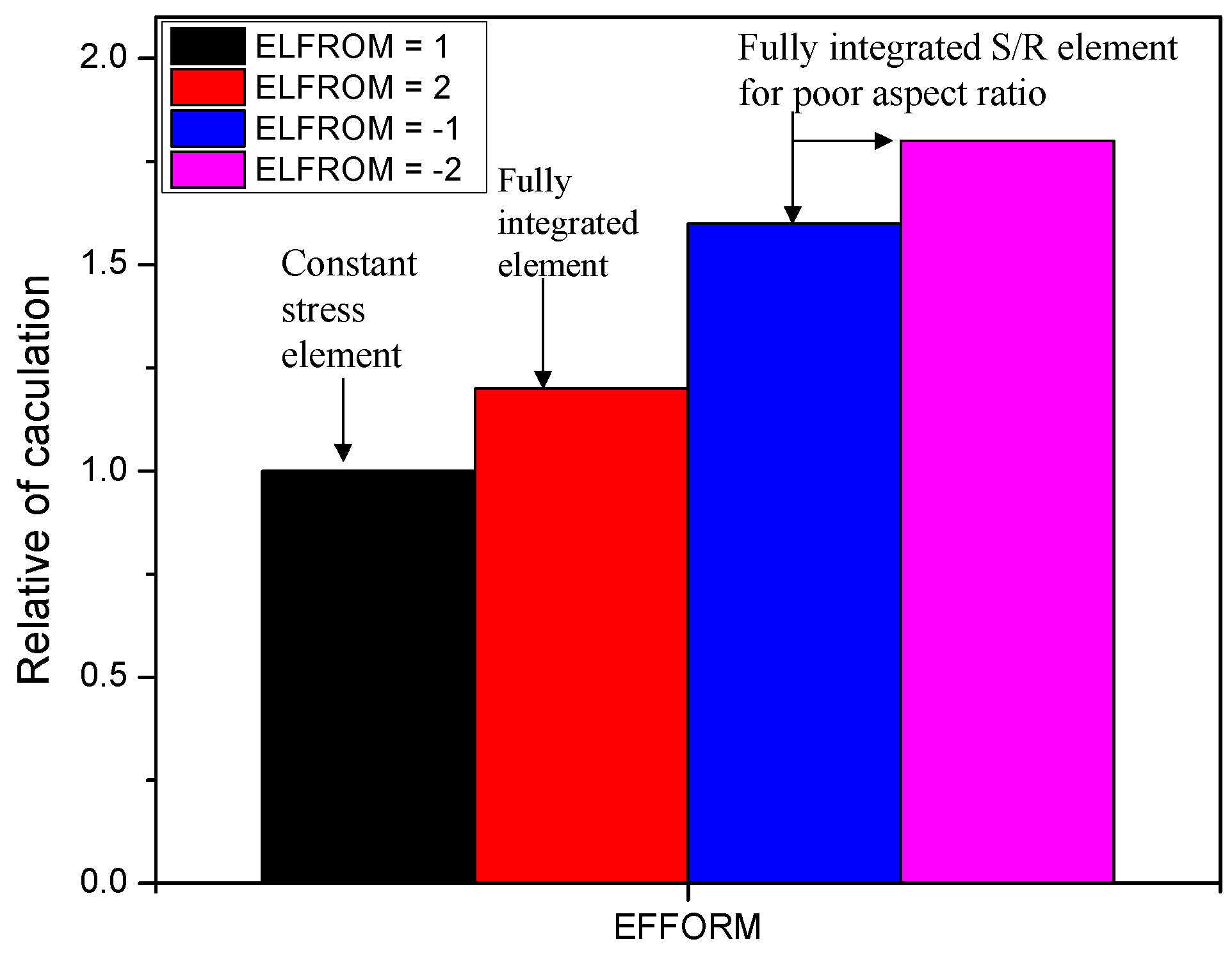
4.1.2. Effect Type of Mesh Size Element
4.1.3. Effect Type of Concrete Element
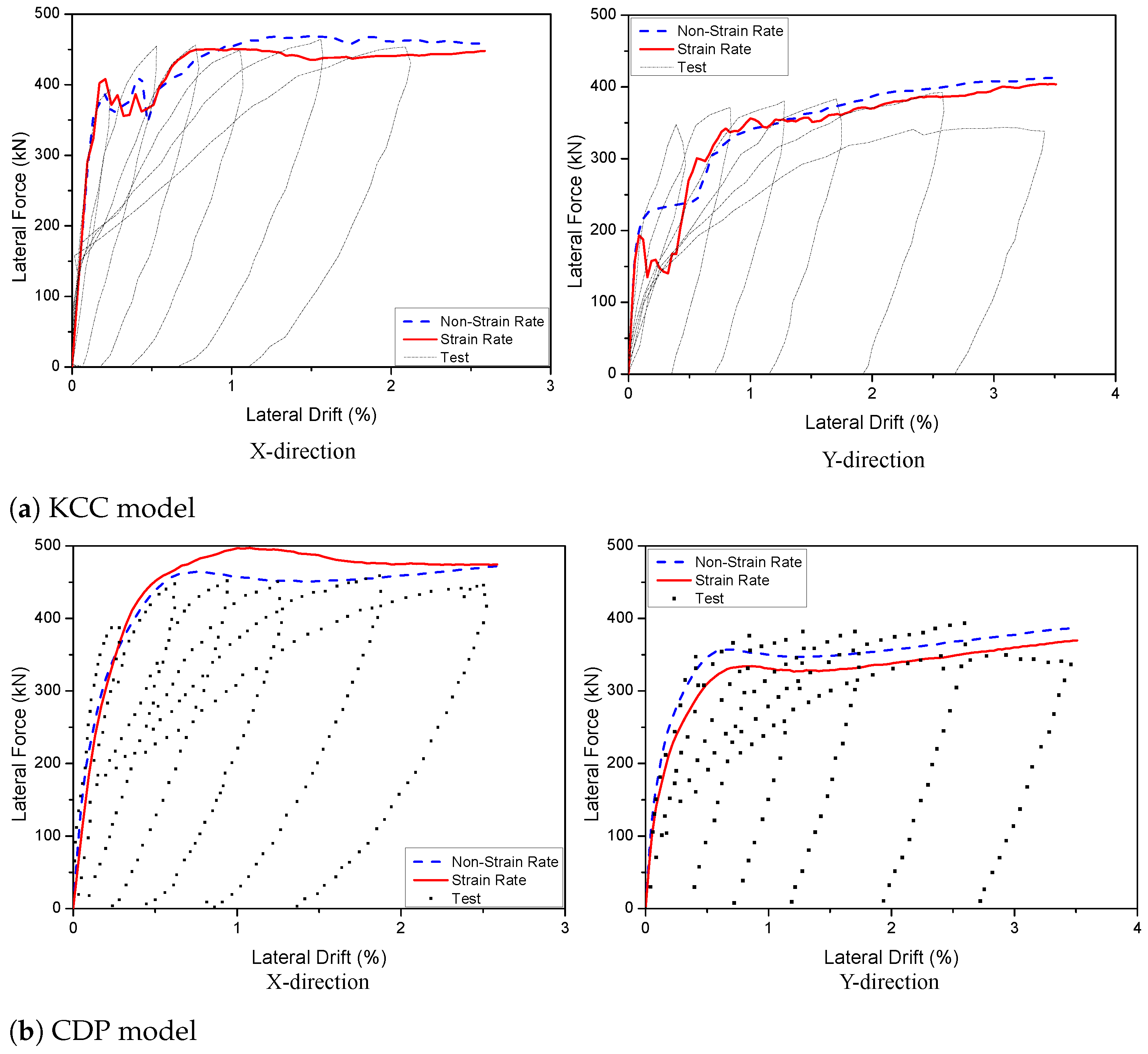
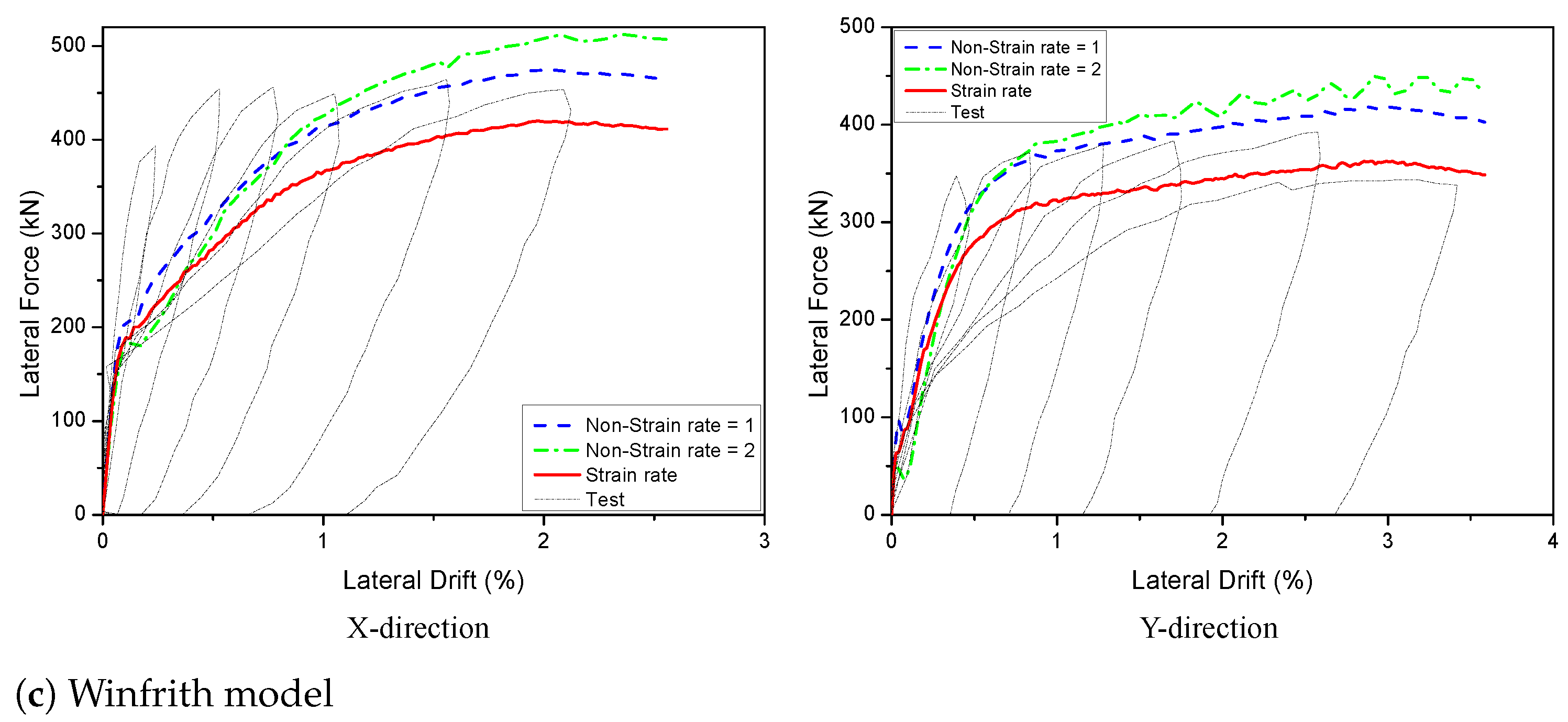
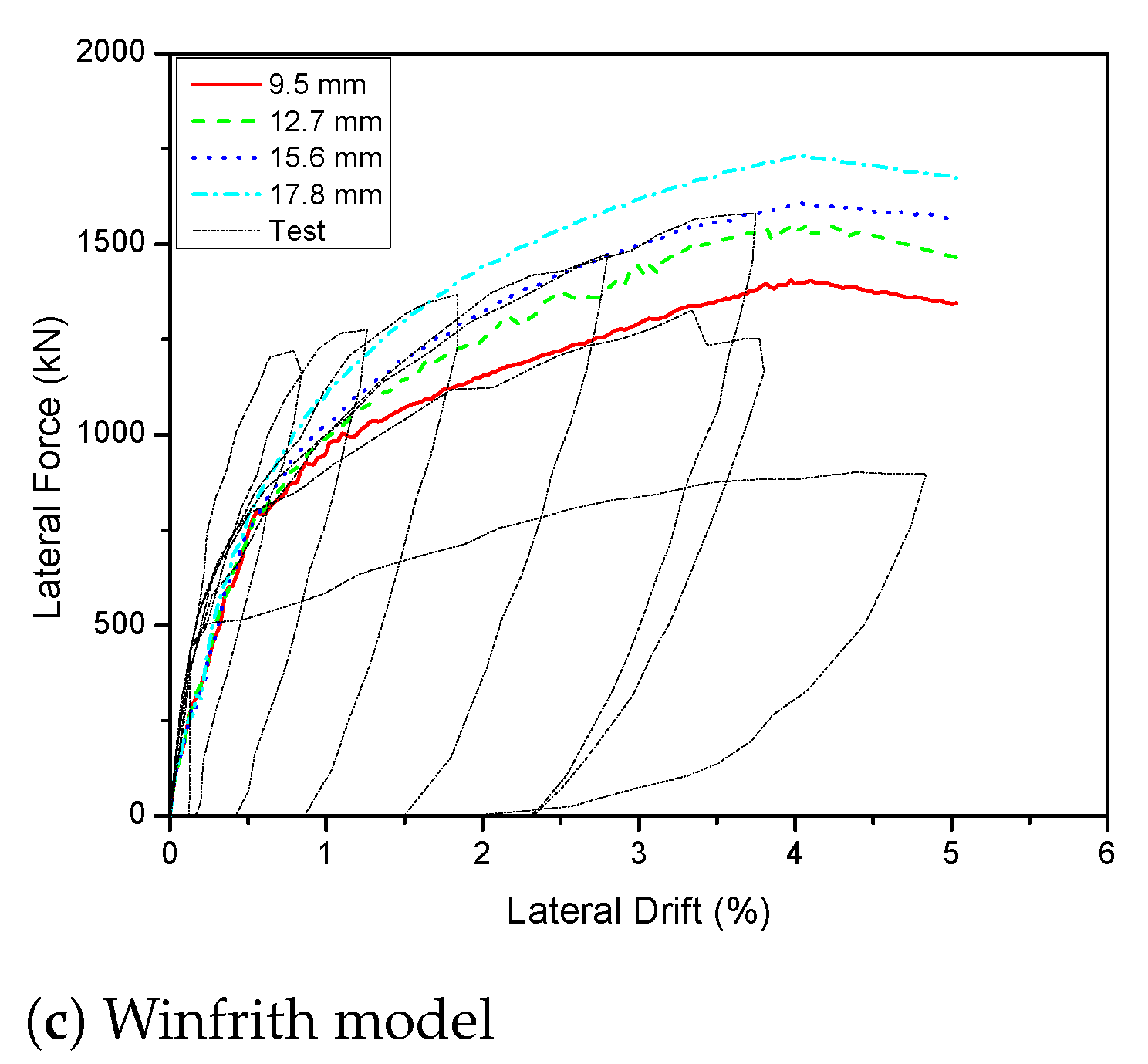
4.1.4. Effect of Strain Rate
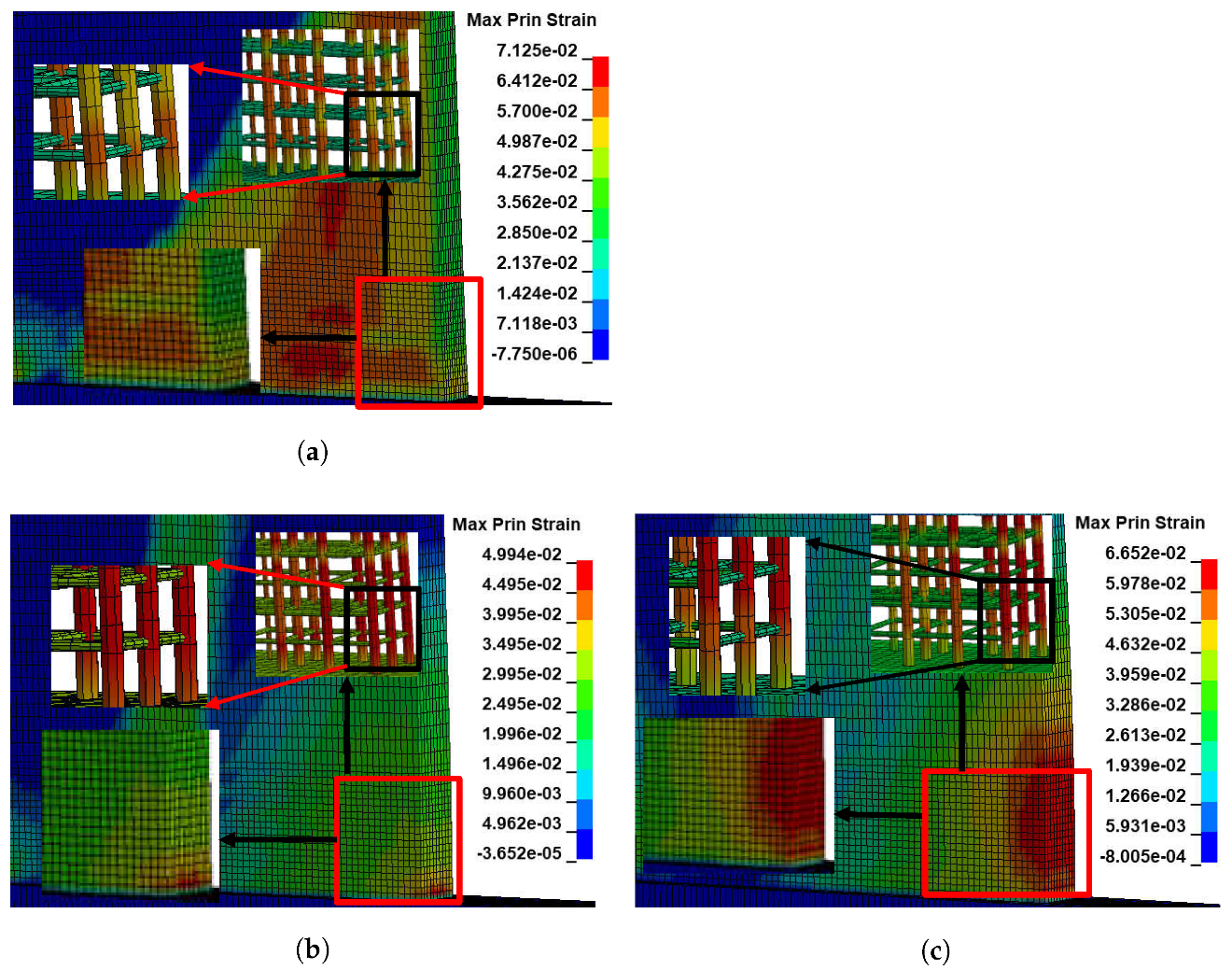
4.1.5. Failure Behaviour
4.2. Analysis of 3D Wall under Pushover Analysis
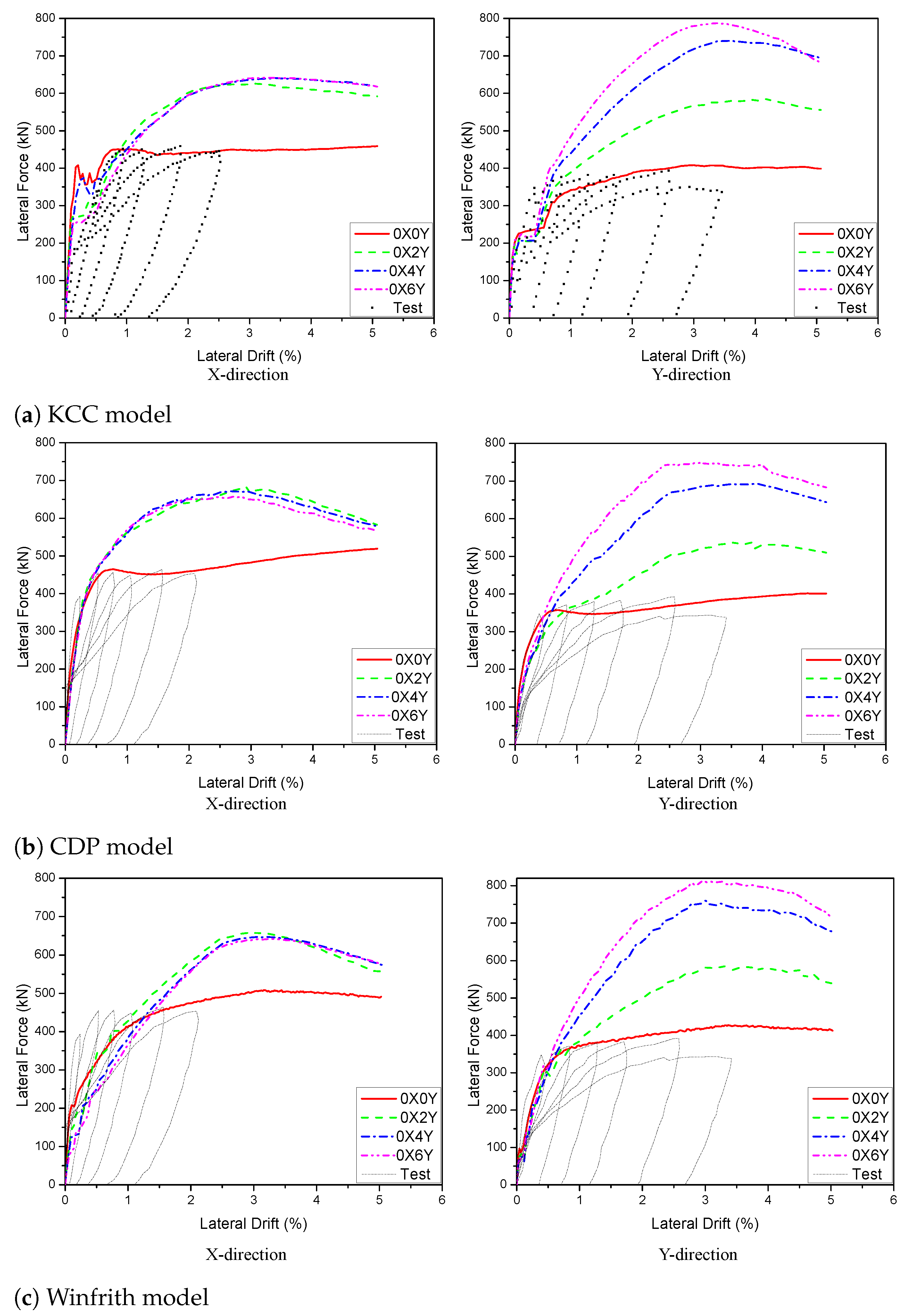
4.2.1. Hysteresis and Backbone Curves
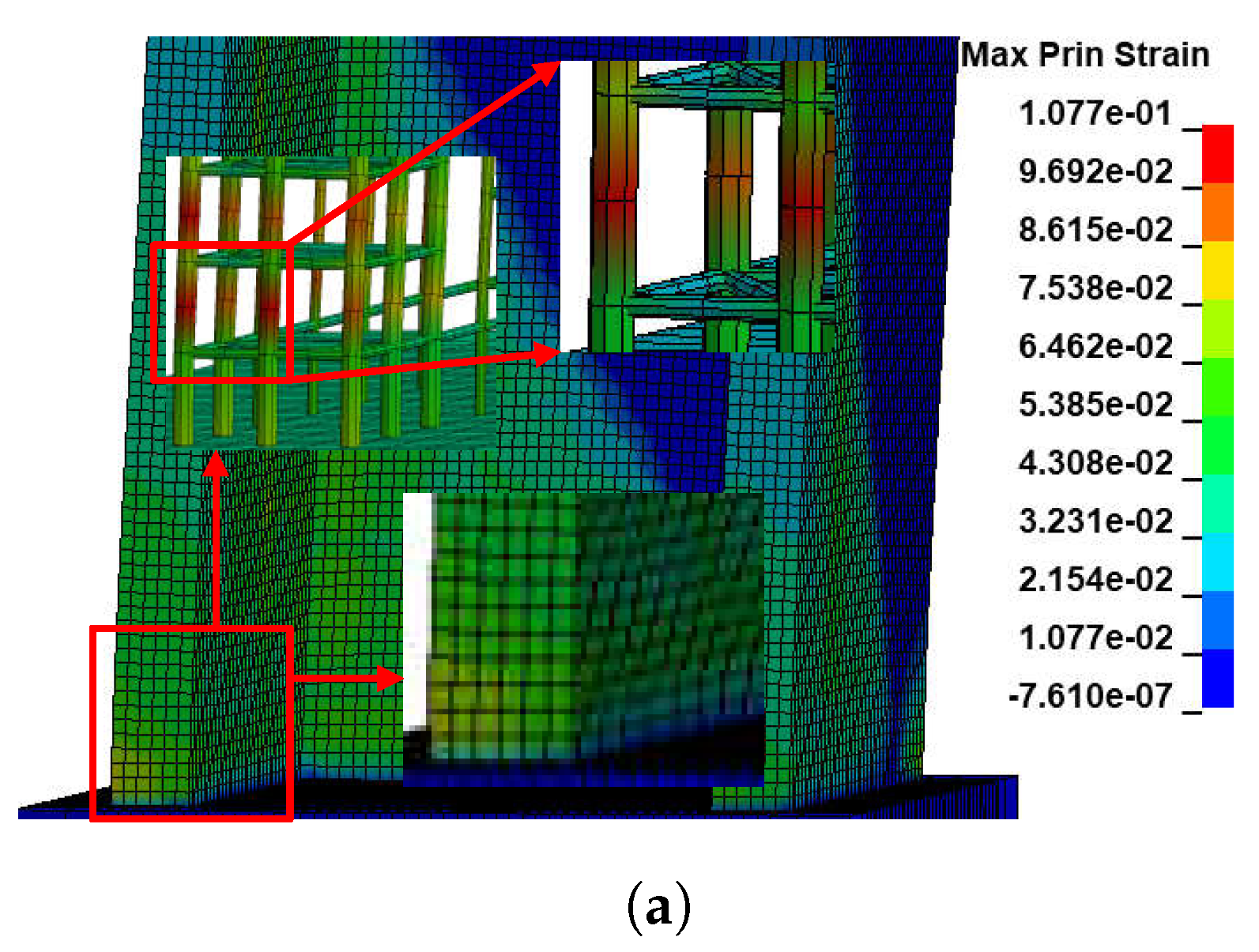
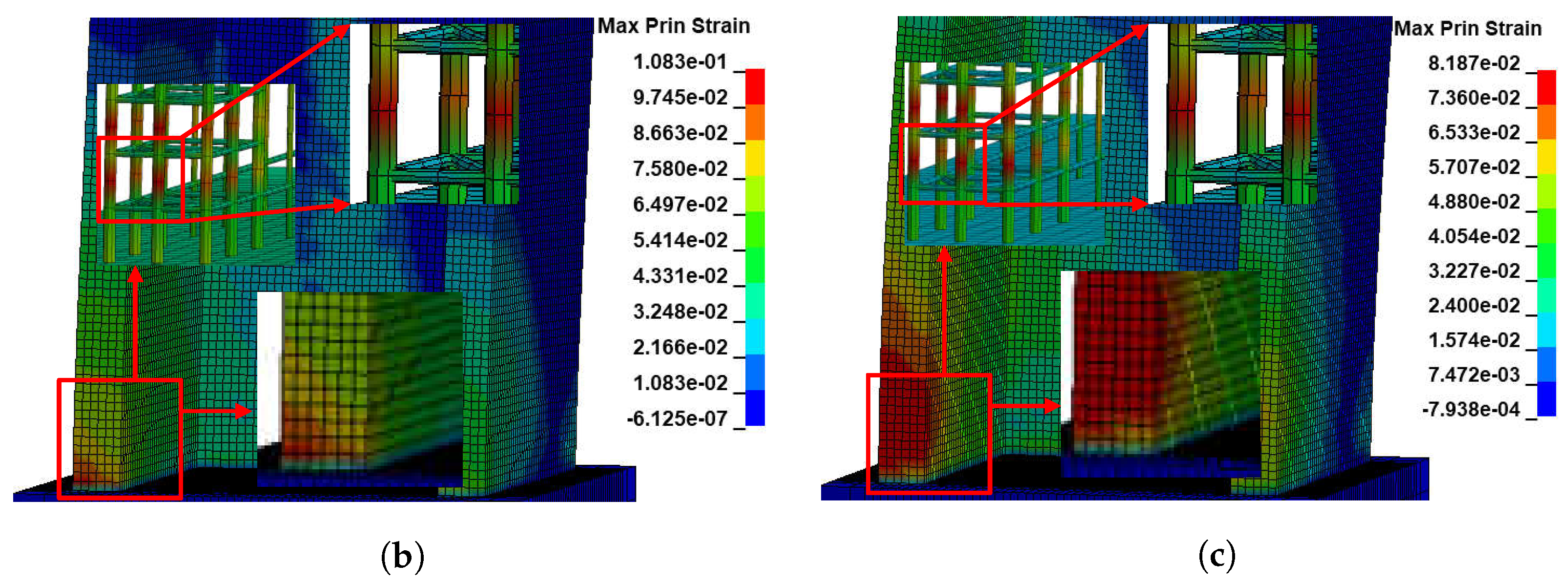
4.2.2. Failure Behaviour
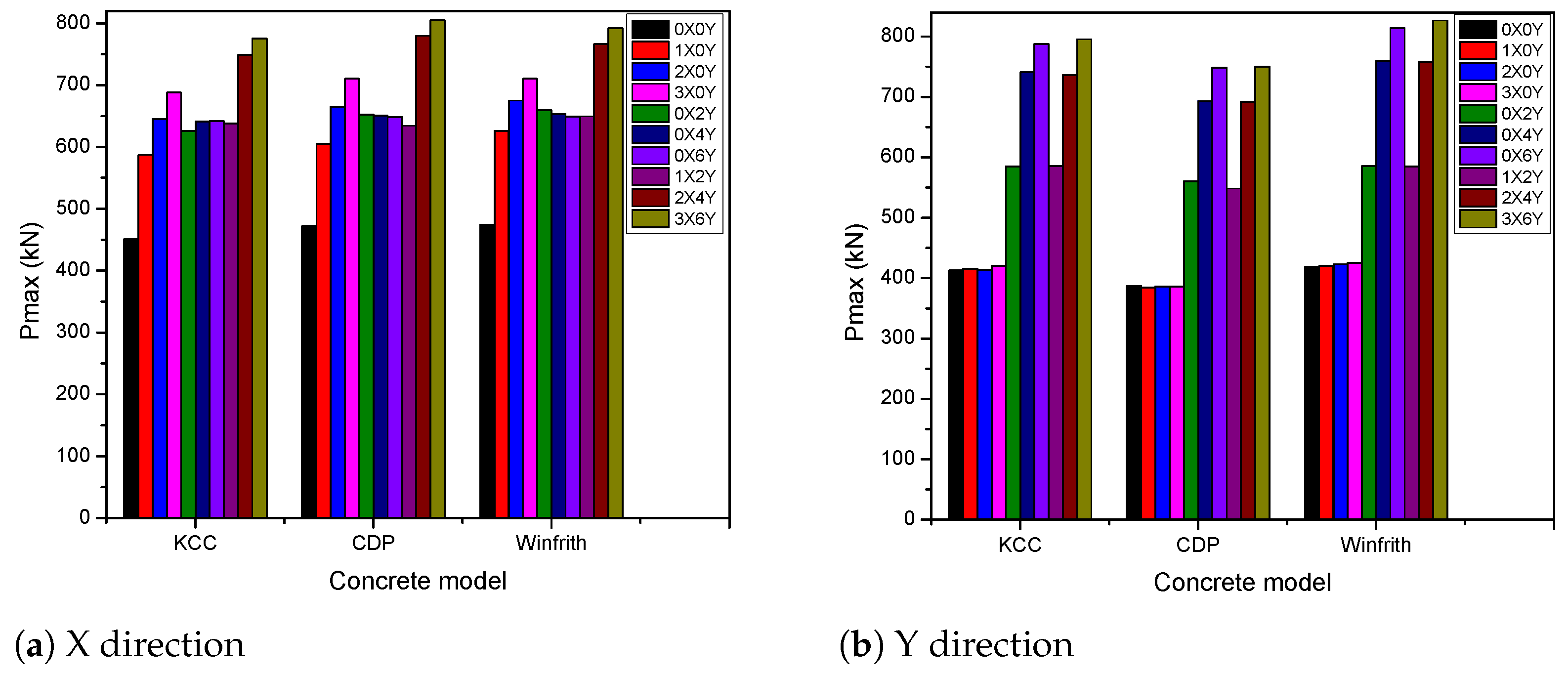
5. Effect of PT Bars for Reinforced Concrete Walls
5.1. Effect of PT Bars for PT 2D Wall
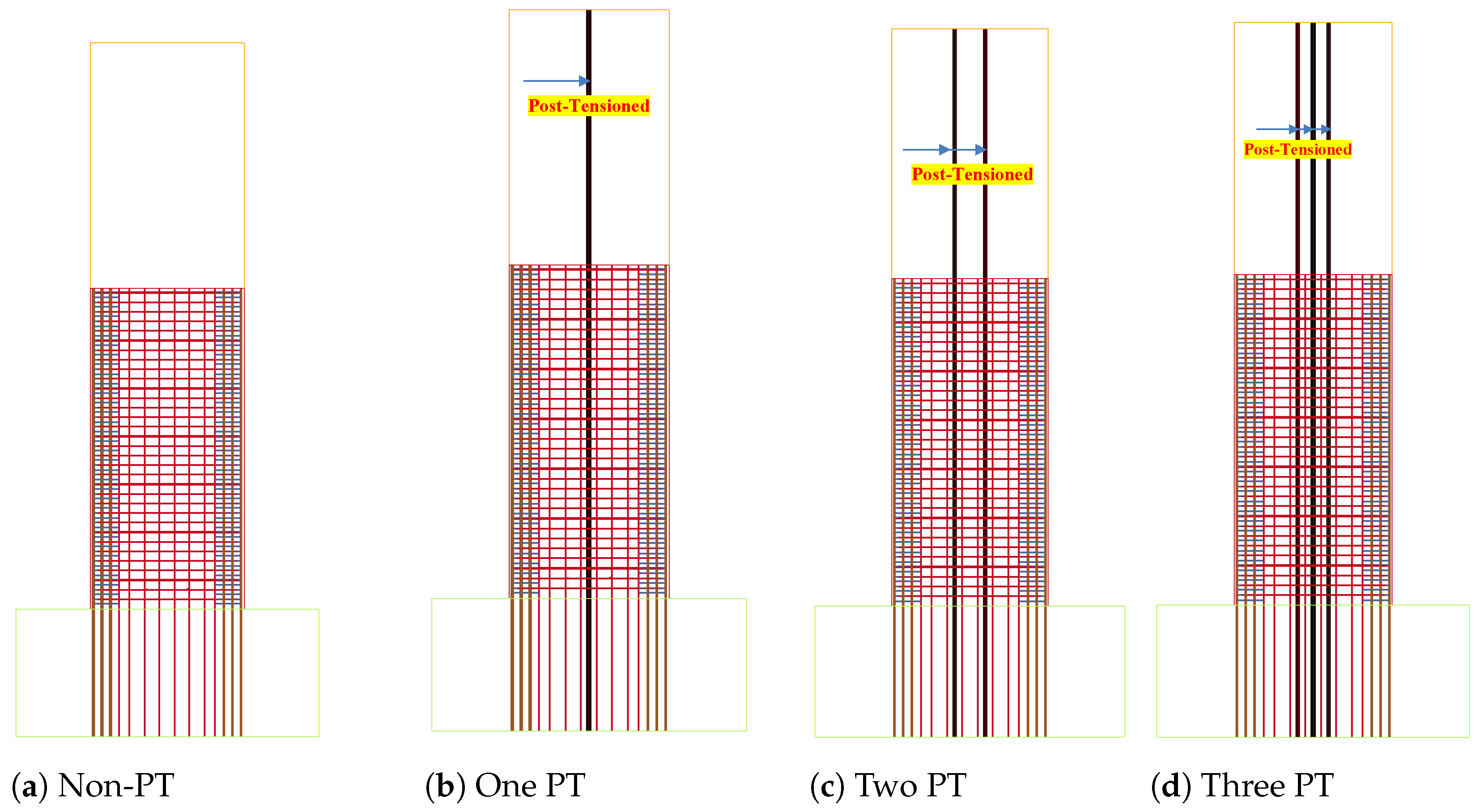
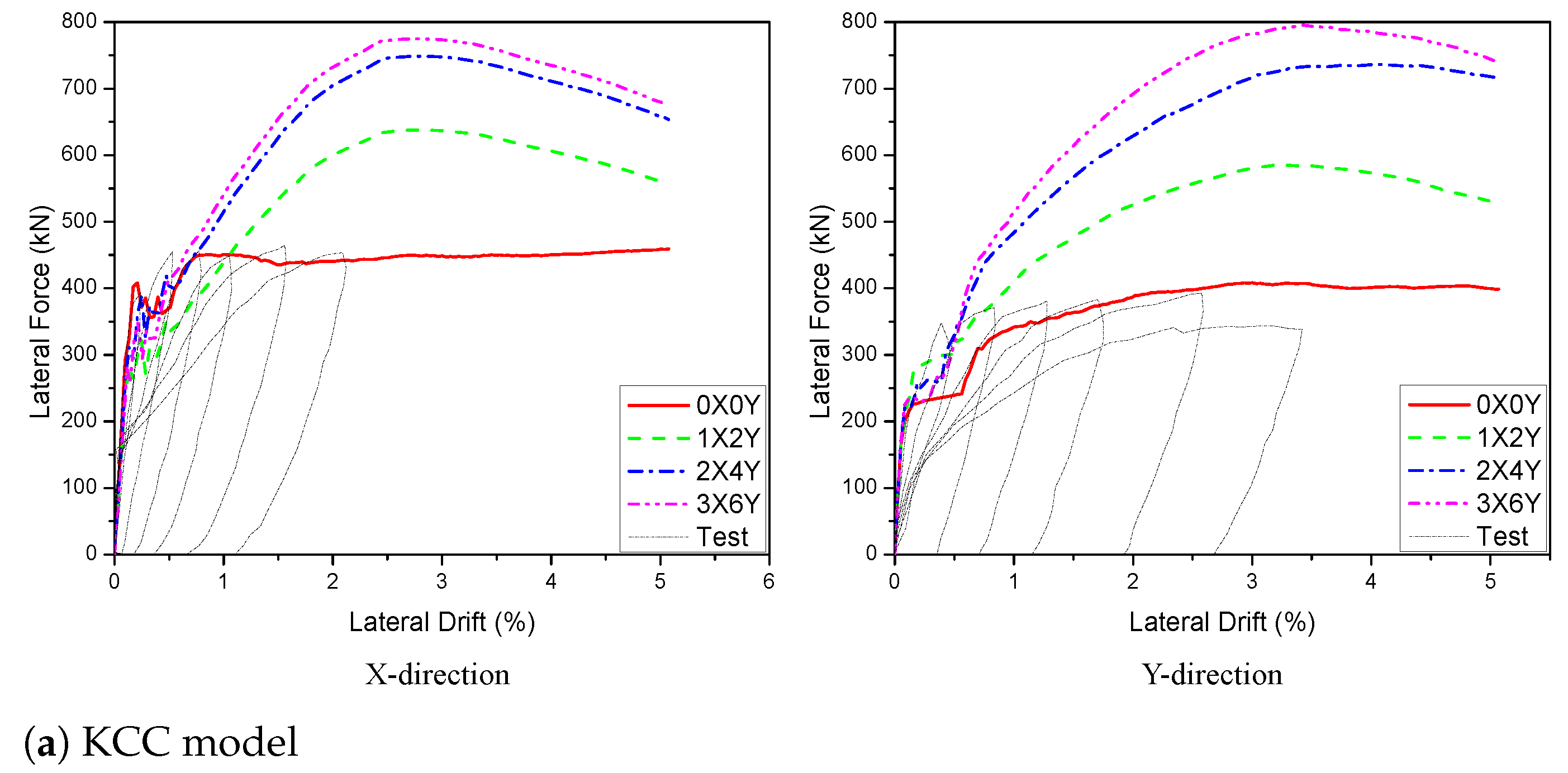
5.1.1. Effect of PT Quantities
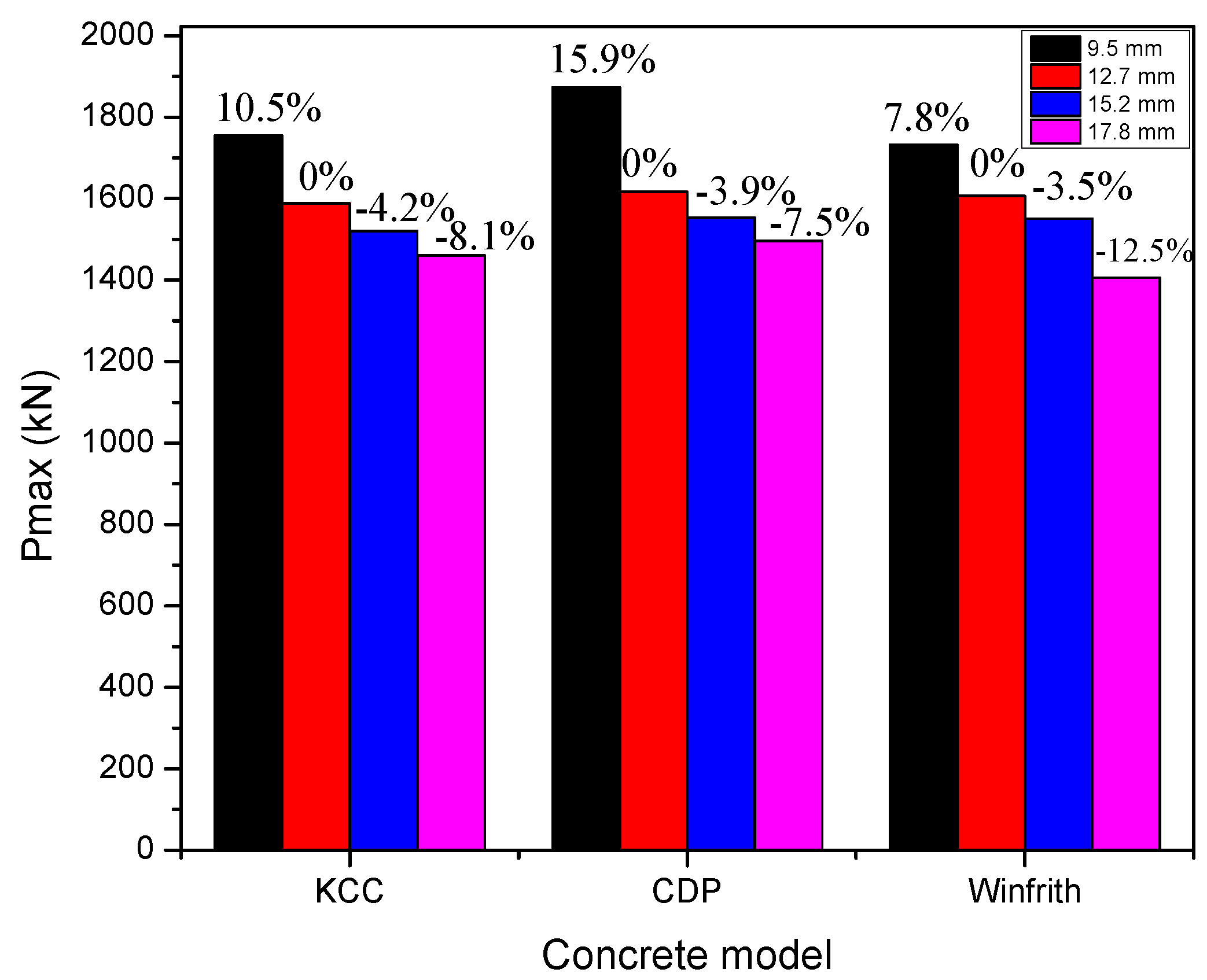
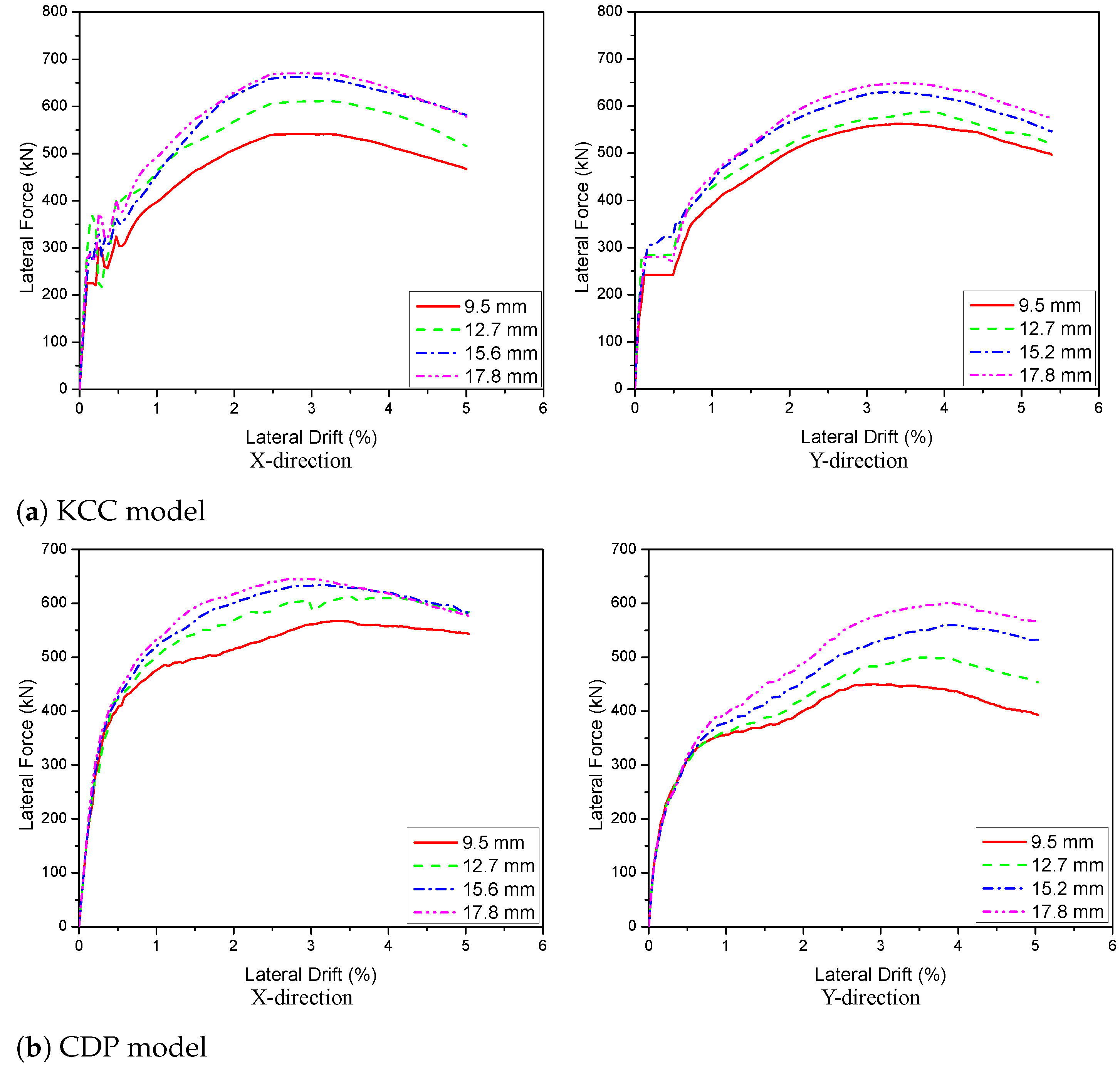
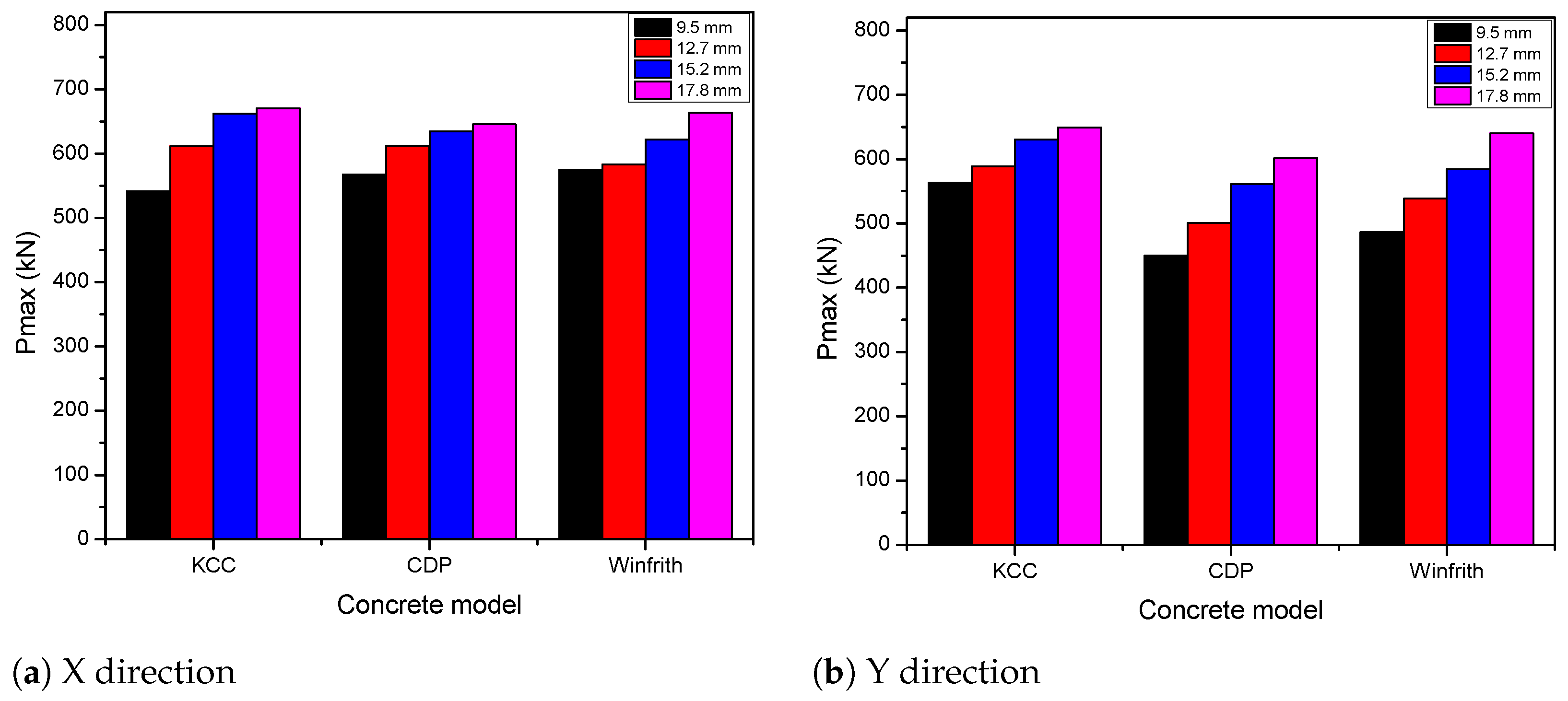
5.1.2. Effect of PT Diameter
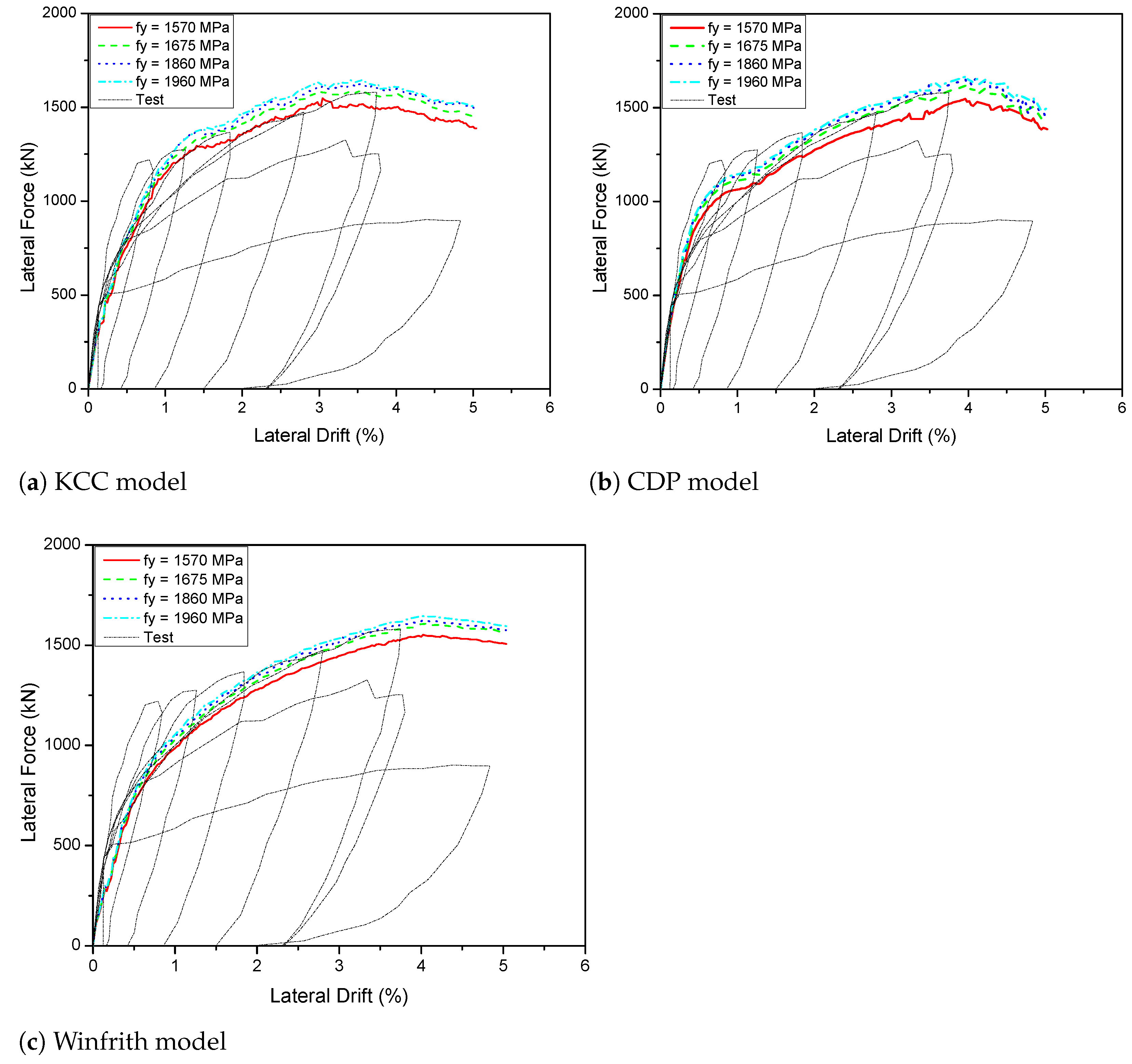
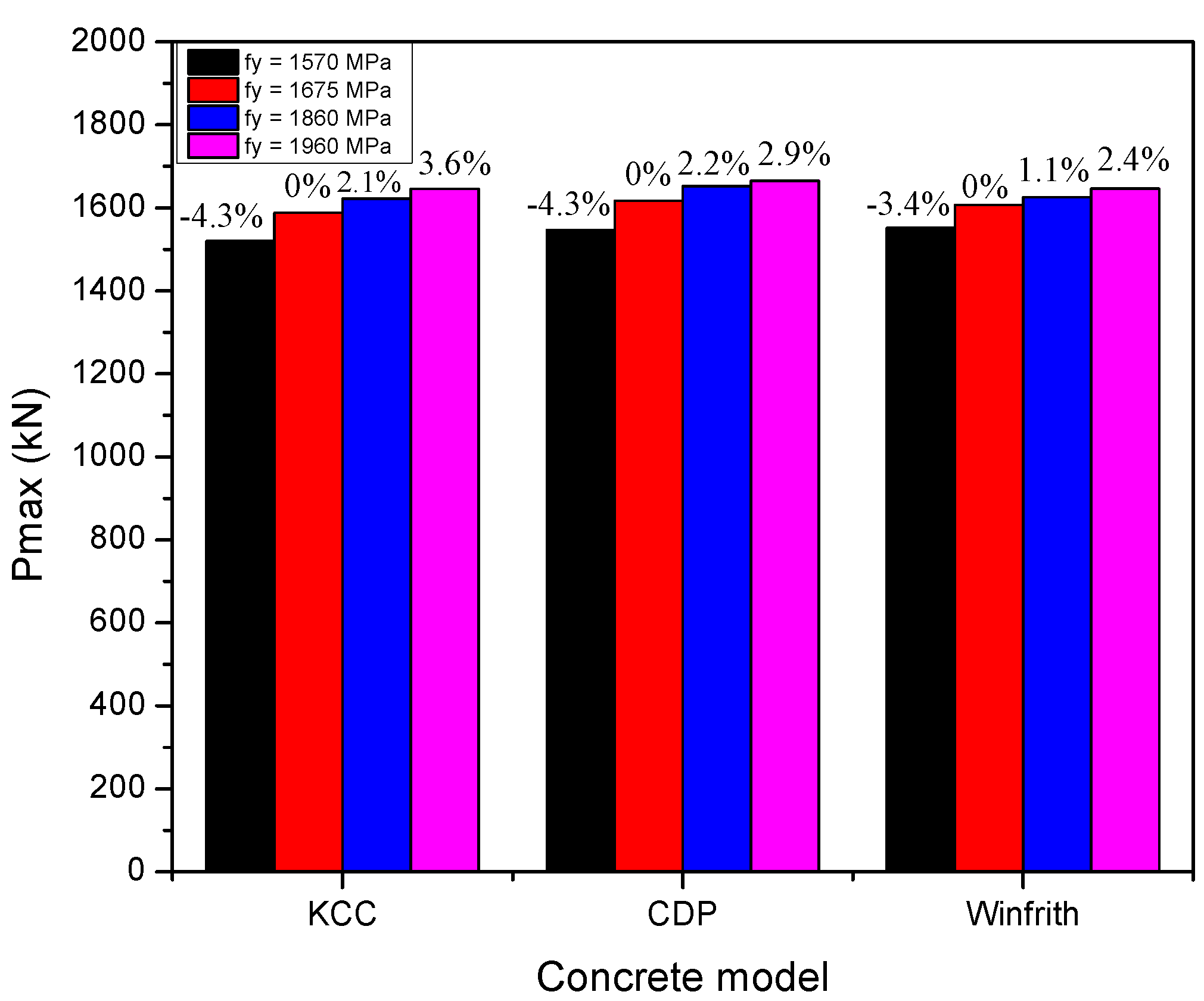
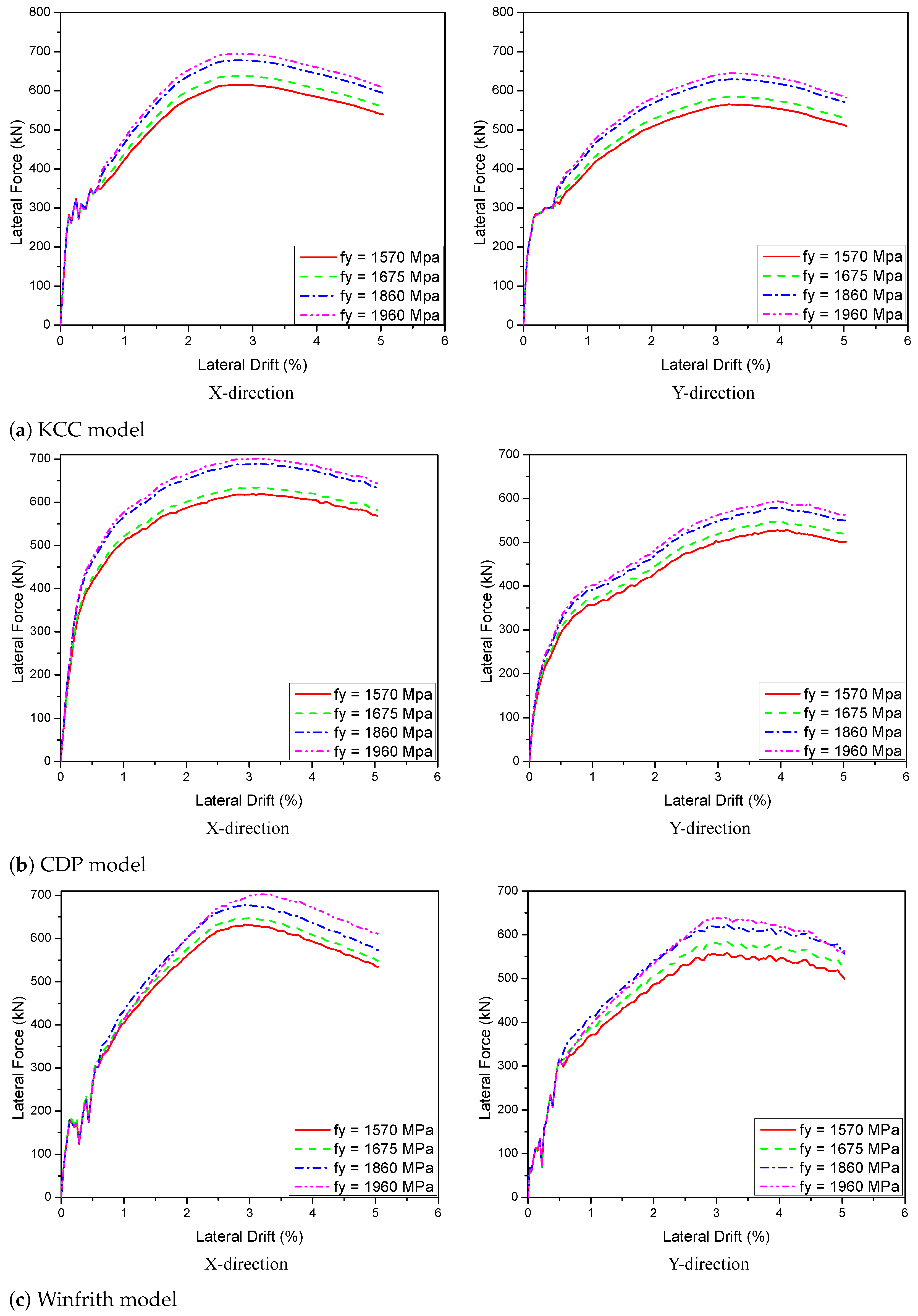
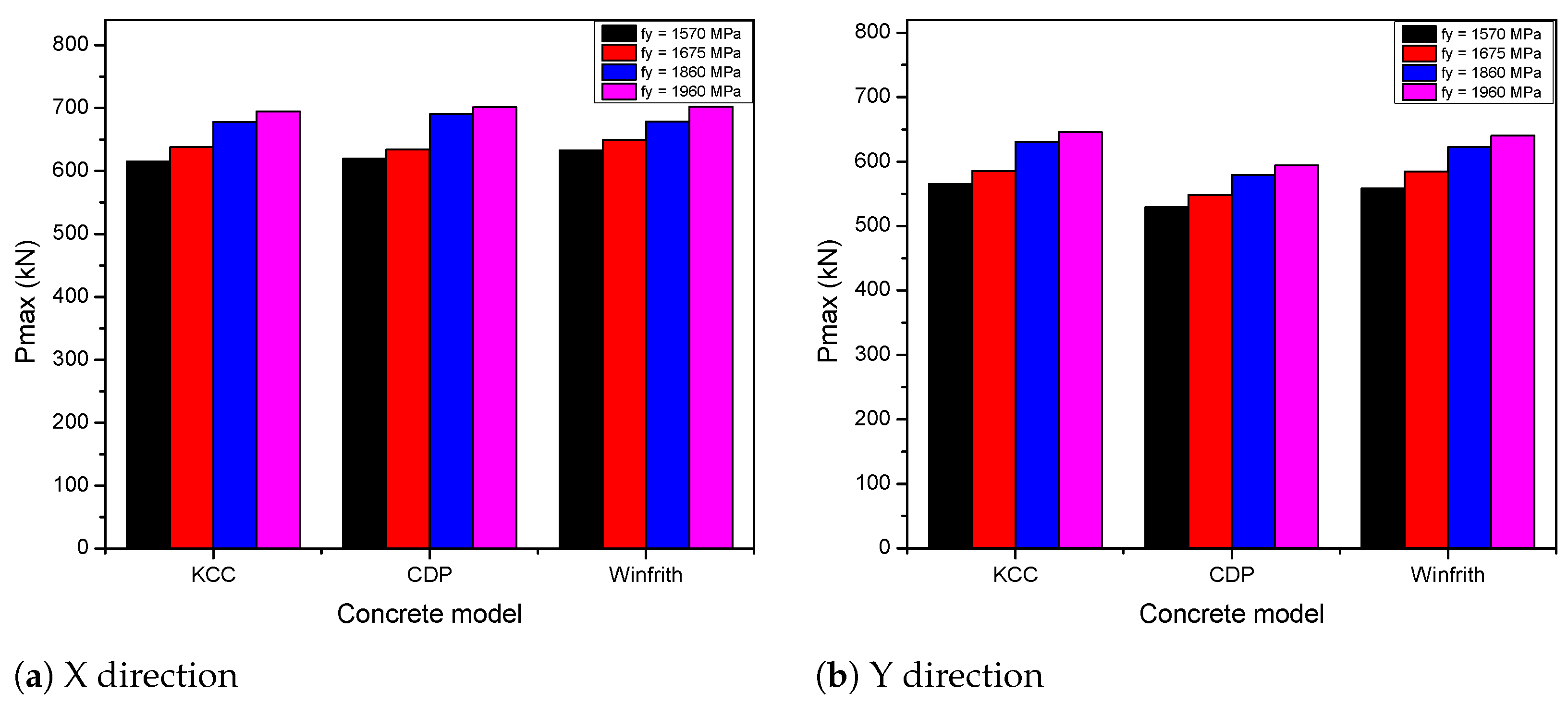
5.1.3. Effect of PT Yield Strength
5.2. Effect of PT Bars for PT 3D Wall
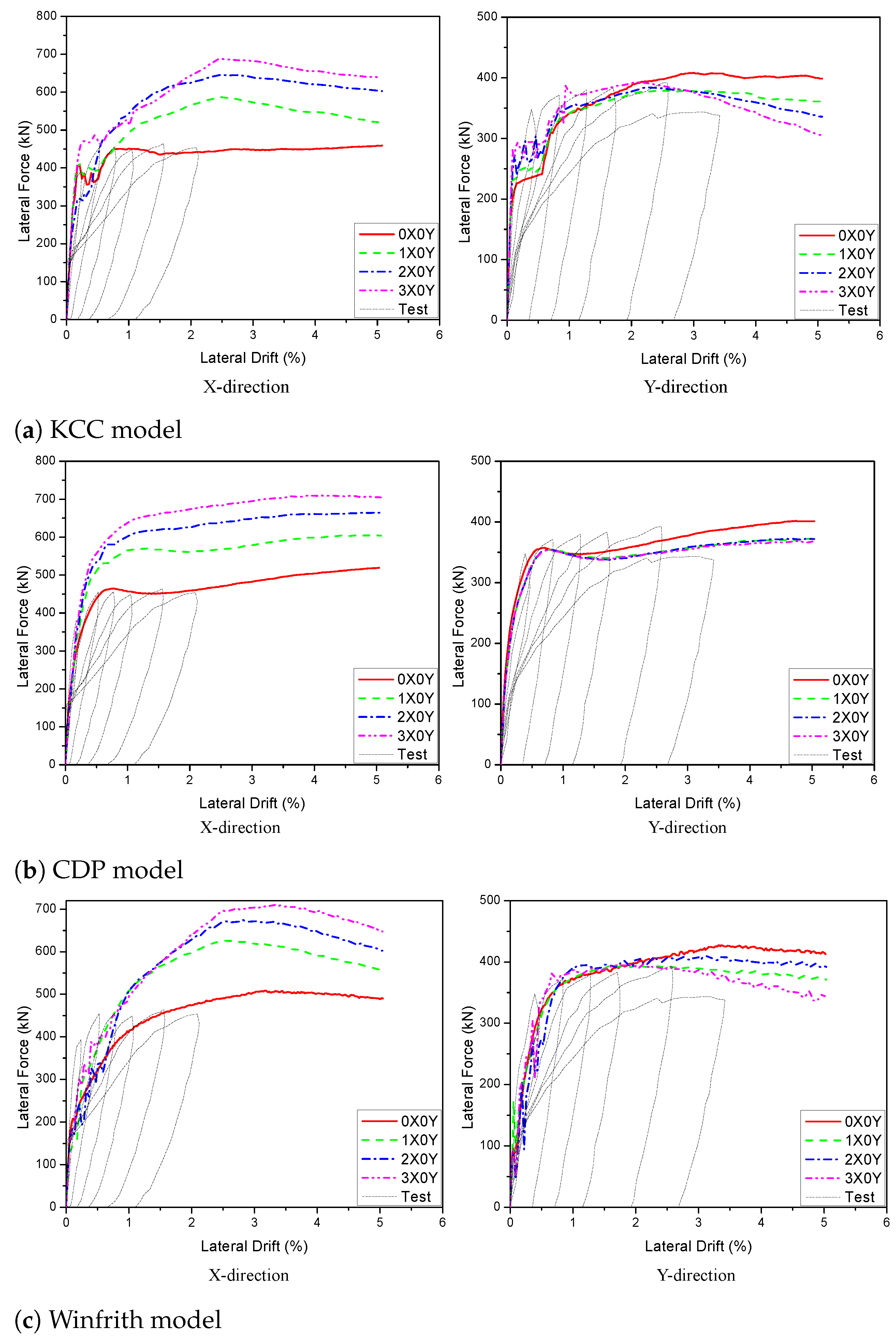
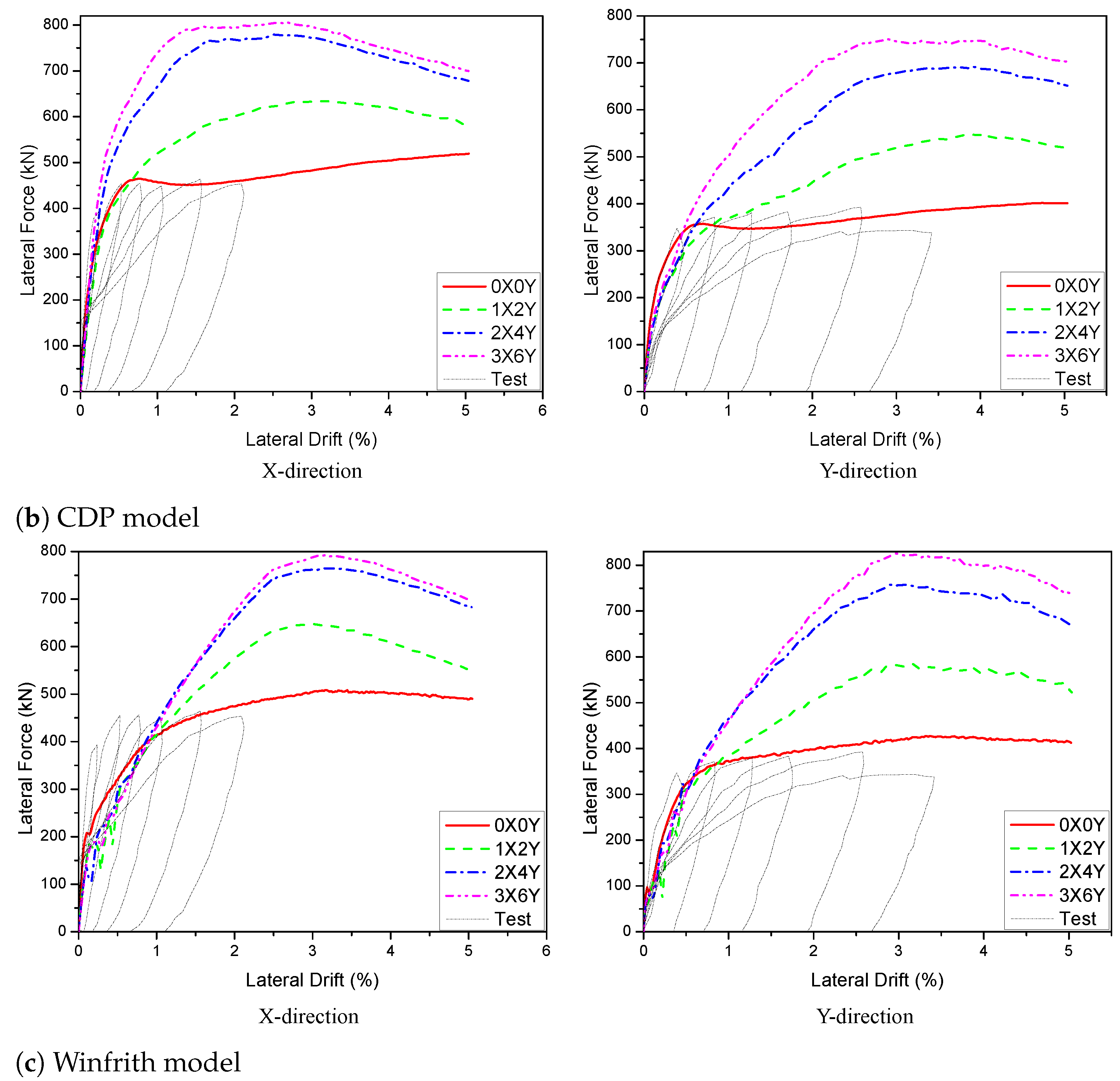
5.2.1. Effect of PT Quantities
5.2.2. Effect of PT Diameter
5.2.3. Effect of the PT Yield Strength
6. Conclusions
- 1.
- All three material models investigated in this study could predict an acceptable peak strength for both PT 2D and 3D walls. The Winfrith model was the best prediction in three models based on the outstanding capability to generate the details of a crack’s location as well as its dimensions. Additionally, not only could it accurately predict the failure position of concrete as compared to the experimental, but the Winfrith model could also identify the regions of maximum flexural stresses in rebars.
- 2.
- The strain rate did not significantly influence the force–displacement relationships for KCC and CDP models but the Winfrith model was converse and the RATE = 1 was appropriate for this model for 2D walls. All three models have a profound effect with the strain rate and the RATE = 1 provided reasonable prediction for the Winfrith model for 3D walls. Because the mesh size of 25 mm and type of element of ELFORM = 1 were suitable for predicting the peak load and minimizing computational time, they were chosen for the numerical simulation.
- 3.
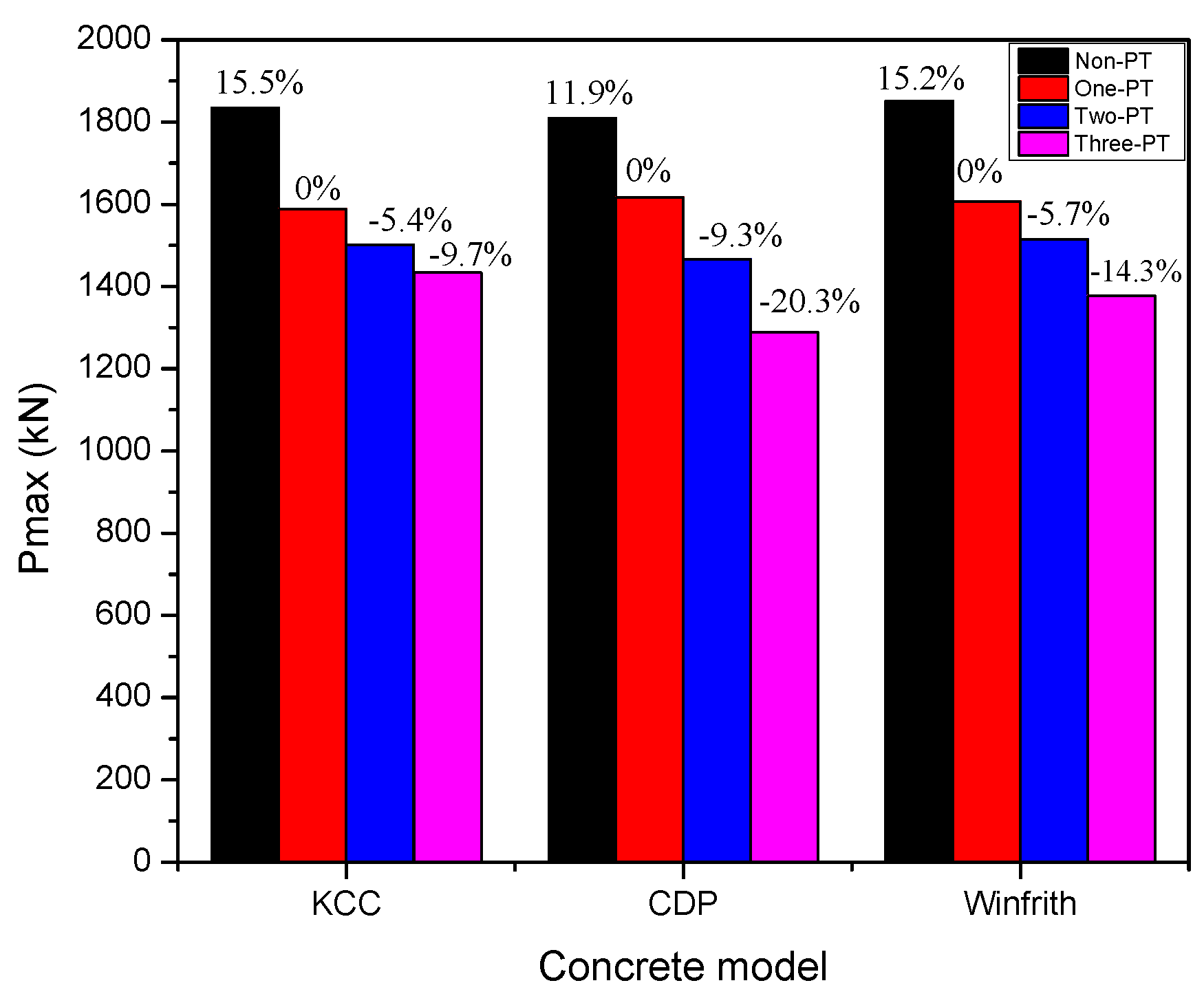
- The number of PT had the greatest influence on lateral strength bearing capacity; yield strength had a negligible effect for PT 2D walls. Based on the numerical simulations, the PT quantity (2X4Y), the PT diameter (15.2 mm) and the yield strength ( = 1860 MPa) were selected to efficiently enhance the bearing capacity of lateral strength for PT 3D walls.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheok, G.S. A hybrid reinforced precast frame for seismic regions. PCI J. 1997, 42, 20–32. [Google Scholar]
- Kurama, Y.; Sause, R.; Pessiki, S.; Lu, L.W. Lateral load behavior and seismic design of unbonded post-tensioned precast concrete walls. Struct. J. 1999, 96, 622–632. [Google Scholar]
- Twigden, K.M. Dynamic Response of Unbonded Post-Tensioned Concrete Walls for Seismic Resilient Structures. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 2016. [Google Scholar]
- Chou, C.C.; Chen, J.H. Analytical model validation and influence of column bases for seismic responses of steel post-tensioned self-centering MRF systems. Eng. Struct. 2011, 33, 2628–2643. [Google Scholar] [CrossRef]
- Kalliontzis, D.; Sritharan, S. Seismic behavior of unbonded post-tensioned precast concrete members with thin rubber layers at the jointed connection. PCI J. 2021, 66, 60–76. [Google Scholar] [CrossRef]
- Christopoulos, C.; Filiatrault, A.; Uang, C.M.; Folz, B. Posttensioned energy dissipating connections for moment-resisting steel frames. J. Struct. Eng. 2002, 128, 1111–1120. [Google Scholar] [CrossRef]
- Newcombe, M.; Pampanin, S.; Buchanan, A.; Palermo, A. Section analysis and cyclic behavior of post-tensioned jointed ductile connections for multi-story timber buildings. J. Earthq. Eng. 2008, 12, 83–110. [Google Scholar] [CrossRef]
- Kurama, Y.C. Seismic design of partially post-tensioned precast concrete walls. PCI J. 2005, 50, 100. [Google Scholar] [CrossRef]
- Aaleti, S.; Sritharan, S. A simplified analysis method for characterizing unbonded post-tensioned precast wall systems. Eng. Struct. 2009, 31, 2966–2975. [Google Scholar] [CrossRef]
- Ou, Y.C.; Chiewanichakorn, M.; Aref, A.J.; Lee, G.C. Seismic performance of segmental precast unbonded posttensioned concrete bridge columns. J. Struct. Eng. 2007, 133, 1636–1647. [Google Scholar] [CrossRef]
- Xu, G.; Li, A. Seismic performance and design approach of unbonded post-tensioned precast sandwich wall structures with friction devices. Eng. Struct. 2020, 204, 110037. [Google Scholar] [CrossRef]
- Hallquist, J.O. LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation: Troy, MI, USA, 2007; Volume 970, pp. 299–800. [Google Scholar]
- Riedel, W. 10 years RHT: A review of concrete modelling and hydrocode applications. In Predictive Modeling of Dynamic Processes; Springer: Berlin/Heidelberg, Germany, 2009; pp. 143–165. [Google Scholar]
- Xu, J.; Lu, Y. A comparative study of modelling RC slab response to blast loading with two typical concrete material models. Int. J. Prot. Struct. 2013, 4, 415–432. [Google Scholar] [CrossRef] [Green Version]
- Tu, Z.; Lu, Y. Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations. Int. J. Impact Eng. 2009, 36, 132–146. [Google Scholar] [CrossRef]
- Bao, X.; Li, B. Residual strength of blast damaged reinforced concrete columns. Int. J. Impact Eng. 2010, 37, 295–308. [Google Scholar] [CrossRef]
- Zhang, C.; Abedini, M.; Mehrmashhadi, J. Development of pressure-impulse models and residual capacity assessment of RC columns using high fidelity Arbitrary Lagrangian-Eulerian simulation. Eng. Struct. 2020, 224, 111219. [Google Scholar] [CrossRef]
- Abedini, M.; Zhang, C. Performance assessment of concrete and steel material models in ls-dyna for enhanced numerical simulation, a state of the art review. Arch. Comput. Methods Eng. 2021, 28, 2921–2942. [Google Scholar] [CrossRef]
- Mutalib, A.A.; Tawil, N.M.; Baharom, S.; Abedini, M. Failure probabilities of FRP strengthened RC column to blast loads. J. Teknol. 2013, 65, 135–141. [Google Scholar] [CrossRef] [Green Version]
- Asgarpoor, M.; Gharavi, A.; Epackachi, S. Investigation of various concrete materials to simulate seismic response of RC structures. Structures 2021, 29, 1322–1351. [Google Scholar] [CrossRef]
- Mohammed, T.A.; Parvin, A. Evaluating damage scale model of concrete materials using test data. Adv. Concr. Constr. 2013, 1, 289. [Google Scholar] [CrossRef] [Green Version]
- Kazaz, l.; Yakut, A.; Polat, G. Numerical Simulation of Dynamic Shear Wall Tests: A Benchmark Study. Comput. Struct. 2006, 84, 549–562. [Google Scholar] [CrossRef]
- Morales, E.; Filiatrault, A.; Aref, A. Sustainable and low cost room seismic isolation for essential care units of hospitals in developing countries. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Sanja, H.; Yves, M.; Urs, B.; Tadeusz, S.; Dimitrios, Z. Beyond Design Seismic Capacity Of Squat RC Shear Walls: Lessons Learnt From Phase 2 Of The CASH Benchmark Exercise Using LS-DYNA. In Proceedings of the Transactions, SMiRT-25, Charlotte, NC, USA, 4–9 August 2019. [Google Scholar]
- Bojanowski, C.; Kulak, R.F. Seismic and Traffic Load Modeling on Cable Stayed Bridge. Technical Report. 2011. Available online: https://trid.trb.org/view/1092530 (accessed on 2 May 2022).
- Coleman, D.K. Evaluation of Concrete Modeling in LS-DYNA for Seismic Application. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2016. [Google Scholar]
- Sturt, R.; Avanes, C.; Muriithi, B.; Bernardi, M.; Huang, Y. A masonry material model for seismic analysis in LS-DYNA: Implementation and validation. In Proceedings of the 16th European Conference on Earthquake Engineering, Thessaloniki, Greece, 18–21 June 2018. [Google Scholar]
- Bocciarelli, M.; Barbieri, G. A numerical procedure for the pushover analysis of masonry towers. Soil Dyn. Earthq. Eng. 2017, 93, 162–171. [Google Scholar] [CrossRef]
- Chomchuen, P.; Boonyapinyo, V. Incremental dynamic analysis with multi-modes for seismic performance evaluation of RC bridges. Eng. Struct. 2017, 132, 29–43. [Google Scholar] [CrossRef]
- Fanaie, N.; Ezzatshoar, S. Studying the seismic behavior of gate braced frames by incremental dynamic analysis (IDA). J. Constr. Steel Res. 2014, 99, 111–120. [Google Scholar] [CrossRef]
- Taghinezhad, R.; Taghinezhad, A.; Mahdavifar, V.; Soltangharaei, V. Seismic Vulnerability Assessment of Coupled Wall RC Structures. Int. J. Sci. Eng. Appl. 2018, 7, 1–7. [Google Scholar] [CrossRef]
- Pan, X.; Zheng, Z.; Wang, Z. Estimation of floor response spectra using modified modal pushover analysis. Soil Dyn. Earthq. Eng. 2017, 92, 472–487. [Google Scholar] [CrossRef]
- Taghinezhad, R.; Taghinezhad, A.; Mahdavifar, V.; Soltangharaei, V. Numerical Investigation of Deflection Amplification Factor in Moment Resisting Frames Using Nonlinear Pushover Analysis. Int. J. Innov. Eng. Sci. 2017, 2, 1–7. [Google Scholar]
- Seible, F.; LaRovere, H.; Kingsley, G. Nonlinear analysis of reinforced concrete masonry shear wall structures—Monotonic loading. Mason. Soc. J. 1990, 9. [Google Scholar]
- Lotfi, H.R.; Shing, P.B. Interface model applied to fracture of masonry structures. J. Struct. Eng. 1994, 120, 63–80. [Google Scholar] [CrossRef]
- Mehrabi, A.B.; Shing, P.B. Finite element modeling of masonry-infilled RC frames. J. Struct. Eng. 1997, 123, 604–613. [Google Scholar] [CrossRef]
- Damoni, C.; Belletti, B.; Esposito, R. Numerical prediction of the response of a squat shear wall subjected to monotonic loading. Eur. J. Environ. Civ. Eng. 2014, 18, 754–769. [Google Scholar] [CrossRef]
- Li, H.; Shi, G. Material modeling of concrete for the numerical simulation of steel plate reinforced concrete panels subjected to impacting loading. J. Eng. Mater. Technol. 2017, 139, 021011. [Google Scholar] [CrossRef]
- Hong, J.; Fang, Q.; Chen, L.; Kong, X. Numerical predictions of concrete slabs under contact explosion by modified K&C material model. Constr. Build. Mater. 2017, 155, 1013–1024. [Google Scholar]
- Xu, M.; Wille, K. Calibration of K&C concrete model for UHPC in LS-DYNA. In Advanced Materials Research; Trans Tech Publications Ltd.: Bach, Switzerland, 2015; Volume 1081, pp. 254–259. [Google Scholar]
- Kong, X.; Fang, Q.; Li, Q.; Wu, H.; Crawford, J.E. Modified K&C model for cratering and scabbing of concrete slabs under projectile impact. Int. J. Impact Eng. 2017, 108, 217–228. [Google Scholar]
- Deng, Y.; Tuan, C.Y. Design of concrete-filled circular steel tubes under lateral impact. ACI Struct. J. 2013, 110, 691. [Google Scholar]
- Pham, T.M.; Hao, Y.; Hao, H. Sensitivity of impact behaviour of RC beams to contact stiffness. Int. J. Impact Eng. 2018, 112, 155–164. [Google Scholar] [CrossRef]
- Wu, J.; Liu, X.; Zhou, H.; Li, L.; Liu, Z. Experimental and numerical study on soft-hard-soft (SHS) cement based composite system under multiple impact loads. Mater. Des. 2018, 139, 234–257. [Google Scholar] [CrossRef] [Green Version]
- Malvar, L.J.; Crawford, J.E. Dynamic Increase Factors for Concrete; Technical Report; Naval Facilities Engineering Service Center: Port Hueneme, CA, USA, 1998. [Google Scholar]
- Grassl, P.; Jirásek, M. Damage-plastic model for concrete failure. Int. J. Solids Struct. 2006, 43, 7166–7196. [Google Scholar] [CrossRef] [Green Version]
- Grassl, P.; Xenos, D.; Nyström, U.; Rempling, R.; Gylltoft, K. CDPM2: A damage-plasticity approach to modelling the failure of concrete. Int. J. Solids Struct. 2013, 50, 3805–3816. [Google Scholar] [CrossRef] [Green Version]
- Broadhouse, B.; Neilson, A. Modelling Reinforced Concrete Structures in DYNA3D; Technical Report; UKAEA Atomic Energy Establishment: Abingdon, UK, 1987. [Google Scholar]
- Pakiding, L.; Pessiki, S.; Sause, R.; Rivera, M. Lateral load response of unbonded post-tensioned cast-in-place concrete walls. In Structures Congress 2015; American Society of Civil Engineers: Reston, VA, USA, 2015; pp. 1338–1349. [Google Scholar]
- Beyer, K.; Dazio, A.; Priestley, M. Quasi-static cyclic tests of two U-shaped reinforced concrete walls. J. Earthq. Eng. 2008, 12, 1023–1053. [Google Scholar] [CrossRef]
- LS-DYNA. Keyword Users Manual-Volume II: Material Models; Livermore Software Technology Corporation: Livermore, CA, USA, 2016. [Google Scholar]
- Abu-Odeh, A. Modeling and simulation of bogie impacts on concrete bridge rails using LS-DYNA. In Proceedings of the 10th International LS-DYNA Users Conference, Dearborn, MI, USA, 8–10 June 2008; Volume 1, pp. 9–20. [Google Scholar]
- Bhargawa, A.; Roddis, W.K.; Marzougui, D.; Mohan, P.K. Analysis of Extended End-Plate Connections Under Cyclic Loading Using the LS-DYNA Implicit Solver. In Proceedings of the 9th International LS-DYNA Conference, Detroit, MI, USA, 4–6 June 2006. [Google Scholar]
- Abedini, M.; Mutalib, A.A.; Raman, S.N.; Akhlaghi, E.; Mussa, M.H.; Ansari, M. Numerical investigation on the non-linear response of reinforced concrete (RC) columns subjected to extreme dynamic loads. J. Asian Sci. Res. 2017, 7, 86–98. [Google Scholar] [CrossRef] [Green Version]
- Lu, G.; Li, X.; Wang, K. A numerical study on the damage of projectile impact on concrete targets. Comput. Concr. 2012, 9, 21–33. [Google Scholar] [CrossRef]
- Majidi, L.; Usefi, N.; Abbasnia, R. Numerical study of RC beams under various loading rates with LS-DYNA. J. Cent. South Univ. 2018, 25, 1226–1239. [Google Scholar] [CrossRef]













| Specimen | ||||
|---|---|---|---|---|
| (MPa) | (MPa) | |||
| Pakiding et al. [49] | 200,000 | 43.4 | 0.0023 | 0.2 |
| PT 2D wall | ||||
| Beyer et al. [50] | 200,000 | 45.0 | 0.0023 | 0.2 |
| 3D wall |
| Specimen | Bar | |||||
|---|---|---|---|---|---|---|
| Type | (MPa) | (MPa) | (MPa) | |||
| Pakiding et al. [49] | #1 | 200,000 | 0.00783 | 0.3 | 519 | 744 |
| PT 2D wall | #2 | 200,000 | 0.00783 | 0.3 | 473 | 742 |
| #3 | 200,000 | 0.00783 | 0.3 | 473 | 742 | |
| #4 | 200,000 | 0.00783 | 0.3 | 441 | 683 | |
| #5 | 200,000 | 0.00783 | 0.3 | 1675 | 2038 | |
| Beyer et al. [50] | #6 | 200,000 | 0.00783 | 0.3 | 519 | 744 |
| 3D wall | #7 | 200,000 | 0.00783 | 0.3 | 518 | 681 |
| Model | Mesh Size | ELFORM | Strain Rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 12.5 mm | 25 mm | 50 mm | 1 | 2 | a | b | c | |||
| KCC | 1558 (0.2%) | 1588 (1.7%) | 1711 (9.6%) | 1612 (3.3%) | 1600 (2.5%) | 1588 (1.7%) | 1578 (1.1%) | 1650 (5.7%) | 1590 (1.9%) | - |
| CDP | 1586 (1.6%) | 1617 (3.6%) | 1698 (8.8%) | 1602 (2.6%) | 1624 (4.1%) | 1617 (3.6%) | 1632 (4.5%) | 1640 (5.1%) | 1620 (3.8%) | - |
| Winfrith | 1589 (1.8%) | 1607 (2.9%) | 1714 (9.8%) | 1617 (3.5%) | 1617 (3.5%) | 1608 (3.0%) | 1595 (2.2%) | 1720 (10.2%) | 1610 (3.1%) | 1790 (14.7%) |
| Test | 1561 (kN) | 1561 (kN) | 1561 (kN) | |||||||
| Model | Mesh Size | ELFORM | Strain Rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 12.5 mm | 25 mm | 50 mm | 1 | 2 | a | b | c | |||
| KCC | 459.9 (0.2%) | 450.9 (1.8%) | 482.6 (5.1%) | 495.7 (8.0%) | 500.9 (9.1%) | 450.9 (1.8%) | 508.0 (10.7%) | 450.9 (1.8%) | 468.6 (2.1%) | - |
| CDP | 464.7 (1.2%) | 472.0 (2.8%) | 487.9 (6.3%) | 527.3 (14.8%) | 526.9 (14.8%) | 472.0 (2.8%) | 511.2 (11.4%) | 512.1 (11.6%) | 464.7 (1.3%) | - |
| Winfrith | 484.1 (5.5%) | 474.6 (3.4%) | 512.6 (11.7%) | 539.9 (17.6%) | 542.1 (18.1%) | 474.6 (3.4%) | 569.4 (24.1%) | 420.0 (8.5%) | 474.6 (3.4%) | 512.1 (11.6%) |
| Test | 459.0 kN | 459.0 kN | 459.0 kN | |||||||
| Model | Mesh Size | ELFORM | Strain Rate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 12.5 mm | 25 mm | 50 mm | 1 | 2 | a | b | c | |||
| KCC | 401.4 (2.0%) | 412.7 (4.9%) | 404.3 (2.7%) | 452.2 (14.9%) | 456.7 (16.1%) | 412.7 (4.9%) | 450.2 (14.4%) | 412.7 (4.9%) | 404.3 (2.7%) | - |
| CDP | 375.5 (4.6%) | 386.8 (1.7%) | 378.9 (3.7%) | 363.6 (7.6%) | 364.2 (7.4%) | 386.8 (1.7%) | 393.2 (0.1%) | 376.6 (4.3%) | 386.8 (1.7%) | - |
| Winfrith | 429.5 (9.1%) | 418.8 (6.4%) | 454.3 (15.5%) | 452.3 (14.9%) | 454.6 (15.5%) | 418.8 (6.4%) | 439.4 (11.7%) | 362.6 (7.9%) | 418.8 (6.4%) | 450.9 (14.6%) |
| Test | 393.5 kN | 393.5 kN | 393.5 kN | |||||||
| PT Quantities | KCC Model | CDP Model | Winfrith Model | |||
|---|---|---|---|---|---|---|
| Values (kN) | Errors (%) | Values (kN) | Errors (%) | Values (kN) | Errors (%) | |
| Three PT | 1834.1 | 15.5 | 1809.8 | 11.9 | 1850.7 | 15.2 |
| Two PT | 1588.3 | - | 1616.8 | - | 1606.8 | - |
| One PT | 1502.1 | −5.4 | 1466.5 | −9.3 | 1514.8 | −5.7 |
| Non-PT | 1433.9 | −9.7 | 1288.8 | −20.3 | 1376.8 | −14.3 |
| PT Diameters | KCC Model | CDP Model | Winfrith Model | |||
|---|---|---|---|---|---|---|
| Values (kN) | Errors (%) | Values (kN) | Errors (%) | Values (kN) | Errors (%) | |
| 17.8 mm | 1754.8 | 10.5 | 1873.4 | 15.9 | 1732.6 | 7.8 |
| 15.2 mm | 1588.3 | - | 1616.8 | - | 1606.8 | - |
| 12.7 mm | 1520.9 | −4.2 | 1553.3 | −3.9 | 1551.2 | −3.5 |
| 9.5 mm | 1460.5 | −8.1 | 1496.2 | −7.5 | 1406.3 | −12.5 |
| Yield Strength | KCC Model | CDP Model | Winfrith Model | |||
|---|---|---|---|---|---|---|
| Values (kN) | Errors (%) | Values (kN) | Errors (%) | Values (kN) | Errors (%) | |
| MPa | 1520.3 | −4.3 | 1546.8 | −4.3 | 1551.8 | −3.4 |
| MPa | 1588.34 | - | 1616.8 | - | 1606.8 | - |
| MPa | 1621.9 | 2.1 | 1652.3 | 2.2 | 1625.2 | 1.1 |
| MPa | 1645.8 | 3.6 | 1665.3 | 2.9 | 1646.1 | 2.4 |
| PT Quantities | KCC Model | CDP Model | Winfrith Model | |||
|---|---|---|---|---|---|---|
| Values (kN) | Errors (%) | Values (kN) | Errors (%) | Values (kN) | Errors (%) | |
| 0X0Y | 450.9 | - | 472 | - | 474.6 | - |
| 1X0Y | 587.1 | 30.2 | 605.1 | 28.2 | 626 | 31.9 |
| 2X0Y | 645.5 | 43.2 | 665 | 40.1 | 674.9 | 42.2 |
| 3X0Y | 687.9 | 52.5 | 710.2 | 50.5 | 710.5 | 49.7 |
| 0X2Y | 625.9 | 38.8 | 652.3 | 38.2 | 659.5 | 38.9 |
| 0X4Y | 640.8 | 42.1 | 650.4 | 37.8 | 652.9 | 37.6 |
| 0X6Y | 641.9 | 42.4 | 648.6 | 37.4 | 649 | 36.7 |
| 1X2Y | 637.9 | 41.5 | 634.3 | 34.4 | 649.3 | 36.8 |
| 2X4Y | 748.8 | 66.1 | 779.5 | 65.1 | 766.5 | 61.5 |
| 3X6Y | 775.1 | 71.9 | 805.4 | 70.6 | 792.2 | 66.9 |
| PT Quantities | KCC Model | CDP Model | Winfrith Model | |||
|---|---|---|---|---|---|---|
| Values (kN) | Errors (%) | Values (kN) | Errors (%) | Values (kN) | Errors (%) | |
| 3X0Y | 420.2 | 1.8 | 385.9 | −0.2 | 425.3 | 1.6 |
| 0X2Y | 585.1 | 41.8 | 560.4 | 44.9 | 585.3 | 39.8 |
| 0X0Y | 412.7 | - | 386.8 | - | 418.8 | - |
| 1X0Y | 415.3 | 0.7 | 384.4 | −0.6 | 420.6 | 0.4 |
| 2X0Y | 414.2 | 0.4 | 386.1 | −0.6 | 423.2 | 1.1 |
| 0X4Y | 740.8 | 79.5 | 692.8 | 79.1 | 759.9 | 81.4 |
| 0X6Y | 787.8 | 90.9 | 748.8 | 93.6 | 814 | 94.4 |
| 1X2Y | 585.5 | 41.9 | 548.2 | 41.7 | 584.4 | 39.5 |
| 2X4Y | 736.5 | 78.5 | 692.4 | 79 | 758.3 | 81.1 |
| 3X6Y | 795.6 | 92.8 | 750.3 | 93.4 | 826.5 | 97.3 |
| PT Diameters | KCC Model | CDP Model | Winfrith Model | |||
|---|---|---|---|---|---|---|
| Values (kN) | Errors (%) | Values (kN) | Errors (%) | Values (kN) | Errors (%) | |
| 9.5 mm | 541.4 | −18.3 | 567.4 | −10.5 | 574.6 | −7.7 |
| 12.7 mm | 611.3 | −7.7 | 612.4 | −3.5 | 583.1 | −6.3 |
| 15.2 mm | 662.4 | - | 634.3 | - | 622.2 | - |
| 17.8 mm | 670.3 | 1.2 | 645.4 | 1.7 | 663.9 | 6.7 |
| PT Diameters | KCC Model | CDP Model | Winfrith Model | |||
|---|---|---|---|---|---|---|
| Values (kN) | Errors (%) | Values (kN) | Errors (%) | Values (kN) | Errors (%) | |
| 9.5 mm | 562.9 | −10.7 | 449.9 | −19.8 | 486.4 | −16.8 |
| 12.7 mm | 588.5 | −6.7 | 500.6 | −10.8 | 538.6 | −7.8 |
| 15.2 mm | 630.5 | - | 561.1 | - | 584.4 | - |
| 17.8 mm | 649.5 | 3.0 | 601.4 | 7.2 | 640 | 9.5 |
| Yield Strength | KCC Model | CDP Model | Winfrith Model | |||
|---|---|---|---|---|---|---|
| Values (kN) | Errors (%) | Values (kN) | Errors (%) | Values (kN) | Errors (%) | |
| 1570 MPa | 615.1 | −3.6 | 619.4 | −2.3 | 632.8 | −2.5 |
| 1675 MPa | 637.9 | - | 634.3 | - | 649.3 | - |
| 1860 MPa | 678.1 | 6.3 | 690.3 | 8.8 | 678.8 | 4.5 |
| 1960 MPa | 694.5 | 8.9 | 701.6 | 10.6 | 702.6 | 8.2 |
| Yield Strength | KCC Model | CDP Model | Winfrith Model | |||
|---|---|---|---|---|---|---|
| Values (kN) | Errors (%) | Values (kN) | Errors (%) | Values (kN) | Errors (%) | |
| 1570 MPa | 565.3 | −3.5 | 528.9 | −3.5 | 558.7 | −4.4 |
| 1675 MPa | 585.5 | - | 548.2 | - | 584.4 | - |
| 1860 MPa | 630.5 | 7.7 | 579.4 | 5.7 | 622.8 | 6.6 |
| 1960 MPa | 645.3 | 10.2 | 593.9 | 8.3 | 640 | 9.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, Q.T.; Lee, K.; Kim, S.-J.; Shin, J. Quantifying Effect of Post-Tensioned Bars for Precast Concrete Shear Walls. Sustainability 2022, 14, 6141. https://doi.org/10.3390/su14106141
Bao QT, Lee K, Kim S-J, Shin J. Quantifying Effect of Post-Tensioned Bars for Precast Concrete Shear Walls. Sustainability. 2022; 14(10):6141. https://doi.org/10.3390/su14106141
Chicago/Turabian StyleBao, Quoc To, Kihak Lee, Sung-Jig Kim, and Jiuk Shin. 2022. "Quantifying Effect of Post-Tensioned Bars for Precast Concrete Shear Walls" Sustainability 14, no. 10: 6141. https://doi.org/10.3390/su14106141
APA StyleBao, Q. T., Lee, K., Kim, S.-J., & Shin, J. (2022). Quantifying Effect of Post-Tensioned Bars for Precast Concrete Shear Walls. Sustainability, 14(10), 6141. https://doi.org/10.3390/su14106141







