Drilling Process of GFRP Composites: Modeling and Optimization Using Hybrid ANN
Abstract
:1. Introduction
2. Material and Methods
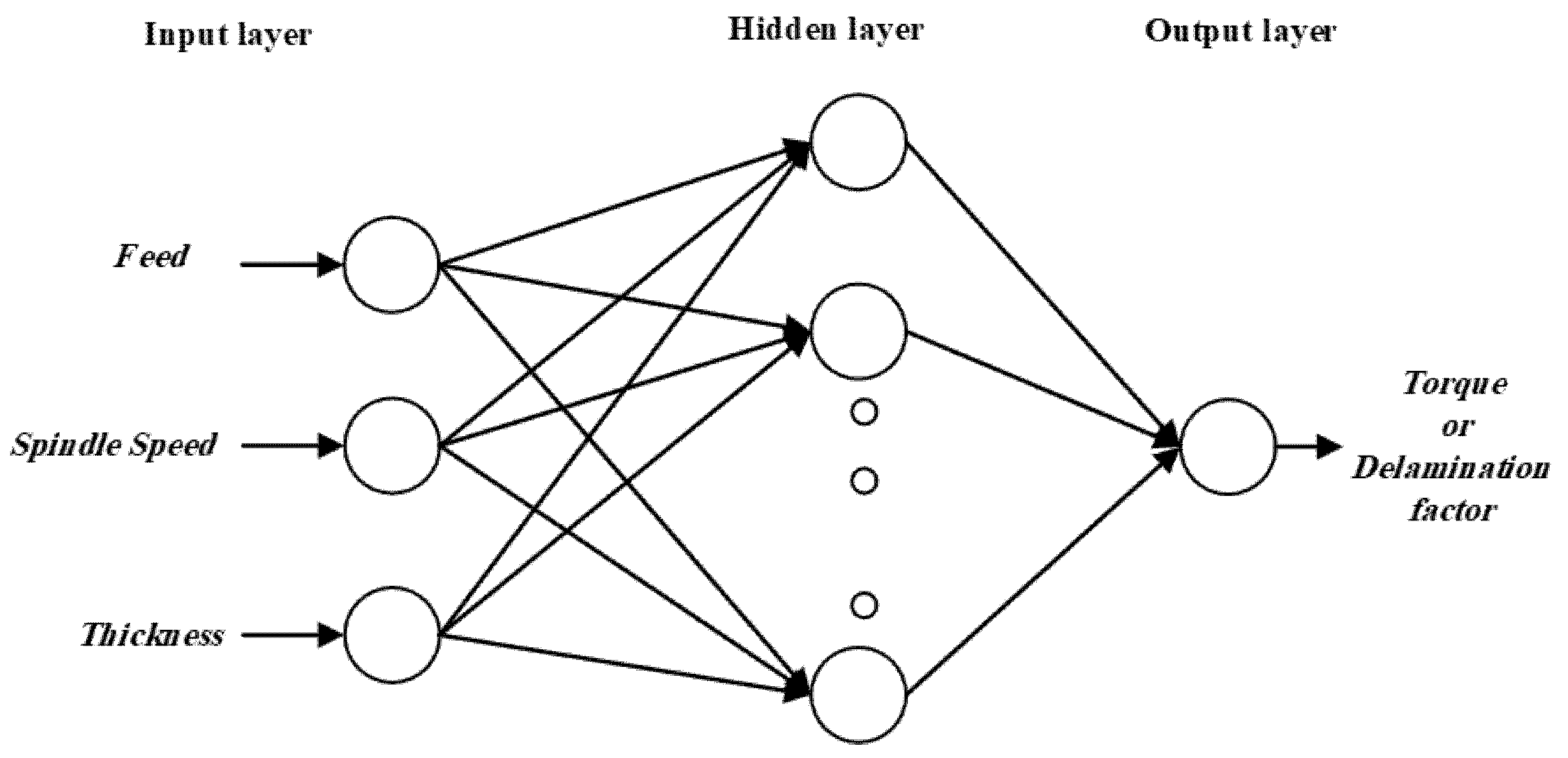
2.1. Artificial Neural Network Models
2.2. Particle Swarm Optimization
2.3. ANN–PSO Model
3. Results and Discussion
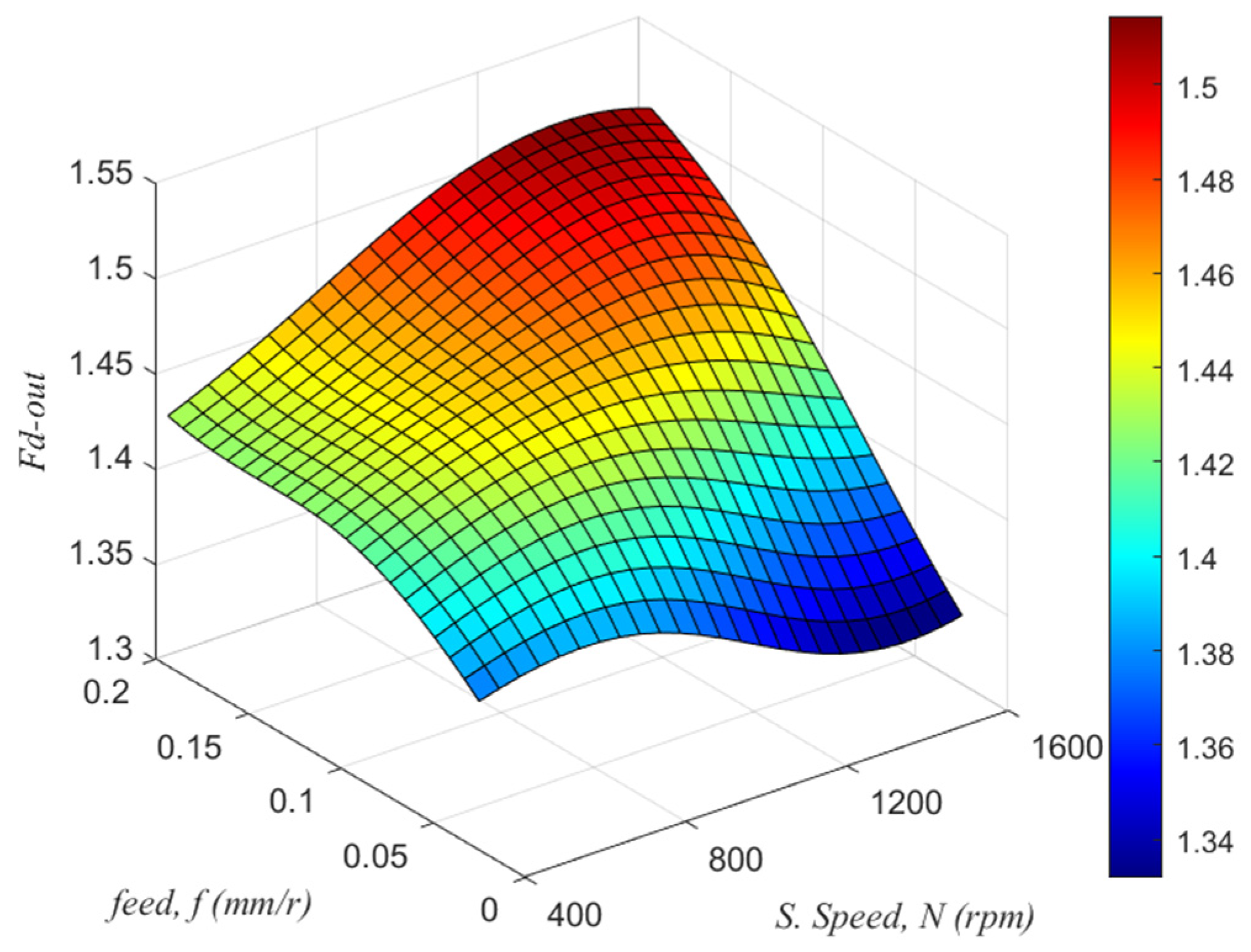
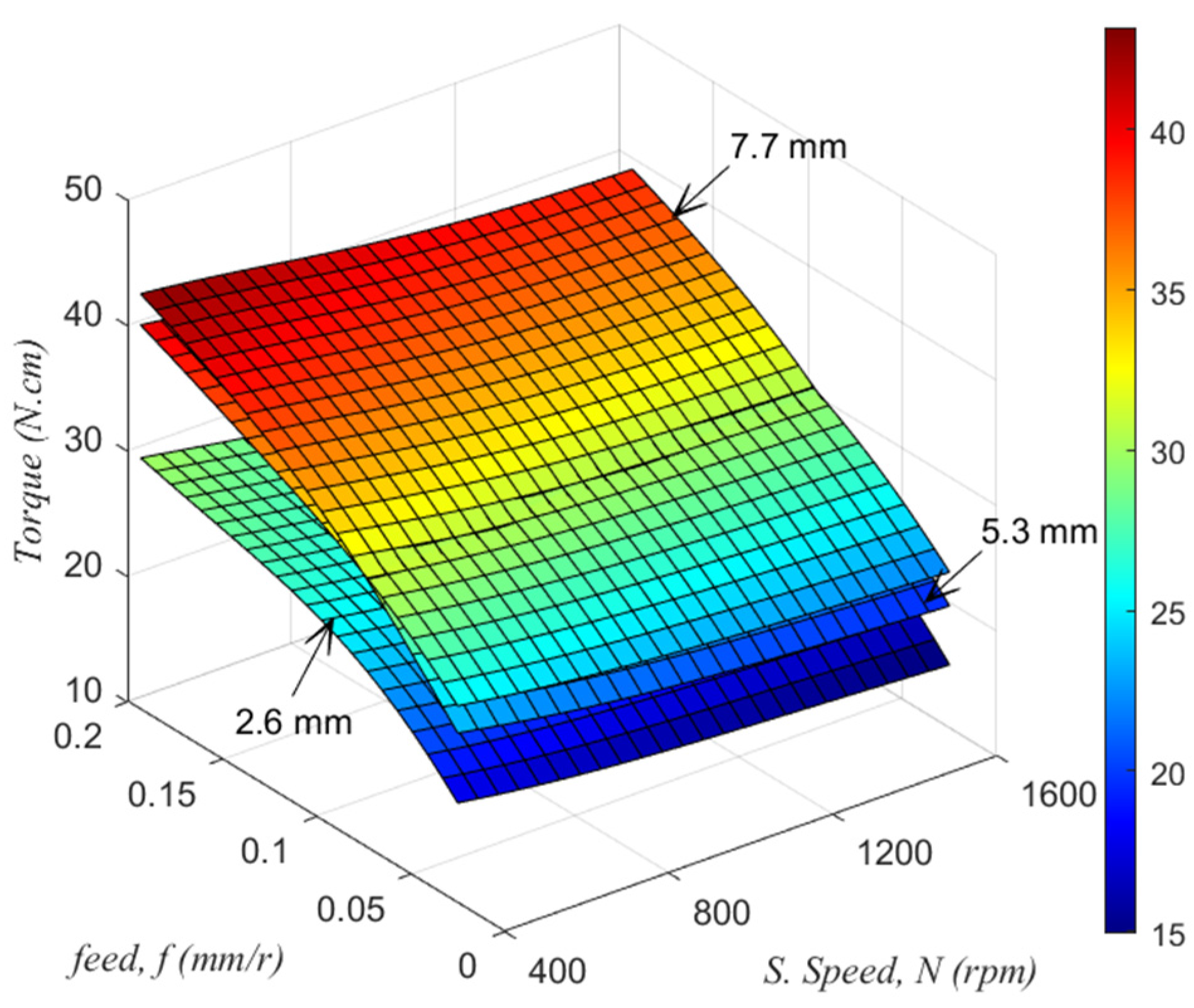
3.1. Effect of Drilling Parameters on the Responses
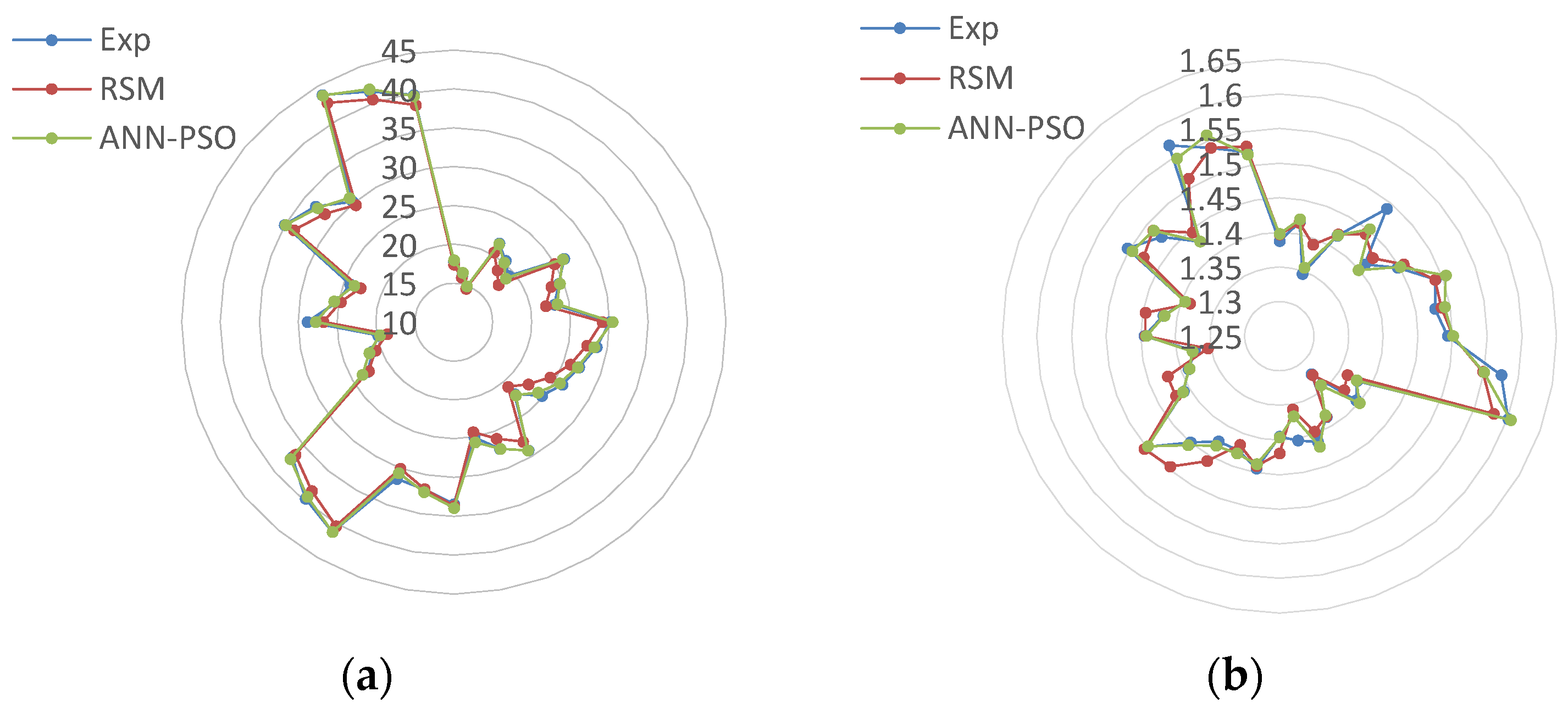
3.2. Prediction of Responses by ANN–PSO Model
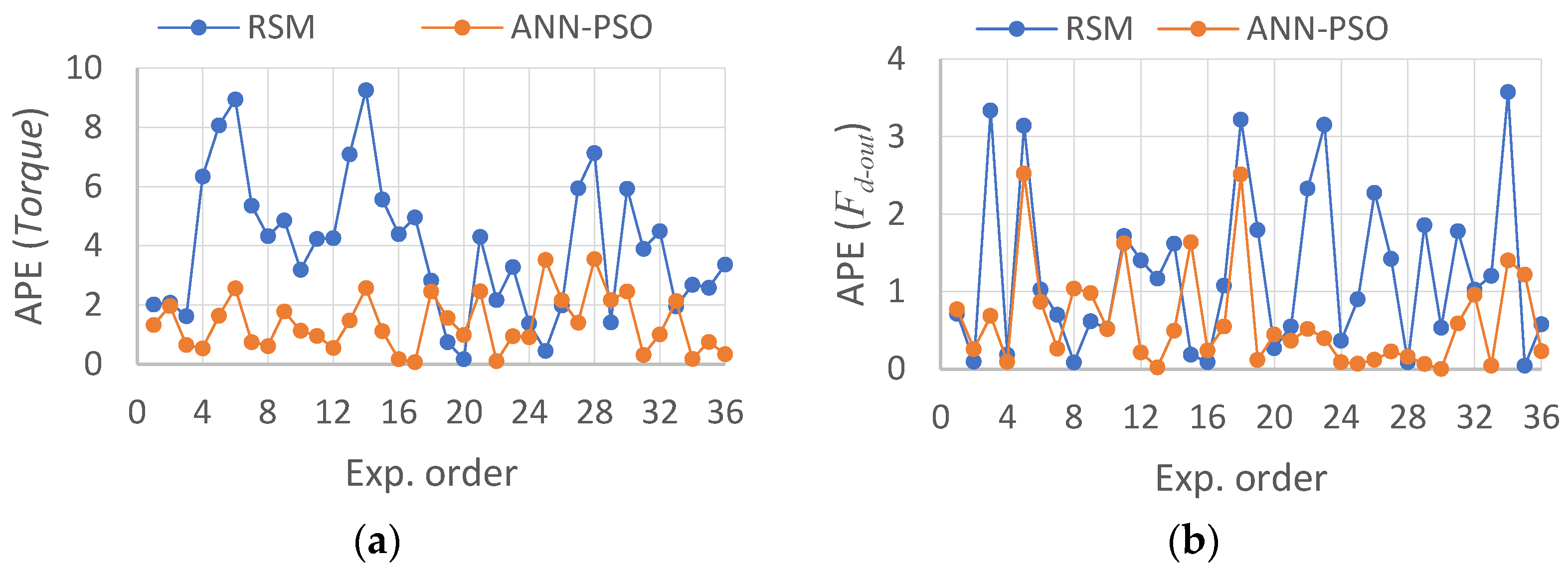
3.3. Comparison of Obtained Predictive Models
3.4. Optimizing Responses
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reisgen, U.; Schiebahn, A.; Lotte, J.; Hopmann, C.; Schneider, D.; Neuhaus, J. Innovative joining technology for the production of hybrid components from FRP and metals. J. Mater. Process. Technol. 2020, 282, 116674. [Google Scholar] [CrossRef]
- Khashaba, U.A.; Othman, R.; Najjar, I.M.R. Effect of Water Absorption on the Impact Behaviors of CFRE Composites. Glob. J. Res. Eng. AMechanical Mech. Eng. 2017, 17. Available online: https://www.engineeringresearch.org/index.php/GJRE/article/view/1693 (accessed on 4 May 2022).
- Malik, K.; Ahmad, F.; Gunister, E. Drilling Performance of Natural Fiber Reinforced Polymer Composites: A Review. J. Nat. Fibers 2021, 1–19. [Google Scholar] [CrossRef]
- Köklü, U.; Mayda, M.; Morkavuk, S.; Avcı, A.; Demir, O. Optimization and prediction of thrust force, vibration and delamination in drilling of functionally graded composite using Taguchi, ANOVA and ANN analysis. Mater. Res. Express 2019, 6, ab2617. [Google Scholar] [CrossRef]
- Khashaba, U.A.; El-Keran, A.A. Drilling analysis of thin woven glass-fiber reinforced epoxy composites. J. Mater. Process. Technol. 2017, 249, 415–425. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Tahboub, K.K.; Rawabdeh, I.A. A design of experiments approach for optimizing an extrusion blow molding process. J. Qual. Maint. Eng. 2004, 10, 47–54. [Google Scholar] [CrossRef]
- Cathie Lee, W.P.; Mah, S.-K.; Leo, C.P.; Wu, T.Y.; Chai, S.-P. Phosphorus removal by NF90 membrane: Optimisation using central composite design. J. Taiwan Inst. Chem. Eng. 2014, 45, 1260–1269. [Google Scholar] [CrossRef]
- El-Midany, T.T.; El-Baz, M.A.; Abdelwahed, M.S. Improve Characteristics of Manufactured Products Using Artificial Neural Network Performance Prediction Model. Int. J. Recent Adv. Mech. Eng. 2013, 2, 23–34. [Google Scholar]
- Khashaba, U.A.; Abd-Elwahed, M.S.; Ahmed, K.I.; Najjar, I.; Melaibari, A.; Eltaher, M.A. Analysis of the machinability of GFRE composites in drilling processes. Steel Compos. Struct. 2020, 36, 417–426. [Google Scholar] [CrossRef]
- Rao, T.B.; Krishna, A.G. Design and Optimization Of Extrusion Process Using FEA And Taguchi Method. Int. J. Eng. Res. Technol. 2012, 1, 1–5. [Google Scholar]
- Nezadi, M.; Keshvari, H.; Yousefzadeh, M. Using Taguchi design of experiments for the optimization of electrospun thermoplastic polyurethane scaffolds. Adv. Nano Res. 2021, 10, 59–69. [Google Scholar]
- Alaoui, A.; El Kacemi, K.; El Ass, K.; Kitane, S. Application of Box-Behnken design to determine the optimal conditions of reductive leaching of MnO2 from manganese mine tailings. Russ. J. Non-Ferr. Met. 2015, 56, 134–141. [Google Scholar] [CrossRef]
- Azizi, A.; Masdarian, M.; Hassanzadeh, A.; Bahri, Z.; Niedoba, T.; Surowiak, A. Parametric Optimization in Rougher Flotation Performance of a Sulfidized Mixed Copper Ore. Minerals 2020, 10, 660. [Google Scholar] [CrossRef]
- Gamal, S.A.; Mohamed, S.; Abd-Elwahed; Hefni, M.A. Controlling Grinding Process Parameters Using Central Composite Design to Reduce Slimes in Phosphate Ore Beneficiation. Rud.-Geol.-Naft. Zb. 2022, 59. [Google Scholar]
- Flores, V.; Keith, B.; Leiva, C. Using Artificial Intelligence Techniques to Improve the Prediction of Copper Recovery by Leaching. J. Sens. 2020, 2020, 2454875. [Google Scholar] [CrossRef] [Green Version]
- Abdelwahed, M.S.; El-Baz, M.A.; El-Midany, T.T. A Proposed Performance Prediction Approach for Manufacturing Processes using ANNs. Int. J. Ind. Manuf. Eng. 2012, 6, 260–265. [Google Scholar] [CrossRef]
- Kharwar, P.; Verma, R. Grey embedded in artificial neural network (ANN) based on hybrid optimization approach in machining of GFRP epoxy composites. FME Trans. 2019, 47, 641–648. [Google Scholar] [CrossRef] [Green Version]
- Tabet, Z.; Belaadi, A.; Boumaaza, M.; Bourchak, M. Drilling of a Bidirectional Jute Fibre and Cork-Reinforced Polymer Biosandwich Structure: ANN and RSM approaches for Modelling and Optimization. Int. J. Adv. Manuf. Technol. 2021, 117, 3819–3839. [Google Scholar] [CrossRef]
- Adda, B.; Belaadi, A.; Boumaaza, M.; Bourchak, M. Experimental investigation and optimization of delamination factors in the drilling of jute fiber–reinforced polymer biocomposites with multiple estimators. Int. J. Adv. Manuf. Technol. 2021, 116, 2885–2907. [Google Scholar] [CrossRef]
- Anarghya, A.; Harshith, D.N.; Rao, N.; Nayak, N.S.; Gurumurthy, B.M.; Abhishek, V.N.; Patil, I.G.S. Thrust and torque force analysis in the drilling of aramid fibre-reinforced composite laminates using RSM and MLPNN-GA. Heliyon 2018, 4, e00703. [Google Scholar] [CrossRef] [Green Version]
- Erturk, A.T.; Vatansever, F.; Yarar, E.; Guven, E.A.; Sinmazcelik, T. Effects of cutting temperature and process optimization in drilling of GFRP composites. J. Compos. Mater. 2020, 55, 235–249. [Google Scholar] [CrossRef]
- Bayraktar, Ş.; Turgut, Y. Determination of delamination in drilling of carbon fiber reinforced carbon matrix composites/Al 6013-T651 stacks. Measurement 2020, 154, 107493. [Google Scholar] [CrossRef]
- Solati, A.; Hamedi, M.; Safarabadi, M. Comprehensive investigation of surface quality and mechanical properties in CO2 laser drilling of GFRP composites. Int. J. Adv. Manuf. Technol. 2019, 102, 791–808. [Google Scholar] [CrossRef]
- Rajaraman, G.; Agasti, S.K.; Jenarthanan, M.P. Investigation on effect of process parameters on delamination during drilling of kenaf-banana fiber reinforced in epoxy hybrid composite using Taguchi method. Polym. Compos. 2019, 41, 994–1002. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X.; Duan, Y. Effects of drilling area temperature on drilling of carbon fiber reinforced polymer composites due to temperature-dependent properties. Int. J. Adv. Manuf. Technol. 2018, 96, 2943–2951. [Google Scholar] [CrossRef]
- Abd-Elwahed, M.; Khashaba, U.; Ahmed, K.; Eltaher, M.; Najjar, I.; Melaibari, A.; Abdraboh, A. Experimental and Numerical FEM of Woven GFRP Composites during Drilling. Struct. Eng. Mech. 2021, 80, 503–522. [Google Scholar] [CrossRef]
- Khashaba, U.A.; Abd-Elwahed, M.S.; Eltaher, M.A.; Najjar, I.; Melaibari, A.; Ahmed, K.I. Thermo-Mechanical and Delamination Properties in Drilling GFRP Composites by Various Drill Angles. Polymers 2021, 13, 1884. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Cater, J.P. Successfully using of peak learning rates of 10 (and greater) in back-propagation networks with the heuristic learning algorithm. In Proceedings of the IEEE First International Conference on Neural Networks, San Diego, CA, USA, 21–24 June 1987; pp. 645–651. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 1944, pp. 1942–1948. [Google Scholar]
- Rukhaiyar, S.; Alam, M.N.; Samadhiya, N.K. A PSO-ANN hybrid model for predicting factor of safety of slope. Int. J. Geotech. Eng. 2017, 12, 556–566. [Google Scholar] [CrossRef]
- Kilickap, E. Analysis and modeling of delamination factor in drilling glass fiber reinforced plastic using response surface methodology. J. Compos. Mater. 2010, 45, 727–736. [Google Scholar] [CrossRef]
- Belaadi, A.; Laouici, H.; Bourchak, M. Mechanical and drilling performance of short jute fibre-reinforced polymer biocomposites: Statistical approach. Int. J. Adv. Manuf. Technol. 2019, 106, 1989–2006. [Google Scholar] [CrossRef]
- Khashaba, U.A.; El-Sonbaty, I.A.; Selmy, A.I.; Megahed, A.A. Drilling analysis of woven glass fiber-reinforced/epoxy composites. J. Compos. Mater. 2012, 47, 191–205. [Google Scholar] [CrossRef]




| Materials of Used Drill | Geometries | ||
|---|---|---|---|
| Material Grade | K200 | D (mm) | 6 |
| ISO Code | K20~K40 | Flute Length (mm) | 28 |
| Tungsten carbide (WC) | 90% | Overall Length (mm) | 66 |
| Cobal (Co) | 10% | Helix Angle | 30° |
| Grain Size (µm) | 0.5~0.8 | Rake Angle | 30° |
| Density (g/cm3) | 14.4 | Clearance Angle | 12° |
| Hardness (HRA) | 91.3 | Point Angles | 100° |
| Rupture Strength Transverse (MPa) | 3920 | Chisel Edge Length (mm) | 0.3 |
| KIC (MPa·m1/2) | 10.5 | ||
| Factors | Levels | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Feed, f (mm/r) | 0.025 | 0.05 | 0.1 | 0.2 |
| Spindle speed, N (rpm) (Cutting speed, m/min) | 400 (7.5) | 800 (15) | 1600 (30) | - |
| Sample thickness, t (mm) | 2.6 | 5.3 | 7.7 | - |
| Spindle Speed, N (rpm) | Feed, f (mm/r) | Thickness, t (2.6 mm) | Thickness, t (5.3 mm) | Thickness, t (7.7 mm) |
|---|---|---|---|---|
| 400 | 0.025 | 17.76 | 26.10 | 22.75 |
| 0.05 | 21.70 | 29.08 | 28.81 | |
| 0.1 | 26.33 | 33.39 | 35.07 | |
| 0.2 | 30.04 | 41.19 | 43.74 | |
| 800 | 0.025 | 16.13 | 24.74 | 21.09 |
| 0.05 | 20.35 | 27.34 | 25.12 | |
| 0.1 | 24.33 | 31.85 | 33.17 | |
| 0.2 | 28.58 | 39.69 | 41.56 | |
| 1600 | 0.025 | 14.83 | 22.08 | 19.91 |
| 0.05 | 19.19 | 25.06 | 24.21 | |
| 0.1 | 23.10 | 31.45 | 30.22 | |
| 0.2 | 27.10 | 37.07 | 39.64 |
| Spindle Speed, N (rpm) | Feed, f (mm/r) | Thickness, t (2.6 mm) | Thickness, t (5.3 mm) | Thickness, t (7.7 mm) |
|---|---|---|---|---|
| 400 | 0.025 | 1.39 | 1.38 | 1.41 |
| 0.05 | 1.42 | 1.39 | 1.44 | |
| 0.1 | 1.45 | 1.39 | 1.50 | |
| 0.2 | 1.49 | 1.43 | 1.57 | |
| 800 | 0.025 | 1.42 | 1.39 | 1.39 |
| 0.05 | 1.49 | 1.41 | 1.42 | |
| 0.1 | 1.49 | 1.44 | 1.47 | |
| 0.2 | 1.58 | 1.45 | 1.54 | |
| 1600 | 0.025 | 1.35 | 1.32 | 1.37 |
| 0.05 | 1.41 | 1.40 | 1.40 | |
| 0.1 | 1.48 | 1.43 | 1.43 | |
| 0.2 | 1.60 | 1.50 | 1.52 |
| Source | Degree of Freedom | Torque (N·cm) | p-Value | Fd-out | p-Value |
|---|---|---|---|---|---|
| f (mm/r) | 3 | 65.48% | 0.000 | 64.22% | 0.000 |
| N (rpm) | 2 | 3.77% | 0.000 | 2.82% | 0.160 |
| t (mm) | 2 | 27.08% | 0.000 | 12.81% | 0.001 |
| Residual/ Error | 28 | 3.67% | 20.05% | ||
| Total | 35 |
| Coeff. Values | ||
|---|---|---|
| Coeff. | T | Fd-out |
| B0 | 2.504821562361 | 1.4573630529957 |
| B1 | 118.92109172956 | 0.94650108016652 |
| B2 | −0.0059756624435889 | 0.00014598690410596 |
| B3 | 7.3417239905438 | −0.06642819426032 |
| B11 | −335.5708004779 | −2.1115459976105 |
| B22 | 0.000002076953125 | −6.7491319444444 × 10−8 |
| B33 | −0.62808747881869 | 0.0073693566932946 |
| B12 | −0.0015827267080745 | 0.00040208364389234 |
| B13 | 9.2268980164296 | −0.015652138293372 |
| B23 | −0.0001833230469607 | −0.00001008312417709 |
| R2 | 0.993 | 0.864 |
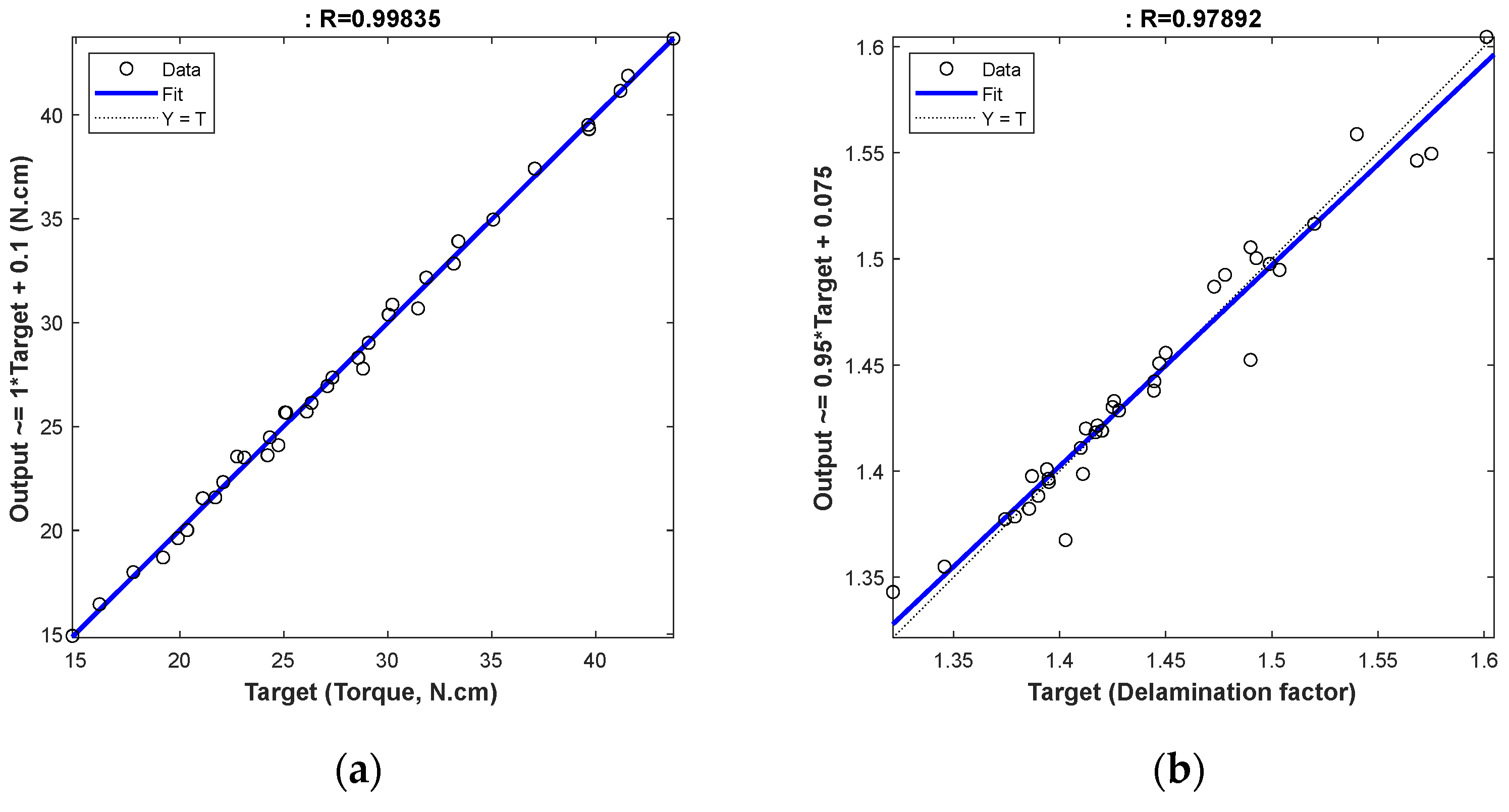
| Model | Network Structure | Mean Square Error | R-Value (R2) |
|---|---|---|---|
| Torque | 3-6-1 | 0.18 | 0.99835 (0.9967) |
| Fd-out | 3-6-1 | 0.16968 × 10−³ | 0.97892 (0.9582) |
| RSM | ANN–PSO | |||||
|---|---|---|---|---|---|---|
| Model | R2 | Mean Square Error | Mean Absolute Percentage Error | R2 | Mean Square Error | Mean Absolute Percentage Error |
| Torque | 0.993 | 1.4277 | 9.249 | 0.9967 | 0.18 | 3.5487 |
| Fd-out | 0.864 | 0.55 × 10−3 | 3.5768 | 0.9582 | 0.17 × 10−3 | 2.5223 |
| Condition | Goal | Lower Limit | Upper Limit | Importance |
|---|---|---|---|---|
| Feed, f (mm/r) | In range | 0.025 | 0.2 | 3 |
| Spindle speed, N (rpm) | In range | 400 | 1600 | 3 |
| Laminate thickness, t (mm) | In range | 2.6 | 7.7 | 3 |
| Fd-out | minimize | 1.3215 | 1.60117 | 4 |
| Torque | minimize | 14.8337 | 43.7449 | 2 |
| Number | N | f | t | Fd_out | Torque | Desirability |
|---|---|---|---|---|---|---|
| 1 | 1600.000 | 0.025 | 5.433 | 1.323 | 21.968 | 0.906 |
| 2 | 1599.998 | 0.025 | 5.413 | 1.323 | 21.959 | 0.906 |
| 3 | 1599.997 | 0.025 | 5.452 | 1.323 | 21.977 | 0.906 |
| 4 | 1599.997 | 0.025 | 5.486 | 1.323 | 21.991 | 0.906 |
| 5 | 1599.990 | 0.025 | 5.366 | 1.324 | 21.935 | 0.906 |
| 6 | 1599.999 | 0.025 | 5.317 | 1.324 | 21.908 | 0.906 |
| 7 | 1599.997 | 0.025 | 5.559 | 1.323 | 22.016 | 0.906 |
| 8 | 1599.998 | 0.025 | 5.583 | 1.323 | 22.022 | 0.905 |
| 9 | 1599.999 | 0.025 | 5.237 | 1.324 | 21.856 | 0.905 |
| 10 | 1599.999 | 0.025 | 5.210 | 1.324 | 21.836 | 0.905 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd-Elwahed, M.S. Drilling Process of GFRP Composites: Modeling and Optimization Using Hybrid ANN. Sustainability 2022, 14, 6599. https://doi.org/10.3390/su14116599
Abd-Elwahed MS. Drilling Process of GFRP Composites: Modeling and Optimization Using Hybrid ANN. Sustainability. 2022; 14(11):6599. https://doi.org/10.3390/su14116599
Chicago/Turabian StyleAbd-Elwahed, Mohamed S. 2022. "Drilling Process of GFRP Composites: Modeling and Optimization Using Hybrid ANN" Sustainability 14, no. 11: 6599. https://doi.org/10.3390/su14116599
APA StyleAbd-Elwahed, M. S. (2022). Drilling Process of GFRP Composites: Modeling and Optimization Using Hybrid ANN. Sustainability, 14(11), 6599. https://doi.org/10.3390/su14116599






