Spatial and Temporal Characteristics of Infiltration Wetting Front of Ring-Shaped Root Emitters
Abstract
:1. Introduction
2. Materials and Methods
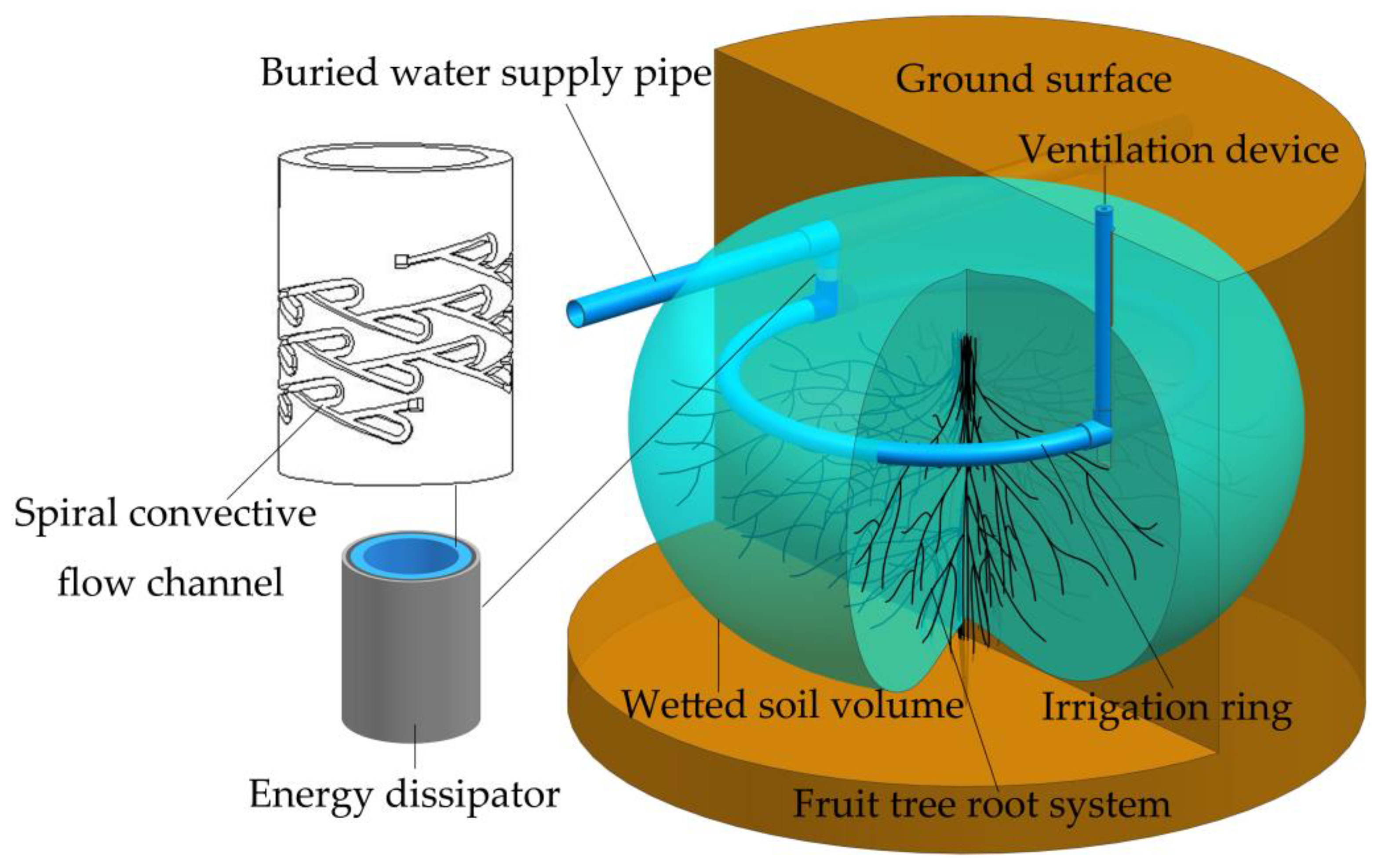
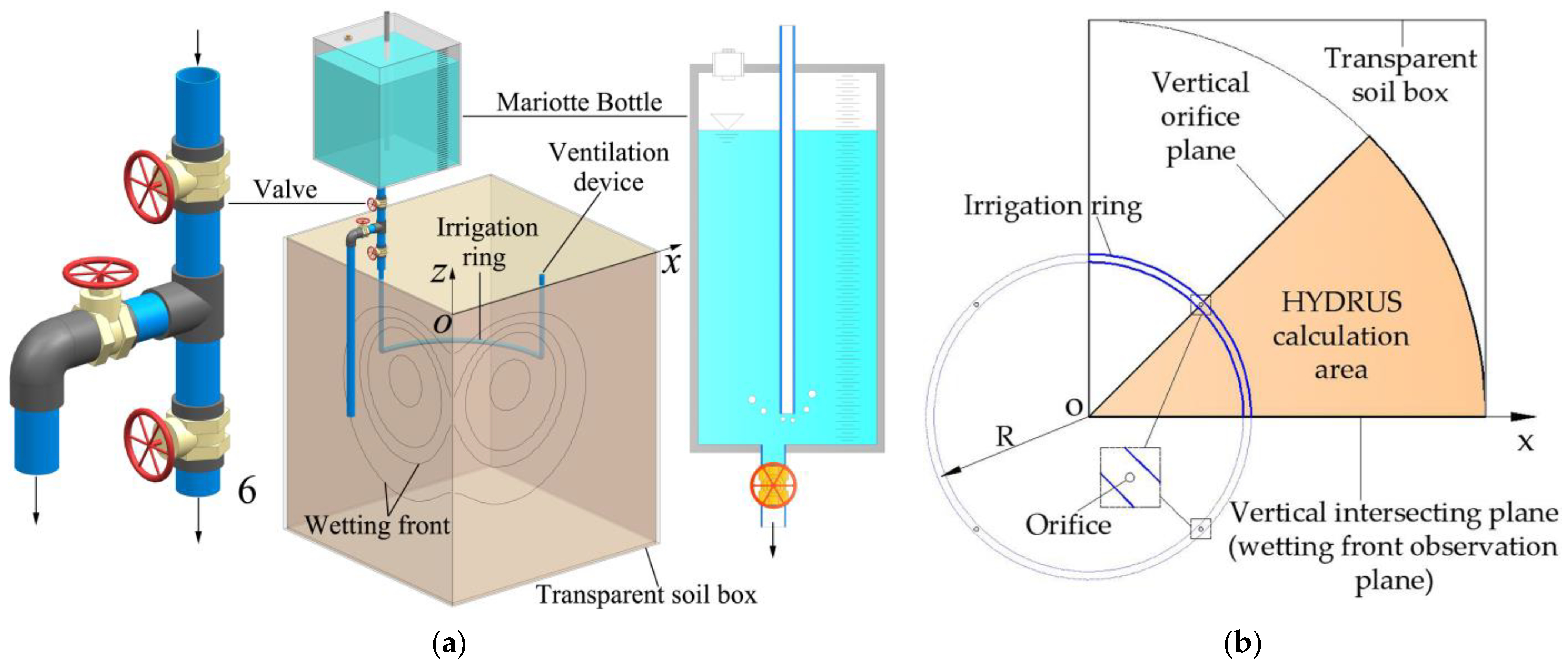
2.1. Test Soil and Apparatus
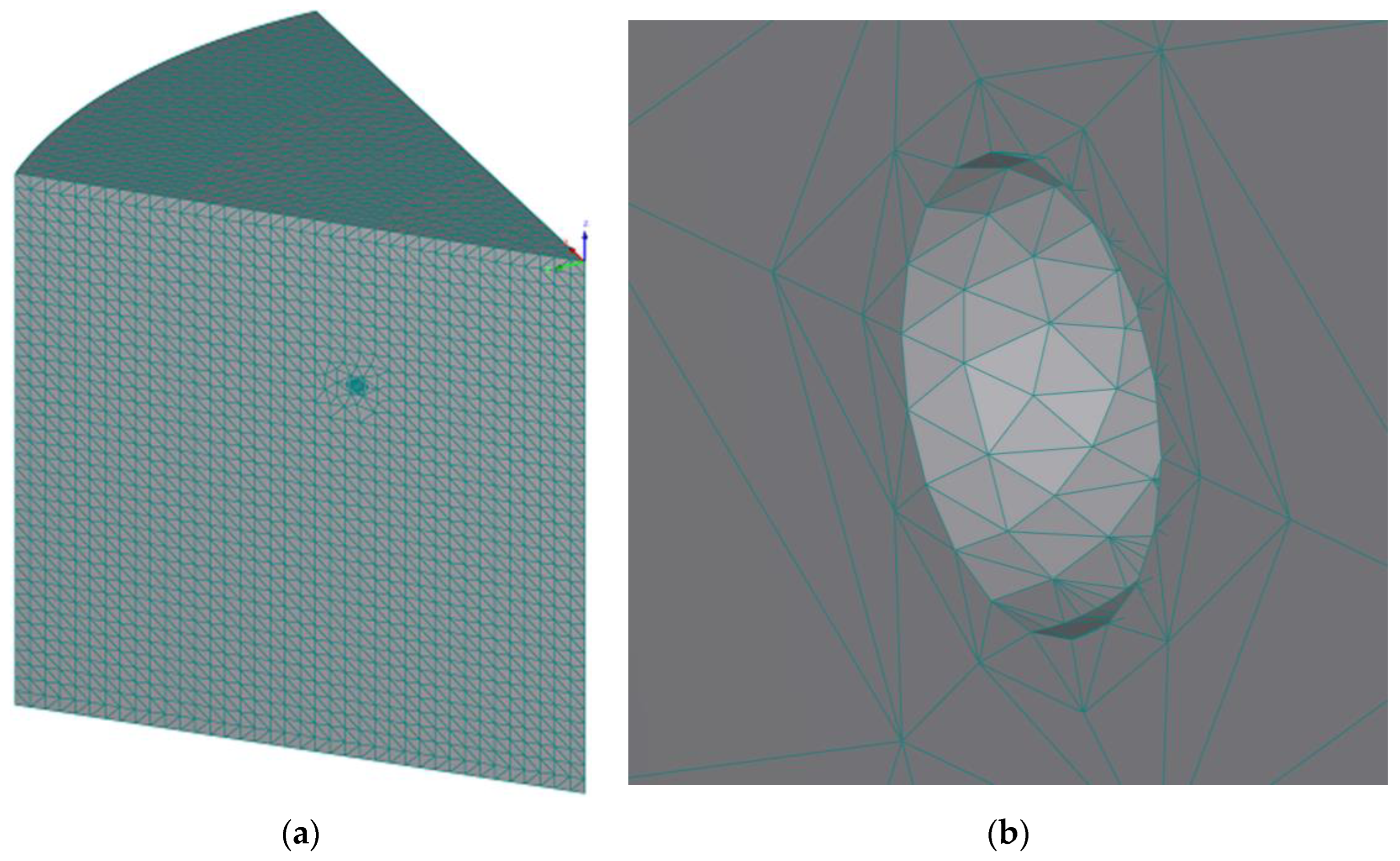
2.2. Numerical Modeling Program
2.3. Statistical Analysis
3. Results and Discussion
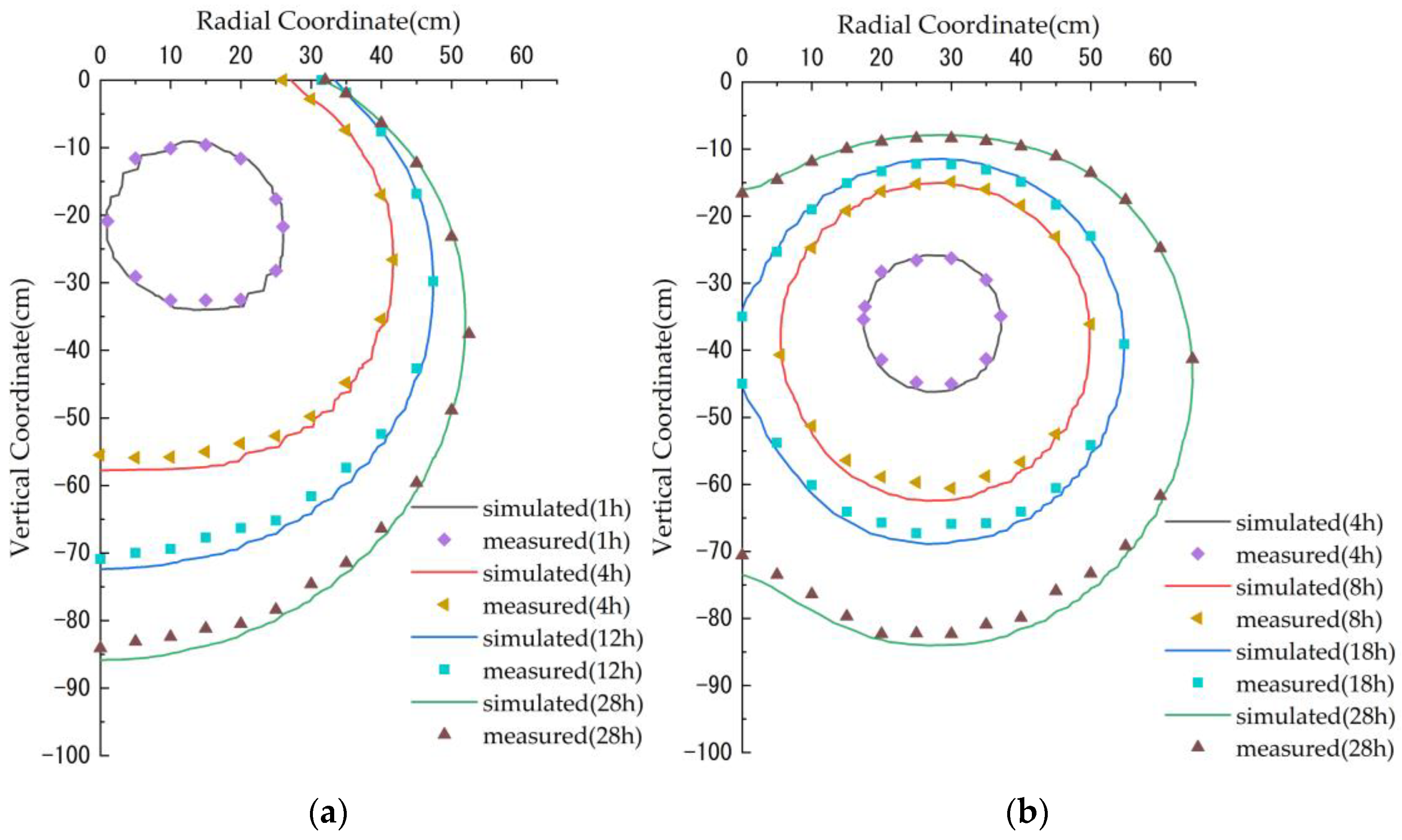
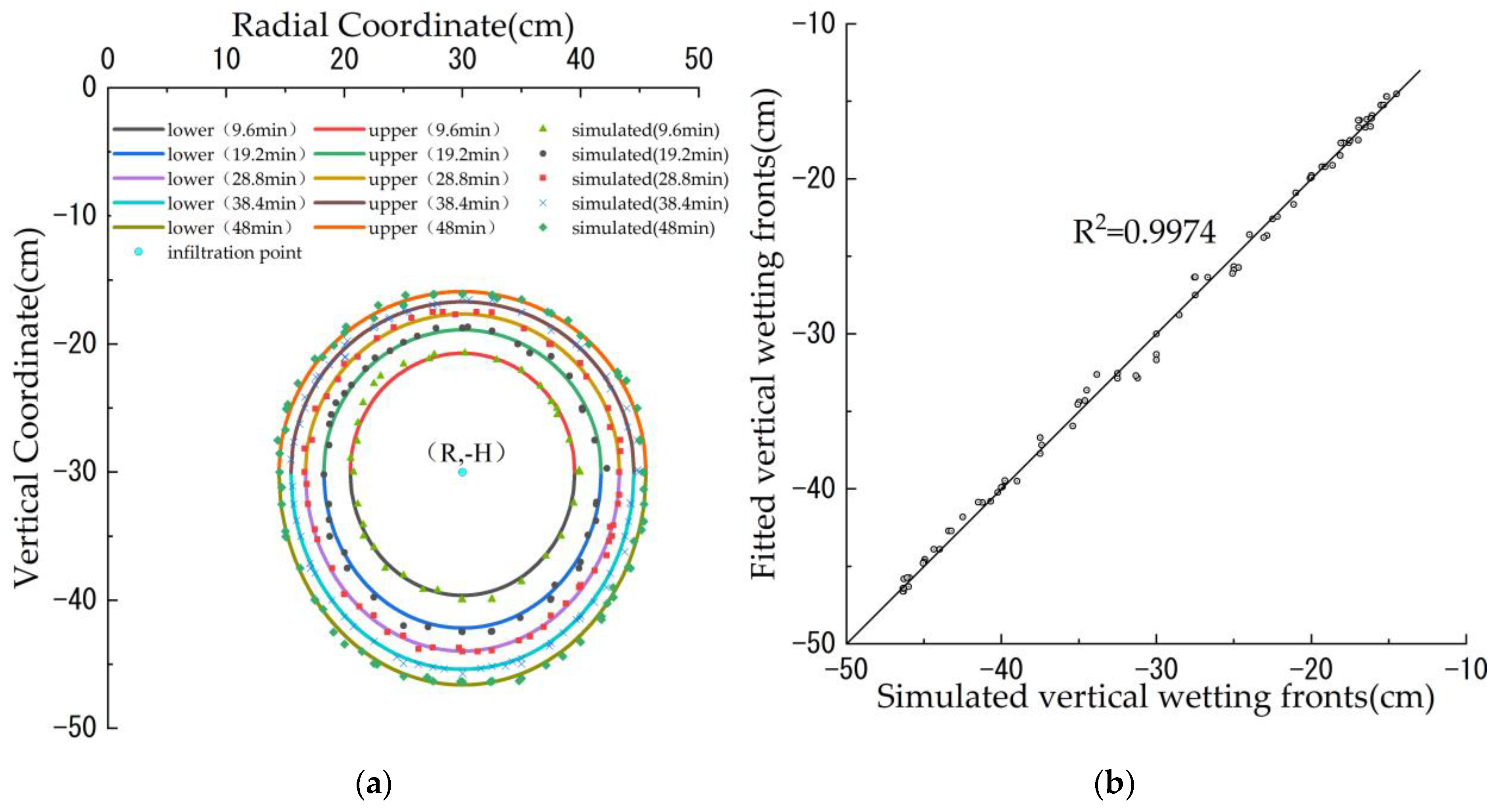
3.1. HYDRUS Model Validation
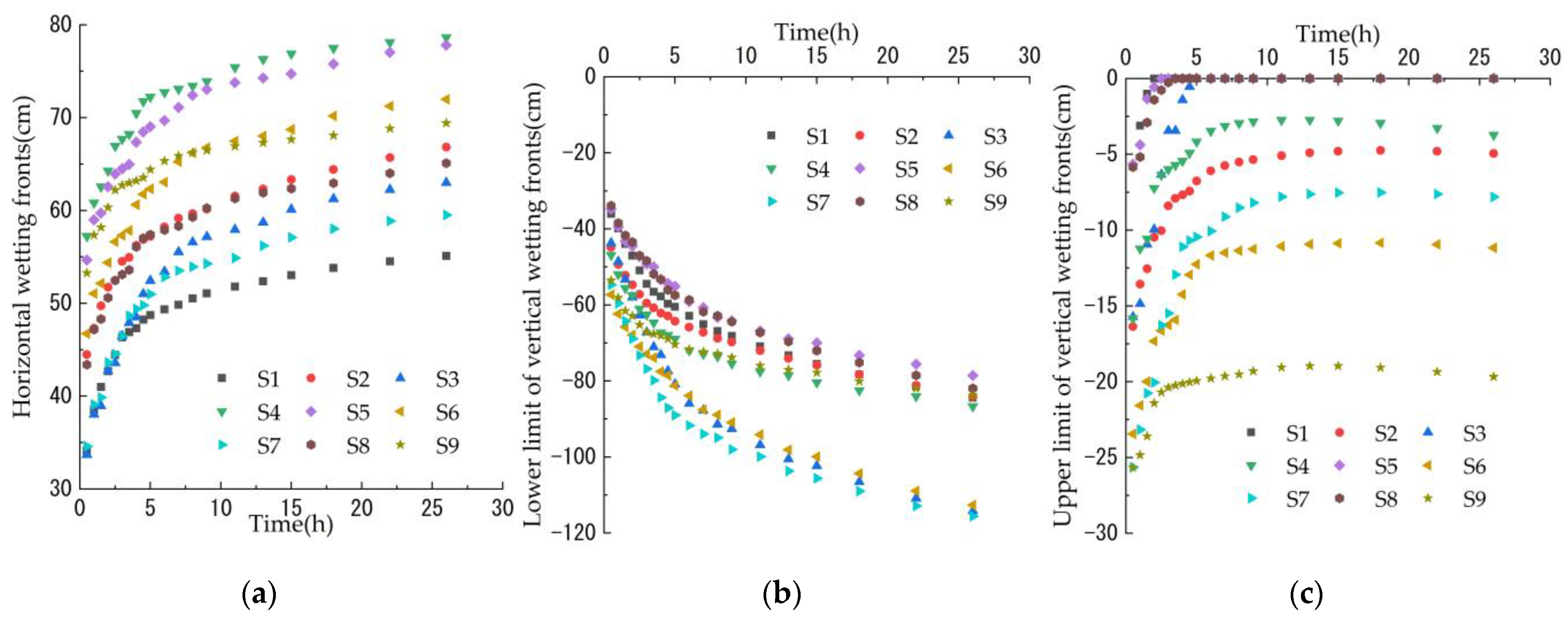
3.2. Spatial and Temporal Variation Characteristics of Wetting Fronts
3.2.1. Pre-Interference Infiltration
3.2.2. Post-Interference Infiltration
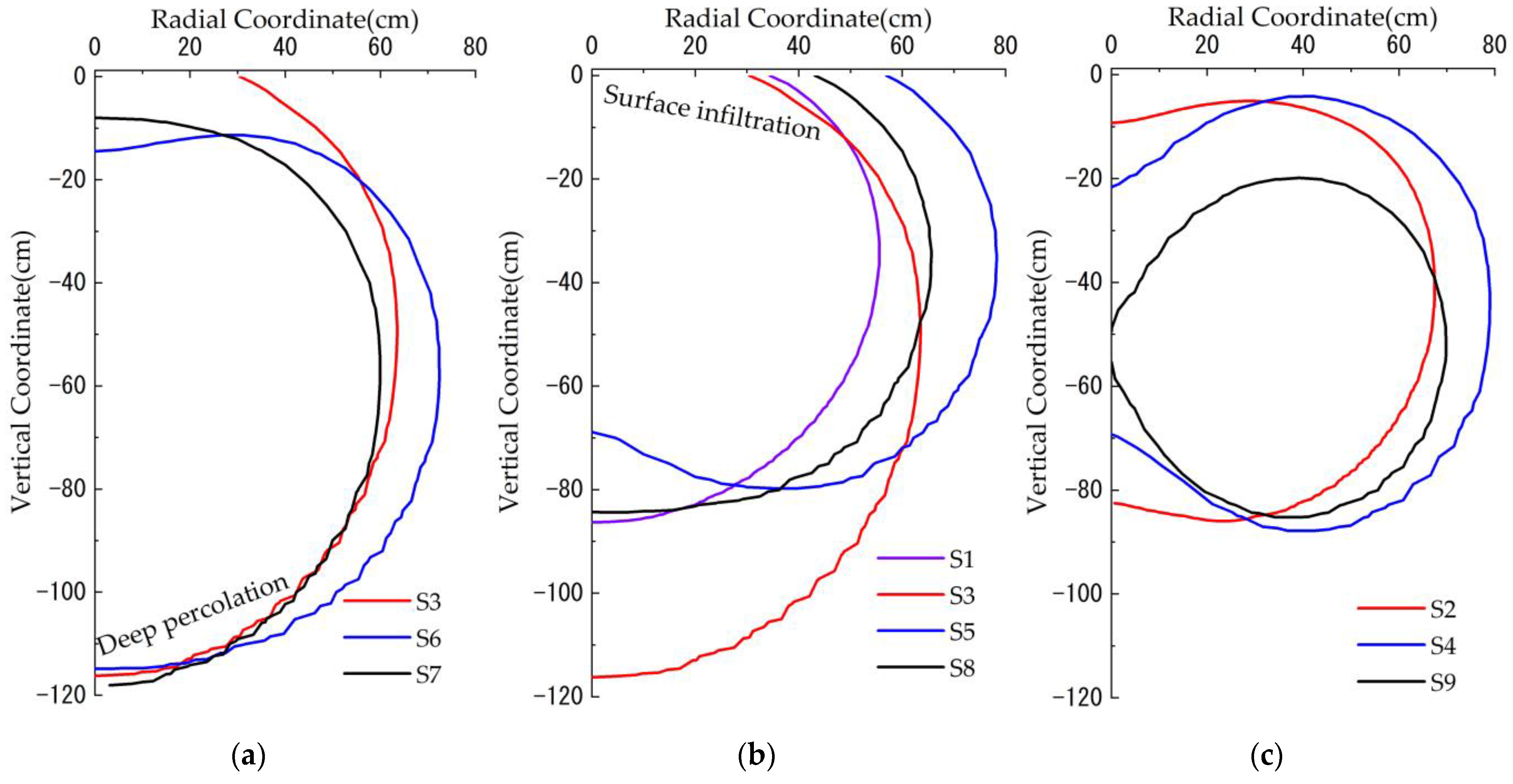
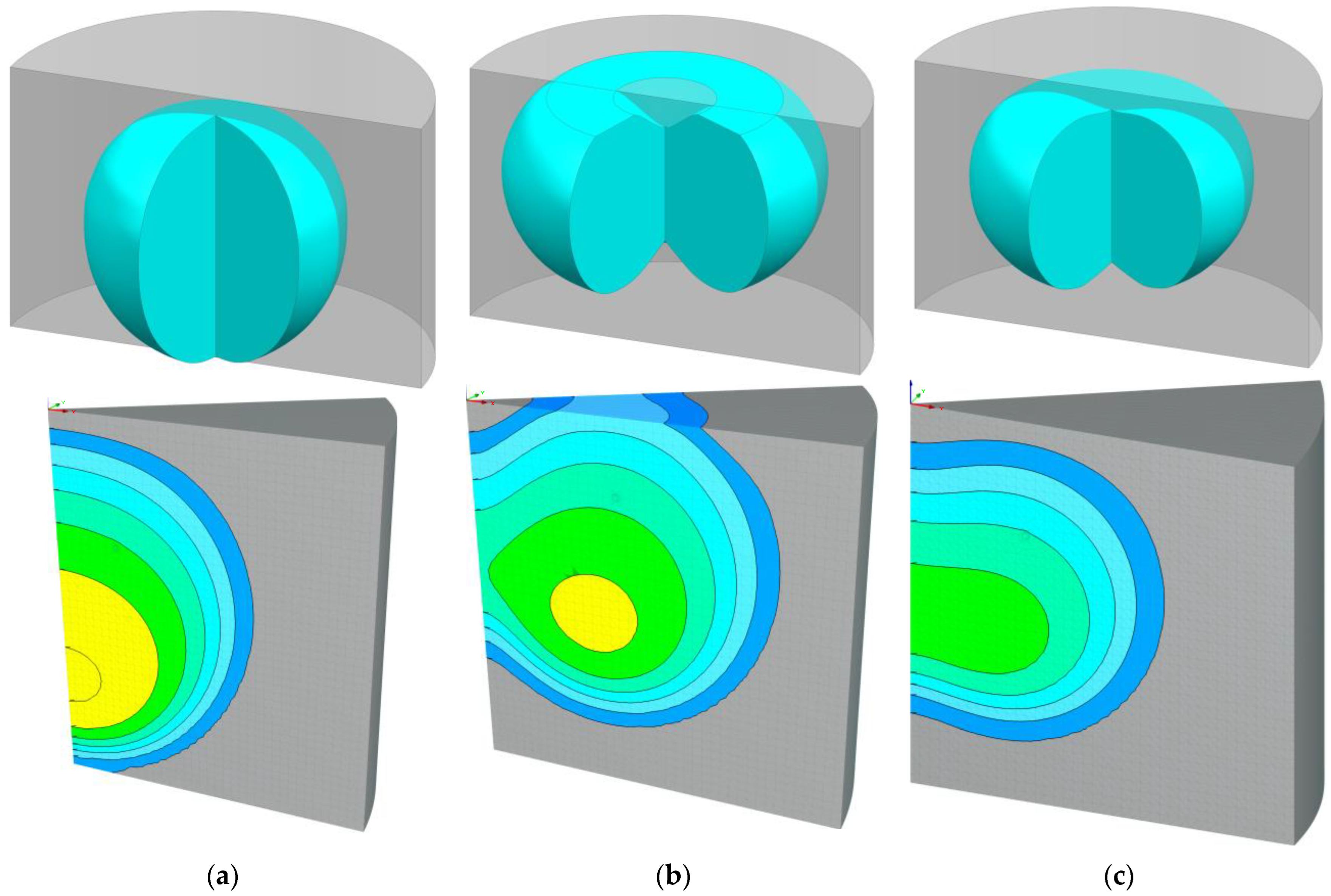
3.3. Shape of Wetted Soil Volume at Steady-State Infiltration
4. Conclusions
- (1)
- The subsurface ring-shaped multi-point source infiltration in sandy loam was simulated using HYDRUS-3D software. The simulated wetting fronts at different moments fitted well with the measured wetting front, with root mean square error less than 1.8 cm, average relative error less than 2.93% and average absolute error less than 1.5 cm. This indicates that it is feasible to use HYDRUS to simulate the multi-point source interference infiltration process.
- (2)
- At the early stage of infiltration, the infiltration belonged to independent subsurface single-point source infiltration before the intersection of the wetting fronts formed by the outflow of each orifice. The interference infiltration moment had a good power function relationship with the irrigation ring radius, the number of orifices and the burial depth while being independent of the irrigation water amount. The wetting fronts before interference infiltration were all in the form of a rotating ellipsoid centered on the infiltration point. The wetting fronts can be expressed by the equations of the upper and lower semi-ellipsoidal curves relative to the infiltration point, and the complex correlation coefficient of the verification results was 0.9974.
- (3)
- With the increase in time, the wetting front infiltrated in all directions with the infiltration point as the center, and the transport rate decreased. The power function relationship between the wetting front and the influencing factors after the interference infiltration in different directions was established, and the coefficients of determination were above 0.888.
- (4)
- The shape of the wetted soil volume after infiltration stabilization can be regarded as a rotating body formed by the vertical wetting front plane around the z-axis. The Wetted soil volume of deep percolation, surface infiltration and suitable infiltration scenarios was nearly rugby-shaped, apple-shaped with a flattened top and complete apple-shaped, respectively. Burying the irrigation ring at slightly deeper than one-third of the crop root zone is recommended, and half of the horizontal range of the crop root system can be selected as the irrigation ring radius.
5. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nazari, E.; Besharat, S.; Zeinalzadeh, K.; Mohammadi, A. Measurement and simulation of the water flow and root uptake in soil under subsurface drip irrigation of apple tree. Agric. Water Manag. 2021, 255, 106972. [Google Scholar] [CrossRef]
- Bainbridge, D.A. Buried clay pot irrigation: A little known but very efficient traditional method of irrigation. Agric. Water Manag. 2001, 48, 79–88. [Google Scholar] [CrossRef]
- Du, S.; Kang, S.; Li, F.; Du, T. Water use efficiency is improved by alternate partial root-zone irrigation of apple in arid northwest China. Agric. Water Manag. 2016, 179, 184–192. [Google Scholar] [CrossRef]
- Cook, F.; Thorburn, P.; Fitch, P.; Bristow, K. WetUp: A software tool to display approximate wetting patterns from drippers. Irrig. Sci. 2003, 22, 129–134. [Google Scholar] [CrossRef]
- Moncef, H.; Khemaies, Z. An analytical approach to predict the moistened bulb volume beneath a surface point source. Agric. Water Manag. 2016, 166, 123–129. [Google Scholar] [CrossRef] [Green Version]
- Philip, J.R. Travel Times from Buried and Surface Infiltration Point Sources. Water Resour. Res. 1984, 20, 990–994. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Development and Applications of the HYDRUS and STANMOD Software Packages and Related Codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef] [Green Version]
- Brandt, A.; Bresler, E.; Diner, N.; Ben-Asher, I.; Heller, J.; Goldberg, D. Infiltration from a Trickle Source: I. Mathematical Models. Soil Sci. Soc. Amer. Proc. 1971, 35, 675–682. [Google Scholar] [CrossRef]
- Malek, K.; Peters, R.T. Wetting pattern models for drip irrigation: New empirical model. J. Irrig. Drain. Eng. 2011, 137, 530–536. [Google Scholar] [CrossRef]
- Al-Ogaidi, A.A.; Wayayok, A.; Rowshon, M.; Abdullah, A.F. Wetting patterns estimation under drip irrigation systems using an enhanced empirical model. Agric. Water Manag. 2016, 176, 203–213. [Google Scholar] [CrossRef]
- Schwartzman, M.; Zur, B. Emitter spacing and geometry of wetted soil volume. J. Irrig. Drain. Eng. 1986, 112, 242–253. [Google Scholar] [CrossRef]
- Zhiguang, D.; Liangjun, F.; Ping, L.; Lin, C.; Yun, Z. Suitable Strategy of Water–Nitrogen Management for Surge-Root Irrigation of Jujube in China. Agron. J. 2018, 110, 1390–1401. [Google Scholar] [CrossRef]
- Dai, Z.; Fei, L.; Huang, D.; Zeng, J.; Chen, L.; Cai, Y. Coupling effects of irrigation and nitrogen levels on yield, water and nitrogen use efficiency of surge-root irrigated jujube in a semiarid region. Agric. Water Manag. 2019, 213, 146–154. [Google Scholar] [CrossRef]
- Cai, Y.; Wu, P.; Zhang, L.; Zhu, D.; Chen, J.; Wu, S.J.; Zhao, X. Simulation of soil water movement under subsurface irrigation with porous ceramic emitter. Agric. Water Manag. 2017, 192, 244–256. [Google Scholar] [CrossRef]
- Cai, Y.; Zhao, X.; Wu, P.; Zhang, L.; Zhu, D.; Chen, J.; Lin, L. Ceramic patch type subsurface drip irrigation line: Construction and hydraulic properties. Biosyst. Eng. 2019, 182, 29–37. [Google Scholar] [CrossRef]
- Dirwai, T.L.; Mabhaudhi, T.; Kanda, E.K.; Senzanje, A. Moistube irrigation technology development, adoption and future prospects: A systematic scoping review. Heliyon 2021, 7, e06213. [Google Scholar] [CrossRef]
- Qi, W.; Zhang, Z.; Wang, C.; Huang, M. Prediction of infiltration behaviors and evaluation of irrigation efficiency in clay loam soil under Moistube irrigation. Agric. Water Manag. 2021, 248, 106756. [Google Scholar] [CrossRef]
- Rodríguez-Sinobas, L.; Zubelzu, S.; Martín-Sotoca, J.J.; Tarquis, A.M. Multiscaling analysis of Soil Water Content during irrigation events. Comparison between surface and subsurface drip irrigation. Geoderma 2021, 382, 114777. [Google Scholar] [CrossRef]
- Mattar, M.A.; El-Abedin, T.; Al-Ghobari, H.M.; Alazba, A.A.; Elansary, H.O. Effects of different surface and subsurface drip irrigation levels on growth traits, tuber yield, and irrigation water use efficiency of potato crop. Irrig. Sci. 2021, 39, 517–533. [Google Scholar] [CrossRef]
- Wei, W.Y.; Xiao, Y.M.; Li, J.; Parkes, M. Simulation of point source wetting pattern of subsurface drip irrigation. Irrig. Sci. 2011, 29, 331–339. [Google Scholar] [CrossRef]
- Singh, D.K.; Rajput, T.; Sikarwar, H.S.; Sahoo, R.N.; Ahmad, T. Simulation of soil wetting pattern with subsurface drip irrigation from line source. Agric. Water Manag. 2006, 83, 130–134. [Google Scholar] [CrossRef]
- Appels, W.M.; Karimi, R. Analysis of soil wetting patterns in subsurface drip irrigation systems—Indoor alfalfa experiments. Agric. Water Manag. 2021, 250, 106832. [Google Scholar] [CrossRef]
- Siyal, A.A.; Skaggs, T.H. Measured and simulated soil wetting patterns under porous clay pipe sub-surface irrigation. Agric. Water Manag. 2009, 96, 893–904. [Google Scholar] [CrossRef]
- Monjezi, M.S.; Ebrahimian, H.; Liaghat, A.; Moradi, M.A. Soil-wetting front in surface and subsurface drip irrigation. Proc. Inst. Civ. Eng. Water Manag. 2013, 166, 272–284. [Google Scholar] [CrossRef]
- Mei, X.N.; Shen, Z.Z.; Ren, J.; Wang, Z.H. Effects of Dripper Discharge and Irrigation Amount on Soil-Water Dynamics under Subsurface Drip Irrigation. Adv. Mater. Res. 2011, 347–353, 2400–2403. [Google Scholar] [CrossRef]
- Zare, E.; Arshad, M.; Zhao, D.; Nachimuthu, G.; Triantafilis, J. Two-dimensional time-lapse imaging of soil wetting and drying cycle using EM38 data across a flood irrigation cotton field. Agric. Water Manag. 2020, 241, 106383. [Google Scholar] [CrossRef]
- Mohammed, A.K.; Abed, B.S. Water Distribution and Interference of Wetting Front in Stratified Soil Under a Continues and an Intermittent Subsurface Drip Irrigation. J. Green Eng. 2020, 10, 268–286. [Google Scholar]
- Assouline, S.; Cohen, S.; Meerbach, D.; Harodi, T.; Rosner, M. Microdrip irrigation of field crops: Effect on yield, water uptake, and drainage in sweet corn. Soil Sci. Soc. Am. J. 2002, 66, 228–234. [Google Scholar] [CrossRef]
- Badr, A.E.; Abuarab, M.E. Soil moisture distribution patterns under surface and subsurface drip irrigation systems in sandy soil using neutron scattering technique. Irrig. Sci. 2013, 31, 317–332. [Google Scholar] [CrossRef]
- Bozkurt, S.; Yazar, A.; Mansuroğlu, G.S. Effects of different drip irrigation levels on yield and some agronomic characteristics of raised bed planted corn. Afr. J. Agric. Res. 2011, 6, 5291–5300. [Google Scholar]
- Lamm, F.R.; Trooien, T.P. Dripline Depth Effects on Corn Production when Crop Establishment is Nonlimiting. Appl. Eng. Agric. 2005, 21, 835–840. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y. Roots Spatial Distribution Characteristics of 9T337 Dwarfing Self-Rooted Rootstock Apple Trees from Different Ages. Master’s Thesis, Northwest Agriculture and Forestry University of Science and Technology, Xianyang, China, 2019. [Google Scholar]
- Zhongjie, L.; Liangjun, F.; Kun, H.; Teng, L.; Nanshu, C.; Quanju, Z.; Deliang, H. Effects of arrangement of surge-root irrigation emitters on growth, yield and water use efficiency of apple trees. J. Drain. Irrig. Mach. Eng. 2020, 38, 7. [Google Scholar]
- Zhang, L.J.; Wang, Y.K.; Xin, X.G.; Hong-Yan, L.I. Appropriate surge spring root irrigation layout and irrigation norm of jujube on mountain land. J. Northwest A F Univ. 2010, 38, 211–217. [Google Scholar] [CrossRef]
- Zhenjia, H.E. Effects of Irrigation Quota under Bubbled-root Irrigation on Soil Water Dynamic Changes and Water Use Efficiency of Jujube. J. Irrig. Drain. 2018, 37, 45–49. [Google Scholar]
- Saefuddin, R.; Saito, H.; Šimůnek, J. Experimental and numerical evaluation of a ring-shaped emitter for subsurface irrigation. Agric. Water Manag. 2018, 211, 111–122. [Google Scholar] [CrossRef]
- Fan, Y.; Shao, X.; Gong, J.; Wang, Y. An Empirical Model for Estimating Soil Wetting Pattern Dimensions during Film Hole Irrigation. Arch. Agron. Soil Sci. 2019, 66, 1765–1779. [Google Scholar] [CrossRef]
- Sun, S.; An, Q.; Yang, P.; Lu, X.; Gu, K. Effect of Irrigation Depth on Root Distribution and Water Use Efficiency of Jujube under Indirect Subsurface Drip Irrigation. Trans. Chin. Soc. Agric. Mach. 2016, 47, 81–90. [Google Scholar]
- Al-Ogaidi, A.; Wayayok, A.; Kamal, M.R. (Eds.) Modelling Soil Wetting Patterns under Drip Irrigation Using Hydrus-3D and Comparison with Empirical Models. In Proceedings of the Global Conference on Engineering and Technology (GCOET), Kuala Lumpur, Malaysia, 1–2 June 2016. [Google Scholar]
- Nagli, B.; Kechavarzi, C.; Coulon, F.; Pintar, M. Numerical investigation of the influence of texture, surface drip emitter discharge rate and initial soil moisture condition on wetting pattern size. Irrig. Sci. 2014, 32, 421–436. [Google Scholar] [CrossRef]
- Sun, Q.; Wang, Y.; Geng, C.; Hui, Y.; Du, T. Water use efficiency was improved at leaf and yield levels of tomato plants by continuous irrigation using semipermeable membrane. Agric. Water Manag. 2018, 203, 430–437. [Google Scholar] [CrossRef]
| Scenario | R (cm) | M | H (cm) | V (cm3) |
|---|---|---|---|---|
| 1 | 20 | 4 | 20 | 40,000 |
| 2 | 30 | 6 | 30 | 40,000 |
| 3 | 20 | 8 | 30 | 80,000 |
| 4 | 40 | 4 | 30 | 60,000 |
| 5 | 40 | 6 | 20 | 80,000 |
| 6 | 30 | 4 | 40 | 80,000 |
| 7 | 20 | 6 | 40 | 60,000 |
| 8 | 30 | 8 | 20 | 60,000 |
| 9 | 40 | 8 | 40 | 40,000 |
| θr (cm3·cm−3) | θs (cm3·cm−3) | α (cm−1) | n | Ks (cm·h−1) | I |
|---|---|---|---|---|---|
| 0.0348 | 0.3742 | 0.0159 | 1.4721 | 2.2089 | 0.5 |
| Differences | S1 | S4 | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 h | 4 h | 12 h | 28 | 4 h | 8 h | 12 h | 28 h | |
| RMSE (cm) | 0.72 | 1.47 | 1.80 | 1.53 | 0.90 | 1.24 | 1.15 | 1.47 |
| RE (%) | 2.77 | 2.92 | 2.93 | 2.36 | 2.14 | 2.22 | 2.74 | 2.52 |
| MAE (cm) | 0.61 | 1.21 | 1.50 | 1.24 | 0.79 | 0.96 | 0.96 | 1.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Li, L. Spatial and Temporal Characteristics of Infiltration Wetting Front of Ring-Shaped Root Emitters. Sustainability 2022, 14, 6712. https://doi.org/10.3390/su14116712
Zhang J, Li L. Spatial and Temporal Characteristics of Infiltration Wetting Front of Ring-Shaped Root Emitters. Sustainability. 2022; 14(11):6712. https://doi.org/10.3390/su14116712
Chicago/Turabian StyleZhang, Jun, and Lin Li. 2022. "Spatial and Temporal Characteristics of Infiltration Wetting Front of Ring-Shaped Root Emitters" Sustainability 14, no. 11: 6712. https://doi.org/10.3390/su14116712
APA StyleZhang, J., & Li, L. (2022). Spatial and Temporal Characteristics of Infiltration Wetting Front of Ring-Shaped Root Emitters. Sustainability, 14(11), 6712. https://doi.org/10.3390/su14116712





