Dynamic Simulation and Experimental Study of the HDPE Double-Walled Corrugated Pipe Grouting Robot

Abstract

The current drainage pipeline repair methods present significant limitations, and this paper proposes a new construction technology applied to the internal collapse repair of high-density polyethylene (HDPE). This study designed the hot-melt, deflection, support, monitoring, and grouting mechanisms of the grouting gun body while deducing the mechanical formulas of the grouting, deflection lifting, support, and travel processes. The grouting gun body was tested by inserting it into soil, confirming that the pipe grouting robot could perform grouting in an actual construction environment. The hot-melt test verified that the hot-melt mechanism of the pipeline grouting robot melted and broke the HDPE double-walled corrugated pipe. The kinematics simulation was performed using the ADAMS software, verifying that the motion of the pipeline grouting robot satisfied the design requirements. In this paper, the dynamic simulation and experimental research of HDPE double-walled corrugated pipe grouting robot were carried out. Compared with existing drainage pipeline repair methods, the pipeline grouting and shaping technology was highly efficient in a construction environment.

1. Introduction

Urban water supply and drainage systems are indispensable for supplying water to residents while removing sewage and rainwater. Urban drainage pipes consist primarily of cement or reinforced concrete pipes. Although these pipes are cheap and used extensively, they require regular cleaning since the friction coefficient is high and impurities accumulate rapidly, affecting the emission efficiency [1,2]. Moreover, cement pipelines are heavy, expensive, and difficult to construct and maintain. Therefore, high-density polyethylene (HDPE), polyvinyl chloride (PVC), polyethylene (PE), and other plastic drainage pipes are gradually replacing traditional cement and reinforced concrete pipes [3,4]. The low internal friction coefficient of plastic pipes makes it difficult for impurities to accumulate when used as sewage discharge pipes. Moreover, since these pipes are made of polymer materials, they are chemically stable, lightweight, and easy to construct and maintain. However, compared with traditional cement pipes or reinforced concrete pipes, they display weak compressive capacity and are prone to collapse or distortion. These pipes are typically located underneath main roads, bearing significant pressure from heavy vehicles using the roads, resulting in considerable pipeline deformation and ultimately internal collapse. Therefore, these pipelines require repair and reshaping, as shown in Figure 1.

The repair process of drainage pipelines can be divided into two categories: overall repair and local repair [5]. Overall pipeline repair refers to the excavation and replacement of a pipeline section. However, this repair method is expensive, requiring extensive construction time and materials. Local pipeline repair refers to repairing local pipeline collapse or loss. The main process can be divided into early internal pipeline exploration, determination of the pipeline damage and location, formulation of a repair scheme, and repair implementation [6,7]. Although this repair method is cost-efficient, quick, and not labor-intensive, the technical requirements are high. Pipes with larger diameters can be repaired manually. However, the current method for repairing pipes with small diameters between 300 mm and 600 mm involves drilling into the ground to insert grout. When the slurry solidifies the soil around the outer pipe wall, the collapsed portion can be milled using a pipe-milling mechanism, after which ultraviolet curing and other repair processes are used for subsequent treatment [8,9]. This construction method presents significant limitations: First, it is necessary to accurately locate the collapsed portion of the pipeline to facilitate drilling and grouting the soil. However, this is often challenging due to the depth of the pipeline and the internal environment, preventing accurate slurry injection during grouting. Furthermore, a large amount of slurry is required to cover the collapsed section of the pipeline, resulting in low construction efficiency and high cost. Second, the presence of other pipeline networks and buildings above the collapsed pipe section interferes with repair efforts. Therefore, a large number of scholars put forward the trenchless repair technology of drainage pipelines. Liu et al. [10] compared and selected four kinds of trenchless pipeline repair processes, determined to select the centrifugal-cast fiberglass reinforced plastic (FRP) pipe, and introduced the technical principle, construction process, and implementation effect of the repair of the inner lined pipe. Ogden [11] studied the repair of coating damage in the trenchless area of a drainage pipeline and put forward repair procedures for different degrees of coating damage. Zare’s [12] case study shows that the underground pipeline damaged by an earthquake cannot be repaired by blasting in situ solidification pipeline and point repair method. Xie et al. [13], combined with the actual engineering case of drainage pipeline repair, introduced the application of an in situ curing method and polyurethane inlay method in drainage pipeline repair and expounds on the selection of the design parameters and the construction processes of those methods. Chin et al. [14] developed a resin transfer molding (RTM) process for repairing underground pipelines through an axiomatic design method. Compared with the traditional trenchless technology, this process has smaller and simpler operation equipment and higher repair efficiency. Fang et al. [15] and Wang et al. [16] studied the polymer grouting technology and discussed the effects of load type, load location, and buried depth on the mechanical properties of the pipeline after grouting. The results show that the dangerous point of the pipeline is located at the socket joint, and the load has a great impact on the range of 3–4 m on both sides of the pipeline. Lin et al. [17] systematically studied the cutting failure mechanism of polymers with different densities, evaluated the influence of cutting depth and cutting-edge radius on cutting effect, and put forward the prediction model of polymer grouting material optimization. Gil et al. [18] adopted flexible die technology to develop a glass fiber fabric polymer composite, which can quickly cure and repair underground pipelines. Orlov et al. [19] summarized the repair technology of loose joints at the connection points of straight pipes and secondary pipes. It is considered that the selection of pipeline maintenance methods mainly depends on the cleaning conditions of pipelines, the results of remote diagnosis, and the situation of on-site special machinery. Zhong et al. [20] and Ji et al. [21] studied the lining process of cured-in-place pipe (CIPP) liner, compounded the lining materials by various methods, and compared and analyzed the structural characteristics of the lining through a bending strength test. Nuruddin et al. [22], Fang et al. [23], and Li et al. [24] analyzed the influence of corrosive environmental conditions on the mechanical properties of CIPP lining. The research showed that the CIPP wall thickness was positively correlated with corrosion depth, traffic load, coverage depth, and water volume and negatively correlated with corrosion width. Primin et al. [25] believe that the cement mortar coating in trenchless repair has high mechanical and anti-corrosion properties, which can reduce accidents on the water supply network and improve the hydraulic characteristics of the repaired pipeline, so as to ensure the quality of water treatment. Lu et al. [26] used ANSYS Workbench software to analyze the stress of inserted hose lining (IHL), and the research shows that the IHL method can effectively reduce the stress of the old pipeline. Under the condition of uniform corrosion, the residual thickness is inversely proportional to the pipeline stress, and the pipeline pressure and diameter are positively related to the pipeline stress.

To sum up, trenchless repair technology has good advantages in the repair of drainage pipelines. This paper proposes a new construction process for collapsed HDPE double-walled corrugated pipes. A grouting robot was designed by us to repair the interior of 300–600 mm small-diameter HDPE pipes, effectively avoiding the primary challenges presented by the current construction process while improving construction efficiency and reducing construction cost, which is vital for the trenchless repair of drainage pipelines. The kinematics simulation is carried out by using ADAMS software to verify whether its motion meets the requirements.

2. Overall Design and Repair Process of the Pipeline Grouting Robot

The pipeline grouting robot needs to have a variety of functions in the grouting solidification treatment, so it needs to design different structures according to different functional requirements and finally determine the design scheme and process flow of the pipeline grouting robot.

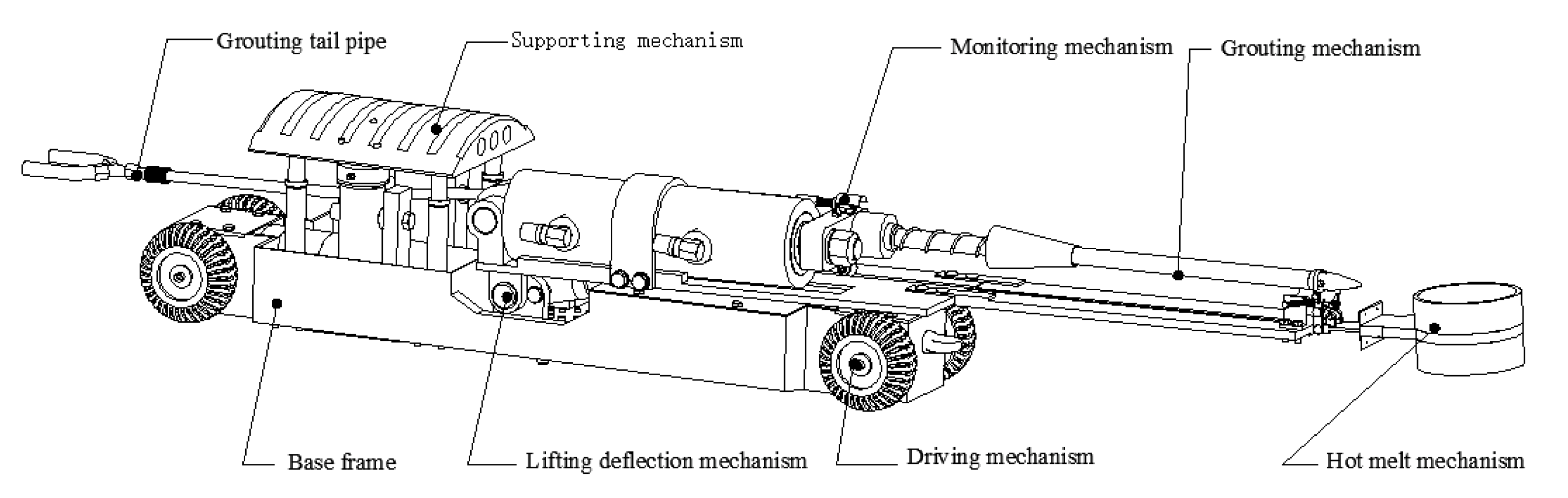
2.1. The Overall Design of the Pipeline Grouting Robot

The pipeline grouting robot requires diverse refinement of grouting solidification treatment, while the wheel structure is used as the mode of motion. Before the grouting pipe can be inserted into the soil, it must first penetrate the inner wall of the HDPE double-walled corrugated pipe, which typically displays high compression, tensile strength, elongation at break, and mechanical properties, rendering a drill bit unsuitable for drilling. However, since its melting point is low at only 131 °C, it can be subjected to the hot-melt method. The goal of the pipeline grouting robot is to conduct grouting in HDPE double-walled corrugated pipes with inner diameters of 300 mm to 600 mm, while it must also be maneuverable to reach different areas of the collapse inside the pipe. Therefore, in addition to deflecting to the left and right to facilitate grouting in different positions, it must also be able to move upward to adapt to pipes with varying inner diameters.

The design of the main mechanism is realized by analyzing the walking, drilling, deflection, and lifting schemes of the grouting robot in the pipe and combining them with the actual technical engineering requirements. It is also necessary to design a support mechanism to ensure the overall stability of the pipeline grouting robot and prevent it from overturning during grouting. Furthermore, overseeing the operational performance of the robot in real-time and locating the damage inside the pipeline requires the installation of a monitoring mechanism. The overall structure of the grouting machine in the pipe is shown in Figure 2.

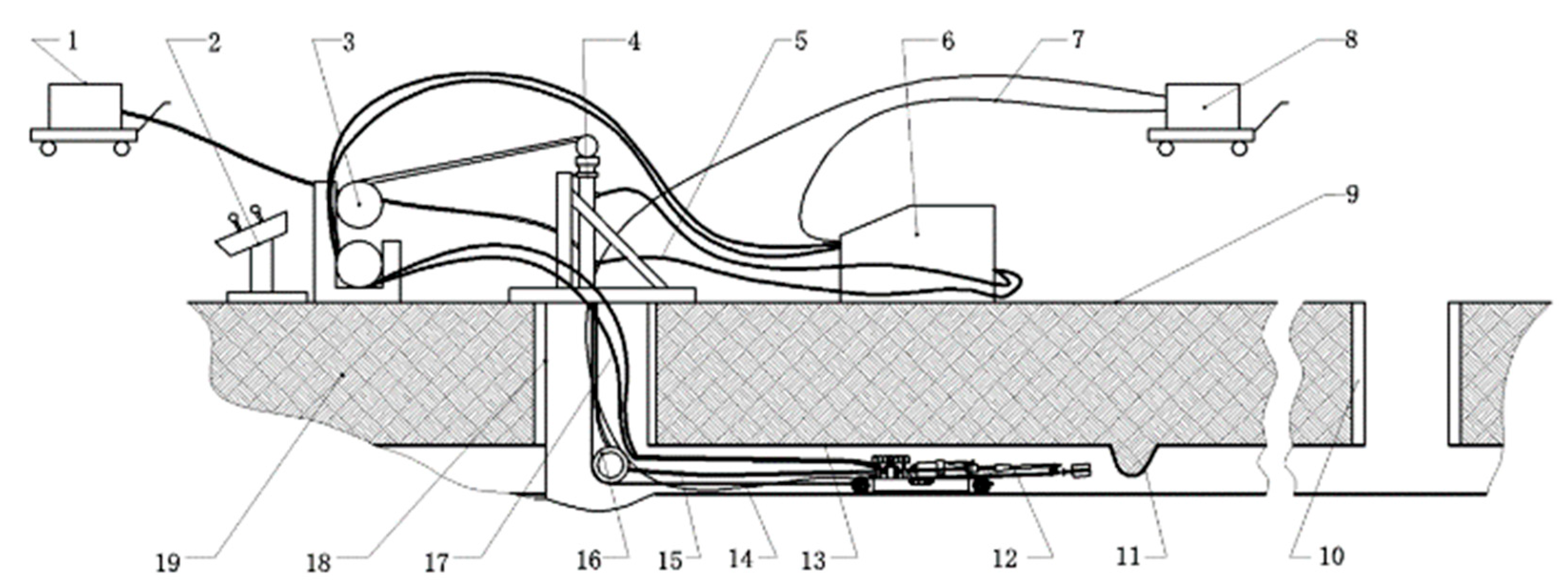
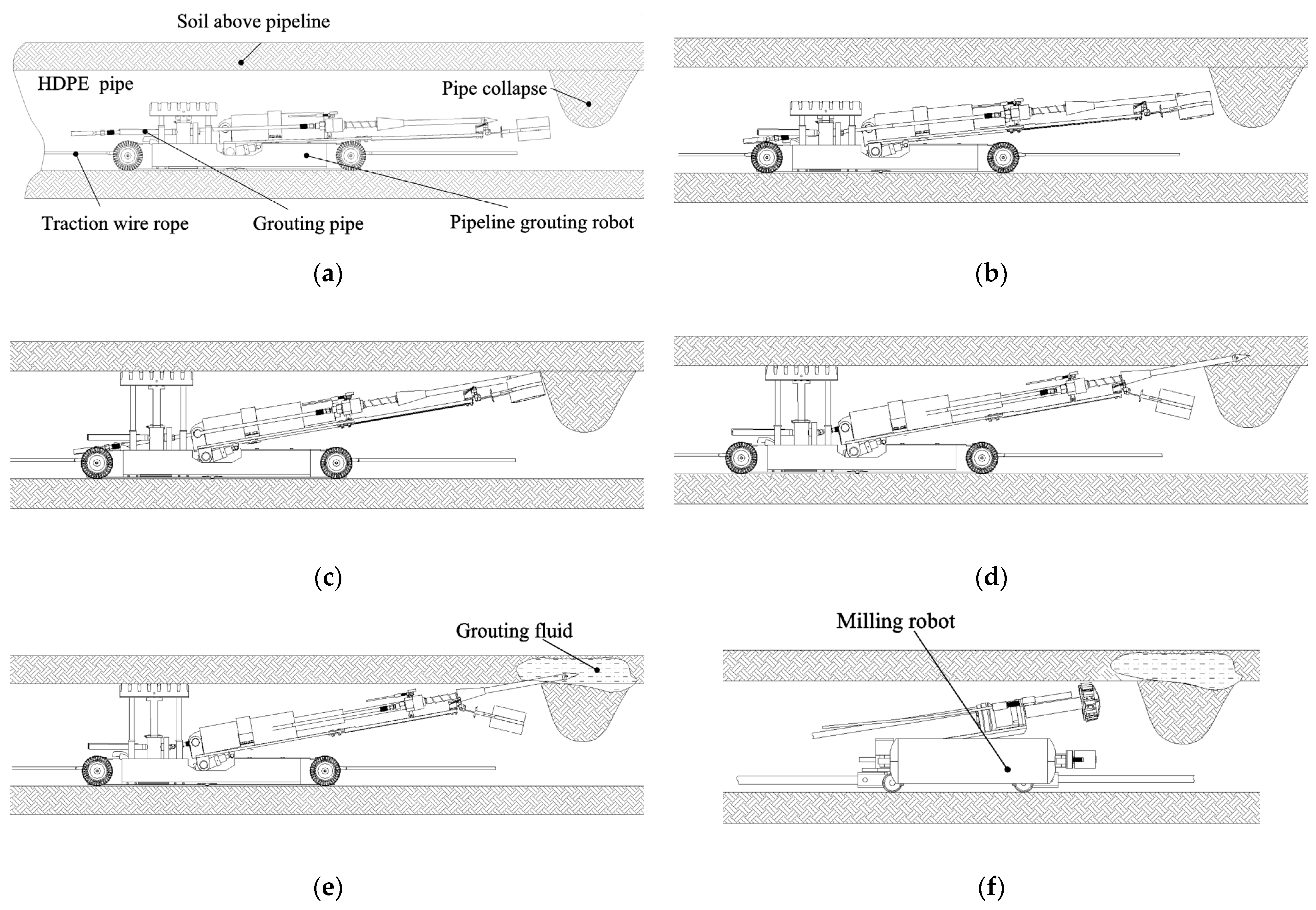
2.2. Technology Used to Repair Internal Pipeline Collapse

Due to the shortcomings of the current construction process, this study proposes a new pipe-grouting shaping technique to repair the collapse of drainage pipelines. As shown in Figure 3, it consists mainly of a grouting system, auxiliary system, and ground control system. The grouting system includes a pipeline grouting robot located inside the pipeline and a grouting pump located on the ground. The grouting pump transmits grouting fluid to the pipeline grouting robot inside the pipeline through the grouting pipe, ensuring effective grouting at the collapsed pipe section. The pipeline grouting robot is equipped with its own power system, independently positioning itself at the damaged location. The auxiliary system includes a power generation vehicle, a traction hoist, a winding machine, a corner device, and a hydraulic pump station. When the pipeline grouting robot fails in the pipeline, it can be withdrawn by pulling a steel wire rope, while the generator car and hydraulic pump station provide power and hydraulic supply.

As shown in Figure 4, after concrete preparation, the grouting robot is positioned at the collapse site in the pipe, and the angle of the grouting gun body is adjusted. The inner wall of the pipe is then melted via the hot-melt mechanism. The grouting gun body is then inserted into the soil above the collapsed pipe section through the melted hole to inject the grouting. After the slurry solidifies the soil above the pipe collapse, the location is milled using the milling robot. Finally, ultraviolet curing technology is used to treat the pipeline.

3. Mechanical Analysis of the Pipeline Grouting Robot

When the pipeline grouting robot moves into the collapse position in the pipeline, the top and bottom supports in the supporting mechanism are pushed by the supporting hydraulic cylinder against the inner wall of the pipeline for fixation. After the inner wall of the pipeline is broken by the hot-melt mechanism, the grouting gun body is inserted into the soil through the melted hole to carry out the grouting operation. In this process, the pipeline grouting robot is subjected to large reaction force and the thrust of the hydraulic cylinder, so it is necessary to conduct the forces on the pipeline grouting robot.

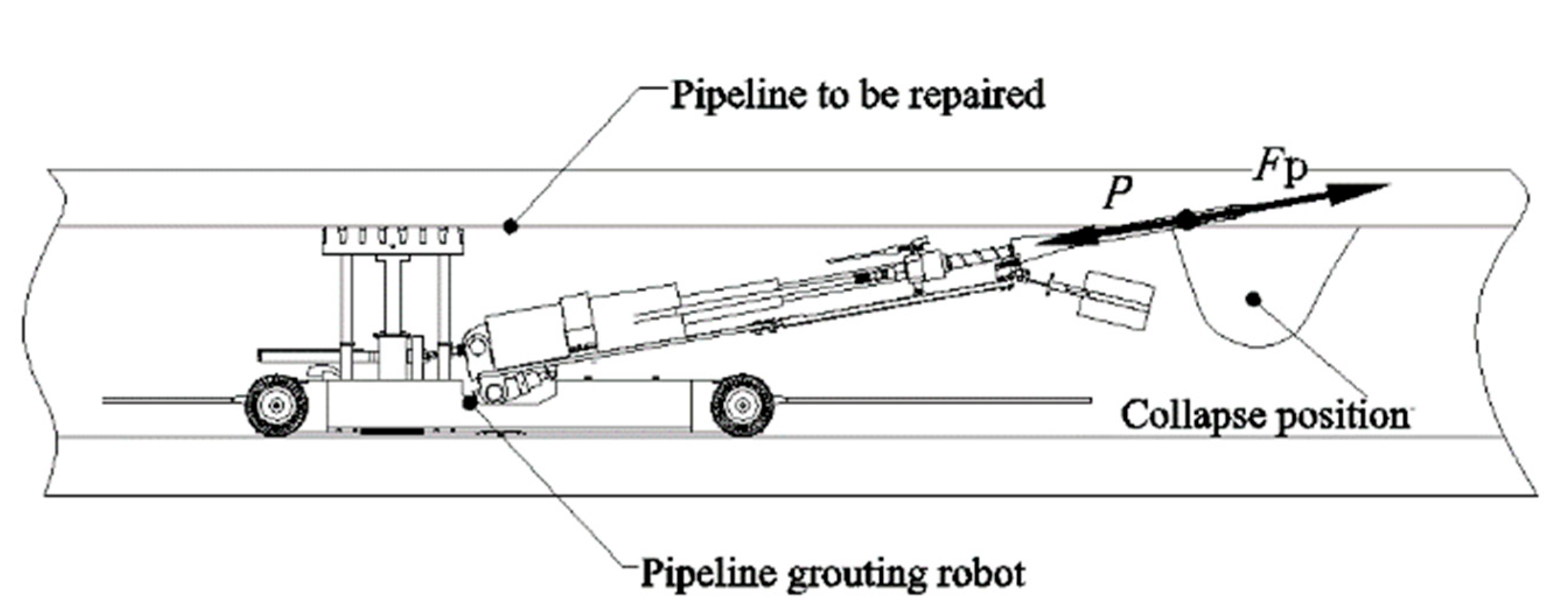
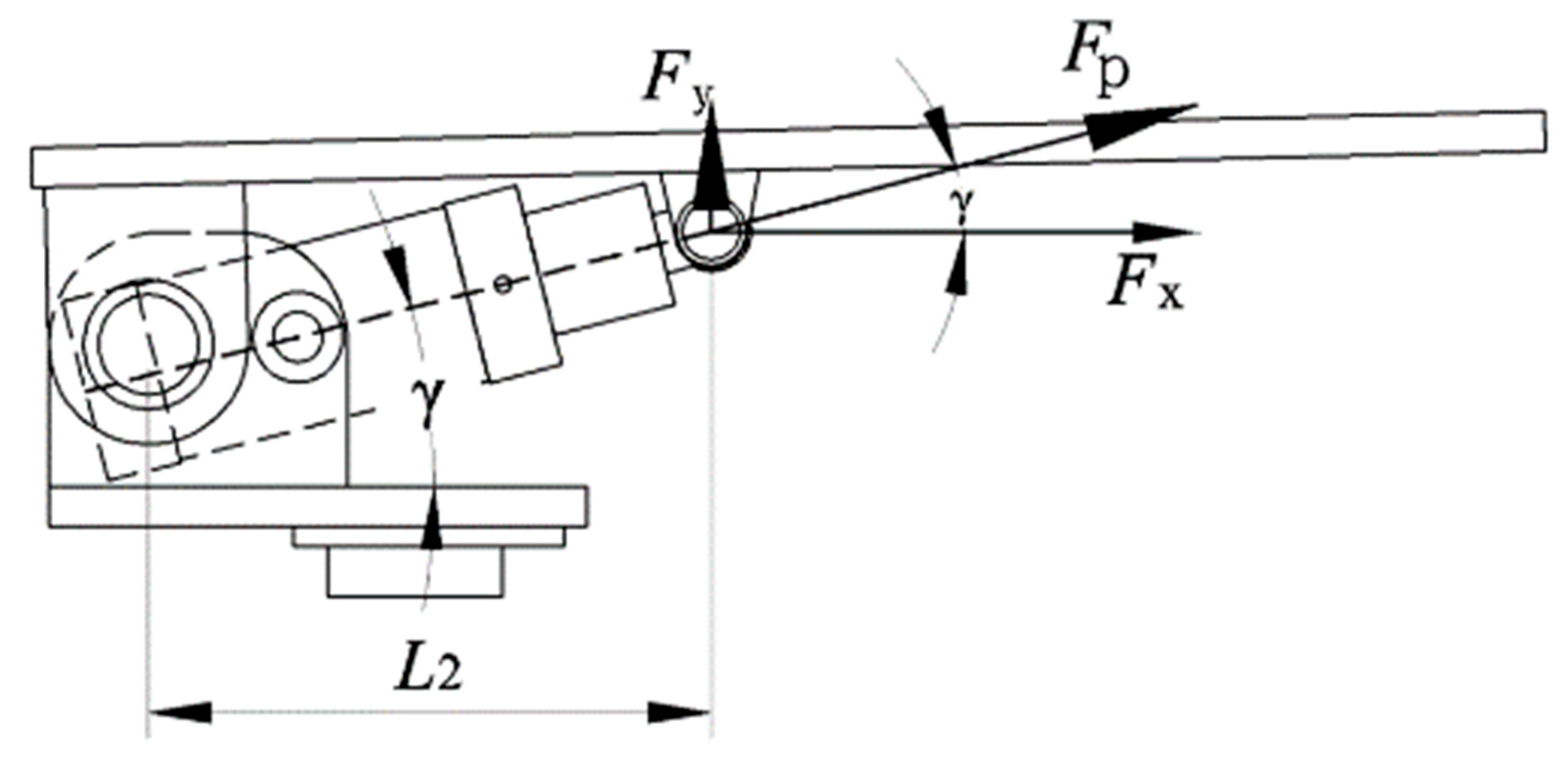
3.1. Mechanical Analysis of the Grouting Process

As shown in Figure 5, when the grouting gun body is inserted into the soil, it is subject to the thrust F_p from the multi-stage hydraulic cylinder and resistance P between the soil and the grouting gun body. When the thrust F_p exceeds the soil resistance P, the grouting gun body penetrates the soil. To determine the required thrust F_p, it is necessary to calculate the soil resistance p value.

Since the grouting gun body is lifted upward at a certain angle for soil insertion, the horizontal component of the soil resistance is defined as p_x, and the upward lifting angle of grouting gun body is $\theta$. According to the trigonometric function relationship, the association between the soil resistance P and its horizontal component is as follows:

$$P=\frac{Px}{\cos \theta }$$

(1)

The grouting gun body can penetrate the soil when its tip and side friction resistance is exceeded by the load applied by the multi-stage hydraulic cylinder. The soil resistance of the grouting gun body in the horizontal direction can be estimated according to the following empirical formula [27,28]:

$$Px=P_{\mathrm{m}}+P_{\mathrm{n}}$$

(2)

$$P_{\mathrm{m}}=W{\displaystyle \sum _i^n{R}_{\mathrm{si}}{l}_{\mathrm{i}}}$$

(3)

$$P_{\mathrm{n}}=R_g{A}_g$$

(4)

where P_m is the side friction resistance of the grouting gun body, P_n is the tip resistance of the grouting gun body, R_si is the dynamic friction resistance of the gun body, R_sk is the standard value of the limit static friction resistance on the side of the gun body, l_i is the length of the grouting gun body in section I, h is the soil penetration depth of the grouting gun body, h_j is the conical tip length of the grouting gun head, W is the perimeter of the grouting gun body, A_g is the cross-sectional area of the tip of the grouting gun head, R_g is the resistance borne by the grouting gun head, R_pk is the standard value of the ultimate resistance borne by the tip of the grouting gun head, and n is the number of sections of the grouting gun body, n = 3.

The soil resistance P of the grouting gun body inserted into the soil after a θ degree lift can be obtained by substituting Equations (2)–(4) into Equation (1), respectively:

$$P=\frac{P_{\mathrm{m}}+P_{\mathrm{n}}}{\cos \theta }=\frac{W{\displaystyle \sum _i^n{R}_{si}{l}_i+R_g{A}_g}}{\cos \theta }$$

(5)

The grouting gun body can be divided into three sections during the soil penetration process, i.e., n = 3. According to the design requirements, the grouting gun body must be inserted into the soil about 300 mm to 500 mm to initiate grouting, h = 500 mm. Since the pipeline grouting robot can operate in different soil layers, a more complex mixed soil layer is selected. The standard value of the ultimate resistance borne by the tip of the grouting gun head is R_pk = 3500 kPa, and the standard value of the ultimate static friction resistance at the side of the gun body is R_sk = 50 kPa. The maximum lifting angle of the grouting gun body of the pipeline robot in different pipe diameters is shown in

Table 1. Upward lifting angle of grouting gun in different pipe diameters.

Pipe Inner Diameter (mm)	Maximum Upward Lifting Angle of Grouting Gun Body
300	5°
400	11°
500	16°
600	22°

, according to the theoretical analysis results.

To ensure that the selected multi-stage hydraulic cylinder can provide a sufficient load, the calculated soil resistance is calculated according to the maximum value, yielding a lifting angle of θ = 22°. The soil resistance P of the grouting gun body inserted into the soil can be obtained by substituting the values of the parameters mentioned above into Equation (5) for calculation:

$$P=\frac{W\left(R_{s1}{l}_1+R_{s2}{l}_2+R_{s3}{l}_3\right)+R_g{A}_g}{\cos \mathsf{\theta }}$$

(6)

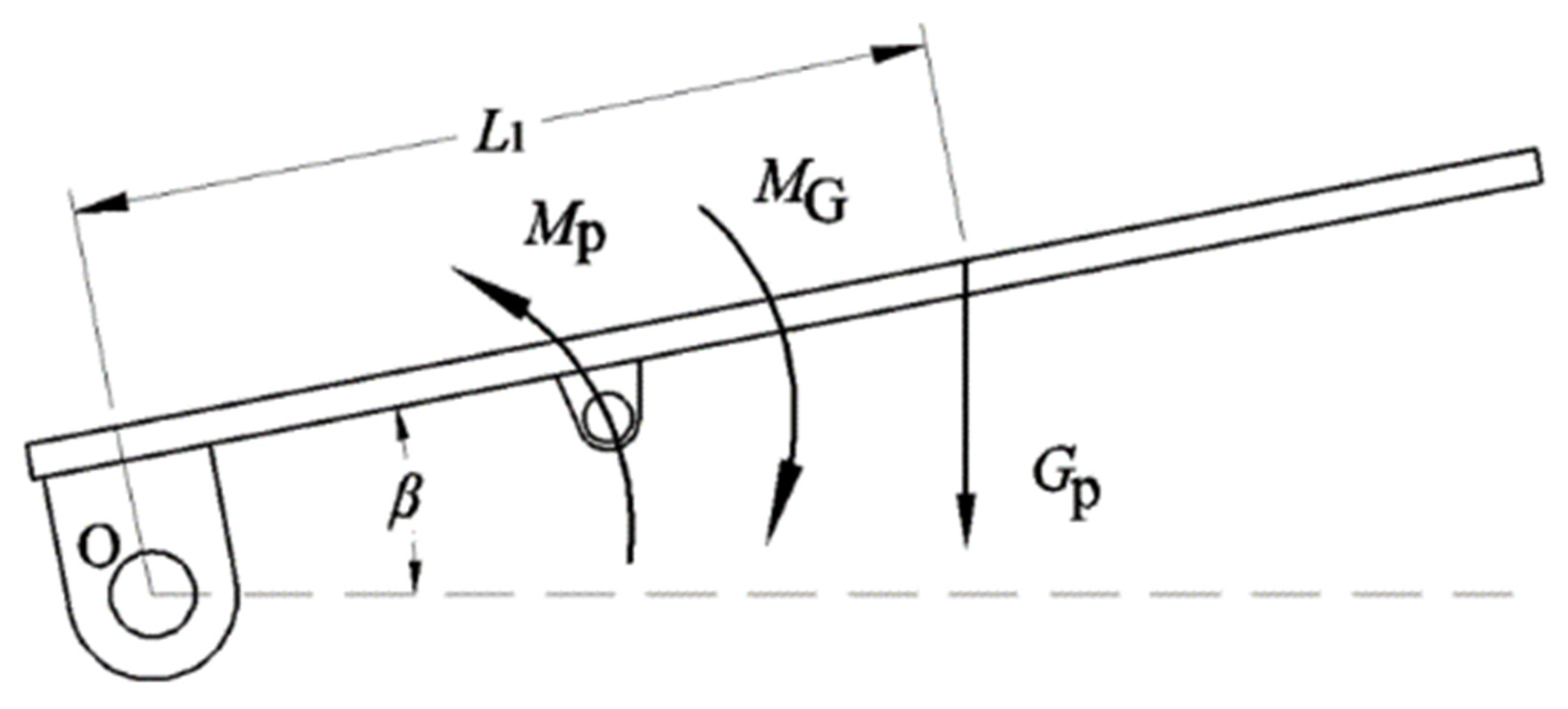
3.2. Mechanical Analysis of the Deflection and Lifting Process

Figure 6 shows the stress analysis when the upper plate is lifted. The torque generated by the weight of the upper plate on the rotation center O of the upper plate is set as M_G, in a clockwise direction. The lifting torque of the hydraulic cylinder on the rotation center of the upper plate is set as M_p, in a counterclockwise direction. When M_p > M_G, the upward lifting of the upper plate is initiated.

$$M_{\mathrm{G}}=G_p\cdot L_1\cdot \cos \beta$$

(7)

where G_p is the gravity of the upper plate, its weight L₁ is the distance from the center of gravity of the upper plate to the rotation center of the upper plate, and β is the lifting angle of the upper plate.

This formula shows that when β = 0, i.e., when the upper plate is horizontal, the MG value is the largest, and the maximum value can be calculated as M_{G max} = 90 N.m. Therefore, only when M_p > M_{G max} = 90 N.m does the hydraulic cylinder lift the upper plate at a certain angle.

As shown in Figure 7, the thrust F_p of the hydraulic lifting cylinder to the upper plate can be divided into a vertical component F_y and a horizontal component F_x:

$$M_{\mathrm{p}}=F_y\cdot L_2$$

(8)

$$F_y=Fp\cdot \sin \gamma$$

(9)

where γ is the original angle of the hydraulic cylinder, γ = 10.68°, L₂ is the horizontal distance from the rotation center of the upper plate to the action point of the hydraulic lifting cylinder, and L₂ = 0.1 m.

Since M_p > M_{G max} = 90 N.m, substituting the relevant parameters yields F_p > 4.856 kN. Therefore, the minimum thrust of the hydraulic lifting cylinder is 4.856 kN.

3.3. Mechanical Analysis of the Support Process

The grouting gun body of the pipeline grouting robot is affected by soil resistance P when inserted into the soil. The soil resistance P is decomposed into horizontal component P_x and vertical component P_y, as shown in Figure 8. The vertical component P_y can be offset by the support force N_ls provided by the inner wall of the pipe, while the horizontal component Px must be offset by the friction between the support mechanism and the inner pipe wall.

N_ts is the support force of the inner pipe wall on the support top, N_ls is the support force of the inner pipe wall on the lower support and wheel, G is the gravity of the grouting robot in the pipe, and f₁ and f₃ represent the friction between the support top, lower support, and the inner pipe wall, respectively. f₂ is the friction between the wheel and the inner pipe wall, and angle α is the included angle between the soil resistance P and its horizontal component P_x, which is the same as the lifting angle of the grouting gun body. The calculation is performed by simplifying these forces and moving their action points to the same coordinate system for analysis, where N_s is the total support force generated by the vertical component of the gravity and soil resistance of the inner pipe wall on the grouting robot in the pipe, as shown in Figure 9.

The force balance shows that stable soil insertion of the pipeline grouting gun can be achieved when f₁, f₂, and f₃ meet the following requirements:

$$f_1+f_2+f_3\ge F$$

(10)

The F_s required to support the hydraulic cylinder can be calculated according to the following formulas:

$$N_{\mathrm{ts}}=N_{ls}=F_s$$

(11)

$$P_x=P\cdot \cos \alpha$$

(12)

$$P_y=P\cdot \sin \alpha$$

(13)

$$f_1=\mu \cdot N_{\mathrm{ts}}$$

(14)

$$f_2=\mu (G+F_y)=\mu \cdot N_{\mathrm{s}}$$

(15)

$$f_3=\mu \cdot Fls$$

(16)

where μ is the friction coefficient of the inner pipe wall.

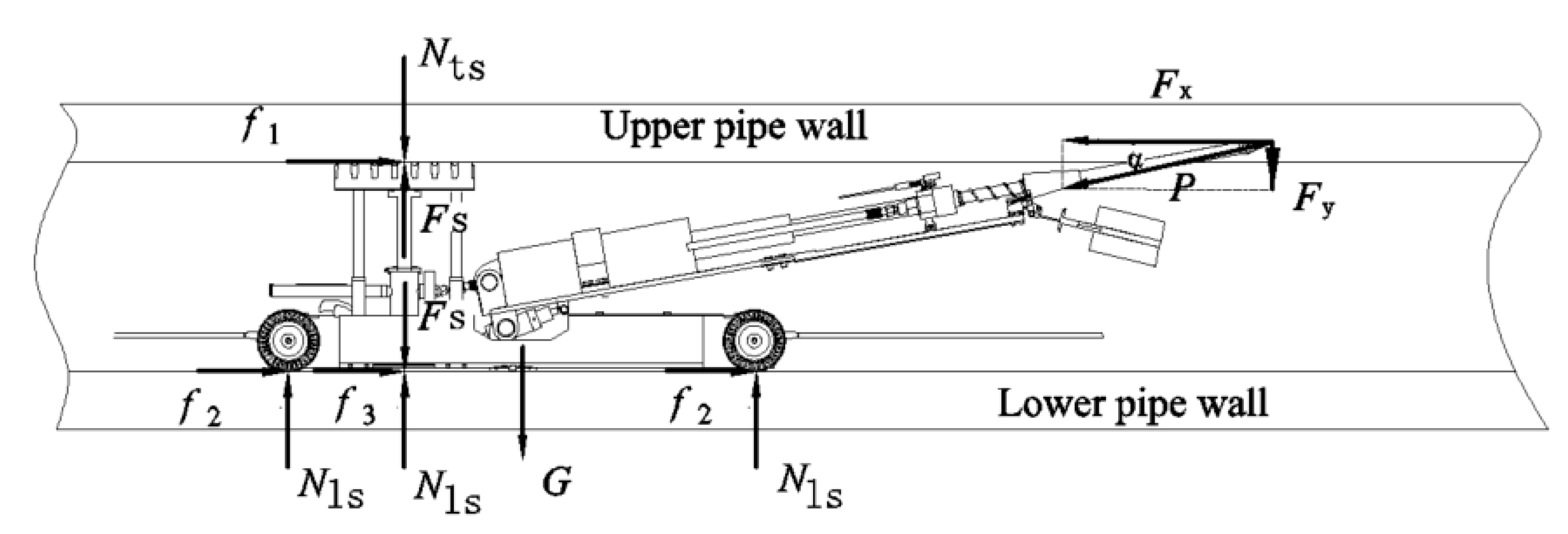
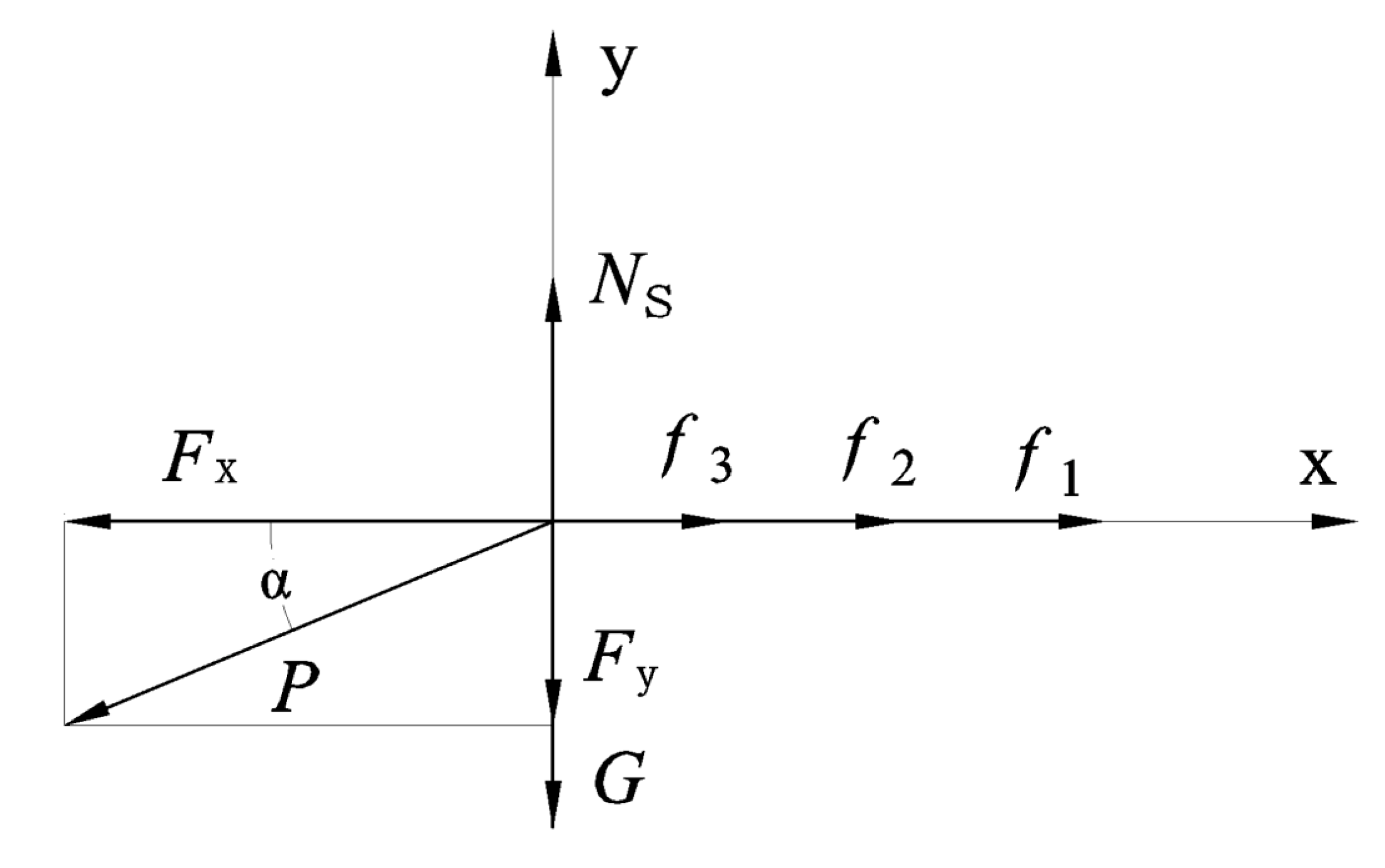
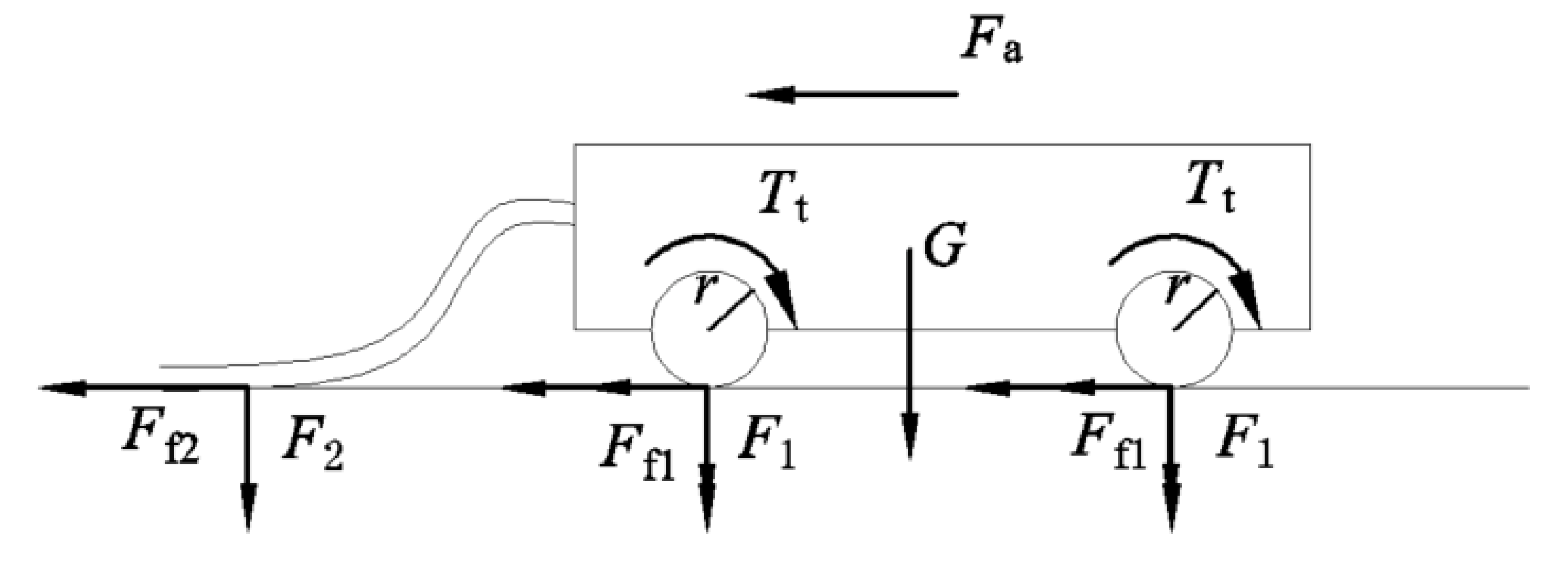
3.4. Mechanical Analysis of the Traveling Process

The pipeline grouting robot must overcome various forms of resistance as it travels in the pipe, such as the friction resistance between the wheel and the inner pipe wall, the friction resistance between the trailing pipe and the inner pipe wall, and the acceleration resistance while in motion. As shown in Figure 10, this resistance must be overcome by the driving force of the wheel. The main parameters of the pipeline grouting robot can be determined according to the design requirements and working conditions, as shown in

Table 2. The pipeline grouting robot parameters.

Project	Parameter
Quality control of in-pipe grouting robot (M1)	300 kg
Mass of 50 m drag pipe (M2)	100 kg
Travel speed (v)	0.5 m/s
Acceleration (a)	0.2 m/s2
Gravitational acceleration (g)	9.8 m/s2
Wheel radius (r)	0.05 m

.

The positive pressure of the grouting robot wheel on the inner pipe wall is:

$$F_1=M_{1}g$$

(17)

If the grouting robot in the pipe travels normally, the driving force F_t required by the wheel is:

$$F_{\mathrm{t}}=F_{\mathrm{f}1}+F_{\mathrm{f}2}+F$$

(18)

F_f1 is the friction between the wheel of the pipeline grouting robot and the inner pipe wall, F_f2 is the friction between the dragging pipe and the inner pipe wall, and F_a represents the acceleration resistance experienced by the pipeline grouting robot while in motion.

According to Newton’s second law, the acceleration resistance F_a is:

$$F_{\mathrm{a}}=(M_1+M_2)\cdot a$$

(19)

Motor driving power is:

$$P_{\mathrm{w}}=K\cdot \frac{F_{\mathrm{t}}\cdot v}{\eta }$$

(20)

where K is the safety factor, V is the traveling speed of the grouting robot in the pipe, and η is the transfer efficiency between the motor and the wheel.

To select the drive motor, it is also necessary to calculate the torque T_a output by the motor. The output torque ultimately reaches the wheel via the two-stage planetary reducer, becoming the torque T_t of the wheel. The calculation formula is:

$$T\mathrm{t}=F\mathrm{t}\cdot r$$

(21)

where r is the wheel radius, r = 0.05 m.

The relationship between the output torque T_a of the motor and the output torque T_t of the wheel is:

$$T\mathrm{a}=\frac{T\mathrm{t}}{i\cdot \eta }$$

(22)

where i is the reduction ratio of the reducer.

4. The Dynamic Simulation and Experimental Research of the Pipeline Grouting Robot

In order to verify the feasibility of the designed pipeline grouting robot, the kinematics simulation was carried out by using ADAMS 2020 software. In order to verify whether the grouting gun body of the pipeline grouting robot can overcome the resistance and smoothly insert into the soil to carry out the grouting operation, the soil insertion test and hot-melt test of the grouting gun body need to be carried out.

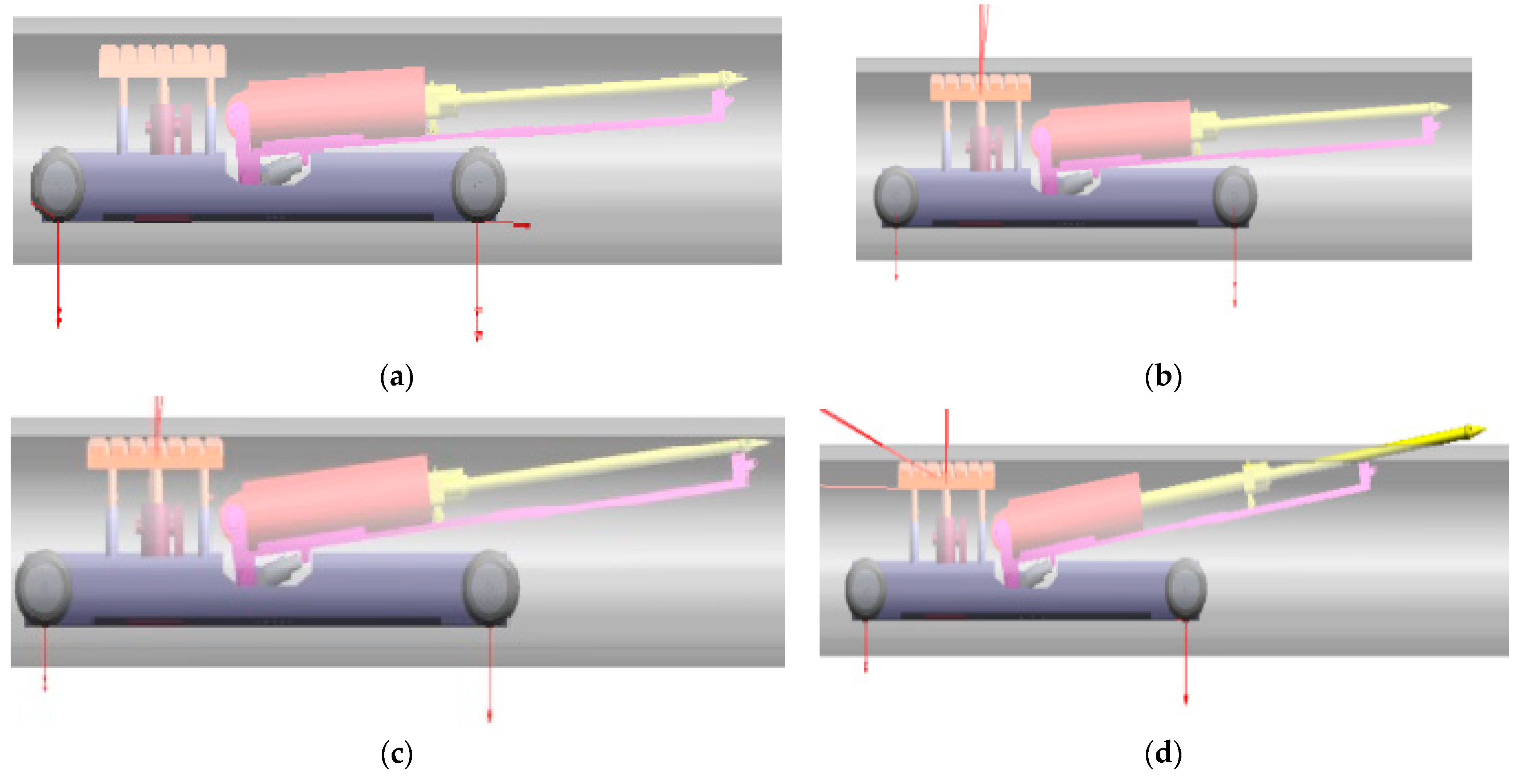
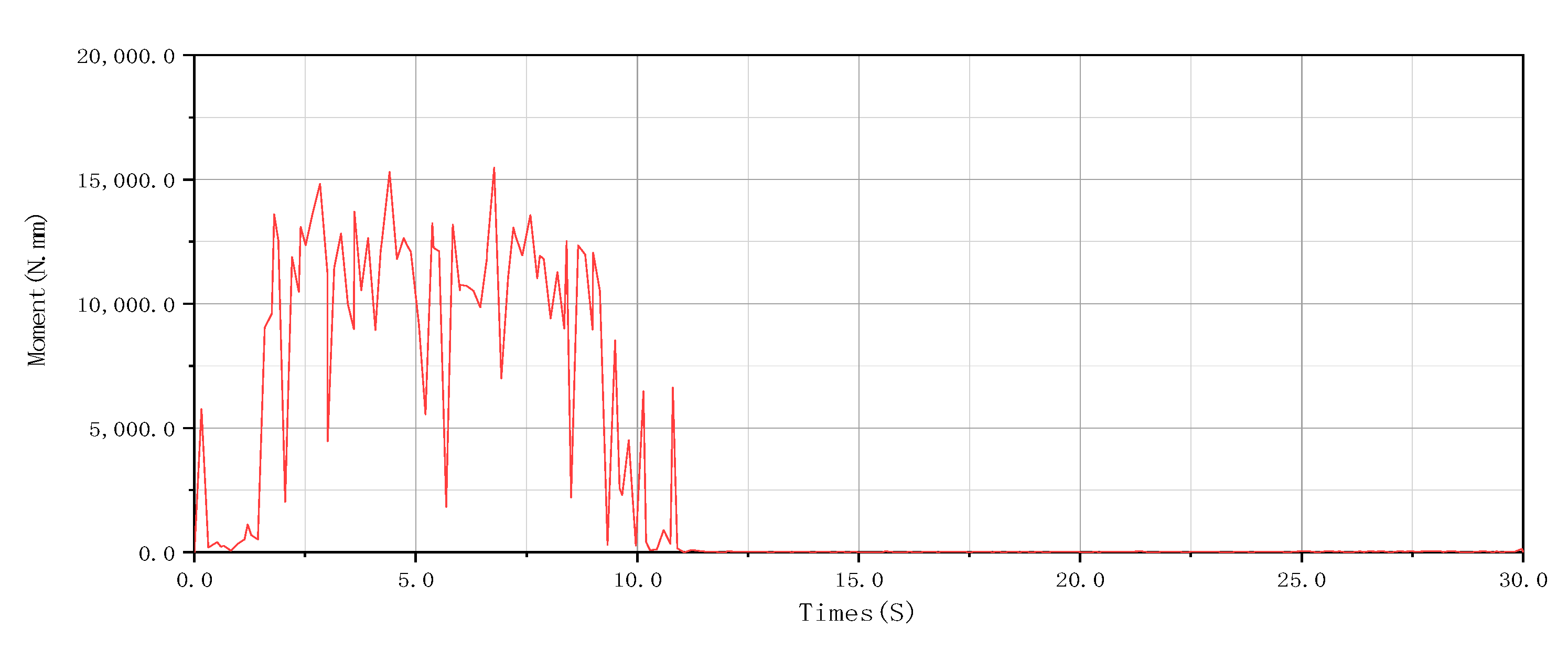
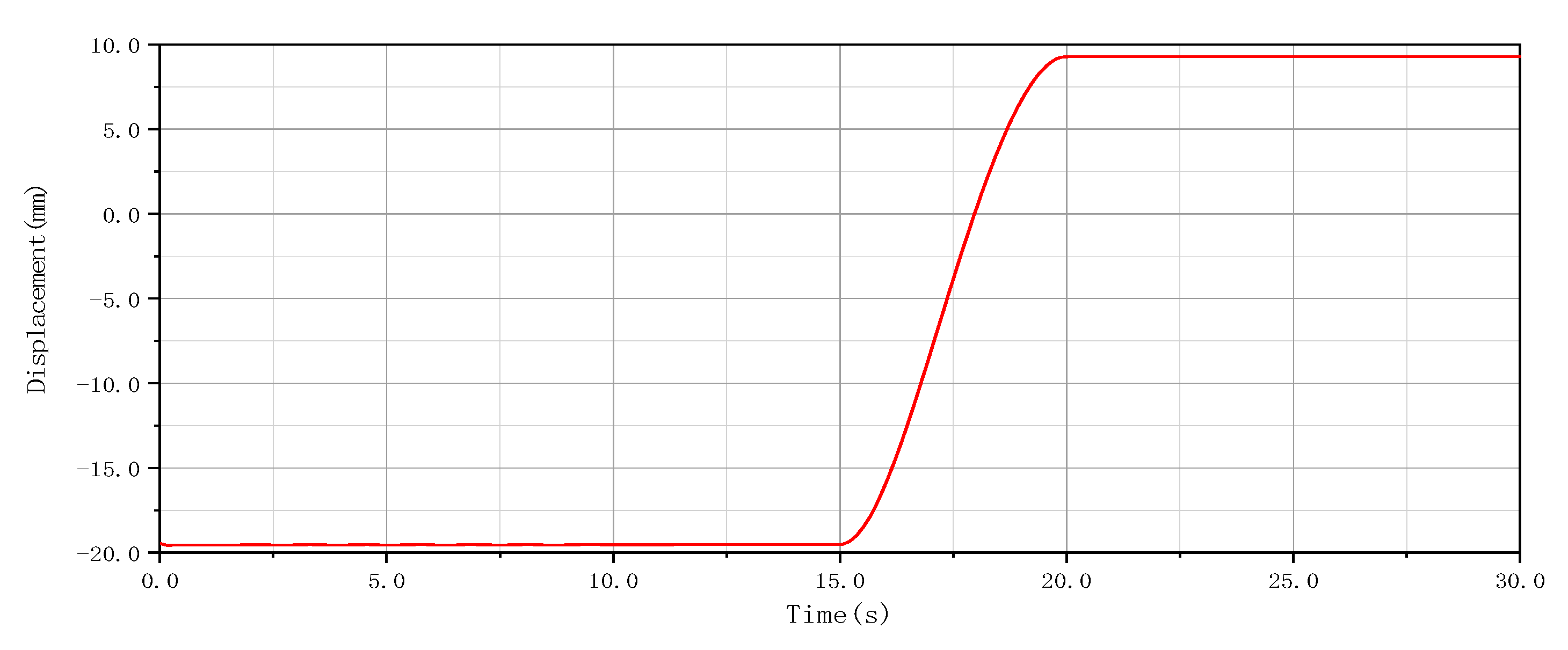
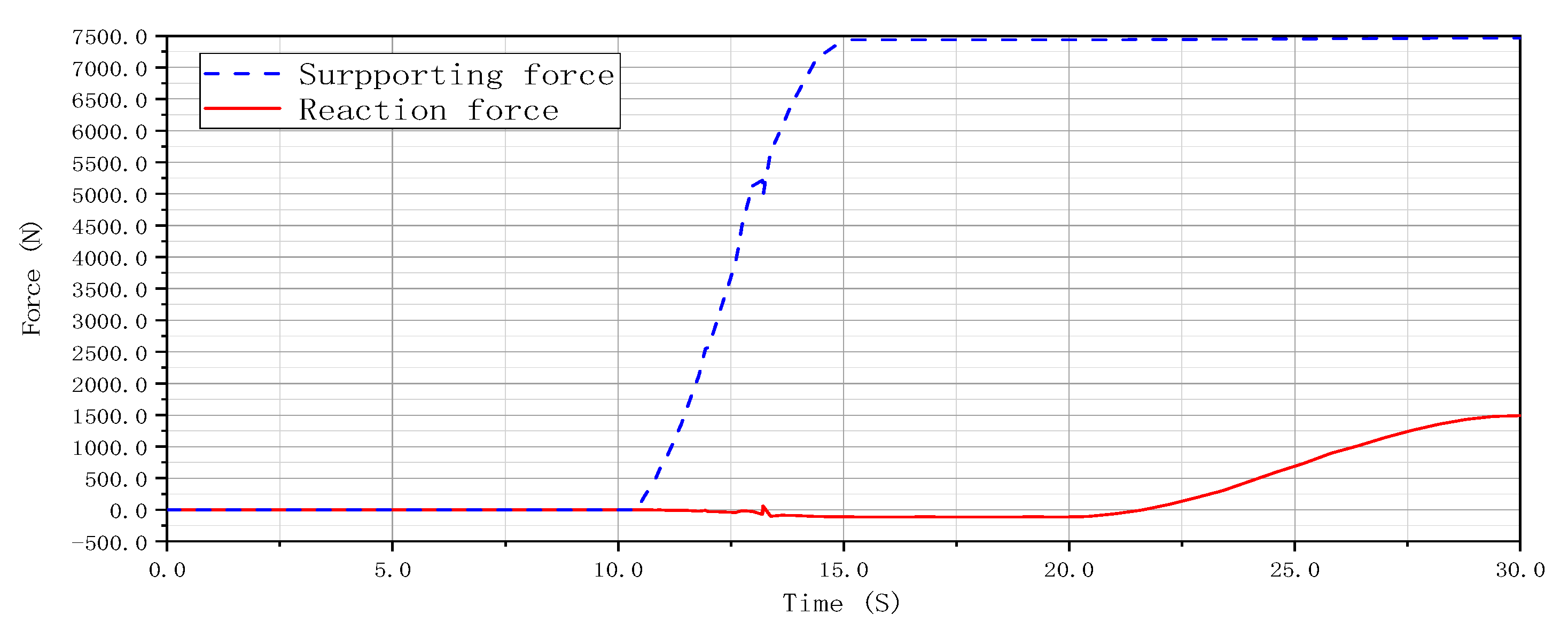
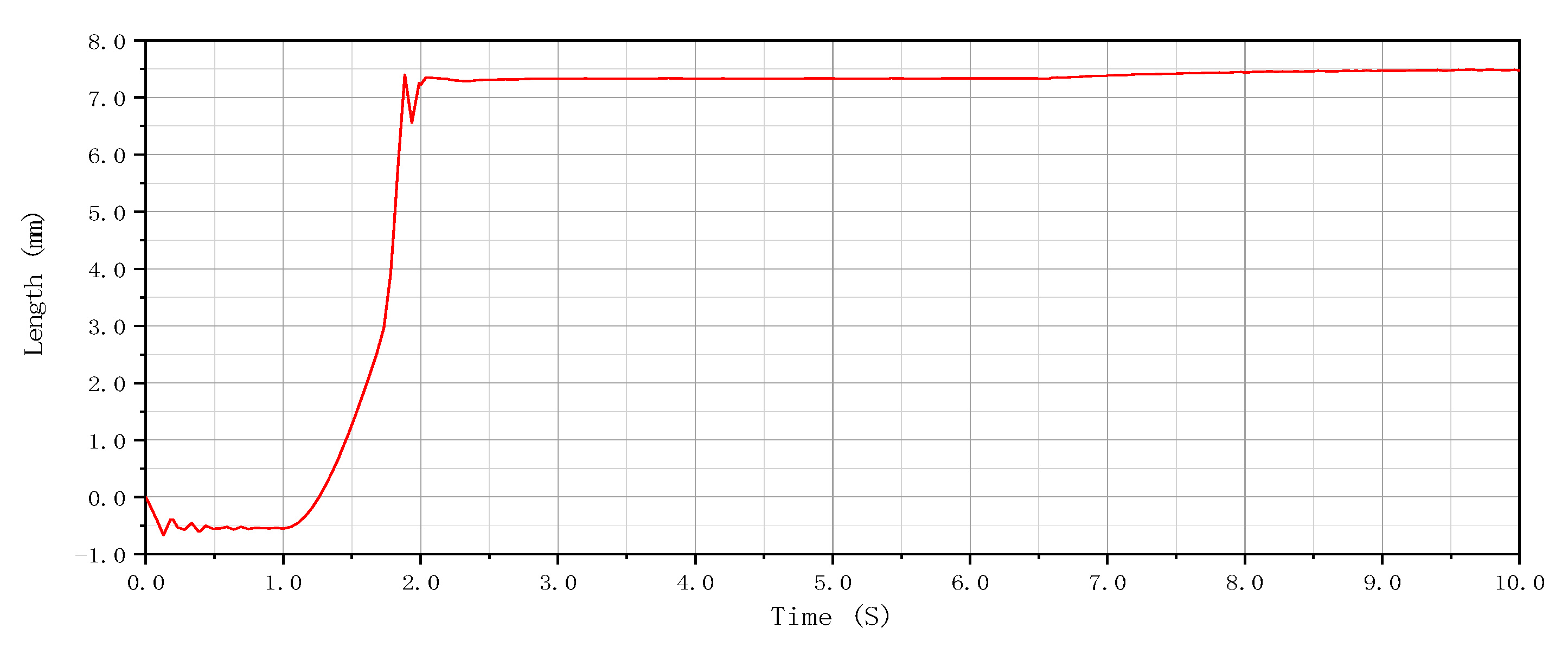
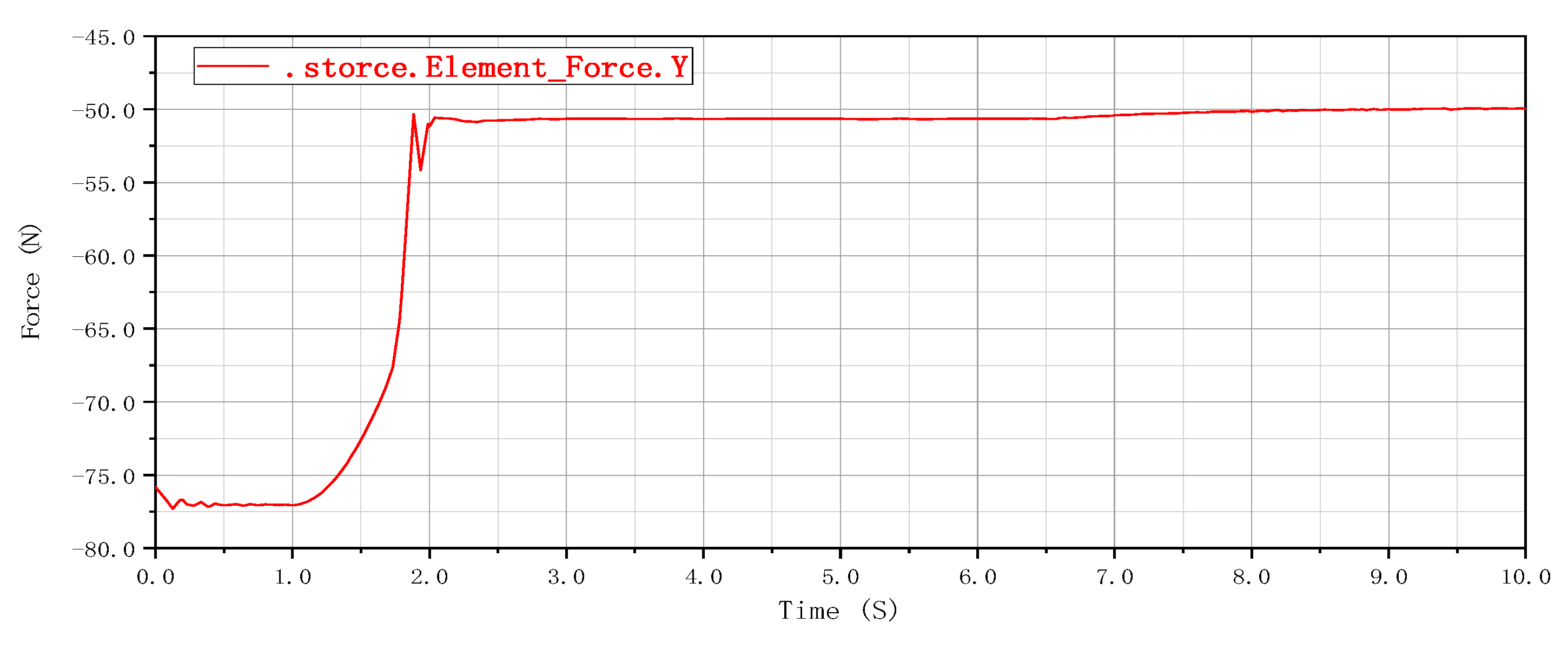
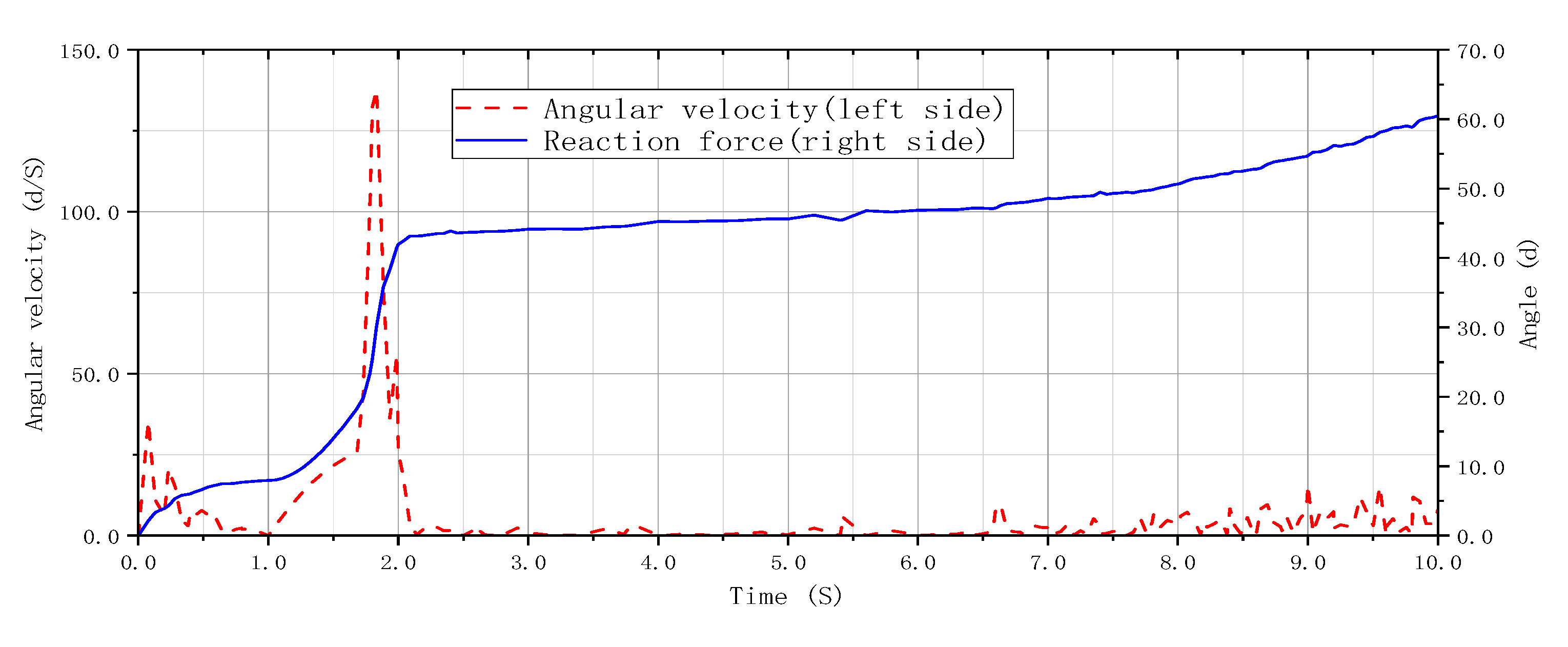
4.1. Dynamic Simulation of the Pipeline Grouting Robot

To reduce the operation time and increase the operation efficiency, the model is divided into two parts: the main body and the hot-melt process of the pipeline grouting robot, which are imported into ADAMS for kinematic simulation. The material parameters of the pipeline grouting robot in ADAMS are shown in

Table 3. Material data of the pipeline grouting robot in ADAMS.

Name	Poisson’s Ratio	Modulus of Elasticity (MPa)	Density (kg/m3)
Rubber	0.45	1 × 10−2	9.6 × 102
35 Steel	0.29	2.05 × 105	7.85 × 103
304 Stainless steel	0.29	1.9 × 105	8 × 103

.

The cylinder barrel supporting the hydraulic cylinder and the two lower supports are integrated into two parts, while the movement constraint is imposed on the base. The rotation drive and movement drive are applied to the two axles, the hydraulic lifting cylinder, the three-stage push hydraulic cylinder, and the hydraulic lifting cylinder, respectively. The contact between the four wheels and the HDPE pipeline is defined as collision contact, while the friction is regarded as Coulomb friction. The relevant parameters are shown in

Table 4. Friction parameter settings.

Parameter Name	Value
Static friction coefficient	0.5
Dynamic friction coefficient	0.43
Static translation speed (mm/s)	0.1
Friction translation speed (mm/s)	10.0

.

The simulation process of the main part of the pipeline grouting robot is shown in Figure 11. The traveling time between the pipeline grouting robot and operational position is set in a range of 1 s to 10 s, from 10 s to 15 s, and the support mechanism applies upward thrust to make the upper support and lower support stick to each other and generate friction with the inner wall of the pipe. The cylinder rod of the hydraulic lifting cylinder extends 0.7 mm from 15 s to 20 s, lifting the upper plate and grouting gun body until reaching a certain angle. The cylinder rod of the 20 s to 30 s three-stage, thrust hydraulic cylinder extends 450 mm, inserting the grouting gun body into the soil and applying backward soil resistance to the main body of the grouting robot in the pipe.

Figure 12 shows a graph of the driving torque of the pipeline grouting machine. The collision contact between the pipeline grouting robot and inner pipe wall, coupled with the influence of the friction between its rubber tire and the inner pipe wall, causes significant torque vibration, with a maximum value of about 15,475 N.mm, which is less than the maximum torque output by the selected drive motor.

Figure 13 shows the output power curve of the hydraulic lifting cylinder, which is parabolic between 15 s and 20 s and has a maximum value of 878 N.mm/s. The level of work completed increases to 2861.42 N.mm between 15 s and 20 s.

Figure 14 shows the output power curve of the hydraulic lifting cylinder and the displacement curve of the upper plate. During this process, the centroid displacement of the upper plate increases by 28.8 mm. Consequently, the maximum thrust of the hydraulic lifting cylinder is 4856 N, exceeding the simulation results, showing that it can successfully lift the upper plate and grouting gun body to a certain angle.

According to Figure 15, the maximum support force is 7500 N, and the maximum reaction force is 1491 N, which is obtained using Equations (14) and (16). During the simulation process, the static friction provided by the support mechanism is about 1500 N, which can form a pair of balanced forces when combined with the reaction force. Therefore, the grouting robot in the pipe can remain stable while inserting the grouting gun into the soil. Similarly, when the grouting gun is pulled from the soil, it is affected by the reaction force, but its value is lower than the reaction force when the grouting gun is inserted into the soil. Therefore, it can be inferred that the support mechanism can also ensure the stability of the entire machine when the grouting gun is recovered from the soil.

Figure 16 and Figure 17 show the deformation and displacement curves generated by the preloaded spring when the turnover baffle in the hot-melt mechanism is turned down at a certain angle. When the grouting gun body extends outward and deflects the turnover baffle and the hot-melt mechanism downward, the maximum shape variable of the preloaded spring is 7.48 mm, and the maximum tension is 49.5 N, showing a rapid initial increase to the maximum value, gradually reaching stability. During this process, the centroid displacement of the turnover baffle changes by about 1.4 mm.

When the grouting gun body protrudes outward and deflects the flip baffle and the fuser downward, in the process, according to Figure 18, the displacement of the center of mass of the flip baffle changes by about 1.4 mm. Figure 19 shows the deflection angle and angular velocity curve of the turnover baffle. During the extension of the grouting gun body, the turnover baffle deflected a total of 60.2°. When the gun head of the grouting gun body first touched the turnover baffle and turned it over, the angular velocity of the turnover was the fastest at about 137.7° per second. The turnover angle increased rapidly to 42°, while the deflection angle increased more slowly to about 60°. This can be attributed to the slightly larger diameter of the grouting gun head than that of the grouting gun body and the conical shape of the gun head. Therefore, when it extends outward, the turnover baffle is close to the outer contour of the grouting gun body. Changes in the outer contour diameter modify the angular velocity of the turnover baffle, the shape variable of the pre-tightening spring connected to it, and the tensile force. The deflection of the turnover baffle tends to be stable until the grouting gun head passes through and the grouting gun body makes contact with it.

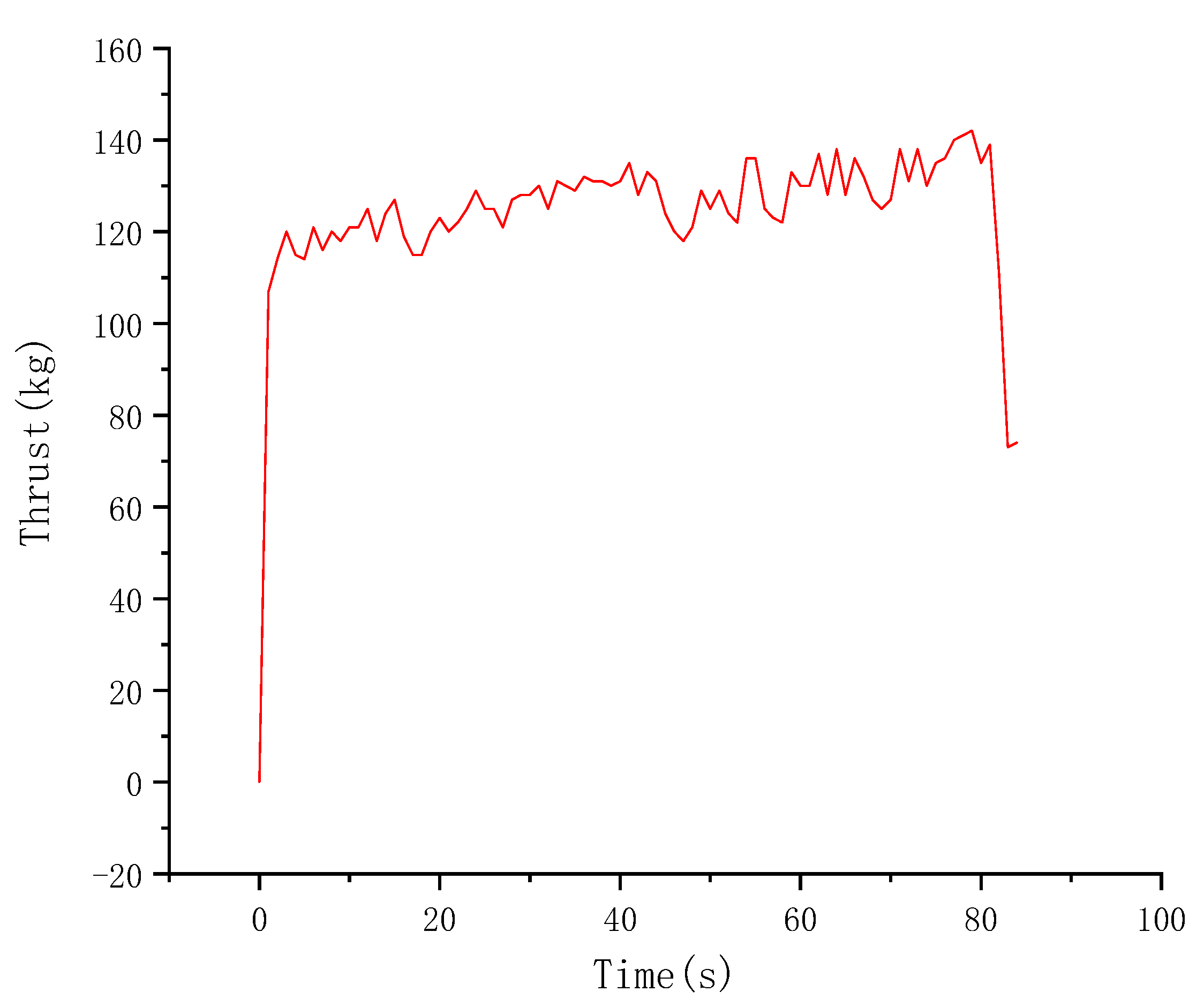
4.2. Horizontal Insertion Test When the Grouting Gun Enters the Soil

The experimental prototype of the pipeline grouting robot is shown in Figure 20. A soil insertion test was performed to verify whether the grouting gun body can successfully overcome the resistance to enter the soil for the grouting process. The test site is selected in the tunnel near the location of the HDPE water supply and drainage pipeline. The soil quality is consistent with that above the pipeline. The grouting robot is fixed to one side of the pipe, its top equipped with a pressure sensor and grouting gun body. When the grouting gun body is inserted into the soil, the thrust applied by the hydraulic cylinder can be read in real-time via a paperless recorder.

The relationship between the thrust and time during the grouting gun insertion measured in the test is shown in Figure 21. The grouting gun penetrates deeper into the soil as the time is extended. The thrust required generally shows an increasing trend, reaching a maximum value of 147 kg in 79 s, followed by a sharp decline, indicating that the grouting gun is completely inserted into the soil. According to the principle of force interaction, the soil resistance is consistent with the required thrust, moves in the opposite direction, and is below the maximum thrust provided by the multi-stage hydraulic cylinder selected by the pipeline grouting robot.

4.3. Hot-Melt Test of the Pipeline Grouting Robot

The pipeline grouting robot melts the inner wall of the HDPE double-walled corrugated pipe using the hot-melt method. A short pipe of the same material is used for the hot-melt test to verify the hot-melt effect. The temperature of the heating head is adjusted to 250 °C and remains unchanged. A certain thrust level is maintained as far as possible when the hot-melt head is in contact with the pipe. The wall thickness of the tested double-walled corrugated pipe is 23.5 mm. The HDPE double-walled bellows are completely penetrated after about 160 s, as shown in Figure 22.

5. Conclusions

This paper proposes a new internal collapse repair process for HDPE double-walled corrugated pipes. The scheme design, structural design, kinematic simulation, and experimental verification are performed according to the process requirements with the pipeline grouting robot as the main research object. The conclusions are as follows:

(1)

A new internal grouting and shaping process for pipelines is proposed, which is suitable for repairing the internal collapse in HDPE double-walled corrugated pipelines. The design requirements and indexes of the pipeline grouting robot are presented. Grouting can be performed in HDPE double-walled corrugated pipelines with inner diameters of 300 mm to 600 mm and can be positioned in different areas of the collapse. This robot can penetrate the wall of the HDPE double-walled bellows since it can move on its own power.

(2)

The overall scheme of the pipeline grouting robot is determined. It consists primarily of hot-melt, deflection, lifting, support, monitoring, and driving mechanisms. A mechanical analysis of the grouting, deflection, lifting, support, and travel processes is performed. Furthermore, the calculation formula of the thrust required for the grouting gun to penetrate the soil is determined while experimental verification is conducted.

(3)

The kinematics simulation of the grouting robot is performed using the ADAMS software, confirming that the thrust of the hydraulic lifting cylinder and the supporting hydraulic rod meets the requirements and that the supporting mechanism of the grouting robot can ensure the stability of the equipment during grouting. The grouting robot designed in this paper has been well applied in practice to avoid the impact of excavation from the ground on traffic.