Food Preservation within Multi-Echelon Supply Chain Considering Single Setup and Multi-Deliveries of Unequal Lot Size
Abstract
:1. Introduction
- What is the set of solutions to optimize deterioration using multiple deliveries and preservation simultaneously?
- Does the SSMD policy affect investment in preservation?
- Does the investment in preservation have any effect on the number of deliveries/shipments within an SSMD setup?
- How does the preservation effect quantitatively the lifetime/deterioration/freshness of a fresh food product?
- What is the effect of SSMD policy on lot size and replenishment cycle?
- How do the preservation and SSMD policies affect total supply chain profit?
2. Literature Review
2.1. Single Setup Multiple Deliveries (SSMD)
2.2. Product Deterioration
2.3. Preservation Policies
| Authors | Two-Echelon SCM | Multiple Retailers | Unequal Lot Size | SSMD | Preservation Policy |
|---|---|---|---|---|---|
| Goyal [13] | ✓ | ✓ | |||
| Lu [15] | ✓ | ✓ | |||
| Goyal [16] | ✓ | ✓ | ✓ | ✓ | |
| Hill [18] | ✓ | ✓ | ✓ | ||
| Goyal and Nebebe [20] | ✓ | ✓ | ✓ | ||
| Woo et al. [59] | ✓ | ✓ | |||
| Yang and Wee [21] | ✓ | ✓ | |||
| Khouja [22] | ✓ | ✓ | |||
| Wang and Sarker [23] | ✓ | ||||
| Siajadi et al. [24] | ✓ | ✓ | ✓ | ||
| Chan and Kingsman [25] | ✓ | ✓ | ✓ | ||
| Ertogral et al. [60] | ✓ | ✓ | |||
| Ben-Daya and Al-Nassar [26] | ✓ | ✓ | ✓ | ||
| Darwish and Odah [27] | ✓ | ✓ | ✓ | ||
| Hsu et al. [50] | Conventional | ||||
| Ben-Daya et al. [11] | ✓ | ✓ | |||
| Dye [51] | Conventional | ||||
| Sana et al. [30] | ✓ | ✓ | |||
| Yang et al. [53] | Conventional | ||||
| Yang et al. [31] | ✓ | ✓ | |||
| Jia et al. [32] | ✓ | ||||
| Dye and Yang [55] | ✓ | ✓ | Conventional | ||
| Giri et al. [56] | ✓ | Conventional | |||
| Azadi et al. [6] | ✓ | ✓ | ✓ | ||
| Sarkar et al. [8] | ✓ | ✓ | ✓ | ||
| This paper | ✓ | ✓ | ✓ | ✓ | MDRDRMIP |
3. Problem Definition, Notation and Assumptions
3.1. Problem Definition
3.2. Assumptions
- A single manufacturer supplies fresh products to the multi-retailers to constitute a supply chain system.
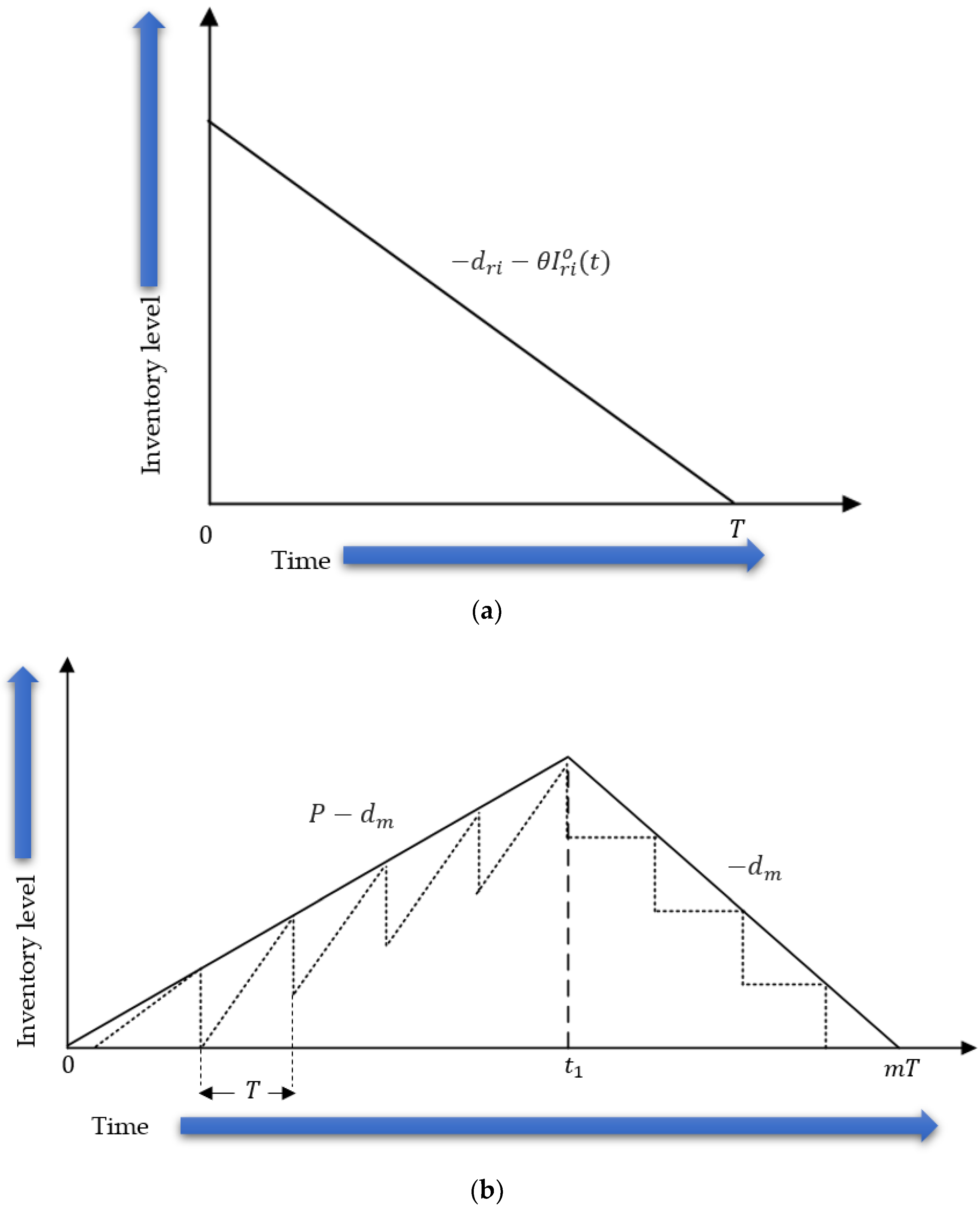
- The manufacturer supplies the produced items to retailers in multiple deliveries, which is known as a single setup multi-delivery (SSMD) policy. Therefore, the cycle time of the manufacturer is the integer multiple of the retailers’ cycle time. This integer is the number of deliveries/shipments to the retailers per cycle of the manufacturer.
- Shipments/deliveries for retailers are prepared from a production batch while the production is continued [26].
- The cycle time of all the retailers is equal, i.e., the inventory is replenished at all the retailers at the same point of time [11].
- The customer demand at all the retailers is known, constant, and different.
- As the demand at each retailer is different, therefore, this model assumes an unequal lot size for each retailer.
- The ordering cost and cost of inventory carrying are different for each retailer.
- The products under consideration are deteriorating in nature, and deteriorate at a constant rate. Practically, the products start deteriorating after being replenished at the retailer. This study includes this fact by considering no deterioration at the manufacturer.
- The rate of production depends on the demand rate [40], i.e., assuming where the production rate and the demand rate at the manufacturer are.
- The inventory holding cost at the manufacturer is less than the inventory holding cost at the retailers, i.e.
- There are no shortages, i.e., all the customers are satisfied to fulfill their demand.
- The supply chain is vertically integrated, such that the optimal value of profit is obtained as a centralized system.
4. Model Formulation and Solution
4.1. Retailers’ Model
4.1.1. Ordering Cost
4.1.2. Purchasing Cost
4.1.3. Inventory Holding Cost
4.1.4. Preservation Cost
4.1.5. Total Cost per Unit Time
4.1.6. Sales Revenue per Unit Time
4.1.7. Retailers’ Profit per Unit Time
4.2. Manufacturer’s Model
4.2.1. Setup Cost
4.2.2. Material Purchasing Cost
4.2.3. Production Cost
4.2.4. Inventory Holding Cost
4.2.5. Total Cost per Unit Time
4.2.6. Sales Revenue per Unit Time
4.2.7. Manufacturer’s Profit per Unit Time
4.2.8. Total Profit per Unit Time of the Supply Chain
5. Solution Methodology
5.1. Solution Algorithm
- Step 1 Start with and input appropriate values of other parameters.
- Step 2 For the first iterative value of , start with and perform the following steps.
- (i)
- Compute the value of that satisfies Equation (9).
- (ii)
- Using the value of , calculated in step (i), compute the value of that satisfies Equation (10).
- (iii)
- Using the value of , calculated in Step (ii), repeat Step (i) and Step (ii) for times, until no further change occurs in the value of and , where denotes the iteration.
- Step 3 For the iteration, using the pair of variables , compute from Equation (8).
- Step 4 Set , then is the optimal solution for given value of m.
- Step 5 Set , repeat Step 2 to Step 4 to attain .
- Step 6 If , go to Step 5, otherwise go to Step 7.
- Step 7 Set , then is a set of optimal solutions.
5.2. Numerical Experiments
5.2.1. Input Parameters
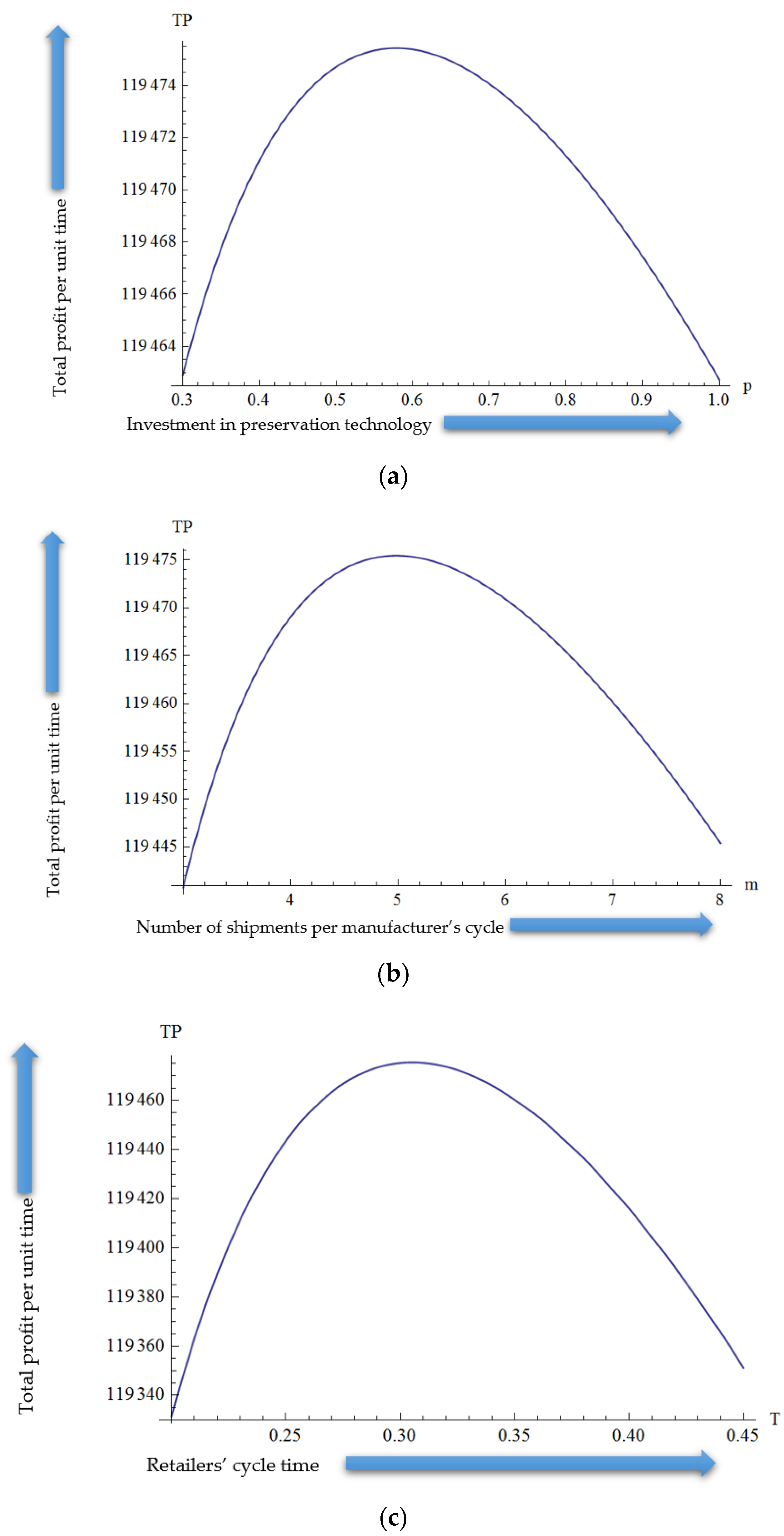
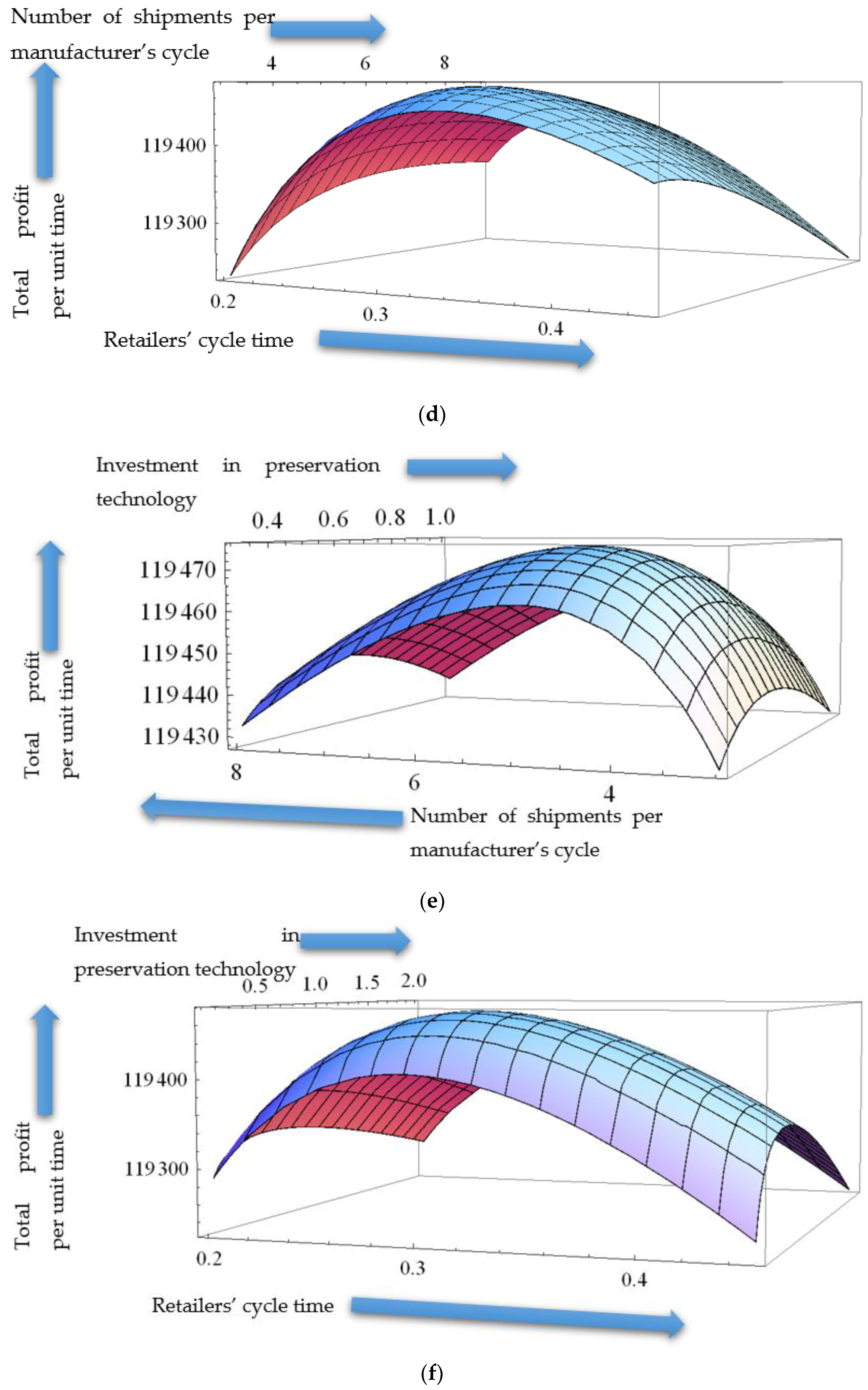
5.2.2. Results and Discussion
Comparative Analysis of the Results from Examples 1 and 2
5.2.3. Sensitivity Analysis
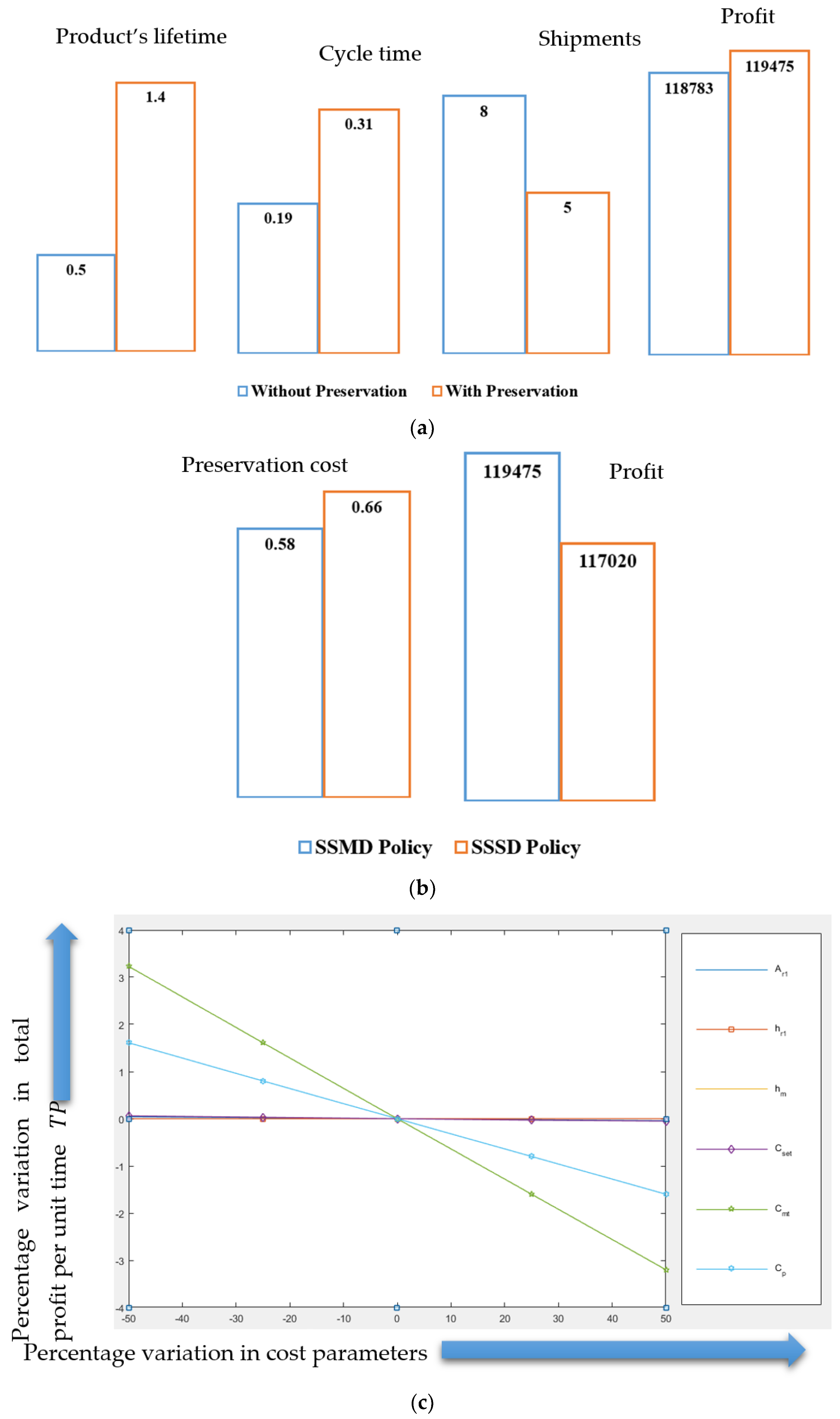
- The magnitude of variation in the value of profit is different from the variation in different cost parameters. The effect of variation in the value of each cost parameter on the value of profit is illustrated in Figure 5c.
- The cost of production and the cost of materials affect the profit the most, while the variation in the value of inventory holding cost of retailer 1 has no effect on the value of the profit. Other cost parameters including manufacturer’s setup cost and inventory holding cost, and retailer’s ordering cost have an insignificant effect on the value of profit.
- Variations in production and material cost have a significant and inverse effect on the value of the retailers’ cycle time. The cycle time varies directly with variations in the retailer’s ordering cost. Retailers’ and manufacturers’ inventory holding costs and setup costs of manufacture have no significant effect on the value of the cycle time.
- The investment in the preservation is affected directly by the variation in the cost parameters. This effect is significant for cost of material and production cost, while other cost parameters do not have a considerable effect on the value of preservation investment.
- Variations in production cost, retailer’s ordering, and inventory holding cost have no effect on the value of the number of deliveries/shipments to the retailers per cycle of the manufacturer. Variations in the cost of material affect directly, while that in the manufacturer’s inventory holding cost and setup cost affect the number of shipments/deliveries inversely.
6. Managerial Insights
6.1. Insight 1—Transportation/Delivery Reduction
6.2. Insight 2—Demand Improvement
6.3. Insight 3—Profit Maximization
6.4. Insight 4—Preservation during Transportation
6.5. Insight 5—Environmental Protection
7. Conclusions
Limitations and Future Research Directions
- This research considered variable ordering cost, inventory holding cost, and selling price due to several demographical, geographical, and setup structure reasons, which can be modeled to extend this research.
- As the demand at each retailer is assumed to be different due to several reasons, those reasons can be considered and modeled to improve the customer demand, e.g., by considering local advertisement-dependent demand for each retailer, as considered by Palanivel and Uthayakumar [64].
- This research assumed a constant size of each replenishment for a single retailer, which can be considered as different for each replenishment, as proposed by Goyal [16].
- The proposed model considered that uniform preservation investment though the lot size is different at each retailer. This model can be extended by relating the amount of preservation investment to the lot size.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Index | |
| . | |
| Variables | |
| number of shipments/deliveries to retailers per manufacturer’s cycle (number) | |
| retailers’ cycle time (time units) | |
| preservation investment at retailers’ level ($/unit/unit time) | |
| Retailers’ Parameters | |
| retailer per unit time (units/unit time) | |
| per cycle (units/cycle) | |
| (units/cycle) | |
| (units/cycle) | |
| (units) | |
| (units/cycle) | |
| ($/order) | |
| ($/unit) | |
| ($/unit/unit time) | |
| ($/unit time) | |
| ($/unit) | |
| ($/unit time) | |
| ($/unit time) | |
| total profit per unit time of all the retailers ($/unit time) | |
| Manufacturer’s Parameters | |
| demand per unit time (units/unit time) | |
| demand per cycle (units/cycle) | |
| rate of production (units/unit time) | |
| (units) | |
| (units) | |
| total inventory carried during one cycle (units/cycle) | |
| number of items produced per cycle (units/cycle) | |
| setup cost per setup ($/setup) | |
| material cost per unit ($/unit) | |
| production cost per unit ($/unit) | |
| inventory holding cost per unit per unit time ($/unit/unit time) | |
| total cost per unit time ($/unit time) | |
| selling price per unit ($/unit) | |
| sales revenue per unit time ($/unit time) | |
| total profit per unit time ($/unit time) | |
| Other Parameters | |
| total profit per unit time of the supply chain as a centralized system ($/unit time) | |
| maximum lifetime of the product (time units) | |
| rate of deterioration | |
| degree of vulnerability to deterioration | |
| degree of effectiveness of preservation cost | |
| scaling parameter within production and demand at manufacturer | |
References
- Gustavsson, J.; Cederberg, C.; Sonesson, U.; Van Otterdijk, R.; Meybeck, A. Global Food Losses and Food Waste; FAO: Rome, Italy, 2011. [Google Scholar]
- Hill, R.; Omar, M. Another look at the single-vendor single-buyer integrated production-inventory problem. Int. J. Prod. Res. 2006, 44, 791–800. [Google Scholar] [CrossRef]
- Yang, P.; Chung, S.; Wee, H.; Zahara, E.; Peng, C. Collaboration for a closed-loop deteriorating inventory supply chain with multi-retailer and price-sensitive demand. Int. J. Prod. Econ. 2013, 143, 557–566. [Google Scholar] [CrossRef]
- Tantiwattanakul, P.; Dumrongsiri, A. Supply chain coordination using wholesale prices with multiple products, multiple periods, and multiple retailers: Bi-level optimization approach. Comput. Ind. Eng. 2019, 131, 391–407. [Google Scholar] [CrossRef]
- Chan, C.K.; Fang, F.; Langevin, A. Single-vendor multi-buyer supply chain coordination with stochastic demand. Int. J. Prod. Econ. 2018, 206, 110–133. [Google Scholar] [CrossRef]
- Azadi, Z.; Eksioglu, S.D.; Eksioglu, B.; Palak, G. Stochastic optimization models for joint pricing and inventory replenishment of perishable products. Comput. Ind. Eng. 2019, 127, 625–642. [Google Scholar] [CrossRef]
- Sufiyan, M.; Haleem, A.; Khan, S.; Khan, M.I. Evaluating food supply chain performance using hybrid fuzzy MCDM technique. Sustain. Prod. Consum. 2019, 20, 40–57. [Google Scholar] [CrossRef]
- Sarkar, S.; Tiwari, S.; Giri, B. Impact of uncertain demand and lead-time reduction on two-echelon supply chain. Ann. Oper. Res. 2021, 1–29. [Google Scholar] [CrossRef]
- Ananno, A.A.; Masud, M.H.; Chowdhury, S.A.; Dabnichki, P.; Ahmed, N.; Arefin, A.M.E. Sustainable food waste management model for Bangladesh. Sustain. Prod. Consum. 2021, 27, 35–51. [Google Scholar] [CrossRef]
- Jeswani, H.K.; Figueroa-Torres, G.; Azapagic, A. The extent of food waste generation in the UK and its environmental impacts. Sustain. Prod. Consum. 2021, 26, 532–547. [Google Scholar] [CrossRef]
- Ben-Daya, M.; As’ad, R.; Seliaman, M. An integrated production inventory model with raw material replenishment considerations in a three layer supply chain. Int. J. Prod. Econ. 2013, 143, 53–61. [Google Scholar] [CrossRef]
- Cárdenas-Barrón, L.E. Optimizing inventory decisions in a multi-stage multi-customer supply chain: A note. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 647–654. [Google Scholar] [CrossRef]
- Goyal, S.K. “A joint economic-lot-size model for purchaser and vendor”: A comment. Decis. Sci. 1988, 19, 236–241. [Google Scholar] [CrossRef]
- Banerjee, A. A joint economic-lot-size model for purchaser and vendor. Decis. Sci. 1986, 17, 292–311. [Google Scholar] [CrossRef]
- Lu, L. A one-vendor multi-buyer integrated inventory model. Eur. J. Oper. Res. 1995, 81, 312–323. [Google Scholar] [CrossRef]
- Goyal, S.K. A one-vendor multi-buyer integrated inventory model: A comment. Eur. J. Oper. Res. 1995, 82, 209–210. [Google Scholar] [CrossRef]
- Thomas, D.J.; Griffin, P.M. Coordinated supply chain management. Eur. J. Oper. Res. 1996, 94, 1–15. [Google Scholar] [CrossRef]
- Hill, R.M. The single-vendor single-buyer integrated production-inventory model with a generalised policy. Eur. J. Oper. Res. 1997, 97, 493–499. [Google Scholar] [CrossRef]
- Hill, R.M. The optimal production and shipment policy for the single-vendor singlebuyer integrated production-inventory problem. Int. J. Prod. Res. 1999, 37, 2463–2475. [Google Scholar] [CrossRef]
- Goyal, S.K.; Nebebe, F. Determination of economic production–shipment policy for a single-vendor–single-buyer system. Eur. J. Oper. Res. 2000, 121, 175–178. [Google Scholar] [CrossRef]
- Yang, P.-C.; Wee, H.-M. A single-vendor and multiple-buyers production–inventory policy for a deteriorating item. Eur. J. Oper. Res. 2002, 143, 570–581. [Google Scholar] [CrossRef]
- Khouja, M. Optimizing inventory decisions in a multi-stage multi-customer supply chain. Transp. Res. Part E Logist. Transp. Rev. 2003, 39, 193–208. [Google Scholar] [CrossRef]
- Wang, S.; Sarker, B.R. An assembly-type supply chain system controlled by kanbans under a just-in-time delivery policy. Eur. J. Oper. Res. 2005, 162, 153–172. [Google Scholar] [CrossRef]
- Siajadi, H.; Ibrahim, R.N.; Lochert, P.B. A single-vendor multiple-buyer inventory model with a multiple-shipment policy. Int. J. Adv. Manuf. Technol. 2006, 27, 1030–1037. [Google Scholar] [CrossRef]
- Chan, C.K.; Kingsman, B.G. Coordination in a single-vendor multi-buyer supply chain by synchronizing delivery and production cycles. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 90–111. [Google Scholar] [CrossRef]
- Ben-Daya, M.; Al-Nassar, A. An integrated inventory production system in a three-layer supply chain. Prod. Plan. Control 2008, 19, 97–104. [Google Scholar] [CrossRef]
- Darwish, M.A.; Odah, O. Vendor managed inventory model for single-vendor multi-retailer supply chains. Eur. J. Oper. Res. 2010, 204, 473–484. [Google Scholar] [CrossRef]
- Roy, M.D.; Sana, S.S.; Chaudhuri, K. An optimal shipment strategy for imperfect items in a stock-out situation. Math. Comput. Model. 2011, 54, 2528–2543. [Google Scholar]
- Sajadieh, M.S.; Fallahnezhad, M.S.; Khosravi, M. A joint optimal policy for a multiple-suppliers multiple-manufacturers multiple-retailers system. Int. J. Prod. Econ. 2013, 146, 738–744. [Google Scholar] [CrossRef]
- Sana, S.S.; Chedid, J.A.; Navarro, K.S. A three layer supply chain model with multiple suppliers, manufacturers and retailers for multiple items. Appl. Math. Comput. 2014, 229, 139–150. [Google Scholar] [CrossRef]
- Yang, G.-Q.; Liu, Y.-K.; Yang, K. Multi-objective biogeography-based optimization for supply chain network design under uncertainty. Comput. Ind. Eng. 2015, 85, 145–156. [Google Scholar] [CrossRef]
- Jia, T.; Liu, Y.; Wang, N.; Lin, F. Optimal production-delivery policy for a vendor-buyers integrated system considering postponed simultaneous delivery. Comput. Ind. Eng. 2016, 99, 1–15. [Google Scholar] [CrossRef]
- Song, Y.; Fan, T.; Tang, Y.; Xu, C. Omni-channel strategies for fresh produce with extra losses in-store. Transp. Res. Part E Logist. Transp. Rev. 2021, 148, 102243. [Google Scholar] [CrossRef]
- Ghare, P.; Schrader, G. A model for exponentially decaying inventory. J. Ind. Eng. 1963, 14, 238–243. [Google Scholar]
- Sachan, R. On (T, S i) policy inventory model for deteriorating items with time proportional demand. J. Oper. Res. Soc. 1984, 35, 1013–1019. [Google Scholar]
- Chang, H.-J.; Dye, C.-Y. An EOQ model for deteriorating items with time varying demand and partial backlogging. J. Oper. Res. Soc. 1999, 50, 1176–1182. [Google Scholar] [CrossRef]
- Skouri, K.; Konstantaras, I.; Papachristos, S.; Ganas, I. Inventory models with ramp type demand rate, partial backlogging and Weibull deterioration rate. Eur. J. Oper. Res. 2009, 192, 79–92. [Google Scholar] [CrossRef]
- Shah, N.H.; Soni, H.N.; Patel, K.A. Optimizing inventory and marketing policy for non-instantaneous deteriorating items with generalized type deterioration and holding cost rates. Omega 2013, 41, 421–430. [Google Scholar] [CrossRef]
- Wu, J.; Ouyang, L.-Y.; Cárdenas-Barrón, L.E.; Goyal, S.K. Optimal credit period and lot size for deteriorating items with expiration dates under two-level trade credit financing. Eur. J. Oper. Res. 2014, 237, 898–908. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, J.; Wei, C. Joint pricing and inventory control for fresh produce and foods with quality and physical quantity deteriorating simultaneously. Int. J. Prod. Econ. 2014, 152, 42–48. [Google Scholar] [CrossRef]
- Iqbal, M.W.; Sarkar, B. Recycling of lifetime dependent deteriorated products through different supply chains. RAIRO-Oper. Res. 2019, 53, 129–156. [Google Scholar] [CrossRef]
- Iqbal, M.W.; Sarkar, B. Application of preservation technology for lifetime dependent products in an integrated production system. J. Ind. Manag. Optim. 2020, 16, 141. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.-C.; Teng, J.-T. Retailer’s optimal ordering policy for deteriorating items with maximum lifetime under supplier’s trade credit financing. Appl. Math. Model. 2014, 38, 4049–4061. [Google Scholar] [CrossRef]
- Wang, W.-C.; Teng, J.-T.; Lou, K.-R. Seller’s optimal credit period and cycle time in a supply chain for deteriorating items with maximum lifetime. Eur. J. Oper. Res. 2014, 232, 315–321. [Google Scholar] [CrossRef]
- Shah, N.H.; Chaudhari, U.; Jani, M.Y. Optimal policies for time-varying deteriorating item with preservation technology under selling price and trade credit dependent quadratic demand in a supply chain. Int. J. Appl. Comput. Math. 2016, 3, 363–379. [Google Scholar] [CrossRef]
- Feng, L.; Chan, Y.-L.; Cárdenas-Barrón, L.E. Pricing and lot-sizing polices for perishable goods when the demand depends on selling price, displayed stocks, and expiration date. Int. J. Prod. Econ. 2017, 185, 11–20. [Google Scholar] [CrossRef]
- Chen, J.; Dong, M.; Xu, L. A perishable product shipment consolidation model considering freshness-keeping effort. Transp. Res. Part E Logist. Transp. Rev. 2018, 115, 56–86. [Google Scholar] [CrossRef]
- Daryanto, Y.; Wee, H.M.; Astanti, R.D. Three-echelon supply chain model considering carbon emission and item deterioration. Transp. Res. Part. E Logist. Transp. Rev. 2019, 122, 368–383. [Google Scholar] [CrossRef]
- Iqbal, M.W.; Kang, Y.; Jeon, H.W. Zero waste strategy for green supply chain management with minimization of energy consumption. J. Clean. Prod. 2020, 245, 118827. [Google Scholar] [CrossRef]
- Hsu, P.; Wee, H.; Teng, H. Preservation technology investment for deteriorating inventory. Int. J. Prod. Econ. 2010, 124, 388–394. [Google Scholar] [CrossRef]
- Dye, C.-Y. The effect of preservation technology investment on a non-instantaneous deteriorating inventory model. Omega 2013, 41, 872–880. [Google Scholar] [CrossRef]
- He, Y.; Huang, H. Optimizing inventory and pricing policy for seasonal deteriorating products with preservation technology investment. J. Ind. Eng. 2013, 2013, 793568. [Google Scholar] [CrossRef]
- Yang, C.-T.; Dye, C.-Y.; Ding, J.-F. Optimal dynamic trade credit and preservation technology allocation for a deteriorating inventory model. Comput. Ind. Eng. 2015, 87, 356–369. [Google Scholar] [CrossRef]
- Tsao, Y.-C. Designing a supply chain network for deteriorating inventory under preservation effort and trade credits. Int. J. Prod. Res. 2016, 54, 3837–3851. [Google Scholar] [CrossRef]
- Dye, C.-Y.; Yang, C.-T. Optimal dynamic pricing and preservation technology investment for deteriorating products with reference price effects. Omega 2016, 62, 52–67. [Google Scholar] [CrossRef]
- Giri, B.; Pal, H.; Maiti, T. A vendor-buyer supply chain model for time-dependent deteriorating item with preservation technology investment. Int. J. Math. Oper. Res. 2017, 10, 431–449. [Google Scholar] [CrossRef]
- Mishra, U.; Wu, J.-Z.; Tsao, Y.-C.; Tseng, M.-L. Sustainable inventory system with controllable non-instantaneous deterioration and environmental emission rates. J. Clean. Prod. 2020, 244, 118807. [Google Scholar] [CrossRef]
- Khakzad, A.; Gholamian, M.R. The effect of inspection on deterioration rate: An inventory model for deteriorating items with advanced payment. J. Clean. Prod. 2020, 254, 120117. [Google Scholar] [CrossRef]
- Woo, Y.Y.; Hsu, S.-L.; Wu, S. An integrated inventory model for a single vendor and multiple buyers with ordering cost reduction. Int. J. Prod. Econ. 2001, 73, 203–215. [Google Scholar] [CrossRef]
- Ertogral, K.; Darwish, M.; Ben-Daya, M. Production and shipment lot sizing in a vendor–buyer supply chain with transportation cost. Eur. J. Oper. Res. 2007, 176, 1592–1606. [Google Scholar] [CrossRef]
- Iqbal, M.W.; Kang, Y. Waste-to-energy supply chain management with energy feasibility condition. J. Clean. Prod. 2021, 291, 125231. [Google Scholar] [CrossRef]
- Liu, A.; Zhu, Q.; Xu, L.; Lu, Q.; Fan, Y. Sustainable supply chain management for perishable products in emerging markets: An integrated location-inventory-routing model. Transp. Res. Part E Logist. Transp. Rev. 2021, 150, 102319. [Google Scholar] [CrossRef]
- Bragg, S.M. Production Cost Reduction. In Cost Reduction Analysis: Tools and Strategies; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 91–105. [Google Scholar]
- Palanivel, M.; Uthayakumar, R. Finite horizon EOQ model for non-instantaneous deteriorating items with price and advertisement dependent demand and partial backlogging under inflation. Int. J. Syst. Sci. 2015, 46, 1762–1773. [Google Scholar] [CrossRef]


| (a) | ||||||
| (b) | ||||||
| (c) | ||||||
| (d) | ||||||
| (a) | |||||||
| Parameters | Without Preservation | With Preservation | Percent Variation | ||||
| Lifetime (month/s) | 0.5 | 1.4 | 180 | ||||
| Cycle time (month/s) | 0.19 | 0.31 | 63 | ||||
| Number of shipments | 8 | 5 | −37.5 | ||||
| Profit/month ($/month) | 118,783 | 119,475 | 0.58 | ||||
| (b) | |||||||
| Percentage Variation in Parameters | Percentage Variation in Optimal Values of Decision Variables and Profit | ||||
|---|---|---|---|---|---|
| −50 | −20 | −31.21 | 14.52 | 3.23 | |
| −25 | 0 | −15.69 | 5.48 | 1.61 | |
| 25 | 0 | 14.83 | −7.42 | −1.60 | |
| 50 | 20 | 29.83 | −11.94 | −3.20 | |
| −50 | 0 | −15.69 | 5.48 | 1.61 | |
| −25 | 0 | −7.93 | 1.61 | 0.80 | |
| 25 | 0 | 7.24 | −4.52 | −0.80 | |
| 50 | 0 | 14.83 | −7.42 | −1.60 | |
| −50 | 0 | −0.52 | −4.68 | 0.04 | |
| −25 | 0 | −0.34 | −3.55 | 0.02 | |
| 25 | 0 | −0.34 | 10.32 | −0.02 | |
| 50 | 0 | −0.17 | 1.94 | −0.04 | |
| −50 | 0 | −0.34 | −1.61 | 0.00 | |
| −25 | 0 | −0.34 | −1.29 | 0.00 | |
| 25 | 0 | −0.34 | −1.61 | 0.00 | |
| 50 | 0 | −0.34 | −1.94 | 0.00 | |
| −50 | 40 | −0.69 | −1.29 | 0.06 | |
| −25 | 20 | −0.52 | −1.61 | 0.03 | |
| 25 | −20 | −0.17 | −1.61 | −0.03 | |
| 50 | −40 | −0.17 | −1.61 | −0.05 | |
| −50 | −20 | −0.69 | −1.61 | 0.06 | |
| −25 | −20 | −0.52 | −1.61 | 0.03 | |
| 25 | 20 | −0.17 | −1.61 | −0.03 | |
| 50 | 20 | −0.17 | −1.61 | −0.05 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iqbal, M.W.; Ramzan, M.B.; Malik, A.I. Food Preservation within Multi-Echelon Supply Chain Considering Single Setup and Multi-Deliveries of Unequal Lot Size. Sustainability 2022, 14, 6782. https://doi.org/10.3390/su14116782
Iqbal MW, Ramzan MB, Malik AI. Food Preservation within Multi-Echelon Supply Chain Considering Single Setup and Multi-Deliveries of Unequal Lot Size. Sustainability. 2022; 14(11):6782. https://doi.org/10.3390/su14116782
Chicago/Turabian StyleIqbal, Muhammad Waqas, Muhammad Babar Ramzan, and Asif Iqbal Malik. 2022. "Food Preservation within Multi-Echelon Supply Chain Considering Single Setup and Multi-Deliveries of Unequal Lot Size" Sustainability 14, no. 11: 6782. https://doi.org/10.3390/su14116782
APA StyleIqbal, M. W., Ramzan, M. B., & Malik, A. I. (2022). Food Preservation within Multi-Echelon Supply Chain Considering Single Setup and Multi-Deliveries of Unequal Lot Size. Sustainability, 14(11), 6782. https://doi.org/10.3390/su14116782







