Method for Setting Weight Tolerance Limits in High-Speed Weigh-in-Motion Systems: A Case Study in Brazil
Abstract
:1. Introduction
2. Weigh-in-Motion of Heavy Goods Vehicles
2.1. Weight Estimation
2.2. Performance and Evaluation Requirements of WIM Systems
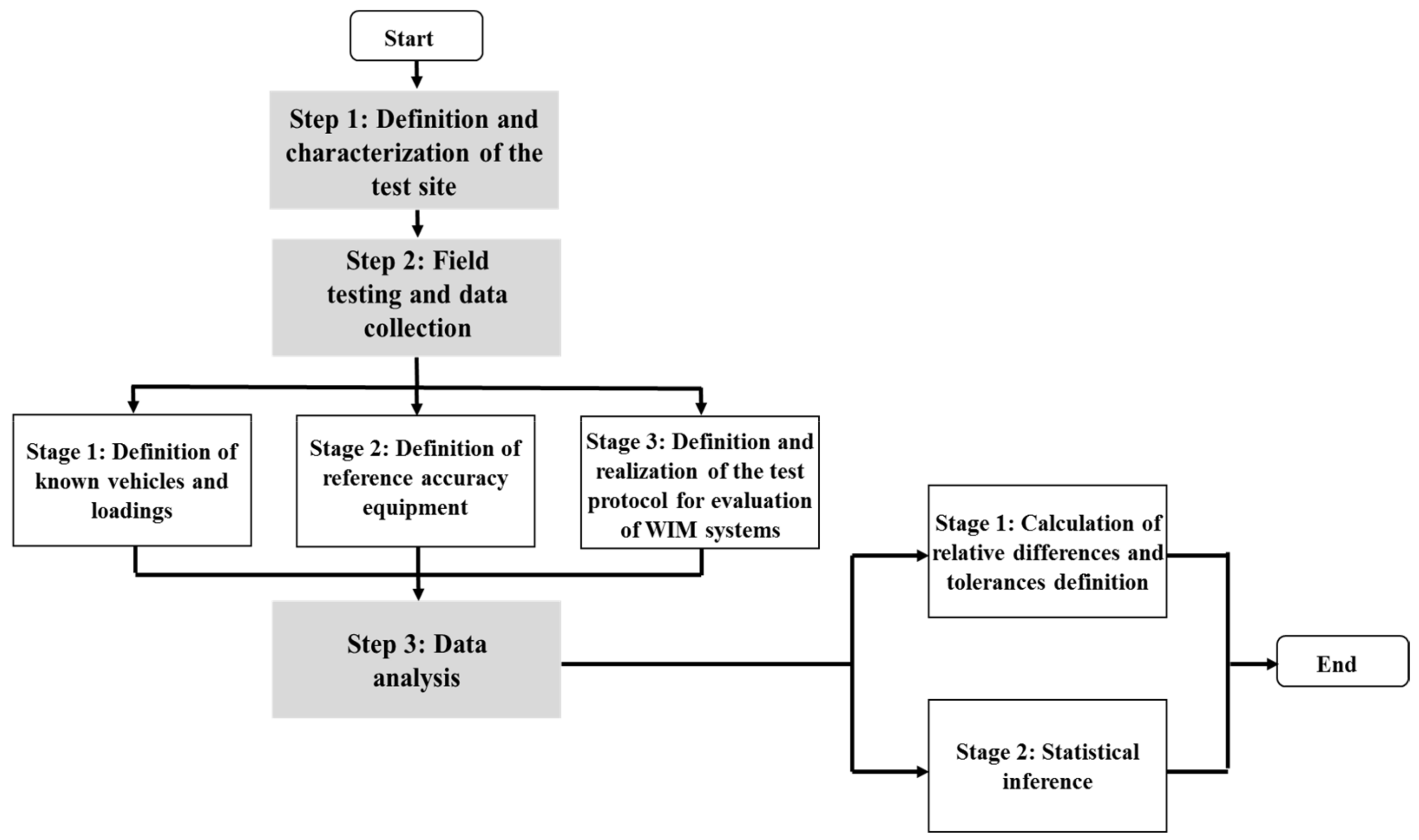
3. Materials and Methods
3.1. Step 1: Definition and Characterization of the Test Site
3.2. Step 2: Field Testing and Data Collection
3.2.1. Definition of Known Vehicles and Loadings
3.2.2. Definition of Reference Accuracy Equipment
3.2.3. Definition and Realization of the Test Protocol for Evaluation of WIM Systems
3.3. Step 3: Data Analysis
3.3.1. Calculation of Relative Differences and Tolerances Definition
3.3.2. Statistical Inference
4. Results of a Case Study
4.1. Step 1: Definition and Characterization of the Test Site
4.2. Step 2: Field Testing and Data Collection
4.2.1. Definition of Known Vehicles and Loadings
4.2.2. Definition of Reference Accuracy Equipment
4.2.3. Definition and Realization of the Test Protocol for Evaluation of WIM Systems
4.3. Step 3: Data Analysis
4.3.1. Calculation of Relative Differences and Tolerances Definition
4.3.2. Statistical Inference
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Neto, C.A.S.C.; Soares, R.P.; Ferreira, I.M.; Pompermayer, F.M.; Romminger, A.E. Gargalos e Demandas da Infraestrutura Rodoviária e os Investimentos do PAC: Mapeamento IPEA de Obras Rodoviárias; Relatório de Pesquisa; Instituto de Pesquisa Econômica Aplicada (IPEA): Brasília, Brazil, 2011. Available online: http://repositorio.ipea.gov.br/bitstream/11058/1637/1/TD_1592.pdf (accessed on 5 January 2017).
- Jacob, B.; La Beaumelle, F.-d.V. Improving Truck Safety: Potential of Weigh-In-Motion Technology. IATSS Res. 2010, 34, 9–15. [Google Scholar] [CrossRef] [Green Version]
- Jacob, B.; Cottineau, L.-M. Weigh-in-Motion for direct enforcement of overloaded commercial vehicles. Transp. Res. Procedia 2016, 14, 1413–1421. [Google Scholar] [CrossRef] [Green Version]
- Han, D.L.; Ko, S.-S.; Gu, Z.; Jeong, K.M. Adaptive weigh-in-motion algorithms for truck weight enforcement. Transp. Res. Part C 2012, 24, 256–269. [Google Scholar] [CrossRef]
- Dolcemascolo, V.; Fernandez, J.; Jacob, B.; Klein, E. French policy to prevent overloading. In Proceedings of the 7th International Conference on Weigh-in-Motion, Foz do Iguaçu, Brazil, 7–10 November 2016; Available online: http://www.is-wim.org/icwim7/doc/icwim7_bookproceedings.pdf (accessed on 13 January 2017).
- Otto, G.G. Estudo da Relação Sensor-Pavimento Para Aumento da Precisão de Sistemas de Pesagem em Movimento. Ph.D. Thesis, Federal University of Santa Catarina (UFSC), Florianópolis, Brazil, 2018; 321p. [Google Scholar]
- Van Loo, H.; Znidaric, A. Guide for Users of Weigh-in-Motion: An Introduction to Weigh-in-Motion, 2nd ed.; International Society for Weigh-in-Motion (ISWIM): Dübendorf, Switzerland, 2019; Available online: https://www.is-wim.net/wp-content/uploads/2020/07/ISWIM_Guide-for-users_press.pdf (accessed on 15 April 2020).
- Zhang, Z.; Huang, Y.; Bridgelall, R.; Palek, L.; Strommen, R. Sampling optimization for high-speed weigh-in-motion measurements using in-pavement strain-based sensors. Meas. Sci. Technol. 2015, 26, 065003. [Google Scholar] [CrossRef]
- Burnos, P.; Gajda, J.; Sroka, R. Application of Vehicle’s Weigh-in-Motion Systems to Enforcement. In Proceedings of the IEEE ICALT’S 2016: 5th IEEE International Conference on Advanced Logistics & Transport, Krakow, Poland, 1–3 June 2016; pp. 61–66. [Google Scholar]
- Al-Qadi, I.L.; Wang, H.; Ouyang, Y.; Grimmelsman, K.; Purdy, J. LTBP Program’s Literature Review on Weigh-in-Motion Systems; FHWA-HRT-16-024; U.S. Federal Highway Administration: Washington, DC, USA, 2016; 42p. Available online: https://www.fhwa.dot.gov/publications/research/infrastructure/structures/ltbp/16024/16024.pdf (accessed on 8 April 2020).
- Jacob, B.; O’brien, E.; Jehaes, S. COST 323–Weigh-in-Motion of Road Vehicles; Final Report (1993–1998); Transport Research Board; Laboratoire Central des Ponts et Chaussées (LCPC): Paris, France, 2002; Available online: https://trid.trb.org/view/723581 (accessed on 22 January 2020).
- Burnos, P.; Rys, D. The Effect of Flexible Pavement Mechanics on the Accuracy of Axle Load Sensors in Vehicle Weigh-in-Motion Systems. Sensors 2017, 17, 2053. [Google Scholar] [CrossRef] [Green Version]
- Otto, G.G.; Simonin, J.-M.; Piau, J.-M.; Cottineau, L.-M.; Chupin, O.; Momm, L.; Valente, A.M. Weigh-in-motion (WIM) sensor response model using pavement stress and deflection. Constr. Build. Mater. 2017, 156, 83–90. [Google Scholar] [CrossRef] [Green Version]
- Jacob, B. Assessment of the accuracy and classification of Weigh-in-Motion systems. Statistical Background. Int. J. Heavy Veh. Syst. 2000, 7, 136–152. Available online: http://www.is-wim.org/doc/ijhd_hvs_jacob.pdf (accessed on 15 April 2020). [CrossRef]
- Jacob, B. Overview of WIM Technologies and Sensors; LCPC: Paris, France, 2007; Available online: http://www.is-wim.org (accessed on 17 April 2017).
- Scheuter, F. Evaluation of Factors Affecting WIM System Accuracy. 1998. Available online: https://pdfs.semanticscholar.org/31cb/0f75e04144c8c353a9f9576ada31d734c0f7.pdf (accessed on 10 April 2020).
- Burnos, P.; Gajda, J.; Sroka, R. Accuracy criteria for evaluation of weigh-in-motion systems. Metrol. Meas. Syst. 2018, 25, 743–754. Available online: https://www.researchgate.net/publication/330082613_Accuracy_criteria_for_evaluation_of_weigh-in-motion_systems (accessed on 6 May 2020).
- OIML. International Recommendation OIML R134-1; Organisation Internationale Métrologie Légale: Paris, France, 2008; Available online: https://www.oiml.org/en/publications/recommendations/publication_view?p_type=1&p_status=1 (accessed on 3 April 2020).
- ASTM. Standard Specification for Highway Weigh-in-Motion (WIM) Systems with User Requirements and Test Methods-ASTM E1318-09; American Society for Testing and Materials: West Conshohocken, PA, USA, 2009. [Google Scholar]
- NMi. Progressive Weighing in Motion. 2020. Available online: https://www.nmi.nl/markets/wim/ (accessed on 6 May 2020).
- INMETRO. Portaria No. 375, de 24 de Julho de 2013; Instituto Nacional De Metrologia, Qualidade e Tecnologia: Brasilia, Brazil, 2013. Available online: http://www.inmetro.gov.br/legislacao/ (accessed on 3 April 2020).
- Oskarbski, J.; Kaszubowski, D. Implementation of Weigh-in-Motion System in Freight Traffic Management in Urban Areas. Transp. Res. Procedia 2016, 16, 449–463. [Google Scholar] [CrossRef] [Green Version]
- Fernandes Junuior, J.L.; Paes, J.C.; Pereira, P.A.A. Effets of traffic loading on portuguese and brazilian pavements performance. In Proceedings of the Transportation Research Board 85th Annual Meeting, Washington, DC, USA, 22–26 January 2006. [Google Scholar]
- Blair, R.C.; Higgins, J.J. Comparison of the power of the paired samples t-test to that of Wilcoxon’s signed-ranks test under various population shapes. Psycho. Bull. 1985, 97, 119–128. [Google Scholar] [CrossRef]
- INMET. Estações Automáticas–Gráficos; Instituto Nacional De Meteorologia: Brasilia, Brazil, 2020. Available online: http://www.inmet.gov.br/portal/index.php?r=home/page&page=rede_estacoes_auto_graf (accessed on 29 May 2020).
- UFSC; DNIT; LABTRANS. Pesagem em Movimento e Análise do Pavimento–Documentos Técnicos: Projetos e Avaliações da Reestruturação da Pista Experimental Para Sistema de Fiscalização Direta WIM; TC No. 497/2012; Universidade Federal De Santa Catarina (UFSC): Florianópolis, Brazil; Departamento Nacional De Infraestrutura De Transportes (DNIT): Brasilia, Brazil; Laboratório De Transportes E Logística (LABTRANS): Florianópolis, Brazil, 2018. [Google Scholar]
- Gillespie, T.D.; Karamihas, S.M.; Cebon, D.; Sayers, M.W.; Nasim, M.A.; Hansen, W.; Ehsan, N. Effects of Heavy Vehicle Characteristics on Pavement Response and Performance; NCHRP Report 353; National Cooperative Highway Research Program–Transportation Research Board (TRB)–National Research Council; Transportation Research Board: Washington, DC, USA, 1993. [Google Scholar]


| Absolute Frequencies—Section A02 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Speed | Lateral Position on the Lane | Vehicles | Total | ||||||
| 3C with 2 Groups of Axles (3C) | 2S3 with 3 Groups of Axles (2S3) | 3S3 with 3 Groups of Axles (3S3) | |||||||
| Pavement Temperatures | Pavement Temperatures | Pavement Temperatures | |||||||
| <37.0 °C | ≥37.0 °C | <37.0 °C | ≥37.0 °C | <37.0 °C | ≥37.0 °C | ||||
| 60 km/h | center | 8 | 0 | 7 | 0 | 7 | 0 | 22 | 56 |
| left | 7 | 0 | 6 | 0 | 7 | 0 | 20 | ||
| right | 2 | 5 | 2 | 5 | 0 | 0 | 14 | ||
| 70 km/h | center | 0 | 5 | 0 | 7 | 0 | 3 | 15 | 51 |
| left | 2 | 5 | 2 | 5 | 1 | 3 | 18 | ||
| right | 6 | 0 | 7 | 0 | 5 | 0 | 18 | ||
| 80 km/h | center | 0 | 6 | 0 | 7 | 0 | 1 | 14 | 48 |
| left | 0 | 9 | 0 | 10 | 0 | 1 | 20 | ||
| right | 1 | 6 | 1 | 6 | 0 | 0 | 14 | ||
| 90 km/h | center | 0 | 3 | 1 | 5 | 0 | 1 | 10 | 22 |
| left | 0 | 4 | 0 | 6 | 0 | 2 | 12 | ||
| right | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Totals | 26 | 43 | 26 | 51 | 20 | 11 | 177 | ||
| 69 | 77 | 31 | |||||||
| Weight Measurements | Speed | Lateral Position | Vehicles | |||||
|---|---|---|---|---|---|---|---|---|
| 3C | 2S3 | 3S3 | ||||||
| Pavement Temperatures | Pavement Temperatures | Pavement Temperatures | ||||||
| <37.0 °C | ≥37.0 °C | <37.0 °C | ≥37.0 °C | <37.0 °C | ≥37.0 °C | |||
| GVW | 60 km/h | Center | 0.0002 * | - | 0.0328 * | - | 0.0001 * | - |
| Left | 0.3141 NS | - | 0.0130 * | - | 0.0026 * | - | ||
| Right | 0.1056 NS5 | 0.0287 * | 0.0036 * | 0.0006 * | - | - | ||
| 70 km/h | Center | 0.3750 NS5 | 0.0038 * | - | 0.4532 NS5 | |||
| Left | 0.5215 NS5 | 0.2314 NS5 | 0.2730 NS5 | 0.0152 * | - | 0.0554 NS5 | ||
| Right | 0.0009 * | 0.8105 NS | 0.0003 * | - | ||||
| 80 km/h | Center | - | 0.0157 * | - | 0.0001 * | - | - | |
| Left | - | 0.1129 NS | - | 0.0001 * | - | - | ||
| Right | - | 0.6554 NS | - | 0.8351 NS | - | |||
| 90 km/h | Center | - | 0.7506 NS5 | - | 0.1172 NS5 | - | - | |
| Left | - | 0.1250 NS5 | - | 0.0435 * | - | 0.2211 NS5 | ||
| Right | - | - | - | - | ||||
| Axle group (G1) | 60 km/h | Center | 0.4226 NS | - | 0.0003 * | - | 0.0001 * | - |
| Left | 0.0285 * | - | 0.0001 * | - | 0.0001 * | - | ||
| Right | 0.0018 * | 0.0151 * | 0.0797 NS5 | 0.0009 * | - | - | ||
| 70 km/h | Center | - | 0.0148 * | 0.3878 NS | - | 0.0001 * | ||
| Left | 0.8335 NS5 | 0.2705 NS5 | 0.6780 NS5 | 0.2494 NS5 | - | 0.0030 * | ||
| Right | 0.0004 * | - | 0.1046 NS | 0.0625 NS5 | - | |||
| 80 km/h | Center | - | 0.2188 NS | - | 0.7409 NS | - | - | |
| Left | - | 0.2985 NS | - | 0.0544 NS | - | - | ||
| Right | - | 0.0008 * | - | 0.1250 NS | - | - | ||
| 90 km/h | Center | - | 0.0992 NS5 | - | 0.0292 * | - | - | |
| Left | - | 0.3092 NS5 | - | 0.5932 NS | - | 0.0288 * | ||
| Right | - | - | - | - | - | |||
| Axle group (G2) | 60 km/h | Center | 0.0001 * | - | 0.0001 * | - | 0.0003 * | - |
| Left | 0.8692 NS | - | 0.0001 * | - | 0.0118 * | - | ||
| Right | 0.1932 NS5 | 0.1363 NS5 | 0.0244 * | 0.0001 * | - | - | ||
| 70 km/h | Center | - | 0.0831 NS5 | 0.0478 NS | - | 0.7749 NS5 | ||
| Left | 0.3627 NS5 | 0.0456 NS5 | 0.8444 NS5 | 0.0864 NS5 | - | 0.0922 NS5 | ||
| Right | 0.0004 * | - | 0.0001 * | 0.0125 * | - | |||
| 80 km/h | Center | - | 0.0003 * | - | 0.0203 * | - | - | |
| Left | - | 0.0186 * | - | 0.6201 NS | - | - | ||
| Right | - | 0.0892 NS | - | 0.1167 NS | - | - | ||
| 90 km/h | Center | - | 0.3227 NS5 | - | 0.0080 * | - | - | |
| Left | - | 0.0130 * | - | 0.5615 NS | - | 0.2460 NS5 | ||
| Right | - | - | - | - | - | - | ||
| Axle group (G3) | 60 km/h | Center | - | - | 0.0009 * | - | 0.0001 * | - |
| Left | - | - | 0.3233 NS | - | 0.0001 * | - | ||
| Right | - | - | 0.1265 NS5 | 0.5827 NS5 | - | - | ||
| 70 km/h | Center | - | - | - | 0.0051 | - | 0.7371 NS5 | |
| Left | - | - | 0.1904 NS5 | 0.0079 * | - | 0.0039 * | ||
| Right | - | - | 0.0154 * | - | 0.3693 NS5 | - | ||
| 80 km/h | Center | - | - | - | 0.0001 * | - | - | |
| Left | - | - | - | 0.0001 * | - | - | ||
| Right | - | - | - | 0.1691 NS | - | - | ||
| 90 km/h | Center | - | - | - | 0.0553 NS5 | - | - | |
| Left | - | - | - | 0.0202 * | - | 0.9767 NS5 | ||
| Right | - | - | - | - | - | - | ||
| Sector A02—(p-Values) and Multiple Comparisons | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Items | Tests | Relative Differences in Weight Measurements (Variables)—ANOVA and Kruskal-Wallis | Relative Differences in Weight Measurements (Variables)—Tukey | ||||||||||
| Description of Distributions | GVW | G1 | G2 | G3 | Description of Distributions | GVW | G1 | G2 | G3 | ||||
| 1 | Comparison between vehicles | 3C | 0.0001 * | 0.0001 * | 0.0001 * | 0.5893 NS | 3C/2S3 (vice versa) | NS | NS | * | - | ||
| 2S3 | 2S3/3S3 (vice versa) | * | * | * | |||||||||
| 3S3 | 3S3/3C (vice versa) | * | * | * | |||||||||
| 2 | Comparison between temperatures | <37.0 °C | 0.0001 * | 0.0257 * | 0.1211 NS | 0.9752 NS | <37.0 °C and ≥37.0 °C | * | * | - | - | ||
| ≥37.0 °C | |||||||||||||
| 3 | Comparison between speeds | 60 km/h | 0.0001 * | 0.0009 * | 0.0004 * | 0.0367 * | 60 and 70 km/h (vice versa) | * | NS | * | NS | ||
| 60 and 80 km/h (vice versa) | * | * | * | NS | |||||||||
| 70 km/h | 60 and 90 km/h (vice versa) | * | NS | NS | NS | ||||||||
| 80 km/h | 70 and 80 km/h (vice versa) | * | NS | NS | * | ||||||||
| 90 km/h | 70 and 90 km/h (vice versa) | NS | NS | NS | NS | ||||||||
| 80 and 90 km/h (vice versa) | NS | NS | NS | NS | |||||||||
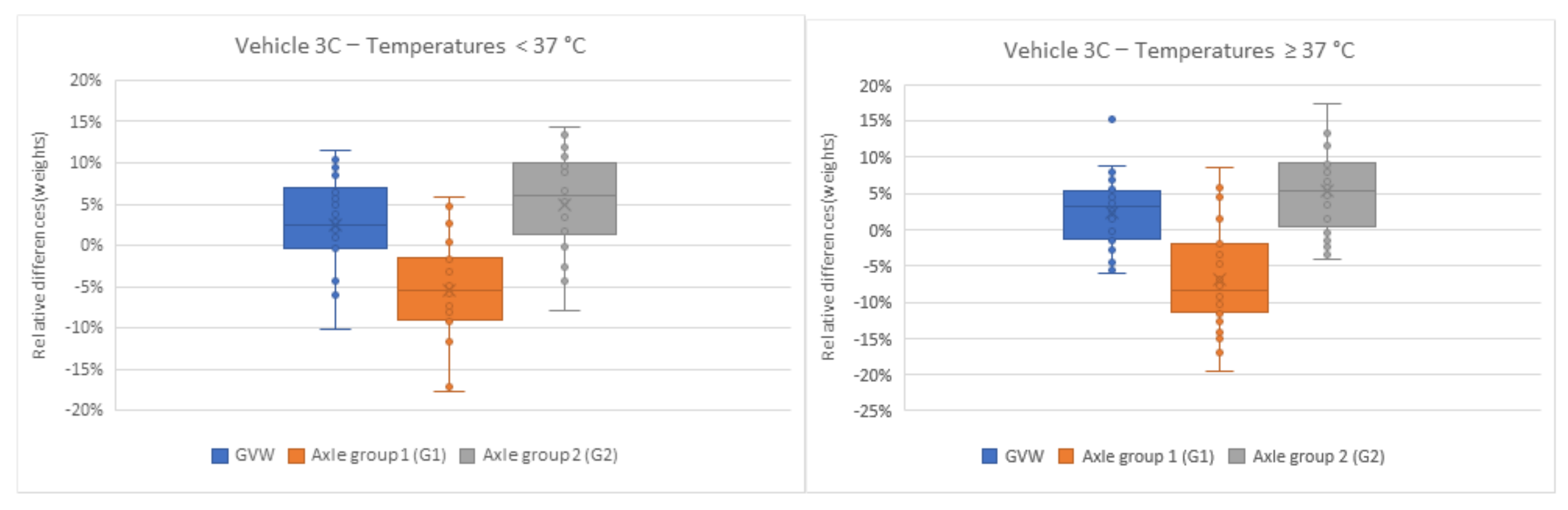
| 4 | Comparison between temperatures by vehicle types | 3C | <37.0 °C | 0.9789 NS | 0.1935 NS | 0.7705 NS | - | 3C | <37.0 °C and ≥37.0 °C | - | - | - | - |
| ≥37.0 °C | |||||||||||||
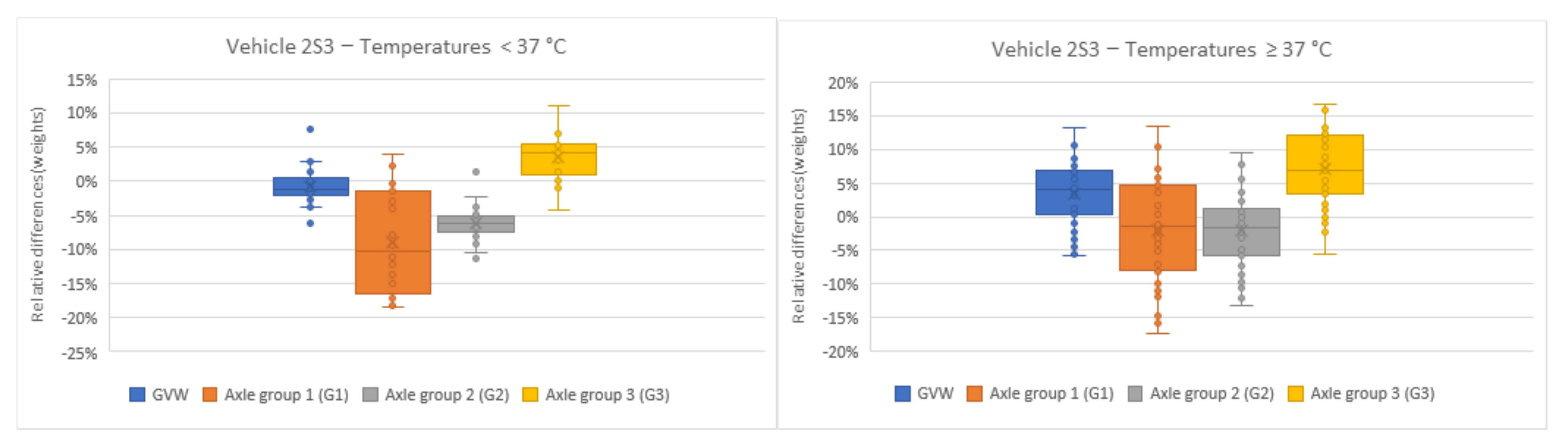
| 2S3 | <37.0 °C | 0.0001 * | 0.0007 * | 0.0003 * | 0.0038 * | 2S3 | <37.0 °C and ≥37.0 °C | * | * | * | * | ||
| ≥37.0 °C | |||||||||||||
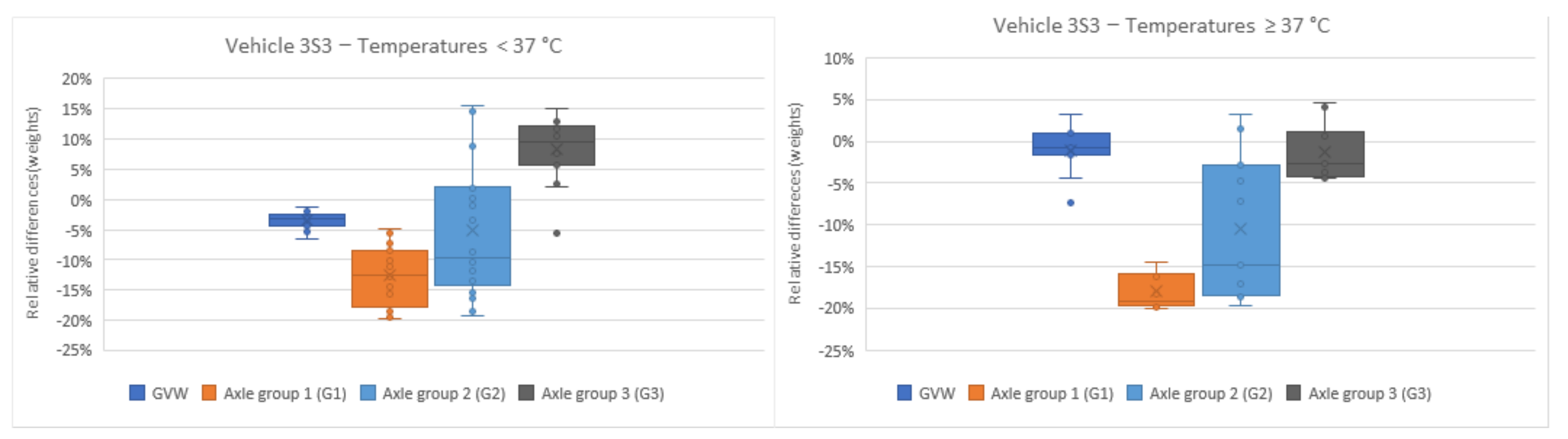
| 3S3 | <37.0 °C | 0.0022 * | 0.0022 * | 0.0002 * | 0.0001 * | 3S3 | <37.0 °C and ≥37.0 °C | * | * | * | * | ||
| ≥37.0 °C | |||||||||||||
| 5 | Comparison between speeds by vehicle types | 3C | 60 km/h | 0.4716 NS | 0.9622 NS | 0.2154 NS | - | 3C | 60 and 70 km/h (vice versa) | - | - | - | - |
| 60 and 80 km/h (vice versa) | |||||||||||||
| 70 km/h | 60 and 90 km/h (vice versa) | ||||||||||||
| 70 and 80 km/h (vice versa) | |||||||||||||
| 80 km/h | 70 and 90 km/h (vice versa) | ||||||||||||
| 90 km/h | 80 and 90 km/h (vice versa) | ||||||||||||
| 2S3 | 60 km/h | 0.0001 * | 0.0001 * | 0.0001 * | 0.0002 * | 2S3 | 60 and 70 km/h (vice versa) | * | * | * | * | ||
| 60 and 80 km/h (vice versa) | * | * | * | * | |||||||||
| 70 km/h | 60 and 90 km/h (vice versa) | * | * | * | NS | ||||||||
| 70 and 80 km/h (vice versa) | NS | NS | NS | NS | |||||||||
| 80 km/h | 70 and 90 km/h (vice versa) | NS | NS | NS | NS | ||||||||
| 90 km/h | 80 and 90 km/h (vice versa) | NS | NS | NS | NS | ||||||||
| 3S3 | 60 km/h | 0.1978 NS | 0.0028 * | 0.0056 * | 0.0001 * | 3S3 | 60 and 70 km/h (vice versa) | - | * | * | * | ||
| 60 and 80 km/h (vice versa) | NS | NS | * | ||||||||||
| 70 km/h | 60 and 90 km/h (vice versa) | NS | NS | * | |||||||||
| 70 and 80 km/h (vice versa) | NS | * | NS | ||||||||||
| 80 km/h | 70 and 90 km/h (vice versa) | NS | * | NS | |||||||||
| 90 km/h | 80 and 90 km/h (vice versa) | NS | NS | NS | |||||||||
| 6 | Comparison between vehicles by speed range | 60 km/h | 3C | 0.0562 NS | 0.0001 * | 0.0001 * | 0.0001 * | 60 km/h | 3C/2S3 (vice versa) | - | * | * | - |
| 2S3 | 2S3/3S3 (vice versa) | NS | NS | * | |||||||||
| 3S3 | 3S3/3C (vice versa) | * | * | - | |||||||||
| 70 km/h | 3C | 0.0001 * | 0.0001 * | 0.0001 * | 0.0009 * | 70 km/h | 3C/2S3 (vice versa) | NS | * | * | - | ||
| 2S3 | 2S3/3S3 (vice versa) | * | * | * | * | ||||||||
| 3S3 | 3S3/3C (vice versa) | * | * | NS | - | ||||||||
| 80 km/h | 3C | 0.0508 NS | 0.0016 * | 0.0001 * | 0.0343 * | 80 km/h | 3C/2S3 (vice versa) | - | * | * | - | ||
| 2S3 | 2S3/3S3 (vice versa) | * | * | * | |||||||||
| 3S3 | 3S3/3C (vice versa) | NS | * | - | |||||||||
| 90 km/h | 3C | 0.4783 NS | 0.0797 NS | 0.0009 * | 0.2482 NS | 90 km/h | 3C/2S3 (vice versa) | - | - | * | - | ||
| 2S3 | 2S3/3S3 (vice versa) | * | |||||||||||
| 3S3 | 3S3/3C (vice versa) | * | |||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pellizzon, N.D.; da Silva, A.R.; Otto, G.G. Method for Setting Weight Tolerance Limits in High-Speed Weigh-in-Motion Systems: A Case Study in Brazil. Sustainability 2022, 14, 7039. https://doi.org/10.3390/su14127039
Pellizzon ND, da Silva AR, Otto GG. Method for Setting Weight Tolerance Limits in High-Speed Weigh-in-Motion Systems: A Case Study in Brazil. Sustainability. 2022; 14(12):7039. https://doi.org/10.3390/su14127039
Chicago/Turabian StylePellizzon, Nayara Donelli, Alan Ricardo da Silva, and Gustavo Garcia Otto. 2022. "Method for Setting Weight Tolerance Limits in High-Speed Weigh-in-Motion Systems: A Case Study in Brazil" Sustainability 14, no. 12: 7039. https://doi.org/10.3390/su14127039
APA StylePellizzon, N. D., da Silva, A. R., & Otto, G. G. (2022). Method for Setting Weight Tolerance Limits in High-Speed Weigh-in-Motion Systems: A Case Study in Brazil. Sustainability, 14(12), 7039. https://doi.org/10.3390/su14127039








