Evaluation of the Durability of Bridge Tension Cables Based on Combination Weighting Method-Unascertained Measure Theory
Abstract
:1. Introduction
1.1. Introduction of Research on Durability Damage Mechanism of Pulling Slings
1.2. Introduction of Existing Durability Evaluation Methods
1.3. Introduction to the Proposed Method in this Study
2. Establishment of the Durability Evaluation Index System for Pulling Sling Structures
2.1. Causes of Damage to the Durability of Pulling Sling Structures
2.2. Pulling Sling Durability Evaluation Index System
2.3. Determine the Durability Evaluation Level of the Pulling Sling Structure
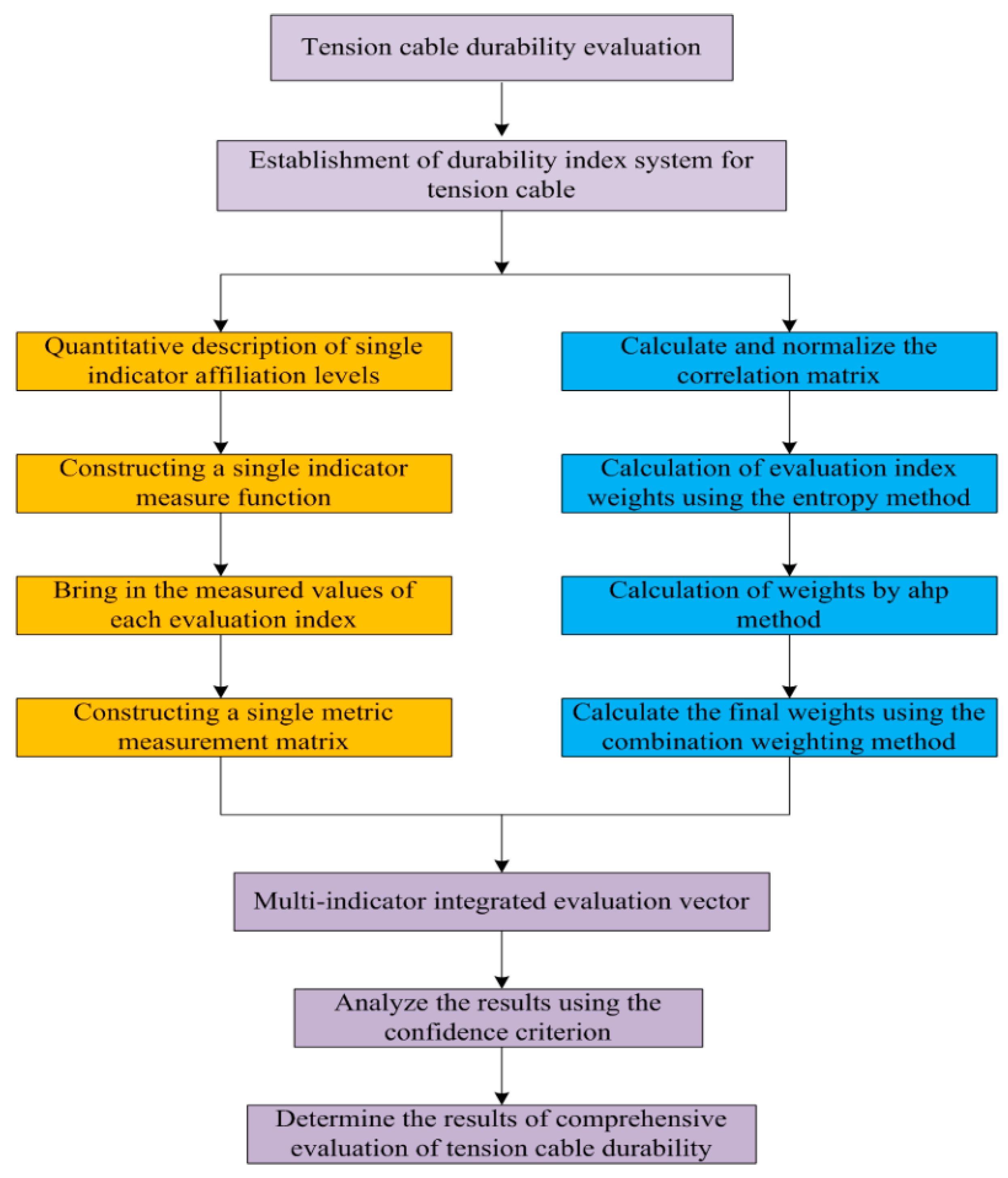
3. Evaluation Methodology and Process of the CWM-UM Method
3.1. Objective Weight Method
3.1.1. The Theory of MEE Method
- (1)
- We determine the classical domain, the section domain, and the matrix of elements [52] to be evaluated.
- (2)
- We calculate the correlation.
- a
- We determine the correlation function for each level of the system to be evaluated.
3.1.2. CRITIC Method
3.1.3. Calculation Steps
- (1)
- We determined the durability evaluation indexes of the system to be evaluated and the grading criteria of each index.
- (2)
- We determined the classical domain, the section domain, and the object element matrix of the system to be evaluated.
- (3)
- We calculated the correlation matrix of the system to be evaluated and normalized the correlation matrix.
- (4)
- We substituted the judgment matrix obtained from Step (3) into Equations (9)–(13) to obtain the weight value of each durability evaluation index.
3.2. IAHP Method
3.3. The Rationality Test
3.4. The Combination Weighting Method
3.5. UM Theory
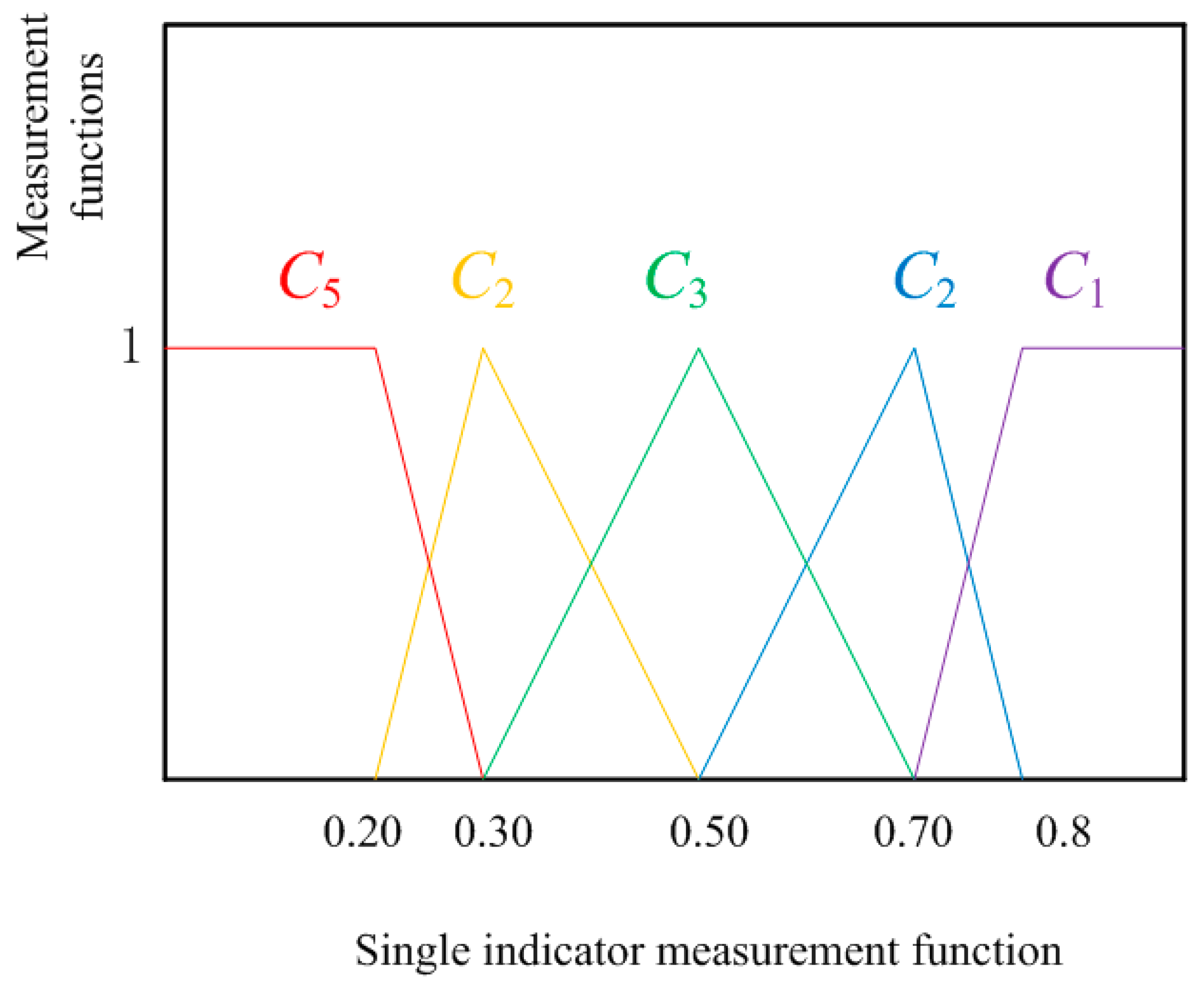
3.5.1. Single-Index Measure
3.5.2. Multi-Index Measure
3.6. Durability Evaluation
4. Example Application
4.1. Determine the Weight Value of the Durability Index of the Pulling Sling Structure
- (1)
- We determine the classical domain, the section domain, and the matrix of elements to be evaluated.
- (2)
- We calculate the correlation.
- (3)
- We then calculate weights using the CRITIC method.
4.2. Calculation Index Weights by the IAHP
4.3. Rationality Test
- (4)
- We use the combination weighting method.
4.4. Determine the Single Indicator Measurement Function and Matrix
4.5. Determine the Multi-Index Comprehensive Measure Evaluation Vector
4.6. Durability Evaluation
5. Comparison between Existing and Proposed Method
5.1. SPA Method
- (1)
- We determine the evaluation index and evaluation level.
- (2)
- We determine the number of t-element links for comprehensive evaluation of each index.
- (3)
- We determine the number of -element links for the total index.
5.2. The Matter Element Extension (MEE) Method
6. Discussion
7. Conclusions
- (1)
- According to the damage mechanism of pulling sling durability, the three-layer durability evaluation index system of the pulling sling structure is established. Seven indexes were selected for the durability evaluation of the pulling sling: PE cracking, PE scratching, corrosion of the rope body, damage to the rope body, damage to the anchorage, damage to the conduit, and damage to the vibration damping device.
- (2)
- There are uncertainties in the factors affecting the durability of pulling sling structures that are difficult to describe quantitatively. The combined weighting method is applied, combining the advantages of IAHP and CRITIC methods to compensate for the bias of a single assignment method. Through the theory of unascertained measure, the multi-indicator comprehensive evaluation vector of pulling sling is obtained, and the results are analyzed according to the confidence criterion.
- (3)
- On the basis of combined weighting method-unascertained-measure theory, a complete durability evaluation model of the pulling sling was established. Taking the Shaoxing Jiahui Bridge pulling sling structure as an example, the durability evaluation was carried out, and the evaluation result was calculated to be level III, which basically matches the actual situation of the bridge. It shows the applicability of the model and provides a new method for the durability evaluation of a pulling cable structure.
- (4)
- Through a comparative study, it was found that the final evaluation results of the three methods are consistent, which proves that the CWM-UM method can make a more accurate evaluation of the durability of the pulling cable structure, and it has the advantages of four theories, the MEE method, the CRITIC method, the IAHP method, and UM theory, with a concise calculation process and more accurate results. It shows the superiority of the CWM-UM method in durability evaluation. In practical application, the method to improve the durability of the cable body can be stated more accurately according to the evaluation results. The proposal and rational use of this method will contribute to the construction of resource-saving highways and the realization of sustainable development.
- (1)
- Since different bridges have different forms of pulling and slinging structures, a more comprehensive durability evaluation system can be established for different forms of pulling and slinging structures to make the evaluation results more reasonable and realistic.
- (2)
- The durability evaluation indexes established in this paper mainly rely on literature collection and theoretical analysis. In subsequent studies, these can be combined with finite element analysis software to identify the factors affecting the durability of the pulling sling structure through real bridge simulation. We can use this standard to establish the evaluation index.
- (3)
- Because of the special structural form and material characteristics of the pulling cable structure compared to the concrete structure, the selection of the environmental index and durability index eigenvalues in this paper is preliminary and rough, and further refinement and research are needed to ensure that the calculation of environmental index eigenvalues and durability index eigenvalues is more accurate and comprehensive.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stallings, J.M.; Frank, K.H. Stay-Cable Fatigue Behavior. J. Struct. Eng. 1991, 117, 936–950. [Google Scholar] [CrossRef]
- Takena, K.; Miki, C.; Shimokawa, H.; Sakamoto, K. Fatigue Resistance of Large Diameter Cable for Cable Stayed Bridges. J. Struct. Eng. 1992, 118, 701–715. [Google Scholar] [CrossRef]
- Matteo, J.; Deodatis, G.; Billington, D.P. Safety Analysis of Suspension-Bridge Cables: Williamsburg Bridge. J. Struct. Eng. 1994, 120, 3197–3211. [Google Scholar] [CrossRef]
- Hamilton, I.H.R.; Breen, J.E.; Frank, K.H. Bridge Stay Cable Corrosion Protection. I: Grout Injection and Load Testing. J. Bridg. Eng. 1998, 3, 64–71. [Google Scholar] [CrossRef]
- Hamilton, I.H.R.; Breen, J.E.; Frank, K.H. Bridge Stay Cable Corrosion Protection. II: Accelerated Corrosion Tests. J. Bridg. Eng. 1998, 3, 72–81. [Google Scholar] [CrossRef]
- Barton, S.C.; Vermaas, G.W.; Duby, P.F.; West, A.C.; Betti, R. Accelerated Corrosion and Embrittlement of High-Strength Bridge Wire. J. Mater. Civ. Eng. 2000, 12, 33–38. [Google Scholar] [CrossRef]
- Mayrbaurl, R.M.; Camo, S. Cracking and Fracture of Suspension Bridge Wire. J. Bridg. Eng. 2001, 6, 645–650. [Google Scholar] [CrossRef]
- Camo, S. Probabilistic Strength Estimates and Reliability of Damaged Parallel Wire Cables. J. Bridg. Eng. 2003, 8, 297–311. [Google Scholar] [CrossRef]
- Haight, R.Q.; Billington, D.P.; Khazem, D. Cable Safety Factors for Four Suspension Bridge. J. Bridg. Eng. 1997, 2, 157–167. [Google Scholar] [CrossRef]
- Faber, M.; Engelund, S.; Rackwitz, R. Aspects of parallel wire cable reliability. Struct. Saf. 2003, 25, 201–225. [Google Scholar] [CrossRef]
- Cremona, C. Probabilistic approach for cable residual strength assessment. Eng. Struct. 2002, 25, 377–384. [Google Scholar] [CrossRef]
- Atienza, J.M.; Ruiz-Hervias, J.; Elices, M. The Role of Residual Stresses in the Performance and Durability of Prestressing Steel Wires. Exp. Mech. 2012, 52, 881–893. [Google Scholar] [CrossRef] [Green Version]
- Atienza, J.M.; Elices, M.; Ruiz-Hervias, J.; Caballero, L.; Valiente, A. Residual stresses and durability in cold drawn eutectoid steel wires. Met. Mater. Int. 2007, 13, 139–143. [Google Scholar] [CrossRef]
- Luo, X.Y.; Li, Z. Study on mechanical properties of unbonded prestressing strand after rusting. J. China Railw. Soc. 2008, 2, 108–112. [Google Scholar]
- Chen, X.-L. Experimental Study on Corrosion Characteristics and Mechanical Properties of Bridge Cable Wires. Master’s Thesis, Southeast University, Nanjing, China, March 2015. [Google Scholar]
- Wu, J. Study on the Damage Classification and the Fatigue Life of Cable Wire. Master’s Thesis, Changsha University of Science & Technology, Changsha, China, April 2015. [Google Scholar]
- Li, X.Z.; Xie, X.; Pan, X.Y.; Sun, W.Z.; Zhu, H.H. Experimental study on fatigue performance of rusted high-strength steel wire for arch bridge boom. China Civ. Eng. J. 2015, 48, 68–76. [Google Scholar] [CrossRef]
- Ye, H.W.; Wang, Y.Q.; Sun, P.P. Fatigue strength test study of corroded galvanized steel wire for bridge cables. World Bridges 2013, 41, 44–49. [Google Scholar]
- Wu, C.; Jiang, C.; Jiang, X. Fatigue test of high-strength steel wire for pre-corroded bridge cables. J. Tongji Univ. (Nat. Sci.) 2018, 46, 1622–1627+1695. [Google Scholar]
- Chen, C.-C.; Wu, W.-H.; Chen, S.-Y.; Lai, G. A novel tension estimation approach for elastic cables by elimination of complex boundary condition effects employing mode shape functions. Eng. Struct. 2018, 166, 152–166. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K.-C.; Chen, C.-C.; Lin, T.-K.; Tullini, N. Bending tests for the structural safety assessment of space truss members. Int. J. Space Struct. 2018, 33, 138–149. [Google Scholar] [CrossRef]
- Wu, W.-H.; Chen, C.-C.; Chen, Y.-C.; Lai, G.; Huang, C.-M. Tension determination for suspenders of arch bridge based on multiple vibration measurements concentrated at one end. Measurement 2018, 123, 254–269. [Google Scholar] [CrossRef]
- Chen, A.; Yang, Y.; Ma, R.; Li, L.; Tian, H.; Pan, Z. Experimental study of corrosion effects on high-strength steel wires considering strain influence. Constr. Build. Mater. 2020, 240, 117910. [Google Scholar] [CrossRef]
- Miao, C.; Li, R.; Yu, J. Effects of characteristic parameters of corrosion pits on the fatigue life of the steel wires. J. Constr. Steel Res. 2019, 168, 105879. [Google Scholar] [CrossRef]
- Yu, X.; Yao, G.; Gu, L.; Fan, W. Numerical and Experimental Study on the Steel Strands under the Coupling Effect of a Salt Spray Environment and Cyclic Loads. Materials 2020, 13, 736. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhang, W.; Zheng, Y. Experimental Study on Corrosion Fatigue Performance of High-Strength Steel Wire with Initial Defect for Bridge Cable. Appl. Sci. 2020, 10, 2293. [Google Scholar] [CrossRef] [Green Version]
- Jie, Z.; Berto, F.; Susmel, L. Fatigue behaviour of pitted/cracked high-strength steel wires based on the SED approach. Int. J. Fatigue 2020, 135, 105564. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, Z.; Li, S. Effect of current density on the cathodic protection efficiency and mechanical properties of pre-stressed high-strength steel wires for stay cable. Constr. Build. Mater. 2021, 314, 125671. [Google Scholar] [CrossRef]
- Hu, X.; Ji, X.; Chen, Z.N. Expert system design for safety and durability assessment of cable-stayed bridges. Chin. J. Appl. Mech. 1998, 4, 125–129. [Google Scholar]
- Sugimoto, I.; Kobayashi, Y.; Ichikawa, A. Durability Evaluation Based on Buckling Characteristics of Corroded Steel Deck Girders. Q. Rep. RTRI 2006, 47, 150–155. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Dan, D.H.; Sun, L.M. Safety and durability assessment of cable-supported bridge by using ANFIS. In Proceedings of the International Conference on Health Monitoring of Structure, Nanjing, China, 16–18 October 2007; Volume 1, pp. 725–731. [Google Scholar]
- Liu, S.Y.; Yang, Z.Y.; Qu, J.B. Preventive measures to ensure durability of cable-stayed bridges. Eng. Struct. Integr. Res. Dev. Appl. 2007, 1, 1350–1352. [Google Scholar]
- Liu, X.Z.; Zhang, C.R.; Chen, S.S. Cables durability evaluation model based on fuzzy neural network. J. East China Jiaotong Univ. 2010, 27, 8–12. [Google Scholar]
- Ma, J.-B.; Pu, Q.; Song, D.-W.; Yang, G.-Q. Fuzzy nearness comprehensive assessment of durability of existing half-through and through concrete arch bridges. J. Highw. Transp. Res. Dev. 2007, 25, 79–84. [Google Scholar]
- Zhu, P.H.; He, X.; Jin, W.L. Research on the application of random layered sampling theory to evaluating durability of existing concrete bridge structures. Int. J. Struct. Eng. 2010, 1, 188. [Google Scholar] [CrossRef]
- Liu, J.Z.; Xu, J.Y.; Bai, E.L.; Gao, Z.G. Durability Evaluation Analysis of Reinforced Concrete Structures Based on Extension Method. Adv. Mater. Res. 2010, 163–167, 3354–3358. [Google Scholar] [CrossRef]
- Zheng, F.; Wang, Y.; Zhang, P.Y. The Application of Fuzzy Synthesis Evaluation Method on Assessing Bridge Durability. In Proceedings of the Global Conference on Civil, Structural and Environmental Engineering/3rd International Symposium on Multi-field Coupling Theory of Rock and Soil Media and its Applications, China Three Gorges University, Yichang, China, 20–21 October 2012. [Google Scholar]
- Tang, Y.B.; Chen, L.; Wang, S.N.; Fan, Z.H. Evaluation of the Corrosion Risk on the Immersed Tunnel of the Hongkong-Zhuhai-Macao Bridge. Appl. Mech. Mater. 2012, 256–259, 1075–1081. [Google Scholar] [CrossRef]
- He, L.; Qian, Y.J. Application of Fuzzy Comprehensive Evaluation Method in Long-Span Arch Bridge Damaged in Wartime. In Proceedings of the 2nd International Conference on Advanced Engineering Materials and Technology (AEMT), Zhuhai, China, 6–8 July 2012. [Google Scholar] [CrossRef]
- Ren, Y.; Tang, H.H.; Huang, Q. Research on Fuzzy Comprehensive Evaluation of Cable-Stayed Bridges. Sustain. Cities Dev. Environ. Prot. 2013, 316-363, 1119. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Chen, J.Y.; Wei, Y.L.; Xu, F.; Liu, X.; Tao, B.X. Health Evaluation for Durability of Harbor Engineering in South China Based on AHP. Adv. Mater. Res. 2013, 842, 489–493. [Google Scholar] [CrossRef]
- Wang, Q.; Xie, F.X.; Hu, X.Y. A method for evaluating the durability of diagonal cables. World Bridges 2015, 43, 79–83. [Google Scholar]
- Zhao, L.; Cheng, L. Application of uncertainty-based hierarchical analysis in bridge safety assessment. J. Luoyang Inst. Sci. Technol. (Nat. Sci. Ed.) 2017, 27, 20–23. [Google Scholar]
- Lin, L. FNN-Based Reinforced Concrete Bridge Evaluation Model. In Proceedings of the International Conference on Smart Grid and Electrical Automation, Changsha, China, 27–28 May 2017; pp. 477–480. [Google Scholar] [CrossRef]
- Cai, J.; Dong, F.; Luo, Z. Durability of Concrete Bridge Structure under Marine Environment. J. Coast. Res. 2018, 83, 429–435. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Guo, Z.Z.; Li, Y.Q. Road slope hazard evaluation model based on entropy power set pair analysis and vehicle-mounted laser scanning. Rock Soil Mech. 2018, 39, 131–141+156. [Google Scholar]
- Li, Z.K.; Li, W.; Ge, W. Environmental impact assessment of dam failure based on set-pair analysis-variable fuzzy set coupling method. J. Tianjin Univ. Sci. Technol. 2019, 52, 269–276. [Google Scholar]
- Liang, L.; Xing, G.H.; Ren, Y.P. Reliability evaluation method of inclined ropes based on cloud theory. J. Northeast. Univ. (Nat. Sci.) 2019, 40, 585–589. [Google Scholar]
- He, W.; Sun, X.; Li, C. Research on Durability Evaluation Method of Bridge Slings Based on Set Pair Analysis. In IOP Conference Series Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 474. [Google Scholar] [CrossRef]
- Liu, F.; Yi, W. Durability Evaluation Method of Reinforced Concrete Beam Bridge Based on Extension Interval Number Theory. In IOP Conference Series Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 510. [Google Scholar] [CrossRef]
- Chinese Standard JTG/T H21-2011; China’s Standards for Technical Condition Evaluation of Highway Bridges. National Standards of the People’s Republic of China: Beijing, China, 2011.
- Liang, G.; Niu, D.; Liang, Y. Core Competitiveness Evaluation of Clean Energy Incubators Based on Matter-Element Extension Combined with TOPSIS and KPCA-NSGA-II-LSSVM. Sustainability 2020, 12, 9570. [Google Scholar] [CrossRef]
- Luo, X.; Wang, Z.; Lu, L.; Guan, Y. Supply Chain Flexibility Evaluation Based on Matter-Element Extension. Complexity 2020, 2020, 8057924. [Google Scholar] [CrossRef]
- Cai, W. Topology and its applications. Chin. Sci. Bull. 1998, 673–682. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFD9899&filename=KXTB199907000&uniplatform=NZKPT&v=q5wWatQV0E66C_n5vjpboWCYMTm8elp7X_y1UyFoKGtPz5-g3UMJljkjR2BgNuFj (accessed on 16 May 2022).
- Cai, W. Overview of Topology. Syst. Eng. Theory Pract. 1998, 77–85. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFD9899&filename=XTLL801.017&uniplatform=NZKPT&v=sUt7xjfRZbhWCHiXl-iAVvAL3oPrRm5NUQkfBVLHjMOh91vI0eJDebUjA2hYqvT_ (accessed on 16 May 2022).
- Hu, Y.-S.; Zhu, C.-L. Credit Evaluation Model of Road Transportation Enterprises Based on the Combination Weighting Method. Math. Probl. Eng. 2021, 2021, 6637164. [Google Scholar] [CrossRef]
- Xu, C.; Ke, Y.; Li, Y.; Chu, H.; Wu, Y. Data-driven configuration optimization of an off-grid wind/PV/hydrogen system based on modified NSGA-II and CRITIC-TOPSIS. Energy Convers. Manag. 2020, 215, 112892. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, H.; Zhang, H. Durability evaluation of highway tunnel lining structure based on matter element extension-simple correlation function method-cloud model: A case study. Math. Biosci. Eng. 2021, 18, 4027–4054. [Google Scholar] [CrossRef]
- Li, X.; Jiangwen, Q.; Tang, J.; Pu, Q.S.; Xia, X.B.; Xu, K. Study on combination weighting method–TOPSIS method-based risk assessment of water in-rush in construction of North Tianshan Mountain Tunnel. Water Resour. Hydropower Eng. 2019, 50, 114–119. [Google Scholar]
- Huang, R.; Zhang, F.X. A comprehensive water quality evaluation method based on an optimized set-pair analysis model. J. Yangtze River Sci. Res. Inst. 2016, 33, 6–10+17. [Google Scholar]
- Wu, S.; Du, X.; Yang, S. Rock Mass Quality Evaluation Based on Unascertained Measure and Intuitionistic Fuzzy Sets. Complexity 2020, 2020, 5614581. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, Q.; Yan, Y.; Wang, J.; Zhao, K.; Cao, S.; Zhang, Y. Geological Structural Surface Evaluation Model Based on Unascertained Measure. Geofluids 2019, 2019, 7. [Google Scholar] [CrossRef]
- Li, Y.; Yang, J.; Shi, H.; Li, Y. Assessment of sustainable urban transport development based on entropy and unascertained measure. PLoS ONE 2017, 12, e0186893. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Tian, S.; Li, Q.; Huang, J. Evaluation of Rock Quality of Tunnel Wall Rock Based on Rough Set Theory and Unascertained Measurement Theory. Math. Probl. Eng. 2018, 2018, 3571028. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, G.; Jiao, Y.; Wang, H. Unascertained Measure-Set Pair Analysis Model of Collapse Risk Evaluation in Mountain Tunnels and Its Engineering Application. KSCE J. Civ. Eng. 2020, 25, 451–467. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of Entropy Weight Method in Decision-Making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
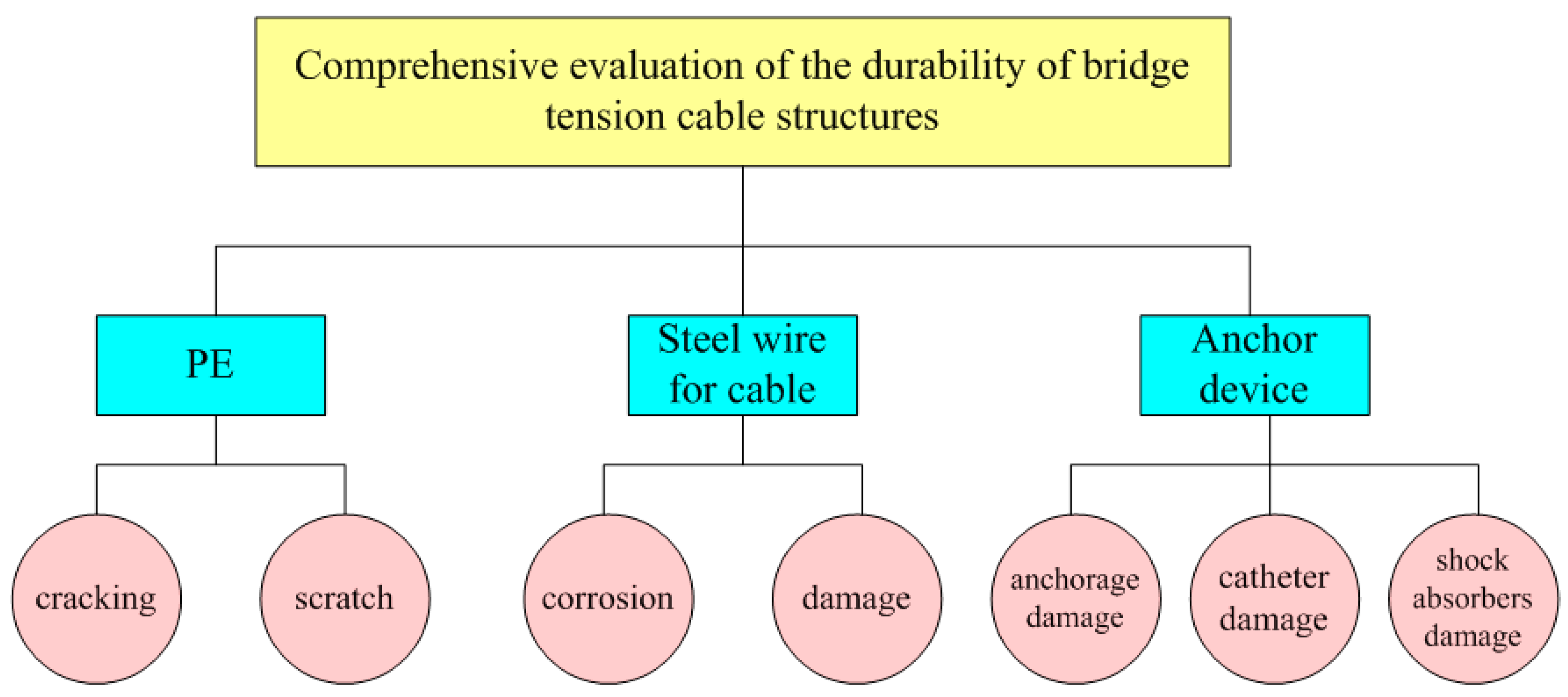



| Level 1 | Level 2 | |
|---|---|---|
| Comprehensive evaluation of the durability of bridge tension cable structures | PE | |
| Steel wire for cable | ||
| Anchor device | ||
| Durability Level | Pull Sling Structure Durability Status | Classification Criteria |
|---|---|---|
| I | In good shape, durability failure risk is very small. | (0.8,1) |
| II | Slightly damaged, durability failure risk is small. | (0.6,0.8) |
| III | Medium damaged, durability failure risk is average. | (0.4,0.6) |
| IV | Severely damaged, durability failure risk is high. | (0.2,0.4) |
| V | Extremely dangerous, durability failure risk is very high. | (0,0.2) |
| Element | Assignment | Meaning |
|---|---|---|
| 1 | In a certain level, indicator j is equally important compared to indicator j′ | |
| 2 | At a certain level, indicator j is slightly more important compared to indicator j′ | |
| 3 | At a certain level, indicator j is important compared to indicator j′ | |
| Guideline Layer | PE | Cable Steel Wire | Anchor Device | |
|---|---|---|---|---|
| 0.196 | 0.311 | 0.493 | ||
| 0.667 | 0.131 | |||
| 0.333 | 0.065 | |||
| 0.333 | 0.104 | |||
| 0.667 | 0.207 | |||
| 0.547 | 0.270 | |||
| 0.190 | 0.094 | |||
| 0.263 | 0.130 |
| Methods | |||||||
|---|---|---|---|---|---|---|---|
| IAHP | 3 | 7 | 5 | 2 | 1 | 6 | 4 |
| CRITIC | 1 | 6 | 7 | 3 | 4 | 2 | 5 |
| Methods | |||||||
|---|---|---|---|---|---|---|---|
| PE | 0.677 | 0.323 | |||||
| Cable steel wire | 0.343 | 0.657 | |||||
| Anchor Device | 0.429 | 0.277 | 0.294 | ||||
| 0.169 | 0.080 | 0.099 | 0.190 | 0.198 | 0.128 | 0.136 |
| Distribution Form | Graphics | Function Expressions |
|---|---|---|
| Linear distribution | 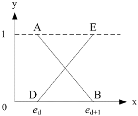 |
| Layer | PE | Cable Steel Wire | Anchor Device | Pulling Cable | Actual Level |
|---|---|---|---|---|---|
| Evaluation Level | II | III | III | III | III |
| Pulling Sling Structure Durability Longevity Evaluation System and Index Level Standard Criteria Division | Index (Weight) | Standard Split Point for Each Grade | Measured Value | ||||
| I | II | III | IV | V | |||
| (0.132) | 90 | 75 | 60 | 50 | 35 | 72 | |
| (0.144) | 90 | 75 | 60 | 50 | 35 | 80 | |
| (0. 142) | 90 | 75 | 60 | 50 | 35 | 65 | |
| (0.151) | 90 | 75 | 60 | 50 | 35 | 55 | |
| (0.156) | 90 | 75 | 60 | 50 | 35 | 63 | |
| (0.142) | 90 | 75 | 60 | 50 | 35 | 45 | |
| (0.133) | 90 | 75 | 60 | 50 | 35 | 85 | |
| Criterion Layer | Indexes | IAHP | CRITIC | EWM | Combined Weight |
|---|---|---|---|---|---|
| PE | Cracking | 0.131 | 0.208 | 0.132 | 0.169 |
| Scratch | 0.065 | 0.094 | 0.144 | 0.080 | |
| Steel wire for cable | Damage | 0.104 | 0.091 | 0.142 | 0.099 |
| Corrosion | 0.207 | 0.166 | 0.151 | 0.190 | |
| Anchor device | Anchorage damage | 0.270 | 0.139 | 0.156 | 0.198 |
| Catheter damage | 0.094 | 0.167 | 0.142 | 0.128 | |
| Shock absorbers damage | 0.130 | 0.136 | 0.133 | 0.136 |
| Pulling Cable | Comprehensive Unascertained Measurement | Evaluation Results | |||||||
|---|---|---|---|---|---|---|---|---|---|
| CWM UM | SPA | MEE | Actual Grade | ||||||
| Jiahui | 0 | 0.313 | 0.627 | 0.060 | 0 | III | III | III | III |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Zhang, T.; Yu, Y. Evaluation of the Durability of Bridge Tension Cables Based on Combination Weighting Method-Unascertained Measure Theory. Sustainability 2022, 14, 7147. https://doi.org/10.3390/su14127147
Li Q, Zhang T, Yu Y. Evaluation of the Durability of Bridge Tension Cables Based on Combination Weighting Method-Unascertained Measure Theory. Sustainability. 2022; 14(12):7147. https://doi.org/10.3390/su14127147
Chicago/Turabian StyleLi, Qingfu, Tianjing Zhang, and Yingqiao Yu. 2022. "Evaluation of the Durability of Bridge Tension Cables Based on Combination Weighting Method-Unascertained Measure Theory" Sustainability 14, no. 12: 7147. https://doi.org/10.3390/su14127147
APA StyleLi, Q., Zhang, T., & Yu, Y. (2022). Evaluation of the Durability of Bridge Tension Cables Based on Combination Weighting Method-Unascertained Measure Theory. Sustainability, 14(12), 7147. https://doi.org/10.3390/su14127147






