3D Numerical Analysis for the Valorization Potential of Spoil Heaps by Shallow Foundations
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Spoil Material
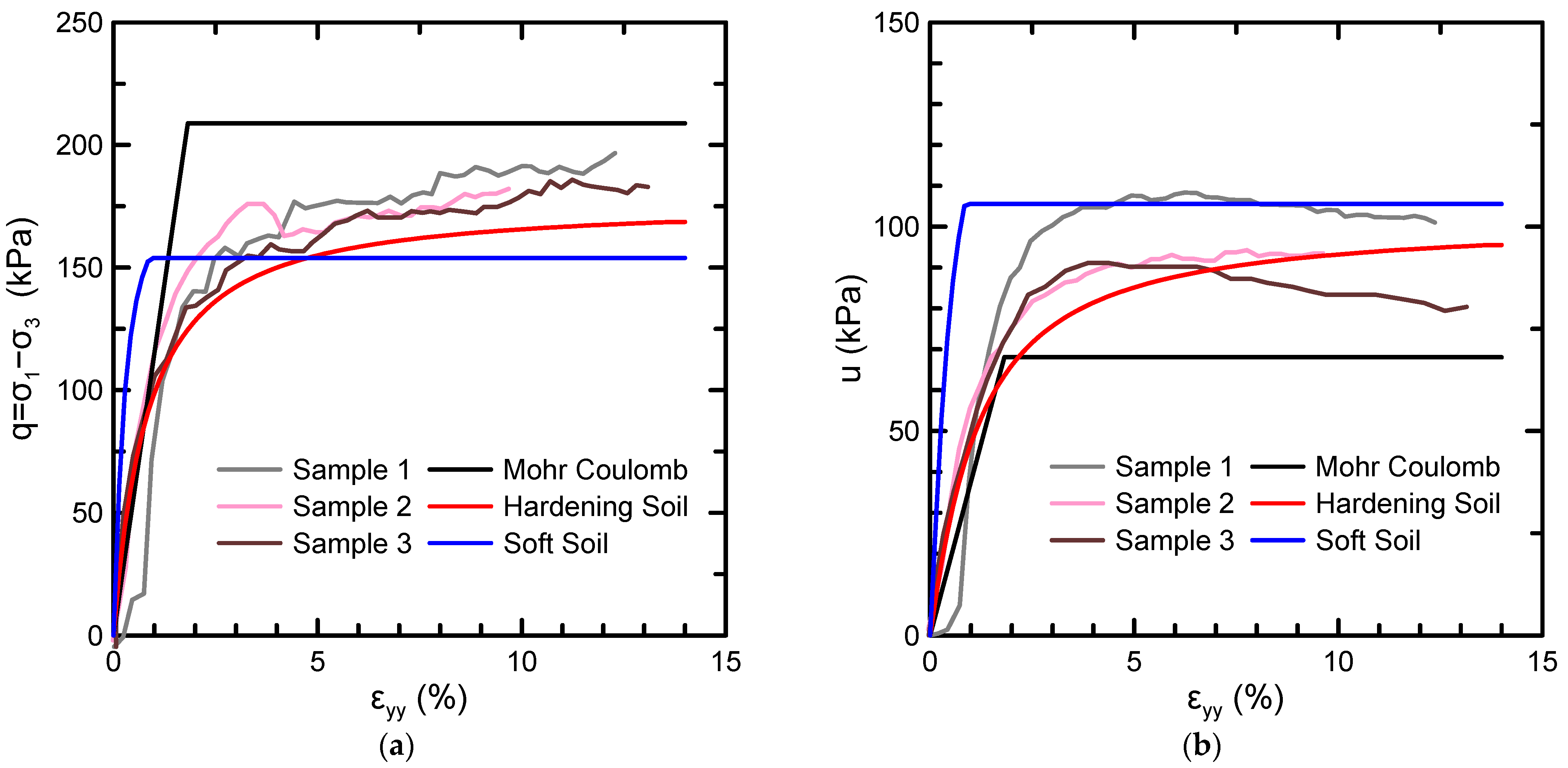
2.2. Numerical Analysis and Constitutive Models
3. Numerical Modeling
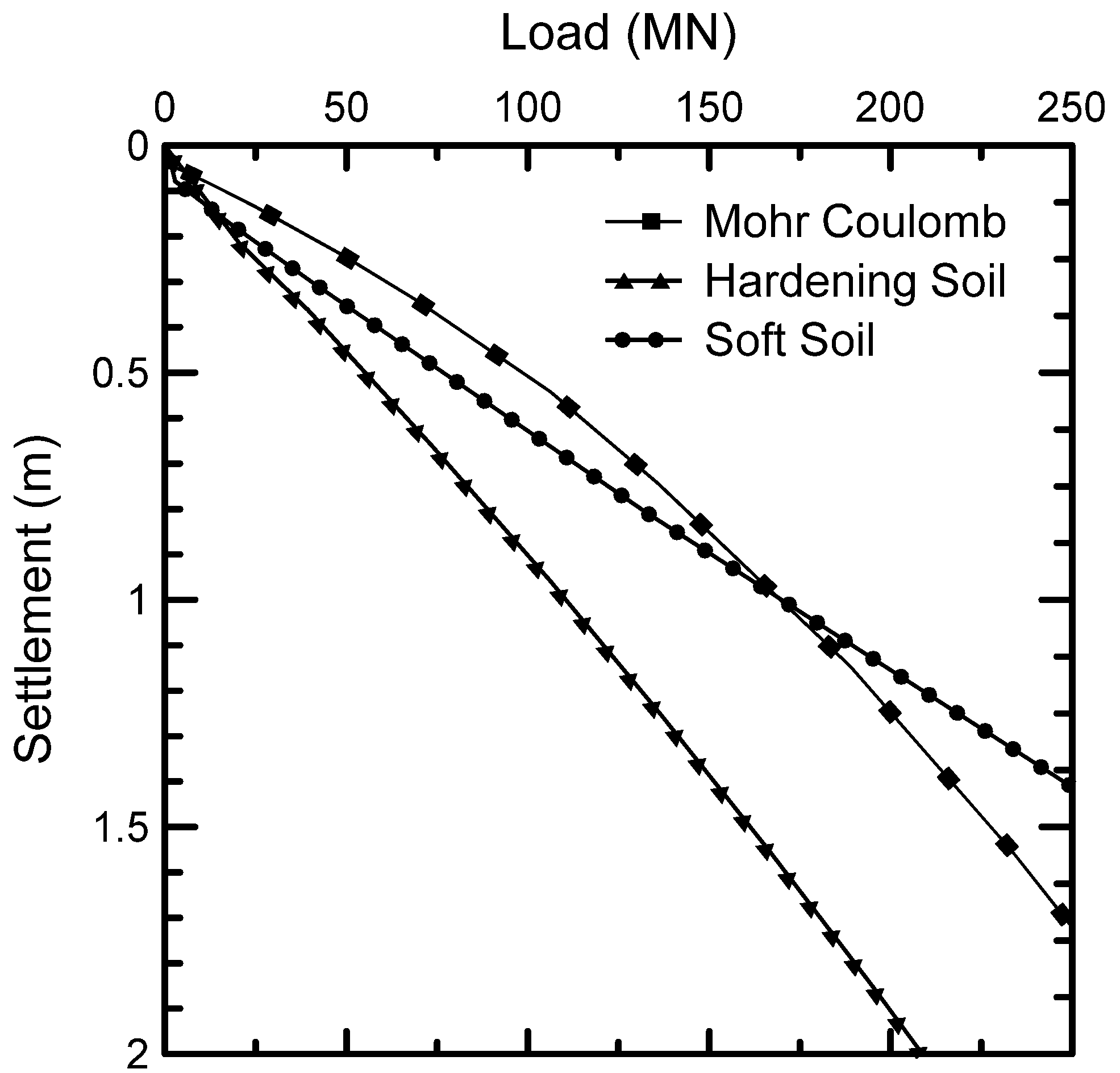
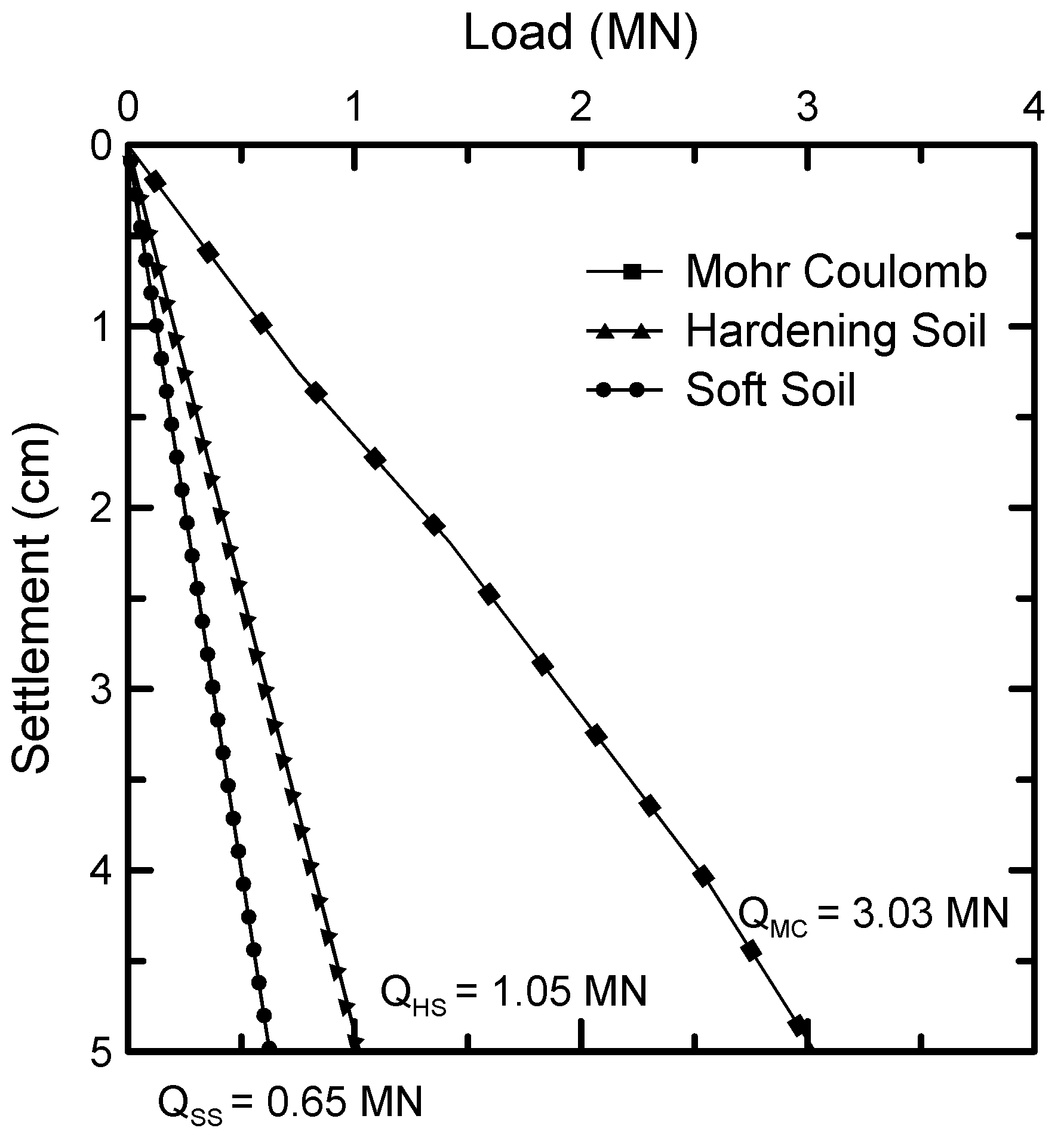
3.1. Wind Turbine Installation with Raft Foundation
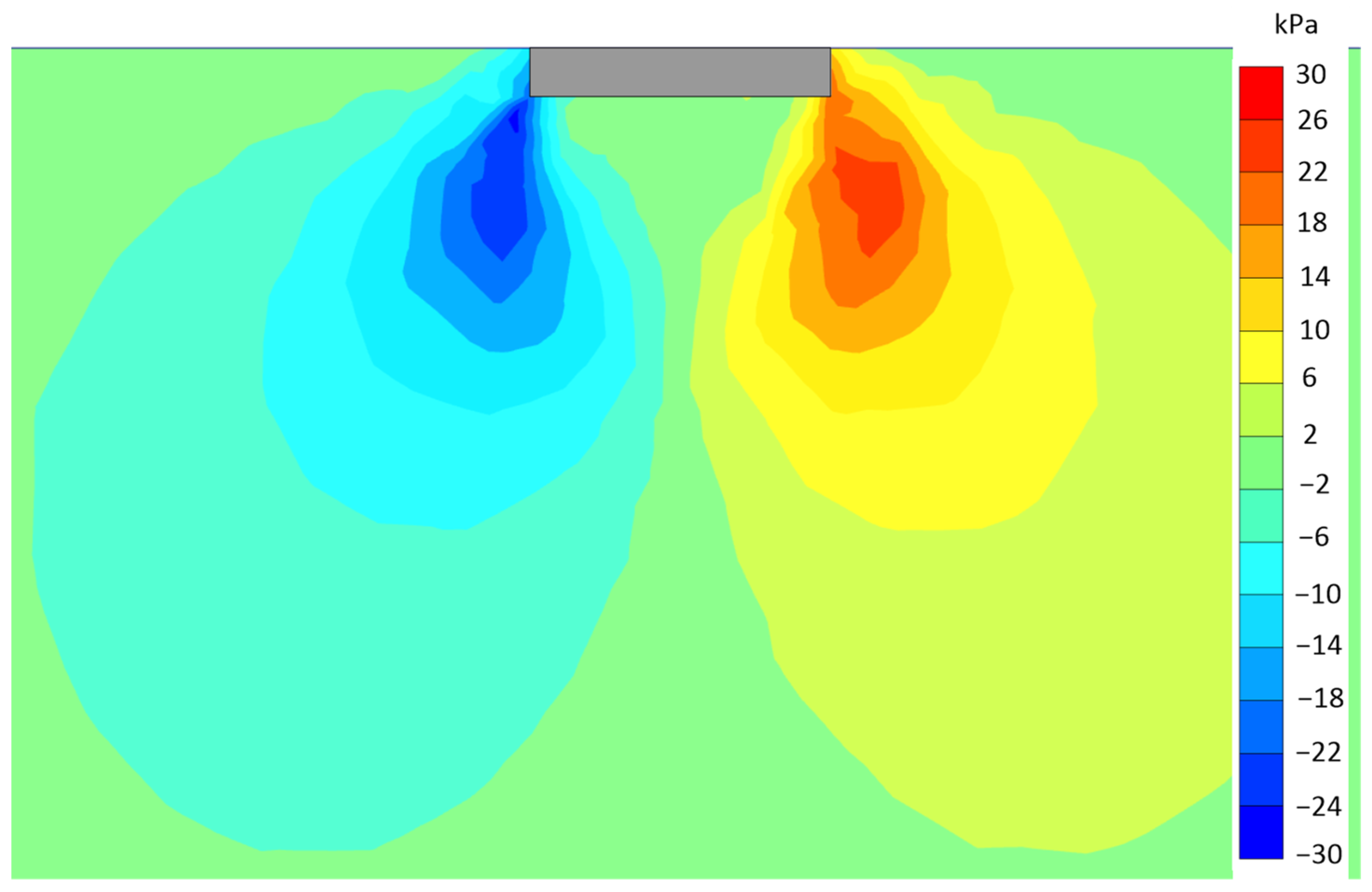
3.2. Building Installation with Isolated Footings
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- BP. BP Statistical Review of World Energy; BP: London, UK, 2021. [Google Scholar]
- Masoudian, M.S.; Zevgolis, I.E.; Deliveris, A.V.; Marshall, A.M.; Heron, C.M.; Koukouzas, N.C. Stability and characterisation of spoil heaps in European surface lignite mines: A state-of-the-art review in light of new data. Environ. Earth Sci. 2019, 78, 505. [Google Scholar] [CrossRef] [Green Version]
- Ichrak, H.; Mostafa, B.; Abdelkabir, M.; Bruno, B. Effect of cementitious amendment on the hydrogeological behavior of a surface paste tailings’ disposal. Innov. Infrastruct. Solut. 2016, 1, 19. [Google Scholar] [CrossRef] [Green Version]
- Hodačová, D.; Prach, K. Spoil heaps from brown coal mining: Technical reclamation versus spontaneous revegetation. Restor. Ecol. 2003, 11, 385–391. [Google Scholar] [CrossRef]
- Hendrychová, M.; Šálek, M.; Tajovský, K.; Řehoř, M. Soil Properties and Species Richness of Invertebrates on Afforested Sites after Brown Coal Mining. Restor. Ecol. 2012, 20, 561–567. [Google Scholar] [CrossRef]
- Spears, D.A. Environmental impact of minerals in UK coals. Geol. Soc. Spec. Publ. 1997, 125, 287–295. [Google Scholar] [CrossRef]
- Kasztelewicz, Z. Approaches to Post-Mining Land Reclamation in Polish Open-Cast Lignite Mining. Civ. Environ. Eng. Rep. 2014, 12, 55–67. [Google Scholar] [CrossRef] [Green Version]
- Alves Dias, P.; Kanellopoulos, K.; Medarac, H.; Kapetaki, Z.; Miranda-Barbosa, E.; Shortall, R.; Czako, V.; Telsnig, T.; Vazquez-Hernandez, C.; Lacal Arántegui, R.; et al. EU Coal Regions: Opportunities and Challenges Ahead—EUR 29292 EN; Publications Office of the European Union: Luxembourg, 2018. [Google Scholar]
- Skinner, H.D.; Watts, K.S.; Charles, J.A. Building on colliery spoil: Some geotechnical considerations. Ground Eng. 1997, 30, 35–40. [Google Scholar]
- Hegde, A.; Das, T. Finite element-based probabilistic stability analysis of rock-fill tailing dam considering regional seismicity. Innov. Infrastruct. Solut. 2019, 4, 37. [Google Scholar] [CrossRef]
- Steiakakis, E.; Kavouridis, K.; Monopolis, D. Large scale failure of the external waste dump at the “South Field” lignite mine, Northern Greece. Eng. Geol. 2009, 104, 269–279. [Google Scholar] [CrossRef]
- Ulusay, R.; Arikan, F.; Yoleri, M.F.; Çaǧlan, D. Engineering geological characterization of coal mine waste material and an evaluation in the context of back-analysis of spoil pile instabilities in a strip mine, SW Turkey. Eng. Geol. 1995, 40, 77–101. [Google Scholar] [CrossRef]
- Kasmer, O.; Ulusay, R.; Gokceoglu, C. Spoil pile instabilities with reference to a strip coal mine in Turkey: Mechanisms and assessment of deformations. Environ. Geol. 2006, 49, 570–585. [Google Scholar] [CrossRef]
- Okagbue, C.O. The geotechnical characteristics and stability of a spoil heap at a southwestern pennsylvania coal mine, U.S.A. Eng. Geol. 1984, 20, 325–341. [Google Scholar] [CrossRef]
- Ashfaq, M.; Heeralal, M.; Moghal, A.A.B. Characterization studies on coal gangue for sustainable geotechnics. Innov. Infrastruct. Solut. 2020, 5, 15. [Google Scholar] [CrossRef]
- Zevgolis, I.E.; Theocharis, A.I.; Deliveris, A.V.; Koukouzas, N.C.; Roumpos, C.; Marshall, A.M. Geotechnical Characterization of Fine-Grained Spoil Material from Surface Coal Mines. J. Geotech. Geoenviron. Eng. 2021, 147, 04021050. [Google Scholar] [CrossRef]
- Euracoal. EURACOAL Market Report 1/2018–5/2018; European Association for Coal and Lignite: Brussels, Belgium, 2018. [Google Scholar]
- Roumpos, C.; Pavloudakis, F.; Liakoura, A.; Nalmpanti, D.; Arampatzis, K. Utilisation of Lignite Resources within the Context of a Changing Electricity Generation Mix. In Proceedings of the 10th Jubilee International Brown Coal Mining Congress, Bełchatów, Poland, 16–18 April 2018; pp. 355–365. [Google Scholar]
- Bentley Systems. 3D Finite Element Geotechnical Analysis Software—Plaxis3D v.2018; Bentley Systems: Dublin, Ireland, 2018. [Google Scholar]
- Theocharis, A.I.; Zevgolis, I.E.; Koukouzas, N.C. Validation of constitutive models for spoil material of brown coal mines. In Proceedings of the 3rd Conference of the Arabian Journal of Geosciences (CAJG), Sousse, Tunisia, 2–5 November 2020. [Google Scholar]
- Grünberg, J.; Göhlmann, J. Concrete Structures for Wind Turbines, 1st ed.; Bergmeister, K., Fingerloos, F., Wörner, J.-D., Eds.; Ernst & Sohn: Hoboken, NJ, USA, 2013. [Google Scholar]
- Shrestha, S.; Ravichandran, N.; Rahbari, P. Geotechnical design and design optimization of a pile-raft foundation for tall onshore wind turbines in multilayered clay. Int. J. Geomech. 2018, 18, 04017143. [Google Scholar] [CrossRef]
- Shrestha, S.; Ravichandran, N. Performance- and cost-based robust design optimization procedure for typical foundations for wind turbine. Int. J. Geotech. Eng. 2020, 14, 395–408. [Google Scholar] [CrossRef]
- Mohamed, W.; Austrell, P.E. A comparative study of three onshore wind turbine foundation solutions. Comput. Geotech. 2018, 94, 46–57. [Google Scholar] [CrossRef]
- Baniotopoulos, C.; Borri, C.; Stathopoulos, T. Environmental Wind Engineering and Design of Wind Energy Structures; Springer: Vienna, Austria, 2011; Volume 531. [Google Scholar]
- Salgado, R. The Engineering of Foundations; McGraw-Hill: Boston, MA, USA, 2008. [Google Scholar]
- DNV-Riso. Guidelines for the Design of Wind Turbines; Det Norske Veritas, Copenhagen and Wind Energy Department, Risø National Laboratory: Copenhagen, Denmark, 2002; Volume 2. [Google Scholar]
- Papagiannis, M. Wind Turbine Foundations in Clay: Technical and Economic Considerations for Proposals for Wind Turbine Foundations; Uppsala University: Uppsala, Sweden, 2018. [Google Scholar]
- European Union. EN 1997-1 (English): Eurocode 7: Geotechnical Design—Part 1: General Rules (Annex H); The European Union: Brussels, Belgium, 2004. [Google Scholar]
- European Union. EN 1997-1 (English): Eurocode 7: Geotechnical Design—Part 1: General Rules; The European Union: Brussels, Belgium, 2004. [Google Scholar]
- European Union. EN 1997-1 (English): Eurocode 7: Geotechnical Design—Part 1: General Rules (Annex D); The European Union: Brussels, Belgium, 2004. [Google Scholar]
- BS:8004; British Standards: Code of Practise for Foundations. British Standards: London, UK, 1986.
- Skempton, A.W.; Macdonald, D.H. The allowable settlements of buildings. Proc. Inst. Civ. Eng. 1956, 5, 727–768. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Pratice, 2nd ed.; John Wiley: New York, NY, USA, 1967. [Google Scholar]









| Parameter | Effective Friction Angle φ′ (°) | Effective Cohesion c′ (kPa) | Compression Index cc | Recompression Index cr | Oedometric Modulus Es (MPa) | |
|---|---|---|---|---|---|---|
| Δσv = 50–100 (kPa) | Δσv = 100–200 (kPa) | |||||
| Population | 43 | 43 | 61 | 61 | 61 | 61 |
| Mean | 25.2 | 17.6 | 0.216 | 0.037 | 1.9 | 2.7 |
| St. Dev. | 6.8 | 18.7 | 0.081 | 0.015 | 1.1 | 1.4 |
| COV (%) | 27 | 106 | 38 | 41 | 58 | 51 |
| Minimum | 8.2 | 0 | 0.064 | 0.090 | 0.6 | 1.0 |
| Maximum | 39.2 | 72.4 | 0.398 | 0.090 | 5.7 | 8.1 |
| Parameter | Mohr–Coulomb | Hardening Soil | Soft Soil |
|---|---|---|---|
| Friction angle φ′ (°) | 25 | 25 | 25 |
| Cohesion c′ (kPa) | 5 | 5 | 5 |
| Dilation angle ψ (°) | 0 | 0 | 0 |
| Elasticity modulus E or E50 (KPa) | 10,000 | 5000 | - |
| Poisson ratio ν | 0.3 | - | - |
| Hardening Soil parameter m | - | 0.5 | - |
| Oedometric modulus Es (kPa) | - | 5000 | - |
| Compression index cc | - | - | 0.2 |
| Recompression index cr | - | - | 0.037 |
| Case Study | Tower Height (m) | Tower Material | Vertical Load (MN) | Horizontal Force (MN) | Bending Moment (MN-m) |
|---|---|---|---|---|---|
| Shrestha, Ravichandran and Rahbari [22] | 120 | Concrete and Steel | 51.71 | 2.26 | 144.89 |
| Shrestha and Ravichandran [23] | 120 | Concrete and Steel | 51.71 | 2.39 | 153.11 |
| Mohamed and Austrell [24] | 80 | Steel | 3.51 | 0.8 | 63.83 |
| Baniotopoulos, Borri and Stathopoulos [25] | 76.15 | Steel | 2.5 | 0.9 | 59.59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Theocharis, A.I.; Zevgolis, I.E.; Roumpos, C.; Koukouzas, N.C. 3D Numerical Analysis for the Valorization Potential of Spoil Heaps by Shallow Foundations. Sustainability 2022, 14, 7363. https://doi.org/10.3390/su14127363
Theocharis AI, Zevgolis IE, Roumpos C, Koukouzas NC. 3D Numerical Analysis for the Valorization Potential of Spoil Heaps by Shallow Foundations. Sustainability. 2022; 14(12):7363. https://doi.org/10.3390/su14127363
Chicago/Turabian StyleTheocharis, Alexandros I., Ioannis E. Zevgolis, Christos Roumpos, and Nikolaos C. Koukouzas. 2022. "3D Numerical Analysis for the Valorization Potential of Spoil Heaps by Shallow Foundations" Sustainability 14, no. 12: 7363. https://doi.org/10.3390/su14127363
APA StyleTheocharis, A. I., Zevgolis, I. E., Roumpos, C., & Koukouzas, N. C. (2022). 3D Numerical Analysis for the Valorization Potential of Spoil Heaps by Shallow Foundations. Sustainability, 14(12), 7363. https://doi.org/10.3390/su14127363









