Impact of Openings on the In-Plane Strength of Confined and Unconfined Masonry Walls: A Sustainable Numerical Study
Abstract
:1. Introduction
2. Methodology
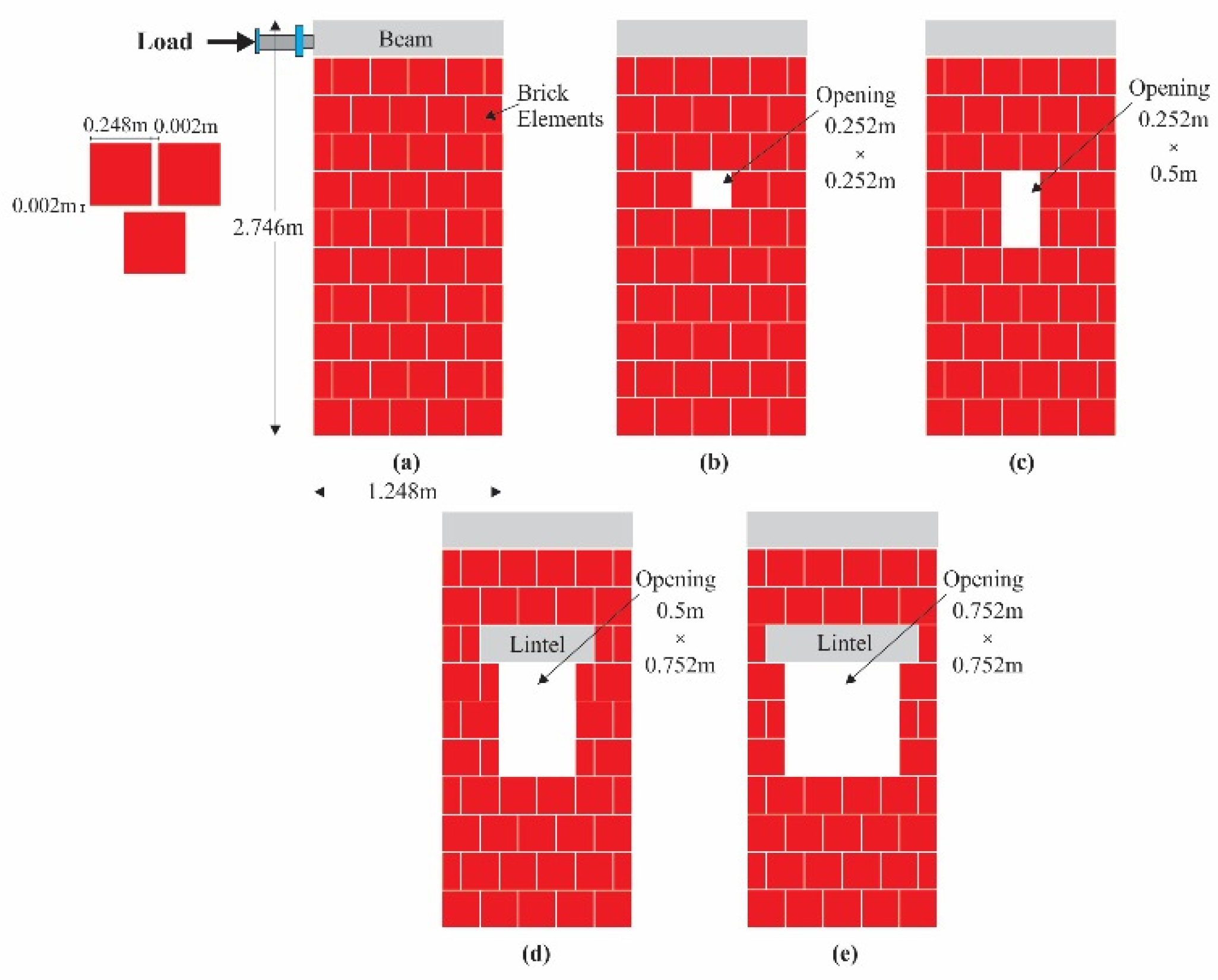
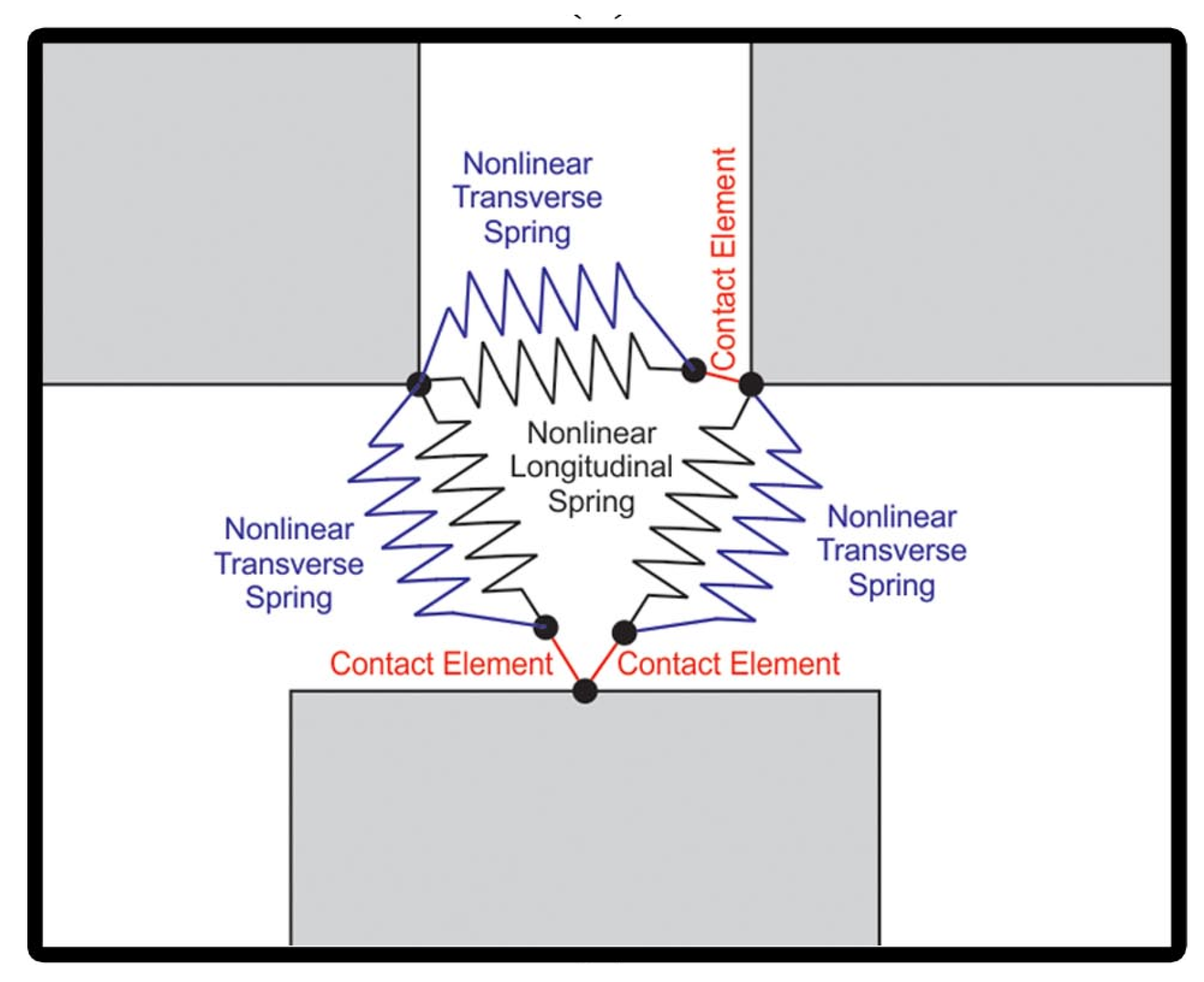
2.1. Numerical Modeling
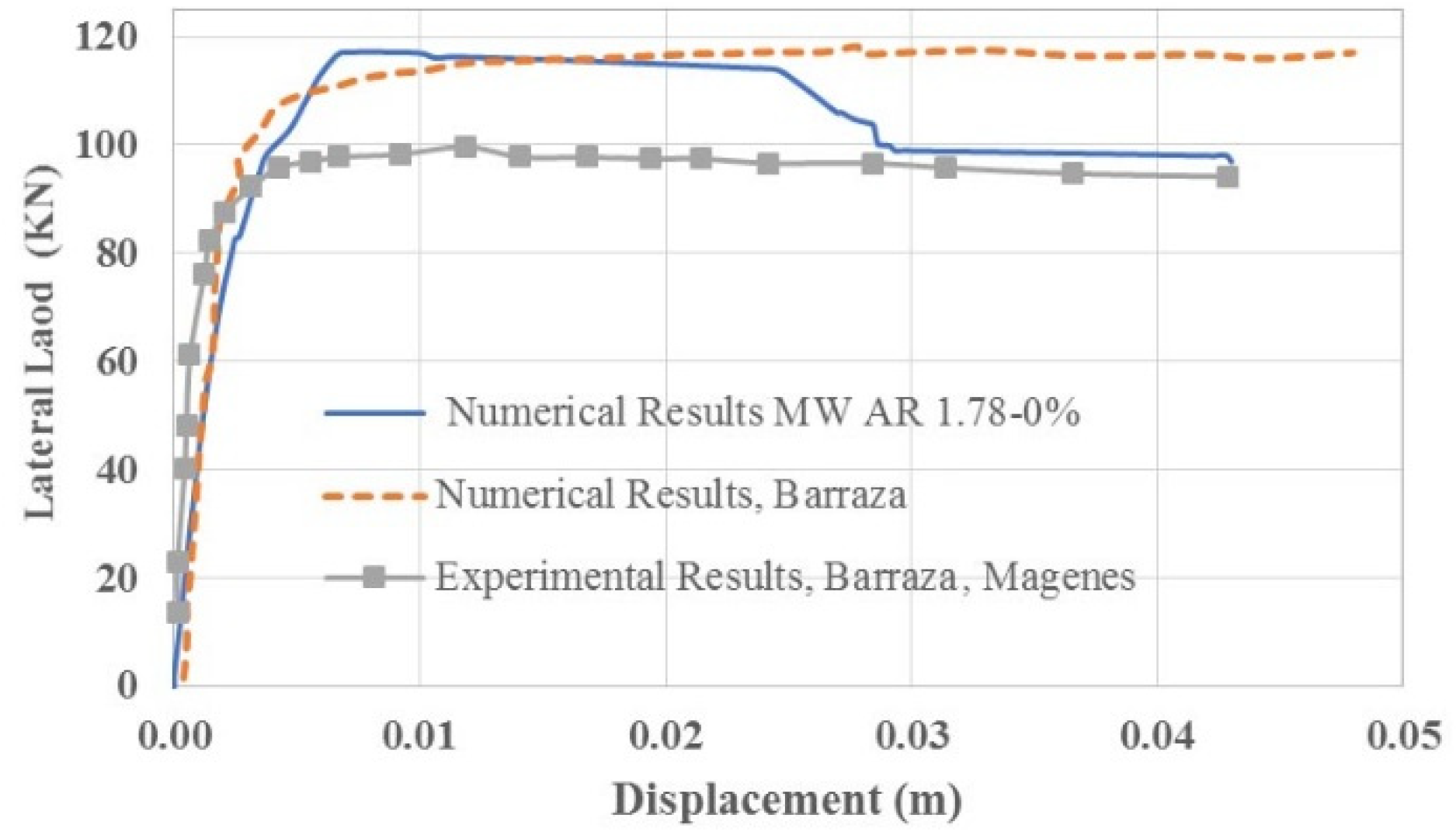
2.2. Experimental Tests and Validation
3. Results and Discussion
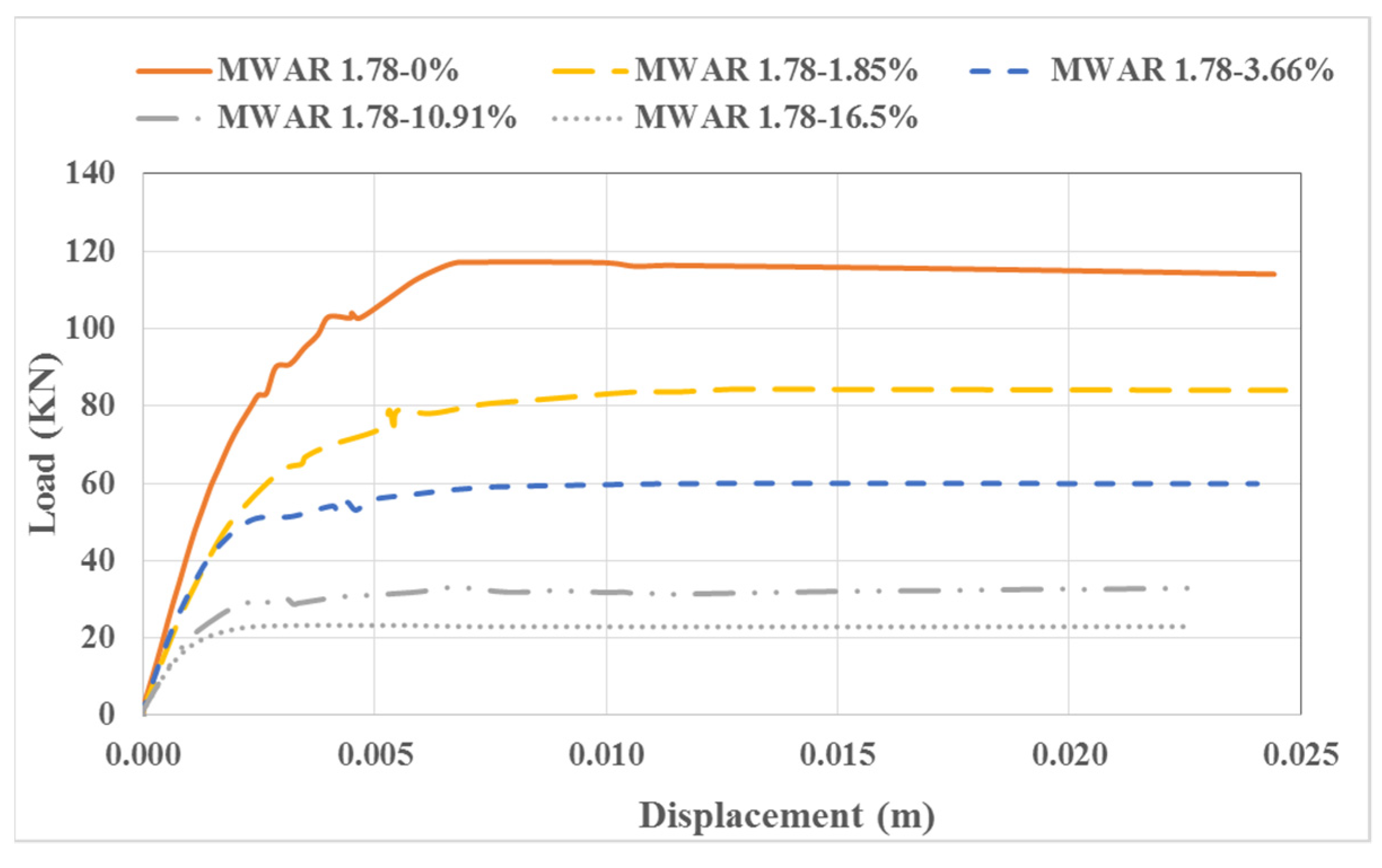
3.1. Performance of Unconfined Masonry Walls against Lateral Loading
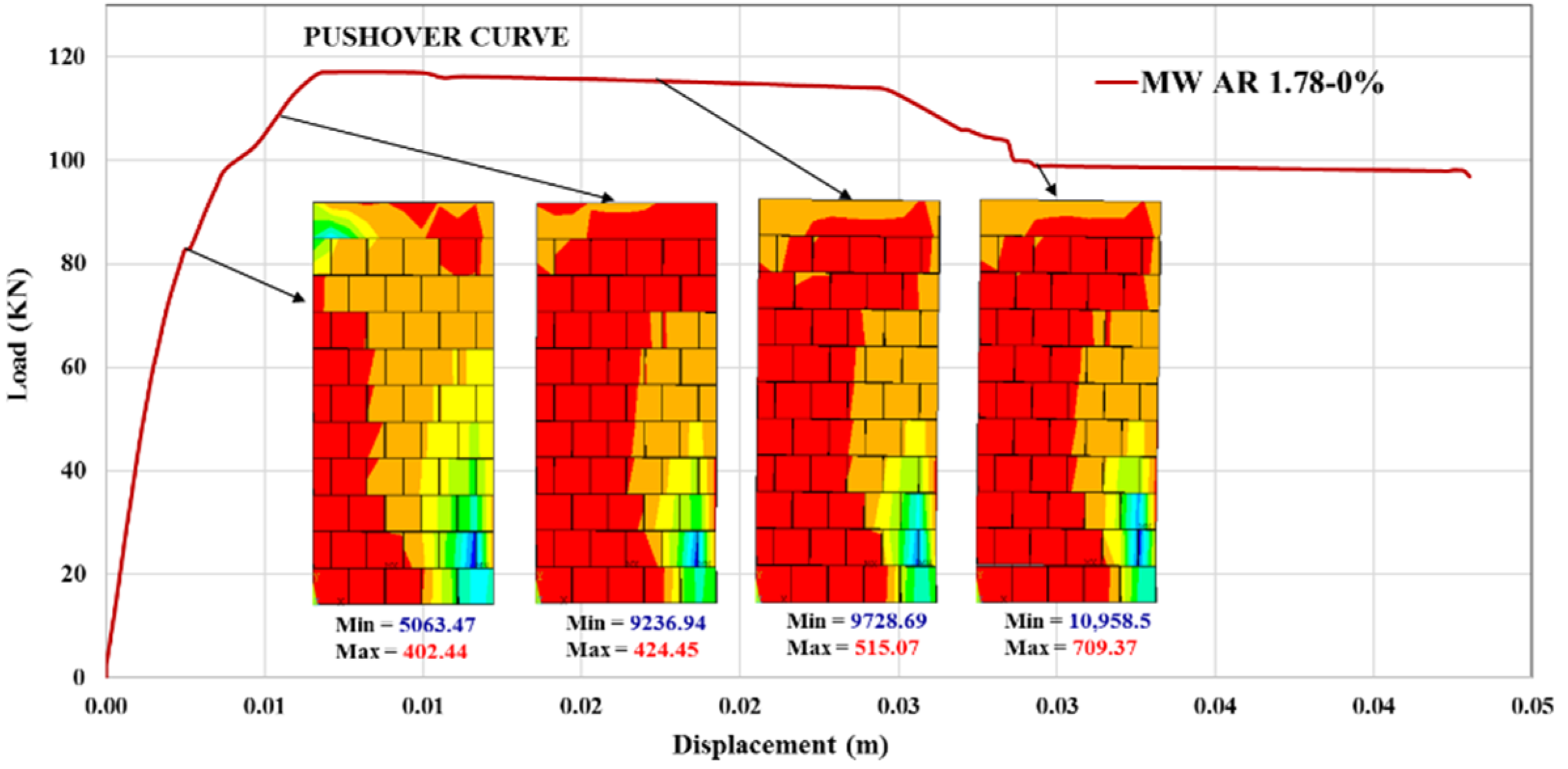
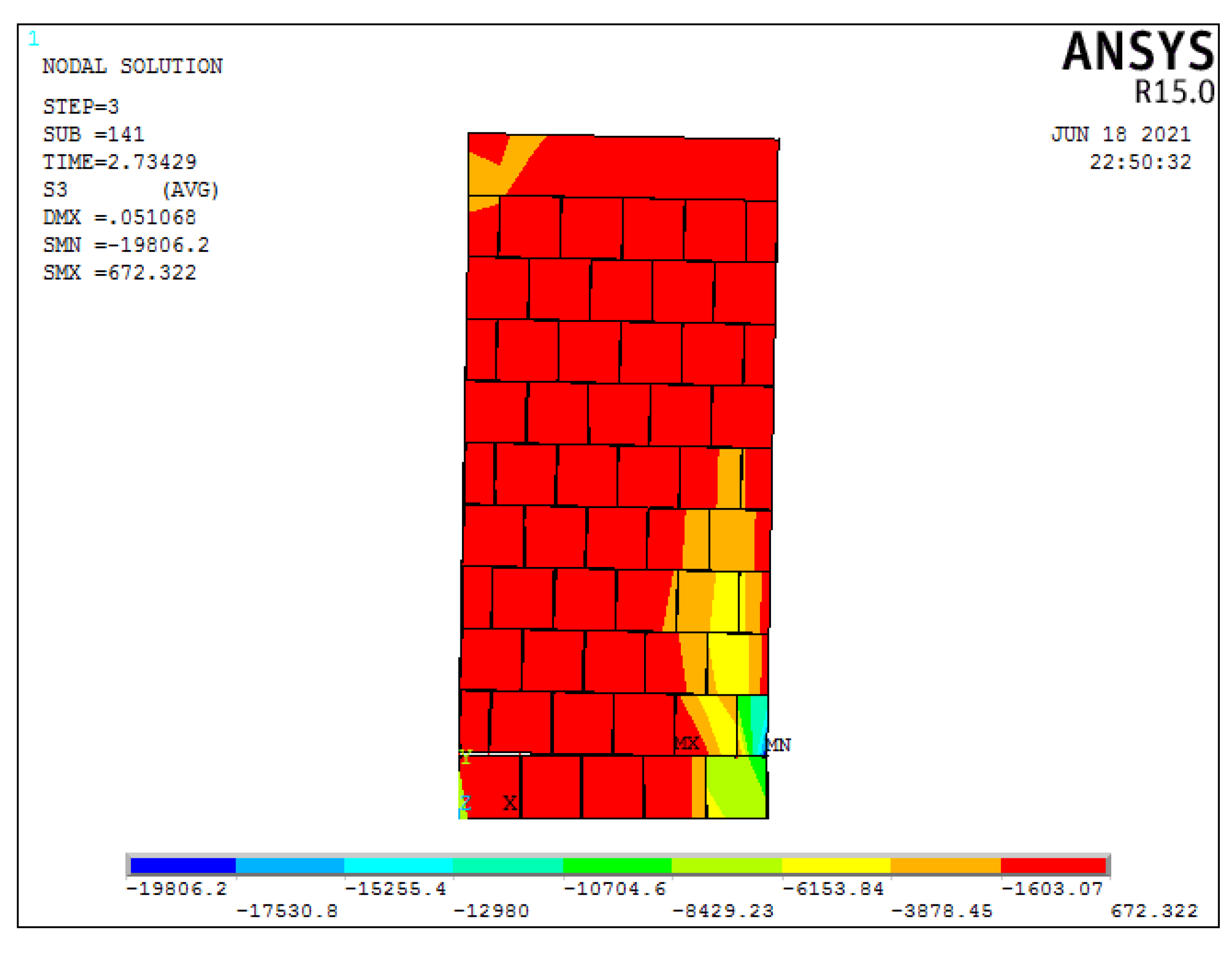
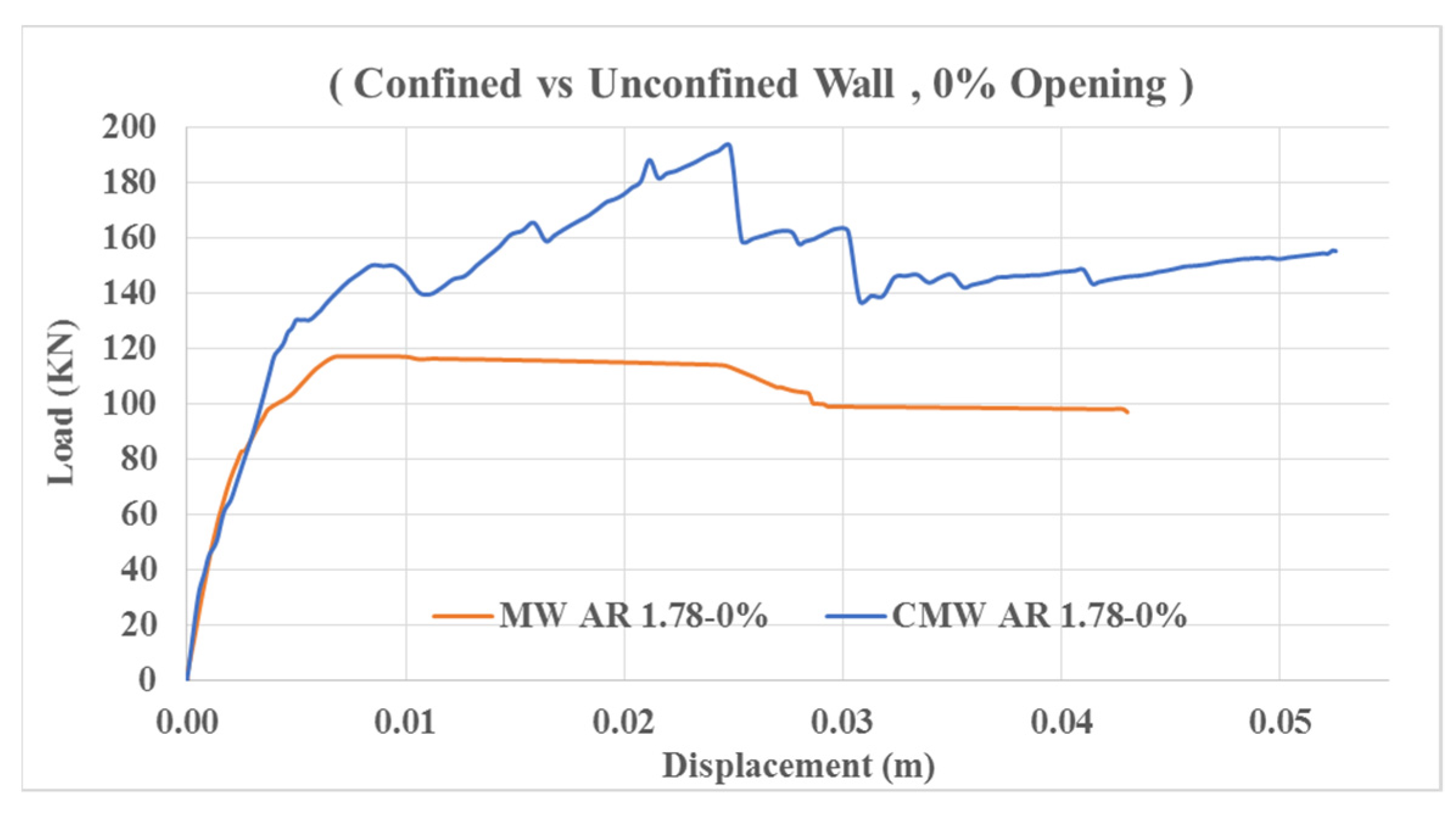
3.1.1. MW AR1.78–0%
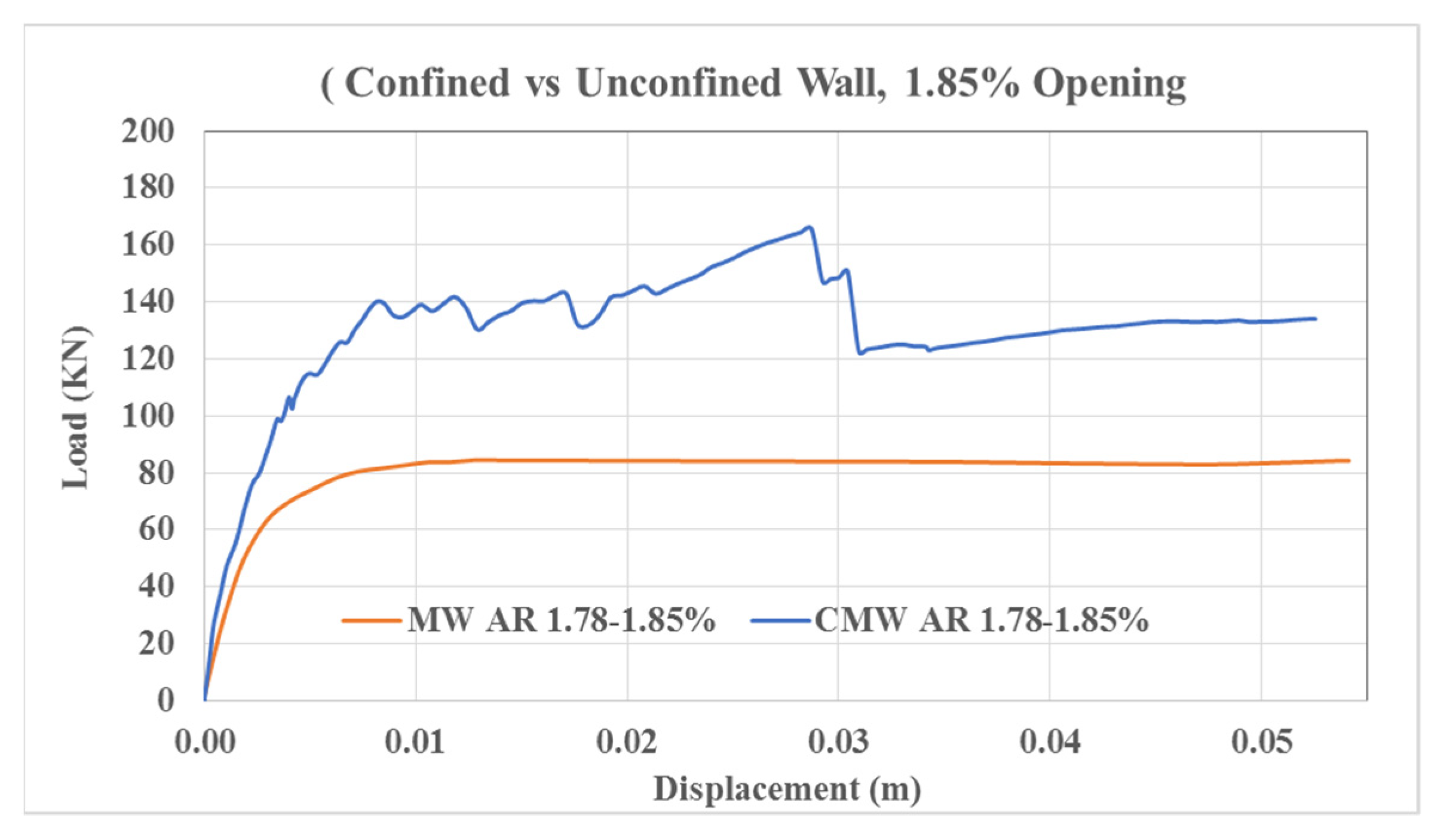
3.1.2. MW AR1.78–1.85%
3.1.3. MW AR1.78–3.66%
3.1.4. MW AR1.78–10.91%
3.1.5. MW AR1.78–16.5%
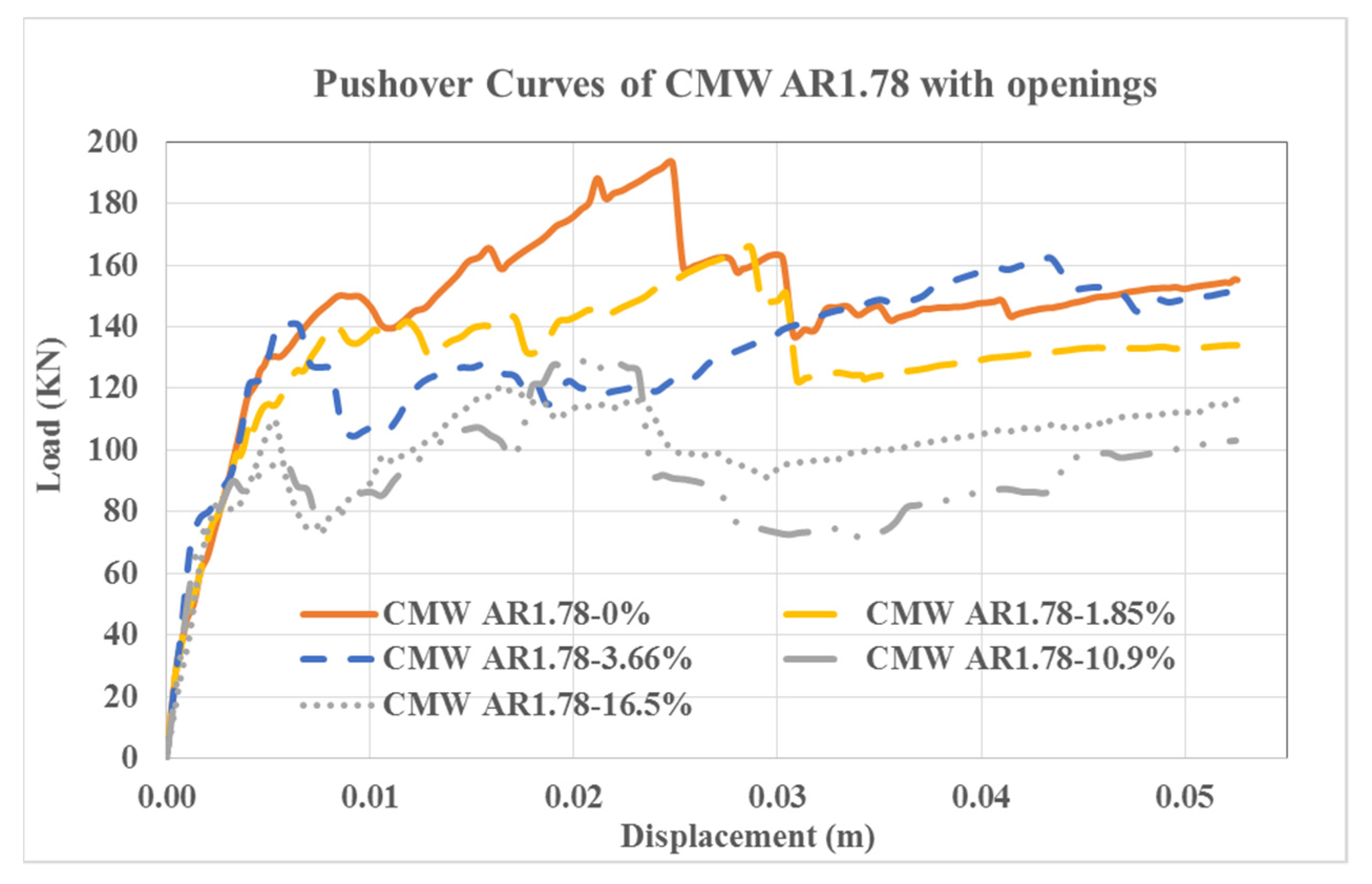
3.2. Performance of Confined Masonry Walls against Lateral Loading
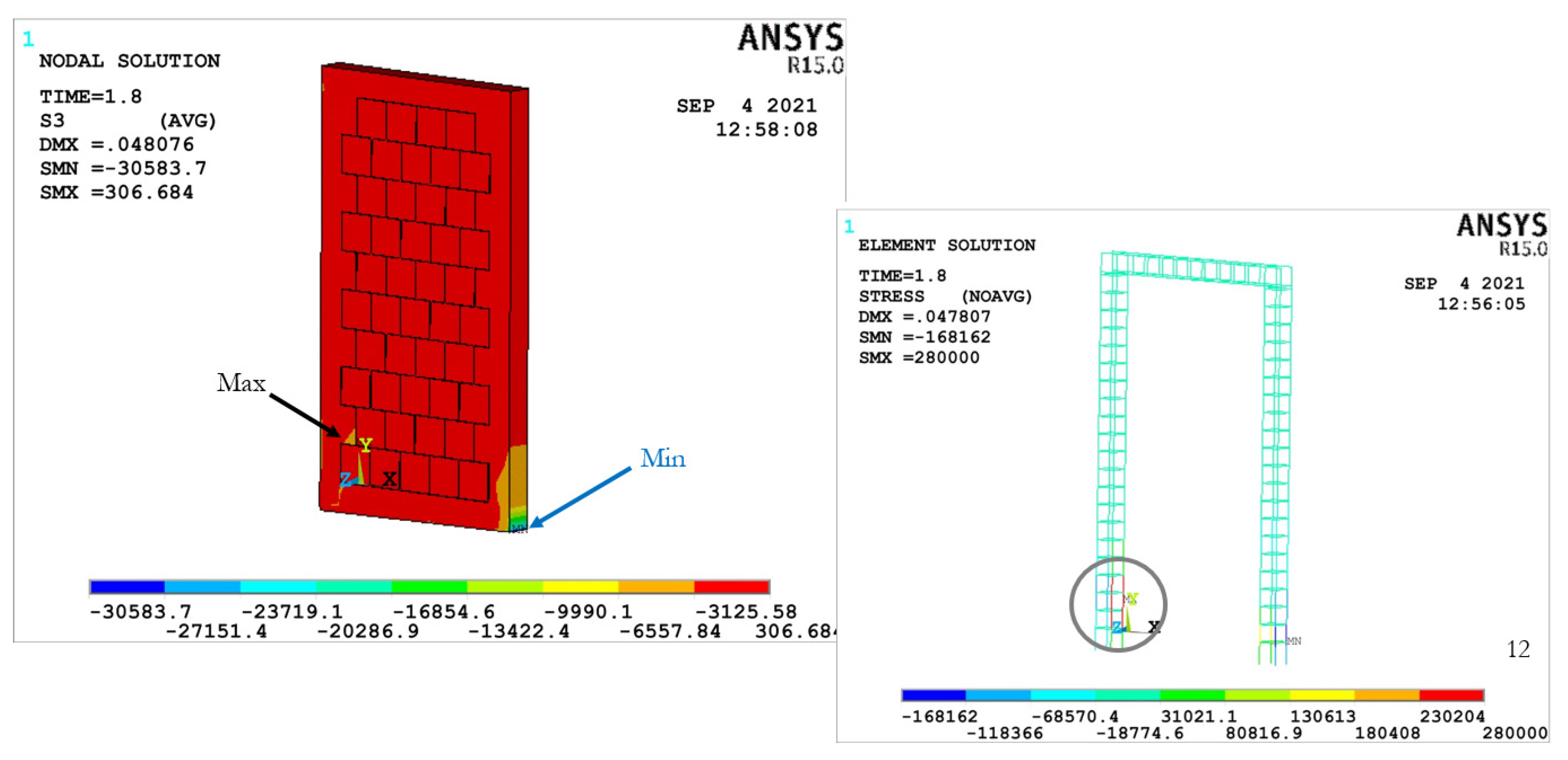
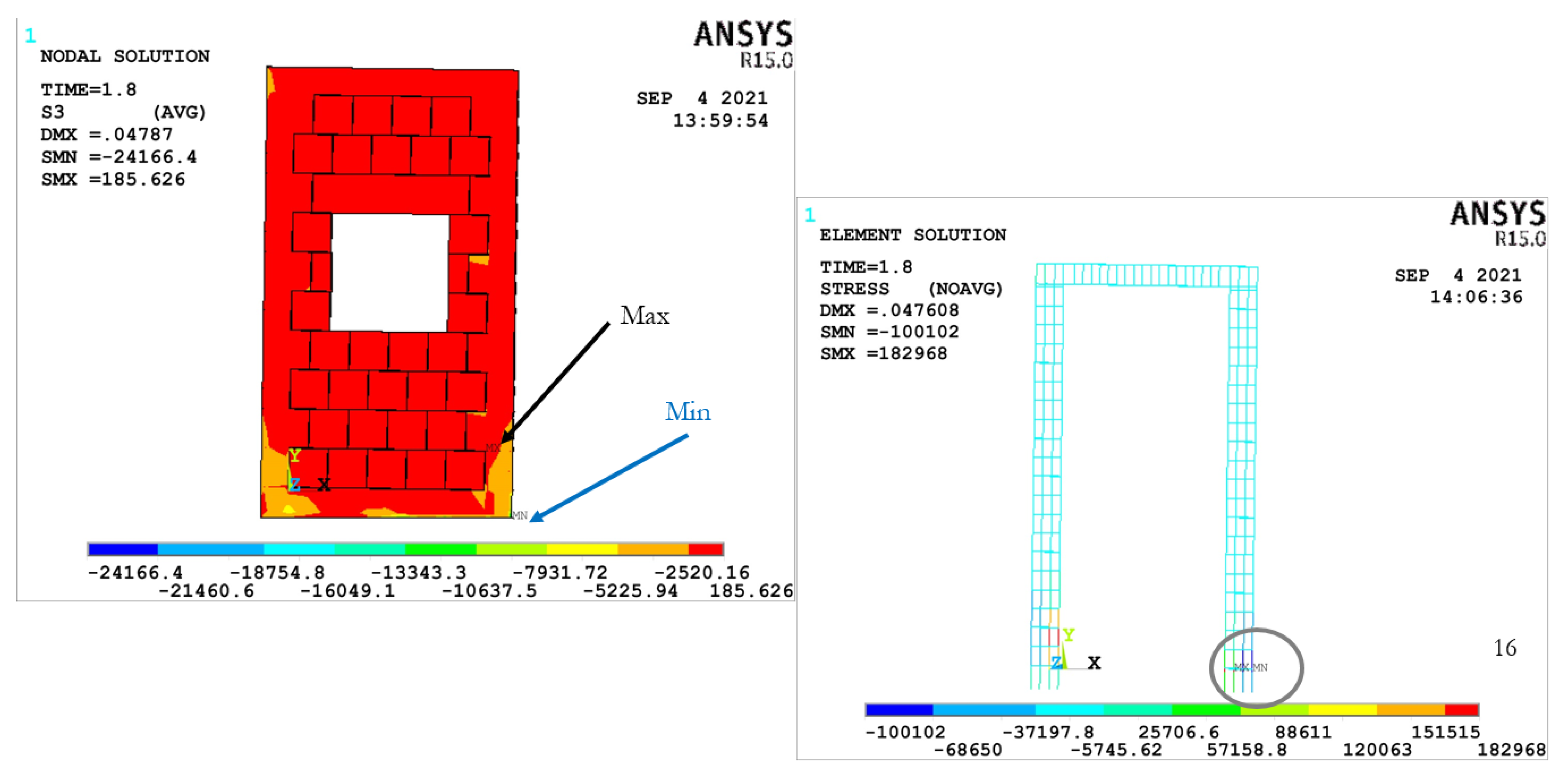
3.2.1. CMW AR1.78–0%
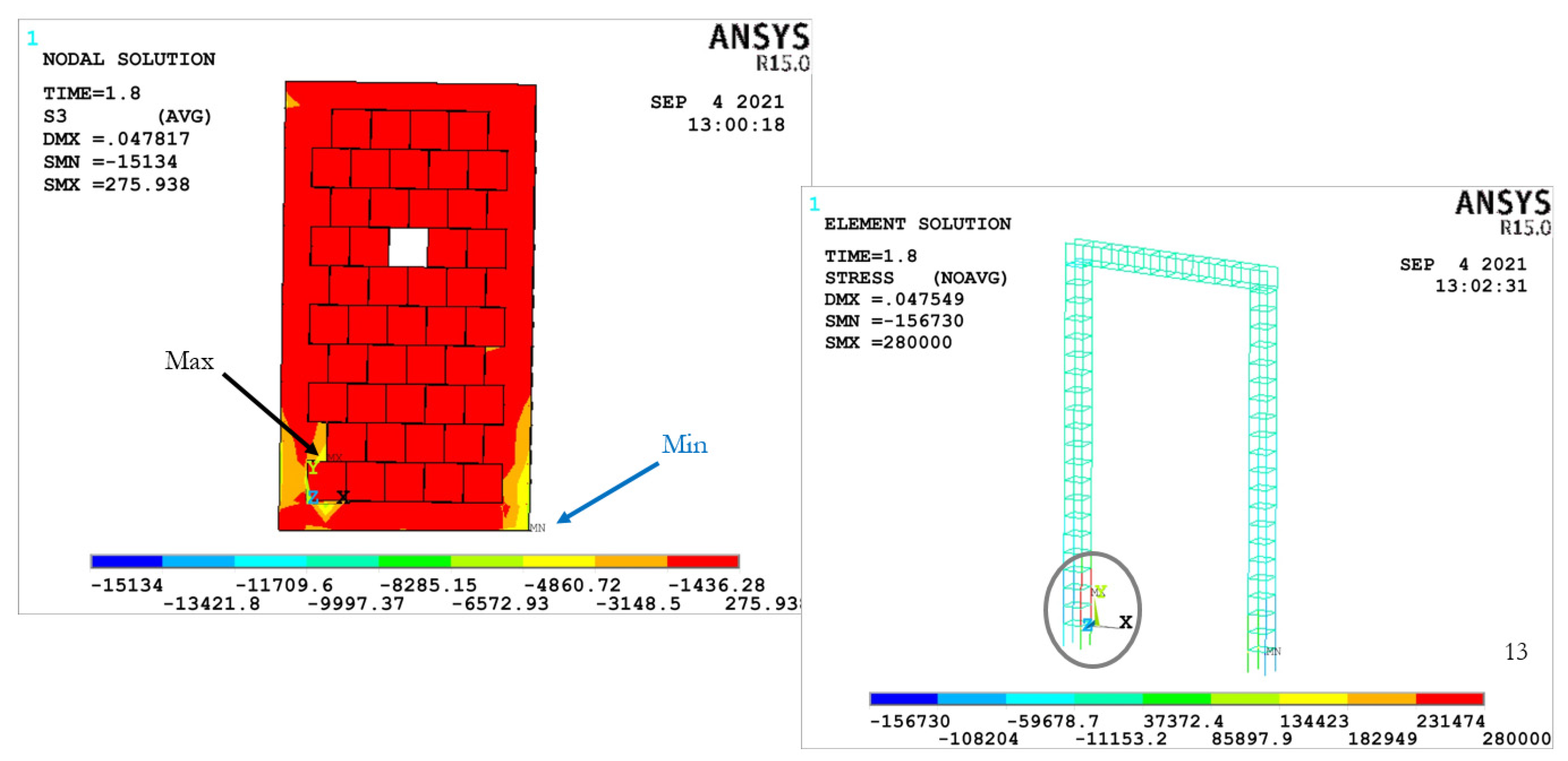
3.2.2. CMW AR1.78–1.85%
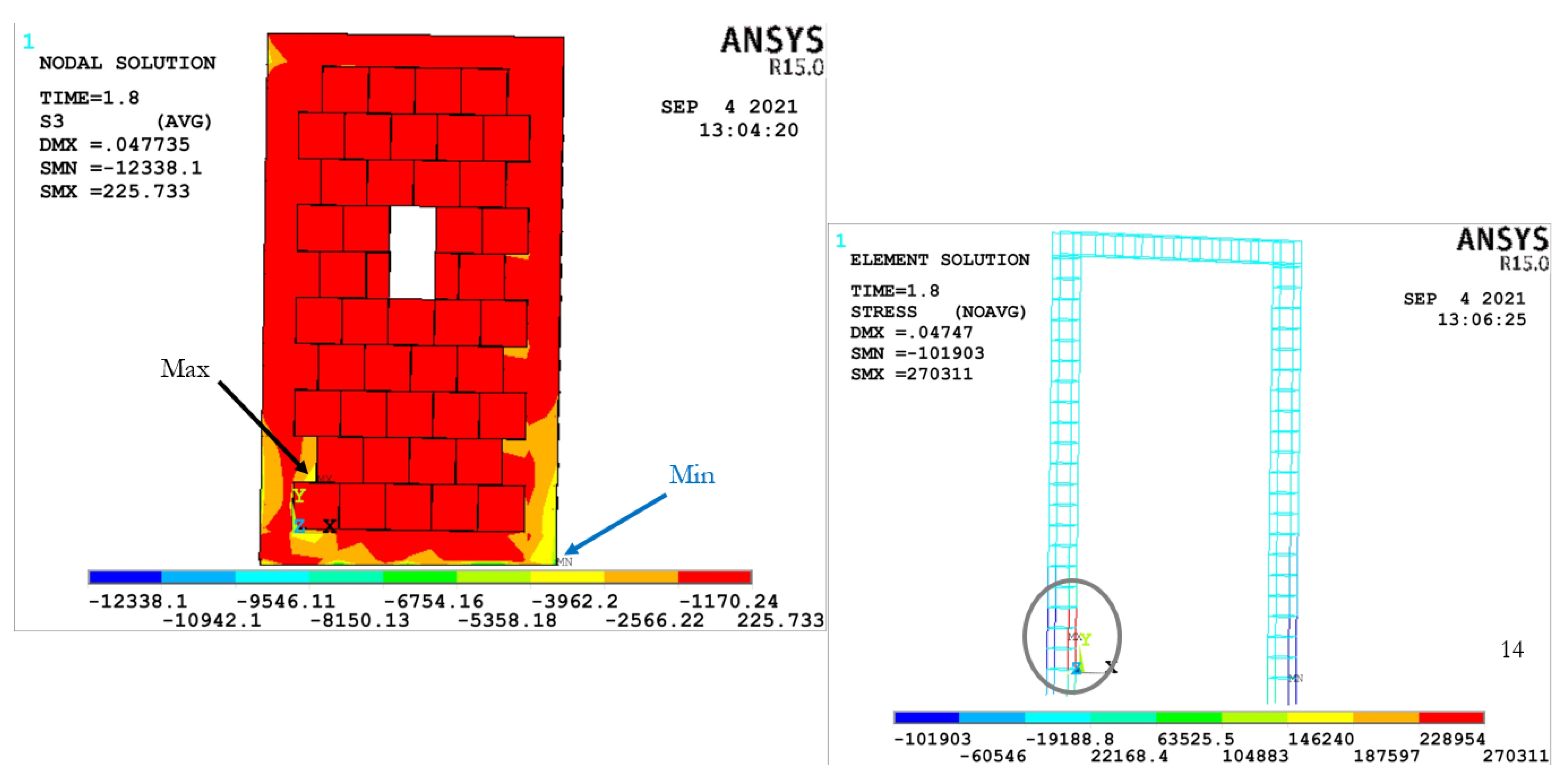
3.2.3. CMW AR1.78–3.66%
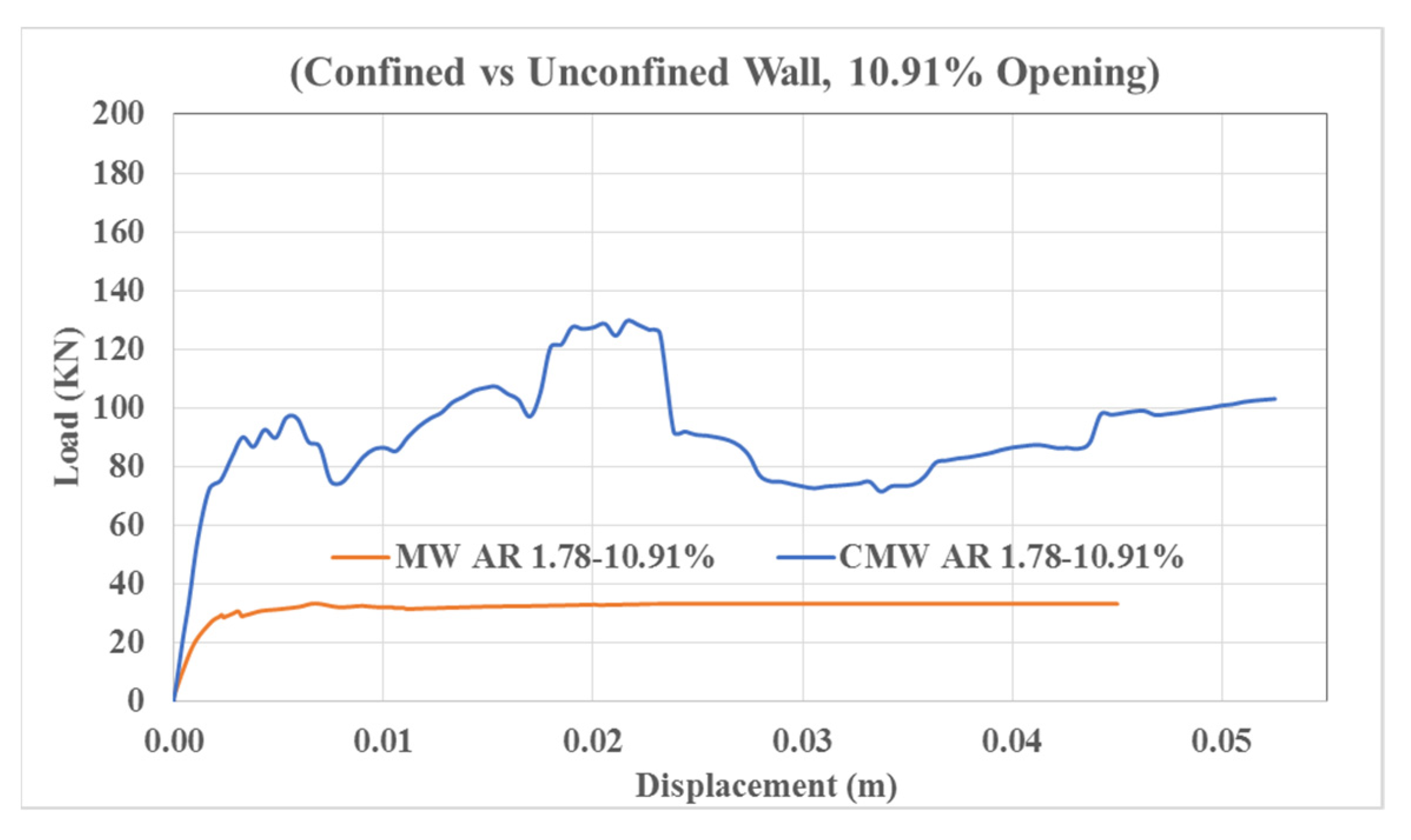
3.2.4. CMW AR1.78–10.91%
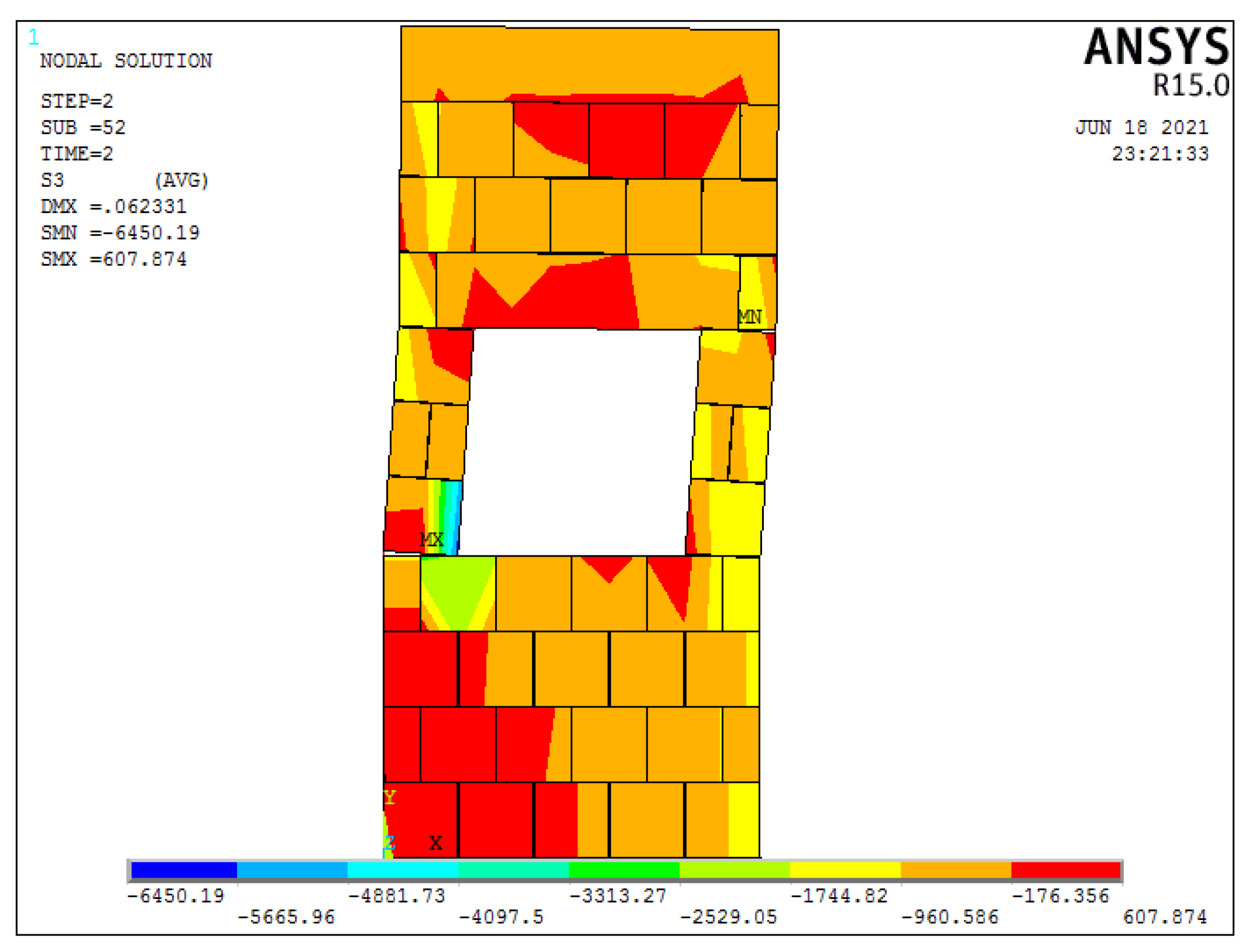
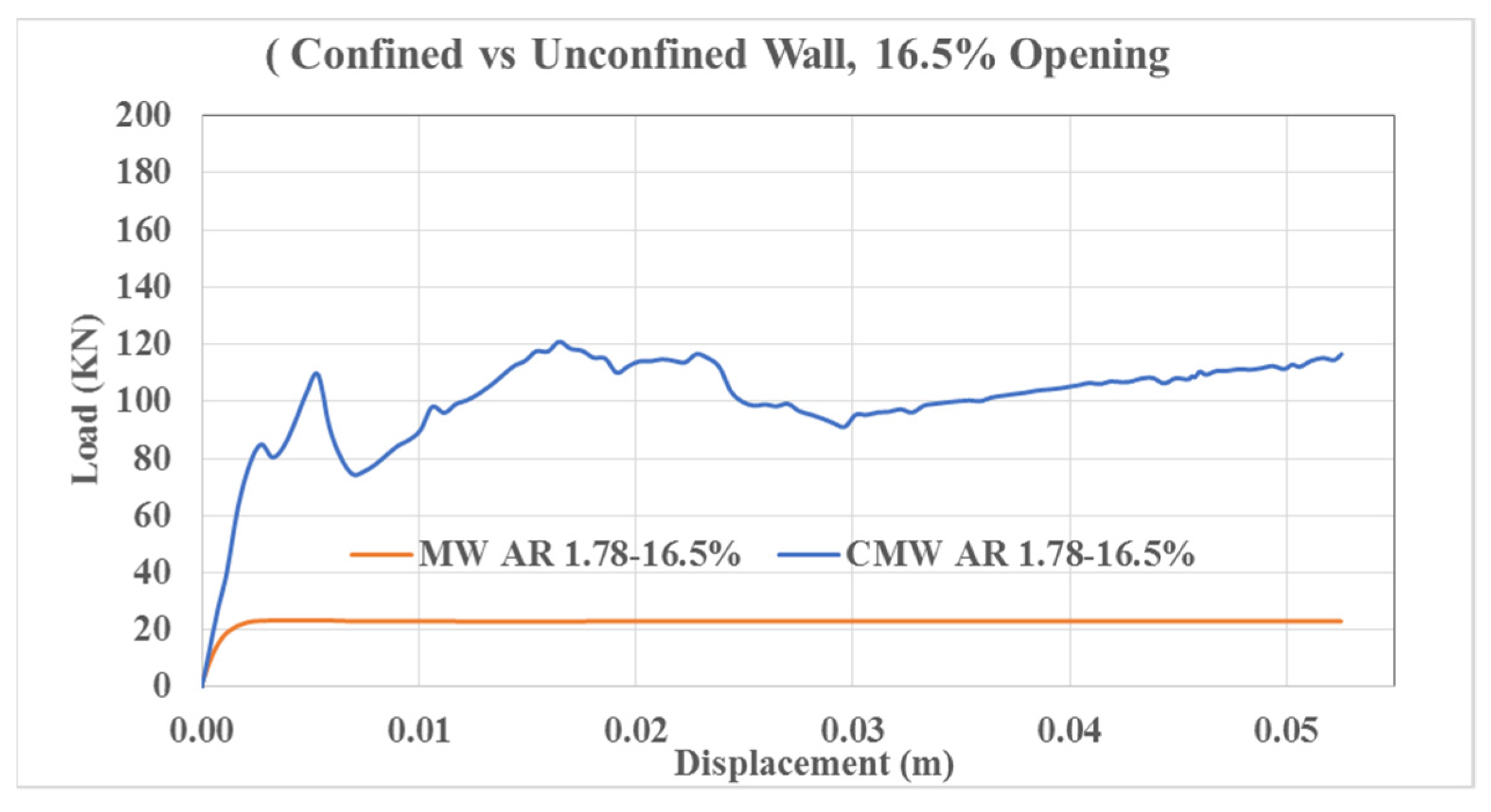
3.2.5. CMW AR1.78–16.5%
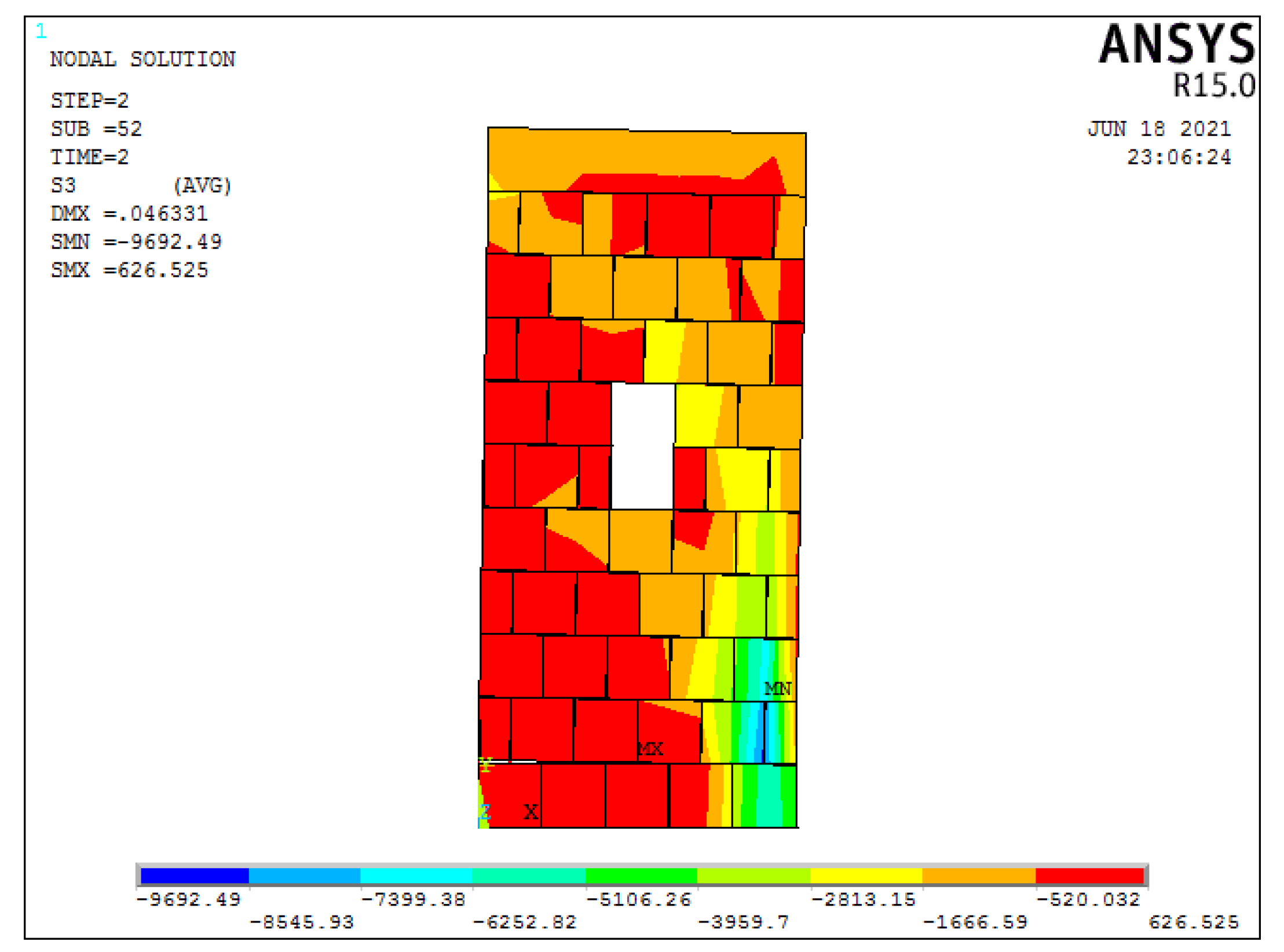
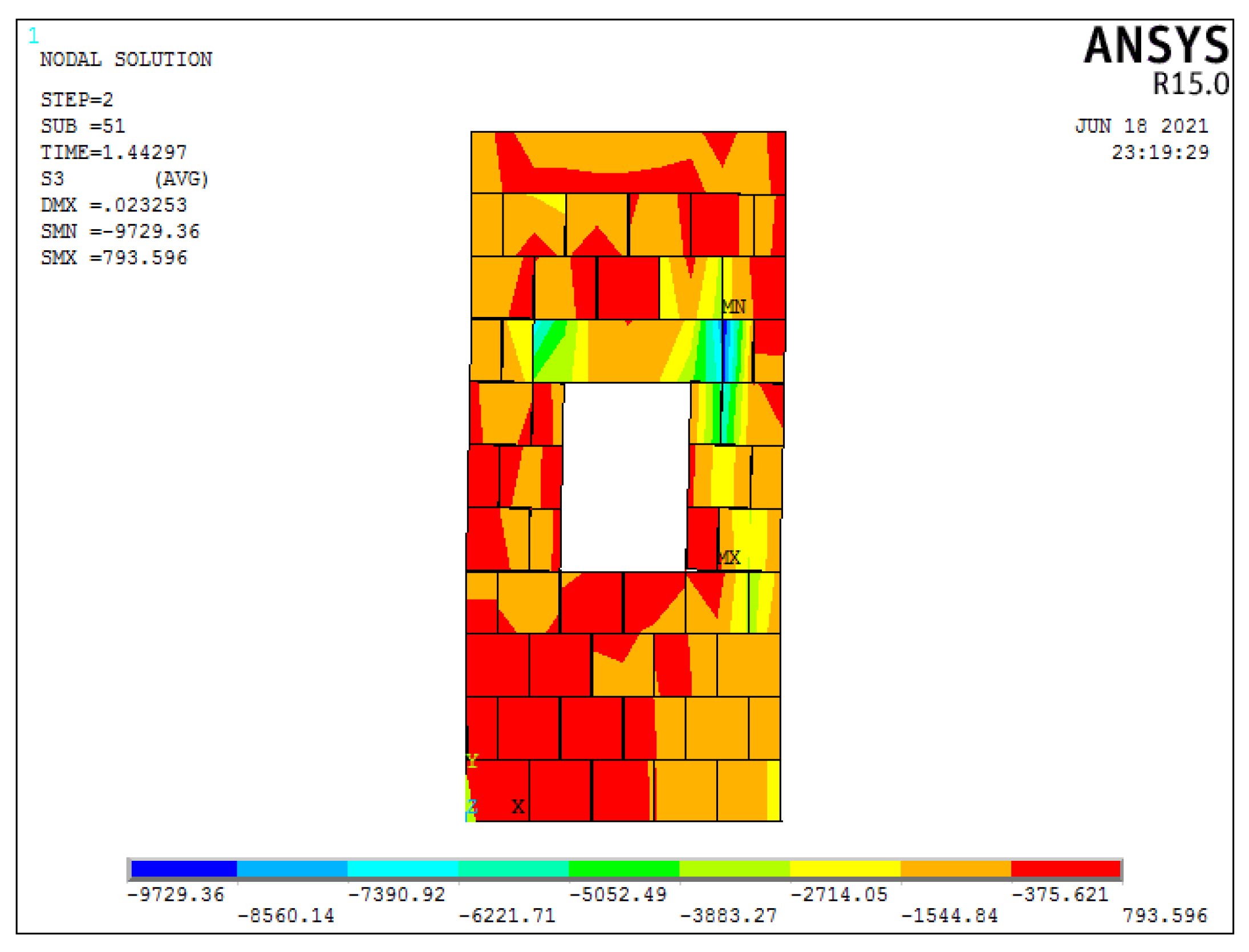
3.3. Impact of Openings on the Unconfined Masonry Walls
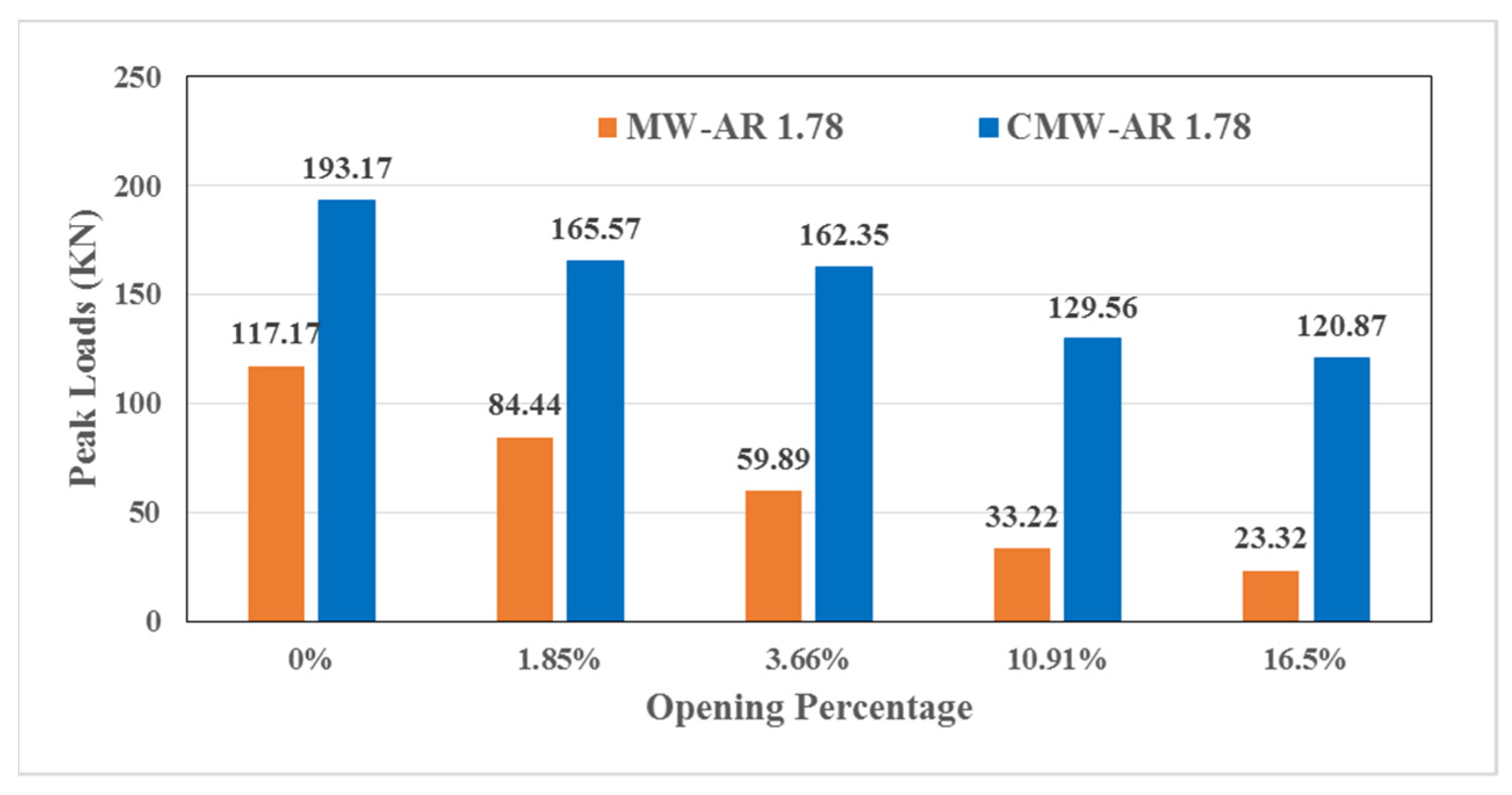
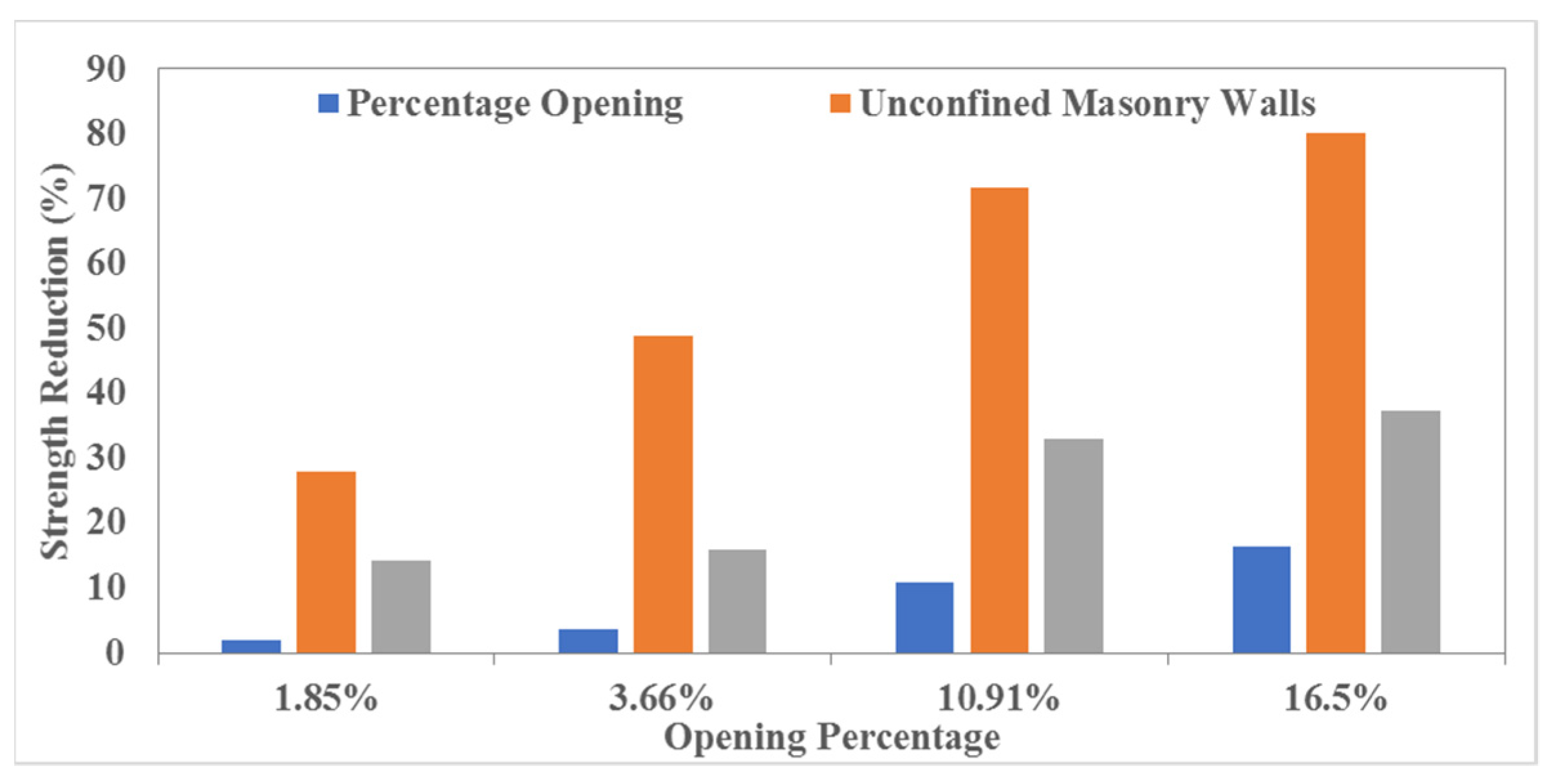
3.3.1. Peak Load and Lateral Strength
3.3.2. Stiffness Reduction
3.3.3. Failure Type
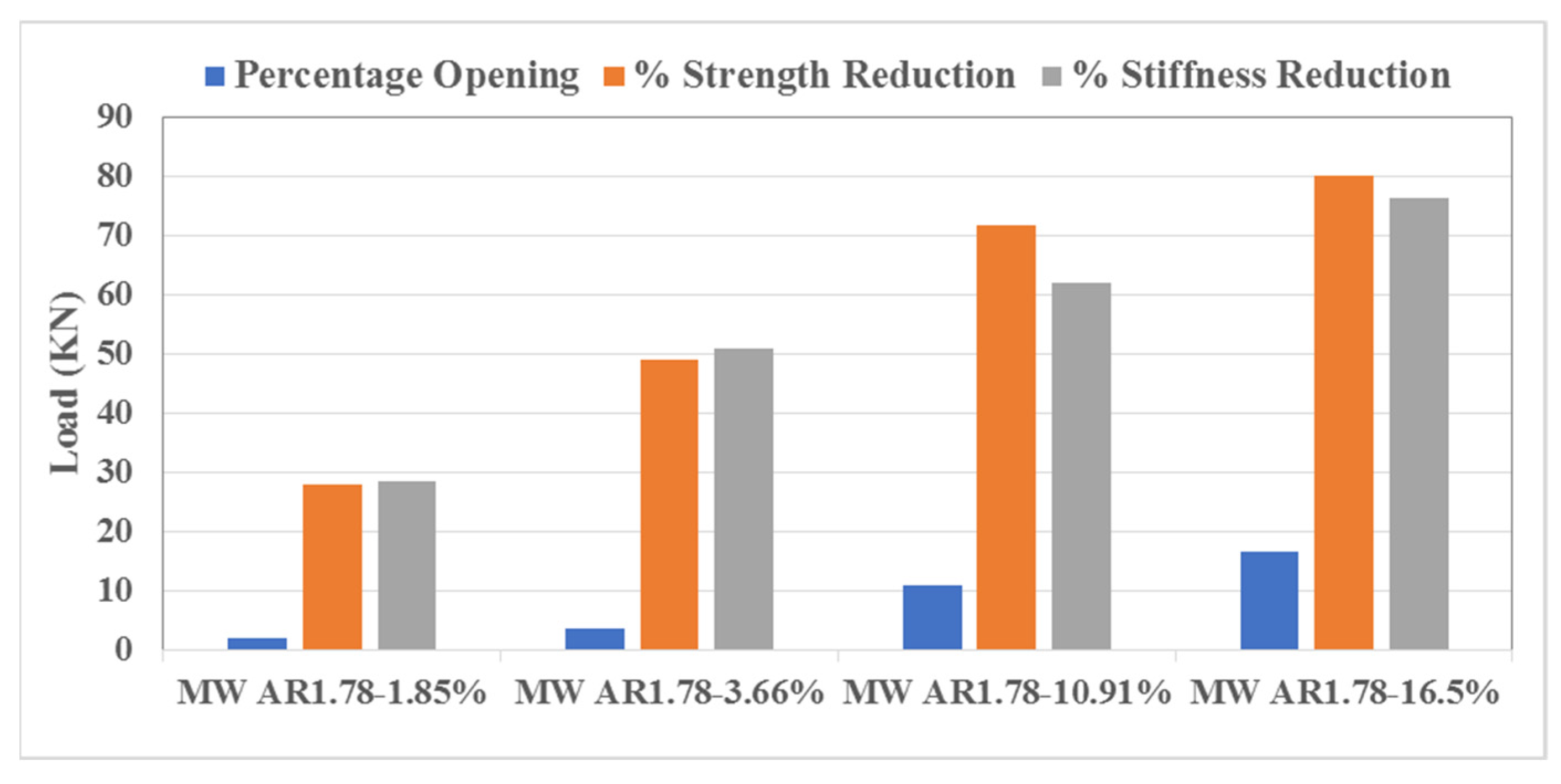
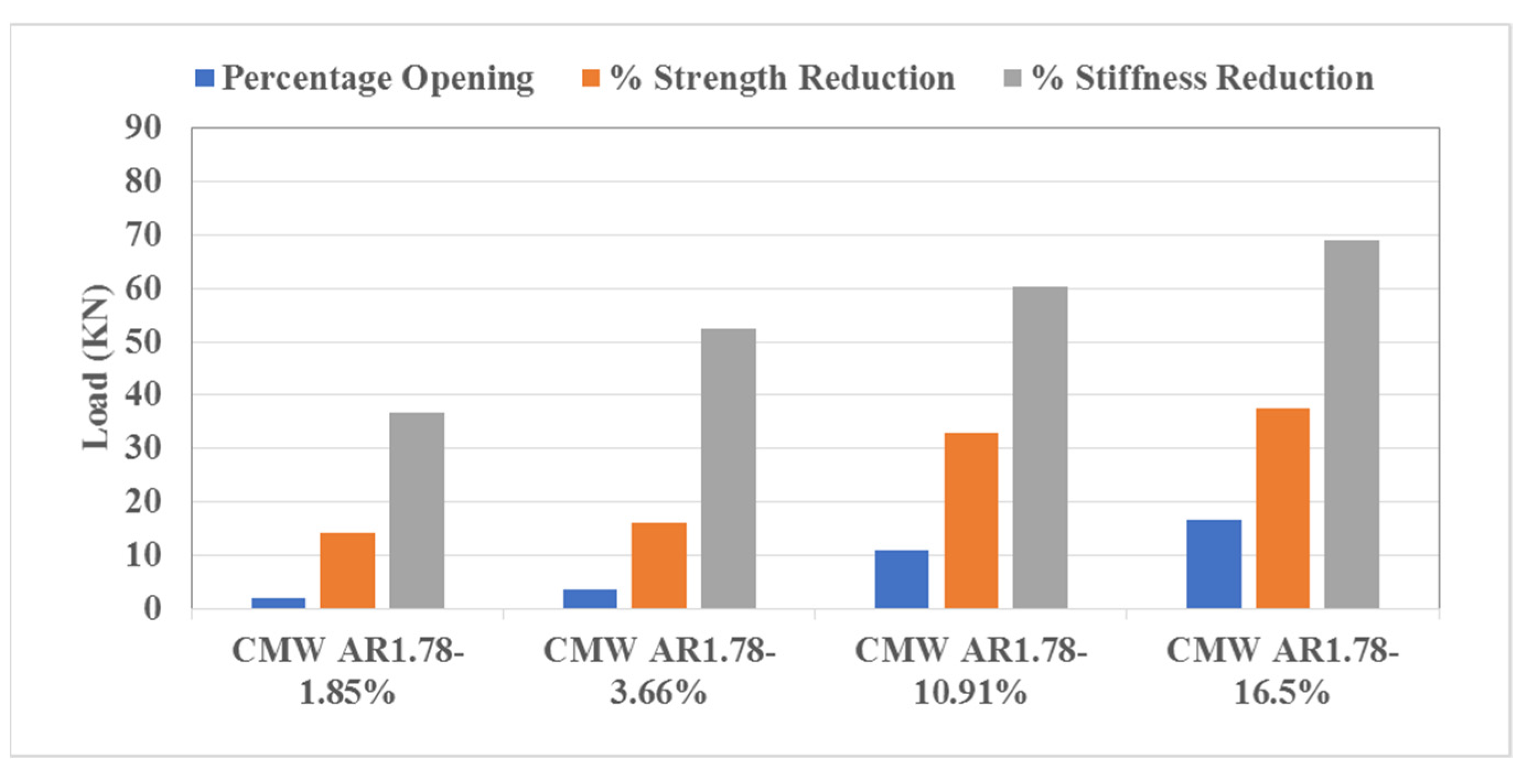
3.4. Impact of Openings on the Confined Masonry Walls
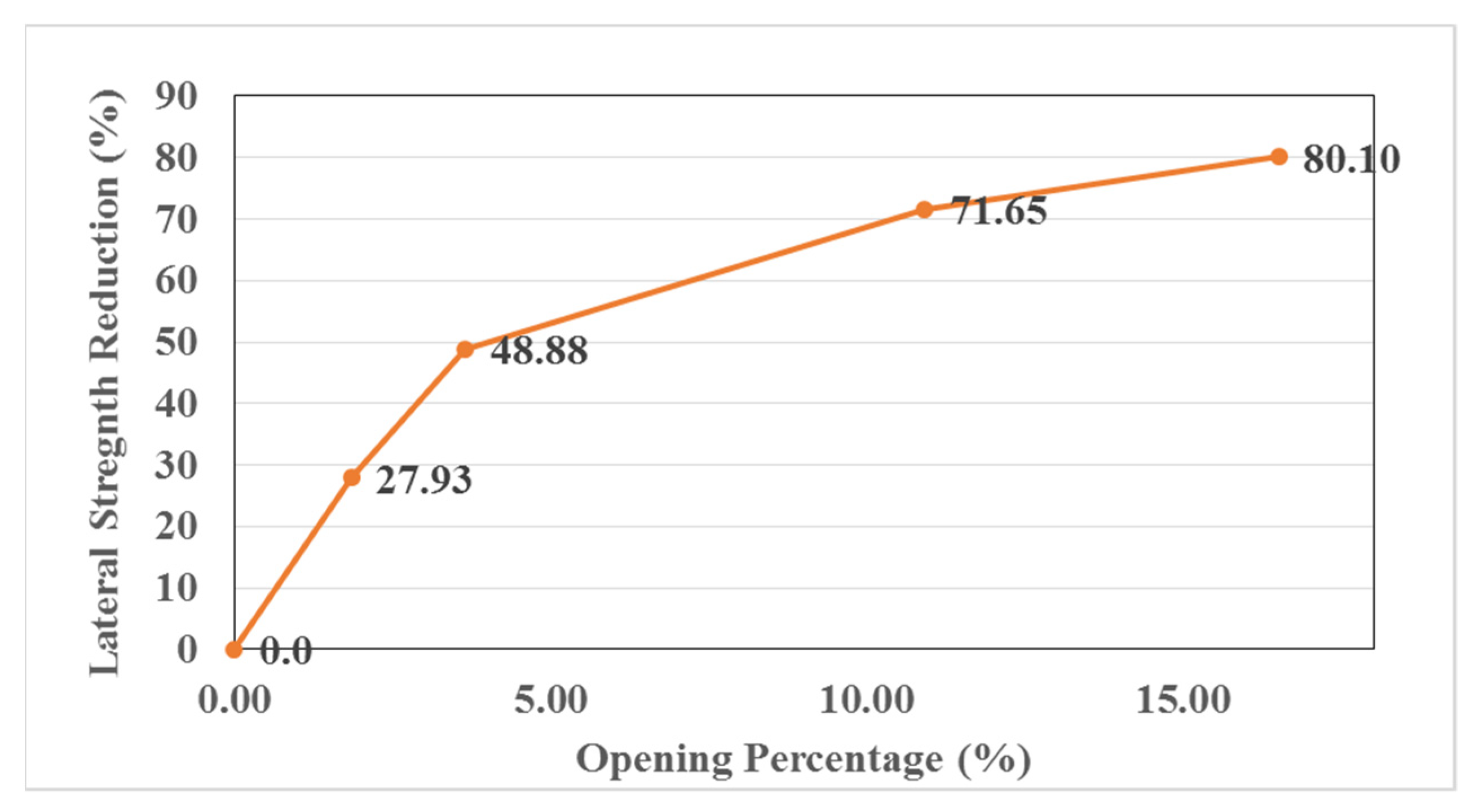
3.4.1. Peak Load and Lateral Strength
3.4.2. Stiffness Reduction
3.4.3. Failure Type
3.5. Benefits of Confinement
3.5.1. Peak Load and Lateral Strength
3.5.2. Stiffness
3.5.3. Failure Type
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Giordano, A.; Guadagnuolo, M.; Faella, G. Pushover analysis of plan irregular masonry buildings. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Gokdemir, H.; Özbaşaran, H.; Dogan, M.; Ünlüoğlu, E.; Albayrak, U. Effects of torsional irregularity to structures during earthquakes. Eng. Fail. Anal. 2013, 35, 713–717. [Google Scholar] [CrossRef]
- Wikipedia Report. Kashmir Earthquake. Available online: https://en.wikipedia.org/wiki/2005_Kashmir_earthquake (accessed on 13 March 2022).
- EN 1998-1:2004; Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions, and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- EN 1998-3:2005; Eurocode 8: Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
- Brzev, S. Earthquake-Resistant Confined Masonry Construction; National Information Center of Earthquake Engineering, Indian Institute of Technology: Kanpur, India, 2007; ISBN 8190419099. [Google Scholar]
- Caliò, I.; Marletta, M.; Pantò, B. A new discrete element model for the evaluation of the seismic behavior of URM buildings. Eng. Struct. 2012, 40, 327–338. [Google Scholar] [CrossRef]
- Raka, E.; Spacone, E.; Sepe, V.; Camata, G. Advanced frame element for seismic analysis of masonry structures: Model formulation and validation. Earthq. Eng. Struct. Dyn. 2015, 44, 2489–2506. [Google Scholar] [CrossRef]
- Tomaževič, M. The Computer Program POR; Report ZRMK; ZRMK: Ljubljana, Slovenia, 1978. (In Slovenian) [Google Scholar]
- Lagomarsino, S.; Penna, A.; Galasco, A.; Cattari, S. TREMURI program: An equivalent frame model for the nonlinear seismic analysis of masonry buildings. Eng. Struct. 2013, 56, 1787–1799. [Google Scholar] [CrossRef]
- Magenes, G.; Della Fontana, A. Simplified non-linear seismic analysis of masonry buildings. In Proceedings of the 5th International Masonry Conference, London, UK, 13–15 October 1998; pp. 190–195. [Google Scholar]
- Vanin, A.; Foraboschi, P. Modelling of masonry panels by truss analogy—Part 1. Mason. Int. 2009, 22, 1–10. [Google Scholar]
- Barraza, J.A.C. Numerical Model for Nonlinear Analysis of Masonry Walls. Ph.D. Thesis, Aachen University, La Serena, Chile, 2012. [Google Scholar]
- Abdullah, K.F.; Cuningham, L.S.; Gillie, M. Simulating masonry wall behaviour using a simplified micro-model approach. Eng. Struct. 2017, 151, 349–365. [Google Scholar] [CrossRef]
- Panday, B.H.; Meguro, K. Simulation of brick masonry wall behavior under in-plane lateral loading using applied element method. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Erdal, M.; Isik, N.S.; Can, O.; Kopraman, Y.; Buyukkaragozet, A. Lateral Strength of Masonry Walls with Openings: Analytical Approach. In Proceedings of the Conference on Application of Efficient & Renewable Energy Technologies in Low Cost Buildings and Construction, Ankara, Turkey, 16–18 September 2013. [Google Scholar]
- Arya, S.K.; Hegemier, G.A. Non-linear response predictions of concrete masonry assemblies. In Proceedings of the Conference North American Masonry, Boulder, CO, USA, 14–16 August 1978; pp. 19.1–19.24. [Google Scholar]
- Page, A.W. A Finite Element Model for Masonry. J. Struct. Div. 1978, 104, 1267–1285. [Google Scholar] [CrossRef]
- Lotfi, H.R.; Shing, P.B. Interface model applied to fracture of masonry structures. J. Struct. Eng. 1994, 120, 63–80. [Google Scholar] [CrossRef]
- Shing, P.; Cao, L. Analysis of Partially Grouted Masonry Shear Walls; US Department of Commerce: Washington, DC, USA, 1997; pp. 97–710. [Google Scholar]
- Kumar, N.; Amirtham, R.; Pandey, M. Plasticity based approach for failure modelling of unreinforced masonry. Eng. Struct. 2014, 80, 40–52. [Google Scholar] [CrossRef]
- Citto, C. Two-Dimensional Interface Model Applied to Masonry Structures. Master’s Thesis, University of Bologna, Bologna, Italy, 2008. [Google Scholar]
- Aref, A.J.; Dolatshahi, K.M. A three-dimensional cyclic meso-scale numerical procedure for simulation of unreinforced masonry structures. Comput. Struct. 2013, 120, 9–23. [Google Scholar] [CrossRef]
- Alcocer, S.M.; Zepeda, J.A. Behavior of multi-perforated clay brick walls under earthquake type loading. In Proceedings of the 8th North American Masonry Conference, Austin, TX, USA, 16–19 June 1999; pp. 235–246. [Google Scholar]
- Alcocer, S.M.; Arias, J.G.; Vazquez, A. Response assessment of Mexican confined masonry structures through shaking table tests. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; p. 2130. [Google Scholar]
- Aguilar, G.; Meli, R.; Diaz, R.; Vazquez-del-Mercado, R.S. Influence of the horizontal reinforcement on the behavior of confined masonry walls. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- Gostic, S.; Zarnic, R. Cyclic lateral response of masonry infilled RC frames and confined masonry walls. In Proceedings of the 8th North American Masonry Conference, Austin, TX, USA, 16–19 June 1999; pp. 477–488. [Google Scholar]
- Gouveia, J.; Lourenço, P. Masonry shear walls subjected to cyclic loading: Influence of confinement and horizontal reinforcement. In Proceedings of the 10th North American Masonry Conference (10NAMC), Saint Louis, MO, USA, 3–5 June 2007. [Google Scholar]
- Irimies, M.T. Confined Masonry Walls: The influence of the tie-column vertical reinforcement ratio on the seismic behaviour. In Proceedings of the 12th European Conference on Earthquake Engineering, London, UK, 9–13 September 2002. [Google Scholar]
- Ahmed, A.; Shahzada, K. Seismic vulnerability assessment of confined masonry structures by macromodeling approach. Structures 2020, 27, 639–649. [Google Scholar] [CrossRef]
- Moghaddam, H.A. Seismic Design of Masonry Building; Sharif University Press: Tehran, Iran, 2006. (In Persian) [Google Scholar]
- Bruneau, M. Performance of masonry structures during the 1994 Northridge (Los Angeles) Earthquake. Can. J. Civ. Eng. 1995, 22, 378–402. [Google Scholar] [CrossRef]
- Ahmed, A.; Shahzada, K.; Ali, S.M.; Khan, A.N.; Shah, S.A.A. Confined and unreinforced masonry structures in seismic areas: Validation of macro models and cost analysis. Eng. Struct. 2019, 199, 109612. [Google Scholar] [CrossRef]
- Cruz, O.; Gavilan, P. Seismic performance of confined masonry walls with joint reinforcement and aspect ratio: An experimental study. Eng. Struct. 2021, 242, 112484. [Google Scholar] [CrossRef]
- Singhal, V.; Rai, D.C. Seismic behavior of confined masonry walls when subjected to inplane and out of plane loadings. In Proceedings of the 10th U.S. National Conference on Earthquake Engineering, Frontiers of Earthquake Engineering, Anchorage, Alaska, 21–25 July 2014. [Google Scholar]
- Sun, J.; Ono, T.; Zhao, Y.; Wang, W. Lateral load pattern in pushover analysis. Earthq. Eng. Eng. Vib. 2003, 1, 99–107. [Google Scholar]
- Makarios, T.K. Optimum definition of equivalent non-linear SDF system in pushover procedure of multistory r/c frames. Eng. Struct. 2005, 27, 814–825. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, G.; Yang, D. A modified approach of energy balance concept based multimode pushover analysis to estimate seismic demands for buildings. Eng. Struct. 2010, 32, 1272–1283. [Google Scholar] [CrossRef]
- Mughal, U.A.; Qazi, A.U.; Hassan, F.; Rasool, A.M.; Hameed, A. Numerical investigation of openings on lateral strength of masonry walls. Key Eng. Mater. 2022, 913, 247–255. [Google Scholar] [CrossRef]
- Lourenco, P.J.B. Computational Strategies for Masonry Structures. Ph.D. Thesis, University of Delft, Delft, The Netherlands, 1996. [Google Scholar]
- Magenes, G.; Morandi, P.; Penna, A. ESECMaSE—Tests Results on the Behaviour of Masonry under Static Cyclic in Plane Loads; ESECMaSE University of Pavia: Pavia, Italy, 2008. [Google Scholar]
- Tripathy, D.; Singhal, V. Estimation of in-plane shear capacity of confined masonry walls with and without openings using strut-and-tie analysis. Eng. Struct. 2019, 188, 290–304. [Google Scholar] [CrossRef]







| Maximum Compressive Strength of Brick = fb = | 26,500 kN/m2 |
| Maximum compressive strength of mortar = fm = | 12,300 kN/m2 |
| Initial elastic modulus of bricks = Eb = | 9,407,500 kN/m2 |
| Initial elastic modulus of mortar = Em = | 2,460,000 kN/m2 |
| Poisson’s coefficient for brick elements = νb = | 0.2 |
| Poisson’s coefficient for mortar = νm = | 0.15 |
| Normal Stiffness = kN = | 66,727,500 kN/m |
| Tangential Stiffness = Ks = | 28,973,783 kN/m |
| Yield Strength of Reinforcement = σy = | 280 MPa |
| Masonry Walls | Opening Size (m) | Peak Load (kN) | % Reduction in Strength | Initial Stiffness (kN/m) | % Reduction in Stiffness |
|---|---|---|---|---|---|
| MW AR1.78–0% | 0.00 | 117.17 | 0.00 | 43,448.24 | 0.00 |
| MW AR1.78–1.85% | 0.25 × 0.25 | 84.44 | 27.93 | 31,049.80 | 28.54 |
| MW AR1.78–3.66% | 0.25 × 0.5 | 59.89 | 48.88 | 21,365.52 | 50.83 |
| MW AR1.78–10.91% | 0.5 × 0.75 | 33.22 | 71.65 | 16,538.58 | 61.93 |
| MW AR1.78–16.5% | 0.75 × 0.75 | 23.32 | 80.10 | 10,253.75 | 76.40 |
| Confined Masonry Walls | Opening Size (m) | Peak Load (kN) | % Reduction in Strength | Initial Stiffness (kN/m) | % Reduction in Stiffness |
|---|---|---|---|---|---|
| CMW AR1.78–0% | 0.00 | 193.17 | 0.00 | 52,808.06 | 0.00 |
| CMW AR1.78–1.85% | 0.25 × 0.25 | 165.57 | 14.29 | 33,437.00 | 36.68 |
| CMW AR1.78–3.66% | 0.25 × 0.5 | 162.35 | 15.95 | 25,165.07 | 52.35 |
| CMW AR1.78–10.91% | 0.5 × 0.75 | 129.56 | 32.93 | 20,987.00 | 60.26 |
| CMW AR1.78–16.5% | 0.75 × 0.75 | 120.87 | 37.43 | 16,412.80 | 68.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mughal, U.A.; Qazi, A.U.; Ahmed, A.; Abbass, W.; Abbas, S.; Salmi, A.; Sayed, M.M. Impact of Openings on the In-Plane Strength of Confined and Unconfined Masonry Walls: A Sustainable Numerical Study. Sustainability 2022, 14, 7467. https://doi.org/10.3390/su14127467
Mughal UA, Qazi AU, Ahmed A, Abbass W, Abbas S, Salmi A, Sayed MM. Impact of Openings on the In-Plane Strength of Confined and Unconfined Masonry Walls: A Sustainable Numerical Study. Sustainability. 2022; 14(12):7467. https://doi.org/10.3390/su14127467
Chicago/Turabian StyleMughal, Ubaid Ahmad, Asad Ullah Qazi, Ali Ahmed, Wasim Abbass, Safeer Abbas, Abdelatif Salmi, and Mohamed Mahmoud Sayed. 2022. "Impact of Openings on the In-Plane Strength of Confined and Unconfined Masonry Walls: A Sustainable Numerical Study" Sustainability 14, no. 12: 7467. https://doi.org/10.3390/su14127467
APA StyleMughal, U. A., Qazi, A. U., Ahmed, A., Abbass, W., Abbas, S., Salmi, A., & Sayed, M. M. (2022). Impact of Openings on the In-Plane Strength of Confined and Unconfined Masonry Walls: A Sustainable Numerical Study. Sustainability, 14(12), 7467. https://doi.org/10.3390/su14127467






